Rotace černých děr - extrakce energie, portály v prostoru
a času?
Kapitola 4
ČERNÉ DÍRY
4.1. Úloha gravitace při vzniku a evoluci
hvězd
4.2. Konečné fáze hvězdné
evoluce. Gravitační kolaps
4.3. Schwarzschildovy statické
černé díry
4.4. Rotující a elektricky nabité Kerrovy-Newmanovy černé
díry
4.5. Teorém "černá díra
nemá vlasy"
4.6. Zákony dynamiky černých
děr
4.7. Kvantové vyzařování a
termodynamika černých děr
4.8. Astrofyzikální význam
černých děr
4.9. Úplný gravitační kolaps -
největší katastrofa v přírodě
4.4. Rotující a
elektricky nabité Kerrovy-Newmanovy černé díry
V předchozích
kapitolách bylo stručně nastíněno, jak úplným
gravitačním kolapsem sféricky symetrické hvězdy (kulové nerotující a elektricky nenabité) vzniká Schwarzschildovská
černá díra. Podmínky přesné sférické symetrie však
nejsou téměř nikdy ve skutečnosti splněny, většina hvězd
především rotuje. Vzniká otázka, zda černá
díra může vzniknout i kolapsem rotující hvězdy, či zda
zrychlující se rotace (odtředivá síla) je schopna kolapsu
zabránit? V newtonovské fyzice by i původně pomalá rotace
hvězdy nakonec převážila a kolaps by zastavila. V obecné
teorii relativity se však ukazuje, že i kolapsem rotující
hvězdy může nakonec vzniknout černá díra, i když
složitějším způsobem [222],[215],[227].
Kolaps rotující hvězdy
Rotující
hvězda, která je vlivem odstředivé síly vždy příslušně
"zploštělá", se při kolapsu (vlivem neustále
zrychlující se rotace v důsledku zachování momentu hybnosti)
stlačí do diskovitého útvaru (obr.4.14a), jakéhosi prudce
rotujícího "lívance", jehož průměr může
několikanásobně převyšovat jeho tloušťku. Jestliže moment
hybnosti není příliš veliký (v porovnání s hmotností
hvězdy), může kolaps pokračovat i v ekvatoriální rovině a
bez dalších komplikací vznikne černá díra. Složitější
situace nastane tehdy, když moment hybnosti je velký, např.
větší než kritická (viz §3.6) hodnota J= M2.
V takovém případě neustále zrychlující se rotace může
roztrhnout diskovitý "lívanec" na několik částí
*) - viz obr.4.14c. Některé části, které obdrží vysoký
moment hybnosti, odletí pryč (a
patřičně tak sníží zbylý moment hybnosti soustavy), většina však bude
gravitačně vázána a bude obíhat kolem společného těžiště.
Tyto fragmenty pak při svém oběhu budou vyzařovat gravitační vlny (soustava
má velký kvadrupólový moment rychle se měnící s časem) odnášející rotační energii
a tím se budou brzdit a sbližovat (obr.4.14c,d), až se nakonec
postupně slijí (obr.4.14e) a vytvoří výslednou rotující černou díru s momentem hybnosti J < M2.
Nejdříve se přitom zbrzdí a sloučí velké fragmenty, protože ty (podle vzorce (2.82)) nejintenzívněji gravitačně
vyzařují.
*) Teoreticky je zde též
možnost, že se vytvoří rotující útvar mající tvar
toroidu, v němž by kolaps proběhl nejdříve podél menšího
poloměru a potom (pokud je "délková" hustota
hmoty~energie postačující) případně i kolaps podél
většího poloměru. Ve skutečnosti však lze očekávat, že v
takovém toroidu hned při jeho vzniku se budou nacházet
určité nehomogenity a deformace, které pak budou růst s
časem - toroidní útvar se rozpadne na několik fragmentů a
další evoluce bude pak již probíhat tak, jak je shora
uvedeno v textu (a dolní části obr.4.14).
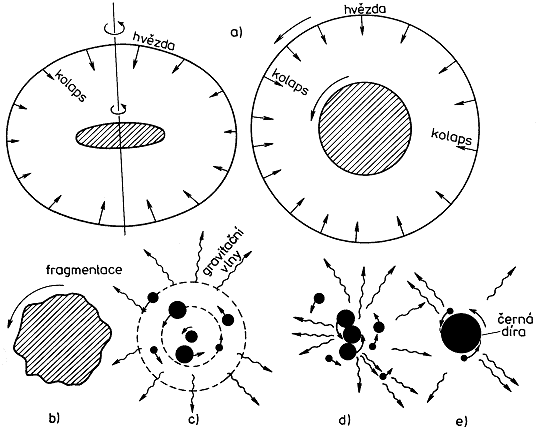
Obr.4.14. Gravitační kolaps rotující hvězdy.
a)
Rotující hvězda se při kolapsu stlačí do prudce
rotujícího diskovitého útvaru. Polkud není rotace natolik
rychlá aby zastavila kolaps v ekvatoriální rovině, vznikne
Kerrova černá díra.
b) Při
velkém momentu hybnosti v důsledku neustále se zrychlující
rotace může dojít k převážení nestabilit a k roztržení
diskovitého útvaru na několik částí.
c,d) Jednotlivé
fragmenty pak obíhají kolem
společného těžiště, vyzařováním gravitačních vln se
brzdí, postupně sbližují a spojují.
e) Nakonec
jsou všechny fragmenty pohlceny a vznikne rotující černá
díra s patřičně sníženým rotačním momentem hybnosti.
Kerrova-Newmanova geometrie
Černá díra vzniklá kolapsem rotující hvězdy však z
důvodu rotace již nebude sféricky symetrická, ale může být
pouze osově symetrická. V současné době se považuje
za obecné řešení (důvod viz
následující §4.5)
pro axiálně symetrickou rotující a elektricky nabitou černou
díru tzv. Kerrova-Newmanova
geometrie prostoročasu, kterou jsme si z geometrického hlediska
popsali v §3.6 "Kerrova a Kerrova-Newmanova
geometrie". Kerrova-Newmanova geometrie je
zobecněním Schwarzschildovy geometrie zhruba řečeno v tom
smyslu, že Schwarzschildova geometrie je kulová, zatímco
Kerrova-Newmanova geometrie je obecně eliptická. Některé aspekty
Kerrovy-Newmanovy geometrie byly rozebírány ve zmíněném
§3.6; zde budeme v tomto rozboru pokračovat za účelem studia
vlastností rotujících a elektricky nabitých černých
děr, jejichž prostoročas tato geometrie popisuje.
Element prostoročasového intervalu
Kerrovy-Newmanovy geometrie (3.41) v Boyerových- Lindquistových
souřadnicích byl uveden v §3.6; zde si
jej napíšeme znovu :
 |
(4.25) |
kde M je celková hmotnost, Q elektrický
náboj, J
vlastní rotační moment hybnosti axiálně symetrického zdroje
této geometrie; a = J/M je specifcický rotační moment
hybnosti na jednotku hmotnosti černé díry. Horizont událostí
r = rg+ má poloměr
 |
(4.26) |
Poloměr horizontu je
zde tedy menší než by měla nenabitá
nerotující černá díra stejné hmotnosti (pro tento případ Schwarzschildovy černé díry
přechází vztah (4.26) ve vztah (3.14), tj. rg = 2M). V běžných
sférických souřadnicích má horizont rotující černé díry
zploštělý elipsoidní tvar (podobně jako rotace odstředivou silou deformuje Zemi
do mírně zploštělého tvaru s rozdílem průměru cca 20km
mezi rovníkem a póly; viz též upozornění na obr.4.16) a to tím výrazněji, čím rychleji černá díra
rotuje, čím vyšší je moment hybnosti J. Vzniká
otázka, zda příliš rychlá rotace by mohla "odstředivou
silou" roztrhnout horizont (podobně
jak by se to stalo při přehnaně rychlém roztočení třebas
kotouče brusky nebo cirkulárky). V §4.6
"Zákony dynamiky černých děr" bude ukázáno, že černou díru nelze
roztočit nad určitou maximální "dovolenou"
či "nepřekročitelnou" rychlost tzv. extrémní
Kerrovy černé díry, kdy M2 = J2/M2. Pokusíme-li se do černé
díry otáčející se téměř extrémní rychlostí vrhnout
těleso, které by ji ještě více roztočilo, odstředivé
síly zabrání tomuto tělesu proniknout dostatečně blízko k
horizontu, proletí mimo a není pohlceno; viz též níže
komentář k nerovnosti (4.36).
Pro fyziku černých děr jsou zajímavé
právě oblasti prostoru r ł rg+ nad vnějším horizontem -
horizontem událostí *). Všechno, co probíhá pod horizontem r = rg+ je totiž příčinně
odděleno
od ostatního vesmíru a nijak se neprojeví. Týká se to
vnitřního horizontu r = rg- = M = Ö(M2-a2-Q2) i prstencové singularity u r = 0,
popsaných v §3.6 "Kerrova a Kerrova-Newmanova
geometrie".
*) V §3.5 a 3.6 byla rozebírána
analytická extenze dovnitř r = rg+. Zdá se
však, že toto vnitřní řešení pod horizontem nemá
fyzikální význam. Jednak je tato oblast zaplněna
vnitřkem kolabujícího tělesa. Kromě toho pro kolaps s
rotací neplatí analogie Birkhoffovy věty (§3.4, teorém 3.3);
Kerrova metrika nepopisuje vnější prostoročas v průběhu
kolapsu, ale až asymptotický tvar metriky po ukončení všech
dynamických procesů. Další důvody, proč se nerealizuje
složitá vnitřní geometricko-topologická struktura
prostoročasu uvnitř rotující černé díry, jsou diskutovány
níže v části "Černé
díry - mosty do jiných vesmírů? Stroje času?", obr.4.19.
Vliv
rotace černé díry. Ergosféra.
Abychom si objasnili podstatu fyzikálních
jevů, které mohou probíhat v okolí Kerrovy-Newmanovy černé
díry (a uvidíme, že zde lze očekávat velice zajímavé
efekty), podíváme se nejprve na vlastnosti pohybu testovacích
částic. Vlastnosti orbit
testovacích částic v poli Kerrovy-Newmanovy geometrie
obecné černé díry jsou podstatně složitější než v
případě Schwarzschildovy geometrie nerotující nenabité
černé díry. Ke kvalitativnímu poznání některých
základních aspektů pohybu však není třeba řešit
komplikované Carterovy rovnice (3.44), vystačíme s
metrickými koeficienty v prostoročasovém elementu (4.25).
Mějme
tedy podle obr.4.15a testovací částici (nenabitou) v místě
se zadanými souřadnicemi r,J, která se pohybuje pouze ve
směru j
; takový pohyb se
nazývá stacionární, protože prostoročasová
geometrie kolem částice se při ní nemění. Bude nás zajímat úhlová rychlost vzhledem k asymptoticky klidové
vztažné soustavě W ş dj /dt = (dj/dt)/(dt/dt) = uj/ut , kde uj a ut jsou příslušné komponenty
čtyřrychlosti (vyšetřujeme stacionární pohyb, tj. jen ve
směru j
, takže
uJ = ur = 0). Tato úhlová rychlost
nemůže být libovolná, přípustné jsou jen takové hodnoty W, pro něž 4-rychlost u leží uvnitř světelného kuželu
budoucnosti :
u 2 = gtt ut ut + 2 gtj ut uj + gjj uj uj < 0 ,
což vyjádřeno pomocí
W dává: gtt (ut)2
+ 2 gtj W (ut)2
+ gjj W2 (ut)2 < 0, tj.
| gtt + 2
W gtj
+ W2 gjj < 0 . |
(4.27) |
Geometrie prostoročasu
tedy "diktuje" tělesu nacházejícímu se v místě se
zadanými r a J přípustnou úhlovou rychlost v
rozmezí
 |
(4.28) |
kde W-max je maximální úhlová rychlost oběhu
proti směru rotace a W+max je maximální rychlost oběhu
ve směru rotace černé díry. Pro velké vzdálenosti r od
černé díry (nebo při jejím malém momentu hybnosti J® 0) je W-max
» - 1/r, W+max » 1/r , takže rychlost částice
u = W.r Î <-1,+1> může být jak ve směru
rotace, tak proti ní, maximálně rovna rychlosti světla
stejně jako je tomu v rovinném prostoročase STR (pohyb
přípustný uvnitř světelného kuželu). S přibližováním k
černé díře se W-max zvětšuje, takže těleso se proti směru rotace černé díry musí
pohybovat pomaleji než kdyby rotace černé díry
nebylo (obr.4.15a).
 |
Obr.4.15. Strhávání
pohybu těles v blízkosti rotující černé díry.
a) Efekt strhávání lokálních inerciálních
soustav (naklánění světelných kuželů do směru
rotace černé díry) vede k postupnému omezování
maximálně možné rychlosti u- pohybu
těles proti směru rotace černé díry při
přibližování k černé díře. Daleko od černé
díry (pro r® Ą) je u+ = c, u-
= -c, v konečných vzdálenostech vně ergosféry je u+> 0, u-<
0, |u-|< |u+|. Na statické mezi však je již u- =
0, v ergosféře dokonce u- > 0 Ţ
těleso se musí nutně pohybovat ve směru rotace
černé díry.
b) Volně padající částice na
rotující černou díru se nejprve pohybuje v
radiálním směru, ale při přiblížení k horizontu
se pohyb stáčí ve směru rotace kolem černé díry;
na horizont částice "dopadá" v
tangenciálním směru a zůstane rotovat spolu s
horizontem.
c) Částice vržená na černou díru v
opačném směru, než se otáčí černá díra, při
přiblížení k horizontu je efektem strhávání
donucena změnit směr obíhání a na černou díru
dopadne jako korotující - stejně jako částice na
obr.b).
Na obr.b),c) jsou pro srovnání
čárkovaně zakresleny trajektorie částice pro
případ nerotující (Schwarzschildovy) černé díry (WH=0). |
Rotace černé díry se
na vnější geometrii prostoročasu projevuje strháváním (unášením) lokálních
inerciálních soustav, které nutí volná tělesa vykonávat rotační pohyb kolem černé díry, a to tím
více, čím blíže jsou k rotující černé díře *). Je to podobné, jako když koule rotující ve
viskózní kapalině strhává do rotace kapalinu v blízkosti
svého povrchu. Efekt "strhávání časoprostoru"
rotující gravitací (momentem hybnosti) umožňuje z černé díry získat určité
množství energie, které souvisí s její rotací (viz níže "Extrakce rotační energie").
*) Efekt strhávání inerciálních
soustav v gravitačním poli rotujícího tělesa (nejen černé
díry) vede k jakési "spin-orbitální interakci" mezi
rotací ("spinem") centrálního gravitujícího
tělesa a momentem hybnosti obíhajících těles: pohyb těles,
např. jejich energie (viz vztah (4.39)), závisí na vzájemné
orientaci momentu hybnosti černé díry a orbitálního momentu
tělesa.
V gravitačním poli rotujících těles existuje též
"spin-spinová interakce" s tělesy, která mají
vlastní rotaci. Například gyroskop v gravitačním poli
tělesa rotujícího úhlovou rychlostí W bude vzhledem k
asymptoticky inerciální soustavě vykonávat precesní pohyb -
jeho rotační osa mající úhel j se bude stáčet s úhlovou
rychlostí w ş dj/dt » W.rg+/r. Tento jev se nazývá Lense-Thirringův
efekt podle autorů, kteří ho poprvé zkoumali [248],
viz §2.5, pasáž "Rotující
gravitace".
Lze říci, že Kerrova-Newmanova
geometrie v jistém smyslu rotuje spolu s černou dírou *) -
prostoročasové světelné kužely jsou natáčeny do směru
rotace černé díry. Pozorovatel nacházející se v místě
se souřadnicemi r,J je vůči lokální geometrii v
klidu a směry + j a - j jsou pro něho ekvivalentní jen
tehdy, když rotuje (obíhá) kolem černé díry
úhlovou rychlostí
 |
(4.29) |
takový pozorovatel se
nazývá lokálně nerotující.
*) U běžných rotujících těles (makroskopických
předmětů, planet, obyčejných hvězd) jsou Lense-Thirringovy
gravitačně-rotační efekty nepatrné, většinou na hranicích
měřitelnosti (je diskutováno v §2.5, část "Rotující
gravitace", pasáž "Možnosti
ověření vlivu rotace"). V okolí rychle rotující
černé díry však vzniká intenzívní gravitační
vír podobný mohutnému tornádu!
Rotace černé díry s sebou unáší okolní prostor a nutí jej
otáčet se ve "víru" v závislosti na rychlosti
rotace černé díry a na vzdálenosti od ní. V dálce od
rotující černé díry se prostor otáčí velmi zvolna,
pozorovatel to ani nepociťuje (podobně
jako daleko od tornáda proudí vzduch jen pomalu). S přibližováním k horizontu se otáčí prostor
rychleji, pozorovatele to "táhne" do směru rotace (podobně jako roste rychlost větru v blízkosti
tornáda). U horizontu se prostor otáčí
stejnou rychlostí jako sám horizont, každý pozorovatel je
neúprosně stržen do víru rotace.
Efekt strhávání pohybu
těles v blízkosti rotující černé díry má výrazný vliv
na pohyb částic a těles padajících do černé díry. Na
obr.4.15b,c jsou schématicky nakresleny trajektorie dvou
testovacích těles padajících do rotující černé díry (z
hlediska souřadnicového systému vnějšího statického
pozorovatele). Částice na obr.4.15b se pohybuje volným pádem
v radiálním směru k černé díře. Kdyby černá díra
nerotovala (statická Schwarzschildova
černá díra), pohybovala by se částice
po přímkové dráze až k horizontu (zpočátku
stále rychleji, těsně u horizontu by z hlediska vnějšího
pozorovatele svůj pád zastavila a zůstala by trvale
"zamrzlá" v daném místě na horizontu - bylo
diskutováno v §4.2, pasáž "Dva různé pohledy na gravitační kolaps
- vnější a vnitřní"). Rotace černé díry však způsobí, že při
přiblížení k horizontu se pohyb částice stáčí ve směru
rotace kolem černé díry. Na horizont částice
"dopadá" v téměř tangenciálním směru a zůstane
rotovat spolu s horizontem (z hlediska
vnějšího pozorovatele opět částice navždy
"zamrzne" na otáčejícím se horizontu; z hlediska
samotné částice tato za krátkou chvíli svého vlastního
času dosáhne horizontu, proletí jím a směřuje ke středu
černé díry...). Druhá částice na
obr.4.15c je vržená na černou díru v opačném směru, než
se otáčí černá díra. Při přiblížení k horizontu je
efektem strhávání postupně donucena obrátit směr obíhání
a na černou díru dopadne jako korotující - skončí stejně
jako částice v případě b).
Protože
reálná tělesa se mohou pohybovat jen uvnitř světelného
kuželu, omezuje toto natočení
prostoročasových světelných kuželů maximální možnou
rychlost pohybu tělesa proti směru rotace černé díry z
původní hodnoty rovné rychlosti světla na hodnotu tím
nižší, čím blíže je k černé díře (jak bylo výše
ukázáno). Na ploše dané rovnicí
| r = rS = M
+ Ö(M2 - a2 cos2 J - Q2) |
(4.30) |
je maximální možná rychlost stacionárního
pozorovatele proti směru rotace černé díry již rovna
nule. Tato plocha (tvaru rotačního elipsoidu,
obr.4.16), na níž se již žádný objekt nemůže pohybovat
proti směru rotace černé díry (gtj = 0),
se nazývá statická mez; vně této meze mohou
existovat statická (nehybná vzhledem k nekonečnu) tělesa,
uvnitř nikoli. Oblast rozprostřená mezi statickou mezí a
horizontem se nazývá ergosféra. Uvnitř
ergosféry je strhávání již tak silné, že žádné těleso
se zde nemůže udržet v klidu; je nevyhnutelně vtaženo
do rotace a jeho obíhání kolem černé díry
nezabrání žádná síla - světelné kužely jsou zcela
obráceny do směru rotace černé díry. Ergosféra (kterou
mají jen rotující černé díry) je nejrozsáhlejší v
"rovníkové" oblasti a zužuje se směrem k pólům,
kde se statická mez r = rS dotýká horizontu r = rg+ (obr.4.16).
 |
Obr.4.16.
Schématické znázornění horizontu, statické meze a
oblasti ergosféry rotující Kerrovy-Newmanovy černé
díry s rotačním momentem hybnosti J ve směru osy Z.
Jedná se o pohled "z boku" - ze strany
rovníku; pohled "shora" (ze strany pólu) je
na obr.4.l7.
Upozornění: Souřadnice r,J , vyznačené na obrázku pro
lepší orientaci, zde nejsou běžné sférické
souřadnice! V blízkosti rotující černé díry se
souřadnice r,J odlišují od
sférických souřadnic, neboť se jedná o
"eliptické" (sféroidální)
Boyerovy-Lindquistovy souřadnice (§3.6). V běžných
sférických souřadnicích má horizont rotující
černé díry zploštělý elipsoidní tvar. |
V ergosféře existují orbity, na nichž
částice mají zápornou celkovou energii
vzhledem k nekonečnu - vazbová energie převyšuje vlastní
hmotnost částice *). Při přechodu přes statickou mez r = rS
totiž časová složka metrického tenzoru goo mění znaménko a
stává se zápornou. Proto energie E = m gik uk = m(goou° + goaua)
částice hmotnosti m pohybující se rychlostí ua se pro
některé orbity testovací částice může stát zápornou.
Taková částice se zápornou energií nemůže opustit
ergosféru a při pohlcení černou dírou vnese pod horizont
zápornou energii vzhledem k nekonečnu - zmenší hmotnost
černé díry. Geodetiky se zápornou energií jsou zcela
uzavřeny uvnitř ergosféry, takže žádná volně pohybující
se částice z vnější oblasti se na orbitu se zápornou
energií nemůže dostat; k dosažení orbity se zápornou
energií je třeba tělesu uvnitř ergosféry udělit dodatečné
(negravitační) zrychlení - viz níže Penroseův proces.
*) Z analýzy obecného vztahu (4.34') pro energii částice v
Kerrově-Newmanově poli plyne, že pro E<0 je třeba orbita s
protisměrným pohybem (Lj<0), jejíž parametry r,.r,Lj splňují určitou (obecně poměrně komplikovanou)
nerovnost [8] ; z této nerovnosti pak vyplývá, že hranicí
oblasti obsahující orbity se zápornou energií je právě
statická mez daná rovnicí (4.30).
Extrakce rotační energie: Penroseův proces ; Superradiace;
Blandford-Znajekův proces
Získat z
černé díry určité množství energie související s její
rotací je obecně umožněno efektem "strhávání
časoprostoru"
(lokálních inerciálních soustav) momentem hybnosti rotujícího
gravitačního pole. Ergosféra má tu zajímavou vlastnost (a odtud též vznikl její název - řec. ergos =
práce), že
jejím prostřednictvím je možno z černé díry získávat tu
část energie (~hmoty), která souvisí s rotací. Penrose [205]
prozkoumal následující efekt (obr.4.17): vnikne-li těleso A do
ergosféry a tam se rozpadne na dvě části B, C
tak, že jedna část, třebas B, se dostane na
protisměrnou orbitu se zápornou energií a je pohlcena černou
dírou, může druhá část C získat zpětný ráz a
vylétnout z ergosféry s větší
energií
než mělo původní těleso, přičemž se zmenší rotační
moment hybnosti černé díry. Tento jev, umožňující
vyextrahovat rotační energii a moment hybnosti z černé díry,
se nyní nazývá Penroseův proces.

Obr.4.17. Penroseův proces získávání energie z ergosféry
rotující černé díry. Těleso A vlétne do ergosféry
a tam se ve vhodném okamžiku rozdělí na dvě tělesa B
a C tak, že těleso B se dostane na orbitu se
zápornou energií (vzhledem k nekonečnu) a je pohlceno černou
dírou. Druhá část C pak vyletí z ergosféry s
větší energií, než mělo původní těleso A.
Jestliže těleso A
mělo (vzhledem k nekonečnu) celkovou energii EA
a pohlcené těleso B energii EB<0 (dostalo se na orbitu se
zápornou energií), bude změna hmotnosti černé díry při
pohlcení DM = EB < 0. Celková energetická
bilance potom bude vypadat takto :
| EC = EA - DM > EA ; |
(4.31) |
celková energie získaná při tomto procesu tedy
je
| D E =
EC
- EA = - DM > 0 . |
(4.31') |
Zajímavá je rovněž
bilance kinetické energie; za tím účelem si celkovou energii
tělesa rozdělíme na kinetickou energii Ekin a klidovou hmotnost: EA
= EAkin + mA.c2 , EC = ECkin + mCc2. Získaná kinetická energie DEkin
= ECkin - EAkin = EC - mCc2
- EA +mAc2 pak po dosazení z (4.31) a mA = mB + mC vychází
| D Ekin
= mB . c2 - DM ; |
(4.32) |
jinými slovy, na
kinetickou energii vylétajícího tělesa C se přeměnila veškerá
klidová hmotnost pohlceného tělesa B a navíc ještě část
hmotnosti černé díry.
Černá díra, pokud má maximální
(extrémní) rychlost rotace, může teoreticky uložit až 42%
(z mc2) své hmotnosti ve formě rotační energie. Tato energie je obsažena v rotujícím
gravitačním poli vně horizontu, takže ji lze v principu čerpat.
Co se týče praktického
(astrofyzikálního) významu Penroseova procesu, byly
navrhovány různé mechanismy a uspořádání pro získávání
energie z rotujících černých děr [204],[205]
*).
*) Penrose dokonce navrhl kuriózní
sci-fi projekt "černoděrové elektrárny"
využívající energii získanou vrháním odpadů do rotující
černé díry. Kontejnerky s odpadem se vrhají do černé díry,
uvnitř ergosféry se otevře víko a odpad se "vysype"
na dráhu se zápornou energií. Kontejnerky tím získávají
Penroseovým procesem značnou kinetickou energii, rychle
vylétají z ergosféry a mohou nárazy pohánět lopatky turbiny
spojené s elektrickým generátorem...
Podrobnější
rozbor pohybu těles při Penroseově procesu, který provedli
Bardeen, Press a Teukolský [8] však ukázal, že rozpad tělesa
uvnitř ergosféry by musel proběhnout s velmi
vysokou vzájemnou rychlostí obou fragmentů - nejméně c/2. Pro
makroskopická tělesa proto Penroseův proces pravděpodobně
nebude astrofyzikálně významný; neznáme totiž fyzikální
procesy, které by mohly udělovat tak velké vzájemné
rychlosti makroskopickým hmotným objektům. Pro nabité
částice však takovým mechanismem může být silné
magnetické pole v okolí černé díry - tzv. Blandfordův-Znajekův proces nastíněný níže.
Další možností by bylo vstřikovat do ergosféry nestabilní
částice
(např. mesony m, p nebo
K , viz "Elementární částice a
jejich vlastnosti") z urychlovače, které by se
uvnitř ergosféry rozpadaly na miony, elektrony a neutrina.
Tyto sekundární částice by se vzájemně rozlétaly
relativistickými rychlostmi (>c/2),
takže by Penroseovým procesem mohly být urychleny vlivem
rotace černé díry. "Praktické využití"
kinetické energie těchto z ergosféry vylétajících
urychlených částic by však bylo velmi obtížné (srov. "Antičástice - antiatomy - antihmota -
antisvěty" ).
Superradiace
Vlnovou (radiační) obdobou Penroseova procesu
je efekt tzv. superradiace [287],[8], kdy vlna dopadající na
rotující černou díru je - pokud má vhodnou vlnovou délku -
černou dírou zesilována na úkor rotační energie
černé díry. Mějme (monochromatickou) vlnu klasického pole s
frekvencí w , momentem hybnosti (axiálním
kvantovým číslem) l a případně elektrickým nábojem q,
která dopadá (z nekonečna) na černou díru. Ve stacionáním
axiálně symetrickém Kerrově-Newmanově poli bude taková vlna
popsána funkcí (řešením vlnové rovnice příslušného
pole) y(t,r,J,j) =
F(r,J) e -i w t e i l j ; pro skalární a elektromagnetické pole
lze provést separaci proměnných, tj. F(r,J)
napsat ve tvaru součinu dvou funkcí: F(r,J) =
R(r).S(J) [43],[246]. Protože prostoročas
Kerrovy-Newmanovy černé díry je stacionární a axiálně
symetrický, budou veličiny w a l integrály pohybu. Část vlnění se
pohltí a po interakci s černou dírou bude v pohybu pokračovat
"rozptýlená" vlna, která bude mít stejnou frekvenci
w , avšak obecně jinou amplitudu.
Změny hmotnosti, náboje, momentu hybnosti a plochy černé
díry při této interakci jsou vázány 1.zákonem
mechaniky černých děr (viz §4.6, rovnice (4.50)):
d M = (k/8p) dA + W dJ + F dQ .
Poměr toku energie,
momentu hybnosti a náboje (obecně připusťme, že vlna může
nést i elektrický náboj q) v dopadající i rozptýlené vlně
je roven w : l : q , takže
díky zachování energie a momentu hybnosti budou ve stejném
poměru i změny příslušných parametrů černé díry dM : dJ : dQ = w : l : q. První zákon dynamiky černých
děr pak dává
dM ( 1 - W l /w - F q / w ) = (k/8p) dA .
Protože podle 2.zákona
dynamiky černých děr (viz §4.6; předpokládáme, že
uvažované vlnění splňuje energetickou podmínku (2.60)
nezápornosti lokální hustoty energie pro každého
pozorovatele) je dA > 0, bude platit nerovnost
dM ( w - l W - q F ) ł 0 .
Jestliže je
w < l W + q F
(dostatečně malá
frekvence vlnění), bude změna hmotnosti černé díry dM < 0 záporná, takže černá díra
bude odevzdávat energii vlnám. Při interakci takového
vlnění s černou dírou se tedy jeho amplituda zvýší: i
když je vlna částečně pohlcována, rozptýlená část
může získat od černé díry více energie, než měla
dopadající vlna - vlnění se zesílí na úkor rotační energie
černé díry. Lze to přirovnat k jakémusi gravitačnímu
"maseru". Efekt superradiace by mohl mít určitý
astrofyzikální význam *); pro černé díry
hvězdných hmotností frekvence w
splňující podmínku superradiace spadají do oblasti radiovln.
Superradiace může vést též k jednomu zajímavému efektu pro
fyziku černých děr. Na konci minulého odstavce bylo
ukázáno, že orbity částic kolem Schwarzschildovy černé
díry jsou v důsledku ztrát gravitačním vyzařováním vždy
nestabilní. Efekt superradiačního zesilování gravitačních
vln však umožňuje v blízkosti rotující černé díry
existenci jakýchsi "plovoucích
orbit",
na nichž jsou ztráty vyzařováním gravitačních vln
kompensovány energií získávanou z černé díry
superradiačním rozptylem těchto vyzařovaných gravitačních
vln [210].
*) Na základě efektu superradiace
byly též navrženy některé myšlenkové projekty [210]
umožňující vysoce rozvinutým civilizacím čerpat z
rotujících černých děr velké množství energie, a též
mechanismus "černoděrové bomby" (black hole
bomb): obklopí-li se černá díra sférickým zrcadlem, budou
elektromagnetické vlny mnohokráte odráženy k černé díře a
jí superradiačně zesilovány (vznikne "kladná zpětná
vazba"), takže jejich intenzita (energie) lavinovitě
poroste až k explozi.
Takto probíhá proces superradiace pro
"bosonová" klasická pole s
celočíselným spinem. V případě "fermionových"
klasických polí se ukazuje, že superradiace nenastává. Je to
způsobeno jednak
tím, že tenzor energie-hybnosti pro klasická pole s
poločíselným spinem nesplňuje energetickou podmínku (2.60) a
proto nelze aplikovat 2.zákon mechaniky černých děr, jednak z
kvantového hlediska Pauliho princip připouští přítomnost
pouze vždy jedné částice pro danou frekvenci
rozptylující se vlny, takže rozptýlená vlna nemůže být
silnější než vlna dopadající. Kvantové aspekty
superradiace a na ně navazující efekt kvantového
vypařování černých děr bude rozebírán v §4.7, část
"Mechanismus
kvantového vyzařování".
Elektromagnetická extrakce
rotační energie - Blandfordův-Znajekův mechanismus
Další zajímavou modifikací Penroseova procesu za účasti silného magnetického pole se zabývali R.Blandford a R.Znajek v
obsáhlé práci [20]. Černá díra jako
taková nemá své magnetické pole (viz
§4.5 "Černá díra nemá vlasy"). Avšak nabité částice, vířící v plasmě
akrečního disku kolem černé díry, představují efektivní
elektrický proud generující magnetické pole.
Ukazuje se, že vnější velmi silné
magnetické pole v okolí rotující černé díry
může rychle se pohybující nabité částice
svým silovým působením uvádět na orbity se
zápornou energií v ergosféře rotující Kerrovy
černé díry, což by Penroseovým procesem mohlo vést k extrakci
rotační energie (a momentu
hybnosti) černé díry. Vyextrahovaná
energie by v ergosféře byla předávána elektromagnetickému
poli, které by pak mohlo urychlovat další nabité částice.
Takovýto Blandfordův-Znajekův mechanismus by
se mohl uplatňovat v nitru akrečních disků kolem černých
děr, kde by mohl přispívat k energii relativistických
výtrysků z kvasarů a aktivních galaktických jader, viz §4.8
"Astrofyzikální význam černých děr", část "Tlusté
akreční disky. Kvasary".
Nachází-li se kolem rotující černé díry
obíhající plasma z nabitých částic - akreční disk,
vytváří rotačními toroidálními proudy, tekoucími v
ekvatoriální rovině, silné poloidální magnetické pole.
Strhávání prostoru a tím i magnetických siločar rotací
černé díry (mag. siločáry se zkroutí
do spirály) pak indukuje
intenzívní elektrické pole, působící na
nabité částice plasmy ve směru podél rotační osy černé
díry. Urychluje tyto částice na relativistické rychlosti - vzniká mohutný elektrický generátor
ve formě proudu nabitých částic podél rotační osy. Z nich
část se dostává na orbity se zápornou energií v ergosféře
a padá do černé díry, přičemž vyextrahovaná energie
posiluje elektromagnetické pole. Jiné nabité částice jsou
pak elektromagneticky urychlovány extrahovanou rotační
energií a tuto svou energii magnetohydrodynamickými efekty
předávají plasmě ve výtryscích. Takové "gravito-magnetické
dynamo", poháněné rotací černé díry, by
mohlo do jetů z akrečního disku dodávat značné množství
energie.
Výše uvedené mechanismy tedy ukazují,
že rotující černé díry jsou "živé" na rozdíl
od "mrtvých" Schwarzschildových černých děr, z
nichž nelze získat žádnou energii (nepřihlížíme-li
k akrečním diskům a ke kvantovým jevům). Tato "živost" rotujících
černých děr může mít značný astrofyzikální
význam (bude diskutováno §4.8., část "Akreční
disky kolem černých děr"
- "Tlusté akreční disky.Kvasary").
Pohyb
částic v poli rotující černé díry
Pohyb
testovacích částic v Kerrově-Newmanově poli obecné černé
díry je dán rovnicemi (3.44). Z rovnic (3.44a) a (3.44b)
dostaneme pro částici s klidovou hmotností mo,
elektrickým nábojem q, energií (vzhledem k nekonečnu) E a
axiální složkou momentu hybnosti Lj (vzhledem k ose rotace černé díry)
vztah
 |
(4.33) |
Pro koeficienty při
jednotlivých mocninách energie E (které jsou funkcemi místa a
parametrů testovací částice a černé díry) si zavedeme
označení [43]
 |
(4.33a)
(4.33b)
(4.33c) |
Výše uvedená rovnice má potom tvar
| (r2 + a2 cos2 J) [ (dr/dl)2
+ (dJ/dl)2 ] = a E2 - 2 b E + g . |
(4.34) |
Vyjádříme-li odtud
energii
 |
(4.34') |
je vidět (vzhledem k
tomu, že a > 0 všude
vně horizontu), že energie splňuje nerovnost
| E
ł |
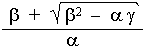 |
. |
(4.35) |
Na horizontě r= rg+ je a = (rg+
2 + a2)2,
b = (Lj a + q Q rg+)(rg+
2 + a2),
g = (Lj a + q Q rg+)2, takže relace (4.35) se zde zjednoduší na
 |
(4.36) |
jen při splnění této
podmínky může částice dosáhnout horizontu a být pohlcena.
Nerovnost (4.36), která zdola omezuje množství energie
vnesené pod horizont při pohlcení tělesa s nábojem q a
momentem hybnosti Lj, hraje důležitou roli v dynamice černých děr - viz §4.6 "Zákony
dynamiky černých děr", kde z ní přímo plyne vztah
(4.51).
Analýza pohybu
testovacích částic v Kerrově-Newmanově geometrii podle
Carterových rovnic (3.44) je v obecném případě značně
komplikovaná [228],[48],[237]. Určitého zjednodušení
dosáhneme, budeme-li vyšetřovat pouze pohyb částic v
"rovníkové" rovině rotující černé díry. Ekvatoriální orbity v poli Kerrovy-Newmanovy černé
díry jsou zároveň nejzajímavější,
nejcharakterističtejší a pro praxi nejdůležitější. V
důsledku efektu strhávání lokálních inerciálních soustav
je např. akreční disk kolem rotující černé díry (§4.8)
natáčen do ekvatoriální roviny a vlastní akrece se děje
především z ekvatoriálních orbit. Ve velkých vzdálenostech
od černé díry je zase vliv její rotace malý a trajektorie částic
zde příliš nezávisí na tom, v jaké rovině a jakým směrem
vzhledem k ose rotace černé díry se částice pohybuje (pohyb
částice ve velkých vzdálenostech je podobný jako ve
Schwarzschildově poli nerotující černé díry).
Rovnici radiální složky pohybu v
ekvatoriální rovině Kerrovy-Newmanovy geometrie dostaneme z
rovnice (4.34) dosazením J = p/2 a
dJ/dl = 0 :
| r
4 (dr/dt)2 = a E2 - 2 b E + g . |
(4.37) |
a, b, g jsou opět označeny veličiny podle
(4.33a,b,c), kde ovšem sin2J = 1 a cos2J = 0. Tuto rovnici lze přepsat též ve
formě
 |
(4.37') |
Jediný činitel, který
zde může měnit znaménko, je činitel II; činitelé I a III
jsou kladní (pokud je energie E kladná). Veličina
| V(r)
= |
 |
. |
(4.38) |
zde tedy hraje roli efektivního potenciálu pro radiální složku pohybu.
Částice s energií E se může dostat pouze do míst,
kde V(r) Ł E ve shodě s obecnou relací (4.35).
Místa, v nichž je V(r)= E jsou body
obratu, kde
radiální složka pohybu mění svůj směr. Kruhové orbity jsou (spolu s podmínkou V(r)=E) dány
podmínkou dV(r)/dr = 0. Tedy kruhové orbity jsou v extrémech
potenciálu V(r), přičemž minimům V(r) odpovídají stabilní kruhové orbity. Podmínky V(r)= E a dV(r)/dr =
0 vedou ke vztahům (pro pohyb v ekvatoriální rovině je Lj = L)
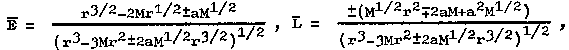 |
(4.39) |
kde `E ş E/mo a `L ş L/mo jsou energie a moment hybnosti
na jednotku hmotnosti testovací částice [8],[81]. Úhlová a
oběžná rychlost na orbitě (z hlediska vzdáleného
pozorovatele) je rovna
 |
(4.39') |
což je zobecněním
3.Keplerova zákona pro kruhové ekvatoriální orbity v Kerrově
metrice rotující černé díry. Vzorce (4.39) jsou pro
jednoduchost uvedeny pouze pro Kerrovu černou díru, tj. pro Q=0
(jinak by klidovou hmotnost mo nebylo možno zahrnout do E a L a
navíc by záleželo na specifickém náboji q/mo
testovací částice). Horní znaménka platí pro pohyb ve
směru rotace černé díry (L.a>0), dolní znaménka pro
orbity proti směru rotace (L.a<0).
Ze vztahů (4.39) je vidět, že kruhové
orbity mohou existovat pouze v takových vzdálenostech od
černé díry, pro které je splněna podmínka
| r
3/2 - 3 M r
1/2 ± 2 a M 1/2 > 0 . |
(4.40) |
Fotonová kruhová orbita (na níž je `E = Ą , `L =
± Ą ) v ekvatoriální rovině
Kerrovy černé díry r = rf, jež je zároveň mezní (nejnižší, nejvnitřnější) kruhovou orbitou, má poloměr rf daný rovnicí r3/2 - 3 M r1/2 ± 2 a M1/2 = 0, tj.
| rf = 2M [1 + cos 2/3 arccos(± a/M)] . |
(4.41) |
Pro a=0 dostáváme rf = 3M ve shodě
se vztahem (4.5) pro fotonovou sféru Schwarzschildovy černé
díry, pro extrémní černou díru a=M je rf = M pro
korotující orbity a rf = 4M pro
protisměrné fotonové dráhy.
Podobně jako ve Schwarzschildově poli, i
zde nejsou všechny kruhové orbity vázané: pro orbity
dostatečně blízké mezní fotonové orbitě se hodnota energie
(4.39) stává větší než jedna (`E ş E/mo > 1) - částice na takové
kruhové dráze E ve vztahu není k černé díře
vázána a pod vlivem sebemenší nahoru směřující poruchy
odlétá z této orbity do nekonečna. Vázané
kruhové orbity existují pouze pro r ł rmv, kde
rmv = 2M + 2M (M ± a)1/2 ± a
je mezní poloměr
vázané orbity odpovídající E/mo = 1. Tento poloměr rmv je zároveň minimálním
"perihéliem" všech parabolických orbit (tj. orbit s
E/mo=1, např. těles padajících z
nekonečna); každá parabolická trajektorie tělesa, které
pronikne blíže než rmv, končí na černé díře. Pro
a=0 dostáváme rmv=4M (srovnej s obr.4.6 vlevo),
pro a=M je pro korotující kruhové dráhy rmv=M, resp. rmv=5,83 M pro protisměrné orbity. Aby
kruhová orbita byla stabilní vůči radiálním perturbacím
(ani všechny vázané kruhové orbity nejsou stabilní!), musí
jí odpovídat minimum efektivního potenciálu, tj. musí být ještě
splněna podmínka d2V(r)/dr2 Ł 0 vedoucí k nerovnosti
| r2 - 6 M r ± 8 a Ö(M r) - 3 a2 ł 0 . |
(4.42) |
Jen pro poloměry
vyhovující této nerovnosti mohou existovat stabilní kruhové
orbity, přičemž rovnítko v (4.42) odpovídá nejnižší (nejvnitřnější) stabilní
kruhové orbitě r = rms [8] :
 |
(4.42') |
Pro a=0 dostáváme
opět poloměr nejnižší, nejvnitřnější stabilní kruhové
dráhy rms=6M ve Schwarzschildově geometrii, u
extrémně rotující černé díry a=M má souhlasně rotující
nejvnitřnější stabilní kruhová orbita poloměr rms=M, zatímco pro nejnižší stabilní
protisměrnou kruhovou orbitu je rms=9M.
Ve velkých
vzdálenostech r od rotující černé díry jsou
parametry (vazbová energie, specifický moment hybnosti,
rychlost oběhu) korotujících a kontrarotujících orbit
téměř stejné. S přibližováním k černé díře (se
zmenšováním r) však vzrůstá vliv momentu
hybnosti černé díry - vazbová energie korotujících orbit se
zvyšuje, zatímco vazbová energie protisměrných
orbit se snižuje ve srovnání se Schwarzschildovými orbitami.
Nejvýraznější rozdíly pohybu testovacích částic oproti
Schwarzschildově geometrii budou v blízkosti extrémní Kerrovy černé díry (a=M), kde se též
budou nejvíce od sebe lišit trajektorie částic
pohybujících se po směru a proti směru rotace černé
díry. Markantně se to projevuje na parametrech mezních
stabilních kruhových orbit. Nejnižší (nejvnitřnější)
stabilní kruhová orbita kolem Schwarzschildovy černé díry
měla tyto charakteristiky (viz §4.3): poloměr r=6M,
specifický moment hybnosti `L = 2Ö(3)M,
energie E = mo.8/9 a vazbová energie částice
Evaz= mo- E = 5,72% mo.
U extrémní Kerrovy černé díry bude
podle vzorců (4.42) a (4.39) nejvnitřnější stabilní
korotující orbita mít poloměr r=M, specifický moment
hybnosti `L = 2M/Ö3,
energii E = mo/Ö3 a
vazbová energie částice bude Evaz = 42,26% mo; při oběhu proti směru rotace
černé díry bude nejnižší stabilní kruhová orbita v
ekvatoriální rovině mít poloměr r=9M, specifický moment
hybnosti `L = 22M/Ö27, energii E=
5M/Ö27, a vazbová energie částice bude jen
Evaz = 3,77% z mo.
Srovnáme-li to s výsledky získanými v
předchozím §4.3 (pasáž "Vyzařování gravitačních vln při pohybu
v poli černé díry"), konkrétně se vztahem (4.21),
nejpozoruhodnější je to, že těleso obíhající po kruhové
orbitě (korotující) v ekvatoriální rovině extrémní
Kerrovy černé díry vyzáří ve formě gravitačních vln
více než 40% své klidové hmotnosti! Tato
hodnota vazbové energie na mezní, nejvnitřnější stabilní
korotující orbitě má též velký význam pro posouzení
potenciální účinnosti uvolňování energie v akrečních discích
kolem černých děr - viz §4.8, část
"Akreční disky".
Šíření
světla v poli rotující černé díry
Podobně
jako u trajektorií testovacích částic, rotace černé díry
má vliv i na šíření světla v jejím poli - ovlivňuje
fotonové orbity. Úhel odklonu fotonů sféricky symetrickou
Schwarzschildovou černou dírou závisí pouze na impaktním
parametru, nikoliv na směru z něhož k černé díře
přicházejí. Kolem Schwarzschildovy černé díry existuje jen
jediná fotonová sféra, na níž se fotony mohou pohybovat pod
všemi úhly podle toho, z jakého směru se na ni dostaly.
Jestliže však černá díra rotuje,
situace je složitější - geometrie není sféricky
symetrická, ale jen axiálně symetrická, takže pro paprsky
přicházející z různých směrů se prostoročas jeví
různě zakřivený. Úhel odklonu paprsků (a celý charakter
jejich trajektorie) může podstatně záviset na směru pohybu
fotonů vzhledem ke směru rotace černé díry. Obecně paprsky
směřující proti směru rotace jsou odchylovány více než
fotony jdoucí po směru rotace - obr.4.18. Tyto rozdíly se
projevují nejvice u fotonů procházejících v těsné
blízkosti černé díry. Skutečně, ze vztahu (4.41) je vidět,
že kolem rotující černé díry existují v ekvatoriální
rovině dvě fotonové kruhové orbity: protisměrná kruhová
fotonová orbita o větším průměru než Schwarzschildovská
fotonová sféra, a korotující fotonová orbita ležící
níže než u nerotující černé díry. Celkový účinný
průřez gravitačního záchytu fotonů rotující černou
dírou se příliš neliší od příslušné hodnoty (4.15) pro
Schwarzschildovu černou díru. Úhel záchytu je však nesymetrický - fotony jdoucí proti směru rotace jsou
zachycovány s větším účinným průřezem než fotony
přicházející po směru rotace - obr.4.18b.

Obr.4.18. Šíření světla v gravitačním poli rotující
černé díry.
a)
Světelné geodetiky v ekvatoriální rovině Kerrovy černé
díry. Úhel odklonu Dj- fotonu pohybujícího se proti směru
rotace je (při stejném srážkovém parametru) větší než
úhel Dj+
odklonu fotonu ve směru rotace
černé díry. Korotující fotonová orbita r = rf+ má větší poloměr než protisměrná
fotonová orbita r = rf-.
b) Účinný
průřez záchytu fotonů (stejně jako jiných částic)
rotující černou dírou je nesymetrický - protisměrně
pohybující se fotony jsou zachycovány účinněji než fotony
jdoucí po směru rotace.
c,d) Rotující (Kerrova) gravitační
čočka: c-
nesymetrický chod paprsků v ekvatoriální rovině; d- odklon paprsků v obecné rovině.
Stáčení světla do
spirály rotací černé díry
V §2.5, pasáži "Rotující gravitace" jsme si ukázali, že prostoročas
kolem rotujícího tělesa v jistém smyslu též rotuje -
Lense-Thirringův efekt strhávání lokálních inerciálních
soustav do směru rotace zdroje. Časoprostor kolem masivního
rotujícího tělesa se deformuje nejen v radiálním směru, ale
vzniklá potenciálová jáma se též stáčí ve směru rotace
zdroje. V blízkosti rotujících černých děr je tento efekt
velmi výrazný a projevuje se i u světla. Moment hybnosti
rotující černé díry by měl obecně způsobovat spirálové
stáčení elektromagnetické vlny ve směru rotace.
Astrofyzikálně by se tento vliv "zkrouceného"
prostoročasu nejvíce mohl projevit na záření, které emituje
akreční disk v ekvatoriální rovině :
-> Toto světlo by se k nám od černé
díry nešířilo po přímce, ale zpočátku po zakřivené
dráze.
-> Když elektromagnetická vlna prochází
rotujícím časoprostorem v blízkosti černé díry, bude se
deformovat její vlnoplocha. Fáze vlny - střídání maxima a
minima - se vlivem strhávání rotujícím gravit. polem budou
posunovat a podél paprsku získají šroubovnicový
tvar, budou tvořit spirálu.
Bylo by to jakési "rotující, stáčející se
či spirálové světlo",
jehož polarizace by se lišila od obvyklé kruhové. Dopadá-li
na nabité částice, způsobí m.j. jejich rotaci kolem směru
šíření paprsku, což lze považovat jako projev momentu
hybnosti tohoto záření. Chová se tedy jako vlnění s orbitálním
momentem hybnosti - srov.
§1.5, pasáž "Vnitřní a orbitální moment hybnosti
elektromagnetických vln".
Parametry Kerrovy-Newmanovy černé díry
Kromě
výrazů (4.26) a (4.30) pro horizont a ergosféru si uvedeme
ještě další důležité vztahy mezi veličinami
charakterizujícími obecnou černou díru. Plocha
horizontu
Kerrovy-Newmanovy černé díry je
A
= r=2M,ňt=const.|gJJ gjj|1/2 dJ dj =
4p (rg+2 + a2) =
= 4p [
2 M2 - Q2 + 2M Ö(M2 - Q2 - a2) ] . |
(4.43) |
v geometrodynamických jednotkách; v obyčejných jednotkách je
plocha horizontu dána vzorcem
| A
= 4pG/c4 [ 2 G M2 - Q2 + 2 Ö(G2 M4 - J2 c2 - G M2 Q2 ) ] . |
(4.43') |
Úhlová rychlost horizontu černé díry (což je úhlová rychlost s jakou vzhledem k nekonečnu
obíhá lokálně nerotující pozorovatel na horizontu) se vypočítá ze vztahu (4.29)
položením r=rg+, což dále můžeme upravit
dosazením ze vztahů (4.26) a (4.43) pro rg+ a plochu A :
 |
(4.44) |
Je vidět, že tato
úhlová rychlost je stejná ve všech místech horizontu
(černá díra rotuje jako "pevné těleso"), takže WH se definuje jako úhlová rychlost černé díry.
Pro úplnost uvedeme též elektrický
potenciál horizontu :
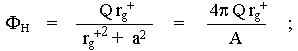 |
(4.45) |
čtyřpotenciál elektromagnetického pole Ai(r,J) kolem Kerrovy-Newmanovy černé díry v
místě se souřadnicemi r,J je (v Lorentzově kalibraci Ai;i = 0) dán vztahem
| A t =
Q r / (r2 + a2cos2 J) , A
j = - a Q r sin2 J / (r2 + a2cos2 J) ; |
(4.46) |
vlivem stacionárnosti a axiální symetrie
nezávisí potenciál na čase t a na úhlu j a jeho ostatní složky jsou rovny
nule.
Povrchová gravitace k na
horizontu (viz §4.3), což je gravitační síla působící na
testovací částici nacházející se na horizontu a mající
stejnou úhlovou rychlost WH
jako horizont (tj. na lokálně nerotující částici na
horizontu) je rovna
 |
(4.47) |
je na první pohled
vidět, že pro extrémní černou díru (pro niž je rg+ = rg- = M) je povrchová gravitace
rovna nule (!).
Je užitečné definovat si tzv. ireducibilní hmotnost černé díry Mired (význam této
veličiny a z něj plynoucí její název bude ukázán v §4.6 v
souvislosti se zákony dynamiky černých děr), což je hmotnost, kterou by
měla Schwarzschildova černá díra se stejnou plochou horizontu
- 16p Mired = 4p(rg+ 2 + a2) :
| Mired ş Ö(A / 16p) = 1/2 Ö(rg+2
+ a2) . |
(4.48) |
Pro černou díru
celkové hmotnosti M je veličina Mired omezena nerovností
M/Ö2 Ł Mired Ł M ,
přičemž horní mez
odpovídá Schwarzschildovské černé díře a dolní mez
extrémní černé díře. Z (4.48), (4.43) a (4.44) lze snadno
odvodit následující vztahy :
 |
(4.49) |
| WH =
a / (4 M2ired) = J / (4 M . 4 M2ired) . |
(4.44') |
Fyzikální význam důležitého vztahu (4.49)
bude rozebírán v §4.6 v souvislosti s 2.zákonem
dynamiky černých děr.
Klasifikace
černých děr
V obecné
Kerrově-Newmanově geometrii, o které si v příštím odstavci
ukážeme, že je zřejmě nejobecnější prostoročasovou
geometrií obecné stacionární černé díry, můžeme
rozlišovat některé význačné speciální případy (srovnej
s klasifikací Kerrovy-Newmanovy geometrie v §3.6) :
- a) Především pro Q = J =
0 dostáváme Schwarzschildovu
geometrii centrálně symetrické
nerotující nenabité černé díry.
- b) Pro Q = 0, 0 < J <
M2 je to Kerrova
geometrie axiálně symetrické rotující nenabité černé díry.
- c) Pro J = 0, 0 < Q <
M dostáváme Reissnerovu-Nordströmovu geometrii nerotující centrálně
symetrické elektricky
nabité černé díry.
- d) Při
M2 = Q2 + J2/M2 to bude
Kerrova-Newmanova geometrie tzv. extrémní černé díry -
nejrychlejší možná rotace (popř. největší možný
elektrický náboj) černé díry vzhledem k její
celkové hmotnosti M; horizont má poloměr rg =M, povrchová gravitace na
horizontu k = 0.
- e) Konečně v případě Q2 + J2/M2 > M2 nepopisuje Kerrova-Newmanova
geometrie již černou díru mající horizont (výraz
(4.26) se stává imaginární), ale tzv. Kerrovu nahou singularitu bez horizontu (vlastnosti nahých singularit a o možnosti
jejich existence jsme diskutovali v §3.9 "Nahé
singularity a princip "kosmické cenzury"").
Kerrova-Newmanova
geometrie má horizont (a popisuje tedy černou díru) jen tehdy,
když je splněna podmínka M2 ł Q2
+ J2/M2, tedy když "příliš
rychle nerotuje" nebo není "příliš elektricky
nabita" ve srovnání se svou celkovou
hmotností M.
Rotace (vlastní moment hybnosti J)
hraje důležitou úlohu pro geometrii prostoročasu v
okolí černých děr vzniklých gravitačním kolapsem, neboť
většina hvězd rotuje a moment hybnosti této rotace se díky
zákonu zachování hybnosti v průběhu kolapsu příliš
nezmění (pokud nenastane případ znázorněný na
obr.4.14, kdy značná část momentu hybnosti může být
odnesena gravitačními vlnami; odnesen je však pouze
"přebytečný" moment hybnosti, zbylý rotační
moment hybnosti je stále ještě značný).
Jinak je to však s elektrickým nábojem černých děr:
Elektricky
nabité černé díry?
Elektrický náboj Q patrně není
důležitý u černých děr ve vesmíru. Aby totiž
elektrický náboj zanechal znatelnou stopu na metrice
prostoročasu, musel by mít obrovskou hodnotu srovnatelnou s
celkovou hmotností M (v geometrodynamických jednotkách).
Jelikož hvězdy jsou většinou elektricky prakticky neutrální,
vznik a udržení tak velkého náboje je velmi
nepravděpodobné; kromě toho tak velké elektrické odpudivé
síly by asi zabránily kolapsu do rozměrů ~2M, protože v
oblastech r > 2M by tyto elektrické odpudivé síly byly
zcela dominantní. I kdyby vznikla silně elektricky nabitá
černá díra, brzy by se v reálné situaci "vybila".
Pokud je kolem černé díry hmotné prostředí (mezihvězdná
látka), budou nabitou černou dírou z okolí přitahovány a
zachycovány opačné náboje (částice, ionty) - tímto selektivním
pohlcováním (akrecí) opačně nabitých částic se
příp. náboj černé díry rychle neutralizuje *). Ale i tehdy,
když silně nabitá černá díra bude ve vakuu, sehrají svou
neutralizační roli kvantové procesy tvorby
elektron-pozitronových párů v silném elektrickém poli,
přičemž náboje souhlasné s černou dírou budou odpuzovány
a opačné náboje přitahovány a pohlcovány černou dírou.
Elektrický náboj stacionární černé díry je tedy prakticky nulový.
Důvod, proč jsme se zde a v §3.5 zabývali vlivem náboje a
Reissnerovou-Nordströmovou geometrií, byl spíše teoretický -
ukázat zajímavé (a přitom aspoň v principu fyzikálně
možné) vlastnosti prostoročasu.
*) Pokud je rotující černá díra
vnořena do prostředí se silným magnetickým polem, může i
ve stacionárním stavu přetrvávat určitá rovnovážná velmi
malá hodnota elektrického náboje, určená rychlostí rotace a
intenzitou vnějšího magnetického pole.
Černé
díry - mosty do jiných vesmírů? Stroje času?
Rotující nebo elektricky nabité
černé díry mají složitou geometrickou a topologickou
strukturu prostoročasu (jak jsme si
ukázali v §3.5 "Reissnerova-Nordströmova geometrie" a §3.6 "Kerrova a Kerrova-Newmanova geometrie"); vyskytly se spekulace,
že by mohly sloužit jako mosty - tunely či portály - do
jiných vesmírů, popř. tunely mezi vzdálenými
místy nebo jinými časy v tomtéž
vesmíru. Pokusíme se kriticky z fyzikálního
hlediska posoudit tyto možnosti.
Červí
díry
Hypotetické "tunely" v prostoročase, které spojují
kratší cestou dvě vzdálená místa v tomtéž vesmíru, nebo
dvě místa v různých, jinak oddělených vesmírech, se
nazývají "červí díry" (angl. worm
hole) - podle podobnosti se spojovacími cestičkami, které
si červ prokousává jablkem.
Červ, který se nachází
na povrchu jablka a má se dostat z jedné strany na druhou, to
může udělat dvěma způsoby. Pokud bude svůj prostor
považovat za dvojrozměrný (povrch jablka), musí se po povrchu
proplazit přes celý obvod jablka. Bude-li však vnímat jablko
jako trojrozměrný objekt, může zvolit cestu jeho nitrem a
prokousat se ke kýženému protilehlému místu po daleko
kratší cestě (nebo také delší v případě křivolaké
chodbičky...). Necestuje dvoudimenzionálně po povrchu jablka,
ale využije třídemenzionální zkratky "červí
dírou".
Červí
díra v jablku umožňuje jen nevýrazné zkrácení cesty mezi
dvěma místy na povrchu-slupce. Při vhodné
geometricko-topologické struktuře ve vesmíru by však červí
díra mohla představovat naprosto zásadní zkrácení cesty
mezi velmi vzdálenými místy ve vesmíru (např. z mnoha
světelných let na stovky metrů či kilometry)! Pozorovatel,
který projde červí dírou nikde nepřekračuje limitní
rychlost světla c, přesto však může překonat
vzdálenost mezi místem startu a cíle daleko rychleji než
světelný paprsek, letící přímo. Hypoteticky by tak červí
díry mohly představovat svérázné zkratky nejen v prostoru,
ale i v čase - umožňovat "cestování časem"
(srov. pasáž "Uzavřené světočáry a
cestování časem"v
§3.3 a "Cesty časem: fantazie nebo fyzikální realita?").
Podle
této analogie s červem si intuitivně představujeme, že
zkratková cesta mezi různými místy či vesmíry se
uskutečňuje přes další, vyšší dimenzi,
skrze hyperprostor. V matematické topologii
(§3.1 "Geometricko-topologické vlastnosti prostoročasu") však může být prostor (varieta) vícenásobně
souvislý svou vnitřní strukturou, takže k
"cestování" mezi různými částmi není třeba
používat další dimenze.
Něco, co by mohlo být předobrazem modelu čeví
díry, poprve posali v r.1935 A.Einstein a N.Rosen jako tzv. Einsten-Rosenův
most (viz §3.4 "Schwarzschildova geometrie", obr.3.18) ve Schwarzschildově řešení
centrálně symetrického gravitačního pole.
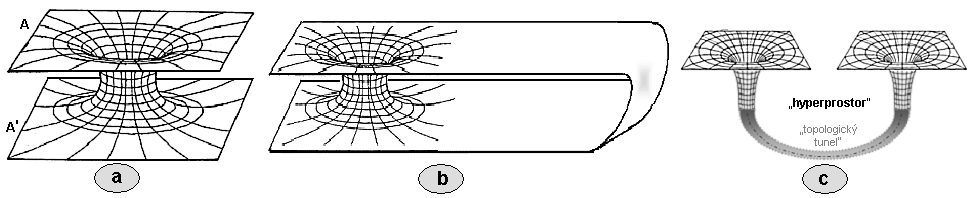 |
Obr.3.18. a) Znázornění geometrické
struktury řezu (prostorové hyperplochy) v = t = 0, J = p/2
Schwarzschildovým prostoročasem ve formě vnoření do
pomocného trojrozměrného eukleidovského prostoru.
Tento pomocný trojrozměrný prostor nemá fyzikální
význam (je pouze prostředkem pro znázornění);
význam má pouze vnitřní geometrie vnořené plochy,
která ukazuje dvě asymptoticky rovinné oblasti A
a A' spojené Einsteinovým-Rosenovým mostem.
b) Topologický tunel mezi dvěma místy
téhož vesmíru. c) "Červí
díra" mezi dvěma místy téhož vesmíru. |
Název "červí díra"
pak v r.1957 navrhl J.A.Wheeler. Ústí či jícen červí díry
by vypadal jako dvourozměrná sféra. Na rozdíl od sférického
horizontu černé díry, který umožňuje jen
"jednosměrnou cestu bez návratu", většinou do
záhuby, je však ústí červí díry obousměrně
průchozí plocha (aspoň v
principu). Červí díra má vstup
i výstup, můžeme jimi projít jak do vnitřku červí
díry, tak ven do vnějšího vesmíru. Pokud hypotetický
astronaut pronikne červí dírou, při výstupu by se mohl
ocitnout v jiném místě vesmíru a v jiném
čase, v budoucnosti nebo minulosti (v závislosti na hodnotách metrického tenzoru v obou
ústích). Příp. i v jiném kauzálně
odděleném vesmíru (podle globální
topologie prostoročasu)..?.. Červí díra
nemá přímou souvislost s černou dírou, avšak v řadě
matematických modelů černých děr se uvnitř vyskytuje i
červí díra.
Z geometricko-topologického hlediska lze červí
díru defnovat jako kompaktní oblast prostoročasu, jehož
prostorová hranice je topologicky ekvivalentní prosté sféře
S3, ale
jejíž vnitřek je topologicky propojen s
místy mimo tuto výchozí oblast. Je to tedy kompaktní oblast W v asymptoticky
plochém prostoročase, jejíiž topologie má tvar W ~ R´S , kde R
je Riemannův prostor a S je 3-rozměrná trubice, jejíž hranice má topologii
tvaru ¶S ~S2
a hyperplocha S opisovaná v prostoročase má prostorový
(prostoru-podobný) charakter.
Z geometrického hlediska máme dva druhy červích děr:
a) Tunely spojující různé oddělené vesmíry;
b) Spojky mezi různými vzdálenými místy téhož
vesmíru (našeho).
Z hlediska "průchodnosti" rozeznáváme rovněž dva
druhy červích děr:
- Traversabilní - stabilní,
umožňující pohyb napříč prostorem (prostoročasem),
červí díry spojující dvě různá a vzdálená místa
našeho vesmíru nebo různých vesmírů. Ke stabilizaci
těchto červích děr je zapotřebí hmota s negativní
hustotou energie (viz níže diskusi
"Mohou
reálně existovat červí díry?").
- Netraversabilní - velmi krátkodobé,
zanikající tak rychle, že žádný reálný objekt nemůže
skrze ně proletět, aniž by byl pohlcen singularitou. Takový
charakter mají červí díry uvnitř černých děr (jako je
Einstein-Rosenův most), spojující různé oddělené vesmíry.
Netraversabilní jsou samozřejmě všechny virtuální červí
mikrodíry v kvantové topologické pěně (opět
je diskutováno níže v pasáži "Mohou reálně existovat červí díry?").
Obyčejný tunel (jako je
železniční) spojuje dvě místa v
prostoru, červí díra spojuje dvě místa v prostoročase.
Pokud by existovala červí díra, teoreticky by umožňovala
překlenout dvě velice vzdálená místa ve vesmíru po daleko kratší
dráze. Pozorovatel (kosmonaut - "červonaut")
prošlý červí dírou - i když by nikde nepřekračoval
rychlost světla - by mohl překonat vzdálenost mezi oběma
místy daleko rychleji, než světelný paprsek letící po
obvyklé přímé dráze (přes prostor mimo červí díru).
Dostihl by vzdálené místo dřív než světlo. Díky tomu, že
pozorovatel touto zkratkou "předběhne" světlo,
může z hlediska teorie relativity "překonat čas" -
může cestovat v čase do budoucnosti i zpátky
do minulosti. Možnosti fiktivního či skutečného cestování
v čase jsou diskutovány v §3.3, část "Uzavřené
světočáry a cestování časem",
systematicky pak v sylabu "Cesty časem: fantazie nebo fyzikální
realita?".
Mohou reálně
existovat červí díry?
Velké "červí díry" by se mohly vyskytovat ve
vesmíru jako pozůstatky bouřlivých procesů s hmotou a
prostoročasem při velkém třesku, které vesmírná inflace
roztáhla na makroskopické nebo dokonce astronomické velikosti.
Mikroskopické červí díry rozměrů cca 10-33cm snad všude a
neustále vznikají a zanikají v důsledku
kvantově-gravitačních fluktuací metriky a topologie
prostoročasu (viz §B.4 "Kvantová
geometrodynamika") - v kvantové topologické pěně.
Červí díry uvnitř černých děr
mají "jepičí" život. Kromě gravitačně
dynamických efektů k tomu přispívají i kvantové efekty
záření. Náhodná kvanta záření, dopadající z vnějšku
na černou díru, se vlivem gravitace urychlí na vysoké energie
a budou "bombardovat" i jícen červí díry, který se
vlivem toho rychle smrští a uzavře. Každý objekt, který by
se pokusil projít takovou červí dírou během jejího
krátkého života, zanikne v okamžiku přetržení červí
díry, spolu s ní, ve vzniklé singularitě. Vzhledem k tomuto
extrémně krátkému trvání topologického tunelu je
problematické vůbec hovořit o existenci červí díry...
Aby se makroskopická červí díra mohla udržet
stabilní a "průchozí", musí být přítomna hmota
nebo pole vyvolávající antigravitační účinky
(hmota s negativní hustotou energie), které by
zabránily tendenci ke gravitačnímu "zaškrcení" do
singularity a vzniku černé díry - podle Raychaudhuryho
rovnice (2.59) deviace geodetik (§2.6 "Deviace a fokusace geodetik") energetická podmínka
opačná než (2.60) způsobuje rozšiřování geodetik po
průchodu červí dírou. Jedinou hypotetickou možností
stabilních červích děr je jejich "vyztužení"
specifickým druhem látky, který by vykazoval antigravitační
účinky a tím efektivně "tlačil" stěny
červí díry od sebe; z hlediska složek tenzoru
energie-hybnosti tato látka musí mít velké napětí v
radiálním směru, přesahující hustotu energie. Ke
stabilizaci červích děr je tedy zapotřebí hmota s
negativní hustotou energie *) (porušující slabou
energetickou podmínku (2.60)), kterou K.Thorne nazval
"exotická hmota".
*) Exotická látka musí mít negativní
energii z hlediska pozorovatele či světelného paprsku prolétajícího
červí dírou, nikoli nutně z hlediska pozorovatele který je v
klidu uvnitř červí díry. Hustota energie může být v teorii
relativity v jedné vztažné soustavě záporná, v jiné
kladná.
Černé díry jsou (aspoň na úrovni nynějších
astrofyzikálních znalostí) zákonitým
fyzikálním důsledkem hvězdného vývoje (§4.1."Úloha
gravitace při vzniku a evoluci hvězd"a §4.2, část "Úplný gravitační kolaps. Černá díra.") a pro jejich existenci
svědčí pádné astronomické pozorovací údaje. Červí díry
jsou však zatím jen pouhou hypotézou -
neznáme žádný přirozený způsob, jak by ve vesmíru červí
díry mohly vznikat mimo vnitřky černých děr.
Dosud neexistují žádné pozorovací
indicie pro červí díry!
Topologické
tunely uvnitř černých děr
O úplné analytické extenzi Kerrovy-Newmanovy geometrie
znázorněné na obr.3.21 až 3.25 a z ní plynoucích
geometricko-topologických důsledcích platí v podstatě
totéž, co o extenzi Schwarzschildovy geometrie (viz konec
§4.3). Všimněme si nejprve Schwarzschildovy geometrie, pro
kterou byl v §3.4 zkonstruován Kruskalův diagram (obr.3.17)
ukazující přítomnost dvou zrcadlově obrácených vesmírů - obr.3.18a. Při gravitačním kolapsu
však Schwarzschildovo řešení popisuje geometrii prostoročasu
pouze nad povrchem kolabující hvězdy. Větší část
idealizovaného (extendovaného) Schwarzschildova řešení na
Kruskalově diagramu se proto nerealizuje - je "odřezáno"
vnitřkem kolabující hvězdy (obr. 4.19a).
V §3.5 "Reissnerova-Nordströmova
geometrie" a §3.6 "Kerrova
a Kerrova-Newmanova geometrie" jsme si
ukázali, že pozorovatel, který při svém pohybu v
Reissnerově-Nordströmově nebo Kerrově-Newmanově
prostoročase protne vnitřní (Cauchyho) horizont r=rg-, se může dostat do jiného
"vesmíru". Podle toho by při gravitačním kolapsu
(elektricky nabité nebo rotující hmoty) existovala možnost,
že po protnutí Cauchyho horizontu r= rg- se smršťující hmota může vyhnout singularitě a začít se znovu rozpínat do jiné oblasti prostoročasu ("jiného vesmíru") -
obr.4.19b.
Einsteinův-Rosenův most a analogické
struktury Kerrovy-Newmanovy geometrie lze chápat jako
"most" spojující dva různé asymptoticky rovinné vesmíry (za předpokladu obvyklé eukleidovské
globální topologie každého z nich). Při vhodné topologii by
takový most mohl spojovat i dvě
různá místa téhož (vícenásobně souvislého) vesmíru - obr.3.18b,c. Takováto "červí díra" (worm hole;
byla definovaná výše) by mohla vytvářet "topologickou
zkratku" mezi dvěma vzdálenými oblastmi prostoročasu.
Spekuluje se dokonce o možnosti, že určitým pohybem obou
konců červí díry by se mohla zformovat uzavřená
časová křivka. Odtud je již jen krok ke sci-fi
představě, jak technicky vyspělá civilizace, disponující
technologií umožňující manipulovat (prostřednictvím
gravitace) s červí dírou, spustí "stroj
času"
("Cesty časem: fantazie nebo fyzikální
realita?") ...
Takovéto cestování
mezi různými vesmíry, popř. mezi různými vzdálenými
místy téhož vesmíru, či dokonce cestování časem, může
být vzrušujícím námětem pro vědecko-fantastickou
literaturu, avšak skutečnost je asi přece jen
prozaičtější. Přesné Schwarzschildovo,
Reissner-Nordströmovo nebo Kerrovo řešení obsahující
"tunely" mezi různými vesmíry platí pouze za
podmínek, pro něž bylo odvozeno, tedy pro jinak úplně prázdný asymptoticky rovinný vesmír.
Na konci §3.5 byla poznámka, že
pozorovatel pohybující se tak, že protne vnitřní horizont
r=rg-, uvidí během konečného intervalu
svého vlastního času celou další historii
"vesmíru", který právě opouští. Každé těleso z
tohoto vesmíru by pozorovatel přibližující se k rg- viděl s fialovým posuvem
narůstajícím do nekonečna. V souvislosti s tím bylo
ukázáno [114],[192], že Cauchyho horizont r=rg- uvnitř černé díry je nestabilní vůči elektromagnetickým a
gravitačním perturbacím vznikajícím vně černé díry
(klasická nestabilita) *). Analýza kvantových procesů tvorby
částic v silných polích uvnitř černé díry dále ukazuje
[192] (viz též §4.7), že zde existuje
rovněž kvantová nestabilita vnitřního horizontu **),
která se projeví i v případě, kdy prostor je z klasického
hlediska prázdný.
*) Obrazně lze říci, že
částice, která by proletěla přes takovou černou díru do
druhého vesmíru, by za sebou "zabořila" tento
teoretický tunel do jiných vesmírů.
**) Existence uzavřených časových světočar by navíc
umožnila částicím časovou smyčkou zasahovat vlastní
minulost. Kvantové úvahy naznačují, že poruchy plynoucí z
takových jevů by se spontánně zesilovaly a svou velkou
energií by nakonec topologický tunel destruovaly.
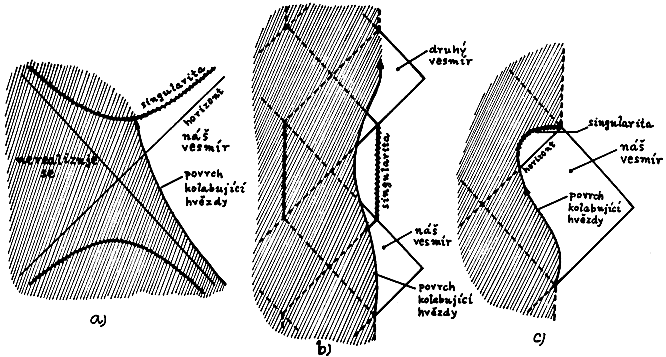
Obr.4.19. Struktura prostoročasu skutečné černé díry.
a) Ve
Schwarzschildově prostoročasu statické černé díry vzniklé
kolapsem (nerotující) hvězdy je značná část struktury
Kruskalova diagramu odřezána vnitřkem kolabující hvězdy.
b) Při
kolapsu rotující hvězdy do černé díry by teoreticky mohla
vzniknout struktura prostoročasu umožňující cestu do
druhého vesmíru. Kolabující hmota by se pak mohla vynořit v
druhém vesmíru ve formě "bílé díry".
c) V
důsledku divergující intenzity přicházejícího záření u
vnitřního horizontu a kvantových produkcí částic v okolí
singularity se však ve skutečnosti značná část teoretické
struktury Kerrrovy-Newmanovy geometrie (zahrnující vnitřní
horizonty a další vesmíry na Penroseově diagramu) nemůže
realizovat. Při kolapsu se vytvoří singularita, která sé
nachází v budoucnosti a nabývá prostorový charakter, což
neumožnuje žádné cestování do jiných vesmírů.
Tyto nestability (vůči
perturbacím a kvantovým procesům) vedou v praxi k destrukci a vymizení
Cauchyova horizontu a vzniku singularity prostorového typu -
obr.4.19c. Lze proto očekávat, že v reálné situaci struktura
prostoročasu uvnitř horizontu událostí r=rg+ bude kvalitativně podobná jako u
Schwarzschildovy černé díry a složité topologické
konstrukce podle
obr.3.25 se neuplatní (hmota by předtím musela
projít singulární oblastí).
Opět tak dospíváme k závěru, že
"exotické" možnosti cestování mezi různými
vesmíry, či cestování časem, by mohly fungovat nanejvýš v
rámci elementárních částic (popř. jen jediné elementární
částice!) - srov. s diskusí o uzavřených
časových křivkách v §3.3., pasáž "Uzavřené světočáry a cestování
časem". Jednotlivé mechanismy jsou
podrobněji popisovány v práci (sylabu) "Cesty
časem: fantazie nebo fyzikální realita?". V
závěru §3.4, poznámka "Dvojí
řešení v analytické extenzi - realita nebo fikce?", jsou diskutovány pochybnosti o
samotném fyzikálním smyslu úplných extenzí geometrie
Schwarzschildova a Kerrova-Newmanova prostoročasu, na nichž
jsou ideově založeny všechny představy o cestování mezi
různými vesmíry nebo v čase..?..
Některé související úvahy o směru toku času jsou dále
nastíněny v §5.6, část "Šipka času".
Černé
díry - "líhně" nových vesmírů?
Vedle myšlenky, že černé díry jsou portály do jiných
světů (vesmírů), vznikla dokonce ještě odvážnější
sci-fi hypotéza (v novější době ji oživil a doplnil Lee
Smolin): že v černých dírách se rodí nové vesmíry.
Celý náš vesmír mohl být zrozen z černé díry z jiného
vesmíru; big-bang by byl ve skutečnosti jen rozšířením
černé díry v jiném vesmíru. Objevila se i myšlenka, že
tyto nově vznikající vesmíry si navíc odnášejí
fyzikální zákony původního ("mateřského")
vesmíru - jako kdyby zde působila jakási "kosmická
dědičnost". Tato spekulativní "evoluční
kosmologie přirozeného výběru" by se pak v
jistém smyslu podobala Darwinovské evoluční biologii, neboť
podle ní budou nejčastějšími druhy vesmírů takové, které
vytvoří nejvíce "kopií sebe samých"; vesmíry v
nichž vzniká velký počet černých děr by měly určitou
"reprodukční výhodu" přecházející na další
"generace" vesmírů...
Z hlediska střízlivého fyzikálního přístupu obecné teorie
relativity a kvantové teorie se však tyto spekulativní
koncepce jeví jako nepodložené:
1. Černé díry neprodukují nové vesmíry
- z klasického (nekvantového) hlediska nevznikají v nitru
černých děr vůbec (jak bylo výše diskutováno), z
kvantového hlediska spontánní fluktuace prostoročasu, které
mohou potenciálně vést ke vzniku nových vesmírů,
probíhají všude a neustále, nejen v nitru
černých děr.
2. Neexistuje žádný mechanismus, kterým by mohla být
jakákoli konkrétní fyzikální informace přenesena z jednoho
vesmíru do druhého. V rámci klasické OTR to zakazují
Hawkingovy a Penroseovy teorémy o singularitách. V přístupu
kvantové kosmologie chaotické kvantové fluktuace polí a
metriky v "topologické pěně" prostoročasu
efektivně stírají a randomizují každou
makroskopickou fyzikální strukturu a informaci z jiného
(předchozího) vesmíru....
Vojtěch
Ullmann