Zpět: Seznam komplexních programů

3.2 Komplexní vyhodnocování radionuklidové angiokardiografie

Pomocí radionuklidové angiokardiografie vyšetřujeme dynamiku krevního průtoku centrální cirkulací, tj. srdečními dutinami, velkými cévami a plícemi. Vyšetření spočívá v tom, že snímáme scintilační kamerou tranzit a ředění radioaktivního bolusu pravým srdcem, plícemi, levým srdcem a systémovou cirkulací. Při počítačovém zpracování se vytvářejí obrazy význačných fází průtoku bolusu a křivky časového tranzitu a diluce bolusu v srdečních komorách a plících. Na scintigrafických obrazech můžeme vizuálně sledovat průtok radioaktivního bolusu jednotlivými částmi srdce a plícemi a rozpoznat tak případné závažnější abnormality v centrální cirkulaci a některé anatomické odchylky. Matematickým zpracováním křivek průchodu a ředění bolusu v srdečních komorách a plících získáme řadu kvantitativních parametrů centrální hemodynamiky, které umožňují detailnější posouzení a odhalení i subtilnějších patologických odchylek. Komparací křivek z pravého a levého srdce se získává hodnota kardiopulmonálního středního tranzitního času. Matematickou analýzou křivky z plic (pulmogramu) můžeme kvantifikovat L-P zkraty (vypočítat průtok zkratem a hodnotu Qp/Qs). Analýzou příslušných křivek lze dále kvantifikovat P-L zkraty, počítat hodnoty ejekční frakce pravé komory, minutového volumu srdečního, kardiopulmonálního objemu krve, v kombinaci s radionuklidovou ventrikulografií též regurgitační frakce.

Střádání dat

Podle indikace k vyšetření provedeme příp. premedikaci neaktivním Sn-pyrofosfátem (viz níže) a detektor scintilační kamery umístíme nad oblast prekordia v přední nebo modifikované LAO projekci.

Do stříkačky si připravíme cca 400-600 MBq (u dětí asi 7MBq/kg) ^99mTc v objemu max. 1ml. a jehlu zavedeme do vnitřní jugulární nebo do antekubitální žíly. Spustíme střádání dynamické studie a vzápětí rychle aplikujeme obsah stříkačky. Rychlou aplikací malého objemu koncentrovaného radioindikátoru dosáhneme toho, že krevním řečištěm se směrem k srdci bude pohybovat kompaktní diskrétní bolus radioaktivity, jehož průchod centrální cirkulací a postupné ředění budeme kamerou mapovat *).
*) Podmínkou kvalitních obrazů a hlavně korektní analýzy křivek je, aby radioindikátor skutečně vstoupil do srdce jako krátký kompaktní bolus. Při obvyklé aplikaci do antekubitální žíly dochází nezřídka (až ve 25% případů) k prodloužení bolusu ve venozní cirkulaci, nebo dokonce k jeho rozdělení a fragmentaci. Takto deformovaný bolus může velice zkreslit analýzu centrální hemodynamiky (např. fragmentovaný bolus může na pulmogramu simulovat zkratovou vlnu). Dodatečné matematické korekce (např. metodou dekonvoluce) zde většinou selhávají. Pro spolehlivější zajištění kvalitního bolusu existuje anatomicky vhodná cesta aplikace bolusu - aplikace do vnitřní jugulární žíly. Dále se doporučuje aplikace bolusu v inspiriuu .

Doporučená předvolba střádání dynamické studie :

Matice 64 ´ 64 , 16 bit

Grupa 1 : 100 snímků po 0.2 sec. (u pomalejší činnosti 0.5 sec./snímek)

Grupa 2 : 50 snímků po 1 sec.

Grupa 3 : 10 obrazů po 30 sec.

(pokud akviziční program neumí grupovat, je třeba předvolit vyšší počet snímků, např. 300 snímků po 0.3 sec.)

Pokud budeme hodnotit pouze první průtok (zpravidla pro diagnostiku kongenitálních srdečních vad), neprovádíme premedikaci neaktivním Sn-pyrofosfátem a střádání scintigrafické studie ukončíme, jakmile je již několik sekund patrná systémová recirkulce (sledujeme na perzistentním osciloskopu nebo na displeji počítače). Chceme-li počítat minutový volum srdeční, pak střádáme studii až do konce. V tomto případě je nutno premedikovat neaktivním Sn-pyrofosfátem cca 20 minut před aplikací bolusu, nebo použít jiný intravazální indikátor značený ^99mTc (erytrocyty značené in vitro, značené plasmatické bílkoviny). Pro výpočet minutového volumu srdečního mimoto vložíme do komentáře hmotnost nemocného v [ kg] , výšku v [ cm] a objem krve v [ ml.] . Objem krve stanovíme buď diluční metodou, nebo jej empiricky odečteme z tabulek podle výšky, váhy a pohlaví pacienta. Pro případný výpočet ejekční frakce pravé komory je nutno sledovat srdeční frekvenci během prvního tranzitu bolusu a tuto hodnotu zapsat pro použití při vyhodnocování.

Vyhodnocování dat

Po vyvolání příslušné radiokardiografické scintigrafické studie pomocí základního systému OSTNUCLINE (pokud jsou jednotlivé grupy nahrány jako oddělené studie, vyvoláme je postupně všechny za použití příkazu ”Další” - spojí se pro vyhodnocení v jednu studii) spustíme komplexní program RKG - bolusová angiokardiografie (jeho první část).

Vizuální hodnocení obrazů průchodu bolusu
Vyhodnocování dynamické radiokardiografické studie začínáme tím, že na scintigrafických obrazech vizuálně sledujeme průtok radioaktivního bolusu jednotlivými částmi srdce a plícemi. Můžeme tak rozpoznat případné závažnější abnormality v centrální cirkulaci a některé anatomické odchylky. Na displeji se zobrazí série vhodně nasumovaných sekvenčních obrazů průchodu radioindikátoru centrální cirkulací, spolu s příslušnými časovými intervaly. Tato série obrazů je nabídnuta k předběžnému vizuálnímu hodnocení. Pokud na obrazech neshledáme žádnou patologii, můžeme použít implicitně zabudovaný text standartního normálního hodnocení, např. :

"Po injekci bolusu radioindikátoru se zobrazují nezvětšené dutiny pravého srdce, následuje plnění nerozšířené plícnice a plicního řečiště, které se přiměřeně rychle vyprazdňují do normálně konfigurovaných dutin levého srdce a aorty. Během průchodu bolusu levým srdcem nepozorujeme předčasný výskyt radioindikátoru v pravém srdci a plících. "

Současně se tím předběžně vygeneruje standartní formulace normálového závěru:

"Z á v ě r: Při vizuálním hodnocení sekvenčních scintigramů průchodu bolusu malým oběhem ani při kvantitativní analýze cirkulačních křivek nepozorujeme patologické změny centrální hemodynamiky.",

kterou však v průběhu dalšího vyhodnocování můžeme upravit (viz níže). V patologickém případě zvolíme nestandartní variantu slovního hodnocení, kdy pomocí klávesnice vpisujeme do vyznačeného rámečku volný text; při této variantě se negeneruje ani žádná standartní formulace závěru. Sérii obrazů včetně slovního hodnocení lze pro dokumentaci vytisknout (má význam jen u výraznějších patologií).

Vyznačení zájmových oblastí
Pro kvantifikaci centrální hemodynamiky je důležitým iniciálním úkonem vyznačení zájmových oblastí (ROI) jednotlivých částí centrální cirkulace. Pomocí šipek nebo jezdce pod obrazem krokujeme obrazy ve studii a zviditelňujeme tak postupně jednotlivé struktury jimiž protéká radioaktivní bolus. Zájmové oblasti vykreslujeme v pořadí:

ROI 1 ......... místo příchodu bolusu
ROI 2 ......... pravá komora
ROI 3 ......... pravá síň (pro posouzení lokalizace L-P zkratu)
ROI 4 ......... plíce
ROI 5 ......... levá komora
ROI 6 ......... aorta (pouze pro kvantifikaci P-L zkratu)

Při zakreslování ROI z pravé komory dbáme na to, aby nebyla zahrnuta část pravé komory přiléhající k septu. Při vymezování ROI plic (obvykle vlevo) nesmí být zahrnuta oblast velkých větví plícnice, mediální hranice musí být vzdálena od aorty a levé komory. Při vyznačování levé komory dáváme pozor, abychom nezabrali i část komory pravé (na příslušném snímku fáze naplněné levé komry je totiž pravá komora již vyprázdněná a není vidět) - doporučujeme během vyznačování na chvíli vrátit šipkami nebo jezdcem obraz naplněné pravé komory.

ROI 3 pravé síně je fakultativní a vyznačujeme ji tehdy, když chceme posoudit, zda příp. L-P zkrat je na úrovni komorového či síňového septa. ROI 6 aorty je rovněž fakultativní a vyznačujeme ji jen tehdy, když chceme kvantifikovat P-L zkrat.

Hemodynamické křivky
Z těchto zájmových oblastí se konstruují křivky (histogramy) časového průběhu aktivity (tj. průchodu a ředění bolusu) v těchto zájmových oblastech, které se korigují na mrtvou dobu systému kamera-počítač (u daného systému efektivní mrtvá doba činí cca 6 m sec.). Dále lze nastavit vhodnou kompresi nebo expanzi měřítka časové osy křivek tak, aby u každého pacienta byly křivky optimálně zobrazeny bez ohledu na průtokový čas. Jeden krok expanze nebo komprese představuje asi 20% stávající délky křivky. Pro zachycení dynamiky prvního průchodu bolusu je vhodné provést takovou expanzi, aby kromě celého primocirkulačního píku byl zobrazen počátek recirkulační vlny. Pro zachycení dynamiky systémové recirkulace je nutno mít s rezervou zobrazenu celou recirkulační vlnu. Optimální časové měřítko si program nastavuje automaticky, takže ruční modifikace expanze a komprese většinou není třeba.

Matematický model dynamiky průchodu a ředění bolusu
Kvantitativní analýza a stanovení hemodynamických parametrů se provádí na základě matematického modelu, který vystihuje hlavní rysy průchodu radioaktivního bolusu srdečními dutinami za postupného ředění. Nejzákladnější model je znázorněn na obr.3.2.1a.

Obr.3.2.1. a) Nejjednodušší model průchodu a ředění bolusu srdeční (diluční) komorou. b) Časový průběh radioaktivity v diluční komoře měřené zevním detektorem (scint.kamerou) po vstřiknutí radioaktivního bolusu do přítokové trubice.

Sestává z průtokové trubice, která ústí do diluční komory o objemu V a zase z ní vyúsťuje ven. Předpokládáme, že v komoře probíhá okamžité a dokonalé rozmíchávání přitékající a odtékající kapaliny. Průtok touto soustavou nechť je roven Q [ ml./sec.] . Do přítokové trubice vstřikneme malou kapku (bolus) radioaktivního roztoku o aktivitě A₀. Po příchodu do diluční komory se kapka okamžitě rozředí do celého objemu V a začne se přitékající a odtékající kapalinou postupně vyplavovat. Aktivita v diluční komoře (měřená příslušným zevním detektorem, např. kamerou) bude mít časový průběh A(t) podle obr.3.2.1b. Zákon zachování aktivity dává rovnici

                                 A(t)
   A(t+dt)  =  A(t) -   --- . Q . dt   ,                                                (3.2.1)
                                  V

neboli

                      A(t)
    dA(t)  =  - --- . Q . dt    .                                                            (3.2.2)
                       V

Zvolíme-li za počátek odečítání času okamžik příchodu a rozmíchání bolusu, je řešením diferenciální rovnice (3.2.2)....                                    _-(Q/V).t
             A(t) =  A₀ . e              ,             t ł 0 .                                    (3.2.3)

Pokles radioaktivity komory bude tedy exponenciální. Náběh by měl být podle našeho idealizovaného modelu okamžitý, ve skutečnosti však bude mít tvar podle obr.3.2.1b (k prokládání se často používá tzv. gama-funkcí, viz níže). Z funkčního vztahu (3.2.3) integrací snadno obdržíme velikost plochy pod křivkou A(t):

                   Ą
                 ó                                V
                 ô A(t) dt     =     A₀ .  ---   .                                             (3.2.4)
                 ő                                Q
                 0

Tento důležitý vztah se dá vyjádřit větou :
Plocha (integrál) pod křivkou časového průběhu průtoku bolusu diluční komorou je přímo úměrná vstupní aktivitě A₀ a objemu komory V a nepřímo úměrná průtoku Q touto komorou.
Tento teorém se někdy označuje jako Steward-Hamiltonův princip.

Komplexnější model srdeční komory je znázorněn na obr.3.2.2a. Diluční komora stejných vlastností jako v předchozím modelu je zde zapojena v uzavřeném okruhu, který začíná a končí v rezervoáru představujícím cévní řečiště obsahující celkový krevní volum V_B.

Obr.3.2.2. a) Realističtějším modelem srdeční komory je diluční komora ("čerpadlo") zapojená v uzavřeném okruhu se zásobníkem reprezentujícím celkový krevní volum v cévním systému. b) Časový průběh radioaktivity v takto zapojené diluční komoře po vstřiknutí radioaktivního bolusu.

Po vstřiknutí bolusu o aktivitě A₀ do vstupní trubice se radioaktivita v diluční komoře bude měnit s časem podle grafu obr.3.2.b. Diluční křivka bude zpočátku stejná jako u předchozího modelu, avšak později nepůjde s časem k nule, ale vlivem recirkulace přes krevní řečiště se radioaktivita v komoře bude blížit určité asymptotické hodnotě AĄ dané podle dilučního principu rozředěním aktivity A₀ v celém krevním volumu V_B :

                                  V
               A_Ą =  A₀ . ---   .                               (3.2.5)
                                 V_B

Pro objem diluční komory tedy platí vztah

                             A_Ą
         V =  V_B  .    ---   .                               (3.2.6)
                             A₀

Abychom nyní mohli použít vztah (3.2.4), je třeba ze skutečné křivky časového průběhu radioaktivity v diluční komoře osamostatnit tu část, která odpovídá primocirkulaci bolusu bez systémové recirkulace. Definujeme si proto funkci A^*(t), která vznikne exponenciální extrapolací píku funkce A(t) odpovídajícího prvnímu průtoku bolusu (na obr.3.2.2b čárkovaná křivka). Pro tuto funkci A^*(t) bez recirkulace budou platit vztahy (3.2.3) a (3.2.4). Dosazením za neznámý volum diluční komory V z (3.2.6) do (3.2.4) obdržíme důležitý vztah

                                A_Ą
          Q =  V_B . ---------    ,                           (3.2.7)
                             Ą
                            ň A^*(t) dt
                           0

podle něhož průtok Q lze stanovit tak, že celkový krevní volum V_B násobíme podílem asymptotické hodnoty aktivity AĄ diluční komory a plochy (integrálu) pod křivkou prvního průtoku A^*(t) touto komorou. Vztah (3.2.7) má pozoruhodnou vlastnost, že platí nejen pro celou komoru, ale i pro její libovolnou část (jestliže A(t) ® k.A(t), pak i A_Ą ® k.A_Ą a A^*(t) ® k.A^*(t), takže příslušný koeficient k se ve zlomku vykrátí). Předpokladem je zde samozřejmě dokonalá diluce. Vztah (3.2.7) je základem pro stanovení krevního průtoku srdcem - minutového volumu srdečního.

Křivky průchodu radioaktivního bolusu jednotlivými částmi centrální cirkulace začínají výrazným píkem prvního průchodu a pokračují méně výrazným platem recirkulace (kromě vždy přítomné recirkulace systémové to může být i event. zkratová recirkulace). Směrem k vyšším časům je sestupná část píku prvního průchodu superponována s touto recirkulací. Pro osamostatnění "čistého" píku prvního průtoku se používají dvě metody. První z nich byla výše popsána - jedná se o exponenciální fitaci rychlé části sestupného ramene píku a extrapolaci k delším časům, čímž vznikne křivka A^*(t). Druhou metodou je proložení tzv. gama-funkce (ve skutečnosti se jedná o integrand funkce G ), která má obecný tvar

        G(t) = Rl . (t-R0) ^R2 . e ^R3.(t-R0) , R2 ł 0, R3 < 0 .         (3.2.8)

Fitovaná gama-funkce se rovněž extrapoluje i mimo prokládaný úsek a nahradí primocirkulační pík - vzniká "čistá" křivka prvního průtoku.

Čtyři parametry gama-funkce se fitují tak, aby tato funkce co nejlépe vystihovala dynamiku prvního průchodu bolusu srdeční komorou nebo plícemi. Parametr R0 vyjadřuje časový posun související s časovým intervalem mezi spuštěním dynamické studie a začátkem příchodu bolusu do daného místa. Parametr R1 souvisí s radioaktivitou bolusu A₀. Parametry R2 a R3 jsou rychlostní koeficienty vzestupné a sestupné části křivky. Užitečnost gama-funkcí tkví v tom, že jsou schopny dobře fitovat i nesymetrické píky díky tomu, že jsou složeny ze dvou částí: koeficient (t-R0)^R2 popisuje exponeciální nárust při vstupu bolusu, zatímco koeficient e^R3.(t-R0) popisuje exponenciální pokles radioaktivity při ředění a vyplavování bolusu.

V programu RKG se fitace gama-funkcí používá jednak u křivek z pravého a levého srdce při stanovení středního tranzitního času centrální cirkulace, jednak u pulmogramu při kvantifikaci zkratů. Úsek křivky, kterým se má gama-funkce prokládat je stanovován automaticky (s možností ruční modifikace) - počáteční bod pomocí maxima druhé derivace, koncový bod na sestupném rameni je vymezen podmínkou definovaného poklesu rychlosti poklesu (většinou na 80% maximální rychlosti vyplavování radioaktivity).

Minutový volum srdeční
Stanovení minutového volumu srdečního je v programu RKG fakultativní. V případě kladné odpovědi stanovíme na dotaz programu hodnotu celkového krevního volumu pacienta. Tuto hodnotu buď určíme diluční metodou a vložíme na dotaz programu, nebo (častěji) si ji program stanoví empirickým vzorcem z výšky, váhy a pohlaví pacienta. Dále zvolíme, ze které křivky chceme minutový volum počítat - doporučujeme buď z levé komory nebo z celého srdce. Na takto zvolené křivce se pak automaticky (s možností ruční modifikace) vymezí počáteční a koncový bod úseku sestupné (diluční) části, kterým se prokládá exponenciální funkce. Vlastní "čistá" křivka A^*(t) prvního průtoku se pak získá spojením úseku původní křivky A(t) od nuly až do místa maximální rychlosti poklesu, a v tomto místě navazující exponenciální funkce extrapolované až do splynutí s vodorovnou osou. Dále se vymezí bod ekvilibria, kde je radioindikátor již rovnoměrně rozmíchán v krevním řečišti. Na základě poměru mezi asymptotickou aktivitou A_Ą v ekvilibriu a plochou (integrálem) pod křivkou prvního průtoku se vypočítá minutový volum srdeční podle vztahu (3.2.7) odvozeného v předchozím odstavci. Vypočtená hodnota se nabídne k odsouhlasení, takže výpočet minutového volumu lze libovolně opakovat pro různé křivky a různě volené úseky diluce na těchto křivkách.

Regurgitační frakce
Za normálních okolností se prakticky všechna krev, vypuzená při systolickém stahu levé komory, stává součástí systémové cirkulace. Při některých kardiopatiích (nedomykavost mitrální nebo aortální chlopně) se však určitá část vypuzené krve vrací při diastole zpět do levé komory - dochází k regurgitaci. Pro kvantifikaci této poruchy, snižující efektivní výkonnost srdce, je důležitým parametrem tzv. regurgitační frakce RGF udávající procentuálně, jaká část tepového objemu se vrací zpět do komory :

                       SV_tot - SV_ef
       RGF  =   --------- . 100 %   ,                         (3.2.9)
                            SV_tot

kde SV_tot je celkový tepový objem vypuzený srdeční komorou při jednom stahu, SV_ef je efektivní tepový objem skutečně vyslaný při jednom stahu do systémového oběhu.

Ke stanovení regurgitační frakce je třeba provést nejprve bolusovou radiokardiografii zahrnující i fázi ekvilibria (při prvním tranzitu sledujeme tepovou frekvenci) a následně rovnovážnou ventrikulografii. Nejdříve vyhodnotíme ventrikulografii, z níž pro stanovení regurgitace použijeme hodnotu tepového volumu SV_ventr, která udává celkový (zdánlivý) tepový objem ^**) : SV_tot = SV_ventr. Pak vyhodnocujeme bolusovou radiokardiografii, která nám poskytne hodnotu minutového volumu srdečního CO [litry/min] - z principu metody plyne, že se jedná o skutečný (efektivní) průtok čerpaný srdcem do systémového oběhu, bez ohledu na případnou regurgitaci. Byla-li tepová frekvence při prvním tranzitu f [ tepů/min.] , je efektivní tepový volum SV_ef = CO/f [ ml.] - nezahrnuje regurgitační frakci. Z výše uvedeného vztahu pak již přímo vychází hodnota regurgitační frakce RGF.
^**) Totální tepový objem vyjadřuje množství krve vypuzené ze srdce při systole, bez ohledu na to, zdali část této krve již během systoly teče zpětně do síní (mitrální regurgitace), nebo se následně v diastole vrací zpátky do komory (aortální regurgitace). Totální tepový objem tedy zahrnuje i regurgitační frakci.

Dotaz, zda počítat regurgitační frakci, se v programu RKG objeví tehdy, byl-li počítán minutový volum srdeční. Vkládáme pak tepovou frekvenci odečtenou při prvním tranzitu bolusu a hodnotu tepového volumu získanou z ventrikulografie.

Za fyziologickou mez lze podle našich zkušeností považovat regurgitační frakci kolem 10%, hodnoty do cca 25% hodnotíme jako lehkou regurgitaci, nad cca 50% jako závažnou regurgitaci. V každém případě je však třeba mít na paměti, že výsledek výpočtu může být ovlivněn kvalitou bolusu a přesností stanovení absolutního volumu srdeční komory.

Ejekční frakce pravé komory
Protéká-li radioaktivní bolus pulzující (čerpající) diluční komorou, je rychlost poklesu sestupné části primocirkulačního píku úměrná tepové frekvenci a ejekční frakci pulzace. Analýzou diluční křivky lze tedy v principu použít ke stanovení ejekční frakce komory. Mezi ejekční frakcí EF a průměrným průtokem Q sdeční komorou totiž platí zřejmý vztah

                                                      V_ED
            Q .=  EF . V_ED . f. =  EF . ----   ,                                 (3.2.10)
                                                        T

kde V_ED je end-diastolický volum srdeční komory, f je tepová frekvence a T perioda srdečního cyklu. Dosadíme-li odtud průtok Q do základní exponenciální funkce (3.2.3) popisující diluční křivku z komory, dostaneme

                                       EF.V_ED .f . t
                                   - -------- . t
                                               V
          A(t)  =   A₀ . e                                        ,                          (3.2.11)

kde V je průměrný objem komory během pulzace. Přesný vztah mezi průměrným objemem komory V a jejím end-diastolickým volumem V_ED závisí na konkrétním tvaru volumové křivky, avšak za oprávněného předpokladu zhruba kosinusového průběhu srdečního cyklu (symetrické ejekce a plnění) můžeme za V považovat průměr mezi end-diastolickým a end-systolickým objemem komory :

                 V_ED + V_ES         V_ED + (V_ED-EF.V_ED)                   2 - EF
       V =    -------   =   --------------   =   V_ED . -----   .
                       2                                 2                                        2

Dosazením posledního výrazu za V do (3.2.11) se V_ED vykrátí a rovnice popisující sestupný diluční úsek křivky bude znít

                                             2. f . EF
                                         - ------ . t
                                              2 - EF
               A(t)   =   A₀ . e                              .                                      (3.2.12)

Proložíme-li tedy sestupným ramenem píku prvního průchodu bolusu srdeční komorou exponenciální funkci

                                        - R .t
                A(t)   =   A₀ . e               ,

pak z takto zjištěného rychlostního koeficientu R úniku radioaktivity z komory můžeme stanovit ejekční frakci srdeční komory:

                              2 . R                     2 . R
             EF   =    ----- . T   =      -------     ,                                (3.2.13)
                             2 + R                   (2+R) . f

kde T je perioda srdečního cyklu a f je tepová frekvence.

Při praktické realizaci této metody je třeba vzít v úvahu, že vzorec (3.2.13) platí pouze v případě, že je splněna dokonalá diluce a že vstupí funkce je Diracova d -funkce, tj. radioindikátor přišel do komory jako dokonalý kompaktní bolus. Podmínka vstupu dokonalého bolusu je (částečně) splněna pro pravou komoru, rozhodně však ne pro levou komoru. Metoda je proto (s omezením) použitelná pouze pro stanovení ejekční frakce pravé srdeční komory.

Fakultativní výpočet ejekční frakce pravé komory v programu RKG začíná tím, že na křivce pravé komory se vymezí sestupný (diluční) úsek, kterým se proloží exponenciela. Zadáme tepovou frekvenci (která se při střádání odečetla na kardiomonitoru v okamžiku naplnění pravé komory bolusem) a program na základě rychlostního koeficientu exponenciální funkce úniku radioaktivity z pravé komory vypočte její ejekční frakci. Vypočtená hodnota EF se zobrazí spolu s křivkou pravé komory a nabídne se k odsouhlasení či opakování výpočtu (třebas s modifikovaným úsekem pro fitaci exponenciely).

Kardiopulmonální střední tranzitní čas
Střední tranzitní čas centrální cirkulace MTT je doba, za kterou element krve projde z pravé komory centrální cirkulací přes plíce do levé komory. Nejjednodušší způsob stanovení kardiopulmonálního tranzitního času je zjištění časového rozdílu mezi vrcholy primocirkulačních křivek pravé a levé komory (metoda "peak to peak"). Jelikož však tyto křivky nejsou symetrické (vzestupná část píku je podstatně srmější než sestupná), může se časový rozdíl mezi vrcholy poněkud lišit od skutečného tranzitního času. Přesnější metodou stanovení kardiopulmonálního tranzitního času je určení časové diference mezi těžišti (centroidy) píků prvního průtoku na křivkách levé a pravé komory. Časová souřadnice těžiště (centroidu) t_C je definována požadavkem, aby plocha (integrál) pod fitovanou gama-funkcí nalevo a napravo od těžiště byla stejná :

                   t_C                     Ą
                  ň G(t) dt     =     ň G(t) dt    .
                 0                        t_C

Průměrný tranzitní čas kardiolulmonální cirkulace MTT je pak dán rozdílem časových souřadnic těžišť (centriodů) fitovaných gama-funkcí levé a pravé komory: MTT = t_C(LK) - t_C(PK) - v sekundách.

Pokud máme kvantifikován minutový volum srdeční Q, můžeme na základě tranzitního času MTT stanovit další parametr centrální hemodynamiky - kardiopulmonální krevní volum V_K-P udávající celkový objem krve v centrální cirkulaci: V_K-P = MTT . Q . Aby tento objem vyšel v mililitrech, je nutno MTT mít v sekundách a Q převést z obvyklých [ litrů/min.] na [ mililitry/sekundu] .

Stanovení tranzitního času centrální cirkulace v programu RKG spočívá v tom, že primocirkulačními píky na křivkách pravé a levé komory se prokládají gama-funkce a z časového rozdílu jejich těžišť (centroidů) se počítá střední kardiopulmonální tranzitní čas MTT). Při běžné tepové frekvenci (cca 60-80 tepů/min.) se normální hodnoty MTT pro dospělé se pohybují kolem 6-8 sec, u dětí (kde je i vyšší tepová frekvence) kolem 3-5 sec. Pokud byl v dřívější fázi vyhodnocení kvantifikován minutový volum srdeční, spočítá se i celkový objem krve v plicním oběhu v [ ml.] . Normální hodnoty u dospělých se zde pohybují kolem 500-800 ml. Vypočtená hodnota MTT a případně i kardiopulmonálního krevního volumu se zobrazí spolu s křivkami z pravého a levého srdce a nabídne se k odsouhlasení nebo k opakování výpočtu (můžeme např. modifikovat úseky pro fitaci gama-funkcí na primocirkulačních vrcholech těchto křivek).

Kvantifikace intrakardiálních zkratů
Za normálních okolností (bez přítomnosti zkratu) je radioaktivní bolus unášen (za postupného ředění) krví z pravého srdce přes plicní oběh do levého srdce (obr.3.2.3). Na křivce pulmogramu se kromě výrazného píku prvního průtoku bolusu objeví po asi 30-50 sec. pouze nižší široký vrchol systémové recirkulace způsobený návratem značně zředěné aktivity přes systémový oběh zpět do srdce a plic.

Obr.3.2.3. a) Schématické znázornění trasy průchodu bolusu radioindikátoru centrální cirkulací. b) Projevy zkratů na cirkulačních křivkách průchodu a ředění bolusu v srdečních komorách, plících a aortě.

Při některých poruchách (defekt síňového nebo komorového septa) však část krve protéká z dutin levého srdce do dutin pravého srdce a následně do plicního oběhu ^*) - dochází k levo-pravému (L-P) zkratu a tím i k předčasné recirkulaci krve v plicním oběhu.
^*) Vzácně se může vyskytnout i zkrat mezi aortou a plícnicí (”dučej”), při němž zkratová recirkulace probíhá jen přes plíce a vynechává pravou komoru.
Tento zkratový průtok s sebou nese i část aktivity bolusu. Na křivce pulmogramu se L-P zkrat projeví tím, že záhy po vrcholu prvního průtoku se objeví další vlna, odrážející předčasnou recirkulaci krve v plících způsobenou zkratem - obr.3.2.3b, obr.3.2.4a. Velikost této recirkulační vlny v poměru k velikosti primocirkulační vlny je mírou závažnosti L-P zkratu. Centrální hemodynamika je schématicky znázorněna na obr.3.2.3a. Za normálních okolností je plicní průtok Qp roven systémovému průtoku Qs. Za přítomnosti L-P zkratu je plicní průtok Qp tvořen součtem systémového Qs a zkratového Qz průtoku: Qp = Qs + Qz. Z toho plyne, že Qz = Qp - Qs a Qs = Qp - Qz .

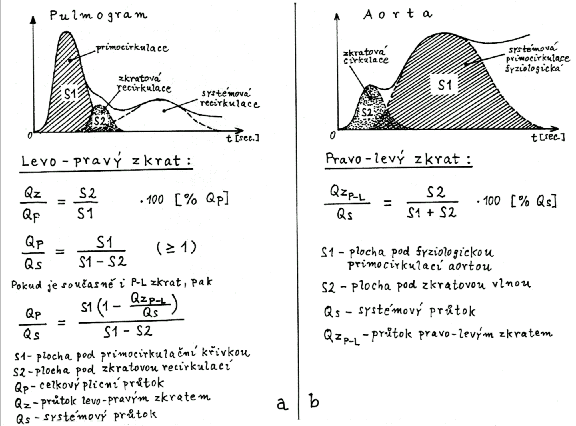Obr.3.2.4. a) Kvantifikace L.-P. zkratu rozkladem pulmogramu b) Kvantifikace P.-L. zkratu rozkladem křivky průchodu radioindikátoru aortou.

Primocirkulace, zkratová recirkulace a systémová recirkulace se částečně časově překrývají a prolínají. Pro kvantifikaci zkratu je třeba rozložit pulmogram na část odpovídající prvnímu průtoku bolusu a na část reprezentující předčasnou (zkratovou) recirkulaci - obr.3.2.4a. První částí pulmogramu (od začátku primocirkulačního píku až po bod maximálního poklesu) se nejprve proloží gama-funkce a extrapoluje se do vyšších časů až po splynutí s vodorovnou osou. Tato gama-funkce představuje první průtok bolusu plicním řečištěm a plocha S1 pod ní (její integrál) je úměrná plicnímu průtoku Qp. Tato fitovaná křivka prvního průtoku se pak odečte od původního pulmogramu. Vzniká tím rozdílová křivka, na které již není pík prvního průtoku, je zde pouze recirkulace jak systémová (pozdní), tak případně zkratová (předčasná). Naším úkolem je teď odseparovat na rozdílové křivce čistou zkratovou vlnu od systémové recirkulace, s níž se částečně prolíná. Za tím účelem širokým píkem systémové recirkulace na rozdílové křivce proložíme další gama-funkci a extrapolujeme ji vlevo do kratších časů, kde právě může být systémová recirkulace superponována se zkratovou (předčasnou) recirkulací. Odečtením této extrapolované křivky (gamma-funkce) systémové recirkulace od původní rozdílové křivky již dostaneme "čistou" křivku předčasné (zkratové) recirkulace. Plocha S2 (integrál) pod ní je úměrná průtoku Qz zkratem. Rozdíl ploch S1 - S2 je úměrný systémovému průtoku Qs - obr. 3.2.4a .

Ke kvantifikaci L-P zkratu se používají dva parametry. Prvním je zkratový průtok Qz vyjádřený v procentech celkového plicního průtoku Qp :

            Qz               S2
          ----     =     ---   . 100 [ % ]                ( ł 0 )  .
            Qp               S1

Bez přítomnosti zkratu je tento parametr blízký nule, normální hranice činí cca 12%. Druhým parametrem používaným pro kvantifikaci L-P zkratu je poměr plicního a systémového průtoku Qp/Qs :

           Qp                     S1
         ----      =       ------                            ( ł 1 ) . ^*)
           Qs                  S1 - S2

Bez přítomnosti zkratu je parametr Qp/Qs blízký jedné, hranice normálu je asi 1,15.
^*) Tento vztah platí pouze tehdy, když není přítomen pravo-levý (P-L) zkrat. Pokud se vyskytuje P-L zkrat, je třeba od primocirkulační plochy S1 odečíst frakci danou průtokem P-L zkratem: S1*(Qz_P-L/Qs), kde Qz_P-L je průtok P-L zkratem, Qs je systémový průtok. Obecný vztah pro poměr plicního a systémového průtoku tedy bude Qp/Qs = S1.(1-Qz_P-L/Qs)/(S1 - S2) .

Metoda odečtení systémové recirkulace není bohužel vždy použitelná. Někdy totiž vlna systémové recirkulace není na křivce pulmogramu dobře vyjádřena a nelze ji tudíž dobře proložit, extrapolovat a odečíst. V takovém případě jsme nuceni pokusit se zkratovou recirkulační vlnu vyextrahovat z počátečního úseku vzestupné části rozdílové křivky. Vhodně volenou částí tohoto úseku rozdílové křivky se metodou nejmenších čtverců proloží taková gama-funkce, jejíž vzestupná rychlost je dána gradientem počátečního růstu rozdílové křivky, avšak rychlostní koeficient sestupné části (která je překryta systémovou recirkulací a není vidět) se předpokládá stejný jako u předchozí gama-funkce prvního průtoku. Tato gama-funkce je pak považována za zkratovou recirkulační vlnu a plocha S2 pod ní je použita ke kvantifikaci zkratového průtoku Qz. Metoda bez odečtení systémové recirkulace se označuje jako metoda Maltze a Trevese. Přesnost a reprodukovatelnost této metody není většinou příliš dobrá. Dosti těžko se zde stanovuje úsek, který ještě není silně ovlivněn systémovou recirkulací. V našem programu RKG se koncový bod pro fitaci zkratové recirkulace stanovuje automaticky jako první maximum konvexnosti rozdílové křivky, samozřejmě s možností ručního posunu.

Metoda bez odečtení systémové recirkulace v každém případě více nebo méně nadhodnocuje zkrat. U normálů nebo slabých zkratů by tato chyba byla významná a znemožnila by nám spolehlivě rozhodnout o přítomnosti a velikosti takového (suspektního) zkratu. Naštěstí však v těchto případech bývá systémová recirkulační vlna většinou dobře vyjádřená a lze proto použít korektní metodu s odečtením systémové recirkulace. Systémovou recirkulaci nelze proložit a odečíst především u výraznějších zkratů, kdy vlna systémové recirkulace je překryta a zahlazena superpozicí postupně se opakujících a stále více rozmazaných vln zkratové recirkulace. V těchto případech však je však první zkratová recirkulační vlna podstatně větší než ta část systémové recirkulace, která by do ní mohla event. zasahovat, takže neodečtením systémové recirkulace se nedopouštíme významné chyby (pokud obezřetně stanovíme vzestupný úsek na rozdílové křivce pro fitaci zkratové gama-funkce).

Pravo-levý zkrat
Prokázání a kvantifikace levo-pravého (L-P) zkratu bývá nejčastější indikací pro bolusové radiokardiografické vyšetření. Méně časté jsou poruchy (převážně kongenitálního původu), při nichž část krve patologicky protéká z dutin pravého srdce přímo do dutin levého srdce aniž projde plicním oběhem (obr.3.2.3) - dochází k pravo-levému (P-L) zkratu a tím k předčasné recirkulaci neokysličené krve v systémovém oběhu. Při radiokardiografii tento zkratový průtok s sebou nese i část radioaktivity bolusu. Vede to k tomu, že se nám předčasně zobrazí levá komora zhruba ve stejné době (nebo dříve) než plíce, takže na křivce z levé komory se objeví předčasná (zkratová) vlna před hlavním primocirkulačním píkem, zhruba v čase kdy bolus dosáhl plic. Podobným způsobem se P-L zkrat projeví na křivce časového průběhu radioaktivity v aortě - před hlavním primocirkulačním píkem se objeví předčasná cirkulační vlna způsobená zkratem - obr.3.2.3b dole. Velikost této předčasné vlny v poměru k velikosti hlavní vlny systémové cirkulace je mírou závažnosti P-L zkratu - obr. 3.2.4b .

Podobně jako u L-P zkratu, i zde se zkratová a systémová cirkulace částečně překrývají a prolínají. Pro kvantifikaci zkratu je proto opět potřeba rozložit křivku z aorty na část odpovídající hlavnímu průtoku bolusu a na část reprezentující předčasnou (zkratovou) cirkulaci. Hlavním primocirkulačním píkem křivky z aorty se proloží gama funkce a extrapoluje se oběma směry. Tato gama-funkce představuje normální první průtok bolusu systémovou cirkulací a plocha S1 (integrál) pod ní je úměrná fyziologické frakci systémového průtoku Qs. Odečtením této fitované a extrapolované gama-funkce systémové cirkulace od původní křivky z aorty vzniká rozdílová křivka, na které již není pík systémové cirkulace, je zde pouze předčasná cirkulační vlna a směrem k vyšším časům se zvedá křivka běžné systémové recirkulace. Tato předčasná cirkulační vlna reprezentuje zkrat a plocha S2 (integrál) pod ní je úměrná průtoku Qz_P-L pravo-levým zkratem. Celková plocha S1+S2 pod oběma vlnami je úměrná celkovému systémovému průtoku Qs. Ke kvantifikaci P-L zkratu se používá poměr průtoků zkratovou a systémovou cirkulací :

           Qz_P-L                  S2
         ------     =     ------     100   [ % ]    .
             Qs                 S1 + S2

Tento parametr udává průtok Qz_P-L pravo-levým zkratem vyjádřený v procentech celkového systémového průtoku - obr. 3.2.4b .

Je třeba upozornit, že na statisticky značně fluktuující křivce z aorty je prokládání gama-funkcí a separace cirkulačních vln dosti problematické, takže kvantifikace P-L zkratu je podstatně obtížnější a méně přesná než je tomu u zkratů levo-pravých.

Nyní stručně popíšeme, jak je kvantifikace L-P zkratu realizována v programu RKG. Na křivce plic - pulmogramu se automaticky (s možností ruční modifikace) vymezí počáteční bod hlavního píku, vrchol a koncový bod primocirkulačního píku. Koncový bod primocirkulačního píku se vymezuje na sestupné části křivky v místě, kde se rychlost sestupu začíná zmenšovat (aby nebyla zahrnuta část zkratové cirkulace). Pokud máme podezření, že automaticky vymezený koncový bod je poněkud vpravo, doporučujeme jeho manuální posunutí do místa těsně za nejprudším sestupem křivky. Takto vymezeným úsekem hlavního píku se nejprve proloží gama-funkce a odečte se od původního pulmogramu. Vznikne rozdílová křivka zachycující jak systémovou, tak případnou zkratovou (a tedy předčasnou) recirkulaci. Objeví se dotaz, zda lze odečítat systémovou recirkulaci. Kladně odpovíme tehdy, když je systémová recirkulační vlna na křivce pulmogramu zřetelně vyjádřená (nesmíme zaměnit zkratovou a systémovou recirkulaci!). V tomto případě se automaticky vymezeným širokým píkem systémové recirkulace proloží další gama-funkce a odečte se od původní rozdílové křivky. Vznikne tím křivka zkratové recirkulace, z jejíž plochy (integrálu) vymezeného úseku (píku) se vypočte hodnota zkratu, tj. Qp/Qs a procento zkratového průtoku krve. Pokud není systémová recirkulace dobře patrná, odpovíme záporně. Na počátečním úseku rozdílové křivky se pak automaticky (s možností ruční modifikace) vymezuje počáteční bod zkratové recirkulace a koncový bod pro proložení gama-funkce. Takto vymezeným počátečním úsekem na rozdílové křivce se pak prokládá gama-funkce způsobem popsaným v teoretické části tohoto odstavce, jejíž plocha (integrál) kvantifikuje zkrat.

Matematická analýza L-P zkratu při vyhodnocení radionuklidové angiokardiografie

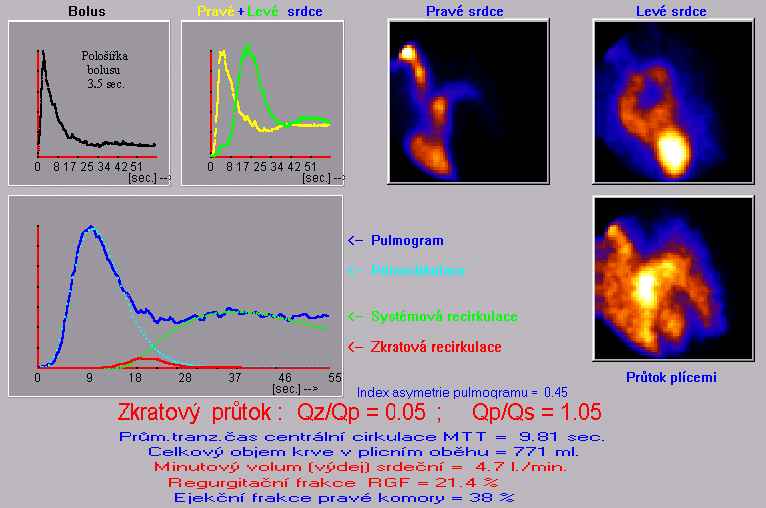
Rozkladem křivky pulmogramu na primocirkulaci, systémovou recirkulaci a předčasnou recirkulaci pozorujeme hemodynamicky významný levo-pravý zkrat. Porovnání křivek průchodu bolusu pravou síní a komorou svědčí pro zkrat na úrovni komorového septa.

Po skončení výpočtu se na obrazovce simultánně (s barevným odlišením) zobrazí křivka pulmogramu, rozložená na křivky primocirkulace, systémové a zkratové recirkulace, spolu s hodnotami nejdůležitějších vypočtených prametrů centrální hemodynamiky; pro dokumentaci můžeme vytisknout.

Závěrečný protokol
Na závěr se na displeji zobrazí sumární obraz obsahující křivky příchodu bolusu, pravého srdce, pulmogramu a levého srdce, obrazy pravého a levého srdce při průchodu bolusu, spolu s hodnotami vypočtených kvantitativních parametrů. V dolní části se zobrazí texty slovního hodnocení pro závěrečnou editaci (doplnění, reformulace) v konfrontaci s obrazy, křivkami a hodnotami kvantitativních parametrů. V tomto místě též vkládáme závěrečné hodnocení, popř. zkontrolujeme a upravíme automaticky vygenerovanou formulaci závěru. Takto připravený výsledný protokol se pak vytiskne na tiskárně v požadovaném počtu exemplářů - obr. 3.2.5 .

Matematická analýza a komplexní vyhodnocení radionuklidové angiokardiografie

Vizuální hodnocení : Po intrajugulární injekci bolusu radioindikátoru se zobrazují nezvětšené dutiny pravého srdce, následuje plnění nerozšířené plícnice a plicního řečiště, které se přiměřeně rychle vyprazdňují do normálně konfigurovaných dutin levého srdce a aorty. Během průchodu bolusu levým srdcem nepozorujeme předčasný výskyt radioindikátoru v pravém srdci a plících. Z á v ě r : Při vizuálním hodnocení sekvenčních scintigramů průchodu bolusu srdečním oběhem, ani při kvantitativní analýze cirkulačních křivek, nepozorujeme patologické změny centrální hemodynamiky.

Struktura programu
Program RKG se skládá z následujících částí (schopných samostatné funkce) :

RKG1 - zobrazení série snímků, vizuální hodnocení, vyznačování ROI, vytvoření křivek
RKG2 - matematické zpracování křivek: korekce na mrtvou dobu, expanze a komprese měřítka, výpočet cardiac output a ejekční frakce pravé komory
RKG3 - matemat. zprac. křivek: výpočet kardiopulmon. tranzitního času (MTT) a kvantifikace zkratu
RKG4 - zobrazení výsledků, editace slovního popisu a tisk protokolu

Z této struktury zároveň plyne, jak pokračovat při přerušení programu nebo při opětovném spuštění za účelem opakování určité části výpočtů. Chceme-li např. změnit pouze slovní hodnocení, stačí spustit RKG4. Pro opětovnou kvantifikaci zkratu nebo MTT spustíme od RKG3. Chceme-li znovu provést celé matematické zpracování křivek, spustíme program od RKG2. Pouze v případě, že chceme vyznačit jinak ROI, je nutno spustit program od začátku, tj. od RKG1.

Obsazení SAVE AREA po skončení programu :

SA1,2,3 - křivky časového průběhu radioaktivity ve vyznačených ROI
SA10 - obraz levého srdce
SA12 - obraz pravého srdce

Zpět: Seznam komplexních programů