 |
(5.21) |
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | Gravitace, černé díry a fyzika |
Kapitola 5
GRAVITACE
A GLOBÁLNÍ STRUKTURA VESMÍRU:
RELATIVISTICKÁ
KOSMOLOGIE
5.1. Základní východiska a principy
kosmologie
5.2. Einsteinův a deSitterův vesmír.
Kosmologická konstanta.
5.3. Fridmanovy dynamické modely vesmíru
5.4. Standardní kosmologický
model. Velký třesk.
5.5. Mikrofyzika a kosmologie.
Inflační vesmír.
5.6. Budoucnost
vesmíru. šipka času. Temná hmota. Temná energie
5.7. Antropický princip a
existence více vesmírů
5.8. Kosmologie a fyzika
5.3. Fridmanovy dynamické modely vesmíru
Je zřejmé, že reálný vesmír, alespoň v současném stádiu jeho vývoje, nelze popsat žádným z modelů založených na předpokladu statičnosti, protože v Einsteinově modelu není rudý posuv světla od vzdálených galaxií a v de Sitterově modelu zase prostor nemůže obsahovat žádnou látku ani záření. Pro modelování reálného vesmíru je proto třeba vzdát se předpokladu statičnosti (který je neslučitelný se současnými astronomickými poznatky) a vytvořit obecnější časově dynamický kosmologický model.
Metrika
nestacionárního homogenního izotropního vesmíru
Budeme tedy uvažovat homogenní izotropní vesmír, který
obecně nebude stacionární. Metrika trojrozměrného
prostoru (tj. prostorová část intervalu) v takovém případě bude mít
opět homogenní izotropní obecný tvar (5.4), avšak poloměr
křivosti a zde bude obecně funkcí času a(t) :
 |
(5.21) |
Připomeňme, že původně ve vztahu (5.4)
jsme jako "a" označili hodnotu křivosti prostoru
"R" (R :-> a). V aplikaci
na dynamický rozšiřující se vesmír však bude a(t) nabývat
význam měřítkového expanzního faktoru.
Délkový
element (5.21) se někdy upravuje na tvar v kartézských
souřadnicích,
v němž je úměrný příslušnému Eukleidovskému výrazu (je to však jen pro názornost, pro kosmologickou
analýzu to význam nemá). Lze to uskutečnit zavedením nové
souřadnice r pomocí transformace r
®
r/(1+r2/a2). Prostorová metrika
(5.21) pak má tvar
 |
. |
Prostorovou vztažnou soustavu je přirozené zvolit tak, aby odrážela izotropii prostoru i rozložení a pohybu hmoty. Nejvhodnější je tedy lokálně "souběžná" vztažná soustava pohybující se v každém místě prostoru spolu s hmotou, která je tam obsažena. Souřadnice jsou "unášeny" spolu s rozšiřováním. Lokální rychlost látky v takové soustavě je tedy všude rovna nule, vztažnou soustavu tvoří samotná hmota vyplňující vesmír. Veškerý pohyb hmoty je vyjádřen deformací vztažné soustavy (kosmologický "měkýš"). Sféricky symetrický souřadnicový systém je tedy vhodné transformovat tak, že původní radiální souřadnici r nahradíme souběžnou souřadnicí: r(t) ®r(t).a(t). Neboli, jelikož poloměr křivosti a může být použit jako přirozená jednotka pro měření vzdálenosti, je výhodné zavést nové bezrozměrné souřadnice r®r/a , ve kterých má délkový element tvar
| (5.21') |
Vzdálenost dl mezi
libovolnými blízkými body je tedy úměrná a(t) - měřítkovému faktoru, takže růst nebo pokles a(t) s
časem znamená zvětšování nebo zmenšování všech
vzdáleností v soustavě - rozšiřování nebo smršťování
veškeré hmoty unášené vesmírným prostorem (srov. diskusi v §5.4, pasáž
"Co se rozpíná při expanzi
vesmíru? (a co se nerozpíná)").
Časovou souřadnici je vhodné zvolit
tak, aby v každém okamžiku metrika prostoru byla stejná ve
všech bodech a ve všech směrech. Aby všechny směry byly
ekvivalentní, komponenty goa metrického tenzoru musejí být v
této vztažné soustavě rovny nule. Prostoročasová
metrika bude mít tedy tvar ds2 = goodx°2 + dl2. Koeficient goo je funkcí pouze x°, takže
vhodnou volbou časové souřadnice lze dosáhnout goo=-1 (=-c2). Časová souřadnice x°,
kterou můžeme označit t, pak udává vlastní čas v
každém bodě prostoru. Prostoročasový interval zde bude mít
jednoduchý tvar ds2 = -c2dt2 + dl2.
Prostoročasová
geometrie
homogenního izotropního vesmíru může být tedy obecně
napsána ve tvaru tzv. Robertsonovy-Walkerovy-Fridmanovy
metriky :
| (5.22) |
kde a(t) je měřítkový faktor, k je
parametr typu křivosti prostoru a r je radiální
souřadnice ve shora zmíněné "souběžné -
souputující" vztažné soustavě, ve sférických
souřadnicích (r, J, j) s
počátkem r=0 v libovolném bodě. Veškerá časová závislost
- evoluce vesmíru - je zde obsažena pouze v měřítkovém
faktoru a(t).
H.P.Robertson a A.G.Walker již v polovině 30.let ukázali, že
výraz typu (5.22) je nejobecnější metrikou která
může popisovat expandující homogenní a izotropní vesmír.
Pro
stanovení časového vývoje a(t) použijeme Einsteinových
rovnic, kam dosadíme potřebné komponenty Ricciho tenzoru
křivosti Rik a skalární křivosti R, které vypočítáme z
metriky (5.22) (použitím metod z §2.4) . Nenulové komponenty zde jsou :
Rtt
= -3.ä/a ; Rrr = [(a.ä + 2..a2)/c2 + 2k]/(1-kr2) ; RJJ = r2.[(a.ä + 2..a2)/c2+ 2k] ; Rjj = r2.[(a.ä + 2..a2)/c2+ 2k].sin2J ;
R = 6.[ä/(c2.a) + .a2/(c2.a2) + k/a2] ,
kde každá tečka nad a znamená derivaci podle času t.
Fridmanovy rovnice evoluce
vesmíru
Rovnice evoluce vesmíru plynou z obecné Einsteinovy rovnice
(5.7) Rik - 1/2 gik R - L.gik = 8pTik , kam dosadíme komponenty
tenzoru energie-hybnosti Tik, komponenty metrického tenzoru gik a Ricciho tenzoru křivosti Rik pro metriku (5.22) (vypočítané
výše). Tenzor
energie-hybnosti Tik kosmologického
"plynu" (3.3) ve všude lokálně klidové vztažné
soustavě má nenulové komponenty pouze Too = r.c2, T11 = T22= T33 = -p, přičemž v homogenním a
izotropním vesmíru mohou být hustota r a
tlak p funkcemi pouze času t. Einsteinovy rovnice (5.7) pro
metriku (5.22) pak vedou po úpravě ke dvěma diferenciálním
rovnicím - jsou to důležité
| Fridmanovy rovnice : |
 |
(5.23a) (5.23b) |
které jsou základem relativistické kosmologie. Spolu se stavovou rovnicí p = p(r) kosmologicke látky (plynu, kapaliny, plasmy, záření) tyto rovnice umožňují určit a, p, r jako funkce času t, tj. určit evoluci vesmíru. Každá tečka nad a značí derivaci podle času. Obě tyto rovnice spolu souvisejí identitou
| d(r.c2 a3) / dt = - p . d(a3) / dt , | (5.23c) |
která je vyjádřením
lokálního zákona zachování energie.
Ortografická poznámka :
V literatuře se většinou autorovo jméno píše "Friedmann",
avšak petrohradský autor kosmologických rovnic se ve
skutečnosti psal "Fridman" (![]() ).
).
Základní kosmologické rovnice (5.23) se v též uvádějí pod
zkratkou FLRW (Fridman–Lemaitre–Robertson–Walker)
rovnice, podle jmen autorů kteří se v letech 1920-30 zabývali
analýzou dynamiky relativistických kosmologických modelů.
Fridmanovy rovnice (5.23)
jsou přesným řešením Einsteinových rovnic
obecné teorie relativity pro homogenní a izotropní vesmír s
Robertson-Walkerovou metrikou (5.22), zaplněný látkou s
hustotou r, vykazující tlak p (podle
příslušné stavové rovnice), s tenzorem
energie-hybnosti (5.3).
V relativistické kosmologii se často místo absolutních hodnot časových změn měřítkového faktoru .a=da/dt , ä=d2a/dt2 zavádějí relativní veličiny od nich odvozené, které mohou být (aspoň v principu) přímo změřeny z astronomických pozorování. Jako míra relativní rychlosti změny poloměru křivosti, tj. míra expanze (nebo hypoteticky i komprese), se používá Hubbleova konstanta H *); výstižnější název by měl být Hubblův rychlostní parametr :
| H =def .a(t) / a(t) . | (5.24) |
*) Veličina H se označuje za "konstantu" pouze v tom smyslu, že je stejná pro všechna místa (nezávisí na souřadnicích); obecně však je funkcí času H(t). Výstižnější název je proto Hubbleův parametr. Nynější hodnota Hubbleovy konstanty H0 se odhadovala většinou v rozmezí H0 ~ (50 ÷100) km s-1/megaparsec. Novější astronomická měření udávají upřesněnou hodnotu :
| H0 ~ 70 km s-1 / megaparsec . | (5.24´) |
Vedle "klasické" Hubbleovy konstanty H0 se někdy používá i tzv. redukovaná bezrozměrná Hubbleova konstanta h, normalizovaná na rychlost 100 km s-1 / Mpc. :
| h =def H0 / 100 km s-1 / Mpc . | (5.24´´) |
Hubbův parametr H byl zaveden již v
§5.1, vztah (5.2), jako koeficient úměrnosti
v Hubbleově expanzním zákonu, který určuje o kolik se
zvětší rychlost vzdalování [km/s] vzdáleného kosmického
objektu (galaxie), když jeho vzdálenost vzroste o 1 megaparsek:
v = H . r, kde r je vzdálenost a v
rychlost vzdalování. Rychlost vzdalování se astronomicky
měří na základě Dopplerova jevu pomocí rudého posuvu
z = Dl/l - relativního
přírustku vlnové délky l záření této galaxie: pro z<1 je přibližně v ~
c . z; přesný vztah mezi rychlostí
vzdalování a rudým posuvem je v = c . [(z+1)2-1]/[(z+1)2+1].
Dále se zavádí tzv. decelerační parametr q
| q =def a . ä / .a2 | (5.25) |
charakterizující zpomalování nebo zrychlování expanze nebo kontrakce. Pomocí veličin H a q lze Fridmanovy rovnice (5.23a,b) vyjádřit ve tvaru
| k.c2/a2 = 8pGr/3 - H2 + L.c2/3 , k.c2/a2 = (2 q - 1) H2 + L.c2 . | (5.23'a,b) |
Dynamika a
evoluce kosmologických modelů
Pomocí Fridmanových rovnic lze analyzovat dynamiku expanze a(t)
vesmíru v závislosti na hustotě hmoty hmoty r, její stavové rovnici p(r) a kosmologické konstantě L. Všimněme si nejprve jednoduššího
případu L = 0, bez kosmologické konstanty :
Z rovnice (5.23'a) je vidět, že o tom,
která z variant k = 1 , 0 , -1 se může realizovat, rozhoduje
znaménko 8pGr/3 -
H2, tj. vztah mezi hustotou hmoty a
rychlostí expanze.
Případ k = 1 odpovídající uzavřenému vesmíru nastává tehdy, když 8pGr/3 > H2 , tj. když střední hustota
hmoty r ve vesmíru je větší než určitá
"kritická hustota"
rkrit
| rkrit = 3 H2 / 8p G . | (5.26) |
Na základě v
současnosti pozorovaných rychlostí vzdalování galaxií
(Hubbleovy konstanty) je tato kritická hustota přibližně 8.10-30 g/cm3, což odpovídá jen asi 5
atomům vodíku na 1m3.
Jestliže r <
rkrit, je k =
-1 - jedná se o
otevřený vesmír, v hraničním případě r=rkrit máme k = 0 - odpovídá Eukleidovskému vesmíru, který je rovněž otevřený.
Rovnice (5.23b) ukazuje, že ekvivalentním kritériem charakteru
křivosti Fridmanova vesmíru je hodnota deceleračního
parametru q : v uzavřeném vesmíru je q > 1/2, v
otevřeném q < 1/2 a Eukleidovskému vesmíru odpovídá q =
1/2. Tyto varianty budou podrobněji analyzovány níže.
V mezním případě r =rkrit bude k = 0, vesmír má nekonečně velký poloměr křivosti - jedná se o model otevřeného vesmíru s plochým prostorem (Eukleidovým). Prostoročasová metrika zde má jednoduchý tvar
| ds2 = - c2 dt2 + a2(t).(dx2 + dy2 + dz2) , | (5.27) |
přičemž časově
proměnný koeficient a(t) nevyjadřuje zakřivení prostoru, ale
jedná se jen o měřítkový faktor.
Je třeba upozornit
na to, že i když pro r=rkrit vychází Eukleidova metrika
trojrozměrného prostoru, celý čtyřrozměrný prostoročas
zde není plochý! Ploché jsou pouze určité speciální řezy
(nadplochy) prostoročasu, odpovídající stejnému vlastnímu
času všech částic vyplňujících vesmír.
Fridmanovy rovnice mají přesné
analytické řešení v případě vesmíru zaplněného "ideální kapalinou" se stavovou rovnicí
| p = w . c2. r , | (5.28) |
kde p je tlak, r je hustota hmoty-energie tekutiny (v lokálně klidové souběžné vztažné soustavě) a w je stavová konstanta. Tenzor energie-hybnosti Tik byl uveden v §5.1, vztah (5.3). Časová závislost měřítkové funkce a(t) se pak získá dosazením p do Fridmanovy rovnice (5.23a). V našem případě k=0 má jednoduchý tvar
| a(t) = a0 . t 2/[3(w+1)] , | (5.29) |
kde a0 je příslušná integrační konstanta závislá na
počátečních podmínkách. Můžeme zde rozlišovat dva
základní případy :
w = 0 je odpovídá nekoherentnímu prachu nevytvářejícímu žádný tlak, p=0.
Vesmír je ovládaný hmotou, kde tlak je vzhledem k hustotě
hmoty zanedbatelný - odpovídá pozdním fázím evoluce. Pak z
obecného řešení (5.29) vychází, že vzdálenost mezi
každými dvěma body roste s časem podle
zákona
| a(t) = a1 . t2/3 , a1 = ...... | (5.30) |
w = 1/3 - radiačně dominantní vesmír. V raných stádiích evoluce vesmíru, kdy je třeba uvažovat maximální tlak p=r.c2/3, z (5.29) pro expanzi dostáváme časovou závislost tvaru
| a(t) = a2 . t1/2 . a2 = ...... | (5.31) |
V obou případech vesmíru s dominantní látkou či zářením při r =rkrit závislost a = a(t) zde má tvar paraboly (obr.5.3a) - poloměr křivosti a monotónně roste od nuly (singularita!) při t = 0 do nekonečna při t®Ą.
Jestliže r > rkrit, je k= 1 - jedná se o uzavřený vesmír. Rovnice (5.23a) pro k=1, L=0 má tvar .a2 + 1 = a2. 8pGr/3. V případě, že vesmír je zaplněn nekoherentním prachem, tj. p = 0, plyne z rovnice (5.23c) r.a3 = const.; jelikož objem uzavřeného vesmíru je V = 2p2a3, je součet hmotnosti v celém prostoru konstantní :
| r . 2p2 a3 = M = const. = 2p2ao3 ro , | (5.32) |
kde ao a ro jsou poloměr a hustota hmoty vesmíru v
nějakém pevném časovém okamžiku to.
Funkce a(t) se často vyjadřuje v
parametrickém tvaru. Po zavedení nové "časové"
proměnné h substitucí dh=a.dt lze řešení rovnice (5.23a) napsat
v parametrickém tvaru
| a = (4GM/6pc2).(1 - cos h) , t = (4GM/6pc2).(h - sin h) . | (5.33) |
Grafické znázornění časové závislosti a = a(t) je tedy cykloida (obr.5.3a), kterou opisuje pevný bod na kružnici o poloměru
| amax = 4GM / 3pc2 | (5.34) |
při jejím valení po
přímce (časové ose t); parametr h je
úhel valení. Hustota hmoty se přitom mění podle zákona r = 3/a2max(1 - cos h)3 = 6H2/8pG(1+cos h). Ve Friedmanově modelu
uzavřeného vesmíru zaplněného prachem s hustotou r > rkrit tedy evoluce vypadá tak
(obr.5.2), že na počátku t=0 vesmír
vychází z počátečního singulárního stavu a = 0 s nulovým objemem a
nekonečnou hustotou hmoty, postupně se rozšiřuje až do
rozměru a = amax, a potom se opět smršťuje do
bodu a = 0 - koncové singularity.
Podle levé části obr.5.2 se evoluce vesmíru často modeluje nafukujícím
se balónkem (a posléze smršťujícím se) , na jehož
povrchu jsou nakresleny galaxie či kupy galaxií. Při takovém
nafukování balónku se všechny body jeho povrchu od sebe vzdalují
rychlostí úměrnou jejich vzájemné vzdálenosti, ve shodě s
Hubbleovým zákonem (5.2). Kritické posouzení a upřesnění
tohoto modelu bude diskutováno v následujícím §5.4, pasáž
"Co se vlastně rozpíná?"

Obr.5.2. Časová evoluce uzavřeného vesmíru.
Vlevo:
Uzavřený Fridmanovský vesmír si lze představit jako
trojrozměrnou sféru, která se postupně "nafukuje"
od nulového poloměru (iniciální singularita v čase t=0) do
jistého maximálního poloměru, a pak se zase smršťuje do
bodu (koncová singularita). Veškeré vzdálenosti Dl
mezi libovolnými objekty (galaxiemi, resp. kupami galaxií) se
při expanzi nebo kontrakci vesmíru zvětšují nebo zmenšují
úměrně poloměru křivosti.
Uprostřed:
Prostoročasový diagram uzavřeného vesmíru vnořený do
fiktivního pětirozměrného prostoru.
Vpravo:
Názorné zobrazení rozpínající a smršťující se hmoty
během evoluce vesmíru.
Ve stádiích a® 0, tj. na počátku a na konci evoluce, však předpoklad stavové rovnice nekoherentního prachu není realistický. Naopak, látka se zde nutně stává ultrarelativistickou, takže blíže skutečnosti bude stavová rovnice p = r.c2/3. Rovnice (5.23c) pak dává r.a4= const. a řešení rovnice (5.23a) zde je
| a = a~ . sin h , t = a~ . (1 - cos h) / c |
(grafem je polokružnice), kde a~ = Ö(8pG.ra4/3c4) = const. = Ö(8pG.roao4/3c4). Globální charakter evoluce bude stejný jako v předchozím případě - žádný tlak látky vyplňující uzavřený vesmír není schopen singulárním bodům a = 0 zabránit.
Jestliže r < rkrit, je k= -1 - jedná se o otevřený vesmír. Pokud je zaplněn prachem, je řešení rovnice (5.23a)
| a = â . (cosh h - 1) , t = â . (sinh h - h) / c , |
kde â = 8pG.ra3/3c2 = const. = 8pG.roao3/3c2). Závislost a = a(t) zde má tvar hyperboly (obr.5.3a) - poloměr křivosti a monotónně roste od nuly (singularita!) při t = 0 do nekonečna při t®Ą. Podobný obraz se dostane i při zahrnutí vlivu tlaku; pro krajní případ p = r.c2/3 je řešení
| a = a~ . sinh h , t = a~ . (cosh h - 1) / c . |
Otevřený Friedmanův vesmír má tedy rovněž singularitu, avšak pouze jedinou - iniciální.
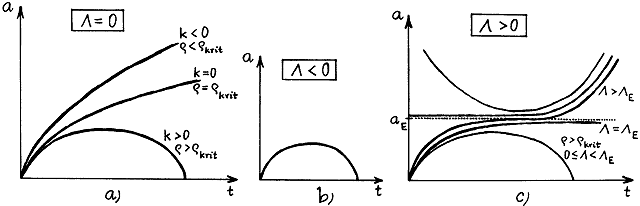
Obr.5.3. Evoluce kosmologických modelů (časový průběh
poloměru a vesmíru)
v závislosti na hodnotě kosmologické konstanty L a
hustotě rozložení hmoty r.
(aE a LE na obr.
vpravo značí hodnoty poloměru vesmíru a kosmologické
konstanty odpovídající Einsteinovu kosmologickému
modelu)
Při zahrnutí nenulové kosmologické konstanty L se
ve vesmíru objevuje navíc určitá přídavná
síla
(odpudivá pro L> 0 a přitažlivá při L< 0), která urychluje nebo zpomaluje
rozšiřování nebo smršťování vesmíru. Tato síla
nezávisí na hmotnosti a roste se vzdáleností. Z hlediska
globální evoluce vesmíru má efektivní
energie vakua, generovaná kosmologickým členem,
důležitou vlastnost (odlišnou od látkové formy hmoty) - nezřeďuje se ani nezhušťuje při rozšiřováví či
smršťování vesmíru, zachovává si konstantní hodnotu. Řešení rovnic (5.23)
pak při L ą 0 vede k následujícím
možnostem :
Pokud je L<0, vždy nakonec převáží přitažlivost a evoluce vesmíru má průběh
podle obr.5.3b při libovolném hustotě hmoty r. Tato varianta se se pravděpodobně ve
vesmíru neuplatňuje.
Pestřejší možnosti evoluce vesmíru
vznikají při L > 0 - jsou
znázorněny na obr.5.3c :
- Pokud
je kosmologická konstanta L<LE menší než Einsteinova hodnota (5.15) LE =4pGr/c2, bude pro nadkritickou hustotu r > rkrit evoluce vesmíru probíhat zhruba
(kvalitativně) stejně jako pro L= 0.
- Při
L>LE se a(t) zvětšuje od nuly do
nekonečna, avšak v určité fázi se expanze na čas výrazně zpomalí - dochází k jakési
"kvazistatické fázi", během níž jsou přitažlivé
síly vyváženy odpudivými ("nerozhodný" vesmír);
později převládnou síly odpudivé *). Doba trvání Tst této kvazistatické fáze, během
níž se poloměr křivosti vesmíru udržuje přibližně na
hodnotě poloměru Einsteinova statického modelu (5.16) a = aE , je tím
delší, čím menší je rozdíl L-LE : Tst ~ ln[L/(L-LE)].
- Při
L®LE se vesmír dostává do stavu Einsteinova
statického vesmíru zmíněného v předchozím odstavci. Tento
Einsteinův model je však nestabilní, protože sebenepatrnější
perturbace hustoty povede k expanzi.
Pro r>rkrit a L=LE existují dvě další řešení
:
1. V nekonečně vzdálené minulosti t®-Ą bylo a= aE, v budoucnu pak neomezená
expanze (nepravděpodobná varianta);
2. Vesmír vyšel v okamžiku t=0 ze stavu a(0)= 0, načež
expanduje a asymptoticky (v nekonečně vzdálené budoucnosti t®Ą) dosahuje poloměr a®aE.
Pro L> 0 existuje, kromě zmíněných
speciálních možností, též řešení, podle něhož při t=
-Ą měl vesmír nekonečný poloměr, pak
probíhala kontrakce do určité minimální
hodnoty amin, načež nastává
neohraničená expanze (nepravděpodobná
varianta).
Zmíněné zvláštnosti kosmologických
modelů s nenulovou kosmologickou konstantou se čas od
času používaly (a používají) při pokusech o překonání
domnělých či skutečných obtíží relativistické kosmologie
(vnitřních potíží i nesrovnalostí s výsledky pozorování)
- srov. ...... .
Tři základní dynamiky
měřítkového faktoru - shrnutí
Pro astrofyzikálně plausibilní scénář evoluce našeho
vesmíru (podle standardního modelu fyzikální kosmologie -
§5.4) by se v jednotlivých etapách evoluce měly uplatňovat
tři základní dynamiky - časové závislosti měřítkového
faktoru a = a(t), plynoucí z řešení Fridmanových rovnic
(5.23) :
- Éra
záření - radiačně dominantní plasmy,
kdy ve hmotném obsahu vesmíru dominuje záření a
relativistické částice, vzbuzující tlak p=r.c2/3. Časová
závislost měřítkové funkce a(t) pak je
a(t) ~ t
1/2 .
Tato situace byla v
raném horkém vesmíru (po inflační
expanzi) a trvala (v "čisté formě") cca 50 000 let.
- Éra látky
,
kdy hustota energie látky (nerelativistických
částic, plynu, prachu) je větší než energie záření . Časová závislost měřítkové funkce a(t) je zde
a(t) ~ t
2/3 .
Obě tyto
závislosti mají podobný parabolický
tvar podle
obr.5.3a (k>=0). Koeficienty úměrnosti závisejí na
konkrétním látkovém obsahu. Éra látky ve vesmíru trvá
stále i nyní...
- Stadium
vakuové energie - kosmologické konstanty
kdy hustota látky a záření je zanedbatelná ve srovnání s
vakuovou energií generovanou kosmologickým členem v
gravitačních rovnicích. Časová
závislost měřítkové funkce a(t) je pak exponenciální
a(t) ~ e H . t
~ e Ö(L/3)
. t
a fakticky
odpovídá speciálnímu případu de
Sitterova modelu.
V §5.5 "Mikrofyzika a kosmologie. Inflační vesmír." uvidíme, že k této
situaci pravděpodobně došlo ve velmi raném vesmíru, těsně
po velkém třesku v časovém rozmezí cca
10-36 ÷
10-32 sec. - inflační
expanze
raného vesmíru. A pak k ní možná dojde zase naopak ve velmi
vzdálené budoucnosti - akcelerovaná
expanze vesmíru, když hustota látky a záření
vlivem expanze vesmíru poklesne na velmi nízké koncentrace a
začne dominovat "temná energie" generovaná
kosmologickou konstantou (§5.6, část
"Temná energie a akcererovaná
expanze vesmíru") .?..
Relativní Omega-parametrizace
kosmologických modelů
Místo absolutních hodnot hustoty hmoty a kosmologické
konstanty se pro modelování evoluce vesmíru často
používají jejich bezrozměrné relativní
poměry W vzhledem k jejich příslušným
význačným (kritickým) hodnotám. Zavádí se poměr
skutečné hodnoty hustoty hmoty r
vzhlem ke kritické hustotě :
| WM =def r / rkrit ( = r . 8p G/3 H2 ) | (5.36) |
a poměr aktuální hodnoty kosmologické konstanty L k Einsteinově hodnotě :
| WL =def L / LE ( = L.c2/3H2 ) . | (5.37) |
Fridmanova rovnice (5.23a) vyjádřená pomocí parametrů W zní :
| k.c2/H2a2 = WM + WL - 1 . | (5.38) |
Decelerační parametr q, zavedený vztahem (5.25), se pomocí parametrů W vyjádří :
| q = WM /2 - WL . | (5.39) |
Pro WL= WM/2 probíhá rozpínání konstantní rychlostí, při WL< WM/2 se expanze
zpomaluje, při WL> WM/2 se rozpínání zrychluje.
Pomocí bezrozměrných hodnot W lze snadněji
testovat evoluci kosmologického modelu. Např. pro plochý model
je WM + WL = 1. Je
též možno konstruovat přehledné grafy chování
kosmologických modelů v souřadnicích, na jejichž osách se
vynášejí hodnoty WM a WL.
Někdy se zavádí ještě poněkud podrobnější
W-parametrizace
kosmologického modelu. Obecná hustota hmoty r (rM) se rozděluje na látku tvořenou nerelativistickými částicemi
rm
(především baryony - značí se
též rB) a relativistickými částicemi a zářením rrad (v raných etapách vesmíru je
to vysokoenergetické záření gama, značí se též rg). Pomocí W-parametru se dále vyjadřuje i parametr křivosti k.
Základní Fridmanova rovnice (5.23a) pro rychlost expanze
vesmíru se pak zapisuje ve tvaru :
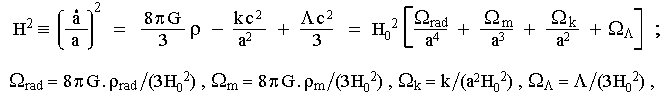 |
(5.40) |
kde Wxxx jsou příspěvky jednotlivých složek hmoty~energie k dynamice expanze: Wrad od relativistických částic a záření, Wm od nerelativistické hmoty, Wk od křivosti prostoru a WL od kosmologické konstanty - "energie vakua". Parametr H0 ~ 70 km s-1/Mpcs je současná hodnota Hubbleovy konstanty.
-----------------------------------------------------
Aktuální poznámka:
Podle posledních astronomických pozorování
vzdálených supernov se vyskytly určité indicie, že v
současné době dochází ke zrychlování expanze
vesmíru, že kromě temné (nezářící) látky se ve
vesmíru vyskytuje i tzv. temná energie, která
vykazuje "antigravitaci". Zdá se tedy, že evoluce
vesmíru probíhá podle křivky na obr.5.3c, případ L>LE (viz §5.6 "Budoucnost
vesmíru.Šipka času.", pasáž "Temná
energie a akcererovaná expanze vesmíru"),
odpovídá WL> WM/2 ...
| 5.2.
Einsteinův a deSitterův vesmír. Kosmologická konstanta. |
5.4. Standardní kosmologický
model. Velký třesk. |
| Gravitace, černé díry a fyzika prostoročasu : | ||
| Gravitace ve fyzice | Obecná teorie relativity | Geometrie a topologie |
| Černé díry | Relativistická kosmologie | Unitární teorie pole |
| Antropický princip aneb kosmický Bůh | ||
| Jaderná fyzika a fyzika ionizujícího záření | ||
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | ||