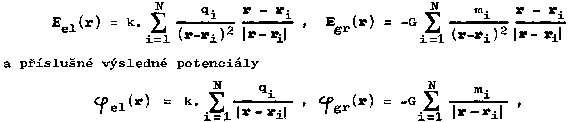 |
(1.25a,b) (1.26a,b) |
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | Gravitace, černé díry a fyzika |
Kapitola 1
GRAVITACE A JEJÍ MÍSTO VE FYZICE
1.1. Vývoj poznatků o přírodě,
vesmíru, gravitaci
1.2. Newtonův gravitační zákon
1.3. Mechanická LeSageova
hypothéza podstaty gravitace;
1.4. Analogie mezi gravitací a elektrostatikou
1.5. Elektromagnetické pole.
Maxwellovy rovnice.
1.6. Čtyřrozměrný prostoročas
a speciální teorie relativity
1.4. Analogie mezi gravitací a elektrostatikou
Newtonův gravitační zákon
| m l . m 2 Fgr = - G . ------------ . r° , r° = r / r , r2 |
(1.20a) |
o vzájemném silovém přitahování dvou těles hmotnosti m l a m 2 ve vzdálenosti r od sebe, se tvarem svého vzorce velice podobá jinému fundamentálnímu zákonu klasické fyziky - Coulombovu zákonu elektrostatiky
| q l . q 2 Fel = - k . ------------ . r° , r2 |
(1.20b) |
který vyjadřuje
vzájemné silové působení dvou (bodových) elektrických
nábojů q1 a q2 umístěných ve vakuu ve
vzdálenosti r od sebe. Hodnota konstanty k
závisí na použité soustavě jednotek. Ve fundamentální
fyzice se pokládá k=1 (čímž se přirozeně definuje jednotka
elektrického náboje pomocí jeho silového působení na
jednotkovou vzdálenost *), v soustavě SI je k = 8,988.109
N m2 C-2 a jednotkou elektrického
náboje je 1 Coulomb (C). Coulombův zákon
ve tvaru (1.20b) platí i v elektricky homogenním a izotropním látkovém
prostředí, přičemž konstanta úměrnosti k se
vyjadřuje ve tvaru k = 1/4pe, kde e je
permitivita (dielektrická konstanta) daného látkového
prostředí.
*) Historický vývoj fyziky však bohužel
vedl k tomu, že v soustavě jednotek SI není náboj primárně
kvantifikován pomocí svých elektrických silových účinků,
ale až zprostředkovaně pomocí magnetických účinků
elektrického proudu (jednotka Ampér; jeden Coulomb
je pak definován jako 1A/1s).
Pozn.: Vývoj poznatků o elektřině a
magnetismu je stručně nastíněn v §1.1 v pasáži "Elektrodynamika,
atomová fyzika, teorie relativity, kvantová fyzika".
Stojí tedy za to sledovat, kam až sahají analogie mezi elektřinou a gravitací. Newtonův a Coulombův zákon mají zcela stejný tvar, takže hmotnosti m1 a m2 dvou gravitujících těles můžeme nazvat jejich "gravitačními náboji". Všechny závěry o pohybu těles pod vlivem gravitace učiněné v §1.2 "Newtonův gravitační zákon" budou platit i o pohybech nabitých těles pod vlivem Coulombova elektrostatického pole. I zde se elektrické náboje pohybují po Keplerovských trajektoriích - obíhají po elipsách, přibližují a vzdalují se po hyperbolách nebo parabolách (nepřihlížíme zde zatím k radiačním efektům způsobeným vyzařováním elektromagnetických vln při nerovnoměrném pohybu elektrických nábojů).
Hned zde však narážíme na první důležitý rozdíl. Zatímco elektrické náboje mohou mít kladné i záporné znaménko (q >=< 0) a elektrostatická síla mezi nimi může být jak přitažlivá (mezi nesouhlasnými náboji) tak odpudivá (souhlasné náboje), je hmotnost vystupující v Newtonově zákoně vždy kladná (resp. nezáporná m ł 0) a gravitační síla je vždy přitažlivá. Tato fundamentální vlastnost gravitace, která je podle Einsteinových rovnic splněna i v obecné teorii relativity (ve všech fyzikálně reálných situacích, kdy tenzor energie-hybnosti je pozitivně definitní - §2.6 "Deviace a fokusace geodetik"), hraje zásadní roli v takových oblastech jako je fyzika černých děr (2.zákon dynamiky černých děr - viz §4.6 "Zákony dynamiky černých děr") nebo kosmologie (teorémy o singularitách - §3.8 "Hawkingovy a Penroseovy teorémy o singularitách", §3.9, kapitola 5 "Relativistická kosmologie").
Stejně jako v elektrostatice je pro vzájemné působení elektrických nábojů užitečné zavést pojem elektrické pole, je i v gravitaci výhodné popisovat vzájemné působení hmotných těles pomocí pojmu gravitační pole. Podle této koncepce každé hmotné těleso vytváří kolem sebe gravitační pole a toto pole pak vykazuje silové účinky na každé další těleso, které se do něho dostane.
Elektrické
a gravitační pole
Každé fyzikální pole je charakterizováno svým působením
na zkušební částice. V elektrostatice jsou
zkušebními částicemi elektricky nabitá tělíska, v
gravitaci to jsou dostatečně malá tělesa, která svými
vlastními účinky znatelně neovlivňují zkoumané
gravitační pole a jeho zdroje. Podobně jako elektrostatické
pole kvantifikujeme vektorem elektrické intenzity Eel, což je síla působící na
jednotkový zkušební náboj, tj.
| Fel = q . Eel , | (1.21a) |
lze gravitační pole popsat rovněž vektorem intenzity pole Egr udávajícím gravitační sílu působící na testovací částici jednotkové hmotnosti, tj.
| Egr = m . Egr . | (1.21b) |
Coulombův zákon je možno vyjádřit prostřednictvím intenzity elektrického pole Eel buzeného v prostoru kolem bodového elektrického náboje Q :
| Eel = k . Q / r2 . r° . | (1.22a) |
Newtonův gravitační zákon pak říká, že bodové těleso hmotnosti M budí kolem sebe centrální gravitační pole o intenzitě
| Egr = - G . M / r2 . r° . | (1.22b) |
Skutečnost, že jak elektrostatické, tak gravistatické pole je konzervativní, umožňuje vyjádřit intenzitu pole pomocí skalárního potenciálu j :
| Eel = - grad jel , Egr = grad jgr | (1.23a,b) |
Pro centrální pole bodového náboje Q nebo tělesa M je
| jel(r) = k . Q / r , resp. jgr(r) = - G . M / r . | (1.24a,b) |
Zkušenost učí, že pro silové působení soustavy většího počtu elektrických nábojů nebo gravitujících těles platí zákon superpozice, podle něhož účinek soustavy objektů (na danou zkušební částici) je roven součtu účinků každého objektu zvlášť, tj. pro soustavu N bodových nábojů nebo hmotných těles bude celková intenzita elektrického nebo gravitačního pole
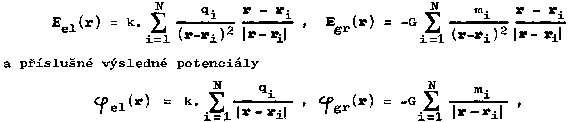 |
(1.25a,b) (1.26a,b) |
kde r je polohový vektor bodu v němž pole určujeme a ri jsou polohové vektory jednotlivých bodových nábojů qi nebo těles mi.
Pozdější rozvoj nauky o gravitaci však ukázal, že zde se skrývá druhý podstatný rozdíl mezi gravitací a elektřinou. Pro elektromagnetické jevy platí princip superpozice naprosto přesně i pro sebevětší náboje a sebesilnější pole. Pro gravitaci ale platí princip superpozice s dostatečnou přesností skutečně pouze v rámci Newtonova zákona, zatímco pro velká nahromadění hmoty a silná gravitační pole již splněn není. Tato nelineárnost souvisí s univerzálností gravitační interakce, jak bude ukázáno v §2.5 "Einsteinovy rovnice gravitačního pole".
Stejně jako je mnohdy užitečné místo soustavy velkého počtu diskrétních elektrických nábojů uvažovat spojité rozložení elektrického náboje s prostorovou hustotou rel = dQ/dV, tj. množství náboje Q obsažené v dané prostorové oblasti V vyjadřovat ve tvaru
| Q = Vňňň rel(x,y,z) dV , | (1.27a) |
zavádí se běžně v mechanice a gravitaci hustota spojitého rozložení hmotnosti r = dm/dV, takže celková hmotnost M obsažená v prostorové oblasti V je pak vyjádřena integrálem
| M = Vňňň r(x,y,z) dV . | (1.27b) |
Souvislost mezi modelem soustavy bodových nábojů qi a představou kontinuálního rozložení náboje se vyjadřuje pomocí Diracovy d-funkce: rel(r) = i=1SN qi.d(r-ri). Analogicky pro hmotnost. Pro spojitě rozložený náboj s hustotou rel(r) nebo pro spojitě rozloženou hmotu s hustotou r(r) pak vzhledem k principu superpozice výsledné elektrické nebo gravitační pole bude
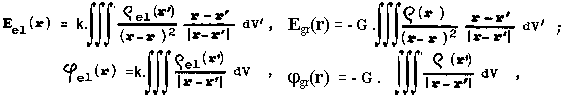 |
(1.25'a,b) (1.26'a,b) |
kde r' je polohový vektor integračního objemového elementu dV'.
Gaussova věta
elektrostatiky a gravitace
Coulombův i Newtonův zákon se dají formulovat ve tvaru Gaussovy věty (obr.1.3a)
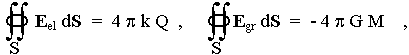 |
(1.28a,b) |
podle níž tok vektoru intenzity pole E přes uzavřenou plochu S je dán celkovým nábojem Q, resp. celkovou hmotností M, obsaženou uvnitř této plochy. Vyjádřením náboje a hmotnosti pomocí integrálů jejich hustoty a užitím Gaussovy věty vektorové analýzy lze vztahy (1.28a,b) přepsat v diferenciálním tvaru
| div Eel = 4p k rel , div Egr = - 4p G r , | (1.28'a,b) |
který říká, že výtok vektoru intenzity pole z jednotkového objemu je dán místní hustotou náboje nebo hmotnosti. Vyjádřením intenzity pole pomocí gradientu potenciálu (1.23) vznikne Poissonova diferenciální rovnice druhého řádu pro potenciál :
| Djel = - 4p k rel , Djgr = 4p G r , | (1.28''a,b) |
kde D ş ¶2/¶x2 + ¶2/¶y2 + ¶2/¶z2 je Laplaceův diferencialní operátor.
Newtonova rovnice pohybu tělesa o hmotnosti m a elektrickém náboji q v elektrickém poli má tvar
| d2r / dt2 = (q/m) . grad jel . | (1.29a) |
zatímco při pohybu v gravitačním poli se hmotnost na obou stranách vykrátí (o rovnosti setrvačné a tíhové hmotnosti, umožňující toto vykrácení, viz §2.2 "Univerzálnost - základní vlastnost a klíč k pochopení podstaty gravitace") :
| d2r / dt2 = grad jgr . | (1.29b) |
Zásadní rozdíl mezi pohybem v elektrickém a v gravitačním poli spočívá v tom, že v elektrickém poli se různá tělesa pohybují různě podle hodnoty svého specifického náboje q/m, zatímco v gravitačním poli trajektorie tělesa nezávisí na žádných individuálních charakteristikách pohybujícího se tělesa - je univerzální vlastností pouze samotného pole jgr(r). Pohybová rovnice (1.29b) je tak vyjádřením univerzálnosti gravitačního působení, která bude v dalším relativistickém popisu gravitace hrát klíčovou roli.
Gravitoelektromagnetismus
?
Elektrostatické pole je speciálním případem obecného pole elektromagnetického (viz následující §1.5 "Elektromagnetické pole. Maxwellovy
rovnice"), které vládne v naší okolní
přírodě, běžném životě, chemii, atomové a jaderné
fyzice a do značné míry i v astrofyzice. Vzniká tak otázka,
zda analogiie mezi Newtonovskou gravitací a elektrostatikou
pokračují i do oblasti dynamických
projevů elektřiny - do elektromagnetismu?
V rámci obecné teorie relativity si
ukážeme, že opravdu existují některé formální
analogie mezi
rovnicemi elektromagnetismu (Maxwellovými
rovnicemi) a
speciálními aproximacemi Einsteinových
gravitačních rovnic v OTR. Tato analogie se označuje jako gravitoelektromagnetismus - některé specifické
kinematické účinky gravitace jsou analogické magnetickým
účinkům pohybujících se nábojů. Jedná se především o
efekt strhávání těles do směru
rotace zdroje
gravitačního pole (Lense-Thirringův
jev - §2.5, pasáž "Rotující gravitace"),
který poněkud připomíná magnetismus. U těchto gravidynamických efektů lze vystopovat určitou analogii s magnetismem v elektrodynamice. Pomocí
speciálních "účelových" transformací lze
Einsteinovy gravitační rovnice upravit do tvaru rovnic
elektromagnetismu.
Z objektivního pohledu jsou však tyto
analogie pouze formální, s malým fyzikálním
významem. Jevy zdánlivě připomínající magnetismus jsou zde
druhého a vyššího řádu ve srovnání s primárním
gravitačním ("gravistatickým") působením.
Skutečný fyzikální magnetismus, způsobený interakcí
pohybujících se "nábojů" - zdrojů pole - v gravitaci obsažen není...
Pozn.: Za magnetismus
v gravitaci by mohly být považovány i známé Coriolisovy
síly Fc=-2m.[v´w ] , které připomínají magnetickou Lorentzovu sílu
Fm= (1/c).q . [ v ´ B ] působící
při pohybu elektrického náboje q rychlostí v
v magnetickém poli intenzity (indukce) B. Tyto
síly jsou však ve skutečnosti kinematickým efektem v
rotující vztažné soustavě (úhlovou rychlostí w),
nastávajícím i v rámci klasické Newtonovy mechaniky...
| Gravitace, černé díry a fyzika prostoročasu : | ||
| Gravitace ve fyzice | Obecná teorie relativity | Geometrie a topologie |
| Černé díry | Relativistická kosmologie | Unitární teorie pole |
| Antropický princip aneb kosmický Bůh | ||
| Jaderná fyzika a fyzika ionizujícího záření | ||
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | ||