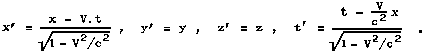h1{font-size:18px;}
Prostor - čas - relativita
Kapitola 1
GRAVITACE A JEJÍ MÍSTO VE FYZICE
1.1. Historický vývoj poznatků o
gravitaci
1.2. Newtonův gravitační zákon
1.3. Mechanická LeSageova
hypothéza podstaty gravitace;
1.4. Analogie mezi gravitací a
elektrostatikou
1.5. Elektromagnetické pole.
Maxwellovy rovnice.
1.6. Čtyřrozměrný prostoročas a speciální teorie
relativity
1.6.
Čtyřrozměrný prostoročas a speciální teorie relativity
Prostoročas a relativita
Budeme
předpokládat, že čtenář je obeznámen se základy speciální teorie relativity (STR), nebo o ní má aspoň
určité povědomí *). Pro ucelenost a kompaktnost knihy však
zařazujeme odstavec se stručným výkladem speciální teorie
relativity z poněkud obecnějšího
pohledu,
směřujícího k teorii prostoru, času, elektromagnetismu a
především gravitace.
*) Základy STR jsou nyní začleněny i do
osnov středoškolské fyziky. K podrobnějšímu studiu STR lze
doporučit především skvělou monografii V.Votruby [263],
dále pak příslušné kapitoly v [183],[250],[271],[135], atd.
Cílem této kapitoly není podrobný a ucelený výklad
speciální teorie relativity, ale spíše připomenout a
zdůraznit klíčové prvky logické
stavby relativistické fyziky a dát přehled základních pojmů,
jevů a vztahů speciální teorie relativity, na které se
budeme v dalším odkazovat. Seznámíme se zde rovněž s
geometrickými vlastnostmi 4-rozměrného prostoročasu a podáme
si 4-rozměrnou tenzorovou
formulaci
zákonů mechaniky a elektrodynamiky; toto bude v dalších
kapitolách často používáno z hlediska obecné
teorie relativity, astrofyziky a kosmologie.
Body a
události v prostoru a čase
Z
faktografického hlediska lze přírodu považovat za svět
událostí: každý fyzikální děj si můžeme rozdělit na
posloupnost jednotlivých elementárních událostí. Událostí je např. srážka
dvou částic, rozpad jádra atomu, bliknutí baterky. Pohyb
testovací částice je sledem událostí "částice se v určitém okamžiku nachází v
určitém místě". Zkušenost nás učí, že každá
událost může být zcela a jednoznačně charakterizována
čtyřmi čísly: místem
"kde" se
stala (3 prostorové souřadnice x,y,z *) a časem "kdy" se stala (časový okamžik t).
*) Číselné hodnoty a geometrický
význam těchto souřadnic, neboli koordinát,
jednotlivých bodů závisí na použité souřadnicové
soustavě. Nejpoužívanější je ortonormální tzv. kartézská
souřadnicová soustava, kterou pro dvojrozměrný případ
roviny zavedl René Descartes (1596-1650); název "kartézská"
souvisí s latinským přepisem Descartesova jména "Cartesius".
Tuto soustavu tvoří navzájem kolmé přímky X,Y,Z - osy,
protínající se ve společném bodě zvaném počátek
souřadnicové soustavy O (z lat. Origin). Poloha
(x,y,z) libovolného bodu P(x,y,z) je zde dána průsečíky
kolmic, spuštěných z tohoto bodu k jednotlivým osám X,Y,Z;
počátku O přiřazujeme nulové hodnoty souřadnic x=y=z=0.
Orientovanou spojnici r z počátku O do bodu P
nazýváme průvodičem či polohovým vektorem
(rádius-vektor) bodu P (o vektorech viz níže).
V dalším výkladu se setkáme i s obecnějšími
souřadnicovými soustavami - přímkovými kosoúhlými
souřadnicemi (viz níže pasáž "Lorentzovy transformace a
relativistická kinematika", obr.1.5c) a především s křivočarými
souřadnicemi (téměř celý zbytek knihy, počínaje §2.1),
kde poloha bodů je určena průsečíky přesně definovaných
křivek. Nejčastějšími příklady křivočarých souřadnic v
rovině jsou polární souřadnice (r,j), v prostoru pak sférické
(kulové) souřadnice (r,J,j) - viz §3.2, §3.4.
Transformace
souřadnic. Skaláry, vektory, tenzory.
Volba počátku, orientace a měřítka souřadnicových os je
zcela libovolná; je zpravidla motivována jen co největší
jednoduchostí vyjádření studované úlohy. Obecně se však
setkáváme se souřadnicovými systémy, jejichž počátky jsou
vůči sobě posunuty, osy jsou vzájemně pootočeny, měřítka
na osách jsou jiná. Potřebujeme pak najít převodové - transformační
- vztahy mezi souřadnicemi bodů a dalšími veličinami,
vyjádřenými v obou soustavách S a S'.
Přepočet hodnot souřadnic bodů, vyjádřených v různých
souřadnicových soustavách, se provádí pomocí
algebraicko-geometrických vztahů, plynoucích z analýzy
pozičních vztahů mezi souřadnicovými osami. V případě
pouhého posunu (translace) počátků O, O'
souřadnicové soustavy o (xo,yo,zo) jsou vztahy mezi souřadnicemi x,y,z a x',y',z' dány
jednoduše x'=x-xo, y'=y-yo, z'=z-zo. Při rotaci kartézské vztažné soustavy o
určitý úhel a kolem některé osy jsou transformační vztahy dány
sinusy a kosinusy úhlu rotace, např. kolem osy Z: x' = x.cosa + y.sina, y' = -x.sina + y.cosa, z'=z. Toto je
příkladem lineárních transformací souřadnic.
Pro kompaktnější zápis transformačních vztahů je výhodné
souřadnice označovat nikoli různými písmeny (x,y,z), ale
různými indexy: (x1,x2,x3). Lineární transformaci pak lze vyjádřit rovnicí
x'i = j=1S3aij.xj , i=1,2,3. Ještě kompaktnější zápis dostaneme
zavedením tzv. Einsteinovy sumační konvence:
vyskytne-li se ve výrazu nějaký index dvakrát, znamená to sumaci
přes tento index, aniž vypisujeme sumační znak "S" a sumační
meze (j=1,2,3 v trojrozměrném prostoru). Uvedenou
transformační rovnici tedy zapíšeme x'i = aij.xj ; je ještě zvykem sumační indexy psát jeden dole a
jeden nahoře (zde je to jen formální, svůj význam to má u
tzv. kovariantních a kontravariantních složek vektorů a
tenzorů, viz níže "Čtyřrozměrné vektory a
tenzory"). Transformační rovnice x'i = aij.xj popisuje i obecné transformace mezi křivočarými
souřadnicemi, přičemž ovšem koeficienty aij nejsou konstantní,
ale jsou funkcemi místa (souřadnic) - viz §2.4.
Matematické a fyzikální veličiny můžeme klasifikovat podle
jejich chování při transformaci souřadnic:
¨ Skalárem nazýváne takovou
veličinu, která nezávisí na volbě souřadnicové soustavy -
je invariantní (neměnná) při transformaci
souřadnic. Číselná hodnota skalární fyzikální veličiny
může záviset pouze na volbě použitých jednotek (odtud
pochází název: lat. scala = stupnice, žebřík).
¨ Vektory jsou v klasické fyzice
označovány veličiny, které kromě své velikosti mají i
určitý směr v prostoru (lat. vector = jezdec,
nosič). Zapisuje se tučným písmem či šipou nad znakem,
znázorňuje se šipkou v prostoru; kolmé průměty jeho délky
do souřadnicových os tvoří složky vektoru.
Typickými příklady je polohový vektor (průvodič,
radius-vektor) určitého bodu r o složkách (x1,x2,x3), rychlost v
o složkách vişdxi/dt, hybnost p
o složkách pişm.vi, zrychlení a
o složkách aişdvi/dt, síla F
o složkách Fişdpi/dt. Jelikož směr je
spojen s volbou vztažné souřadnicové soustavy, jeho složky
se transformují stejně jako souřadnice. Z tohoto hlediska tedy
definujeme vektor A jako trojici
veličin A1,
A2, A3 (složky
neboli komponenty vektoru), která se při transformaci
souřadnic x'i = aij.xj transformuje stejně jako souřadnice: A'i = aij.Aj. Délka, neboli
absolutní hodnota či velikost vektoru, je veličina A ş |A| ş (Ai.Ai)1/2, která je skalárem.
¨ Tenzory se nazývají soubory
veličin, které se při transformacích souřadnic transformují
jako součiny souřadnic. Tenzor druhého řádu
nazýváme soubor veličin Tij, které se při transformacích souřadnic x'i = aik.xk transformují podle
zákona T'ij = aik.ajl.Tkl (sčítá se přes k,l). Tenzory jsou zobecněním
vektorů a popisují veličiny, které jsou tvořeny součiny
komponent vektorů (jako je moment hybnosti či kvadrupólový
moment). Název "tenzor" pochází z
latinského slova tensio = napětí; nejprve se
používaly k popisu deformací těles působením vektoru síly
na vektorově orientovaný plošný element. Analogicky se
definují tenzory vyšších řádů.
4-rozměrný prostoročas
Z matematického
hlediska lze tedy každou událost zobrazit jako bod v myšleném
čtyřrozměrném prostoru, tzv. prostoročasu
(časoprostoru), na jehož osách se vynášejí tři prostorové
souřadnice a čas; body (události) v prostoročasu se nazývají světobody. Pohybu částice pak
odpovídá určitá čára - tzv. světočára - v tomto
čtyřrozměrném prostoročase, jejíž body určují
souřadnice částice v jednotlivých časových okamžicích
(lze říci, že v průběhu času se světobod odpovídající
dané částici přemísťuje v prostoročase a opisuje určitou
čáru - světočáru). Rovnoměrně přímočaře se
pohybující částici odpovídá přímková světočára,
zrychlený pohyb je vyjádřen zakřivenou světočárou, světočára
částice "stojící" v klidu vzhledem k dané
vztažné soustavě je přímka rovnoběžná s časovou osou. Z
fyzikálního hlediska světočára vyjadřuje kinematickou
historii částice, neboť každý světobod vyjadřuje polohu
částice v určitém bodě prostoru a v určitém čase.
Protože prostoročas v jeho čtyřrozměrné podobě si nijak
nedovedeme představit, pro grafické znázornění se jeden nebo
dva prostorové rozměry vypouštějí, čímž vzniká prostoročasový
diagram sledovaného děje (obr.1.6).
Zavedení čtyřrozměrného prostoročasu
v klasické mechanice je zatím jen čistě formální. Není v
něm definována ani metrika, protože prostorové dimenze a
časová dimenze spolu nijak nesouvisejí. Nalezení hlubokých
souvislostí mezi prostorem a časem a zavedení metriky ve
čtyřrozměrném prostoročase je právě hlavní zásluhou
speciální teorie relativity.
Klasická Newtonova mechanika
Klasická mechanika je založena na třech Newtonových
zákonech :
1. Zákon setrvačnosti :
Těleso, na nějž nepůsobí vnější síla, zůstává v klidu
nebo v rovnoměrném přímočarém pohybu, tj. v ş dr/dt =const.
Pozn.: Tato formulace se
vztahuje na idealizovanou hmotnou částici bez
makroskopických rozměrů a vnitřní struktury. Pro reálná
makroskopická tělesa lze z fenomenologického hlediska zákon
setrvačnosti pro translační pohyb doplnit i o možnost setrvačného
otáčení: "Těleso setrvává v klidu nebo v
rovnoměrném přímočarém či otáčivém pohybu, dokud není
donuceno tento stav změnit působením síly".
Přívlastek "vnější" u síly zde již nemusí
platit - viz např. "efekt piruety" u
krasobruslařky, která připažením rukou (vnitřním
silovým působením) zmenší svůj moment
setrvačnosti, což vede ke zvýšení rychlosti jejího
otáčivého pohybu.
Při fundamentálním fyzikálním rozboru však
tyto vnější složité okolnosti není třeba brát v úvahu -
ve skutečnosti jsou sumárně způsobeny zákony
mechaniky pro jednotlivé částice, z nichž se těleso
skládá. Rotační setrvačný pohyb tělesa je tvořen
rovnoměrným kruhovým pohybem jednotlivých částic
tělesa kolem rotační osy, při němž je odstředivá síla
kompenzována mechanickou pevností materiálu tělesa (v podstatě to jsou elektrické vazbové síly mezi
atomy a molekulami). Vnitřně se jedná o
nerovnoměrný pohyb částic s dostředivým zrychlením,
vyvolaným vnitřními silami podle 2.Newtonova zákona; nemění
se velikost, ale jen směr rychlosti. Tyto pohyby, vznikající
koprodukcí zákona setrvačnosti se zákonem síly a zrychlení,
spadají do oblasti mechaniky pevných těles, avšak
uplatňují se i v hydrodynamice. Do základní
formulace zákona setrvačnosti - v duchu "Occamovy
břitvy" - není nutno rotační pohyb zavádět.
Skutečný fundamentální zákon setrvačnosti
tedy spočívá ve výše uvedené základní formulaci 1
pro translační pohyb.
2. Zákon pohybu (síly a
zrychlení) :
Zrychlení tělesa
je přímo úměrné na něj působící síle, tj. F = m.a, kde F je působící síla, a ş dv/dt ş d2r/dt2 je zrychlení, m je (setrvačná) hmotnost tělesa.
3. Zákon akce a reakce :
Při vzájemném
působení dvou těles je síla, kterou druhé těleso působí
na první, téže velikosti ale opačného směru než síla,
kterou působí první těleso na druhé: FAB = - FBA.
Z
formálně-matematického hlediska je první zákon speciálním
případem zákona druhého (pro F=0
je a=0, t.j. v = const.). Přesto však má zákon
setrvačnosti zásadní a samostatný fyzikální význam,
protože pojmy "rychlost", "zrychlení",
"klid", "přímočarý pohyb", vystupující
v Newtonových zákonech, mohou být definovány teprve tehdy,
když je předem dána vztažná
soustava, vzhledem k níž se pohyb těles vyšetřuje.
Newtonovy zákony 2. a 3. platí pouze v inerciální vztažné soustavě, dané zákonem
setrvačnosti 1.
K těmto třem základním zákonům
"pozemské" mechaniky se přidružuje Newtonův gravitační zákon (§1.2
"Newtonův gravitační zákon"),
který je východiskem tzv. "nebeské" mechaniky pohybu
hvězd, planet a měsíců kolem nich.
Vztažná
soustava. Měření polohy a času.
Kdykoliv mluvíme o pohybu, máme vždy na mysli pohyb vůči
vztažné soustavě. Pod vztažnou soustavou *) se rozumí
soustava prostorových souřadnic udávajících polohu těles v prostoru a hodiny sloužící ke stanovování časových intervalů. Nejjednodušší způsob
měření polohových souřadnic a vzdáleností těles v
prostoru je pomocí přikládání dostatečně tuhých a
přesných - standardních, ideálních - měřících tyčí.
Nejčastější způsob měření času je použití nějakého periodického procesu (regulárně se opakujícího); kritériem
správnosti je přitom to, že periodičnost jednoho procesu
souhlasí s periodičností jiných procesů. Faktory, které ovlivňují
jen některé takové procesy (např. teplota materiálu) jsou
"neuniverzální", působí rušivě a při
objektivním měření musejí být odstraněny nebo
odkorigovány. V dalším budeme předpokládat, že všechna
prostorová a časová měření se provádějí pomocí standardních (ideálních) hodin a měřících tyčí,
tj. takových tyčí a hodin, u nichž jsou odstraněny nebo
vykorigovány všechny neuniverzální rušivé vlivy (je ještě diskutováno níže v odstavci "Exaktní
- ideální - měření prostoru a času"). Naproti tomu faktory stejně
ovlivňující všechny periodické
procesy (chod všech hodin) a délky všech měřících tyčí - univerzální vlivy - nelze nijak odkorigovat a je nutno
považovat je za ovlivňující běh samotného času a
vlastnosti samotného prostoru. V moderní fyzice se totiž na
prostor a čas nedíváme jako na nějaké metafyzické
kategorie, ale jsou vyjádřením vzájemného vztahu předmětů
a událostí.
*) Pojmy "vztažná soustava" a "souřadnicová
soustava" se často ztotožňují. Lze říci, že
:
vztažná
soustava |
= |
soustava
prostoro-
časových souřadnic |
+ |
způsob,
jakým jsou tyto souřadnice
jednotlivým bodům přiřazovány |
. |
Mezi vztažnou soustavou a souřadnicovou
soustavou je zhruba takový rozdíl, jako mezi krajinou se
skutečnými orientačními "body" a její mapou s
kartografickými souřadnicemi. Základem vztažné soustavy jsou
určitá reálná tělesa tvořící "opěrné body"; s
jejich pomocí se vytyčují myšlené čáry a jednotlivá
místa se opatřují čísly - vytváří se soustava souřadnic.
Je třeba si uvědomit, že obecně:
| transformace
souřadnic |
Ü/Ţ |
přechod
k jiné vztažné soustavě |
. |
Z fyzikálního hlediska však většinou oba
pojmy není nutno příliš rozlišovat (výjimku tvoří např.
problematika gravitační energie - viz §2.8).
Exaktní - ideální - měření
prostoru a času
Pro přesné měření fyzikálních veličin je obecně třeba
používat takové metody, pomůcky a přístroje, které
dostatečně citlivě reagují na měřenou veličinu a přitom nejsou
ovlivňovány ostatními rušivými vlivy a okolnostmi
měření. Pokud toto není splněno, musí být aspoň možná
přesná korekce na tyto rušivé a
zkreslující vlivy. Pro měření prostoru a času ve
fundamentální fyzice, zvláště v teorii relativity, se
modelově zavádějí standartní idealizované hodiny
a měřící tyče:
Ideální
hodiny
jsou takové kalibrované hodiny, jejichž rychlost chodu
(frekvence použitého periodického děje) není ovlivňována
žádnými neuniverzálními vlivy jako je teplota či
působící síly. Naprosto nepoužitelné by zde tedy byly
kyvadlové nebo přesýpací hodiny (jejichž rychlost chodu je
přímo dána tíhovou silou, v beztížném stavu se zastaví);
podobně i jiné mechanické hodiny by mohly být ovlivňovány
mechanickými deformacemi jejich konstrukčních dílů.
Nejvhodnější z tohoto hlediska jsou elektronické
oscilátory, jejich nejpřesnější variantou jsou
atomové hodiny :
Atomové hodiny
Elektronickým základem atomových hodin je oscilátor
řízený krystalem - drobným precizně vybroušeným
piezoelektrickým křemenným krystalem, naladěným na vysokou
gigahertzovou frekvenci odpovídající kmitům použitých
atomů. Relativní přesnost samotného tohoto
elektro-mechanického oscilátoru dosahuje až cca 10-7 (pro většinu aplikací naprosto postačující). Další podstatné zvýšení přesnosti je zde
dosaženo citlivým elektronickým laděním oscilátoru pomocí
zpětnovazební smyčky s rezonanční frekvencí použitého
druhu atomů. Nejčastěji jsou to atomy cesia s
rezonanční frekvencí 9,192631770 GHz.
Zesílený signál z krystalového oscilátoru je připojen na
vysílač rádiových vln, kterým jsou v komůrce vystaveny
atomy cesia. Pokud dojde ke shodě frekvence - rezonanci
- oscilátoru s frekvencí přechodu mezi základní a
excitovanou hladinou hyperjemného rozštěpení energetických
hladin v elektronovém obalu cesia (způsobené
interakcí spinů jádra a elektronů),
přejdou atomy cesia do excitovaného stavu.
Aplikací magnetického pole jsou tyto excitované atomy
separovány a detekovány. Pomocí množství excitovaných
atomů cesia se elektronicky ve zpětné vazbě
průběžně ladí frekvence krystalového
oscilátoru tak, aby se neustále shodovala s rezonanční
frekvencí přechodů atomů cesia - 9 192 631 770
Hz *). Počet těchto kmitů pak velmi přesně
měří čas. Zdroj přesné frekvence zde pochází
přímo z elektronového obalu atomů, který je
stabilní a není ovlivňován žádnými běžnými vnějšími
vlivy. V konečném výsledku tak dostáváme "oscilátor
řízený atomovým obalem" cesia, který
dosahuje relativní přesnosti 10-13.
*) Na základě atomových hodin byla v
r.1967 zavedena nová definice sekundy - jako
časový interval odpovídající 9 192 631 770 periodám
elektromag. záření vznikajícího při přechodu mezi dvěma
hladinami velmi jemné struktury základního stavu atomu cesia
133-Cs.
Současné atomové hodiny jsou značně složitým a dosti
rozměrným laboratorním zařízením. S pokrokem techniky však
lze v blízké budoucnosti očekávat jejich aspoň částečnou
miniaturizaci a kompaktifikaci, aby mohly být používány v
"terénu" a v kosmických sondách.
Ideální
měřící tyče
jsou taková délkově kalibrovaná měřítka, jejichž délka
není ovlivňována žádnými neuniverzálními vlivy
jako je teplota nebo působící síly. Ideální meřící tyče
by tedy měly být z teplotně neroztažného materiálu,
dostatečně pevného a tuhého.
Pokud se nelze vyhnout vlivu neuniverzálních
faktorů (což většinou není 100-%
možné), je na tyto neuniverzální vlivy
nutno provést korekci. Ve fyzikální praxi,
zvláště v teorii relativity, se pro měření časů a délek
většinou nepoužívají přímo "hodiny" a
"tyče", ale složitější metody využívající
elektromagnetického záření - metody optické
a radiolokační. Měřící tyče a precizní
hodiny slouží spíše pro kalibraci těchto
metod.
V praxi je vztažná
soustava vždy realizována nějakými materiálními tělesy.
Vztažnou soustavou mohou být stěny laboratoře, zemský
povrch, střed naší Galaxie, stěny kabiny kosmické rakety
atd. Principiálně jsou použitelné libovolné vztažné
soustavy, i když v konkrétních případech mohou být
některé z nich vhodnější k popisu určitých dějů než
ostatní. Je jasné, že pro studium pohybu planet je
výhodnější vztažná soustava spojená se Sluncem než
soustava spojená s některým z Jupiterových měsíců, nebo
pro sledování tenisového míčku se lépe hodí vztažná
soustava tvořená kurtem než soustava spojená s okolo
projíždějícím automobilem.
První Newtonův zákon je pak vlastně
tvrzením, že existují tzv. inerciální vztažné soustavy,
v nichž platí zákon setrvačnosti. Je jasné, že každá
vztažná soustava S', která se vzhledem k dané inerciální
soustavě S pohybuje rovnoměrně přímočaře, je
též inerciální; existuje tedy nekonečně mnoho
inerciálních soustav. Naopak, soustavy které se vůči
inerciální soustavě pohybují s nenulovým zrychlením, nejsou
inerciální - zákon setrvačnosti v nich neplatí. Inerciální
vztažná soustava je idealizace; v obecné teorii relativity se
ukazuje, že globální inerciální
soustavy neexistují, avšak vždy lze najít lokální inerciální soustavu, která v dostatečně omezené
prostorové oblasti má všechny vlastnosti skutečné
inerciální vztažné soustavy.
Galileiho
transformace a relativita
Mějme dvě inerciální vztažné soustavy S a S' s rovnoběžně orientovanými
kartézskými prostorovými souřadnicemi x,y,z a x',y',z'
(obr.1.5a) takové, že soustava S' se vůči soustavě S
pohybuje ve směru osy X rychlostí V; za počátek t=0=t'
odečítání času v obou soustavách zvolíme okamžik, kdy
počátky O a O' obou soustav splývaly. Pokud
polohové souřadnice a časové intervaly v obou soustavách
měříme stejnými standartními tyčemi a hodinami (což budeme
vždy v dalším předpokládat), vztah mezi souřadnicemi a
časy měřenými v nečárkované a čárkované soustavě bude - tzv. Galileiho transformace :
| x = x' + V.t , y =
y' , z = z' , t = t' . |
(1.64) |
V obecnějším
případě, kdy se inerciální soustava S' pohybuje vůči S
rychlostí V v obecném směru, má Galileiho
transformace vektorový tvar
| r = r' + V.
t , t = t' . |
(1.64') |
Galileiho transformace
(1.64) je vyjádřením běžných kinematických a
geometrických představ plynoucích z každodenní zkušenosti.
Z Galileiho transformace plyne obyčejný aditivní
zákon skládání rychlostí: jestliže se těleso pohybuje rychlostí
v' vzhledem k soustavě S', pak v soustavě
S jeho rychlost činí
neboli rychlost tělesa
v nečárkované soustavě se zvětší o rychlost V
čárkované soustavy vzhledem k soustavě nečárkované (resp.
obě rychlosti se vektorově složí).
Zkušenost
vyjádřená v klasické (Galileiho a Newtonově) mechanice
učí, že neexistuje absolutní klid ani absolutní rychlost
rovnoměrného přímočarého pohybu. Galileův princip relativity
tvrdí, že zákony mechaniky jsou stejné pro každou
inerciální vztažnou soustavu - všechny inerciální soustavy
jsou z hlediska klasické mechaniky rovnocenné; žádným
vnitřním mechanickým pokusem nelze zjistit, jak rychle se
daná inerciální soustava pohybuje. Galilei k tomuto závěru
došel pozorováním, že mechanické děje na lodi plovoucí
stálou rychlostí po klidné hladině probíhají stejně, jako
kdyby loď byla v klidu, takže mechanickými pokusy se nelze
přesvědčit, zda je loď v klidu nebo v přímočarém
rovnoměrném pohybu.
Skutečně, zákony klasické mechaniky
jsou invariantní vzhledem ke Galileiho
transformacím (1.64). Např. 2.Newtonův zákon F = m.a ş m.d2x/dt2 = m.d2(x+V.t)/dt2 = m.d2x/dt2 = F (pokud vnější síla nezávisí
na rychlosti pohybu tělesa, tj. F = F') zachovává svůj tvar a
číselnou hodnotu koeficientu úměrnosti m při Galileiho transformacích
mezi dvěma inerciálními soustavami, podobně jako při
libovolných posunech nebo pootočeních prostorových
souřadnicových os. Invariantní vůči Galileiho transformaci
jsou pak i zákony zachování energie a hybnosti.
Při formulaci Newtonových zákonů
klasické mechaniky se mlčky předpokládá splnění dvou
(zdánlivě) samozřejmých předpokladů :
a) Předpoklad o univerzálním (absolutním) čase, podle něhož časové
intervaly mezi událostmi jsou nezávislé na volbě vztažné
soustavy.
b) Vzdálenosti současných poloh
bodů (a tedy i rozměry těles) jsou absolutní, tj. nezávislé na volbě
vztažné soustavy vzhledem k níž jsou polohy těchto bodů
určovány.
Oba tyto předpoklady jsou obsaženy v
Galileiho transformačních rovnicích (1.64). Newton zavedl pojem "absolutního prostoru" a setrvačnost považoval
za snahu hmotných těles o zachování "pohybového
stavu" v tomto absolutním prostoru. Pojem absolutního
prostoru je však v rámci klasické mechaniky prázdný, neboť
vzhledem k platnosti Galileiho principu relativity se
sebepečlivějším zkoumáním žádných mechanických jevů
nedá zjistit, které těleso nebo vztažná soustava je v
"absolutním klidu". Pomocí žádného mechanického
experimentu od sebe nelze odlišit dvě inerciální soustavy.
Kdyby se některé fyzikální zákony lišily pro různé
vzájemně se pohybující pozorovatele, bylo by možné na
základě těchto rozdílů určit, které objekty jsou v
prostoru v (absolutním) klidu a které se pohybují.
Dlouhou dobu se myslelo, že takovými
jevy umožňujícími odlišit různé inerciální soustavy (a
tedy rozlišit absolutní pohyb a klid), jsou jevy elektromagnetické. Galileiho princip relativity se totiž
ukázal být neslučitelný s klasickou Maxwellovou
elektrodynamikou. Použijeme-li Galileiho vztahů (1.64) k
vzájemné transformaci ekvivalentních veličin v soustavách S a S', budou mít Maxwellovy rovnice
odlišný tvar. Elektromagnetické
jevy by tedy probíhaly různě v různých inerciálních
soustavách. Maxwellovy rovnice nejsou invariantní
vzhledem ke Galileiho transformacím. Ze zákona skládání
rychlostí (1.65) plyne, že je-li rychlost světla vzhledem k
nějaké "základní" inerciální soustavě S rovna c, pak vzhledem k jiné inerciální
soustavě S' se tato rychlost zmenší nebo zvětší
podle toho, pohybuje-li se světelný paprsek ve směru nebo
proti směru pohybu čárkované soustavy vzhledem k
nečárkované soustavě. Rychlost světla by tedy byla v
různých inerciálních soustavách různá.
Maxwellova teorie by podle toho mohla
platit pouze v jediné z nekonečně mnoha inerciálních
soustav; tuto význačnou soustavu bychom mohli považovat za
"absolutní vztažnou soustavu" ve shodě s Newtonovou
koncepcí. Podle éterové hypothézy je taková soustava
reprezentována nehybným světlonosným éterem, popř. by to mohla být
soustava spojená s těžištěm veškeré hmoty vesmíru.
Přesná měření Michelsona a Morleye,
kteří (s úmyslem přímého experimentálního potvrzení
existence éteru, stanovení absolutní vztažné soustavy a
zjištění rychlosti absolutního pohybu Země vůči ní) v
letech 1881 až 1904 měřili rychlost světla ve směru a proti
směru pohybu Země, ukázala, že rychlost
světla ve
vakuu je v různých inerciálních soustavách stejná.
Einsteinova
speciální teorie relativity
Negativní výsledek pokusů Michelsona a Morleye, který byl
později několikrát znovu a přesněji ověřen, se
fyzikové snažili zpočátku vysvětlit (nebo spíš smířit
jej s klasickými fyzikálními představami) zaváděním
některých umělých předpokladů a dodatečných hypothéz.
Tyto hypothézy však neobstojí v konfrontaci s výsledky
jiných pokusů a pozorování. Např. nejjednodušší z nich -
předpoklad, že éter je v okolí Země "strháván"
jejím pohybem a je proto vůči ní lokálně v klidu - je
neslučitelný s pozorovanou aberací světla stálic. Lorentz na
základě své elektronové teorie vyslovil hypothézu o
kontrakci, podle níž se délka každého tělesa pohybujícího se
rychlostí v zkracuje ve směru pohybu v poměru Ö(1 - v2/c2) ve srovnání se svou klidovou
délkou. Zavádění dodatečných hypothéz ad hoc, které nahrazují jednu záhadu záhadou
jinou, však nemůže být uspokojivým vysvětlením žádného
jevu.
Princip relativity
Nové, zcela principiální stanovisko k rozporu mezi mechanikou
a elektromagnetismem, nezatížené předsudky mechanistických
představ, zaujal A.Einstein. Einstein si uvědomil, že
měření rychlosti světla v libovolné inerciální soustavě
dává tentýž výsledek c @ 2,998 .108 m/s, což vůbec není v
rozporu, ale naopak v plném souladu s principem relativity
platným v mechanice. Ve své epochální práci z r.1905 "O elektrodynamice pohybujících se těles" [78] Einstein zobecnil Galileiho princip relativity z mechaniky
na všechny fyzikální jevy:
| Teorém 1.1 (Eisteinův speciální
princip relativity) |
| Fyzikální
zákony jsou stejné pro všechny inerciální vztažné
soustavy. |
Všechny inerciální
soustavy jsou tedy pro popis všech fyzikálních dějů zcela rovnocenné, při stejných fyzikálních
podmínkách probíhají fyzikální jevy stejně v každé
inerciální soustavě nezávisle na rychlosti jejího pohybu.
Každý fyzikální pokus dopadne stejně, ať ho provedeme v
libovolné inerciální soustavě. Einsteinův speciální
princip relativity je tak vyjádřením nezjistitelnosti
a neexistence univerzální (absolutní) vztažné soustavy.
Speciální princip relativity je rovněž odrazem jednoty fyziky, společné materiální
podstaty
přírody. Žádný elektromagnetický experiment totiž nemůže
být uskutečněn bez použití hmotných těles
řídících se zákony mechaniky a naopak, každého
mechanického děje se účastní elektromagnetické interakce
mezi částicemi materiálu pohybujících se těles. Z platnosti
(Galileiho) principu relativity v mechanice tedy plyne, že i
elektromagnetické a ostatní jevy by měly principu relativity
vyhovovat.
Proč název "speciální"
a "obecná" ?
Einsteinova práce z r.1905 založila teorii
relativity
jako takovou. Zabývala se inerciálními vztažnými soustavami,
pohybujícími se relativně vůči sobě navzájem. V zásadě
však mohla pracovat i se zrychlujícími se vztažnými
soustavami, kde však vznikají "fiktivní" síly (jako
je odstředivá síla).
Einstein se pak snaži najít obecnější
přístup, který by s inerciálními i zrychlenými soustavami
zacházel stejně, jako ze "sobě rovnými". Dospěl k
zásadní myšlence univerzálnosti gravitace - k principu ekvivalence gravitace a akceleračních sil.
V r.1915 tak vznikla novější zobecněná teorie relativity,
která zahrnovala setrvačnost a gravitaci ve vzájemné
ekvivalenci a v koprodukci se zobecněnými Lorentzovými
transformacemi i geometrii zakřiveného prostoročasu.
Při absenci gravitace se
nová zobecněná teorie redukuje na původní relativitu z
r.1905 - je speciálním případem za nepřítomností
gravitace. Proto se teorie z r.1905 začala nazývat "speciální
teorie relativity" a novější teorie z r.1915,
zahrnující gravitaci, se nazývá "obecná teorie
relativity".
Princip konstantní rychlosti
světla
V Newtonově mechanice je speciální princip relativity
samozřejmě splněn. Aby speciální princip relativity platil i
pro jevy elektromagnetické popsané Maxwellovými
rovnicemi,
musí mít veličina c (obsažená
v Maxwellových rovnicích buď přímo nebo přes permitivitu
vakua), rovná rychlosti šíření elektromagnetických vln ve
vakuu, ve všech inerciálních soustavách stejnou
hodnotu (z obecně-fyzikálního hlediska je rychlost světla
diskutována v §1.1, pasáž "Rychlost světla").
Aplikace speciálního principu relativity na elektrodynamiku tak
přirozeně vysvětluje výsledek Michelsonova pokusu.
Při axiomatické výstavbě obecné
teorie, která by měla být základem celé fyziky, je však
použití složitých Maxwellových rovnic (popisujících
konkrétní oblast elektromagnetických jevů) jako výchozího
axiómu nevýhodné. Einstein proto vzal poznatek o konstantnosti
rychlosti světla jako primární nezávislý postulát spolu se
speciálním principem relativity:
| Teorém 1.2 (princip konstantní
rychlosti světla) |
| Rychlost
světla ve vakuu je stejná ve všech inerciálních
soustavách bez ohledu na jakýkoliv pohyb zdroje nebo
pozorovatele. |
Klasická Newtonovská
fyzika vychází z předpokladu o okamžité interakci těles:
změna, polohy (nebo obecně nějaké charakteristiky) jednoho z
interagujících těles se projeví na ostatních tělesech v
tomtéž okamžiku, nezávisle na jejich vzdálenosti. Formálně
je to vyjádřeno popisem interakce částic pomocí
potenciální energie U(x1,x2,...,xn), která je funkcí pouze
polohových souřadnic částic xi. Ve skutečnosti však žádné
bezprostřední okamžité působení "na dálku" v
přírodě neexistuje. Jestliže nastane nějaká změna s
jedním tělesem, pak na druhém tělese, které je s ním v
interakci, se tato změna začne projevovat až po uplynutí konečného
časového intervalu. Tuto dobu potřebuje interakce (pole které
ji zprostředkovává) k překonání vzdálenosti mezi tělesy.
Vzájemné působení se tedy šíří konečnou rychlostí,
takže existuje určitá maximální (mezní) rychlost
šíření interakcí. Z prvního postulátu STR (speciálního
principu relativity) pak plyne, že tato rychlost šíření
interakcí je stejná ve všech inerciálních soustavách - je
tedy univerzální konstantou. Z elektrodynamiky plyne, že
tato rychlost je rovna rychlosti elektromagnetických vln - rychlosti světla ve vakuu c. Druhý základní postulát STR
lze proto též formulovat ve tvaru :
| Teorém 1.2' (princip univerzální
rychlosti šíření interakcí) |
| Existuje
maximální rychlost šíření interakcí ve vakuu,
rovná rychlosti světla c,
která je stejná pro všechny inerciální vztažné
soustavy. |
Postuláty 1.2 a 1.2' nejsou zcela ekvivalentní; formulace 1.2'
vylučuje např. možnost existence tachyonů (částic pohybujících se
nadsvětelnou rychlostí), protože jejich prostřednictvím by
bylo možno uskutečnit interakci rychlostí převyšující
maximální rychlost šíření interakcí. Tachyony můžeme však
doposud považovat za výplod fantazie fyziků, neboť pro jejich
existenci nesvědčí žádné teoretické ani experimentální
důvody (viz níže). Na problematiku relativistické astrofyziky
a kosmologie jemné rozdíly v obou formulacích druhého
základního postulátu STR nemají vliv.
Druhý postulát
speciální teorie relativity - existence univerzální
rychlosti, která se co do velikosti neskládá s žádnou jinou rychlostí - je
v ostrém rozporu s obvyklými kinematickými představami
vyjádřenými Galileiho transformacemi a založenými na
koncepci absolutního prostoru a času. Neplatí zde běžné
pravidlo skládání rychlostí, jednoduché Galileiho
transformace souřadnic mezi inerciálními soustavami musejí
být nahrazeny obecnějšími transformacemi (Lorentzovými).
Prostorové vzdálenosti a časové intervaly přestávají
být objektivními absolutními veličinami *), ale závisejí na vztažné
soustavě z níž se měří - stávají se relativními. Principy STR tak boří obvyklé
intuitivní pojmy prostoru a času založené na zkušenosti s
pohybem běžných makroskopických těles.
*) Pokud se rychlost světla jeví stejná
pro pozorovatele pohybujícími se různými rychlostmi, je to
možné jen tehdy, když se liší jejich "hodinky" a
"pravítka" - čas a prostor je pro různé
pozorovatele různý.
Dá se říci, že když se rychlost světla c
ukázala být absolutní, prostorová měřítka
a časové intervaly musejí být relativní...
Kdo má pravdu? - či
se mýlí ?
V rámci STR se pozorovatelé, pohybující se rozdílnými
rychlostmi, často rozcházejí v názoru na
velikost délkových proporcí, trvání časových intervalů,
časové následnosti (či současnosti) událostí. Nemusí to
však být tím, že jeden z nich by měl pravdu a druhý se
mýlil - každý má pravdu ve své vlastní
vztažné soustavě... V čem se ale všichni pozorovatelé
zákonitě musejí shodovat, je objektivní existence
a průběh přírodních dějů! To, zda se dvě
pohybující tělesa srazí nebo se minou, nezáleží na
pozorovací vztažné soustavě; z hlediska různých soustav se
může lišit jen časový údaj kdy a v jakých prostorových
souřadnicích se tak stane..?.. Tyto otázky jsou dále
diskutovány níže v pasáži "Paradoxy
ve speciální teorii relativity".
Lorentzovy transformace a relativistická kinematika
Spolu s
některými dalšími předpoklady, jako je homogenita
a izotropie prostoru a času a jejich eukleidovské
geometrické a topologické vlastnosti, umožňují tyto dva základní
postuláty 1.1 a 1.2. stanovit nové
transformační vztahy, zobecňující
Galileiho
transformaci (1.64) pro přechod od jedné inerciální soustavy
k druhé a vybudovat novou kinematiku
a dynamiku
pohybu hmotných těles - Einsteinovu speciální
teorii relativity (STR).
Terminologická poznámka:
Název "speciální" proto,
že je omezena jen na inerciální (rovnoměrně se pohybující)
soustavy, "relativita" proto,
že pouze relativní pohyb je fyzikálně důležitý. Slovo
"relativita" dále odráží vývody STR, že
některé fyzikální veličiny - jako jsou časové a
prostorové intervaly, současnost a soumístnost událostí,
hmotnosti těles - ztrácejí svůj dřívější absolutní
význam a stávají se relativními veličinami, závislými na
pohybu vztažných soustav ("pozorovatelů"). Nelze
však souhlasit s často uváděným tvrzením, že "podle
teorie relativity je všechno relativní"! Některé
důležité veličiny, jako je rychlost světla či
prostoročasové intervaly, jsou naopak "absolutní",
nezávislé na vztažné soustavě (na rychlosti pohybu
pozorovatele).
Mějme inerciální
soustavu S s počátkem O, souřadnicemi x,y,z a časem t, a
další inerciální soustavu S' s počátkem O', souřadnicemi
x',y',z' a časem t', pohybující se vzhledem k S rychlostí V. Fyzikální měření ve vztažné
soustavě S' se přitom provádějí stejným způsobem (za použití stejných pomůcek - standartních
měřících tyčí a synchronizovaných hodin) jako v soustavě S. V
čase t=t'=0 nechť je vyslán z počátku O, který v tomto okamžiku
splývá s O', světelný záblesk (obr.1.5b). V soustavě S je
šíření tohoto světelného signálu vyjádřeno rovnicí
| s2 ş x2 + y2 + z2 - c2.t2 = 0 |
(1.66) |
popisující kulovou
vlnoplochu, jejíž poloměr r = c.t se zvětšuje rychlostí c.
Ve vztažné soustavě S' se zdroj světla pohybuje rychlostí -V, avšak vzhledem k principu stálé
rychlosti světla (c'= c bez ohledu na rychlost a směr pohybu
zdroje) bude šíření světelného signálu vypadat stejně
jako v soustavě S :
| (s')2 ş (x')2
+ (y')2 + (z')2 - (c.t')2
= 0 . |
(1.66') |
Aby bylo možno vyhovět
principu stálé rychlosti světla, je nutno předpokládat v
obou soustavách různý čas. Ze současného splnění
rovností (1.66) a (1.66') vyplynou hledané transformační vztahy mezi souřadnicemi (t,x,y,z) a
(t',x',y',z').
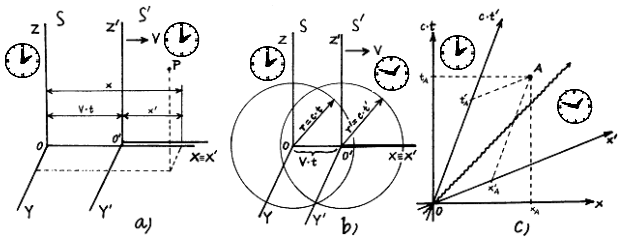
Obr.1.5. Transformace souřadnic mezi inerciálními vztažnými
soustavami.
a) Galileiho transformace.
b) K odvození
Lorentzovy transformace. Světelný záblesk vyslaný v časovém
okamžiku t=t'=0 z počátku O (který v té době splýval s O')
se z hlediska obou soustav S i S' šíří na všechny strany stejnou
rychlostí c, takže v
čase t vyplňuje
kulovou vlnoplochu o poloměru r = c.t, resp. r'= c.t'.
c)
Geometrické znázornění Lorentzovy transformace. Je-li
výchozí vztažné soustavě S v prostoročase připsána
(pseudo)kartézská souřadnicová soustava c.t,x, pak přechod k
pohybující se vztažné soustavě S' geometricky
znamená deformaci na kosoúhlé prostoročasové
souřadnice c.t',x'.
Pozn.: Pomocí
obrázku hodin je symbolicky znázorněna rychlost plynutí času
v soustavách S a S' (viz níže - dilatace času).
Těleso pohybující se
rovnoměrně přímočaře z hlediska
soustavy S se
podle principu relativity musí pohybovat rovnoměrně
přímočaře i v soustavě S'. Proto souřadnice x', y',z',t'
musejí být lineárními funkcemi souřadnic x,y,z,t. Aby
rovnice (1.66) a (1.66') byly splněny současně, musí platit
s'2= k.s2, kde k je nějaký činitel. Tento
koeficient nemůže záviset na souřadnicích a na čase,
protože různé body a časové okamžiky by nebyly rovnocenné, což
odporuje homogenitě prostoru a času. Koeficient k
nemůže záviset ani na směru rychlosti V, protože prostor ve STR
předpokládáme izotropní; k by
mohl být funkcí nanejvýš velikosti rychlosti V = |V|,
tj. s'2=
k(V).s2.
Soustavy S a S' jsou však rovnocenné. Proto
stejná úvaha provedená z hlediska soustavy S' vzhledem k níž se
nečárkovaná soustava pohybuje rychlostí -V
ukazuje, že s2= k(|-V|).s'2 = k(V).s'2, z čehož plyne k2=
1, takže k = 1 (platí kladné znaménko aby zůstala zachována
identičnost transformace soustavy S samé na sebe při V=0).
Veličina s, tzv. interval, definovaná v rovnicích
(1.66), zůstává tedy při transformaci mezi dvěma
inerciálními soustavami invariantní:
| s'2 ş x'2 + y'2 + z'2 - c2t'2 = x2 + y2 + z2 - c2.t2 ş s2 . |
(1.67) |
Uvažujme, stejně jako
u Galileiho transformace, speciální případ podle obr.1.5, kdy
osy obou vztažných soustav jsou rovnoběžné a stejného
smyslu, osy X a X' splývají a soustava S' se
vzhledem k S pohybuje konstantní
rychlostí V
v kladném směru osy X. Potom je-li
y=0, musí být i
y'=0 při libovolném z a podobně je-li z=0, musí být
z'=0 při libovolném y (plochy XY a X'Y', stejně jako
plochy XZ a X'Z', se transformují samy na sebe). Proto y'=k.y,
z'= k.z, kde koeficient k ze stejných důvodů jako
předtím u intervalu nezávisí na x,y,z,t a může být funkcí
pouze V. Koeficient k je zde tedy (opět vzhlesem k
nerozlišitelnosti obou soustav) roven jedné, takže souřadnice
kolmé na směr pohybu se nemění: y'= y, z'= z. Hledaná
speciální transformace bude mít tedy (vzhledem k linearitě) tvar
| x' = A . x + B . t
, y' = y , z' = z , t' = P . x + Q . t . |
(1.68) |
Dosazením do podmínky invariantnosti
intervalu (1.67) dostaneme
(A2-c2P2)x2 + 2(AB-c2PQ)x.t + (B2-c2Q2) = x2 - c2.t2 .
Tento vztah musí být
splněn identicky ve všech místech prostoru a v každém čase,
takže se musejí sobě rovnat koeficienty u x a t na obou stranách:
A2-c2P2
= 1 , AB-c2PQ
= 0 , c2Q2 - B2 = c2 .
Čtvrtou rovnici
zízkáme z toho, že soustava S' se vůči S pohybuje ve směru osy X rychlostí V. Bod O' má v okamžiku t souřadnice O'= (x=V.t,y=0,z=0)
z hlediska S, zatímco z hlediska S'
je stále O'= (x'=0,y'=0,z'=0). Z první rovnice (1.68) tak
dostáváme mezi A a B vztah x'= A.V.t + B.t = 0, tj. A.V + B =
0. Řešením této soustavy čtyř rovnic dostaneme pro
transformační koeficienty v (1.68) výsledky
A = 1/Ö(1-V2/c2) , B = -V/Ö(1-V2/c2) , P = (-V2/c2)/Ö(1-V2/c2) , Q = 1/Ö(1-V2/c2) ,
přičemž záporné
znaménko u B a P a kladné u
A a Q je
opět z důvodu identičnosti transformace při V® 0.
Po dosazení do (1.68) hledaná speciální
transformace je
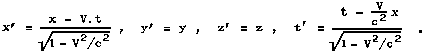 |
(1.69) |
Tato transformace,
která zobecňuje Galileiho transformaci (1.64) a zaručuje
splnění obou základních postulátů STR, se nazývá Lorentzova transformace. Lorentz a Poincaré totiž ještě před
vznikem speciální teorie relativity ukázali, že Maxwellovy
rovnice elektromagnetického pole zachovávají stejný tvar ve
dvou vzájemně se pohybujících inerciálních soustavách S a
S' tehdy, jestliže mezi těmito soustavami platí nikoliv
jednoduché Galileiho transformace, ale složitější
transformace (1.69) nazývané nyní Lorentzovy
transformace.
A.Einstein však ve své speciální teorii relativity podal
obecné odvození těchto transformací a ukázal, že se
nejedná jen o nějakou zvláštnost konkrétního
(elektromagnetického) pole, ale řídí se jimi všechna pole a
veškerý pohyb - jsou vyjádřením strukturních
vlastností prostoru a času.
Prostoročasové
diagramy
Pro přehledné
grafické znázornění prostorových pohybů těles v
závislosti na čase, jejich světočar, se často kreslí tzv. prostoročasové diagramy v souřadnicích x , t. Jelikož se ve
STR zabýváme pohyby o rychlostech blízkých rychlosti světla,
je vhodné v prostoročasových diagramech na časové ose místo
prostého času t vynášet jeho c-násobek - časovou souřadnici x°= c.t, aby měřítko na
časové ose bylo souměřitelné se škálami na osách
prostorových. Takový prostoročasový diagram, na němž
je vyznačena vodorovná osa x a k ní kolmá časová osa c.t (souřadnice y a z jsou pro
jednoduchost vynechány), odpovídající výchozí vztažné
soustavě S, je znázorněn na obr.1.5c. Na těchto
souřadnicových osách lze odečítat prostoročasové
souřadnice libovolného světobodu (události) ve vztažné
soustavě S. Aby bylo možno odečítat
prostoročasové souřadnice těchto událostí i ve vztažné
soustavě S', pohybující se vzhledem k S ve směru osy x rychlostí V, je třeba na tomto diagramu vytyčit
souřadnicové osy x' a x'°= c.t' odpovídající soustavě S'.
Osa x', která je dána podmínkou t'= 0, je podle (1.69)
přímka ct =(V/c).x ; osa t', daná podmínkou x'=0, je přímka
x = (V/c).ct. Jak je tedy vidět z obr.1.5c, přechod k jiné
inerciální soustavě pomocí Lorentzových
transformací geometricky znamená přechod ke kosoúhlé soustavě prostoročasových souřadnic,
jejíž osy jsou vůči původním osám nakloněny o úhel a
daný vztahem tg a=
V/c. Tento úhel sklonu a roste s rychlostí soustavy S'
vůči S; při V®c se blíží 45°, kde osy x' a
ct' splývají. Z takového geometrického vyjádření
Lorentzovy transformace velmi názorně plynou kinematické
efekty STR jako je kontrakce délek nebo dilatace
času; rovněž
se zde elegantně řeší známý paradox
hodin
[232],[242] - je podrobněji analyzováno
níže v pasáži "Paradoxy STR".
Obrácené Lorentzovy
transformace ze soustavy S' do S dostaneme vzhledem k rovnocennosti obou
soustav jednoduše tak, že ve vztazích (1.69) zaměníme
čárkované a nečárkované souřadnice a rychlost V nahradíme -V
 |
(1.69') |
Obecnou Lorentzovu transformaci, platnou při
libovolném směru rychlosti V inerciální soustavy S'
vzhledem k soustavě S, lze získat
ze speciální Lorentzovy transformace (1.69) tak, že se nejprve použije pomocných
souřadnic takových, že pohyb se v nich děje podél osy X,
aplikuje se (1.69) a pak se provede zpětná transformace do
původních souřadnic. Obecná Lorentzova transformace se
obvykle zapisuje ve vektorovém tvaru
 |
(1.69'') |
kde r ş [O, (x,y,z)] je polohový vektor
od počátku O k události (t,x,y,z). Složením dvou
Lorentzových transformací S® S' a S® S''
vznikne správná Lorentzova transformace mezi S a S'' jen tehdy,
když rychlost soustavy S'' vůči soustavě S' má stejný směr
jako rychlost S' vůči S. Fyzikálně to souvisí s tím,
že velikost rychlosti světla c se neskládá s žádnou jinou
rychlostí, zatímco směr rychlosti světla se obecně mění
(aberace světla, viz níže). Proto
obecnou Lorentzovu transformaci nelze získat prostým
skládáním speciálních Lorentzových transformací v
jednotlivých osách X,Y,Z.
Kinematické
efekty STR
Z Lorentzových transformací (1.69) plynou známé kinematické
efekty
speciální teorie relativity - dilatace času,
kontrakce délek a neaditivní zákon skládání rychlostí :
Máme-li
v soustavě S dvě soumístné události x,y,z,t a
x,y,z,t+Dt oddělené časovým intervalem
Dt, pak podle (1.69), vzhledem k tomu, že Dx = 0 (soumístnost), bude časový
interval mezi těmito událostmi měřený
ze soustavy S' roven
| Dt' = Dt / Ö(1 - v2/c2) . |
(1.70) |
Čas měřený
ideálními hodinami pohybujícími se spolu s daným tělesem se
nazývá vlastní čas tohoto tělesa. Vlastní čas t souvisí s prostoročasovým intervalem
vztahem (jelikož dx=dy=dz=0)
a je tedy rovněž
invariantní. Ze vztahu (1.70), nebo ekvivalentně zavedením
rychlosti v2 = (dx2+dy2+dz2)/dt2 ve vztahu dt = ds/c = (1/c)Ö(-c2dt2+dx2+dy2+dz2), dostaneme
| dt = Ö(1 - v2/c2) . dt ; |
(1.72) |
interval vlastního
času pohybujícího se tělesa je tedy vždy menší než odpovídající interval
souřadnicivého času. Pozorovatel porovnávající chod
klidových a pohybujících se hodin zjistí, že pohybující se
hodiny jdou podle vztahu (1.70) tím pomaleji, čím rychleji se pohybují;
tento jev se nazývá dilatace času.

Obr.1.5 - uvedený pro přehlednost znova
a) V klasické mechanice (Galileiho transformace) je rychlost
toku času stejná ve všech inerciálních soustavách,
nezávisle na jejich rychlosti.
b), c) Ve speciální teorii relativity se uplastňuje efekt
dilatace času - v pohybující se soustavě S' teče čas
pomaleji, než ve výchozí klidové soustavě S.
V předrelativistické
fyzice se o současnosti dvou událostí probíhajících v
různých místech dalo přesvědčit pomocí vhodného signálu,
např. světelného, pro jehož rychlost platil běžný zákon
skládání rychlostí. Dvě události současné z hlediska
jedné vztažné soustavy jsou pak současné i v každé jiné
inerciální soustavě - pojem současnosti má v klasické fyzice absolutní význam
a nezávisí na pohybovém stavu pozorovatele. Z Lorentzových transformací (a
vlastně již z jednoduché úvahy o nezávislosti rychlosti
světla na pohybu vztažné soustavy) však plyne, že dvě
události probíhající v různých místech, které se z
hlediska jedné vztažné soustavy jeví jako současné,
probíhají z hlediska jiné soustavy v různých
časových okamžicích. Ve STR je tedy současnost pojem
relativní, závisí na pohybovém stavu pozorovatele. K
definování současnosti je přitom třeba podle STR použít
světelných signálů, u nichž je zaručena nezávislost jejich
rychlosti na vztažné soustavě.
Podobně rozměry těles a vzdálenosti
mezi nimi v nerelativistické kinematice nijak nazávisí na tom,
zda je sleduje klidový nebo pohybující se pozorovatel. Pro
určení délky nějakého tělesa (tyče, měřítka) v STR je
nutno v dané vztažné soustavě S stanovit současné hodnoty
souřadnic x1,y1,z1 a x2,y2,z2 jeho konců v daném časovém
okamžiku; délka ve směru x pak je Dx = x2-
x1, podobně ve směrech y a z. Provedeme-li totéž z hlediska
vztažné soustavy S' pohybující se rychlostí V, potom z Lorentzových transformací (kde Dt = 0 -
současnost) plyne
| Dx = Dx'/Ö(1 -V2/c2) , Dy = Dy' , Dz = Dz' . |
(1.73) |
Vlastní délkou dané tyče se rozumí její délka lo
měřená ve vztažné soustavě vzhledem k níž je tato tyč v
klidu. Ze vztahu (1.73) plyne, že délka tyče pohybující se v
podélném směru rychlostí v bude
| l = lo . Ö(1 - v2/c2) , |
(1.73') |
Tento poznatek nazývaný Lorentzova kontrakce
délek říká,
že rozměr každého tělesa se ve směru pohybu jeví zkrácený v poměru Ö(1 -
v2/c2) ve srovnání s klidovým
rozměrem; rozměry kolmé ke směru pohybu se nemění, jsou stejné jako klidové.
Z Lorentzových
transformačních vzorců (1.69) rovněž plynou vztahy mezi
rychlostí částice měřenou v různých inerciálních
soustavách. Jestliže v soustavě S', pohybující se vůči
soustavě S rychlostí V ve směru osy X,
bude mít vyšetřovaná částice rychlost v ş (v'x=dx'/dt', v'y=dy'/dt', v'z=dz'/dt') , potom ze vztahů
(1.69) přepsaných v diferenciálním tvaru plynou pro složky
rychlosti v v soustavě S transformační vztahy
 |
(1.74) |
představující Einsteinův
zákon skládání rychlostí. Speciálně, pohybuje-li se v
S' částice ve směru osy X
rychlostí v,
pak výsledek jejího složení s rychlostí V
(stejného směru) soustavy S' vůči S
bude
| v = (v' + V)/(1
+ v'.V/c2) , |
(1.74') |
Je vidět, že součet
dvou rychlostí menších nebo rovných rychlosti světla vždy
dává rychlost nepřevyšující rychlost světla. Jestliže ve
vztahu (1.74) položíme |v'|= c (jedná se třebas o
foton), dostaneme |v| = Ö(vx2+vy2+vz2) = c - rychlost světla se co do
velikosti neskládá se žádnou rychlostí. Dokonce i kdyby se soustava
S' vůči S pohybovala rychlostí V=c a v soustavě
S' prolétala částice rychlostí v'= c ve směru pohybu
soustavy S', výsledná rychlost pohybu této částice vůči S podle vztahu (1.74') v = (c + c)/(1 + c.c/c2)
= c by přesto byla rovna opět jen rychlosti světla. To
potvrzuje vlastnost rychlosti světla c jakožto horní meze
možných rychlostí pohybu. Pokud jsou obě rychlosti v i V malé oproti rychlosti světla c,
přechází vzorec (1.74) v běžný aditivní zákon skládání rychlostí (1.65), t.j. v = v' + V.
Důležitým
speciálním případem Einsteinova zákona skládání
rychlostí je vztah popisující změnu směru šíření světla
při přechodu od jedné inerciální soustavy ke druhé - tzv. aberaci
světla. Pohybuje-li se foton v rovině XY soustavy S' tak,
že směr jeho pohybu svírá s osou X (tj. se směrem rychlosti pohybu V
soustavy S') úhel J, budou složky jeho rychlosti v
soustavě S' rovny v'x=c.cosJ', v'y=c.sinJ'. Pro úhel J
pohybu tohoto fotonu v soustavě S (vx=c.cosJ, vy=c.sinJ) plyne z transformačních vztahů (1.74)
sin J = [(1 - V2/c2)/(1 + (V/c)cosJ')] sin J' , cos J = (cosJ' + V/c)/(1 + (V/c)cosJ')
Pro případ V « c (s
přesností do členů prvního řádu ve V/c) odtud plyne pro
úhel aberace světla DJ = J'- J klasický vztah DJ =
(V/c).sinJ.
Relativnost
kinematických efektů STR
Je třeba upozornit, že výše uvedené kinematické efekty,
způsobené rychlostí pohybu tělesa, jsou pozorovatelné jen relativně
při vzájemném pohybu pozorovaného tělesa a pozorovatele.
Pokud by se pozorovatel *) rozhodl "přistihnout
pohybující se objekt při činu" (co tam, k čertu, s
těmi měřítky a hodinami čaruje..?!..), skočil
by za ním, dostihl jej a začal se pohybovat spolu s ním
stejnou rychlostí, nezjistil by vůbec nic -
měřítka i hodiny by byly v pořádku a všechny
relativistické efekty by při takovém pozorování vymizely..!..
V teorii relativity neexistuje absolutní úhel pohledu.
*) Samotné slovo "pozorovatel"
je obecně ve fyzice třeba brát s rezervou: musí být
oproštěn od jakýchkoli subjektivních vlivů, zdání a
pocitů! Objektivním "pozorovatelem" může být i
přístroj či průběh nějakého přírodního děje...
Paradoxy speciální teorie relativity
Neobvyklost kinematických zákonitostí speciální teorie
relativity, které zdánlivě odporují "zdravému rozumu"
*), vyvolávala (a v laické veřejnosti
vyvolává někdy i dnes) řadu námitek formulovaných často
pomocí "paradoxů". Všechny tyto paradoxy
vznikají chybným nebo nedůsledným použitím zákonitostí
STR (nejčastěji se zapomíná na
relativnost současnosti); část úvahy se provede relativisticky,
část klasicky: Ţ rozpor. Nyní
jsou již zdánlivé paradoxy tohoto druhu spolehlivě vyřešeny [232],[242], mají jen historický
význam, avšak sehrály důležitou úlohu při formulování a
tříbení myšlenkových postupů STR.
*) STR není teorií "selského
rozumu", nýbrž - ať se nám to líbí či je nám to
proti mysli - popisuje vlastnosti skutečného
prostoročasu, v němž žijeme. Lze říci, že tato
teorie představuje vítězství skutečného objektivního
rozumu nad tzv. "selským rozumem",
vycházejícím z omezené zkušenosti každodenního života
lidí v našich pozemských podmínkách...
Paradox času
Nejpodivnějším vývodem teorie relativity se jeví efekt dilatace
času - tvrzení o různé rychlosti běhu času
v různých vztažných soustavách, pro různé pozorovatele.
Máme-li výchozí inerciální vztažnou soustavu S a druhou
soustavu S', kerá se vůči S pohybuje velkou rychlostí V, bude
pozorovatel v S vidět, že hodiny v S' jdou ve srovnání s jeho
"klidovými" hodinami pomaleji, podle relativistické
dilatace času. Pozorovatel v S' však může stejným právem
tvrdit, že jeho soustava je "klidová" a naopak
soustava S je pohybuje rychlostí -V, takže naopak hodiny v S
jdou pomaleji. Kdo má pravdu? Tento zdánlivý nesoulad se
často formuluje jako paradox hodin, zvaný
též paradox dvojčat :
Představme si v myšleném ("sci-fi") experimentu dva pozorovatele A a B,
kteří jsou dvojčata stejného stáří (mají příp.
na rukou přesné, "ideální" hodinky). Pozorovatel A
zůstane zde na Zemi (odhlédneme od její
tíže, rotace a oběhu), zatímco B
nasedne do rakety a odletí na mezihvězdnou vesmírnou cestu
rychlostí blízkou rychlosti světla. Pokud budou spojeni
rádiovými signály, podle STR se pozemskému pozorovateli A
bude na raketě B jevit pomalejší běh času; astronaut B
bude naopak registrovat dilataci času na pozemské základně A.
Po návratu za několik let se oba bratři opět
setkají a porovnají své stáří a hodinky.
Budou mít stejný fyzický věk *) a časový údaj na
hodinkách? - nebo který z nich bude "starší" či
"mladší"?
*) Na otázku, zda cestovatel bude
stárnout v souhlase s chodem svých standardních
"ideálních" hodin, odpovídá biochemie kladně:
stárnutí je důsledkem biochemických procesů na molekulární
a atomární úrovni, jejichž rychlost odpovídá fyzikálnímu
běhu času, měřenému standardizovanými hodinami. Z
filosofického hlediska lze s trochou nadsázky říct, že
"všichni jsme jakýmisi hodinami - a naše tváře jsou
ciferníky let"... (A.Eddington)
K relativistické
analýze tohoto myšleného experimentu podle STR si v
prvé řadě zavedeme jednu stálou inerciální vztažnou
soustavu S s počátkem O ve světobodě startu,
spojenou s "klidovým" pozorovatelem A; ta
zůstáva neměnná během celého pokusu. Pohyb astronauta B
si můžeme rozdělit na 5 etap:
I. Zrychlování pohybu po zapálení
raketových motorů v bodě O, na jejímž konci dosáhne
raketa rychlost V ve směru osy O-x, blízkou rychlosti světla c.
II. Rovnoměrný pohyb rychlostí V po vypnutí
raketových motorů směrem od Země k pozorovacímu cíli
(třebas vzdálené hvězdě).
III. Zrychlený pohyb - po dosažení
pozorovacího cíle (vzdálené hvězdy) se znovu zapálí raketové motory, aby se směr pohybu
sondy změnil na opačný, k Zemi.
IV. Rovnoměrný pohyb opět relativistickou
rychlostí -V, po vypnutí raketových motorů, směrem k Zemi.
V. Zpomalený pohyb po zapnutí raketových
motorů k zabrzdění z vysoké rychlosti V, k přistání na
Zemi.
V tomto idealizovaném myšleném pokusu budeme
pro jednoduchost předpokládat, že raketové motory jsou velmi
výkonné (a kosmonaut B velmi
odolný proti přetížení, jakož i jeho standardní hodinky), takže fáze urychlení (I.), zpětný manévr (III.)
a zabrzdění (V.) budou velmi rychlé, s dobou trvání
zanedbatelně krátkou vzhledem k etapám II. a IV.
rovnoměrného pohybu relativistickou rychlostí V. Pro pohyb
astronauta B pak můžeme nakreslit prostoročasový
diagram :
 |
Prostoročasový diagram
mezihvězdného letu a návratu kosmonauta B při
analýze "paradoxu dvojčat".
Pohyb kosmonauta B je
znázorněn silnější linií O-K´-L´-M´´-N´´-P,
která má krátké zakřivené úseky O-K´, L´-M´´ a
N´´-P, odpovídající urychlování a brzdění
rakety, a dlouhé přímé úseky odpovídající
inerciálnímu pohybu tam a zpět. Šikmými tenšími
čarami je vyznačeno několik linií současnosti mezi
soustavou S´ odlétající rakety a změněnou
soustavou S´´ vracející se rakety - ty mají
opačný sklon!
Pozn.: Vlastní kosoúhlé souřadnicové osy soustav S´
a S´´ v diagramu nejsou zakresleny, obrázek by
se stal nepřehledným. |
Světočára klidového pozorovatele A
je svislá úsečka O-P podél časové osy t v klidové
inerciální soustavě S; odpočítávání času pro
pozorovatele A je na svislé ose t (resp. c.t).
Pohyb "dvojčete"-kosmonauta B je znázorněn
čárou O-K´-L´-M´´-N´´-P, která je nejprve po startu
nakloněná šikmo doprava (úsek O-L´), pak se po návratovém
manévru láme směrem doleva (úsek M´´-L´´) a nakonec
přistává na Zemi ve světobodě P. Při časové
analýze mezi dvěma vzájemně se pohybujícími inerciálními
soustavami je v prostoročasovém diagramu obecně potřeba
používat souřadnicové linie současnosti,
které jsou nakloněny šikmo pod úhlem daným
podílem V/c (srov. obr.1.5). Pro odečet času je v našem případě důležitou
"fintou" uvědomit si, že po obrácerní směru pohybu
v etapě III. se již v etapě IV. jedná o jinou
inerciální soustavu, která má linie současnosti nakloněny opačně
než v etapě II. - ve směru "-V"! Podrobná analýza
vede k výsledku, že součet úseků O-L+M-P zobrazuje kratší
časový interval, než odpovídá úseku OP pro
pozorovatele A. Do společného bodu P se tedy
astronaut B vrátí za kratší vlastní
čas - mladší - než mezi tím uplynul čas
klidovému pozorovateli A. V našem zjednodušeném
případě, kde astronaut B letěl tam i zpět rychlostí V (a úseky zrychlených pohybů jsou zanedbatelně
krátké), bude diference časových
intervalů DtA
a DtB obou pozorovatelů
odpovídat standardnímu vzorci pro dilataci času (1.72):
DtB
= DtA . Ö(1 - V2/c2) .
Pokud by se tedy astronaut B
vydal k nejbližší hvězdě Proxima Centauri, vzdálené 4,2
světelných let, rychlostí např. 0,8 c (cca 240 000 km/s) tam i zpět, pak podle pozemského
pozorovatele A by se vrátil za 14 let; o tuto dobu by
pozemský pozorovatel A zestárnul. Astronaut B by
však při tomto letu zestárnul pouze o 8,2 let vlastního
času, byl by tedy po návratu o 5,5 let mladší než jeho
pozemský bratr A.
V obecném případě dvou
standardních hodin, které se v učitém okamžiku od sebe rozletí
a později se znova setkají, bude časová
diference záviset na "historiích" jejich pohybů -
rychlostech a směrech inerciálních pohybů a dynamikách
neinerciálních změn. Resp. na symetriích
obou pohybů. Pokud se oba pozorovatelé pohybují symetricky
- rakety se rozletí v opačných směrech stejnými rychlostmi a
zrychleními a pak se zase vrátí stejnými pohyby, v místě
setkání se vzájemné relativistické dilatace anulují.
V druhém krajním případě - úplné asymetrie,
který odpovídá zde rozebíranému případu, se projeví plná
hodnota relativistické dilatace času.
Pozn.: V popularizační
literatuře se občas tvrdí, že k řešení paradoxu dvojčat
je třeba použít obecnou teorii relativity (OTR), neboť
vztažná soustava cestovatele je neinerciální: že
příslušný časový rozdíl vzniká právě ve fázi brzdění
a opačného urychlování pohybu druhého pozorovatele. Toto
tvrzení je zavádějící a nepřesvědčivé; zavedení OTR je
jen jiným alternativním způsobem řešení, který je
zbytečně komplikovanější a nepřináší nové informace,
pokud nejsou přítomná "reálná" gravitační pole,
buzená distribucí hmoty-energie. Ve skutečnosti lze vlastní
paradox dvojčat korektně vyřešit v rámci samotné
speciální teorie relativity s použitím tří
inerciálních vztažných soustav: jedné klidové soustavy S
prvního pozorovatele a dvou rozdílných
pohybujících se soustav S´ a S´´ druhého
pozorovatele při jeho pohybu tam a pak zpět, jak bylo výše
nastíněno.
Paradox délky
Druhým podivným vývodem speciální teorie relativity je efekt
kontrakce délek v různých vztažných
soustavách - různé délky pro různé pozorovatele. Máme-li
výchozí inerciální vztažnou soustavu S a druhou
soustavu S', kerá se vůči S pohybuje velkou
rychlostí V, bude pozorovatel v S vidět, že standardní
tyče jsou v S' ve srovnání s jeho
"klidovými" tyčemi kratší, podle relativistické
kontrakce délek. Pozorovatel v S' však může stejným právem
tvrdit, že jeho soustava je "klidová" a naopak
soustava S je pohybuje rychlostí -V, takže naopak tyče
v S jsou zkrácené. Opět vyvstává otázka "kdo
má pravdu?". Tento zdánlivý nesoulad se obecně označuje
jako paradox délek a ilustruje se na různých
pohybujících se tělesech - tyč a stodola, automobil a
garáž, letadlo a hangár, vlak a nádraží či tunel. V
nejjednoduší formulaci "paradox tyče a stodoly"
spočívá v následujícím :
Postavme v myšleném experimentu jednoduché
stavení (přístřešek, kůlnu, stodolu) délky
třebas L= 10 m, která má v přední a zadní stěně dveře.
Tuto stodolu obhospodařuje (a přední a zadní dveře otvírá
či zavírá) pozorovatel A ve výchozí klidové
vztažné soustavě S. Dále je zde vzdálený pozorovatel
B, který ve směru středů těchto dvou dveří vrhne
relativistickou rychlostí např. V= 0,8c (cca
240 000 km/s) tyč délky l= 12 m
a bude se pohybovat spolu s ní jakožto pozorovatel B´ v
inerciální soustavě S´. Co se stane při vniknutí
tyče a jejím průletu stodolou? - "vejde"
se tam ta tyč nebo ne? Z hlediska pozorovatele A
se tyč jeví relativistickou kontrakcí podle vzorce (1.73')
zkrácena na délku l´= 7,2 m a tudíž by se měla do 10m
stodoly v pohodě vejít. Pozorovateli B´ se však naopak
délka stodoly jeví zkrácená na L´= 6 m, takže bude
očekávat problémy při průletu své 12m tyče stodolou. Pro
posouzení toho, zda se prolétající tyč do stodoly vejde či
nikoli, mohou sloužit okamžiky otevření a zavření
předních a zadních dveří. Pokud ze svého hlediska soustavy S
pozorovatel A uzavře oboje dveře v okamžiku, kdy tyč
bude celá uvnitř (konec tyče proletěl
zadními dveřmi), prokáže se tím
zkrácení tyče. Z hlediska pozorovatele B´ se to však
jeví jinak: zadní dveře byly uzavřeny, když moje tyč již
předtím narazila do přednách dveří; moje tyč byla delší
než stodola pozorovatele A. Jejich nesouhlas spočívá v
načasování zavření dveří. V tom, co se rozumí současností
dvou vzdálených událostí (byť zde
vzdálených jen o několik metrů, časové údaje se liší o
pouhé pikosekundy) . Z tohoto hlediska je
vztah současnosti mezi soustavami S a S´ potřeba
analyzovat pomocí linií současnosti, rovnoběžných
s osou X´ na kosoúhlém prostoročasovém diagramu (poněkud podobném jako u výše uvedeného obrázku
"Paradox času"; vzhledem k celkové
marginálnosti tohoto problému jsme zde speciální obrázek
nekreslili...). Podle pozorovatele A
(v jeho vztažné soustavě S) byly v jistém okamžiku
oba konce tyče uvnitř stodoly. Z pohledu pozorovatele B´
nebyly konce tyče nikdy současně uvnitř stodoly,
tyč je delší než stodola. Z formálního hlediska mají oba
pozorovatelé pravdu, jedná se svým způsobem o "optický
klam". Z fyzikálního hlediska je zde důležitá
jedině situace, kdy se oba pozorovatelé setkají v
"zabrzděném" stavu a z hlediska společné vztažné
soustavy snadno zjistí, zda se tyč do stodoly vejde či ne.
Všechno ostatní je jen "STR folklór",
který může být sice pěkný a zajímavý, ale se skutečnou přírodní
realitou již nemusí mít nic společného..!..
Důležité jsou pouze fyzikální interakce
částic a těles. Pokud probíhají vysokými
(relativistickými) rychlostmi, mohou se při nich reálně
uplatňovat efekty dilatace času a kontrakce délek - viz např. "Vysokoenergetické srážky těžších jader.
Kvark-gluonová plasma.",
kde je na obrázku vlevo dole vidět, že při vysokých
energiích se jádra srážejí nikoli jako "kuličky",
ale jako "ploché disky", vlivem kontrakce délky...
Zdánlvě nadsvětelné rychlosti
pohybu ?
Kinematická rychlost, stanovovaná formálně jako rychlost
změny souřadnic nějakého objektu či jevu, může v
některých případech překračovat rychlost světla ve vakuu.
Jednoduchým příkladem může být světelná stopa
- skvrna paprsku z rotujícího kolimovaného zdroje na
stínítku ve velké vzdálenosti (jako je
v dálce pohyb světelného "prasátka" při otáčení
zrcátkem odrážejícím sluneční paprsky, nebo světelná
stopa majáku ve velké vzdálenosti).
Takováto nadsvětelná rychlost však není
rychlostí fotonů které světelnou stopu tvoří. Světelná
stopa v různých místech je tvořena pokaždé jinými fotony (které přicházejí ze směru kolmého ke zdánlivému
pohybu stopy). Mezi jednotlivými
"prasátky" v různých místech není žádný
kauzální vztah, nepřenáší se mezi nimi žádná informace.
Principy STR tedy nejsou nijak narušeny.
V kvantové fyzice se
nadsvětelné rychlosti mohou virtuálně uplatňovat v
souvislosti s kvantovými fluktuacemi a relacemi neurčitosri
(viz např. část "Kvantová fyzika" v monografii "Jaderná
fyzika a fyzika ionizujícího záření"). Pro virtuální částice, které vznikají a
zanikají v průběhu interakcí, jsou možné lokálně
nadsvětelné rychlosti; jejich rychlosti fluktuují mezi
pomalejším a rychlejším pohybem než světlo. Pro skutečné
částice, které existují v počátečním a koncovém
stavu interakce, však nadsvětelné rychlosti nevznikají. Tyto
výchozí a vzniklé částice spolu neinteragují a
intermediální virtuální částice nejsou schopny přenášet
informace.
Důsledkem principiální nelokálnosti kvantového
popisu částic pomocí vlnových funkcí je jev zvaný kvantová
provázanost. Spočívá v tom, že dvě částice, jejichž
kvantový stav je "provázán" původně společnou
vlnovou funkcí, zůstávají v jistém smyslu spojeny i
nadále - korelovány, a to i na libovolně velkou
vzdálenost. Změní-li se stav jedné z provázaných částic,
dojde i ke změně stavu druhé částice, a to
"okamžitě" - nastává jakási "teleportace"
informace, přenos nekonečnou rychlostí (pasáž "Kvantová provázanost a teleportace" v téže kapitole). Pro
reálné změření kvantového stavu je však nutná informace o
měření ve výchozím systému, která musí být přenesena
klasickým komunikačním kanálem, tedy podsvětelnou
rychlostí. Kvantová teleportace tedy neumožňuje přenos
informace rychlostí větší než je rychlost světla.
V kvantové mechanice ani v kvantové teorii pole
tedy neexistují žádné procesy o
nadsvětelné rychlosti, které by bylo možné použít k
přenosu hmoty nebo k informační komunikaci nadsvětelnou
rychlostí.
V relativistické kosmologii, v
globálně zakřiveném prostoročase rozpínajícího se
vesmíru, se velmi vzdálené objekty mohou od sebe vzdalovat
rychlostí překračující rychlost světla. V §5.3 a §5.4
"Standardní kosmologický model.
Velký třesk. Formování struktury vesmíru." bude ukázáno, že galaxie vzdálené více než
c/H (Hubbleoba konstanta H~ 70 km/s/Mpc) se od sebe vzdalují rychlostí větší než je
rychlost světla c. Zmizí za horizont událostí a již
nebudou moci vzájemně interagovat. V relativistické kosmologii
spolu s hmotou expanduje i samotný prostor - resp.
rozpínání je dynamickou vlastností samotného
"volného" protoročasu. Částice hmoty jsou jím jen
unášeny. Z tohoto
pohledu se zde tedy nejedná o mechanický pohyb, takže
vzájemné rychlosti částic při kosmologické expanzi mohou
být i nadsvětelné (aniž by to porušovalo zákonitosti speciální teorie
relativity)....
Pozorování nadsvětelných
rychlostí vzdálených astronomických zdrojů
Pozorujeme-li nějaký vzdálený objekt (emitující světlo) ve
vzdálenosti d, pohybující se prostorem skutečnou
rychlostí v v určitém směru q, bude mít obecně
určitou složku rychlosti pohybu v.cos q směrem k nám a
také kolmo k naší linii pohledu v.sin q. Astronomicky
pozorovaná rychlost v´ zářících objektů se
přímočaře stanovuje tak, že vzdálenost d se
vynásobí pozorovanou úhlovou rychlostí w: v´ = d.w. Úhlová rychlost
se stanoví ze změny pozorované úhlové polohy j1, j2 objektu ve dvou
různých časech t1, t2 : w = (j2-j1)/(t2-t1). Toto však nebude skutečná rychlost v
objektu, jakou bychom změřili u zdroje, ale jen příčná zdánlivá
rychlost v´, vzniklá průmětem skutečné
rychlosti do směru pozorovatele. Tato zdánlivá příčná
rychlost je jediná rychlost astronomických objektů,
kterou lze na obloze přímo měřit. Přitom se zde neuvažuje
konečná rychlost světla, předpokládá se okamžité
šíření. Ve skutečnosti však časový interval t2-t1 mezi oběma
pozorováními je pro příčný pohyb zkrácen v důsledku
přibližování objektu k pozorovateli ...
Z relativistického hlediska má tento fenomen
zajímavé důsledky u vysokých rychlostí blízkých rychlosti
světla, které se často vyskytují ve výtryscích
vysokoenergetických částic z akrečních disků u kvasarů a
aktivních jader galaxií (obrázek vlevo).
Pokud se ve výtrysku nachází nějaká
astronomicky pozorovatelná zřetelná struktura, můžeme
přesným pozorováním její polohy A, B ve dvou
časech t1, t2 (s
odstupem několika měsíců) stanovit
rychlost pohybu této struktury na obloze - v zásadě změřit rychlost
plynu v jetu. Podrobná měření světla (a
obecně elektromagnetického záření)
výtrysků z kvasarů a aktivních jader galaxií ukázala, že v
řadě případů se pohyb struktur zářících plynů v jetech
jeví rychlejší než světlo. Tento klamný efekt se
vyskytuje tehdy, když je rychlost výtrysku blízká rychlosti
světla (>0,9c) a je vysoká složka rychlosti směrem k Zemi
(malý úhel jetu q cca 10°-40°). V takovém případě, jak se
pozorovaná struktura v jetu pohybuje směrem k Zemi, zkracuje
se vzdálenost d2 oproti d1 a tím i časové zpoždění detekce v obou polohách A,
B o hodnotu (v/c).cosq. Jako kdyby sledovaná struktura vzdálenost mezi
oběma místy A-->B stihla překonat dříve. To znamená, že
zdánlivá pozorovaná rychlost v´ se
jeví větší než skutečná rychlost
v, v poměru 1/[1-(v/c).cosq]. Pozorovaná
rychlost v' není limitována rychlostí světla c,
protože je způsobena retardačními efekty.
 |
Skutečná a zdánlivá rychlost
výtrysků z kvasarů.
Vlevo:
Výtrysk z akrečního disku centrální černé díry,
směřující pod určitým úhlem q vzhledem k pozorovateli.
Vpravo:
Trigonometrická analýza pohybu vyšetřovaného
elementu ve výtrysku a pozorovaných světelných
paprsků ve dvou časech.t1, t2. |
Na obrázku vpravo je
znázorněna geometrická situace při vyzáření určitého
sledovaného elementu ve výtrysku z bodu A v čase t1 a jeho příchodu do
bodu B v čase t2. Z těchto míst a v těchto časech jsou přitom
vyslány světelné paprsky k pozorovateli O - jsou
provedena dvě astronomická pozorování polohy j1, j2 na Zemi v časech t1´ a
t2´.
Z trigonometrické analýzy podle obrázku vpravo
tedy plyne, že skutečná příčná-transversální rychlost
sledovaného objektu bude vT = v.sin q. Pozorovaná zdánlivá příčná (úhlově měřená) rychlost
sledovaného objektu pak vzhledem ke zkrácené vzdálenosti d2 = d1 - v.(t2-t1).cos q *), a tedy
kratšímu časovém intervalu mezi detekcemi t2´- t1´ =
(t2-t1)/[1-(v/c).cos q], bude mít hodnotu v´ = v. sin q
/[1 - (v/c). cos q].
*) Jejikož úhel j, pod nímž jsou ze Země
pozorovány detaily výtrysků v blízkosti kvasaru, je velmi
malý (cosj~1), v
rozdílu vzdáleností d1 a d2 není potřeba jej uvažovat. U vzdálených kvasarů
se rychlost koriguje faktorem d.(1+z), kde d je
vzdálenost a z je kosmologický rudý posuv, aby se
získala hodnota rychlosti, kterou by naměřil pozorovatel
pohybující se spolu se zdrojem (tj. v klidu vzhledem ke
zdroji).
Pohybuje-li se sledovaný
objekt směrem k pozorovateli, může docházet k nadhodnocení
pozorované rychlosti vzhledem ke skutečné. Tento efekt
nadhodnocení rychlosti je maximální, pokud úhel q má hodnotu cosq=v/c. Pro určité
kombinace skutečné rychlosti v a úhlu paprsku q může zdánlivá
příčná rychlost vycházet větší než c.
Je to např. tehdy, když v>0,9.c a úhel q je v rozmezí
kolem 5°-40°. Při opačném pohybu - směrem od pozorovatele
(výtrysk na opačnou stranu) by naopak docházelo k podhodnocování
pozorované rychlosti. A když jet směřuje přímo k Zemi (q=0), není
samozřejmě patrný žádný pohyb...
Tato situace se často vyskytuje u výtrysků z
aktivních jader galaxií - z akrečních disků kolem
supermasivních černých děr - kvasarů - je diskutováno v
§4.8, část "Tlusté akreční disky.
Kvasary." a "Mechanismus kvasarů a aktivních jader galexií".
Relativistická dynamika
Zatím jsme
vyšetřovali jen čistě kinematické zákonitosti speciální
teorie relativity. Aplikací relativistické
kinematiky na zákony dynamiky vzniká relativistická
dynamika, poskytující další pozoruhodné efekty.
Newtonovu pohybovou rovnici hmotného bodu dp/dt
= F , která
je invariantní vzhledem ke Galileiho transformaci, je třeba
modifikovat (zobecnit) tak, aby byla invariantní vůči
Lorentzově transformaci, a přitom pro malé rychlosti
přecházela v původní Newtonovu rovnici. Každé hmotné
částici pohybující se vůči inerciální soustavě S rychlostí v se přiřazuje vektor hybnosti p
p =def. m . v
úměrný rychlosti v;
koeficient úměrnosti m představuje setrvačnou hmotnost částice.
Aby Newtonova pohybová rovnice a zákon
zachování hybnosti byly slučitelné s relativistickou
kinematikou, nebude hmotnost m již na pohybu nezávislou
konstantou jako v klasické mechanice, ale bude univerzální
funkcí m = f(v) velikosti rychlosti částice v ş |v| (na směru rychlosti nemůže
záležet vzhledem k izotropii prostoru). Z principu relativity
plyne, že při přechodu k jiné vztažné soustavě S', vůči
níž se sledovaná částice pohybuje rychlostí v', bude p'= m'.v', kde m'=f(v') je tatáž funkce argumentu v', jako funkce m = f(v) argumentu v
(form-invariantnost). Tvar této funkce f je jednoznačně dán
požadavkem, aby zákon zachování hybnosti platil v libovolné
inerciální soustavě. Nejsnadněji lze k němu dojít analýzou
srážky dvou stejných částic prováděnou z hlediska dvou
různých vztažných soustav S a S' za použití relativistické
kinematiky, tj. Lorentzových transformací (tvar funkce f
lze rovněž zízkat z požadavku, aby se p
chovala jako vektor
při Lorentzových transformacích). Vychází f(v) = f(0)/Ö(1 - v2/c2), takže hmotnost částice
pohybující se rychlostí v
je rovna
| m = mo / Ö(1 - v2/c2)
, |
(1.75) |
kde mo je vlastní neboli klidová hmotnost částice shodná s hmotností v
Newtonovské mechanice. Pohybující se těleso tedy vykazuje vyšší
setrvačnou hmotnost, klade větší odpor proti
dalšímu urychlování. V našem běžném životě jsou
rychlosti těles malé, takže žádnou změnu hmotnosti
nepozorujeme. V mikrosvětě se však částice často pohybují
rychlostmi blízkými rychlosti světla a změna hmotnosti je zde
již nezanedbatelná. V urychlovačích se připravují
vysokoenergetické částice, které mají mnohonásobně
vyšší hmotnost než je jejich hmotnost klidová.
Při v®c roste hmotnost m
nade všechny meze, což je dynamickou překážkou
zabraňující tělesům s nenulovou klidovou hmotností mo dosáhnout rychlosti světla
v=c. Existují však i částice (kvanta) s nulovou
klidovou hmotností mo=0,
např. fotony nebo dosud hypotetické gravitony. U těchto částic s mo=0 může hybnost zůstat konečná i při
dosažení rychlosti světla (vztah (1.75) dává při v=c
neurčitý výraz 0/0). Rychlost částic s nulovou klidovou
hmotností dokonce vždy musí být rovna
přesně rychlosti světla c a jejich relativistická
hmotnost je dána velikostí energie kterou přenášejí (tato energie je přímo úměrná frekvenci
vlnění, jehož kvantem je daná částice: E=h.f). Hybnost takové částice s
nulovou klidovou hmotností je pak třeba udávat zvlášť -
nezávisle na její rychlosti (která je
identicky rovna c).
Rychlost,
a tedy i hybnost volné částice, je časově konstantní.
Interaguje-li částice s okolím, rychlost jejího pohybu se
obecně mění, přičemž měřítkem působící síly
je změna hybnosti částice za jednotku času:
Tuto definici síly je výhodné ponechat i v relativistické
mechanice, protože (na rozdíl od součinu hmotnosti a
zrychlení) vede k ekvivalenci zákona akce a reakce se zákonem
zachování hybnosti. Pokud je síla F, která je příčinou změny
hybnosti částice, dána jako funkce místa a času, je vztah
(1.76) rovnicí pohybu dané částice. Na rozdíl od Newtonovy
mechaniky proměnnost m způsobuje, že vektory síly a
zrychlení nemusejí mít stejný směr.
Práce vykonaná silou F s danou částicí hmotnosti m
se, stejně jako v Newtonově mechanice, definuje jako součin
působící síly a vzdálenosti, kterou během tohoto působení
částice prošla:
Pokud síla F působí na jinak volnou částici, lze
předpokládat, že dodaná práce se přemění na kinetickou
energii částice:
dEkin =def. dA
= F.dr .
Pohybuje-li se částice
hmotnosti m rychlostí v, po
dosazení z (1.76) a (1.75) dostaneme
dEkin = m (dv/dt) .dr + (dm/dt) .v.
dr = mv.dv - v2dm =
= mov.dv/Ö(1 -v2/c2)3 = c2 dm . |
(1.78) |
Integrací od 0 do v vznikne vztah
| Ekin = moc2/Ö(1 - v2/c2) - moc2 = c2(m - mo) |
(1.79) |
udávající kinetickou
energii částice s klidovou hmotností mo pohybující se
rychlostí v,
tj. se setrvačnou hmotností m. Při rychlostech v<<c
malých ve srovnání s rychlostí světla tento vztah nabývá
přibližný tvar Ekin»(1/2).mov2 odpovídající známému vzorci
pro kinetickou energii v klasické mechanice.
Vztah
(1.78) udává, že vzrůst kinetické energie tělesa je
doprovázen úměrným zvětšením jeho (setrvačné) hmotnosti m. Z
analýzy mechanických dějů, jako je dokonale nepružná
srážka dvou hmotných těles, s použitím relativistické
kinematiky a zákona zachování energie plyne, že podobný
vztah přímé úměrnosti platí i mezi dodanou energií a
vzrůstem klidové hmotnosti tělesa, přičemž zachovávající
se celková energie
| E = m . c2 = moc2/Ö(1 - v2/c2) = Eo + Ekin |
(1.80) |
se skládá z kinetické energie
| Ekin = (m - mo) . c2 |
(1.80a) |
a z klidové energie
Mezi změnou hmotnosti a
energie platí univerzální Einsteinův vztah "ekvivalence hmoty a energie"
nezávisle na tom, čím
je změna energie nebo hmotnosti způsobena. Z (1.80) a definice
hybnosti p = m.v plyne (vyloučením v)
důležitý obecný vztah mezi energií a
hybností:
| E2 = p2 c2 + mo2 c4 . |
(1.81) |
Vztahy (1.75) a
(1.78)-(1.81), které jsou dynamickým důsledkem relativistické
kinematiky, byly zcela přesně
ověřeny
experimenty v atomové fyzice, jaderné fyzice a fyzice
elementárních částic; staly se již
"inženýrskou
součástí" jaderné techniky.
V
nerelativistické fyzice platily dva zcela samostatné a
izolované zákony zachování: hmoty a energie. Mezi
(setrvačnou) hmotností a energií tělesa neexistoval žádný
univerzální vztah. V Einsteinově teorii relativity však
platí obecný vztah E = m.c2, podle něhož hmotnost m a energie E každého hmotného objektu jsou si
vzájemně úměrné s univerzálním koeficientem c2.
Hmotnost a energie, které v klasické fyzice popisují
kvalitativně různé vlastnosti matérie,
se v teorii relativity ukazují být ekvivalentními
charakteristikami
množství hmoty.
Geometrie prostoročasu. Čtyřtenzory.
V
předrelativistické fyzice prostor a čas vystupovaly jako
nezávislé pojmy pro popis pohybu těles. STR však ukazuje, že
ve skutečnosti se prostor a čas nerozlučně prolínají.
Lorentzovy transformace "promíchávají" časovou
souřadnici se souřadnicemi prostorovými při přechodu od
jedné vztažné soustavy ke druhé. Fyzikální veličinu, k
jejímuž změření stačí jednomu pozorovateli jen pravítko,
musí jiný pozorovatel měřit pomocí pravítka i hodinek.
Čtyřrozměrný prostoročas, který jsme si zavedli na
začátku tohoto odstavce, tak přestává být jen formálním
modelem, ale nabývá hluboký geometricko-fyzikální
význam. K vyjasnění
tohoto významu je třeba zavést v prostoročase metriku, tj. definovat prostoročasové
"vzdálenosti" (odlehlosti) mezi událostmi.
Prostoro-časový
interval a metrika
Důležitou vlastností vzdálenosti l = Ö[(x2-x1)2
+(y2-y1)2 +(z2-z1)2] dvou bodů (x1,y1,z1)
, (x2,y2,z2) v trojrozměrném
Eukleidovském prostoru je její neměnnost při přechodu k jiné soustavě
prostorových souřadnic (třebas při posunech nebo pootočení
souřadnicových os). Výše jsme si ukázali, že veličina s definovaná v (1.66) zachovává svou
hodnotu v libovolné inerciální soustavě, při libovolných
Lorentzových transformacích prostoročasových souřadnic.
Invariantní veličina s definovaná
vztahem
| s1,22 = -c2(t2-t1)2 + (x2-x1)2 + (y2-y1)2 + (z2-z1)2 |
(1.82) |
a nazývaná prostoročasovým intervalem mezi událostmi (t1,x1,y1,z1) a (t2,x2,y2,z2), hraje
tedy úlohu prostoročasové vzdálenosti (odlehlosti) dvou
událostí *).
*) Prostočasový interval s a jeho
diferenciální element ds hraje v teorii relativity
klíčovou úlohu. Vyjadřuje, jak jsou prostoročasové
události od sebe "daleko" - v prostoru i čase. Podle
našich konvenčních představ dvě události mohou být od sebe
"daleko" ze dvou důvodů:
1. Buď se odehrály v různých od sebe
vzdálených místech prostoru;
2. Nebo se staly v různou dobu, proběhl mezi
nimi dlouhý "časový interval".
Teorie relativity "promíchává" prostor a čas a
slučuje je do jednotného prostoročasového kontinua.
Prostoro-časová "vzdálenost" mezi dvěma událostmi
"1" a "2" se pak vyjadřuje pomocí
prostoročasového intervalu s1,2 podle vztahu (1.82). Něco jako Pythagorova věta
zobecněná na 4-rozměrný (pseudo)eukleidovský prostoročas.
Tato hodnota prostoročasového intervalu nezávisí na vztažné
či souřadnicové soustavě, vzhledem k níž je stanovována
(plyne to z konstantní rychlosti světla c; a z toho pak plynou
výše odvozené Lorentzovy transformace (1.69) STR) - je zcela
objektivní.
V STR vystačíme zpravidla s makroskopickým vyjádřením
intervalu s, resp. s2. V následující kapitole 2 (jakož i ve všech
dalších kapitolách knihy) uvidíme, že v zakřiveném
prostoročase obecné teorie relativity je třeba použít diferenciální
element intervalu ds (resp. jeho kvadrát ds2), který má
speciální funkční vyjádření, charakterizující zakřivení
prostoročasu - že v různých místech jsou odlišná
prostorová měřítka a různá rychlost plynutí
(souřadnicového) času.
Jestliže známe prostoročasový interval, tj. závislost
elementu ds2 na souřadnicích, víme o prostoročasu
"všechno" a můžeme pomocí toho zkoumat, jak se v
něm budou pohybovat tělesa (částice) a šířit světlo
(fotony). Jinými slovy, známe metrický tenzor gik a rovnice geodetických
čar - trajektorií volných částic v gravitačním poli
(§2.4 "Fyzikální zákony v zakřiveném prostoročase").
Tím máme v prostoročase zavedenou tzv. Minkowského metriku, kterou v diferenciálním tvaru můžeme
zapsat
ds2 = -c2dt2 + dx2 + dy2 + dz2 ;
zavedeme-li nové
označení x°ş ct, x1şx, x2şy, x3şz , bude Minkowskiho metrika mít tvar *)
| ds2 = -(dx°)2 + (dx1)2
+ (dx2)2 + (dx3)2 . |
(1.83) |
Od normální
Eukleidovské metriky se liší záporným znaménkem u časové
souřadnice. Taková metrika se označuje jako pseudoeukleidovská. Zatímco v Eukleidově geometrii je
vzdálenost mezi dvěma body rovna nule jen tehdy, když oba body
splývají, interval mezi dvěma událostmi v prostoročase
může být nulový i tehdy, když obě události jsou od sebe
velmi daleko (např. jednou takovou
událostí může být vyslání rádiového signálu zde na Zemi
a druhou událostí jím vyvolaný manévr kosmické rakety
třebas někde u Jupitera).
*) Ve speciální teorii relativity (zvláště ve starší literatuře) se často používá imaginární
časová souřadnice x4= ict,
která byla Minkowským zavedena proto, aby se geometrie
prostoročasu formálně podobala geometrii Eukleidova prostoru: ds2 = (dx4)2 + (dx1)2 + (dx2)2 + (dx3)2 .
Tento formalismus má při geometrické intetepretaci STR
některé výhody, např. Lorentzova transformace může být znázorněna jako pootočení souřadnicového systému. Použití
imaginární časové souřadnice má však též nevýhody.
Zakrývá některé důležité strukturní vlastnosti plynoucí
z pseudoeukleidovského charakteru prostoročasu a k výpočtu
některých fyzikálních
veličin, které jsou reálné, se zbytečně používají
operace s komplexními čísly. Hlavně však použití
imaginární časové souřadnice ztrácí jakýkoliv význam v
obecné teorii relativity, kde geometrii zakřiveného
prostoročasu nelze nijak "připodobnit" Eukleidově geometrii. A protože STR nám zde slouží
jako základ pro vybudování obecné teorie relativity a studium
obecných vlastností prostoročasu, budeme zásadně používat reálnou
časovou souřadnici x° =
c t .
Jelikož se ve STR
zabýváme pohyby o rychlostech blízkých rychlosti světla, je
vhodné v prostoročasových diagramech na časové ose místo
prostého času t vynášet časovou
souřadnici
x°= c.t, aby měřítko na časové ose bylo souměřitelné se
škálami na osách prostorových. Takový prostoročasový
diagram, na němž je vyznačena osa x a k ní kolmá časová osa c.t (souřadnice y a z jsou pro
jednoduchost vynechány), odpovídající výchozí vztažné
soustavě S, je znázorněn na obr.1.5c. Na těchto
souřadnicových osách lze odečítat prostoročasové
souřadnice libovolného světobodu (události) ve vztažné
soustavě S. Aby bylo možno odečítat
prostoročasové souřadnice těchto událostí ve vztažné
soustavě S', pohybující se vzhledem k S ve směru osy x rychlostí V, je třeba na tomto diagramu vytyčit
souřadnicové osy x' a x'°= c.t' odpovídající soustavě S'.
Osa x', která je dána podmínkou t'= 0, je podle (1.69)
přímka ct =(V/c).x ; osa t', daná podmínkou x'=0, je přímka
x = (V/c).ct. Jak je tedy vidět z obr.1.5c, přechod k jiné
inerciální soustavě pomocí Lorentzových
transformací geometricky znamená přechod ke kosoúhlé soustavě prostoročasových souřadnic,
jejíž osy jsou vůči původním osám nakloněny o úhel a
daný vztahem tga= V/c. Tento úhel sklonu a roste s rychlostí soustavy S' vůči S, a
při V®c se blíží 45°, kdy osy x' a ct'
splývají. Z takového geometrického vyjádření Lorentzovy
transformace velmi názorně plynou kinematické efekty STR jako
je kontrakce délek nebo dilatace času; rovněž se zde
elegantně řeší známý paradox hodin [232],[242] - je podrobněji analyzováno výše v pasáži "Paradoxy
STR".
Kauzální vztahy v prostoročase
Prostorové a časové souvislosti mezi událostmi a tělesy jsou
vyjádřeny geometrickými vztahy mezi příslušnými útvary ve
čtyřrozměrném prostoročase. Nejjednoduššími
geometrickými objekty v prostoročase jsou již zmíněné
světobody představující jednotlivé elementární události.
Základem našeho
poznávání objektivní reality jsou příčinné
(kauzální) vztahy mezi jevy a událostmi. Podívejme se
proto, jaká omezení na příčinné vztahy mezi událostmi
kladou zákonitosti STR. Sledujme dvě události Aş(tA,xA,yA,zA) a Bş(tB,
xB,yB,zB) z hlediska vztažné soustavy S
(obr.1.6a). Časový interval mezi nimi označíme tAB = tB - tA a jejich prostorovou vzdálenost
lAB: lAB2 = (xB-xA)2 +(yB-yA)2 + (zB-zA)2;
prostoročasový interval sAB mezi nimi bude sAB2 = -c2t2AB + l2AB. Událost B může mít nějakou
příčinnou souvislost s událostí A pouze tehdy, když tyto
události mohou být spojeny signálem šířícím se pomaleji
než světlo, tj. za předpokladu, že lAB < c.tAB, neboli
sAB2 < 0 .
Interval splňující
tuto nerovnost se nazývá časový (časového typu,
"času-podobný"). Zda dvě události spojené
intervalem časového typu spolu skutečně souvisejí, záleží
na konkrétních okolnostech - v zásadě však vždy mohou.
Je-li interval mezi dvěma událostmi
časového charakteru, lze vždy nalézt takovou vztažnou
soustavu S', v níž obě události proběhnou ve stejném
místě rostoru (l'AB=0). Časový interval mezi
oběma událostmi v této soustavě pak je t'AB = Ö(-s2AB/c2) > 0. Pokud interval mezi
dvěma událostmi A a B je časového charakteru a z
hlediska vztažné soustavy S
událost B
nastala později než A, tj. tB > tA, platí tato časová relace i v
každé jiné inerciální soustavě (neexistuje žádná
vztažná soustava, v níž by událost B předcházela události A) - událost B je tedy absolutně budoucí vzhledem k A. Probíhají-li dvě události A a B s týmž tělesem, je interval mezi nimi
vždy časového typu, protože dráha lAB, kterou těleso mezi oběma
událostmi proběhne, je vždy menší neš c.tAB (rychlost tělesa nemůže být větší
než c), takže s2AB = l2AB - c2t2AB < 0.
Jsou-li naopak dvě události A a C odděleny intervalem splňujícím
nerovnost
s2AC > 0 - interval prostorového typu,
je lAC > c.tAC, takže mezi těmito událostmi
nemůže být žádná příčinná
souvislost (událost A nemohla události C o sobě "dát
vědět", protože událost C nastala dříve, než by
jakýkoliv signál mohl překonat vzdálenost lAC). Pro každé dvě události A a C oddělené intervalem prostorového
charakteru lze vždy nalézt takovou vztažnou soustavu S', v
níž t'AC=0, tj. v níž obě události proběhnou
současně; prostorová vzdálenost obou událostí je zde
přitom rovna lAC = sAC. Navíc, pokud v soustavě S událost C nastala později než A (tC
> tA), existuje vztažná soustava S'', z
jejíhož hlediska je časový sled obou událostí opačný: t''A>
t''C. Přitom neexistuje žádná vztažná
soustava, v níž by takové události A
a C byly
soumístné - události oddělené prostorovým intervalem jsou
tedy od sebe absolutně vzdálené.

Obr.1.6. Příčinná struktura a pohyb částic v Minkowského
prostoročase speciální teorie relativity.
a)
Prostoročasový diagram třech událostí A,B,C. Událost B může příčinně souviset s A
(s2AB < 0), zatímco událost C nemůže na události
A nijak záviset (s2AC > 0).
b) Hmotná
tělesa (částice) se v prostoročase pohybují po
světočárách časového typu ležících uvnitř světelných
kuželů, světlo se šíří po izotropních světočárách
ležících na plášti světelného kuželu, hypotetické
tachyony opisují světočáry prostorového typu.
c)
Světelný kužel rozděluje pro každý světobod prostoročas
na příčinně související oblasti absolutní budoucnosti a
minulosti a na absolutně vzdálené oblasti bez příčinné
souvislosti.
Jednorozměrné křivky
- světočáry - ve 4-rozměrném prostoročase
reprezentují pohyby částic. Protože rychlost každého
hmotného tělesa je limitována rychlostí světla, bude na
prostoročasovém diagramu světočára každé částice svírat
s časovou osou x° úhel menší než 45°; množina všech
světočar zkušebních částic procházejících daným bodem
O tedy vyplňuje v prostoročase
"kužel" (4-kužel)
x2 + y2 + z2 - c2.t2 < 0
s vrcholem v tomto bodě
O podle obr.1.6b (kde je událost O vzata jako počátek
souřadnicové soustavy). Takové světočáry se nazývají časového
typu, protože interval mezi jejich dvěma
libovolnými světobody (t,x,y,z) a (t+dt,x+dx,y+dy,z+dz)
splňuje relaci ds2 < 0 - je časového
charakteru.
Foton se pohybuje po světočáře dx2
= (dx°)2, tj. po přímce nakloněné 45° k
časové ose. Množina světočar všech fotonů procházejících bodem O (tj. z bodu O vyzářených nebo do bodu O
přicházejících) tvoří v prostoročase "plochu"
(hyperplochu)
x2 + y2 + z2 - c2.t2 = 0 ,
tj. plášť
zmíněného kužele - tzv. prostoročasového světelného
kužele rozbíhajícího se z bodu O
na všechny strany pod úhlem 45° k časové ose x°. Tento plášť
světelného kuželu v prostoročase vyjadřuje šíření
kulové světelné vlny vycházející z počátku O
(x=y=z=0) v časovém okamžiku t=0. Světočáry ležící na
plášti světelného kuželu se nazývají světelné, izotropní nebo nulové; prostoročasový interval mezi
libovolnými jejich světobody je roven nule:
ds = 0.
Světelný
kužel namířený z dané události O
do budoucnosti obsahuje všechny události, které mohou být
událostí O
ovlivněny; světelný kužel sbíhající se v bodě O z minulosti obsahuje všechny události, které
mohly událost O ovlivnit. Množina všech dvojitých
světelných kuželů vycházejících z každého bodu
(události) prostoročasu v něm vytváří rozvětvující
se příčinnou strukturu. Příslušný světelný kužel
pro každou událost (světobod) rozděluje prostoročas na tři
oblasti (obr.1.6c): oblast absolutní
budoucnosti a absolutní minulosti uvnitř světelného kužele, a
mimo něj ležící oblast obsahující
"absolutně
vzdálené" události bez příčinné souvislosti.
V prostoročase si dále můžeme
představit též světočáry prostorového
typu, které
leží mimo světelný kužel a interval mezi jejichž světobody
ds2> 0 je prostorového charakteru.
Světočáry prostorového typu
reprezentují pohyb nadsvětelnou
rychlostí a nemohou proto odpovídat žádnému reálnému
tělesu. Mohly by vyjadřovat pohyb hypotetických tachyonů
(viz níže). Pohyb po světočárách prostorového typu je
doprovázen "patologickým" kinematickým a kauzálním
chováním: na prostoročasovém diagramu lze snadno nalézt
vztažnou soustavu, v níž taková částice bude současně na
dvou různých místech, i soustavy v nichž tachyon doletí do
svého cíle dříve, než byl svým zdrojem vyzářen - poruší
příčinnost (existuje sice interpretace, v níž porušení
kauzality nenastává, avšak i zde jsou určité problémy
[102]). V dalším nebudeme proto světočárám prostorového
typu připisovat fyzikální význam. Zařadíme zde ale
stručnou pasáž o tachyonech :
Tachyony - částice rychlejší než světlo?
Ze speciální teorie relativity plyne, že žádné hmotné
těleso či částice se nemůže pohybovat rychleji než
světlo, přičemž rychlostí světla se pohybují pouze
částice s nulovou klidovou hmotností. Někteří fyzikové se
však s tímto omezením a asymetrií v oblasti rychlostí
nechtěli smířit a vyslovili spekulativní hypotézu, že by
mohly existovat exotické částice zvané tachyony (řec.
tachyos = rychlý), které by se pohybovaly vyšší
rychlostí než světlo [80],[102] *).
*) Zastánci hypotézy tachyonů
rozdělují částice na tři druhy: Částice s (reálnou)
nenulovou klidovou hmotností, pohybující se podsvětelnou
rychlostí, nazývají bradyony či tardyony.
Částice s nulovou klidovou hmotností, pohybující se
rychlostí světla, označují jako luxony. A
částice, které by se pohybovaly nadsvětelnou rychlostí, se
všeobecně nazývají tachyony.
Ze
základních vztahů (1.75) a (1.81) relativistické dynamiky
mezi (setrvačnou) hmotností, rychlostí, hybností a energií,
plynou některé neobvyklé "exotické" vlastnosti
tachyonů. Ze vztahu m = mo/Ö(1 -
v2/c2) při v>c vychází imaginární
hmotnost tachyonu; totéž platí pro jeho energii E.
Pokud tachyon urychlujeme, snižuje se jeho energie; tachyon s
nulovou energií by se pohyboval nekonečně rychle. Z hlediska
kvantové fyziky by se naráželo na problém, že při vzniku
virtuálních párů tachyonů by se tyto od sebe vzdálily velmi
rychle na větší vzdálenost než je Comptonova a nemohly by
zpětně anihilovat - vakuum by se tím stalo zcela nestabilní.
Pokud by byl tachyon elektricky nabitý, při svém pohybu vakuem
nadsvětelnou rychlostí by snad vyzařoval Čerenkovovo
elektromagnetické záření *) - to by snižovalo jeho
energii a tedy zvyšovalo jeho rychlost, elektricky nabité
tachyony by samovolně vyzářily veškerou svoji energii. I u
elektricky nenabitého tachyonu lze podle obecné teorie
relativity očekávat, že při svém pohybu vakuem rychlostí
větší než c by měl tachyon vyzařovat gravitační
Čerenkovovo záření (vytvářející kužel
táhnoucí se za ním), které by odnášelo energii tachyonu,
který by se tím urychloval na stále vyšší rychlost.
*) Čerenkovovo záření
je elektromagnetické záření vznikající tehdy, když se
elektricky nabitá částice pohybuje v optickém prostředí
rychlostí převyšující rychlost světla v tomto prostředí
(která je menší než c). Toto záření je jakousi
"rázovou vlnou" podobnou akustickému třesku v
atmosféře u letadla pohybujícího se nadzvukovou rychlostí.
Fyzikální mechanismus vzniku Čerenkovova záření je popsán
v pasáži "Čerenkovovo záření" §1.6 "Ionizující záření" knihy
"Jaderná fyzika a fyzika ionizujícího záření". "Klasické" Čerenkovovo záření
vzniká interferencí depolarizačních elektromagnetických vln
látkového prostředí z jednotlivých míst dráhy částice. V
případě tachyonu ve vakuu však látkové prostředí chybí,
snad by se zde mohla projevit elektrická polarizace vakua,
jejíž "virtualitě" by částice "uletěla"
a polarizace by se stala reálnou..?..
Jelikož podobně jako v elektrodynamice zrychleným pohybem
elektrických nábojů vznikají elektromagnetické vlny, podle
obecné teorie relativity vznikají zrychleným pohybem hmoty
gravitační vlny šířící se rovněž rychlostí c,
lze očekávat i gravitační analogii
Čerenkovova záření (k tomuto je autor této knihy skeptický
- jakým mechanismem by se parciální vlny budily..?..).
Tyto "divoké" dynamické vlastnosti
tachyonů, stejně jako shora zmíněné kinematické a
kauzální patologie, jsou z fyzikálního hlediska jen těžko
přijatelné. Proto je reálná existence tachyonů ve fyzice
obecně odmítána. Žádné jevy svědčící
pro účast tachyonů nebyly pozorovány, tyto částice nemají
ani žádnou úlohu v logické stavbě teoretické fyziky, nejsou
nutné k vysvětlení žádného dosud pozorovaného jevu. Podle
principu Occamovy břitvy (je diskutován v §1.1) se
tedy předpokládá, že neexistují.
Tachyony se občas objevují jako některá
řešení ve formalismu unitárních teorií pole, viz. §B.6
"Sjednocování fundamentálních interakcí.
Supergravitace. Superstruny.".
Zařazení tachyonů mezi další "exotické" a
hypotetické částice do systematiky elementárních částic je
zmíněno v §1.5 "Elementární
částice", pasáž "Hypotetické a modelové částice" knihy "Jaderná fyzika a fyzika
ionizujícího záření".
_____________________________________________
Vzhledem k
invariantnosti intervalu má klasifikace prostoročasových
intervalů mezi událostmi a světočar částic na časové,
izotropní (nulové) a prostorové, stejně jako rozdělení
oblastí prostoročasu podle kauzální souvislosti na absolutně
budoucí nebo minulé a absolutně vzdálené, absolutní význam, nezávislý na vztažné soustavě. I když
konkrétní prostorové a časové relace mezi událostmi obecně
závisejí na vztažné soustavě z níž jsou pozorovány, u
příčinně souvisejících událostí mají pojmy
"dříve" a "později" absolutní význam.
Jen tak mohou mít smysl pojmy příčiny a následku. Teorie relativity tedy fyzikálně konkretizuje
pojem příčinnosti na základě vlastností šíření
interakcí. Souvislosti mezi příčinností a strukturou
prostoročasu budou podrobněji rozvedeny v §3.2 a 3.3.

Obr.1.7. Vyjádření evoluce a pohybu těles ve
čtyřrozměrném prostoročase.
a) Těleso T
v trojrozměrném prostoru a jeho projekce do roviny XY.
b)
Hyperrovina x° = const. = c.t ve čtyřrozměrném prostoročase
představuje celý nekonečný trojrozměrný prostor v časovém
okamžiku to.
c) Těleso T
opisuje ("vyřezává") při svém pohybu v
prostoročase čtyřrozměrnou "světovou trubici".
d) Světová
trubice pulzujícího tělesa.
Dalšími geometrickými
útvary v prostoročase jsou dvojrozměrné plochy a
trojrozměrné hyperplochy ("nadplochy").
Hyperrovina x° = const., tj. t = const.= to v prostoročase je vlastně
celý nekonečný trojrozměrný prostor v časovém okamžiku t
= to. Máme-li nějaké (trojrozměrné)
těleso T (obr.1.7a) v okamžiku to,
bude v prostoročase vyjádřeno jako příslušný ohraničený
útvar v hyperrovině x°= c.to= const. (obr.1.7b), jehož
(dvojrozměrná) hranice představuje povrch tělesa T v
čase t = to. Fyzikální soustava
konečných rozměrů (např. vnitřek tělesa T)
při svém pohybu a vývoji opisuje ("vyřezává") v
prostoročase jakousi čtyřrozměrnou "trubici" zvanou
prostoročasová neboli světová trubice, která
vyjadřuje množinu všech bodů soustavy (tělesa) ve všech
časech t (obr.1.7c). Trojrozměrný
"plášť" této trubice představuje povrch tělesa ve
všech časech - evoluci tvaru tělesa. Např. povrch kulového
tělesa o konstantním poloměru R se středem v počátku
souřadnic (tj. kulová plocha x2+y2+z2 = R2= const.) ve všech časech t
bude v prostoročase tvořit válcovou hyperplochu s osou x°.
Důležitým speciálním případem
4-rozměrné prostoročasové (světové) trubice je světelný
kužel, analyzovaný výše v části "Kauzální
vztahy v prostoročase", obr.1.6. Jeho trojrozměrný
plášť daný rovnicí x2+y2+z2-c2t2 = 0 (světelný
"hyperkužel") představuje povrch obyčejné koule
(vlnoplochu světelného signálu) se středem v počátku,
jejíž poloměr se nejprve zmenšuje rychlostí světla z
nekonečna až k nule, a potom zase roste
rychlostí c
do nekonečna. Většinou se však bere jen ta polovina
světelného kužele, která směřuje do budoucnosti.
Podobně jako světočáry, i hyperplochy v prostoročase se
klasifikují na prostorové, izotropní (světelné) a časové
podle toho, zda čtverec intervalu mezi jejich světobody je
vždy kladný, může být nulový nebo záporný. Např.
hyperrovina t=const. je prostorového typu, plášť světelného
kuželu je izotropní hyperplochou.
Čtyřrozměrné vektory a tenzory
Prostoročasové souřadnice a komponenty veličin v
prostoročase budeme označovat latinskými indexy
i,j,k,..,m,n,..., které nabývají hodnoty 0,1,2,3; např. xi
ş (x°,x1,x2,x3). Čistě prostorové
souřadnice a komponenty budeme opatřovat řeckými indexy a,b,....,m,n,..., probíhajícími hodnoty 1,2,3;
např. xaş (x1,x2,x3). Při zápise algebraických
operací s těmito indexovanými veličinami je velmi výhodné
používat tzv. Einsteinova sumačního pravidla, podle
něhož přes každý index, vyskytující se v součinu
dvakrát, se provádí sčítání, přičemž sumační symbol S se vynechává. Například i=0S3AiAi = A°Ao+A1A1+A2A2+A3A3 ş AiAi;
zjednodušení zápisu je evidentní.
Výraz pro
prostoročasový interval (1.83) STR je speciálním případem
obecné kvadratické formy
| ds2 = gik dxi dxk = hik dxi dxk , |
(1.84) |
jejíž koeficienty,
tzv. metrický tenzor gik (viz §2.1) *), má speciální
tvar
| gik = hik ş |
/ |
-1 |
0 |
0 |
0 |
\ |
; |
|
|
|
|
| | |
0 |
1 |
0 |
0 |
| |
| | |
0 |
0 |
1 |
0 |
| |
| \ |
0 |
0 |
0 |
1 |
/ |
hik se někdy nazývá Minkowského metrický tenzor.
*) Zde v STR je zavedení metrického tenzoru jen formální,
při použití běžných kartézských souřadnic má
triviální hodnoty komponent. V kap.2 (a ve všech dalších)
uvidíme, že metrický tenzor má klíčový význam v obecné
teorii relativity - popisuje gravitaci jakožto geometrii
zakřiveného prostoročasu.
Přechod od inerciální
soustavy S se souřadnicemi xi ş
(x°,x1,x2,x3) k soustavě S' se souřadnicemi
x'i ş (x'°,x'1,x'2,x'3) musí být lineární transformací prostoročasových souřadnic
| x'i = k=0S3aik xk + bi = aik xk + bi , i=0,1,2,3 |
(1.86) |
(aik a bi
jsou konstanty nezávislé na x), protože podle principu
relativity částice, pohybující se rovnoměrně přímočaře
v inerciální soustavě S, se musí rovnoměrně
přímočaře pohybovat i z hlediska každé jiné inerciální
soustavy S'. Aby byl splněn princip stálé
rychlosti světla, musí tato transformace dále vyhovovat
podmínce
| s2 = hik xi xk = hik x'i x'k = s'2 |
(1.87) |
invariantnosti intervalu. Transformace xi®x'i (1.86) vyhovující podmínce
(1.87) jsou čtyřrozměrným vyjádřením obecných
Lorentzových transformací mezi inerciálními soustavami S a S'. Jestliže souřadnice a čas měříme
takovým způsobem, že při t=t'=0 počátky kartézských
souřadnic v obou soustavách S a S'
splývají, jsou bi = 0 - jedná se o tzv. homogenní Lorentzovy
transformace
Na obr.1.5c jsme si
ukázali, že Lorentzova transformace geometricky znamená
přechod mezi kosoúhlými prostoročasovými souřadnicemi.
Transformační vztah (1.86) obsahuje
celkem 4´4=16 zdánlivě nezávislých
koeficientů aik. Dosazením z transformačního
vztahu (1.86') do (1.87) však dostaneme podmínku hik = hlm ali amk, která tyto koeficienty svazuje 10-ti
rovnicemi (vzhledem k symettrii v indexech i,k). Zůstává proto
pouze 6 nezávislých transformačních koeficientů v (1.86')-
odpovídají třem parametrům udávajícím směr os x',y',z' a
třem komponentám vektoru rychlosti pohybu soustavy S' vůči
S. Množina všech homogenních
Lorentzových transformací (1.86') tvoří grupu - spojitou
6-parametrovou Lorentzovu grupu (Ą6).
Rovněž
množina všech nehomogenních Lorentzových transformací
(1.86), které z homogenních transformací vznikají přidáním
čtyř transformací posunu počátku prostoročasových
souřadnic x'i®x'i + bi, tvoří 6+4=10-parametrovou
grupu - tzv. Poincarého grupu.
V
případě speciální Lorentzovy transformace vztah (1.86')
přejde v (1.69), takže koeficienty aik mají hodnoty
 |
(1.86'') |
Hlavním úkolem
speciální teorie relativity je formulace fyzikálních zákonů
nezávisle na inerciální vztažné soustavě. Ve
čtyřrozměrném prostoročase tyto fyzikální zákony
přecházejí v geometrické vztahy mezi objekty v prostoročase,
které jsou nezávislé na volbě prostoročasových souřadnic.
Podobně jako v trojrozměrném prostoru klasické fyziky
vektorový zápis fyzikálních zákonů zaručuje jejich
platnost nezávisle na použitých prostorových souřadnicích
(neměnnost např. při posunech nebo pootočeních souřadnicových os),
splnění principu relativity ve STR lze nejlépe vyjádřit
tím, že fyzikální zákony budou formulovány jako vektorové a tenzorové rovnice ve čtyřrozměrném
prostoročase. Taková vektorová nebo tenzorová rovnice platná
v jedné souřadnicové soustavě, automaticky platí i v každé
jiné soustavě souřadnic. Navíc zákony mechaniky a
elektrodynamiky nabývají zvláště jednoduchý a názorný
charakter, jsou-li vyjádřeny pomocí vztahů mezi vektory a
tenzory ve čtyřrozměrném prostoročase - viz níže "Čtyřrozměrná
mechanika"
a "Čtyřrozměrná elektrodynamika".
Souřadnice (ct,x,y,z) = (x°,x1,x2,x3)
ş xi dané události lze považovat
za komponenty čtyřrozměrného "polohového vektoru"
příslušného světobodu v prostoročase. Čtverec
"délky" tohoto polohového 4-vektoru lze pak definovat
jako interval mezi počátkem (0,0,0,0) a daným světobodem
(x°,x1,x2,x3): (xi)2 = -(x°)2 +(x1)2+(x2)2 +(x3)2 = hik xi xk ; je to veličina invariantní
vzhledem k Lorentzovým transformacím. V kontextu s obecnou
definicí vektorů v n-rozměrném prostoru se pod čtyřrozměrným
vektorem (4-vektorem) Ai rozumí soubor čtyř veličin
A°,A1,A2,A3, které se při transformacích
(1.69') prostoročasových souřadnic transformují stejně jako
souřadnice xi :
| A'i = aik Ak = (¶x'i/¶xk) . Ak . |
(1.88) |
Kromě uvedených
komponent 4-vektorů Ai s indexy nahoře, zvaných kontravariantní, se zavádějí též tzv. kovariantní složky Ai s indexy dole pomocí vztahu
| Ai ş hik Ak , tj. Ao = -A° , A1 = A1 , A2 = A2 , A3 = A3 . |
(1.89) |
Lze
snadno ukázat, že transformační vlastnosti kovariantních
složek jsou
| A'i = (¶xk/¶x'i) . Ak , |
(1.88') |
tj. kovariantní a kontravariantní složky se transformují
navzájem "kontragredientně".
Pod skalárním
součinem
dvou 4-vektorů A a B se rozumí algebraický výraz AiBi
= A°Bo + A1B1 + A2B2 + A3B3 = hikAiBk = -A°B°+A1B1+A2B2+A3B3 = AiBi; jedná se o skalár
invariantní vzhledem k transformacím souřadnic. Čtverec
velikosti daného 4-vektoru A se definuje jako jeho skalární
součin samého se sebou: (A)2 ş AiAi
= -(A°)2+(A1)2 +(A2)2+ (A3)2. Podle znaménka čtverce
4-vektoru se prostoročasové čtyřvektory rozdělují na tři
skupiny : AiAi < 0 - vektor
časového typu; AiAi = 0 - nulový neboli izotropní
vektor; AiAi > 0 - vektor prostorového
typu. Tři prostorové složky A1,A2,A3 4-vektoru Ai tvoří trojrozměrný vektor A (vzhledem k transformacím čistě
prostorových souřadnic), takže soubor komponent 4-vektoru lze
symbolicky zapsat jako Ai ş
(A°,A). Takové rozložení 4-vektoru
na prostorovou a časovou část lze provést v každé
inerciální soustavě, mění se však samozřejmě při
Lorentzových transformacích. Čtverec 4-vektoru Ai
potom je AiAi = -(A°)2+ A2. Pro vektor Ai
časového typu lze vždy nalézt takovou soustavu S', v níž
prostorový vektor A'=0 (je to soustava S', jejíž
časová osa má směr 4-vektoru Ai); podobně pro každý vektor Bi
prostorového typu lze najít soustavu S', v níž je jeho
časová komponenta B'°= 0.
V prostoročase se dále
pomocí svých transformačních vlastností zavádějí
složitější veličiny - tenzory. Kontravariantním 4-tenzorem
r-tého řádu se rozumí souhrn 4r veličin Ti1,i2,...,ir, které se při transformaci
souřadnicové soustavy xi®x'i = aikxk transformují jako součin
r-souřadnic xi :
T'i1,i2,...,ir = ai1k1. ai2k2 ... airkr
. Tk1,k2,...,kr .
Analogicky kovariantní
a smíšené tenzory - viz obecnou definici v §3.1. Skalár je
tenzorem 0.řádu, vektor tenzorem 1.řádu.
Souvislost mezi kovariantními a
kontravariantními složkami tenzorů, tj. "zvedání"
a "spouštění" indexů, se uskutečňuje přes
metrický tenzor, ve STR tedy přes Minkowského tenzor hik. Např. Tik =himTmk = hil.hkm.Tlm. Při použité Minkowskiho
metrice platí jednoduché pravidlo: při zvedání a
spouštění prostorových indexů (1,2,3) se hodnoty
komponent nemění, při zvedání a spouštění časového
indexu (o) se mění znaménko této složky.
Aritmetické operace mezi tenzory
(složkami tenzorů) se řídí jednoduchými a přirozenými
pravidly tenzorové algebry
[214],[163],[33]. Pomocí tenzorového součinu vznikají
tenzory vyšších řádů, např. součinem tenzoru 2.řádu Aij a 1.řádu Bk (tj. čtyřvektoru) vzniká
tenzor 3.řádu Tijk = Aij.Bk ; analogicky pro smíšené
tenzory. Naopak, pomocí operace "zúžení",
spočívající v sumaci přes dvojici indexů v daném tenzoru,
vznikají tenzory nižších řádů. Např. z tenzoru čtvrtého
řádu Aiklm zúžením vznikne tenzor
druhého řádu Aik = Aikll; zúžením tenzoru 2.řádu Aik dostaneme skalár A = Aii = A°o+A11+A22+A33 , který
se nazývá stopou tenzoru Aik.
Mezi
tenzory 2.řádu zaujímají zvláštní postavení Minkowskiho
tenzor hik a hik, a rovněž tzv. Kroneckerův
delta-symbol dik : dik=1 pro i=k, dik=0 pro iąk -
jeho stopa dii= 4; komponenty těchto tenzorů jsou
stejné ve všech souřadnicových soustavách STR. Takové
tenzory se nazývají izotropní. Platí him.hmk = dik a pro každý vektor Ai
je dkiAi= Ak; tenzor dki má tedy charakter jednotkového
4-tenzoru 2.řádu. V tenzorovém počtu se rovněž často
používá jednotkový izotropní tenzor 4.řádu - Levi-Civitův tenzor eiklm antisymetrický ve všech indexech, jehož složka e0123 = +1 a ostatní nenulové složky (tj.
ty, u nichž jsou všechny čtyři indexy různé) jsou rovny +1
nebo -1 podle toho, zda daná posloupnost indexů i,k,l,m je z
posloupnosti 0,1,2,3 utvořena sudým nebo lichým počtem permutací.
Máme-li skalární,
vektorové nebo tenzorové veličiny definovány nejen v jednom
bodě, ale v každém bodě dané oblasti prostoru (zde
prostoročasu), mluvíme o skalárních, vektorových a
tenzorových polích. Pravidla a operace vektorové
analýzy, tak užitečné ve fyzice pole a kontinua, je
přirozené přenést a zobecnit na čtyřrozměrný
prostoročas.
4-gradient skalárního pole j = j(xi) se definuje jako čtyřvektor,
jehož kovariantní složky jsou
 |
(1.90) |
Čtřdivergencí vektorového pole Ai = Ai(xk) se rozumí skalární pole
| Ai,i
ş ¶Ai/¶xi = ¶A°/¶t + div A ; |
(1.91) |
analogicky 4-divergencí
tenzorového pole Tik je čtyřvektor (vektorové
pole) Ti = Tik,k ş ¶Tik/¶xk.
Diferenciální operátor ¶/¶xi
je výhodné označovat prostě indexem s čárkou " ,i ", což podstatně zjednodušuje
zápis takových vztahů. Operátor ¶/¶xi je zobecněním Hamiltonova
operátoru Ń = i. ¶/¶x + j.¶/¶y +k.¶/¶z . Prostoročasovým zobecněním
Laplaceova diferenciálního operátoru D = ¶2/¶x2
+ ¶2/¶y2 + ¶2/¶z2 je d'Alembertův operátor
 |
(1.92) |
Tedy žj = j ,i,i = ¶2j/¶x2 + ¶2j/¶y2 + ¶2j/¶z2 - (1/c2) ¶2j/¶t2.
Gaussova
věta vektorové analýzy v trojrozměrném Eukleidovském
prostoru
 |
(1.93) |
podle níž integrál
divergence vektoru A přes nějaký objem V je
roven toku tohoto vektoru přes uzavřenou plochu S = ¶V ohraničující tento objem, se ve
čtyřrozměrném prostoročase zobecňuje na tvar
 |
(1.93') |
kde dW = dx0dx1dx2dx3 = c.t.dV je element 4-objemu v
prostoročase a dSi jsou složky 4-vektoru elementu
hyperplochy S = ¶W
ohraničující 4-objem W, přes který se integruje na
levé straně; dS° =dx1dx2dx3 = dV, dS1 = dx0dx2dx3 = c.dt.dy.dz, podobně dS2
a dS3.
Vztah mezi křivkovým integrálem vektoru
přes uzavřenou křivku C a plošným integrálem přes
plochu S, ohraničenou křivkou C,
je v trojrozměrné vektorové analýze dán Stokesovou větou
 |
(1.94) |
Integrál podél uzavřené čtyřrozměrné křivky C se
převádí na integrál přes hyperplochu S ohraničenou touto křivkou C obecně
tak, že dxi se nahradí dSik ¶/¶xi.
Přímé zobecnění Stokesovy věty pro křivkový integrál
4-vektoru Ai pak zní :
 |
(1.94') |
kde komponenty
antisymetrického tenzoru plochy dSik = dxidx'k - dxkdx'i udávají projekce plošného
elementu (braného jako rovnoběžník se stranami dxi
a dx'i) do souřadnicových rovin). Analogicky
pro tenzory vyšších řádů.
Čtyřrozměrná mechanika
Pohyb hmotné
částice je v klasické mechanice popsán trajektorií v trojrozměrném Eukleidově
prostoru
r = r(t)
, tj. xa = xa(t) , a = 1,2,3 .
Ve čtyřrozměrném
prostoročase je pohyb částice reprezentován její světočárou, kterou lze popsat parametrickou rovnicí
kde l je vhodný parametr. Jako parametr l lze použít buď souřadnicový čas t,
lépe však invariantní veličiny - vlastní čas t nebo přímo "délku"
světočáry danou prostoročasovým intervalem s.
Vektory rychlosti v = dx/dt a
zrychlení a = dv/dt = d2x/dt2
hrají důležitou úlohu v klasické mechanice, takže je
užitečné zavést jejich čtyřrozměrné analogie. Přímým
zobecněním vzniklá veličina dxi/dt se nehodí, protože to není
čtyřvektor (dt není invariant). Invariantni mírou času je
vlastní čas t, takže jako čtyřrychlost
je přirozené definovat 4-vektor se složkami *)
| ui =def dxi/dt =
c . dx i/ds . |
(1.96) |
Vzhledem ke vztahu
(1.72) mezi dt a dt lze složky čtyřrychlosti
vyjádřit pomocí obyčejné rychlosti v
ve tvaru
 |
(1.96') |
při malých rychlostech
v«c prostorová část 4-rychlosti přechází v obyčejnou
rychlost v. Ze vztahu dxidxi = c2dt2 snadno plyne
Z geometrického
hlediska je čtyřvektor c.ui jednotkový tečný vektor ke
světočáře dané částice.
*) Často se 4-rychlost
definuje jako ui = dxi/ds = c-1dxi/dt ; takto definovaná čtyřrychlost je
bezrozměrnou veličinou.
4-zrychlení částice se definuje jako
| ai =def dui/dt =
d2xi/dt2 = c2 d2xi/ds2 , |
(1.98) |
Z derivace vztahu (1.97) podle t pak plyne
tj. čtyřvektory
rychlosti a zrychlení v prostoročase jsou vzájemně kolmé.
Pohyb volné částice, který probíhá rovnoměrně
přímočaře (v=const., a = 0), je ve čtyřrozměrném
tvaru vyjádřen rovnicí
| a i ş d2xi/dt2 = 0 |
(1.100) |
popisující přímkovou
světočáru.
Čtyřrozměrným zobecněním hybnosti p = mo.v klasické mechaniky je 4-vektor
| p i =def mo . u i |
(1.101) |
zvaný čtyřhybnost. Dosazením složek u i z (1.96') dostáváme

Srovnáním se vztahy (1.75) a (1.80) pro
hybnost a energii ve STR je vidět, že prostorová část 4-hybnosti
je rovna relativistické hybnosti p
= m.v = mo.v/Ö(1-v2/c2) a časová komponenta je p° =
E/c. Složky 4-hybnosti lze proto zapsat jako
| p i = (
E/c , p ) . |
(1.101') |
Z prostoročasového
hlediska jsou tedy energie E a
hybnost p
částice složkami jediného čtyřvektoru - 4-hybnosti, kterou
lze proto označit za jakýsi "vektor energie-hybnosti"
jednoznačně charakterizující pohybový stav částice.
Čtverec 4-hybnosti pipi = (moui).(moui) = mo.c2 je podle (1.101) roven pipi
= E2/c2 - p.c2, což vede ke vztahu (1.81).
4-vektor síly neboli čtyřsíla se definuje jako
časová změna 4-hybnosti částice
| f i =def dpi/dt =
mo
dui/dt . |
(1.102) |
S obyčejným
trojrozměrným vektorem síly F = dp/dt
souvisejí komponenty 4-síly vztahem
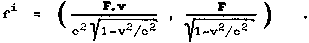 |
(1.102') |
Mezi 4-sílou a
4-hybností platí vztah f i.ui = 0, tj. 4-síla je v
prostoročase "kolmá" k 4-rychlosti.
Newtonova pohybová rovnice
dp/dt = F má ve čtyřrozměrném zobecnění tvar
prostorová část této
rovnice popisuje změnu hybnosti, časová komponenta změnu
energie částice pod vlivem působící síly.
V teoretické fyzice se
pohybové zákony často odvozují pomocí variačního
principu nejmenší akce [165]. Volná (relativistická) částice o
klidové hmotnosti mo, pohybující se v prostoročase
od bodu A bo bodu B, se popisuje integrálem akce

kde s je
prostoročasový interval a t vlastní čas částice. Tato
akce S je úměrná délce světočáry částice, tj. relativistickému
intervalu s. Variační princip nejmenší akce dS = 0 pak vede k Lagrangeovým
rovnicím,
z nichž plynou pohybové rovnice relativistické mechaniky (1.100).
Tenzor energie-hybnosti
Veličiny
energie a hybnost se užívají buď jako charakteristiky
jednotlivých diskrétních částic a těles, nebo jako úhrnné
veličiny charakterizující danou soustavu jako celek. Máme-li
však částice ve vyšetřovaném systému rozloženy
dostatečně hustě tak, že je můžeme považovat za kontinuum,
nebo se jedná dokonce o pole (v §1.5 jsme si ukázali, že
pole je určitou "rozprostřenou" formou hmoty), je
třeba vyšetřovat hustotu, s jakou jsou základní
fyzikální charakteristiky jako je hmotnost, energie, hybnost,
moment hybnosti, elektrický náboj a pod., v prostoru
rozloženy. Kromě toho je užitečné popsat, jak tyto veličiny
v systému proudí z jednoho místa
na druhé.
Označíme-li
hustoru energie e = dE/dt, je lokální zákon
zachování energie vyjádřen rovnicí
kontinuity
| ¶e / ¶t +
div (v.e ) = 0 . |
(1.104) |
Díky univerzálnímu vztahu (1.81) mezi
energií, hmotností a hybností je hustota rozložení hybnosti P = dp/dV
dána hustotou proudu energie v.e : P = v.e/c (=v.r pro
nekoherentní prach). Lokální zákon zachování hybnosti
může být napsán ve tvaru
| div (v. Pa)
+ ¶Pa/¶t
= 0 , (a = 1,2,3) |
(1.105) |
(zachovává se každá
komponenta Pa hybnosti).
Víme,
že energie a hybnost jsou v prostoročase složkami 4-vektoru
energie-hybnosti (4-hybnosti). Stejně tak rovnice (1.104) a
(1.105) zachování energie a hybnosti lze sloučit do jedné
tenzorové rovnice
| ¶ Tik/¶xk ş T ik,k
= 0 , |
(1.106) |
kde
| Tik = e . |
/ |
1 |
vx/c |
vy/c |
vz/c |
\ |
(1.107') |
| | |
vx/c |
vxvx/c2 |
vyvx/c2 |
vzvx/c2 |
| |
| | |
vy/c |
vxvy/c2 |
vyvy/c2 |
vzvy/c2 |
| |
| \ |
vz/c |
vxvz/c2 |
vyvz/c2 |
vzvz/c2 |
/ |
je tenzor energie-hybnosti.
Tenzor
energie-hybnosti, který úplně popisuje rozložení
a pohyb energie a hybnosti v dané fyzikální soustavě, má
obecně strukturu :
| Tik = |
/ |
hustota energie |
hustota proudu energie,
tj. (hustota hybnosti)/c |
\ |
(1.107) |
| | |
| |
| | |
hustota proudu energie,
tj. (hustota hybnosti)/c |
hustota proudu hybnosti,
tj. tlaky a napětí
(tenzor napětí) |
| |
| \ |
/ |
Fyzikální význam jednotlivých komponent
tenzoru energie-hybnosti Tik je tedy následující:
- T°° - hustota energie
(~hmotnosti); tato složka je ve fyzikálně reálných
situacích nejdůležitější a dominantní
- T a° - a-složka proudu energie = a-složka hustoty hybnosti
- T ab - a-složka hustoty b-složky hybnosti, tj. a-složka síly působící na
daný objemový element přes jednotkovou plošku s
normálovým vektorem eb.
Rozepsáním
tenzorového zákona zachování (1.106) ve složkách a
oddělením prostorových a časových derivací dostaneme
rovnice
(1/c) (¶T°°/¶t) + ¶T°a/¶xa = 0
, (1/c) (¶Ta°/¶t) + ¶Tab/¶xb = 0 .
Jejich integrací přes
nějakou (libovolnou) prostorovou oblast V:
(1/c) ¶/¶t VňT°°
dV+ Vň(¶T°a/¶xa) dV = 0
, (1/c) ¶/¶t VňTa° dV+ Vň(¶Tab/¶xb) dV = 0
a po úpravě pomocí
Gaussovy věty (trojrozměrné) vznikají dvě rovnice
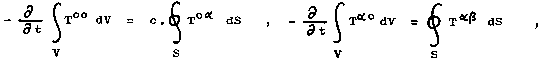 |
(1.106'') |
kde integrály na pravé straně se berou přes uzavřenou
plochu S = ¶V obklopující objem V.
Podle první z těchto rovnic je rychlost změny energie
obsažené v objemu V rovna toku energie přes
uzavřenou plochu S ohraničující tento objem.
Podobně druhá rovnice říká, že změna hybnosti obsažené v
objemu V za jednotku času je rovna proudu hybnosti přes
ohraničující plochu S. Rovnice (1.106'') vyjadřují zákon zachování energie a hybnosti v
integrálním tvaru. Obecně, celková čtyřhybnost pi
je pomocí tenzoru energie-hybnosti vyjádřena integrálem
p i = (1/c) ň T ik dSk
přes hyperplochu
zahrnující celý trojrozměrný prostor. Rovnice (1.106) je pak
ekvivalentní tvrzení, že tato 4-hybnost
se zachovává.
Obyčejný
(trojrozměrný) vektor momentu hybnosti J
klasické mechaniky, definovaný jako J = r ´ p (vektorový součin), se ve STR
nahrazuje obecnějším 4-tenzorem
momentu hybnosti
J ik = xi pk - xk pi .
Je to antisymetrický
tenzor, jehož prostorové složky jsou rovny složkám
trojrozměrného vektoru J. Pro kontinuum je Jik = ň(xidpk -xkdpi) = (1/c) ň(xiTkm - xkTim)dSm. Aby platil zákon zachování
momentu hybnosti Jik,k = 0, musí být (xiTkm - xkTim),m = 0; kromě zákona (1,106) je k
tomu zapotřebí, aby tenzor energie-hybnosti byl symetrický (Tik = Tki).
Nejjednodušším typem látky - kontinua - je soubor vzájemně neinteragujících
částic označovaný jako nekoherentní
prach. Hustota
čtyřhybnosti částic v takové soustavě pak je r.ui, takže T°a = r.c2ua (a = 1,2,3). Hustota energie je
T°°=r.c2 a hustota proudu hybnosti Tab = r.c.dxa/dtdxb/dt . Tenzor
energie-hybnosti nekoherentního prachu tedy je
T ik = r . u i u k .
Použijeme-li při
sledování ideální kapaliny vztažnou soustavu v níž
uvažovaný objemový element je v klidu, bude platit Pascalův zákon podle něhož tlak p je stejný ve všech
směrech. V takové vztažné soustavě tenzor napětí bude
roven s ab = p.d ab =Tab
; hustota
hybnosti je zde rovna nule, takže T°a = 0, a hustota energie T°°= e = r.c2.
Tenzor energie-hybnosti ideální kapaliny v klidové
vztažné soustavě tedy je
| T ik = |
/ |
e |
0 |
0 |
0 |
\ |
. |
|
|
| | |
0 |
p |
0 |
0 |
| |
| | |
0 |
0 |
p |
0 |
| |
| \ |
0 |
0 |
0 |
p |
/ |
Po transformaci do
obecné vztažné soustavy, v níž daný objemový element se
pohybuje čtyřrychlostí ui, bude tenzor energie-hybnosti
ideální kapaliny dán vztahem
| Tik = (p + e)
ui uk + p.hik , resp. Tik = (p + e) ui uk + p.dik
. |
(1.108) |
Koncepci tenzoru
energie-hybnosti je výhodné zachovat i v případě, kdy se
nejedná o skutečné kontinuum. Sestává-li vyšetřovaná
soustava z N "bodových" částic o hmotnostech ma (a=1,2,...,N),
které se pohybují čtyřrychlostmi uia, pak tenzor energie-hybnosti
může být definován jako
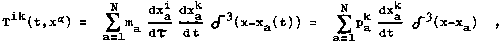
kde d3(x) je trojrozměrná Diracova
delta-funkce.
Čtyřrozměrná elektrodynamika
Maxwellovy
rovnice elektrodynamiky, i když původně vznikly na základě
klasických nerelativistických představ, jsou invariantní
vzhledem k Lorentzově transformaci. Elektrodynamika je proto od základu relativistická - elektromagnetické jevy jsou vlastně
jediným případem, kdy se s relativistickými efekty
setkáváme v běžném životě (není ale
snadné si toho všimnout!). Elektrodynamika tedy nepotřebuje
žádnou relativistickou reformulaci, teorie relativity nevede k
žádným novým a neočekávaným elektromagnetickým jevům.
Aplikace zákonitostí speciálni teorie relativity však
zavádí v elektrodynamice jasnější a jednotnější řád a
ukazuje na hluboké vnitřní
souvislosti jevů, které jsou z klasického hlediska
chápány jako nezávislé empirické skutečnosti. Tato
jednota elektromagnetických zákonitostí zvláště zřetelně
vystupuje při čtyřrozměrné prostoročasové formulaci.
Základní veličinou elektrodynamiky je elektrický náboj, pro nějž platí zákon zachování
(1.31). Elektrický náboj je definován jako invariantní skalární veličina, takže velikost náboje
tělesa je stejná ve všech inerciálních vztažných
soustavách:
dq' = r'. dV = r dV ş r . dx1dx2dx3 = dq
.
Jelikož objem se při
přechodu k jiné inerciální soustavě transformuje
podle vztahu dV' = Ö(1 - V2/c2) dV , je transformační zákon
pro r stejný jako pro dx°: r' = r/Ö(1 -
V2/c2). Hustota elektrického náboje
se tedy transformuje jako časová složka nějakého
čtyřvektoru. Složky vektoru proudové hustoty j = r.v, které jsou ja = r.va = r .dxa/dt (a = 1,2,3), se
vzhledem k chování
r transformují jako dxa, tj. jako prostorové složky
čtyřvektoru. Veličiny r a j je proto přirozené sjednotit
do jednoho 4-vektoru ji ş (c.r, j), tzv. čtyřproudu,
jehož komponenty jsou
| j° = c.r , j1 = jx , j2 = jy , j3 = jz . |
(1.109) |
Protože složku j° =
c.r můžeme vyjádřit pomocí x° = c.t
jako j°= r.dx°/dt, lze komponenty 4-proudu
definovat takto :
| j k = r . dxk / dt . |
(1.109') |
Rovnici kontinuity
(1.31b) ¶r/¶t + div j = 0, vyjadřující zákon zachování
elektrického náboje, lze potom zapsat ve čtyřrozměrném tvaru
| ¶ j k / ¶x k = 0
, neboli j k ,k = 0 |
(1.110) |
(4-divergence
čtyřproudu je rovna nule).
Podobně pro potenciál z rovnic (1.46a,b)
plyne, že co do transformačních vlastností se veličina j chová jako časová a veličiny Aa =(A) jako
prostorové složky
4-vektoru, takže elektrický skalární potenciál j a magnetický vektorový potenciál A lze sjednotit do jednoho 4-vektoru
| A k ş ( j , A
) , |
(1.111) |
který se nazývá čtyřpotenciál. Rovnice
(1.46a) a (1.46b) lze potom sloučit do jedné prostoročasové
rovnice
| ž A k ş ¶2Ak/¶xm¶xm = -(4p/c) . j k , |
(1.112) |
přičemž Lorentzova
kalibrační podmínka (1.45) ve čtyřrozměrném tvaru
| ¶Ak/¶xk ş A k ,k
= 0 |
(1.113) |
značí, že
4-potenciál je volen tak, aby jeho čtyřdivergence byla rovna
nule. Rozepsání vztahů E = -gradj -(1/c)¶A/¶t , B = rot
A mezi potenciály a intenzitami elektrického a
magnetického pole
ukazuje, že složky vektorů E a B
lze interpretovat jako komponenty antisymetrického 4-tenzoru Fik
| F ik =def ¶Ak/¶xi - ¶Ai/¶xk , |
(1.114) |
který se nazývá tenzor
elektromagnetického pole. Tento tenzor elektromagnetického pole,
vyjádřený pomocí komponent vektorů E
a B, má strukturu :
| F ik = |
/ |
0 |
Ex |
Ey |
Ez |
\ |
. |
(1.114') |
| | |
-Ex |
0 |
0 |
0 |
| |
| | |
-Ey |
Bz |
0 |
-Bx |
| |
| \ |
-Ez |
-By |
Bx |
0 |
/ |
Je to určitý
sjednocující "konglomerát" složek elektrického a
magnetického pole, který ve čtyřrozměrném prostoročase
úplně popisuje elektromagnetické pole.
Pozn.: Tenzor
elektromagnetického pole Fik se někdy nazývá Faradayův tenzor,
ačkoli ve Faradayově době ještě žádné tenzory (a už vůbec ne 4-rozměrné!)
nebyly známé. Odráží totiž sjednocení elektrického a
magnetického pole v duchu Faradayova zákona
elektromagnetické indukce.
Lorentzovy pohybové rovnice (1.30 )
nabité hmotné částice v elektromagnetickém poli

lze interpretovat jako
prostorové složky čtyřrozměrné rovnice pohybu nabité
částice
| mo du i / dt
= (q/c) Fik uk ; |
(1.115) |
časová komponenta
této rovnice popisuje změny energie částice v důsledku
práce vykonané elektromagnetickými
silami.
První
dvojici Maxwellových rovnic (1.40)-(1.41) lze zapsat jako jednu
rovnici pro složky tenzoru
elektromagnetického pole :
 |
(1.116a) |
Druhou dvojici Maxwellových rovnic (1.38)-(1.39) lze pak pomocí Fik sjednotit do jediné čtyřrozměrné
rovnice
 |
(1.116b) |
popisující buzení elektromagnetického pole čtyřproudem ji.
Pro formulaci elektrodynamiky pomocí
Hamiltonova principu nejmenší akce je lagrangián elektromagnetického pole ve
4-rozměrném tvaru :
| L
= (1/16pc) FikFik + (1/c2)Ai ji ; |
(1.117) |
z variačního principu dS= d
ňL dW = 0 (při variaci
složek 4-potenciálu při zadaném rozložení a pohybu
nábojů) pak
můžeme získat Maxwellovy rovnice elektromagnetického pole
(116a,b).
Vztahy (1.52)-(1.56), vyjadřující
hustotu a proud energie a hybnosti v elektromagnetickém poli,
lze shrnout pomocí tenzoru energie-hybnosti elektromagnetického
pole, který je roven
| Tikelmag. = - 1/4p
Fim Fkm + 1/16p
Flm
Flm |
(1.118) |
Po dosazení hodnot Fik z (1.114') je vidět, že T°°elmag. je rovna hustotě energie (1.52) a
komponenty T°aelmag. jsou rovny složkám Poyntingova vektoru
(1.55). Prostorové složky
T abelmag. = sab
= 1/4p [1/2(E2 + B2) dab - EaEb - BaBb]
tvoří trojrozměrný
tenzor zvaný Maxwellův tenzor napětí.
Pro jevy mechanické a elektrodynamické
je tedy speciální teorie relativity dokonale rozpracována a exrimentálně
ověřena. Je však nutno přiznat, že pro jiné jevy
než elektromagnetické není speciální teorie
relativity přímo ověřena... Nepřímé
indicie jsou však velmi pádné..!..
Nelineární elektrodynamika
Při všech intenzitách, které pozorujeme v přírodě i
laboratoři, se nám elektické a magnetické pole ve vakuu jeví
jako lineární - pro hodnoty intenzit E
a B, jakož i pro potenciály, přesně platí princip
superpozice. Otázkou je, jak je to u extrémně
silných elektromagnetických polí? Pro tuto situaci
byly zkonstruovány varianty zobecněné nelineární
elektrodynamiky NED, v níž neplatí
princip superpozice (výsledné
elektromagnetické pole dvou nábojů není rovnou součtu polí
jednotlivých nábojů). Projevuje se zde samointerakce
pole - dochází např. k rozptylu "světla na
světle". Očekává se, že tyto jevy nelineární
elektrodynamiky *) by se mohly projevovat v oblasti velmi
silných elektromag. polí a vysoce intenzívních svazků
elektromagnetického záření (zatím
nedosažených v našich experimentech).
*) Máme zde na mysli chování polí ve
vakuu, nikoli jevy nelineární optiky
způsobené nelineární polarizací či magnetizací v
látkových prostředích.
Motivace pro zobecnění klasické
elektrodynamiky se začaly objevovat již na počátku 20.stol. v
souvislosti s ne zcela uspokojivým modelem nabité částice (bodová nabitá částice v centru vykazovala
nekonečné hodnoty Coulombova pole, s nekonečnou energií - singularitu). V r.1912 G.Mie navrhl, že elektromagnetické pole by
mohlo být složeno ze součtu klasického Maxwellova pole a
druhého nelineárního přídavného členu (složeného z potenciálů A), který by byl významný pouze v oblasti atomárních
rozměrů (tato varianta nepronikla do
širšího povědomí fyzikální veřejnosti).
Zkoušely se i některé jiné modifikace
Coulombova zákona pro intenzitu E a potenciál F :
- Malá oprava "e" v zákonu obrácených čtverců: E(r) = Q/r2+e ;
- Do standardního Coulombovského potenciálu F(r) = Q/r zařadit
složku s Yukawovým potenciálem F´(r) = Q.e-m.r/r
(používaným v jaderné fyzice - je
zmíněn např. v pasáži "Silná
jaderná interakce" §1.1
monografie "Jaderná fyzika a ionizující záření"). Toto by bylo ekvivalentní zavedení nenulové
hmotnosti fotonu mf s Comptonovou délkou m = mf.c/h......
Žádný z těchto prvotních pokusů o nelineárních
rozšíření elektrodynamiky nevedl k uspokojivým
výsledkům...
Základní konzistentní variantu nelineárního
zobecnění klasické Maxwellovy elektrodynamiky NED
navrhli v r.1934 M.Born a L.Infeld [23] - Born-Infeldova
elektrodynamika (B-I). Motivací bylo odstranění
singularity v bodovém náboji - s cílem stanovení konečné
hodnoty vlastní elektrické energie elektronu. Pro tento účel
zde zavedli hypotézu maximální možné hodnoty
intenzity elektrického pole Emax a potenciálu Fmax, analogicky jako v
relativistické mechanice STR existuje maximální možná
(limitní) rychlost c pohybu hmotných těles. Realizovali
to zavedením speciálního parametru nelinearity "b"
v modifikovaných rovnicích pole tak, aby intenzita
elektrického pole bodového náboje Q (místo
standardního Coulombova zákona E=Q/r2) závisela na vzdálenosti r podle zákona :
(tečkovaná křivka na obr.1.8 vpravo), při němž je intenzita elektrického pole v
počátku r=0 konečná a rovněž celková
energie elektrického pole je konečná (vztahy
(1.122-123)).
Pozn.: Někdy
se parametr "b" značí řeckým "b" a používá
se jeho převrácená hodnota 1/b či 1/b.
V klasické Maxwellově elektrodynamice je
lagrangián ve 4-rozměrné formulaci dán výše uvedeným
vztahem (1.117):
L = (1/16pc) FikFik + (1/c2)Ai ji
.
Lagrangián elektromag. pole v B-I je modelován ve zobecněném
tvaru obsahujícím parametr nelinearity "b" (který pak v rovnicích charakterizuje maximální
možnou intenzitu elektrického pole - viz
níže vztahy (1.123))
:
| LBI = b-2 [(1
- Ö[1 + b2.FikFik/2 - b4.(FikFikeiklm)2/16]] + Ai ji , |
(1.119) |
kde Fik je tenzor elektromagnetického pole (1.114) (F ..= F.. . eiklm. je jeho ..sdružený.., násobený jednotkovým
... Levi-Civitův
tenzor eiklm antisymetrický ...doplmit,upravit ; v lagrangiánech
zatím vynecháváme c (konvence c=1)............).
Pro čistě elektrické pole E, tj. při B=0, je
L = b-2 [1 - Ö(1 - b2.E2)].
V 3-rozměrné vektorové
symbolice elektrické intenzity E a magnetické
indukce B je standardní Maxwellovský
lagrangián (1.42): L = 1/8p (E2-B2) + j.A - r.j , zatímco v B-I
NED má lagrangián tvar :
| LBI = b-2 [(1
- Ö[1 + b2(B2-E2) - b4.(B.E)2]] + j.A
- r.f . |
(1.119´) |
V limitě b-->0 dostáváme standardní
Maxwellovu elektrodynamiku, pro b>0 jsme ve variantě
nelinearity.
Z principu nejmenší akce s lagrangiánem LBI (1.119´) plynou
rovnice elektromagnetického pole v BI modelu :
 |
(1.120) |
které jsou formálně stejné jako standardní
lineární Maxwellovy rovnice (1.38-41). Nelinearita
je "skryta" ve veličinách D ("elektrická indukce")
a H ("magnetická
intenzita") :
D
= ¶L/¶E = [E + b2(B.E) B]/Ö[1 + b2(B2-E2) - b4.(B.E)2]] ,
H = ¶L/¶B
= [B - b2(B.E) E]/Ö[1 + b2(B2-E2) - b4.(B.E)2]] , |
(1.121) |
které obsahují faktor "b". Je to
analogické jako v elektrodynamice kontinua, kde
vztahy mezi E a D=E/e , B
a H=B/m obsahují matriálové
koeficienty elektrické permitivity e a magnetické permeability m (včetně příp. nehomogenit a nelinearit polarizace a
magnetizace).
Řešení rovnic pole (1.120-121) pro sféricky
symetrické elektrostatické pole vede k funkční
závislosti potenciálu F a intenzity E elektrického pole na radiální
vzdálenosti r od bodového náboje Q :
 |
(1.122) |
Integrál obsažený ve funkci F(r) pro potenciál
lze explicitně vyjádřit pomocí dvou druhů speciálních
funkcí :
kde "F(...)" je Legenderova
eliptická funkce 1.druhu a "2F1(...)"
je tzv. hypergeometrická funkce (složitější
mocninná řada z Q2b2/r4). Konkrétní hodnoty těchto složitých funkcí lze pro
fyzikální výpočty nalézt ve speciálních tabulkách, v
poslední době pro ně existují i počítačové programy.
Lze zapsat též :
E(r) = q/Ö[ro4 +
r4] ; Emax = 1/b ,
kde ro = Ö(q.b/4p) je "efektivní poloměr bodového
náboje" .
F(r) = F(r/ro).q/ro (F je kombinovaná
eliptická funkce) , číselně
vychází F(0) = 1,854 Emax . |
(1.122b) |
Tyto závislosti elektrického potenciálu a
intenzity v B-I NED modelu (čárkované křivky na obr.1.8) jsou
ve větších vzdálenostech r podobné standardnímu
Coulombovu zákonu (plné křivky na obr.1.8). V malých
vzdálenostech se však podstatně liší: zatímco podle
Coulombova zákona s přibližováním r-->0 roste potenciál
a intenzita do nekonečna, v BI modelu dosahují konečné
hodnoty F(r=0)=Fmax, E(r=0)=Emax ~ 1/b .
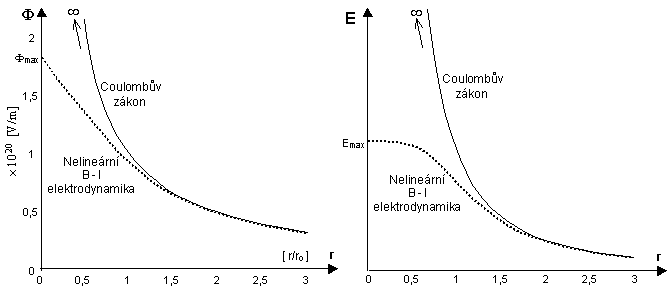 |
| Obr.1.8. Závislost potenciálu F (vlevo) a intenzity E (vpravo)
elektrického pole na vzdálenosti r
od bodového náboje (elektronu) podle standardního
Coulombova zákona (_____) a
podle nelineární B-I elektrodynamiky (........). |
Konkrétní hodnotu
základního parametru "b" v
nelineární B-I elektrodynamice lze stanovit z fyzikálního
rozboru elektrického pole elektronu - elektron
je totiž fundamentální elementární částice bez vnitřní
struktury - není z ničeho "složen", z hlediska
klasické fyziky jej lze považovat za "polní
objekt". Lze proto fyzikálně požadovat, aby
veškerá klidová hmotnost elektronu me byla elektrického
původu. Klidová energie elektronu me.c2 s nábojem q=e by
tedy v klasické fyzice měla být dána celkovou energií
jeho elektrického pole: me.c2 = e . 0ňĄdr/Ö[ro4 + r4]. Pro elektron tak
vychází :
r0e = 1,2361.e2/mec2 = 2,28 . 10-13 cm ;
Emax = 1,187.1020 V/m . |
(1.123) |
Hodnota Emax platí nejen pro elektron, ale je to v B-E
elektrodynamice fundamentální maximální
možná hodnota intenzity elektrického pole, daná parametrem
"b".
V klasické fyzice se B-I elektrodynamika považuje především
za model elektronu.
Z fyzikálního
hlediska - atomové, jaderné a částicové fyziky - jsou
otázky "velikosti" či rozměrů částic mikrosvěta
diskutovány v §1.5 "Elementární
částice a urychlovače",
pasáži "Velikost, rozměry a tvar
částic? -problematické!" monografie "Jaderná fyzika a fyzika
ionizujícího záření".
V poslední době se
někdy zavádí modifikované varianty nelineární
elektrodynamiky NED s lagrangiánem v exponenciálním
či logaritmickém tvaru :
LNED = b-2[exp(-FikFik/b2) - 1] nebo
LNED = -8 b-2 ln[(1 + FikFik/(8b2)] , za
účelem širších možností gravitačně-elektrodynamických
řešení...
Nelineární elektrodynamika, i když je zatím
jen teoretická a hypotetická, poskytuje
zajímavé možnosti řešení v teorii elektricky
nabitých černých děr, kde za určitých okolností
umožňuje zbavit se singularit (!) - §3.5, pasáž "Reissner-Nordstromovo řešení s nelineární
elektrodynamikou", §3.6,
pasáž "Kerr-Newmanova geometrie s nelineární
elektrodynamikou" a
zmínka v §4... .... . Je určitá
naděje, že nelinearita elektrodynamiky by se mohla
"vyrušit" s nelinearitou gravitace v
OTR, za vzniku fyzikálně realističtějších regulárních
řešení..?.. - bude jistě předmětem
budoucích teoretických výzkumů...
Zda se toto někde v přírodě "realizuje" se
zatím neví - na experimentální ověření není naděje v
dohledné budoucnosti...
Klasická, kvantová a
gravitační nelineární elektrodynamika
V klasické NED se maximální možná hodnota intenzity
elektrického pole Emax v blízkosti bodového náboje "uměle"
hypoteticky postulovala zavedením parametru
"b" nelinearity v rovnicích pole. V kvantové
elektrodynamice limitní elektrická intenzita vychází
fyzikálně - dynamicky jako důsledek
zvýšené produkce elektron-pozitronových párů
z polarizovaného vakua v silném poli v blízkosti bodového
náboje.
Nelinearita elektrodynamiky, geometricky indukovaná
gravitačním zakřivením prostoročasu v OTR, je
jinou záležitostí - bude analyzovaná v §2.4, část
"Gravitační elektrodynamika a
optika".
"Exotickým" efektem je zakřivení prostoročasu energií
elektromagnetického pole - mohutných
elektromagnetických vln v rámci geometrodynamiky
(§B3 "Klasická geometrodynamika. Gravitace a
topologie.",
geony, obr.B2).
Vojtěch
Ullmann