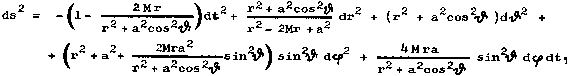 |
(3.37) |
h1{font-size:18px;}
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | Gravitace, černé díry a fyzika |
Kapitola 3
GEOMETRIE A
TOPOLOGIE PROSTOROČASU
3.1. Geometricko-topologické vlastnosti
prostoročasu
3.2. Minkowského rovinný
prostoročas a asymptotická struktura
3.3. Cauchyova úloha,
příčinnost a horizonty
3.4. Schwarzschildova geometrie
3.5. Reissnerova-Nordströmova
geometrie
3.6. Kerrova a Kerrova-Newmanova geometrie
3.7. Prostoročasové singularity
3.8. Hawkingovy a Penroseovy
teorémy o singularitách
3.9. Nahé singularity a princip
"kosmické cenzury"
3.6. Kerrova a Kerrova-Newmanova geometrie
Jestliže těleso,
které je zdrojem gravitačního pole rotuje, nebude již buzené vnější
gravitační pole centrálně symetrické, ale může být pouze osově
symetrické (pokud je distribuce hmoty-energie v rotujícím
tělese symetrická vzhledem k ose rotace).
V §2.5, pasáž "Rotující gravitace",
jsme v aproximaci slabého pole odvodili vliv rotace
gravitujícího tělesa na vnější buzené gravitační pole.
Viděli jsme, že rotace zdroje zanechává na vnějším
gravitačním poli (tj. na metrice
prostoročasu)
charakteristické "stopy" ve formě nediagonálních členů, způsobujících strhávání vnějších
těles rotujícím gravitačním polem do směru rotace zdroje (tzv. Lense-Thirringův efekt).
Přesné řešení Einsteinových rovnic
(ve vakuu) pro takový rotací způsobený axiálně symetrický
případ nalezl R.Kerr [152] v r.1963; toto řešení bylo potom
E.Newmanem zobecněno na případ přítomnosti elektrického
náboje [186].
Kerrova geometrie
Kerrova geometrie je zobecněním Schwarzschildovy
geometrie zhruba řečeno v tom smyslu, že Schwarzschildova
geometrie je "kulová", zatímco Kerrova geometrie je
obecně eliptická. V tzv. Boyerových-Lindquistových souřadnicích (které jsou eliptickým zobecněním
Schwarzschildových souřadnic) [28] má prostoročasový element Kerrovy
geometrie tvar
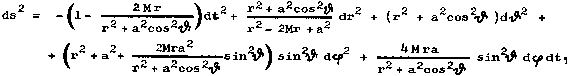 |
(3.37) |
kde M je celková hmotnost (hmotnostní
parametr), a = J/M je "specifický
moment hybnosti"
- celkový rotační moment
hybnosti J
dělený celkovou hmotností M;
nazývá se též Kerrův parametr a charakterizuje
míru rotace zdrojového tělesa (černé díry). Pokud je a = 0 (zdrojové těleso
nerotuje), přechází Kerrova metrika na Schwarzchildovu (3.13).
Z výrazu pro prostoročasový element (3.37) je
patrné (a potvrzuje to výpočet složek
tenzoru křivosti Riklm a jeho skalárního invariantu),
že Kerrova geometrie má fyzikální singularitu
danou vztahem
| r2 + a2 cos2J = 0 . |
Není to však bodová singularita jako ve Schwarzschildově řešení, ale prstencová singularita, která má v rovině kolmé k ose rotace tvar kružnice s poloměrem a.
Podobně
jako v Reissnerově-Nordströmově geometrii, jsou i zde tři
vyznačné speciální případy lišící se globální
geometrickou strukturou prostoročasu: a2 < M2 , a2 = M2 , a2 > M2.
Kerrova geometrie má obzvláštní důležitost pro případ M2
> a2, kdy popisuje vnější pole stacionárních rotujících objektů, především černých děr
*). Když R.Kerr příslušné řešení odvodil [152], jistě
netušil, jak toto "algebraicky speciální" řešení
se ukáže důležité a obecné; ve světle teorému 4.1
"černá díra nemá vlasy" bude každá stacionární
nenabitá černá díra mít Kerrovu geometrii prostoročasu.
*) Přesně to platí pouze
pro černou díru, kdy Kerrova geometrie je vakuovým řešením
Einsteinových rovnic. Nalézt však materiální zdroj přesné
Kerrovy geometrie, vedoucí podle Einsteinových rovnic k
plynulému přechodu vnitřní metriky k vnější Kerrově
metrice, není nikterak snadné. Tvar takového elipsoidního rotujícího
zdroje a distribuce hmoty v něm musí splňovat určité velmi
speciální podmínky [82]. Kolem rotujících materiálních
těles (planet, hvězd, galaxií) je tedy gravitační pole jen
přibližně Kerrovské.
Vnější a vnitřní horizont
V uvažovaném případě a2 < M2 existují dvě hodnoty r,
pro něž je ve jmenovateli prostorové části metriky v (3.37)
r2-2Mr+a2 rovno nule :
| rg+ = M + Ö(M2 - a2) , rg- = M - Ö(M2 - a2) . | (3.38) |
Jsou zde tedy opět (podobně jako v Reissnerově-Nordströmově geometrii) přítomny dva horizonty, na nichž je metrika (3.37) pseudosingulární. Vnější horizont r = rg+ je horizontem událostí (s podobnými vlastnostmi jako Schwarzschildův horizont). Každý objekt potřebuje k dosažení horizontu rg+ nekonečně dlouhý souřadnicový čas (avšak konečný interval vlastního času) a navíc též nekonečný úhel (j ®Ą) - vlivem strhávání inerciálních soustav momentem hybnosti (viz §4.4) musí vykonat nekonečně mnoho oběhů kolem horizontu. Vnitřní horizont r = rg- je Cauchyovým horizontem se složitými kauzálními vztahy (je rozebíráno v §3.3 "Cauchyova úloha, příčinnost a horizonty" a v §3.5 "Reissnerova-Nordströmova geometrie"). Podobně jako v Reissnerově-Nordströmově geometrii i zde je vnitřní Cauchyho horizont nestabilní vůči vnějším perturbacím.
Rotující gravitace,
ergosféra
Důležitou vlastností je zde efekt strhávání
prostoročasu
rotací zdrojového objektu (§2.5 "Einsteinovy
rovnice gravitačního pole", pasáž "Rotující
gravitace"). Tato rotující gravitace nutí
každou částici, která se dostane do blízkosti, obíhat
souhlasným směrem. Nad horizontem se vyskytuje oblast tzv. ergosféra, ohraničená eliptickou plochou zvanou statická mez danou rovnicí r =
rS = M+Ö(M2 - a2 cos2 J). Uvnitř této
oblasti musí každé těleso obíhat ve směru rotace zdroje.
Prostřednictvím ergosféry je teoreticky možné čerpat
energii rotojící gravitace (černé díry). Je podrobněji
rozebíráno v §4.4 "Rotující a elektricky
nabité černé díry",
část "Vliv rotace černé díry.
Ergosféra", pasáž
"Extrakce rotační energie. Penroseův proces.".
Analytická extenze
Kerrovy geometrie
K odstranění souřadnicových pseudosingularit (tj. k analytickému prodloužení metriky přes tyto
plochy) se
používá přechodu ke Kerrovým
souřadnicím
[127],[41] (v+,r, J,j~+)
transformací
| dv+ = dt + [(r2+a2)/(r2-2Mr+a2)].dr , dj~+ = dj + [a/(r2-2Mr+a2)].dr . | (3.39) |
Tato transformace provádí nekonečné "stlačení" souřadnicového času t a nekonečné "rozkroucení" úhlové souřadnice j v okolí horizontu. Metrika (3.37) pak má v Kerrových souřadnicích tvar
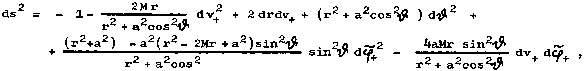 |
(3.40) |
který je již
analytický na r=rg+ a r=rg-. Úplná
analytická extenze se získá kombinací této metriky v souřadnicích (v+,r,
J,j~+) a analogické metriky v
souřadnicích (v-,r, J, j~- ) daných transformací
dv- = dt - [(r2+a2)/(r-2Mr+a)].dr, dj~- = dj - [a/(r2-2Mr+a2)].dr.
Konformní
prostoročasový diagram této úplné
extenze Kerrovy geometrie je na obr.3.25a. Globální struktura je zde podobná
struktuře Reissnerova-Nordströmova prostoročasu (srovnej s
obr.3.21 v předchozím §3.5) *), poněkud odlišná je však
povaha skutečné singularity r=0. Ukazuje se, že v Kerrově
prostoročase má tato singularita prstencovou
strukturu a
je možno přes ni extrapolovat geometrii do záporných hodnot
radiální souřadnice r [43],[28].
*) I zde se vyskytuje nekonečný počet
"vesmírů", mezi nimiž lze teoreticky (modelově)
"cestovat". Kritické
posouzení podobných možností bude v §4.4, část "Černé
díry - mosty do jiných vesmírů?".
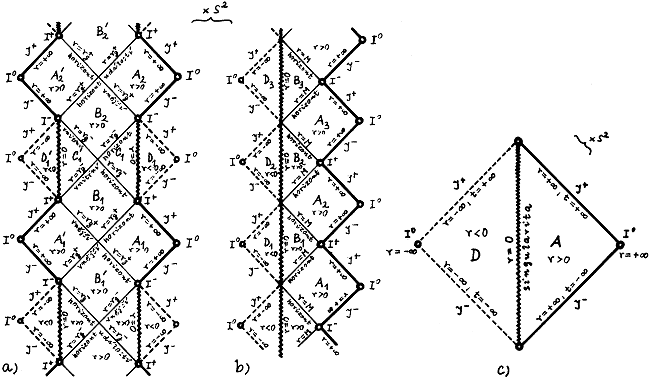
Obr.3.25. Konformní prostoročasový diagram úplné extenze
Kerrovy geometrie podél osy symetrie.
a) Případ M2 > a2 > 0
. b)
Případ M2 = a2 (extrémní Kerrova geometrie). c) Případ a2 > M2
(Kerrova nahá singularita).
V případě M2
= a2 je rg+ = rg- = M , vnitřní a vnější horizont
spolu splývají. Úplná extenze této metriky znázorněná na
obr.3.25b má opět podobnou strukturu jako
Reissnerova-Nordströmova
geometrie při M2=Q2 s tím rozdílem, že je možné
analytické prodloužení přes prstencovou singularitu do
záporných r. Kerrova metrika v tomto případě
popisuje prostoročasovou geometrii extrémní Kerrovy černé díry s
maximálně možnou rychlostí rotace (§4.4).
Pro a2 > M2 je metrika (3.37) singulární
pouze pro r=0, což je skutečná
singularita
s prstencovou strukturou. Přes vnitřek této prstencové
singularity lze řešení analyticky prodloužit do záporných hodnot r (obr.3.25c). Žádný horizont zde není
a singularita proto může oboustranně "komunikovat" s
celým okolním prostoročasem - jedná se o Kerrovu nahou singularitu (viz §3.9 a §4.4).
Kerrova - Newmanova
geometrie
Další
zobecnění dostaneme, jestliže budeme uvažovat přítomnost
osově symetrického elektromagnetického pole, tj. rotující
axiálně symetrický zdroj bude mít elektrický
náboj, který
je rovněž axiálně symetricky rozložen. Geometrie
prostoročasu kolem takového objektu se nazývá Kerrova-Newmanova geometrie [186]; je to fakticky zkombinovaná
Kerrova a Reissnerova-Nordströmova geometrie. Element
prostoročasového intervalu (v Boyerových-Lindquistovýeh souřadnicích) má tvar
 |
(3.41) |
kde Q je celkový elektrický náboj měřený vzdáleným pozorovatelem - buď pomocí toku vektoru elektrické intenzity E uzavřenou plochou, nebo pomocí analýzy trajektorií nabitých testovacích částic. Stejně jako u Kerrova řešení, je i zde geometrie prostoročasu stacionární a axiálně symetrická. Vnější horizont r = rg+ (horizont událostí) a vnitřní horizont r = rg- (Cauchyho horizont) mají poloměry
| (3.42) |
Pozn.: Horizont událostí r = rg+ se též někdy označuje jako Killingův horizont, neboť Killingovo vektorové pole xo ş ¶/¶t (zavedené v §2.4), jeho časová složka, zde mění prostoročasový chrakter: vně horizontu je časového typu, zatímco uvnitř horizontu nabývá prostorový charakter.
Globální geometrická
struktura Kerrova-Newmanova prostoročasu je analogická jako u
výše popsané Kerrovy geometrie. Jsou zde opět tři
speciální případy:
a2+Q2 < M2 (černá díra) ,
a2+Q2 = M2 (extrémní
Kerrova-Newmanova geometrie) ,
a2+Q2 > M2 (nahá singularita)
.
Carter [43] ukázal, že
v okolí prstencové singularity je oblast, v níž gjj< 0; zde axiální Killingův vektor ¶/¶j nabývá časový charakter,
takže se zde objevují uzavřené světočáry
časového typu (např. kružnice t=const, r=const, J =const). V těchto oblastech kolem
singularity tedy může dojít k porušení
kauzality.
Posouzení fyzikálního významu některých aspektů úplné
extenze Kerrovy-Newmanovy geometrie pro černé díry je v
zúvěru §4.4, pro nahé singularity v
§3.9.
Velký
význam Kerrovy-Newmanovy geometrie spočívá v tom, že je
nejobecnějším řešením pro stacionární axiálně
symetrický asymptoticky rovinný prostoročas který má
horizont událostí, tedy nejobecnějším řešením
popisujícím černou díru
- v duchu teorému
"černá díra nemá vlasy", viz §4.5 "Teorém
"černá díra nemá vlasy"".
Trajektorie testovacích
částic
Pohyb
testovacích částic (obecně nabitých) v obecném
Kerrově-Newmanově prostoročase je podstatně
komplikovanější než ve Schwarzschildově geometrii. I ve
speciálním případě, když pohyb se bude dít jen v
ekvatoriální rovině a nebudeme uvažovat elektrický náboj,
bude trajektorie testovací částice v blízkosti horizontu
(zvláště v ergosféře, viz §4.4) rozhodujícím způsobem
záviset mimo jiné na tom, zda moment hybnosti částice má
souhlasný nebo opačný směr vzhledem k
momentu hybnosti J - tj. pohybuje-li se částice ve směru nebo proti
směru
rotace zdroje Kerrova pole.
Pohyb nabitých testovacích částic v
důsledku působení elektromagnetických sil již obecně nebude
probíhat po geodetikách; na pravé straně rovnice geodetiky
bude místo nuly figurovat Lorentzova síla
:
| (3.43) |
kde q je elektrický
náboj testovací částice a Fik je tenzor elektromagnetického
pole spolupůsobícího jako zdroj dané Kerrovy-Newmanovy geometrie.
Analýza
pohybu testovacích částic v Kerrově-Newmanově poli se
většinou provádí nikoli ze základní rovnice (3.43), ale pomocí jí
ekvivalentních Hamiltonových-Jacobiho rovnic [165],[43], z
nichž se snadněji na základě symetrie stanovují integrály
pohybu. Výsledné rovnice pohybu testovací částice s nábojem
q, klidovou hmotností mo, energií E vzhledem k nekonečnu, axiální
složkou momentu hybnosti Lj a složkou pJ hybnosti odvodil
Carter [43],[181] :
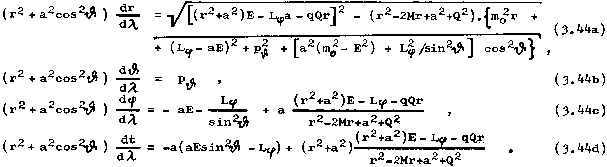
Jelikož gravitační i elektromagnetické pole je stacionární a axiálně symetrické (tj. jak složky metriky gik, tak čtyřpotenciál Ak nezávisí na t a na j), budou při pohybu testovací částice následující veličiny konstantami (integrály) pohybu: energie E vzhledem k nekonečnu, axiální složka L.. momentu hybnosti vzhledem k ose symetrie, elektrický náboj q částice a její klidová hmotnost mo (která v každém bodě trajektorie souvisí se čtyřhybností částice vztahem mo =(-gikpipk)1/2). Další integrál pohybu, který neplyne z uvedených symetrií, nalezl Carter [43]:
| C = PJ2 + a2(m2 - E2) + (Lj2/sin2J).cos2J ; | (3.45) |
protože tuto veličinu
v dalším nebudeme potřebovat, do rovnic pohybu (3.44) jsme ji
nezavedli.
Obecnou
analýzu pohybu částic v Kerrově-Newmanově prostoročase na
základě rovnic (3.44) zde provádět nebudeme, zájemce může
najít podrobnosti např. v [8],[81],[237]. Některých
důsledků plynoucích za patřičných podmínek z rovnic (3.44)
pro pohyb částic v Kerrově-Newmanově prostoročase však
použijeme v §4.4 "Rotující a elektricky
nabité Kerrovy-Newmanovy černé díry", kde si rozebereme
fyzikálně nejdůležitější aspekty Kerrovy-Newmanovy
geometrie (jako je efekt strhávání lokálních lokálních
inerciálních soustav, existence ergosféry, Penroseův proces,
superradiace a pod.) v souvislosti s vlastnostmi černých děr.
Kerr-Newmanova geometrie s nelineární
elektrodynamikou
Na konci předchozího §3.5, věnovaného Reissner-Nordströmovu
prostoročasu s centrálně-symetrickým elektrickým nábojem,
jsme krátce zmínili možnost zobecnění pro případ nelineární elektrodynamiky - pasáž "Reissner-Nordstromovo řešení s nelineární
elektrodynamikou". Analogické zobecnění lze
udělat i pro Kerr-Newmanovu geometrii . Při použití Born-Infeldovy nelineární elektrodynamiky (§1.6, pasáž
"Nelineární
elektrodynamika") s parametrem nelinearity b v
prostoročasovém intervalu (3.41):
 |
(3.41) |
bude místo prostého kvadrátu náboje "Q2" figurovat složitější funkce "f(r,Q)"
analogická jako v metrice (3.36), obsahující eliptické integrály
kde "F(...)" je Legenderova
eliptická funkce 1.druhu a "2F1(...)"
je je tzv. hypergeometrická funkce (složitější mocninná řada z Q2b2/r4)..
Pro tuto "Kerr-Newman-Born-Infeld" metriku se pro
přílišnou výpočetní složitost zatím nepodařilo nalézt
zcela obecnou analýzu pohybu testovacích částic. Zkoušejí
se přibližná řešení pro případ pomalé rotace (a<<1), s
použitím metod perturbační analýzy. ............
...............
| Gravitace, černé díry a fyzika prostoročasu : | ||
| Gravitace ve fyzice | Obecná teorie relativity | Geometrie a topologie |
| Černé díry | Relativistická kosmologie | Unitární teorie pole |
| Antropický princip aneb kosmický Bůh | ||
| Jaderná fyzika a fyzika ionizujícího záření | ||
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | ||
Vojtěch Ullmann