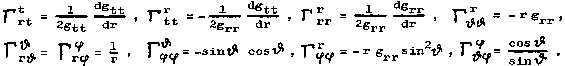 |
(3.12) |
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | Gravitace, černé díry a fyzika |
Kapitola 3
GEOMETRIE A
TOPOLOGIE PROSTOROČASU
3.1. Geometricko-topologické vlastnosti
prostoročasu
3.2. Minkowského rovinný
prostoročas a asymptotická struktura
3.3. Cauchyova úloha,
příčinnost a horizonty
3.4. Schwarzschildova geometrie
3.5. Reissnerova-Nordströmova
geometrie
3.6. Kerrova a Kerrova-Newmanova
geometrie
3.7. Prostoročasové singularity
3.8. Hawkingovy a Penroseovy
teorémy o singularitách
3.9. Nahé singularity a princip
"kosmické cenzury"
3.4. Schwarzschildova geometrie
Jak bylo řečeno již v §2.5, problém řešení Einsteinových rovnic se značně zjednoduší, když si předepíšeme vysoký stupeň symetrie; tím se sníží počet neznámých funkcí (metrických koeficientů) a rovnic. Skutečně, první přesné (a zároveň netriviální) řešení Einsteinových gravitačních rovnic bylo nalezeno hned v r.1916 K.Schwarzschildem pro sféricky symetrický případ. V §4.3 uvidíme, že toto řešení popisuje sféricky symetrickou černou díru.
Centrálně
symetrické Schwarzschildovo řešení
Pro centrálně
symetrické rozložení hmoty předpokládáme, že i
vzbuzované gravitační pole bude centrálně symetrické.
Nejprve budeme uvažovat případ, kdy centrálně symetrické
rozložení hmoty se s časem nemění a gravitační pole je
statické (níže však uvidíme, že tento
předpoklad není nutný, výsledek bude stejný i pro
nestatický případ při zachování centrální symetrie). Potom všechny fyzikální
veličiny budou funkcí pouze vzdálenosti od středu symetrie.
Dále budeme předpokládat, že prostoročas je asymptoticky rovinný - v dostatečně velkých vzdálenostech
přechází postupně v rovinný Minkowskiho prostoročas.
Vztažnou soustavu v tomto případě je přirozené spojit se středem symetrie a použít sférické prostorové souřadnice (r, J, j) s počátkem r=0 rovněž ve středu symetrie. Element prostoročasového intervalu lze potom hledat ve tvaru
| ds2 = - A(r).dt2 + B(r).dr2 + r2(dJ2 + sin2J dj2) , | (3.10) |
takže metrické koeficienty
| gtt = -A(r) , grr = B(r) , gJJ = r2 , gjj = r2sin2J | (3.11) |
jsou funkcemi pouze vzdálenosti r od středu symetrie. Souřadnice tohoto typu se nazývají Schwarzschildovy souřadnice. Jsou to v podstatě sférické souřadnice (r, J, j) prostorové, kde radiální souřadnice r je definována jako vlastní délka příslušné kružnice (se středem v centru symetrie r=0) o poloměru r dělená 2p, popř. odmocnina z vlastní plochy koule dělená 4p. Souřadnicový čas t je měřen vzhledem ke vzdálené, asymptoticky rovinné oblasti.
Předpokládejme dále, že zdrojové těleso je prostorově omezené a sahá jen do vzdálenosti R; při r > R je již vakuum (Tik=0). Nejdříve budeme hledat tzv. vnější řešení, tj. metriku prostoročasu pro r > R vně tělesa - ve vakuu. Je tedy třeba řešit vakuové Einsteinovy rovnice Rik = 0. Christoffelovy koeficienty konexe v metrice (3.10) jsou
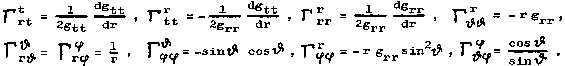 |
(3.12) |
Einsteinovy rovnice Rik = 0 pak po úpravě dávají jen dvě nezávislé diferenciální rovnice
dgtt/dr = (1/r) gtt (1 + grr) , dgrr/dr = - (1/r) grr (1 + grr) ,
které mají řešení
gtt = C1 . (1 + C2/r) , grr = (1 + C2/r)-1 ,
kde C1 a C2 jsou integrační konstanty. Konstantu C1 volíme měřítkem škály časové souřadnice t (transformací t = C1.t se konstanty C1 zbavíme). Z limitního přechodu k Newtonovu zákonu (gtt ~ (1 - M/r) pro r®Ą) dostáváme, že konstanta C2 musí být rovna -2M, kde M je hmotnost zdrojového tělesa (tj. celková hmotnost uzavřená v kouli o poloměru r při r®Ą). Dostáváme tak přesné řešení Einsteinových rovnic ve vakuu pro sféricky symetrické gravitační pole; v této tzv. Schwarzschildově geometrii má element prostoročasového intervalu tvar
| (3.13) |
v geometrodynamických jednotkách; v běžných jednotkách je to
| (3.13') |
Komponenty metrického tenzoru gik ve Schwarszchildově geometri jsou tedy (v geometrodynamických jednotkách) :
| gik = | / | -(1-2M/r) | 0 | 0 | 0 | \ | . | |||
| | | 0 | (1-2M/r)-1 | 0 | 0 | | | |||||
| | | 0 | 0 | r 2 | 0 | | | |||||
| \ | 0 | 0 | 0 | r2 sin2 J | / |
Zatím jsme uvažovali statický případ a předpokládali, že gravitační pole bude statické. Kdybychom tento předpoklad vypustili a připustili možnost závislosti metrických koeficientů (3.11) na čase při zachování sférické symetrie, tj. gtt = - gtt(r,t), grr = grr(r,t), z Einsteinových rovnic Rik= 0 dostaneme po úpravě, že ¶grr/¶t = 0 (takže grr nezávisí na čase) a gtt = f(t)/grr, kde f(t) je funkce pouze času. Protože pro r®Ą přechází vyšetřovaná metrika v metriku Minkowského, kde je gtt=-1 a grr=1, musí být f(t)=const. a na čase tedy nezávisí ani gtt. Dospíváme tak k výsledku, že centrálně symetrické gravitační pole ve vakuu musí být automaticky statické, a to i tehdy, kdyby se budící těleso smršťovalo, expandovalo nebo radiálně pulzovalo (ovšem při zachování přesné sférické symetrie). Získané výsledky můžeme shrnout do nasledujícího tvrzení :
| Teorém 3.3 (Schwarzschildova-Birkhoffova věta) |
| V
asymptoticky rovinném prostoročase je centrálně
symetrické gravitační pole ve vakuu popsáno
Schwarzschildovou geometrií s metrickou formou (3.13) ve
Schwarzschildových souřadnicích. Toto pole je tedy statické a je určeno jen jediným parametrem - celkovou hmotností M. |
Tento poznatek je velmi důležitý při studiu gravitačního kolapsu a vlastností černých děr (kap.4) - je to vlastně speciální případ teorému 4.1 "černá díra nemá vlasy" (odvozeného v §4.5 "Teorém "černá díra nemá vlasy"").
Vnitřní metrika
centrálně symetrického statického tělesa
Jak je tomu uvnitř běžného tělesa (hvězdy, planety)
budícího gravitační pole? Ve zjednodušeném případě
nerotujícího tělesa hmotnosti M a poloměru R,
sestávajácího z nestlačitelné látky s konstatní
hustotou (ideální nestlačitelné kapaliny) s nulovým
tlakem na povrchu, je geometrie prostoročasu dána poněkud
složitějším tzv. vnitřním Schwarzschildovým
řešením, které zde uvádíme bez odvození :
| ds2 = 1/4 [3Ö (1-2GM/c2)/R) - Ö(1 - r2.2GM/c2/R3)]2 c2dt2 - (1 - r2.2GM/c2/R3)-1dr2 + r2(dJ2 + sin2J dj2) . | (3.13b) |
Tato metrika je všude regulární. Pro r>R plynule přechází ve vnější Scharzschildovu geometrii (3.13).
Schwarzschildova geometrie
prostoročasu - pohyb těles
Rozeberme si vlastnosti (vnější) Schwarzschildovy
geometrie. Protože nás bude zajímat celé
Schwarzschildovo
vnější řešení, budeme předpokládat, že budící hmota je
soustředěna ve středu r=0 a všude jinde je vakuum.
Podíváme-li se na prostoročasový element Schwarzschildovy
geometrie (3.13), je na první pohled vidět, že není všude regulární. Při r®2M
časová složka metrického tenzoru gtt®0 a prostorová radiální složka grr®Ą. Poloměr
| rg = 2 M ş 2 G M /c2 | (3.14) |
se nazývá gravitační neboli Schwarzschildův poloměr a příslušná sféra r = rg = 2 M Schwarzschildova sféra. Metrika (3.13) je samozřejmě singulární rovněž pro r=0. Abychom si vyjasnili povahu těchto "singularit" Schwarzschildovy metriky (a uvidíme, že mezi oběma případy je principiální rozdíl), podívejme se nejprve na vlastnosti pohybu testovacích částic ve Schwarzschildově prostoročasu.
Pohyb volné testovací částice ve Schwarzschildově poli je dán rovnicí geodetiky (2.5b)
kde koeficienty konexe Gikl vypočítáme ze složek metrického tenzoru v (3.13) :
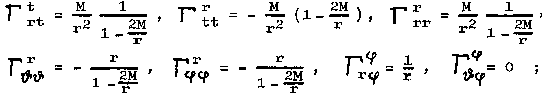 |
(3.15) |
ostatní složky jsou buď s nimi symetrické nebo jsou rovny nule. Sférická symetrie nám umožňuje pro rovinu pohybu položit J = p/2 (sledovat pohyb v ekvatoriální rovině), čímž rovnice pro souřadnici J odpadá. Zbývající rovnice jsou
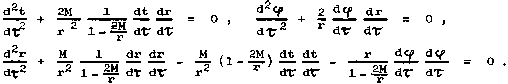 |
(3.16) |
Vydělení první rovnice dt/dt dá
![]()
neboli
| dt = K ( 1 - 2 M / r ) dt , | (3.17) |
kde integrační konstanta K souvisí s rychlostí částice (viz níže). Analogická úprava druhé rovnice dává ln (dj/dt) + 2.ln r = const., z čehož dostaneme rovnici
| r2 dj/dt = const. =def `L | (3.18) |
vyjadřující zákon zachování momentu hybnosti `L. Z třetí rovnice (3.16) pak dostaneme
| (dr / dt)2 = 1/K2 - (1 - 2M/r) (1 + `L2/r2) . | (3.19) |
Radiální
pohyb částice
Mějme nyní částici padající radiálně ve Schwarzschildově
poli ve směru ke středu r=0. V rovnici (3.19) bude nyní `L = r2dj/dt = 0, takže (dr/dt)2 = 1/K2 - 1 + 2M/r. V limitě r®Ą
dostáváme (dr/dt)2 = 1/K2 - 1, takže 1/K2
- 1 je rovno čtverci vlastní rychlosti vĄ, kterou by měla částice v nekonečně
velké vzdálenosti od středu. Tedy
| (dr/dt)2 = vĄ2 + 2.M/r , | (3.20) |
což je shodou okolností stejný výsledek jako v Newtonově teorii. Z této rovnice můžeme vypočítat interval vlastního času t, který potřebuje částice aby se dostala z nějaké (konečné) vzdálenosti r=r2 do vzdálenosti r=r1 od středu :
 |
(3.21) |
Tento interval vlastního času je vždy konečný, a to i pro r1=0. Tedy volně padající testovací částice dosáhne jak "kritického" poloměru r=2M, tak dokonce i bodu r=0, za konečný vlastní čas.
Abychom stanovili tomu odpovídající interval souřadnicového času t (který je vlastním časem pozorovatele v nekonečnu), použijeme rovnic (3.19) a (3.17), což dává :
| (dr/dt)2 = (1 - 2M/r)2 - K2(1 - 2M/r)3 . | (3.22) |
Limitní přechod r®Ą ukazuje, že 1-K2 zde má význam souřadnicové rychlosti vĄ v nekonečnu. Interval souřadnicovího času potřebného pro pohyb ze vzdálenosti r2 do vzdálenosti r1 je pak roven
 |
(3.23) |
Interval
souřadnicového času potřebného k dosažení bodu r=r1
se blíží nekonečnu při r1®2M *).
*) Skutečně
nekonečně dlouhý čas?
Je třeba upozornit, že z fyzikálního hlediska je tento
výsledek nekonečně dlouhého času jen "matematickou
fikcí" - platí pro idealizovaný případ
"nehmotné" testovací částice
bodových rozměrů (která nijak
neovlivní studovaný prostoročas). Pohyb
takových částic je vhodné analyzovat pro studium
geometricko-topologických vlastností daného prostoročasu a
používaných souřadnicových soustav.
Pro skutečná hmotná tělesa
padající na černou díru bude situace poněkud odlišná. Při
přiblížení takového tělesa k černé díře bude vzájemnou
gravitací docházet k deformaci horizontu,
který bude (vzniklým hrbolkem či
výstupkem) dopadajícímu tělesu "vycházet
vstříc". Extrémní případ takového procesu při
fúzi černých děr je znázorněn ve zvětšených výřezech
na obr.4.13-GW v §4.8, pasáž "Binární gravitačně vázané
systémy černých děr. Srážky a splynutí černých děr". Skutečný efektivní čas
pohlcení tělesa černou dírou, či splynutí dvou černých
děr v jedinou, je tedy konečný.
Vztahy (3.21) a (3.24) můžeme zjednodušeně
zrekapitulovat :
Částice pohybující se ze vzdálenosti r0
> rg
radiálně ve Schwarzschildově prostoročasu směrem ke středu (k horizontu, k černé díře)
překročí horizont událostí r = rg za konečný
interval vlastního času t = (2rg/3c). [(r0/rg)3/2
-1]; pak bude
pokračovat v pohybu až do středové singularity r=0,
přičemž tuto dráhu urazí rovněž za konečný vlastní
čas. Z hlediska měření vnějším pozorovatelem se
každý interval vlastního času Dt dilatací času
prodlužuje na interval Dt = Dt/(1-rg/r)1/2 ; čím více se částice blíží k horizontu, její
pohyb se z pohledu vnějšího pozorovatele zpomaluje a
na horizontu r = rg se úplně zastaví,
na nekonečně dlouhý čas "zamrzne". Tato rozdílná časová
dynamika radiálního pohybu částic při vnějším a vnitřním pohledu je způsobena efektem gravitační dilatace času v obecné teorii relativity (diskutovali jsme ji v §2.4 "Fyzikální
zákony v zakřiveném prostoročase", pasáži "Prostor a čas v gravitačním poli").
Přicházíme tedy k poznatku, že z
hlediska vnějšího pozorovatele se každá částice při
přiblížení k poloměru r=2M zpomaluje a potřebuje k jeho
dosažení nekonečně dlouhý souřadnicový čas (s uvážením shora uvedené výhrady "Skutečně nekonečně dlouhý čas?").
Naproti tomu z hlediska pozorovatele padajícího spolu s
částicí je poloměru r=2M dosaženo za konečný interval
vlastního času, tímto místem částice volně projde a
posléze za konečný vlastní čas dosáhne i středu r=0. A
stejným způsobem se bude chovat povrch gravitačně
kolabující hvězdy do černé díry, jak bude analyzováno v §4.2,
pasáži "Dva různé pohledy na gravitační kolaps -
vnější a vnitřní".
Singularita souřadnicová a
fyzikální
Vypočítáme-li na základě koeficientů konexe (3.15)
komponenty Riemannova tenzoru křivosti ve Schwarzsehildově
prostoročase a přetransformujeme je do vztažné soustavy
padajícího pozorovatele, budou (ty z nich, jež jsou nenulové)
úměrné M/r3, např.
| Rtrtr = -2M/r3 , RtJtJ = Rtjtj = M/r3 , RJjJj = 2M/r3 , RrJrJ = Rrjrj = -M/r3 , | (3.24) |
takže na Schwarzschildově sféře dosahují hodnot řádu 1/M2; podobně skalární invarianty (např. R= RiklmRiklm= 48M2/r6) tenzoru křivosti, které nezávisí na souřadné soustavě. Křivost prostoročasu, a tedy i gradienty gravitačních sil (slapové síly), jsou na Schwarzschildově sféře konečné - a tím menší, čím je hmotnostní parametr M větší.
Dospíváme tak k závěru, že singulární chování Schwarzschildova prostoročasového elementu (3.13) pro r=2M nemá svůj původ v singulárním charakteru geometrie prostoročasu na Schwarzschildově sféře, ale je způsobeno použitými Schwarzschildovými souřadnicemi, které se zde nehodí. Přechodem k jiné vhodné vztažné soustavě, např. k soustavě spojené s volně padajícími testovacími částicemi, tato pseudosingularita na Schwarzschildově sféře zmizí.
To, jakým způsobem může nevhodná souřadnicová soustava způsobovat zdánlivou singularitu, si můžeme názorně ilustrovat na jednoduchém příkladě podle obr.3.15. Sledujeme-li kulovou plochu pomocí souřadnic udávajících "zeměpisnou" šířku a délku J a j (obr.3.15a), budou se všechny "poledníky" sbíhat v bodech "severního" a "jižního" pólu, takže pro tyto body není zeměpisná délka definována, metrický tenzor gjj je zde roven nule. Nebo podobně, děláme-li mapu zeměkoule pomocí válcové projekce podle obr. 3.15b, budou se obrazy P' pólu P nacházet v nekonečnu a metrický tenzor gJJ®Ą. Přitom však samotná geometrie kulové plochy v těchto pólech je zcela normální - stačí pootočit kouli o určitý úhel a body, které se v dřívější souřadnicové soustavě jevily singulární, budou naprosto regulární a singulárními se budou zdát jiné body, nové "póly".
 |
Obr.3.15.
Příklad pseudosingularity způsobené nevhodnou souřadnicovou
soustavou. a) Bod P na kulové ploše (pól) se zdánlivě jeví jako singulární, protože v použitých souřadnicích pro něj není definována "zeměpisná délka". b) Zhotovujeme-li mapu zeměkoule pomocí válcové projekce, bude se pól P zdát singulární, protože jeho obraz P' bude v nekonečnu. |
Geometrie samotného prostoročasu je na Schwarzschildově sféře zcela regulární, pozorovatel může přes Schwarzschildovu sféru volně projít během konečného intervalu vlastního času, nezjistí zde lokálně ani nic zvláštního a bude pokračovat dále ve svém pohybu. Zvláštnost prostoročasové geometrie na Schwarzschildově sféře nespočívá tedy v nějakých nenormálních lokálních vlastnostech, ale jak uvidíme dále, má význačnou globální vlastnost - je horizontem událostí.
Jinak je to s druhým singulárním místem v metrice (3.13) - bodem r=0. Zde jak složky tenzoru křivosti (3.24), tak i jeho skalární invarianty dosahují nekonečných hodnot, jsou zde tedy nekonečně velké gradienty gravitačních sil. Částice, která se dostane do bodu r=0 již ve svém pohybu nemůže pokračovat dále, je těmito nekonečnými slapovými silami rozdrcena, doslova přestane existovat v rámci daného prostoročasu. Zde se jedná o skutečnou, fyzikální singularitu geometrie prostoročasu, kterou nelze odstranit žadnou volbou vztažné soustavy. Vlastnostem prostoročasových singularit a posouzení možností jejich existence jsou věnovány §3.7 a 3.8.
Pohyb světla ve Schwarzschildově
poli
Nebudeme zde již dále pokračovat v rozboru pohybu testovacích
částic ve Schwarzschildově poli, odsuneme to do §4.3, kde
tento rozbor bude mít bezprostřední fyzikální souvislost s
vlastnostmi černých děr. Zde se soustředíme spíše na
geometrické vlastnosti Schwarzschildova řešení. Za tím
účelem si ještě ukážeme některé vlastnosti šíření světla ve Schwarzschildově poli (pro geometricko-topologické vlastnosti
Schwarzschildova gravitačního pole je důležité šíření
světla v radiálním směru). Souřadnicovou rychlost cr
světla v radiálním směru dostaneme, jestliže ve výrazu pro prostoročasový interval (3.13) položíme
ds2=0 při dj = dJ = 0
| cr = dr/dt|(ds=0) = 1 - 2M/r . | (3.25) |
Na Schwarzschildově sféře je souřadnicová rychlost světla v radiálním směru rovna nule. Čas, který potřebuje světlo aby se dostalo z bodu o souřadnici r=r1 do bodu r=r2 bude podle (3.25)
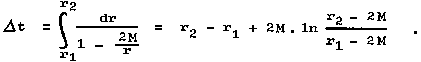 |
(3.26) |
Pro r1®rg = 2M se tento čas blíží
nekonečnu pro libovolnou hodnotu cílového r2
> r1. Světlo vyzářené ze Schwarzschildovy
sféry r=rg potřebuje nekonečně
dlouhý čas
k tomu, aby se dostalo do kteréhokoliv místa více vzdáleného
od středu. Z míst o souřadnicích r < rg
- z pod Schwarzschildovy sféry - se proto žádný objekt
nemůže dostat ven, protože se odtud nemůže dostat ani světlo (a
žádný objekt se nemůže pohybovat rychleji než světlo).
Žádná událost, která probíhá uvnitř Schwarzschildovy
sféry, se tedy nijak nemůže projevit vně a nemůže být z
vnějšku nijak pozorovatelná. Schwarzschildova sféra je proto horizontem událostí, který ve smyslu příčinnosti odděluje vnitřní oblast od
ostatního prostoročasu (viz §3.3).
Pozn.: Tento
horizont událostí se též někdy označuje jako Killingův
horizont, neboť Killingovo vektorové pole xo ş ¶/¶t (zavedené v §2.4), jeho časová složka, zde mění
prostoročasový chrakter: vně horizontu je
časového typu, zatímco uvnitř horizontu nabývá prostorový
charakter.
Pro
gravitační spektrální posuv (rudý posuv)
světla v radiálním směru ve Schwarzschildově metrice
vyplývá jednoduchý vzorec wĄ = wr .(1 - 2M/r)1/2, kde wr je frekvence signálu vyslaného
statickým pozorovatelem ze vzdálenosti r od středu černé díry a wĄ je frekvence tohoto signálu
detekovaná vzdáleným pozorovatelem (v nekonečnu). Tento
vzdálený pozorovatel bude detekovat tento signál s menší
hodnotou frekvence wĄ způsobenou tím, že tento signál
ztrácí energii při překonávání gravitačního pole černé
díry. Pokud by signál libovolné frekvence wr byl vyslán ze Schwarzschildovy
sféry r=2M, bylo by wĄ=0 - nebyl by detekován žádný signál... Z obecného relativistického hlediska
je problematika gravitačního spektrálního posuvu diskutovaná
v §2.4, pasáži "Gravitační spektrální posun".
V oblasti Schwarzschildova horizontu
mění složky metrického tenzoru grr =(1 - 2M/r)-1 a gtt= -(1 - 2M/r) svá znaménka: pro r >
2M je grr > 0 a gtt< 0, zatímco při r< 2M je
grr < 0 a gtt > 0. Lze říci, že časová
t a radiální prostorová r souřadnice si v jistém smyslu
vzájemně vymění úlohy. Uvnitř horizontu úlohu toku
času do budoucnosti přejímá neustálé zmenšování r.
Prostoročasové světelné kužely jsou zde zcela obráceny dovnitř, takže každé reálné těleso se zde
bude pohybovat tak, že r se neustále zmenšuje - musí
tedy "padat" směrem ke středu r=0 (obr.3.16).
Katastrofální důsledky tohoto jevu si ukážeme v kapitole 4 o
gravitačním kolapsu a černých dírách.
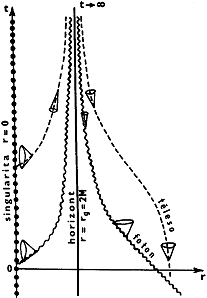 |
Obr.3.16. Prostoročasový diagram radiálního pohybu testovacích částic a fotonů ve Schwarzschildově prostoročasu za použití obyčejných Schwarzschildových souřadnic. |
Zakřivování
světelných paprsků - efekt gravitační čočky
Pro analýzu
geometricko-topologických vlastností Schwarzschildova
gravitačního pole, kterou se zde zabýváme, je důležité
šíření světla v radiálním směru. Z
astrofyzikálního hlediska jsou však důležitější
vlastnosti šíření elektromagnetického záření (a tedy i
světla) v azimutálním směru - gravitační
ohyb dráhy fotonů a zakřivování
světelných paprsků při průchodu kolem
gravitujících těles a sytémů.. O tomto šíření světla v gravitačním
poli a o efektu "gravitační čočky" bude podrobněji pojednáno v §4.3, část "Gravitační
čočky. Optika černých děr".
Analytická extenze Schwarzschildovy
geometrie
Protože zdánlivá singularita na horizontu Schwarzschildovy
geometrie je způsobena jen charakterem použité vztažné
soustavy (Schwarzschildových souřadnic), nabízí se sledovat
Schwarzschildův prostoročas pomocí souřadnic, které nemají
tuto nepříjemnou vlastnost. Nejjednodušší co do realizace by byla
vztažná soustava spojená s radiálně padajícími
testovacími částicemi. Taková soustava sice nemá
souřadnicovou singularitu, avšak není vhodná pro studium
globálních geometrických vlastností (příliš
složité a nepřehledné transformačni vztahy). Pro sledování geometrických
vlastností Schwarzschildova prostoročasu je velmi výhodná
tzv. Kruskalova-Szekeresova
souřadnicová
soustava [160], která vznikla spojením dříve zavedené Eddingtonovy-Finkelsteinovy smršťující se a
rozšiřující se souřadnicové soustavy [76],[84]. Pro tento účel
se nejprve zavádí modifikovaná souřadnice r*
| (3.27) |
[ rÎ(0, +Ą) Ţ r*Î(-Ą, +Ą) ] a dále izotropní souřadnice p a q :
| p = t + r* , q = t - r* . | (3.28) |
Význam těchto souřadnic je ten, že světelné geodetiky směřující ven jsou dány rovnicí q = const. a geodetiky směřující dovnitř rovnicí p = const. Schwarzschildova metrika v souřadnicích (q,r,J,j) má pak tvar
ds2 = - (1- 2M/r)dq2 + 2dqdr + r2(dJ2 + sin2J dj2) ;
tato tzv. smršťující se Eddingtonova-Finkelsteinova souřadnicová soustava dobře (bez pseudosingularity) popisuje pád částic směrem pod gravitační poloměr, nikoliv však v opačném směru. Rozšiřující se Eddingtonova-Finkelsteinova souřadnicová soustava používá místo r a t souřadnice r a p, takže výraz pro metriku zde je
ds2 = - (1- 2M/r)dp2 + 2dpdr + r2(dJ2 + sin2J dj2) ;
zde je naopak dobře popsán pohyb částic směrem ven, zatímco při pádu částic pod gravitační poloměr se objevuje pseudosingularita. Pro odstranění pseudosingularit a získání úplné extenze Schwarzschildovy geometrie se nabízí spojit obě tyto soustavy, tj. vyloučit r a použít souřadnice (p,q,J,j). Prostoročasový element Schwarzschildovy geometrie pak má tvar
ds2 = - (1- 2M/r)dpdq + r2(dJ2 + sin2J dj2) ;
Pro odstranění singulárního koeficientu 1-2M/r je dále třeba provést vhodnou transformaci p' = p'(p), q' = q'(q). Takovou transformaci nalezl Kruskal ve tvaru
p' = e p/4M , q' = e -q/4M .
V těchto nových souřadnicích má metrika tvar
ds2 = - (16.M2/r).e-r/2M dp'dq' + r2(dJ2 + sin2J dj2) .
Abychom dostali tuto metriku v obvyklém tvaru se separovanými časovými a prostorovými členy, zavedeme nakonec místo izotropních souřadnic p' a q' časovou u a prostorovou v souřadnici:
u = (q' - p')/2 , v = (q' + p')/2 .
V Kruskalově soustavě jsou tedy souřadnice t a r nahrazeny bezrozměrnými časovými a radiálními prostorovými souřadnicemi u a v pomocí transformace
| u = |r - 2M|1/2 e r/4M cosh(t/4M) , v = |r - 2M|1/2 e r/4M sinh(t/4M) pro r > 2M | (3.29) |
a analogicky pro r < 2M se záměnou "cosh" za "sinh" a naopak. Jsou to tedy ve skutečnosti dvě navazující souřadnicové mapy (podobně jako např. u rovinného zobrazení zeměkoule). Prostoročasový element Schwarzschildovy geometrie má potom v Kruskalových souřadnicích tvar
| ds2 = - (16.M2/r).e-r/2M (du2 - dv2) + r2(dJ2 + sin2J dj2) . | (3.30) |
kde r jako funkce u a v je dáno rovnicí
| (r - 2M) e r/2M = u2 - v2 . | (3.30') |
Z (3.30) je vidět, že metrika Schwarzschildovy geometrie v Kruskalových souřadnicích je regulární všude s výjimkou středu r=0 (kde se jedná o skutečnou fyzikální singularitu neodstranitelnou žádnou transformací souřadnicové soustavy).

Obr.3.17. Kruskalův prostoročasový diagram Schwarzschildovy
geometrie.
a) Souřadnicová
síť ve vztahu ke Schwarzschildovým souřadnicím r
a t.
b) Celková struktura
prostoročasu a pohyb testovacích částic a fotonů. A je vnější asymptoticky rovinná
oblast, B je vnitřní
oblast pod horizontem.
Některé základní rysy Schwarzschildovy geometrie v Kruskalových-Szekeresových souřadnicích jsou schématicky znázorněny na Kruskalově diagramu (což je prostoročasový diagram v Kruskalových souřadnicích u a v) na obr.3.17b, který můžeme srovnávat s odpovídajícím diagramem ve Schwarzschildových souřadnicích na obr.3.16. Především singularita r=0 je zde dána vztahem v2-u2 = 1, což popisuje dvě oddělené singularity tak, jak je hyperbolami znázorněno na obr.3.17. Horizont r=2M je zde tvořen dvěma přímkami u = ± v. Vnější oblast r > 2M je vyjádřena nerovností u2 > v2, což opět popisuje dvě vnější oblasti. Pro radiální nulové (izotropní) geodetiky ds=0 dostáváme du = ± dv; tyto radiální světelné geodetiky jsou tedy přímky pod úhlem 45° k osám Kruskalovy soustavy. Tato vlastnost je velmi výhodná, protože světelné kužely vypadají úplně stejně jako v diagramu Minkowskiho rovinného prostoročasu STR. Reálná hmotná tělesa se tedy mohou v tomto Kruskalově diagramu pohybovat pouze pod úhlem menším než 45° od svislé osy v (uvnitř prostoročasových světelných kuželů). Rozbor geometrických vlastností Schwarzschildova prostoročasu a sledování přičinných vztahů a pohybu hmotných objektů je zde proto daleko snadnější a názornější než v obyčejných Schwarzschildových souřadnicích (srovnáme-li obr.3.16 a 3.17b vidíme, že pohyb testovacích částic i fotonů vypadá daleko přehledněji na Kruskalově diagramu.
Velmi podivné je to, že z původního Schwarzschildova řešení obsahujícího jen jednu asymptoticky rovinnou vnější oblast r®Ą, jeden horizont r=2M a jednu singularitu r=0, jsme přechodem ke Kruskalovým souřadnicím dostali prostoročas se dvěma vnějšími oblastmi, dvěma horizonty a dvěma singularitami. Vysvětlení je v tom, že prostoročas získaný přechodem ke Kruskalovým souřadnicím je úplnou analytickou extenzí původní Schwarzschildovy geometrie, tedy příkladem procedury zmíněné v závěru §3.1. Skutečný prostoročas M, který je řešením Einsteinových rovnic pro ostrovní sféricky symetrický případ, je rozsáhlejší varietou, než by se dalo očekávat z původního řešení (3.13) ve Schwarzschildových souřadnicích. Schwarzschildovy souřadnice jsou schopny obsáhnout jen část této úplné variety, zatímco Kruskalovy souřadnice ji obsáhnou celou.
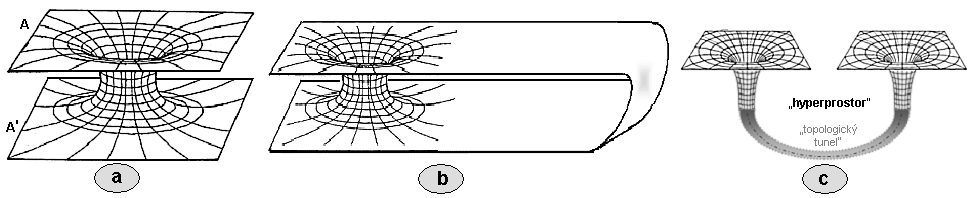 |
|
| Obr.3.18. a) Znázornění geometrické
struktury řezu (prostorové hyperplochy) v = t = 0, J = p/2
Schwarzschildovým prostoročasem ve formě vnoření do
pomocného trojrozměrného eukleidovského prostoru.
Tento pomocný trojrozměrný prostor nemá fyzikální
význam (je pouze prostředkem pro znázornění);
význam má pouze vnitřní geometrie vnořené plochy,
která ukazuje dvě asymptoticky rovinné oblasti A
a A' spojené Einsteinovým-Rosenovým mostem. b) Topologický tunel mezi dvěma místy téhož vesmíru. c) "Červí díra" mezi dvěma místy téhož vesmíru. |
|
Jestliže oblast A na
obr.3.17 je původní vnější asymptoticky rovinnou oblastí
Schwarzschildovy geometrie ("náš vesmír"), objevuje
se ještě jedna zrcadlově obrácená asymptoticky rovinná
oblast A' na druhé straně diagramu, jakýsi
"druhý vesmír". Vezmeme-li si řez
Kruskalovým diagramem podél osy u (tedy řez t=0 podle obr.3.16), vidíme,
že kulové plochy r=const. s ubývajícím r nejprve normálně zmenšují
svoje plochy, avšak ne k nule, ale k minimální hodnotě 16pM2, a potom znovu rostou, jako
kdyby se rozšiřovaly do druhého
asymptoticky rovinného
prostoru. Názorně je tato situace zachycena na obr.3.18a,
který je vnořením řezu t=0 s jedním vynechaným rozměrem do
pomocného trojrozměrného prostoru. Úplná geometrie obsahuje
v časovém řezu určitý "most",
zvaný Einsteinův-Rosenův
most, spojující dva různé asymptoticky rovinné vesmíry
*). Jak je jasně vidět z Kruskalova diagramu,
Einsteinovým-Rosenovým mostem nemůže nikdo proniknout do
druhého (zrcadlově obráceného) vesmíru, protože by se musel
pohybovat nadsvětelnou rychlostí aby stačil uniknout
singularitě.
*) Za předpokladu obvyklé eukliedovské
globální topologie; při složitější topologii by takový
most mohl spojovat i dvě různá místa jednoho vícenásobně
souvislého vesmíru- obr.3.18b,c.
Další zajímavou vlastností Schwarzschildova řešení, která je vidět z Kruskalova diagramu, je to, že v oblasti r < 2M má geometrie dynamický charakter. Sledujeme-li časové řezy (rovnoběžné s osou u) Kruskalovým diagramem postupně od velkých záporných hodnot v až do velkých kladných hodnot v (tj. v postupu časové evoluce), budeme vidět zpočátku dva nesouvisející asymptoticky rovinné vesmíry, z nichž každý má svou singularitu r=0. Jakmile řez přestane procházet dolní (minulou) singularitou, objeví se mezi oběma vnějšími oblastmi Einsteinův-Rosenův most. Tento most se bude rozšiřovat (maximální bude v řezu t=0) a pak zase zužovat, až nakonec při dotyku řezu s horní singularitou zanikne a opět zbudou dva nesouvisející vesmíry se svými singularitami. Lze říci, že most zanikne tak rychle, že jím žádný reálný objekt nemůže proniknout do druhého vesmíru (skončí vždy v singularitě). Geometrie Schwarzschildova řešení má v oblasti r < 2M dynamický charakter vlivem toho, že zde v důsledku výměny úloh časových a prostorových metrických komponent úlohu časové evoluce přebírá "evoluce" prostorová.
Důsledným rozborem Schwarzschildovy geometrie se nám tak objevuje úplně jiná globální topologie, než by se dalo očekávat z "nevině vyhlížejícího" Schwarzschildova výrazu (3.13). Je na první pohled vidět, že topologie nebude eukleidovská v bodě r=0 kde je singularita; mohlo by se ale zdát, že toto je jediný rozdíl od obyčejných topologických vlastností. Úplná extenze však ukazuje zcela jinou globální topologii - dva různé asymptoticky rovinné "vesmíry" spojené "mostem", který má dynamický charakter.
Některé vlastnosti Schwarzschildovy geometrie v Kruskalových souřadnicích jsou stejné jako u Minkowskiho prostoročasu (stejné tvary světelných kuželů). Proto ze stejných důvodů jako jsme to v §3.2 udělali pro Minkowskiho prostoročas, je výhodné Kruskalův diagram ještě dále "vylepšit" zavedením konformní transformace převádějící oblasti nekonečna do konečných souřadnic. Vhodný transformační vztah bude opět podobný jako (3.5) :
c = arctg(v + u) - arctg(v - u) , h = arctg(v+ u) + arctg(v- u) .
Vzniklá metrika má potom tvar
 |
(3.31) |
Příslušný konformní Penroseův prostoročasový diagram úplné analytické extenze Schwarzschildova řešení je znázorněn na obr.3.19. Vlastnosti geometrie, pohyb částic a příčinné vztahy mezi jednotlivými částmi Schwarzschildova prostoročasu jsou zde vidět ještě názorněji než na Kruskalově diagramu.

Obr.3.19. Penroseův-Kruskalův konformní prostoročasový
diagram úplné extenze Schwarzschildovy geometrie.
a) Souřadnicové
čáry ve vztahu ke Schwarzschildovým souřadnicím
(hyperplochy r=const. a t=const.).
b) Tvary světelných
kuželů a radiální geodetiky časového a světelného typu.
Kritická
poznámka: Dvojí
řešení v analytické extenzi - realita nebo fikce?
Neobvyklé vlastnosti analytických extenzí Schwarzschildovy, a zvláště pak Reissnerovy-Nordströmovy a Kerrovy-Newmanovy geometrie (§3.5 a 3.6), vzbuzují
časté diskuse a rozdílné názory mezi odborníky i širší odbornou
veřejností. Odrážejí fyzikální realitu? - nebo se jedná jen o umělé
matematické konstrukce, které
se v přírodě a vesmíru nikdy a nikde neuplatňují?
Na
jedné straně se jedná o přesná řešení osvědčených Einsteinových
gravitačních rovnic,
takže bychom se k nim měli stavět zcela
vážně, alespoň na
teoretické úrovni. Na druhé straně však máme i z jiných
oblastí aplikací matematiky ve fyzice a přírodovědě zkušenost,
že pokud použité (správné) rovnice mají dvě nebo několik
řešení, nemusí některá tato řešení být použitelná -
neodpovídají zadání, nedávají smysl, např. jsou záporná
či imaginární.
Jednoduchým příkladem může být
použití kvadratických rovnic v geometrických
úlohách stanovení rozměrů geometrických útvarů (např.
vztahů obvodů, ploch a úhlopříček pozemků). Tyto rovnice
mají zpravidla dva kořeny, přičemž jen jeden z nich
vyhovuje zadání úlohy a je použitelný, zatímco druhý
bývá často záporný či imaginární. Tomuto druhému
výsledku nemůžeme přikládat technický či přírodovědný
význam. V samotné teorii rovnic je však nutno uvažovat
všechna řešení...
Podobně
některá rozšířená řešení Einsteinových rovnic, i když
jsou matematicky korektní, pravděpodobně neřeší žádnou skutečnou situaci v přírodě
(ve vesmíru). Z (astro)fyzikálního hlediska jsou tyto otázky
podrobněji diskutovány v §4.4 "Rotující a
elektricky nabité Kerrovy-Newmanovy černé díry", část "Černé
díry - mosty do jiných vesmírů? Červí
díry".
| Gravitace, černé díry a fyzika prostoročasu : | ||
| Gravitace ve fyzice | Obecná teorie relativity | Geometrie a topologie |
| Černé díry | Relativistická kosmologie | Unitární teorie pole |
| Antropický princip aneb kosmický Bůh | ||
| Jaderná fyzika a fyzika ionizujícího záření | ||
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | ||
Vojtěch Ullmann