Kdy lze očekávat vznik singularit ?

Kapitola 3
GEOMETRIE A TOPOLOGIE PROSTOROČASU
3.1. Geometricko-topologické vlastnosti prostoročasu
3.2. Minkowského rovinný prostoročas a asymptotická struktura
3.3. Cauchyova úloha, příčinnost a horizonty
3.4. Schwarzschildova geometrie
3.5. Reissnerova-Nordströmova geometrie
3.6. Kerrova a Kerrova-Newmanova geometrie
3.7. Prostoročasové singularity
3.8. Hawkingovy a Penroseovy teorémy o singularitách
3.9. Nahé singularity a princip "kosmické cenzury"

3.8. Hawkingovy a Penroseovy teorémy o singularitách

Z předchozího rozboru jsme viděli, že ony nepříjemné singularity prostoročasu se objevují v některých přesných řešeních Einsteinových gravitačních rovnic, např. ve Schwarzschildově nebo Kerrově-Newmanově geometrii (viz §3.4 a 3.5). Vzniká otázka, zda se singularity budou vyskytovat i v realističtějších fyzikálních situacích. Svého času (šedesátá léta) se doufalo, že singularity v řešeních gravitačních rovnic jsou důsledkem předpokladů o přesné symetrii a že narušení symetrie (např. rotace) by snad mohlo singularitám zabránit.

Na to by ukazovala i analogie s klasickou Newtonovou mechanikou. Jestliže vezmeme přesně symetrické rozložení malých tělísek a necháme je vlastní gravitací padat, "srazí se" všechny současně ve středu a vytvoří jakousi "singularitu" v rozložení hmoty (nekonečná hustota). Stačí však poněkud porušit přesnou symetrii (popř. výchozí stav nechat rotovat) a tělíska prolétnou poblíž středu kolem sebe (popř. převládne odstředivá síla neustále se zrychlující rotace) aniž se něco tak špatného jako singularita stane.

Potom by singularity byly jen akademickou otázkou: byly by vlastností některých idealizovaných a nerealistických modelů. Protože ve skutečné přírodě přesná symetrie není nikdy splněna, nevyskytovaly by se ve skutečnosti ani sigularity - neměly by žáddný fyzikální význam.

Výzkumy Penrose a Hawkinga však ukázaly, že v obecné teorii relativity (která si činí nárok býti správnou fyzikou gravitace) tomu tak není - prostoročasové singularity jsou zde zákonitým jevem a vyskytují se v řešení gravitačních rovnic za značně obecných podmínek (i bez symetrie), které jsou v praxi pravděpodobně splněny. Penrose a Hawking formulovali své výsledky ve formě několika existenčních teorémů specifikujících podmínky, za nichž se prostoročasové singularity zákonitě objevují. V tomto odstavci si stručně přiblížíme tyto důležité věty o singularitách.

První z těchto vět je vlastně zobecněním známého faktu, že v OTR sféricky symetrický kolaps pod Schwarzschildův poloměr (viz §3.4, 4.2, 4.3) vede ke vzniku singularity. Schwarzschildovu sféru (která je definována pro sféricky symetrický případ) Penrose ve svém teorému nahrazuje obecnějším objektem, tzv. zachycenou plochou :

Zachycená (pohlcující) plocha se objevuje tehdy, když gravitační pole je tak silné, že i paprsky vyzářené ven jsou gravitací "staženy zpět" (obr.3.28). Protože nic se nemůže pohybovat rychlostí větší než světlo, bude hmota nacházející se uvnitř zachycené plochy "uvězněna, ulovena v pasti" v prostorové oblasti, jejíž hranice (a tedy i objem) se smršťuje k nule za konečný časový interval.

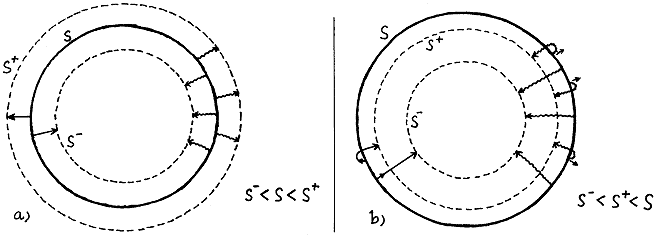
Obr.3.28. Mějme uzavřenou dvojrozměrnou plochu S, ze které je v určitém okamžiku vyzářen světelný impuls kolmo směrem dovnitř i směrem ven. Množina bodů, kam za jednotku času dospěje světlo vyzářené dovnitř bude uzavřená plocha S^-, množina bodů dosažených za jednotku času světlem vyzářeným kolmo ven bude uzavřená plocha S⁺.
a) Za normálních okolností bude plocha S^- menší než plocha S a plocha S⁺ větší než S.
b) V případě, že S je zachycenou plochou, bude jak plocha S^-, tak i plocha S⁺ menší než S - i paprsky vyzářené ven z S budou ve skutečnosti zataženy dovnitř.

Penroseovu větu lze pak formulovat takto :

Nastíníme si důkaz věty 3.4 podle obr.3.29. Na Cauchyho hyperploše S zvolíme bod p_o uvnitř oblasti omezené uzavřenou zachycenou plochou F. Zde je konvergence geodetik Cł C_o > 0, kde C_o je nějaká minimální hodnota konvergence. Protože podle a) je splněna energetická podmínka, bude na základě Raychaudhuriho rovnice (2.59) dC/dl ł C_o²/3 > 0 (viz teorém 2.5 v §2.6). Pro l větší než počáteční hodnota l₁ na ploše S tedy bude C ł 3/[l-(l₁+3/C_o)] takže C se stane nekonečnou ne dále jak ve "vzdálenosti" l_o = 3/C_o od plochy S, a to podél každé geodetiky procházející oblastí hyperplochy S omezené zachycenou plochou F. Sousední geodetiky se tedy protínají, objevují se fokální body.

Obr.3.29. K důkazu teorému 3.4. V oblasti (trojrozměrné) prostorové hyperplochy S omezené dvojrozměrnou zachycenou plochou F je konvergence geodetik C ł Co> 0. To způsobí, že geodetika G a nekonečně blízká geodetika G ' se protnou v bodě f ve vzdálenosti menší než 3/Co.

Bodem p_o nechť prochází geodetika G, na níž si zvolímé bod p ve "vzdálenosti" větší než l_o. Sousední (nekonečně blízká) geodetika G' protne geodetiku G v bodě f bližším než p. Lomenou světočáru p'_o- f - p můžeme "narovnat" tak, jak je naznačeno na obr.3.29, čímž dostaneme světočáru jdoucí od hyperplochy S do bodu p, která má větší délku než geodetika G. A zde dospíváme k prvnímu sporu: časová světočára o největší délce jdoucí od hyperplochy S do bodu p musí být normálová geodetika; jestliže však normálová geodetika má délku větší než l_o = 3/C_o, potom to není světočára maximální délky jdoucí od hyperplochy S do bodu p (ukázali jsme si možnost nalézt delší světočáru). Jestliže tedy zvolíme nějaký bod p v dostatečně velké vzdálenosti (větší než 3/C_o podél nějaké geodetiky) od hyperplochy S, nebude existovat časová světočára maximální délky jdoucí od hyperplochy S do bodu p.
Podle předpokladu b) je hyperplocha S globální Cauchyho hyperplochou prostoročasu M, takže každá časová světočára v M protíná S (právě jednou). Protože tedy každá časová světočára jdoucí bodem p protíná hyperplochu S, musí mezi nimi existovat světočára maximální délky jdoucí od hyperplochy S do bodu p (měla by to být tedy geodetika).
Avšak před chvílí jsme si ukázali, jak je možno nalézt bod p, do něhož nelze od plochy S vést světočáru maximální délky. Dostáváme tak logický spor, který lze uspokojivě vyřešit jedině tím, že do bodu p, majícího uvedené sporné vlastnosti, se vůbec žádná geodetika z S dostat nemůže - žádná geodetika směřující z oblasti obklopené zachycenou plochou F hyperplochy S do budoucna nemá délku větší než 3/C_o. V M se tedy vyskytují nekompletní geodetiky.

Všimněme si stručně významu a účelu jednotlivých podmínek ve větě 3.4. Podmínku c) jsme si již nastínili výše - je to právě ta základní specifická podmínka, aby gravitační pole bylo natolik silné, že z něho nemůže uniknout ani světlo. Podmínka a) říká podle Raychaudhuriho rovnice (2.59), že gravitace má přitažlivý charakter a na geodetiky fokusující účinek (derivace konvergence geodetik C je nezáporná). Jak bylo ukázáno v §2.6, je pro splnění podmínky R_ikVⁱV^k ł 0 třeba, aby vlastní hustota energie byla nezáporná pro každého pozorovatele. Je to tedy energetická podmínka, která je splněna pro všechny známé formy hmoty a pole (kvantové výjimky budou zmíněny níže).

Problematičtější je podmínka b) - existence (nekompaktní) globální Cauchyho hyperplochy v prostoročase M, která činí teorém 3.4 poměrně slabým. Jak jsme viděli v §3.5 a 3.6, některá řešení Einsteinových rovnic (např. Reissnerova-Nordströmova nebo Kerrova geometrie) vedou k prostoročasu, který nemá globální Cauchyovy hyperplochy. Věta 3.4 fakticky říká, že za přítomnosti uzavřené zachycené plochy (např. při gravitačním kolapsu) bude existovat buď singularita nebo Cauchyho horizont; v obou těchto případech se ztrácí možnost všude v M předpovídat budoucnost. Mezi těmito dvěma eventualitami však věta 3.4 rozhodnout nedovede.

Při použití věty 3.4 na "lokální" případ gravitačního kolapsu (kap.4, §4.2-4.4) je navíc nevýhodné to, že musíme znát globální geometrickou strukturu celého vesmíru (být Cauchyho hyperplochou je vlastnost nejen samotné hyperplochy, ale i celého prostoročasu M). Bylo by tedy užitečné zbavit se podmínky b) (nutnosti existence globální Cauchyovy hyperplochy).

Když to uděláme, tj. hyperplocha S bude jen částečnou Cauchyho hyperplochou, budou argumenty vedoucí k větě 3.4 platit pouze v Cauchyho oblasti evoluce D(S) hyperplochy S. Rozbor situace na Cauchyho horizontě H(S) (který je vždy izotropní plochou) vede k tomu, že aby byla splněna podmínka kauzality pro izotropní geodetiky, musí být H(S) nekompaktní. Platí-li energetická podmínka a je-li přítomna zachycená plocha, lze nalézt geodetiku, která není kompletní. Příslušná věta zní takto :

*) Generická podmínka (lat. genericus = rodový, druhový; též obecný, základní..),
zvaná též rodová či typová podmínka, je poněkud speciální a odtažitý požadavek (hranaté závorky [..i,j,m,n..] znamenají, že se berou antisymetrické indexy).
Fyzikálně tato podmínka znamená, že každá částice nebo kvantum, pohybující se volně po geodetice, se během své historie setká s místem, kde je prostoročas zakřiven nějakou formou látky nebo záření. Za běžných okolností, které se mohou astrofyzikálně vyskytovat, by stačilo např. R_jklmK^kK^l ą 0. Speciální složitější tvar generické podmínky vychází z podrobností matematického důkazu teorému 3.5 [130], k vyloučení některých speciálních metrik, v nichž se zakřivení anuluje v některých směrech.

Hawking pak zformuloval ještě další větu :

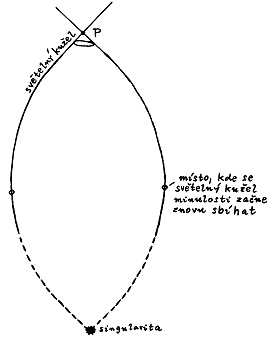Obr.3.30. Jestliže z bodu p sledujeme světelný kužel ve směru minulosti a zjistíme, že se jeho izotropní geodetiky začnou znovu sbíhat (vlivem fokusace křivostí prostoročasu), lze na základě teorému 3.6 očekávat přítomnost prostoročasové singularity v minulosti (např. "big bang" v minulosti vesmíru).

Obě tyto věty mají výhodu v tom, že není třeba činit žádné předpoklady (kromě kauzality) o globální struktuře vesmíru; jsou proto výhodné pro analýzu ohraničených ("lokálních") jevů jako je gravitační kolaps hvězd. Teorém 3.6 je jednak (ve verzi "v budoucnosti") použitelný pro dostatečně homogenní případy gravitačního kolapsu (bod p odpovídá středu kolapsu), hlavně však (ve verzi "v minulosti") se dá použít v kosmologických problémech (kap.5). Věta se vztahuje jen na vnitřek a plášť světelného kuželu minulosti bodu p, což jsou oblasti jež mohou být principiálně pozorovatelné z p. Vezmeme-li za světobod p událost našeho pozorování vesmíru, můžeme v principu na základě tohoto pozorování (např. stanovení pozorované hustoty hmoty ve vesmíru) rozhodnout, zda geodetiky v minulosti změnily znaménko své konvergence (obr.3.30). Podle rozboru Hawkinga a Ellise [127],[128] by hustota pozorovaného reliktového záření (které přichází izotropně s teplotou asi 2,7°K) mohla být postačující k tomu, aby podmínka c) věty 3.6 byla splněna. Potom by v minulosti měla (podle klasické OTR) existovat singularita prostoročasu - "velký třesk".

Speciálně pro singularity v kosmologii je určena následující věta :

Podmínky b) a c) znamenají, že prostoročas M je uzavřený a expandující (resp. smršťující se) v každém bodě hyperplochy S.

Výše zmíněné teorémy 3.4 - 3.7 svědčí o přítomnosti prostoročasových singularit v široké skupině řešení Einsteinových rovnic za podmínek, které se zdají být v přírodě splněny. To bude ukázáno v kap.4 pro gravitační kolaps za vzniku černé díry a též v kap.5 pro vesmír jako celek. Hawkingovy a Penroseovy teorémy jsou větami existenčními a obsahují málo informací o povaze a vlastnostech předpovídaných singularit - o jejich "rozměrech", "tvaru", "poloze" v prostoru a čase a pod. Z hlediska fyzikální důležitosti pro evoluci prostoročasu je též třeba znát "počet" geodetik nekompletních v důsledku singularit: je to jen jedna geodetika, celá kongruence v určité části prostoročasu, nebo úplně všechny geodetiky (a světočáry vůbec)? O tom je možno si učinit určitou představu i z existenčních vět; např. v případě splnění podmínek teorému 3.4 a nepřítomnosti Cauchyových horizontů žádná geodetika z hyperplochy S nemůže být prodloužena dále něž do 3/C_o (C_o ł 0 je minimální hodnota konvergence na S). Pokud je přítomen Cauchyho horizont, nemusí se každá geodetika setkat se singularitou, protože se může dostat do oblasti v níž nelze předvídat budoucnost z hyperplochy S. Z teorémů o singularitách lze tedy obecně nanajvýš dokázat existenci trojrozměrné kongruenee neúplných geodetik nacházejících se v rámci Cauchyho oblasti evoluce plochy S.

Povahu singularit lze analyticky zjistit v případě přesných řešení Einsteinových rovnic (§3.4-3.6). Úloha teorémů o singularitách je jiná: ukázat, zda jsou singularity přítomny i v takových řešeních Einsteinových rovnic, které nedovedeme analyticky popsat. A to rozhodně není triviální otázka. Přitom očekáváme, že povaha singularit v těchto případech bude alespoň trochu podobná jako u těch přesných řešení, která jsou jim fyzikálně blízká.

3.7. Prostoročasové singularity		3.9. Nahé singularity a princip "kosmické cenzury"

Vojtěch Ullmann