| (3.32) |
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | Gravitace, černé díry a fyzika |
Kapitola 3
GEOMETRIE A
TOPOLOGIE PROSTOROČASU
3.1. Geometricko-topologické vlastnosti
prostoročasu
3.2. Minkowského rovinný
prostoročas a asymptotická struktura
3.3. Cauchyova úloha,
příčinnost a horizonty
3.4. Schwarzschildova geometrie
3.5. Reissnerova-Nordströmova geometrie
3.6. Kerrova a Kerrova-Newmanova
geometrie
3.7. Prostoročasové singularity
3.8. Hawkingovy a Penroseovy
teorémy o singularitách
3.9. Nahé singularity a princip
"kosmické cenzury"
3.5. Reissnerova-Nordströmova geometrie
Předchozí sféricky
symetrický případ je možno poněkud zobecnit při zachování
sférické symetrie tím, že budící těleso budeme uvažovat elektricky nabité s nábojem Q. Pro zachování sférické
symetrie musí být distribuce tohoto elektrického náboje též
sféricky symetrická, protože gravitační pole je buzeno nejen
hmotou zdrojového tělesa, ale i tenzorem energie-hybnosti
elektromagnetického pole. Nesymetrické rozložení náboje by
vedlo k nesymetrickému elektrickému poli, které by budilo
nesymetrické gravitační pole.
Element prostoročasového intervalu bude
mít opět stejný sféricky symetrický základní tvar (3.10)
ds2 = gttdt2 + grrdr2 + r2(dJ2 + sin2J dj2) .
Rozdíl oproti předchozímu Schwarzschildovu řešení je nyní v tom, že vnější řešení nebude řešením Einsteinových rovnic bez pravé strany, ale pravou stranou zde bude tenzor energie-hybnosti elektromagnetického pole Tikelmag (1.118). V tomto případě se jedná o Coulombovské centrálně symetrické elektrostatické pole o intenzitě E = E(r).er, kde er je jednotkový bázový vektor radiálního směru. Protože Schwarzschildova radiální souřadnice r si zachovává ten význam, že plocha koule se středem v bodě symetrie, mající poloměr r, je rovna 4pr2, podle Coulombova zákona (Gaussovy věty) je E(r)= Q/r2. Tenzor energie-hybnosti tohoto elektrického pole potom je (nediagonální složky jsou nulové)
Tttelmag = -Trr = TJJ = Tjj = E(r)2/8p = Q2/8p.r 4 ;
ten dosadíme do Einsteinových rovnic Rik - (1/2)gikR = 8pTikelmag a pro sféricky symetrickou metriku (3.10) dostaneme podobným postupem jako při odvozování Schwarzschildova řešení opět dvě nezávislé diferenciální rovnice
dgtt/dr = (1/r) gtt (1 + grr - grr.Q2/r2) , dgrr/dr = - (1/r) grr (1 + grr - grr.Q2/r2) .
Řešení této soustavy je
gtt = C1(1 - C2/r + Q2/r2) , grr = (1 - C2/r + Q2/r2 )-1 ,
kde ze stejných důvodů jako ve Schwarzschildově případě musí být integrační konstanty C1=1 a C2=-2M. Konečný výraz pro element prostoročasového intervalu sféricky symetrického gravitačního pole buzeného sféricky symetrickým tělesem o celkové hmotnosti M a elektrickém náboji Q má tedy tvar
| (3.32) |
v geometrodynamických jednotkách; v běžných jednotkách je to
 |
(3.32') |
Tato geometrie se nazývá Reissnerova-Nordströmova geometrie (R-N). Parametr M zde má opět význam celkové hmotnosti, parametr Q význam celkového elektrického náboje měřeného vzdáleným pozorovatelem pomocí Gaussových integrálních toků vektoru E, popř. pomocí analýzy pohybu nabitých testovacích částic. V případě 0<Q2<M2 by R-N pole mohlo teoreticky popisovat elektricky nabitou černou díru (§4.4 "Rotující a elektricky nabité Kerrovy-Newmanovy černé díry").
Odvození
gravitačně-elektrického řešení z principu nejmenší akce
Obecné odvození struktury prostoročasu za přítomnosti
kombinovaného gravitačního +
elektromagnetického pole se někdy provádí pomoci
variačního principu nejmenší akce s
použitím kombinovaného Lagrangiánu
gravitačního LG a elektrodynamického LEL
:
L = LG + LEL
= (R - 2L) - FikFik ...... ,
kde R je Ricciho skalární křivost, L kosmologická
konstanta, Fik je tenzor elektromagnetického pole.
Variační princip nejmenší akce pak dává Einsteinovy-Maxwellovy
rovnice gravitačního a elektromagnetického pole :
Gik + Lgik = 1/2 gik....................,
.............................
............... ...................
Vlastnosti
Reissnerova-Nordströmova pole
R-N geometrie s prostoročasovou metrikou (3.32) je statickým
sféricky symetrickým řešením Einsteinových-Maxwellových
gravitačních rovnic. Tato geometrie je asymptoticky rovinná a
její horizont má sférickou topologii. Je charakterizována
hmotností M a elektrickým nábojem Q a je singulární v
počátku r=0 radiální souřadnice.
Podle vzájemného poměru hodnot M a Q
můžeme v Reissnerově-Nordströmově prostoročase rozlišovat
čtyři význačné případy lišící se globální
geometrickou strukturou :
a) Při Q = 0, M > 0 dostáváme
Schwarzschildovu geometrii z předchozího §3.4 ;
b) 0 < Q2 < M2 ;
c) 0 < Q2 = M2 ;
d) Q2 > M2 > 0 .
Nejprve rozebereme případ 0 < Q2
< M2, který je fyzikálně
nejzajímavější.
Vnější a vnitřní horizont
Reissnerova-Nordströmova metrika (3.32) je značně podobná
Schwarzschildově metrice (3.13), avšak liší se tím, že
výraz
1 - 2 M r + Q2/r2
je v případě 0 < |Q| < M roven nule pro dva "kořeny" r= rg+ a r = rg- :
| rg+ = M + Ö(M2 - Q2) , rg- = M - Ö(M2 - Q2) . | (3.33) |
V obyčejných jednotkách jsou to hodnoty
| rg+ = (G/c2) [M + Ö(M2 - Q2)] , rg- = (G/c2) [M - Ö(M2 - Q2)] . | (3.33') |
V R-N geometrii tedy existují dva "horizonty", kde metrika (3.32) není regulární - "vnější" horizont r=rg+ a "vnitřní" horizont r=rg-. Vnější horizont r=rg+ má podobný význam jako Schwarzschildova sféra ve Schwarzschildově prostoročase je to horizont událostí, oddělující příčinně vnitřní oblast od vnější; z (3.33) vidíme, že za přítomnosti elektrického náboje je gravitační poloměr rg+ menší než rg =2M ve Schwarzschildově případě. Pod r=rg+ jsou světelné kužely obráceny dovnitř směrem k r=0 (protože gtt > 0) a zdálo by se, že každý objekt jež se tam dostane nutně skončí v singularitě r=0. Avšak na vnitřním horizontu r=rg- se světelné kužely opět začínají napřimovat (časová složka metrického tenzoru opět mění znaménko: gtt < 0) - je zde tedy možný pohyb částice tak, aby se vyhnula singularitě (obr.3.20). Nemůže se však dostat přes vnější horizont (tj. horizont událostí) zpět do původního prostoročasu, ale nutně do "jiného vesmíru", který leží vzhledem k původnímu v absolutní budoucnosti (viz níže).
 |
Obr.3.20 Kerrův prostoročasový diagram Reissnerovy-Nordströmovy geometrie (podobně bude situace vypadat i v Kerrově a Kerrově-Newmanově geometrii - §3.6). Vnější horizont r= rg+ je horizontem událostí (světelné kužely pod ním jsou obráceny dovnitř směrem k r=0). Pod vnitřním horizontem r= rg- se však světelné kužely začínají opět "napřimovat", takže světočára tělesa, které proniklo pod horizont r=rg+, nemusí nutně skončit v singularitě r=0. |
Singulární chování metriky (3.32) ve standardních souřadnicích na těchto horizontech je opět jen zdánlivé a může být odstraněno přechodem k vhodnějším souřadnicím podobným Kruskalovým. S pomocí modifikované souřadnice r*
 |
(3.34) |
podobně jako při extenzi Schwarzschildovy geometrie zavedeme izotropní souřadnice p = t + r*, q= t - r*. Ty potom za účelem odstranění singulárního koeficientu v metrice dále přetransformujeme :
| (3.34') |
Po zavedem nových časových a prostorových souřadnic u = (q' - p')/2 a v = (q' + p')/2 má Reissnerova-Nordströmova metrika tvar
| (3.35) |
Po konformní transformaci (analogické (3.5) v §3.2) za účelem názornější prezentace asymptotické struktury bude Reissnerova-Nordströmova geometrie popsána intervalem
 |
(3.35´) |

Obr.3.21. Penroseův konformní prostoročasový diagram úplné
extenze Reissnerovy-Nordströmovy geometrie pro případ Q2<M2.
a)
Souřadnicová síť - hyperplochy r=const. a t=const.
b) Globální
geometrická struktura - nekonečně mnoho periodicky se
opakujících vnějších oblastí ("vesmírů") A...,-1,1,2,.., vnitřních oblastí B...,-1,1,2,.. a C...,-1,1,2,.., horizontů a singularit.
Cestování do jiných
vesmírů ?
Prostoročasový diagram konformního obrazu R-N geometrie pro fyzikálně
nejpravděpodobnější případ 0 <|Q|< M je na obr.3.21.
Geometrická struktura této úplné
extenze Reissnerova-Nordströmova řešení je neočekávaně
složitá. Objevuje se zde nekonečné množství periodicky se
opakujících "vesmírů" (samostatných asymptoticky
rovinných vnějších oblastí A…,-1,1,2,…), horizontů a singularit. Oproti
Schwarzschildově geometrii (obr.3.19), kde singularity jsou
prostorového typu (a tedy pro každý objekt v oblasti B nevyhnutelné), jsou singularity
Reissnerovy-Nordströmovy geometrie podle obr.3.21 časového typu - jsou
takříkajíc "časově omezené" a lze se jim vyhnout.
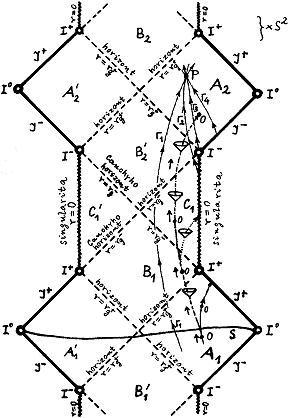 |
Obr.3.22. Pozorovatel O pohybující se ve vnější
asymptoticky rovinné oblasti A1 Reissnerova- Nordströmova
prostoročasu má tři
možnosti. Buďto se bude neustále pohybovat v A1 (plná čára), takže se v limitě dostane do I+ nebo do Á+. Pokud však pozorovatel pronikne pod horizont r=rg+ (čárkovaná tra jektorie) do vnitřní oblasti B1, projde i horizontem vnitřním r=rg- do oblasti C1, kde má dvě možnosti: buď narazí na singularitu (tečkovana dráha) kde je pohlcen a zničen, nebo se může vyhnout singularitě (čerchovaná trajektorie) a dostane se do další asymptoticky rovinné vnější oblasti A2. Situace v tomto dalším "vesmíru" A2 přitom není zcela určena počátečními podmínkami na Cauchyho hyperploše S, jak je vidět např. v bodě pÎA2. |
Sledujme osud
pozorovatele (jak je naznačeno na obr.3.22), který při svém
pohybu Reissnerovým-Nordströmovým prostoročasem pronikl pod
vnější horizont r = rg+. Protože se dostal pod horizont
událostí, nemůže se již nijak vrátit do původního
vnějšího prostoru (oblasti A1) a má v podstatě dvě možnosti. Jednak
doletět do singularity, kde jeho světočára (a tedy i jeho
existence v rámci uvažované variety) definitivně skončí. To
však není (na rozdíl od Schwarzschildova prostoročasu)
nevyhnutelné, pozorovatel se může singularitě vyhnout
a pohybovat se dále, až se objeví v
druhé asymptoticky rovinné oblasti A2, v druhém "vesmíru", který leží vzhledem k
výchozímu A1 v absolutní budoucnosti.
Vidíme tedy, že reálný hmotný objekt pohybující se v R-N
geometrii v rámci světelného kuželu může v principu
"cestovat" mezi jednotlivými "vesmíry" *),
aniž by musel projít singularitou (na
rozdíl od Schwarzschildovy geometrie, kde
Einsteinovým-Rosenovým mostem by se dalo projít pouze
nadsvětelnou rychlostí).
*) Je třeba upozornit, že
toto "cestování mezi různými vesmíry" (a samotná
existence těchto dalších vesmírů) je možné pouze
teoreticky v krajně idealizovaném modelu asymptoticky
rovinného vesmíru bez jiných těles a polí, s přesnou
Reissnerovou-Nordströmovou nebo Kerrovou geometrií. Kritické
posouzení podobných možností bude v §4.4, část "Černé
díry - mosty do jiných vesmírů?".
Podíváme-li se na kauzální
vztahy tohoto druhého vesmíru vzhledem k původnímu, vidíme,
že vnitřní horizonty r=rg- jsou zároveň Cauchyovými horizonty.
Vezmeme-li si nějakou událost P v oblasti A2 a sledujeme, čím může být
principiálně ovlivňována, vidíme, že sice může být
ovlivňována geodetikami (např. G1) přicházejícími z oblasti A1
(a danými tedy počátečními podmínkami na vhodné Cauchyho
hyperploše v A1), avšak mohou tam rovněž
"nekontrolovaně" přicházet nové informace
geodetikami (např. G2,
G3, G4) z oblastí nekonečna minulosti
I-, Á- a ze singularity, která je odtud
"vidět". Tyto informace mohou narušit každou předpověď učiněnou
na základě počátečních podmínek v oblasti A1.
Pozorovatel se tedy vynořil v oblasti prostoročasu (jiném
"vesmíru"), který není jednoznačně určen
počátečními podmínkami na žádné Cauchyho hyperploše v
původní oblasti A1.
Zkonfrontujme to s
deterministickou ideou klasické (nekvantové) fyziky, kterou zformuloval již
Laplace: Kdybychom v určitém okamžiku zjistili všechny
fyzikální veličiny ve všech místech vesmíru (tj. okamžitý
stav vesmíru - úplný soubor počátečních podmínek na
Cauchyho hyperploše) a znali fyzikální zákony, kterými se
všechny tyto veličiny řídí, mohli bychom neomezeně předpovídat evoluci vesmíru, tj. jeho stav kdykoliv v
budoucnosti (nebo i minulosti). V úplné extenzi
Reissnerovy-Nordströmovy geometrie však toto není splněno,
existují zde Cauchyho horizonty (a tedy neexistují globální Cauchyovy
hyperplochy) a jsou zde proto oblasti, jejichž stav není
jednoznačně určen žádným souborem počátečních
podmínek. Pouze ve vnější asymptoticky rovinné oblasti lze
jednoznačně "předvídat" budoucnost z parciálních
Cauchyho hyperploch. Tedy i v klasické fyzice (na níž je
Reissnerova-Nordströmova geometrie jakožto řešení
Einsteinových rovnic založena) může být možnost předvídat
budoucnost omezena nejen praktickou nedostupností fyzikálních
veličin ve všech místech vesmíru v určitém časovém
okamžiku, ale principiálně též globální
geometricko-topologickou strukturou prostoročasu.
Nestabilita vnitřního Cauchyova
horizontu vůči perturbacím; "Mass
inflation" ?
Shora uvedený scénář možnosti cestování pozorovatele skrze
vnitřní Cauchyův horizont do jiného asymptoticky plochého
vesmíru předpokládá, že tento vnitřní horizont je stabilní při zhruba neměnných parametrech
černé díry (zde hmotnosti a náboje). Pertubační analýza však
ukázala, že může vykazovat nestabilitu a dokonce divergenci.
Již prostá analýza dopadajících radiovln ukazuje, že tyto
vlny se při cestě do nitra černé díry zahustí a vykazují
silné gravitační a dopplerovské frekvenční modré-fialové
posuny. Toto zesilování ve směru k vnitřnímu Cauhyho
horizontu pokračuje do nekonečna, což vede k její nestabilitě i vůči malé vnější perturbaci. A
podrobnější perturbační analýzy potvrdily, že tato exponenciální divergence může vést na singularitu. Padající
cestovatel tedy nepřežije setkání a průchod vnitřním
Cauchyovým horizontem..?..
Nebo jiná argumentace: Na obr.3.21
každý bod oblasti B mezi rg+ a rg- (kde plochy r=const. jsou prostorového
typu) reprezentuje dvojrozměrnou kulovou plochu, která je
uzavřenou pohlcující plochou (viz
definici 3.10). Pozorovatel O při svém průchodu plochou r=rg- (obr.3.22) uvidí celou další
historii asymptoticky rovinné vnější oblasti A1,
kterou opouští, za konečný čas. Každé těleso z této
oblasti proto bude vidět s neomezeně narůstajícím fialovým
posuvem. Z toho plyne, že Cauchyho horizont r=rg- je nestabilní vůči
perturbacím počátečních podmínek na výchozí prostorové
hyperploše S [192]. Je jasné, že
"kosmologické" otázky evoluce "vesmíru" A1,
který pozorovatel opouští, budou pro něj velmi důležité.
Jestliže vesmír A1 bude v budoucnu třebas
kolabovat, nevyhne se tomuto osudu ani pozorovatel O;
na horizontu r=rg- se setká s nekonečnou hustotou
hmoty~energie, tedy nakonec vlastně se singularitou.
Tato
hmotnostní nestabilita vnitřního Cauchyova horizontu se někdy
poněkud zavádějícím způsobem nazývá "Mass
inflation", s analogií na inflační expanzi
vesmíru.

Obr.3.23. Penroseův konformní prostoročasový diagram úplné
extenze Reissnerovy-Nordströmovy geometrie pro případ Q2 = M2.
a) Hyperplochy (souřadnicové čáry) r =
const. a t = const.
b) Globální geometrická struktura -
nekonečně mnoho periodicky se opakujících vnějších
oblastí A a vnitřních oblastí B.
Extrémní R-N geometrie
Pro případ Q = M má příslušný konformní prostoročasový
diagram úplné extenze Reissnerovy-Nordströmovy geometrie tvar
znázorněný na obr.3.23. Je vidět opět nekonečně mnoho
periodicky se opakujících "vnějších" oblastí A
(M<r<Ą) a vnitřních oblastí B
(0<r<M). Vnější a vnitřní horizonty splývají (rg- = rg+ = M), jedná se o speciální případ extrémní
černé díry (viz §4.4).

Obr.3.24. Penroseův konformní prostoročasový diagram
Reissnerovy-Nordströmovy geometrie v případě Q2> M2.
a)
Souřadnicové čáry - hyperplochy r=const. a t=const.
b)
Globální geometrická struktura - tvary světelných kuželů a
radiální pohyb těles a fotonů. Nejsou zde horizonty,
singularita r=0 je "nahá" (je
viditelná z kteréhokoliv světobodu).
R-N nahá singularita
V případě Q2 > M2 není třeba žádnou extenzi
hledat, protože prostoročas je nerozšiřitelný již v
původních souřadnicích; je všude regulární kromě bodu r=0
- neodstranitelné fyzikální
singularity
prostoročasu. Konformní prostoročasový diagram pro tento
případ je na obr.3.24. Horizont
událostí zde není, jedná se o nahou singularitu (viz
§3.9 a §4.4).
Zobecněné
Reissnerovo-Nordströmovo řešení v nelineární
elektrodynamice
V §1.6, závěrečné pasáži "Nelineární elektrodynamika", byla diskutována teoretická možnost, že
elektrické pole by se při extrémně vysokých intenzitách
nemuselo chovat přesně lineárně podle zákonitostí
standardní Maxwellovy elektrodynamiky, ale mohla by
existovat fundamentální hranice - maximálně možná
intenzita elektrického pole Emax. Tato alternativní možnost by se mohla výrazně (se zajímavými důsledky)
uplatnit v Reissner-Nordströmově řešení,
jakož i v Kerr-Newmanově geometrii (§3.6) - a obecně v černých
dírách (příp. i v dalších
kompaktních objektech jako jsou neutronové hvězdy a
jejich speciální případy magnetary) s velmi silnými elektrickými a
magnetickými poli (§4..., §.....) .......
Nahradíme-li při odvozování statického
sféricky symetrického Reissner-Nordströmova elektro-gravitačního řešení (3.32),
kterému je věnován tento §3.5, standardní Maxwellovu
elektrodynamiku nelineární Born-Infeldovou
elektrodynamikou (1.120) - buď s použitím
lagrangiánu (1.119) nebo tenzoru energie hybnosti elektromag.
pole, dostaneme zobecněné Reissner-Nordströmovo
řešení :
 |
(3.36) |
Funkce f(r,Q) vyjadřuje vliv elektrického
pole na metriku. Intenzita elektrického pole v B-N
elektrodynamice závisí na radiální souřadnici r podle
zákona E(r) = Q/Ö(r4 + Q2.b2). Při b=0, t.j. bez
elektrické nelinearity, je f(r,Q) = Q2/r2 - dostáváme základní R-N geometrii (3.32) s
Coulombovskou elektrickou intenzitou E(r) = Q/r2.
Integrál obsažený ve funkci f(r,Q) lze
explicitně vyjádřit pomocí dvou druhů speciálních funkci
| (3.36´) |
kde "F(...)" je Legenderova
eliptická funkce 1.druhu a "2F1(...)"
je je tzv. hypergeometrická funkce (složitější mocninná řada z Q2b2/r4). Konkrétní hodnoty těchto složitých funkcí lze pro
fyzikální výpočty nalézt ve speciálních tabulkách, v
poslední době pro ně existují i počítačové programy.
Tento prostoročas
zobecněného R-N řešení s metrikou (3.36), který je
řešením Einstein-Born-Infeldových rovnic, je charakterizován
třemi parametry: hmotností M, nábojem
Q a Born-Infeldovým parametrem nelinearity
"b" (jehož inverzní hodnota
udává konečnou hodnotu intenzity elektrického pole v
počátku souřadnic r=0). I při b>0 ve
větších vzdálenostech r>0 asymptoticky přechází v R-N
řešení.
......................
Je zajímavé, že v řešení nelineární elektrodynamiky
představují nulové (izotropní) geodetiky jen dráhy (hypotetických-modelových) gravitonů,
obecně však nikoli fotonů! Dráhy fotonů zde
mohou být totiž ovlivňovány "samointerakcí" s
nelineárním elektromagnetickým polem... ...........
...........
....... .. ..................
| Gravitace, černé díry a fyzika prostoročasu : | ||
| Gravitace ve fyzice | Obecná teorie relativity | Geometrie a topologie |
| Černé díry | Relativistická kosmologie | Unitární teorie pole |
| Antropický princip aneb kosmický Bůh | ||
| Jaderná fyzika a fyzika ionizujícího záření | ||
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | ||
Vojtěch Ullmann