Zakázané nahé singularity bez horizontu

Kapitola 3
GEOMETRIE A TOPOLOGIE PROSTOROČASU
3.1. Geometricko-topologické vlastnosti prostoročasu
3.2. Minkowského rovinný prostoročas a asymptotická struktura
3.3. Cauchyova úloha, příčinnost a horizonty
3.4. Schwarzschildova geometrie
3.5. Reissnerova-Nordströmova geometrie
3.6. Kerrova a Kerrova-Newmanova geometrie
3.7. Prostoročasové singularity
3.8. Hawkingovy a Penroseovy teorémy o singularitách
3.9. Nahé singularity a princip "kosmické cenzury"

3.9. Nahé singularity a princip "kosmické cenzury"

Teorémy zmíněné v předchozím odstavci předpovídají existenci singularit v řadě fyzikálně reálných situací. Mnohá přesná řešení Einsteinových rovnic, z nichž některá byla rozebírána v §3.4-3.6 (např. Schwarzschildova nebo Kerrova-Newmanova geometrie), mají singularity. Singularity uvnitř černých děr mají tu důležitou vlastnost, že jsou obklopeny horizontem událostí, který je brání "vidět" a znemožňuje jakékoliv ovlivňování ostatního vesmíru danou singularitou.

Vzniká otázka, zda mohou existovat "nahé" ("obnažené") singularity bez horizontu. Například formálním položením Q² + J²/M² > M² ve výrazu (3.37) pro Kerrovu-Newmanovu geometrii dostaneme tzv. Kerrovu nahou singularitu bez horizontu.

Podle dnešních poznatků je vysoce pravděpodobné, že taková nahá singularita vzniknout nemůže, každá singularita je "oblečena" do horizontu, což R.Penrose metaforicky nazval principem kosmické cenzury [202],[204] (uvádíme zde jeho stručné znění) :

Princip kosmické cenzury je vlastně hypothézou, která není obecně dokázána. Svědčí pro něj jednak rozbor gravitačního kolapsu, kde pro sférický kolaps toto přímo dostáváme analyticky, a při nevelkých odchylkách od symetrie lze pomocí pertubačních metod rovněž ukázat, že kolaps nevede ke vzniku nahé singularity [211],[246]. Především však je princip kosmické cenzury rozumným fyzikálním požadavkem. Přítomnost nahé singularity by totiž vedla k porušení determinovanosti další evoluce prostoročasu *). Do jednotlivých míst prostoročasu M by od takové nahé singularity (která není prvkem M!) mohly nekontrolovatelně přicházet nové informace prostřednictvím geodetik nepokračujících do minulosti; situace je zde trochu podobná jako na obr.3.10a. Neexistovaly by tedy žádné Cauchyho hyperplochy. V úplné extenzi Kerrovy-Newnamovy geometrie existují sice rovněž Cauchyovy horizonty, avšak jen ve "vnitřní" oblasti pod horizontem událostí, zatímco ve vnější asymptoticky rovinné oblasti lze jednoznačně předvídat budoucnost z vhodné Cauchyho hyperplochy. Nahá singularita by však toto znemožňovala všude, o další evoluci prostoročasu by nebylo možné nic určitého říci. A to je proti deterministickému duchu klasické fyziky.
*) Nahá singularita bez horizontu by mohla, obrazně řečeno, "nakazit" okolní vesmír svou "patologií" - nepředvídatelností fyzikálních jevů, porušením kauzality. Kdyby např. i někde ve větší vzdálenosti ve vesmíru obíhala planeta kolem hvězdy podle Newtonových-Kepplerových zákonů, mohla by nahá singularita náhodně vyslat silnější gravitační vlny, které by mohly porušit a nepředvídatelně změnit tuto oběžnou dráhu.

Princip kosmické cenzury má kromě své samostatné fyzikálně-filosofické důležitosti též klíčový význam ve fyzice černých děr, např. pro 2.zákon dynamiky černých děr (viz §4.6).

Hypothéza kosmické cenzury je v klasické obecné teorii relativity pravděpodobně splněna ve všech fyzikálně reálných situacích (samozřejmě však s výjimkou předpokládané iniciální singularity vesmíru při velkém třesku, která by byla evidentně nahá - viz kapitolu 5). V §4.7 o kvantové evaporaci černých děr si však ukážeme, že kvantové efekty mohou ve svých důsledcích vést k nesplnění hypothézy kosmické cenzury a k porušení determinovanosti evoluce prostoročasu. Dojde pak i k porušení klasického druhého zákona dynamiky černých děr, pro jehož platnost je třeba splnění principu kosmické cenzury. Při konečném stádiu kvantové evaporace černé díry - její kvantové explozi - se pak (na okamžik) přímo objeví nahá singularita (§4.7).

Nejčastěji rozebíraným typem nahé singularity je Kerrova-Newmanova nahá singularita zmíněná v §3.6; tam jsme uvedli poznámku, že v blízkosti prstencové singularity Kerrovy-Newmanovy geometrie může docházet k porušení kauzality (existují zde uzavřené časové křivky). U černých děr je tato "patologická" oblast od ostatního prostoročasu oddělena horizontem událostí, takže vně černé díry se narušení příčinnosti neprojeví. V případě nahých singularit je však možná oboustranná komunikace mezi vnější asymptoticky rovinnou oblastí a oblastí kauzálních poruch; uzavřené časové křivky lze "protáhnout" tak, aby procházely libovolným bodem takového prostoročasu [43]. Částice vyslaná ze vzdáleného místa by se do výchozího bodu mohla vrátit dříve, než byla odeslána.

Představme si, že by na chvíli došlo k porušení principu kosmické cenzury a nějakým způsobem by přece jen vznikla nahá singularita. Otázka pak zní, zda taková nahá singularita by zůstala stále nahou, nebo zda by i pak přišel ke slovu "kosmický cenzor" v osobě určitého fyzikálního procesu a dodatečně by tuto singularitu "oblékl" do horizontu. Ukazuje se, že hned dva druhy fyzikálních jevů mohou sehrát roli "vesmírného cenzora", vytvořit kolem nahé singularity horizont a přeměnit ji tak na černou díru.

První "kosmický cenzor" je čistě klasický: je to akrece okolní hmoty na nahou singularitu, při níž se poměr J/M a Q/M neustále zmenšuje, až se utvoří horizont. Při akreci dochází k účinné extrakci rotační energie [205] a k vybíjení případného elektrického náboje (singularita přitahuje opačně nabité částice).

Druhým mechanismem, fungujícím i bez přítomnosti okolní hmoty jako "kosmický cenzor", jsou kvantové efekty v silně nehomogenním poli kolem nahé singularity. Párová produkce částic-antičástic v poli nahé singularity vede k toku kvantového záření z ní, čímž singularita ztrácí hmotnost a rotační moment hybnosti. Mechanismus kvantového vyzařování je poněkud odlišný než u černých děr (§4.7) a závisí na konkrétní prostoročasové struktuře nahé singularity (na tom, kam mohou jednotliví partneři v páru částice-antičástice "tunelovat", obr.3.32). Kvantové vyzařování nahé singularity vede k jejímu "oblékání" do horizontu, tedy k přeměně na černou díru.

Pohlédneme-li na Penroseův diagram úplné extenze Reissnerovy-Nordströmovy nebo Kerrovy-Newmanovy geometrie (obr.3.21, 3.22, 3.25), vidíme, že singularita jež je v jednom vesmíru součástí rotující nebo nabité černé díry a tedy "zahalena" horizontem, je pro další "vesmír" (ležící v budoucnosti) nahá. Podobně kdybychom připustili bizarní topologii prostoročasu (zmíněnou v §3.5) odpovídající stočení a slepení Penroseova diagramu vystřihnutého z papíru do válcové plochy, objevila by se nahá singularita i v "našem vesmíru"; podobné topologické varianty vedoucí k časovým smyčkám a "stroji času" jsme však vyloučili již v §3.1. V §4.4 bude ukázán kosmický cenzor, který jak na klasické, tak na kvantové úrovni odřezává větší část struktury Penroseova diagramu a znemožňuje tak přechod černé díry v bílou díru doprovázeny nahou singularitou v dalším vesmíru (viz obr.4.19).

Pod nahými singularitami podléhajícími kosmické cenzuře jsme zatím rozuměli "globálně" nahé singularity viditelné z nekonečna. Princip kosmické cenzury ve formulaci teorému 3.8 zabraňuje sice singularitám nekontrolovatelně ovlivňovat fyzikální děje "v nekonečnu" (v dostatečné vzdálenosti od singularity), nic však nehovoří o situaci v blízkosti samotné singularity. To je ale poněkud "egoistické" stanovisko, protože kdyby pozorovatel pohybující se v blízkosti singularity (třebas uvnitř horizontu černé díry) tuto singularitu "viděl" ještě před tím než jí bude pohlcen, setkal by se se stejnou nepředvídatelností, jakou jsme popisovali u nahé singularity. Jednalo by se tedy o "lokálně nahou" singularitu. Pro singularity uvnitř černých děr hvězdných hmotností lze sice tvrdit, že každý pozorovatel který pronikne pod horizont bude zničen za zlomek sekundy a nebude mít proto čas provádět žádná pozorování nebo experimenty v nichž by se případný vliv singularity mohl projevit. V obecné teorii relativity (která je škálově invariantní teorií) však mohou v principu existovat i obří černé díry, v nichž pozorovatel (astronaut který tam vletí) má k dispozici dny nebo i měsíce času, kdy nepocítí účinek velkých slapových sil a může beze spěchu provádět experimenty a pozorování a analyzovat důsledky neurčitosti vnášených působením singularity. Rozšířený (objektivně chápaný) princip kosmické cenzury by měl tedy zakazovat i tyto lokálně nahé singularity.

Obr.3.31. Nestabilita prostoročasovéhu charakteru singularity ve Schwarzschildově a Kerrově-Newmanově řešení vůči perturbacím ve vztahu k principu kosmické cenzury.
a) Pro přesně sféricky symetrický případ (bez perturbace) má v odpovídajícím Schwarzschildově řešení síngularita všude prostorový charakter, takže žádný pozorovatel nemůže tuto singularitu uvidět předtím, než se s ní srazí - rozšířený princip kosmické cenzury je splněn.
b) Přidání i nepatrného momentu hybnosti nebo elektrického náboje vede ke Kerrově nebo Reissner-Nordströmově řešení, v němž singularita nabývá časový charakter. Pozorovatel pod vnitřním (Cauchyovým) horizontem může takovou singularitu vidět - je lokálně nahá.
c) Cauchyho (vnitřní) horizont H⁺ z obr.b) je však nestabilní vůči perturbacím ve vnější oblasti: signály z nekonečně vzdálených oblastí S nabudou na H⁺ nekonečně velký fialový posuv, takže slabá pole perturbací budou na H⁺ divergovat - v místě H⁺ tak vznikne singularita křivosti, která bude izotropního typu (nelineární efekty v poli velké křivosti by dokonce mohly vést ke vzniku singularity prostorového typu - srovnej s obr.4.19). Princip kosmické cenzury by tak byl rovněž splněn.

Podívejme se, jak z tohoto hlediska obstojí singularity s nimiž jsme se v §3.4-3.6 setkali u nejjednodušších přesných řešení Einsteinových rovnic. Singularita r=0 ve Schwarzschildově sféricky symetrickém prostoročase zřejmě vyhovuje rozšířenému principu kosmické cenzury, protože má všude prostorový charakter (obr.3.31a), takže lokálně nahá singularita zde není (singularitu nelze vidět před srážkou s ní). Schwarzschildova singularita je však nestabilní: dodání i nepatrného momentu hybnosti nebo elektrického náboje vede ke Kerrově nebo Reissnerově-Nordströmově řešení, kde singularita přestává být prostorová, ale je časového typu (obr.3.31b). Z obr.3.31b je vidět, že taková singularita je lokálně nahá, protože např. pozorovatel, jehož světočára je vyznačena, ji může vidět aniž se s ni srazí; na obr.3.22 jsme dokonce viděli situaci, kdy se pozorovatel může zcela vyhnout pohlcení singularitou a proniknout do dalšího "vesmíru", pro nějž zmíněná singularita bude globálně nahá (bude zde vidět i z nekonečna). Pro strukturu prostoročasu je zde však rozhodující vnitřní horizont r = r_g^-, který je Cauchyovým horizontem každé prostorové hyperplochy sahající do prostorového nekonečna. Pozorovatel, který prochází tímto vnitřním horizontem H⁺(S), uvidí celou budoucí historii vnějšího světa zhuštěnou do jediného časového okamžiku.

Pokud budou v počátečních podmínkách na Cauchyho hyperploše S přítomny nějaké perturbace (obecného charakteru - např. nějaká slabá pole), potom signály ze vzdálených oblastí S budou u horizontu H⁺ dosahovat nekonečně velký "fialový posuv", což povede k divergenci podél H⁺. Vnitřní horizont je tedy nestabilní vůči perturbacím v prostorovém nekonečnu, takže v obecném případě (tj. ve skutečnosti) lze v místě H⁺ očekávat singularitu křivosti, která bude izotropního typu (obr.3.31c); nelineární efekty v poli velké křivosti by mohly vést i k singularitě prostorového typu, jak je vyznačeno na obr.4.19. Zdá se tedy, že v asymptoticky plochých prostoročasech OTR je rozšířený princip kosmické cenzury splněn.

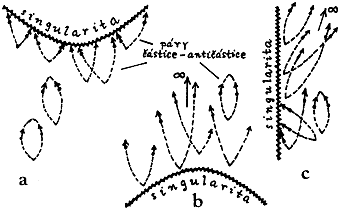Obr.3.32. Možnosti kvantové produkce částic a antičástic v silném gravitačním poli v blízkosti singularity. a) Pokud je singularita prostorového typu a nachází se v budoucnosti, nemají tyto částice kam odlétnout a jsou vždy pohlcovány singularitou. b,c) Jestliže se singularita nachází v minulosti nebo je časového typu, existují časové nebo izotropní světočáry, podél nichž tyto částice a antičástice mohou odcházet pryč od singularity.

Charakteristickou vlastností lokálně nahé singularity je její "časová omezenost": existence takové křivky časového typu (světočáry po níž by se mohl pohybovat pozorovatel), na níž existují body A a B takové, že singularita leží v budouonosti bodu A a v minulosti bodu B. Co se tedy týče všezahrnující kosmologické singularity "velkého třesku", princip kosmické cenzury se na něj vlastně nevztahuje; nejedná se o lokálně nahou singularitu, protože před velkým třeskem žádný pozorovatel neexistoval.

3.8. Hawkingovy a Penroseovy teorémy o singularitách		4. Černé díry ve vesmíru

Vojtěch Ullmann