h1{font-size:18px;}

Děsivé singularity prostoročasu

Kapitola 3
GEOMETRIE A TOPOLOGIE PROSTOROČASU
3.1. Geometricko-topologické vlastnosti prostoročasu
3.2. Minkowského rovinný prostoročas a asymptotická struktura
3.3. Cauchyova úloha, příčinnost a horizonty
3.4. Schwarzschildova geometrie
3.5. Reissnerova-Nordströmova geometrie
3.6. Kerrova a Kerrova-Newmanova geometrie
3.7. Prostoročasové singularity
3.8. Hawkingovy a Penroseovy teorémy o singularitách
3.9. Nahé singularity a princip "kosmické cenzury"

3.7. Prostoročasové singularity
Regulární a singulární řešení
V klasické fyzice mají tělesa a pole obvyklé a očekávané fyzikální, geometrické a topologické vlastnosti . Jsou (relativně) hladké a spojité, mají konečné rozměry a konečné hodnoty svých fyzikálních veličin. Takové chování označujeme jako regulární. A může být matematicky modelováno pomocí regulárních zobrazení, což jsou prostá vzájemně jednoznačná zobrazení, k nimž jsou k dispozici jednoznačná invezní zobrazení.
  Při matematickém modelování v teoretické fyzice se však setkáváme i se situacemi, kdy příslušné rovnice divergují a formálně dávají nekonečné či neurčité hodnoty fyzikálních veličin. Jednoduchým příkladem je níže uvedená idealizace bodového elektrického náboje, kdy podle Coulombova zákona je v místě o nulové vzdálenosti (r=0) nekonečně velká intenzita elektrického pole. Takovéto anomální chování fyzikální veličiny se obecně označuje jako singulární (je to opak chování regulárního). A místo či bod anomálního chování fyzikální veličiny se nazývá singularita (lat. singularis = ojedinělý, vyjímečný, jedinečný).
  Při rozboru některých přesných řešení Einsteinových gravitačních rovnic (např. Schwarzschildova řešení) jsme viděli, že v některých místech tato řešení nejsou regulární. Ukázali jsme si, že některé z těchto "singularit" jsou způsobeny jen nevhodnou souřadnicovou soustavou a přechodem k jiným souřadnicím může být příslušné singulární chování odstraněno (příkladem může být pseudosingularita Schwarzschildovy sféry). V takových případech se tedy nejedná o singularity samotného prostoročasu (prostoročas je zde regulární).
  Existují však místa, kde singulární chování nelze odstranit přechodem k jiné souřadné soustavě, např. bod r=0 ve Schwarzschildově geometrii. V takovém případě se jedná o skutečnou, fyzikální singularitu samotného prostoročasu (kde např. invarianty tenzoru křivosti dosahují nekonečných hodnot). Pod singularitami prostoročasu budeme v dalším rozumět právě jen podobné "neodstranitelné" singularity. Zde si ujasníme některé základní rysy prostoročasových singularit a pokusíme se podat jejich obecnou definici. O podmínkách, za nichž singularity vznikají, si povíme v příštím §3.8 "Hawkingovy a Penroseovy teorémy o singularitách".

Fyzikální nereálnost singularit
V této a dalších matematicky zaměřených kapitolách naší knihy (§3.4-3.9, §5.3) se singularitami zabýváme "vážně, jako kdyby skutečně existovaly". Je však třeba mít na paměti, že se jedná jen o matematické abstrakce. Tyto singularity vznikají jako důsledek "přímočaré" striktní extrapolace přesných řešení rovnic obecné teorie relativity k určitým speciálním hodnotám souřadnic (např. k t=0, r=0).
  Skutečné "fyzikální" singularity, v nichž by reálné fyzikální veličiny nabývaly nekonečných hodnot, nemohou v přírodě existovat! Opravdové nekonečno nikdy v přírodě nevidíme (analýza různých druhů nekonečna byla provedena v §3.1, v oddíle "Nekonečno v prostoročase"). Pokud je nějaká teorie předpovídá, je to její vážný nedostatek, svědčící buď o její chybnosti či přílišné idealizaci, nebo o tom, že se v dané situaci dostává k mezím své platnosti. Pokud se nekonečno objeví v nějaké teorii, snažíme se ho odstranit (proces renormalizace v kvantové teorii), aspoň do doby, než bude vytvořena nová dokonalejší teorie.
  Ukazuje se, že v oněch "exotických" situacích hrají důležitou úlohu kvantové zákonitosti gravitace i ostatních druhů interakcí, které se zde imanentně vynořují (jako důsledek kvantových fluktuací polí ve vakuu) společně s "klasickou" gravitací. Zahrnutí těchto kvantových interakcí do obecně-relativistického gravitačního modelu může tuto singularitu odstranit - prostoročas zde nemusí být singulární, může mít sice velmi vysokou, ale konečnou křivost, při konečné koncentraci polí, konečné hustotě a teplotě gravitující látky. Z kvantového hlediska lze očekávat, že singularita se "rozpustí" v kvantové pěně. Toto je, zatím neurčitý, pohled kvantové gravitace a kvantové geometrodynamiky (§B.4 "Kvantová geometrodynamika").
  Přesto však je užitečné matematicky prozkoumat, za jakých okolností v (nekvantové) teorii vznikají singularity a jaké mají vlastnosti, z nichž by se něco mohlo "potenciálně" uplatnit i v praxi.

Singulatity v elektrodynamice a v gravitaci
Porovnejme nejprve situaci kolem singularit v gravitaci s příslušnou situací v elektrodynamice. V elektrodynamice se též vyskytují singularity, např. v místě bodového elektrického náboje (klasická idealizace!) dosahuje intenzita elektrického pole nekonečných hodnot. Metrika Minkowského prostoročasu, na jejímž pozadí (a s pomocí níž) elektrické pole sledujeme (a měříme) zůstává však všude regulární *). Naproti tomu v obecné teorii relativity nemáme "nezúčastněnou" metriku, s jejíž pomocí sledujeme chování (a tedy i případné singularity) nějakého pole. Zde je metrika prostoročasu tím samým polem, jehož singularity vyšetřujeme. Singularita prostoročasu má proto mnohem hlubší důsledky než singularita např. v klasické elektrodynamice. V prostoročasové singularitě, kde přestává existovat regulární prostor a čas, ztrácejí platnost všechny fyzikální zákony, protože všechny dosavadní fyzikální zákony jsou formulovány na bázi klasického prostoru a času.
*) Tak je tomu ve STR, když elektromagnetické pole bereme izolovaně. Ve skutečnosti však elektromagnetické pole vzbuzuje i gravitační pole (zakřivuje prostoročas), takže v místě nekonečné intenzity elektromagnetického pole by vzniklo i nekonečně silné gravitační pole (nekonečné zakřivení prostoročasu), a tedy prostoročasová singularita.
  Singulární bod nelze považovat za součást sledované prostoročasové variety, nelze v něm principiálně provádět žádná fyzikální měření. Aby prostoročas zůstal varietou, je nutno všechny singulární body z něj vyloučit ("vyříznout"). Zbylý prostoročas bude potom opět varietou, kde v každém bodě budou platit obvyklé fyzikální zákony a kde je možno provádět fyzikální měření. Nelze však zbylý prostoročas prohlásit za regulární a myslet si, že jsme se tím úplně zbavili singularit. Jak uvidíme níže, má tento zbylý prostoročas určité "patologické" vlastnosti (související s tím, že některé geodetiky končí svou existenci v místech "vyřezaných" singulárních bodů) bránící považovat jej za regulární.
  Pokusme se vystihnout společné charakteristické vlastnosti prostoročasových singularit. Jinými slovy: jaká principiální "nebezpečí" mohou při pohybu prostoročasem čekat na reálného pozorovatele (pohybujícího se po světočárách časového nebo světelného typu)? Omezíme se zatím pro jednoduchost na pohyb po geodetikách. Příklad jednoho takového nebezpečí jsme viděli při analýze pohybu částic ve Schwarzschildově geometrii centrálně symetrického gravitačního pole. Dostane-li se pozorovatel pod Schwarzschildovu sféru, je jeho osud zpečetěn - za krátký interval vlastního času se nutně dostane do bodu r=0, kde bude zničen nekonečnými slapovými silami.

Singularity souřadnicové a fyzikální
Z matematického hlediska se v obecné teorii relativity vyskytují singularity - místa kde dochází k divergenci metriky prostoročasu - v zásadě dvou druhů :
-> Singularity souřadnicové - zdánlivé
Jsou to body, kde singulární hodnoty metriky vznikají díky výběru souřadnic, nikoli skutečné fyzické singularitě v prostoročase.
  Můžeme si to ukázat na Schwarzchildově geometrii :
Vypočítáme-li na základě koeficientů konexe (3.15) komponenty Riemannova tenzoru křivosti ve Schwarzschildově metrice (3.13) a přetransformujeme je do vztažné soustavy padajícího pozorovatele, budou (ty z nich, jež jsou nenulové) úměrné M/r³, např.

takže na Schwarzschildově sféře dosahují hodnot řádu 1/M²; podobně skalární invarianty (např. R= R_iklmR^iklm= 48M²/r⁶) tenzoru křivosti, které nezávisí na souřadné soustavě. Křivost prostoročasu, a tedy i gradienty gravitačních sil (slapové síly), jsou na Schwarzschildově sféře konečné - a tím menší, čím je hmotnostní parametr M větší.
  Dospíváme tak k závěru, že singulární chování Schwarzschildova prostoročasového elementu (3.13) pro r=2M nemá svůj původ v singulárním charakteru geometrie prostoročasu na Schwarzschildově sféře, ale je způsobeno použitými Schwarzschildovými souřadnicemi, které se v tomto místě pro popis metriky nehodí. Přechodem k jiné vhodné vztažné soustavě, např. k soustavě spojené s volně padajícími testovacími částicemi, tato pseudosingularita na Schwarzschildově sféře zmizí.
  To, jakým způsobem může "nevhodná" souřadnicová soustava způsobovat zdánlivou singularitu, si můžeme názorně ilustrovat na jednoduchém příkladě mapy zeměkoule. Sledujeme-li kulovou plochu pomocí souřadnic udávajících "zeměpisnou" šířku a délku J a j (obr. a), budou se všechny "poledníky" sbíhat v bodech "severního" a "jižního" pólu, takže pro tyto body není zeměpisná délka definována, metrický tenzor g_jj je zde roven nule. Nebo podobně, děláme-li mapu zeměkoule pomocí válcové projekce podle obr. b, budou se obrazy P' pólu P nacházet v nekonečnu a metrický tenzor g_JJ®Ą. Přitom však samotná geometrie kulové plochy v těchto pólech je zcela normální - stačí pootočit kouli o určitý úhel a body, které se v dřívější souřadnicové soustavě jevily singulární, budou naprosto regulární a singulárními se budou zdát jiné body, nové "póly".

Příklad pseudosingularity způsobené použitou souřadnicovou soustavou. a) Bod P na kulové ploše (pól) se zdánlivě jeví jako singulární, protože v použitých souřadnicích pro něj není definována "zeměpisná délka". b) Zhotovujeme-li mapu zeměkoule pomocí válcové projekce, bude se pól P zdát singulární, protože jeho obraz P' bude v nekonečnu.

Geometrie samotného prostoročasu je na Schwarzschildově sféře zcela regulární, pozorovatel může přes Schwarzschildovu sféru volně projít během konečného intervalu vlastního času, nezjistí zde lokálně ani nic zvláštního a bude pokračovat dále ve svém pohybu. Použitím jiných souřadnicových systémů, jako jsou Eddington-Filnkelstein nebo Krustal-Szekeres souřadnice (§3.4 "Schwarzschildova geometrie), lze singularitu na horizontu událostí odstranit (převést ji na dvě navazující souřadnicové mapy). Zvláštnost prostoročasové geometrie na Schwarzschildově sféře nespočívá tedy v nějakých nenormálních lokálních vlastnostech prostoročasu, ale v její globální vlastnosti horizontu událostí.
  Souřadnicové singularity jsou odstranitené, neboť nejsou spojeny s žádným lokálním fyzikálním jevem *). Souřadnicové singularity mohou být odstraněny-transformovány změnou souřadnic.
*) Tak je tomu z hlediska klasické fyziky makrosvěta. V kvantové fyzice však mohou horizonty události lokálně "odseparovat" vznikající virtuální částice a antičástice a způsobit tím fyzikální jev emise reálných částic (§4.7 "Kvantové vyzařování černých děr").
-> Singularity fyzikální - esenciální
Jinak je to s druhým singulárním místem v metrice (3.13) - bodem r=0. Zde jak složky tenzoru křivosti (3.24), tak i jeho skalární invarianty dosahují nekonečných hodnot, jsou zde tedy nekonečně velké gradienty gravitačních sil. Částice, která se dostane do bodu r=0 již ve svém pohybu nemůže pokračovat dále, je těmito nekonečnými slapovými silami rozdrcena, doslova přestane existovat v rámci daného prostoročasu. Zde se jedná o skutečnou, esenciální fyzikální singularitu geometrie prostoročasu, kterou nelze odstranit žadnou volbou vztažné soustavy.
Vlastnostem skutečných prostoročasových singularit a posouzení možností jejich existence je věnován tento §3.7 a následující §3.8 a 3.9.
  Názorným příznakem fyzikální singularity by tedy mohla být gravitační singularita křivosti - neomezeně velká křivost prostoročasu v blízkém okolí singulárního bodu. S trochou nadsázky si názorně můžeme gravitační singularitu připodobnit k situaci, kdy nás gravitace neúprosně stlačuje až do nekonečně malého bodu, čímž efektivně redukuje naši existenci na nicotu!

Jak rozlišit souřadnicovou a fyzikální singularitu ?
Metrika prostoročasu se obvykle vyjadřuje pomocí obecné kvadratické formy elementu prostoročasového intervalu ds² = g_ik dxⁱ dx^k, jejímiž koeficienty jsou komponenty metrického tenzoru g_ik(x⁰,x¹,x²,x³) zadané jako funkce souřadnic - časové x⁰ a prostorových x^1,2,3. V Minkovského rovinném prostoročase STR se používají (pseudo)Euklidovské katrézské souřadnice, v nichž ds² = -dt² + dx² + dy² + dz² - vztah (3.3). V polárních souřadnicích (r,J,j) je to ds² = -dt² + dr² + r²(dJ² + sin²J dj²) - vztah (3.4). V zakřiveném prostoročase ve sférických prostorových souřadnicích (r,J,j) s počátkem r=0 je metrika ds² = -g_tt dt² + g_rr dr² + r²(dJ² + sin²J dj²) s metrickými koeficienty g_tt(r), g_rr(r), g_JJ = r², g_jj = r² sin²J. Konkrétně Schwarzschildova metrika je (3.13)
Z metrických koeficientů g_ik se vypočítají Christiffelovy koeficienty konexe Gⁱ_kl , komponenty tenzoru křivosti Rⁱ_klm a rovnice geodetiky pro pohyb testovacích částic. Tyto údaje nám již umožňují úplnou analýzu vlastností zkoumané metriky (§3.2, 3.4, 3.5, 3.6).
  Ve funkčních závislostech metrických komponent můžeme najít místa (hodnoty souřadnic), kde metrika vykazuje "patologické" vlastnosti - divergence, nespojitosti, nekonečna. Avšak na první pohled zpravidla nepoznáme, zda se jedná jen o zdánlivé souřadnicové singularity, nebo o skutečné singularity prostoročasu. Pro specifikaci povahy těchto singularit můžeme postupovat dvěma způsoby :
-» Explicitně vyšetřovat geodetické pohyby testovacích částic - zda se při určité zkoumané souřadnici nesetkají s nějakou divergencí či nekonečnem, které by jim znemožňovalo pokračování v pohybu.
-» Číselné hodnoty metrických koeficientů i složek tenzoru křivosti sice závisejí na použité vztažné soustavě - vektorové bázi (která může v blízkosti singularity degenerovat), avšak algebraickou kombinací složek metrického tenzoru g_ik a tenzoru křivosti Rⁱ_klm lze vytvořit skalární invarianty křivosti, jejichž hodnoty jsou nezávislé na souřadnicové soustavě. Jsou to určité kvadratické polynomy - součty druhých mocnin složek tenzoru křivosti a metrického tenzoru. Základním takovým skalárním invariantem křivosti je

který vzniká zúžením Riemannova tenzoru křivosti ve všech kovariantních a kontravariantních složkách (nazývá se někdy Kretschmanův skalár podle E.J.Kretchmanna, který jej prozkoumal v r.1915; později bylo zformulováno několik dalších invariantů křivosti). Takovéto veličiny jsou účinným prostředkem pro detekci fyzikální singularity. Kvantifikují míru zakřivení prostoročasu nezávisle na souřadnicové soustavě. Pokud v určitém bodě tato veličina diverguje do nekonečna, znamená to, že singularita zde existuje univerzálně - napříč všemi souřadnicovými systémy.
  Pro Schwarzschildův prostoročas (3.13) skalární invariant křivosti vychází

Při dosažení r=0 je R_Schw nekonečný (zakřivení se stane nekonečně velkým) - fyzikální singularita, avšak na horizontu r=2M zůstává konečný - souřadnicová singularita.

Nekompletnost geodetik
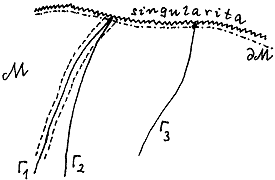
Singularity mají jednu společnou charakteristickou vlastnost: světočára pozorovatele při setkání se singulárním bodem (např. s r=0 ve Schwarzschildově geometrii) zde nespojitě končí za konečný interval vlastního času. Tuto geodetiku nelze v rámci existující variety dále prodloužit, objekt opisující geodetiku prostě pro ni přestal existovat a nemůže být tedy již popsán žádným světobodem z dané variety (obr.3.26) :

Obr.3.26. Nekompletní geodetika G, která končí po uplynutí konečného vlastního času (resp. při konečné hodnotě afinního parametru) a dále ji již v rámci M nelze prodloužit, je příznakem prostoročasové singularity.

Můžeme tedy říci, že např. ve Schwarzschildově prostoročase existují geodetiky (jsou to konkrétně všechny ty geodetiky, jež protínají Schwarzschildovu sféru), které mají jen konečnou celkovou délku a nespojitě končí v oblasti r=0 po uplynutí konečného intervalu vlastního času (popř. při konečné hodnotě afinního parametru v případě izotropních geodetik). Takové geodetiky jsou "neúplné" (nekompletní). Pojem kompletnosti a nekompletnosti lze rozšířit z geodetik i na obecné světočáry, přičemž afinní parametr se nahradí zobecněným afinním parametrem *).
*) Zobecněný afinní parametr se zavádí následujícím způsobem [225],[127]:
1. V bodě pÎM, jímž prochází křivka C: x = x(t), se zvolí trojrozměrná vektorová báze (e1,e2,e3) v tečném prostoru.
2. Paralelním přenosem podél křivky C lze získat vektorovou bázi v každém bodě křivky (pro každou hodnotu t).
3. Tečný vektor V(t) = (¶ /¶t)_x(t) v každém bodě křivky lze vyjádřit pomocí přenesené báze: V = V^a(t).e_a .
4. Zobecněný afinní parametr se pak definuje integrálem l = _pň^x(t) (Vi Vⁱ)^1/2 dt; závisí na bodu p a na vektorové bázi e_a v bodě p.
Jestliže x(t) je geodetika, je l afinním parametrem na C: x=x(t). Zobecněný afinní parametr l však lze zavést na libovolné křivce v M.

Jinými slovy, v kompletním prostoročase M každá světočára G(l) konečné "délky" (měřené zobecněným afinním parametrem l) má koncový bod v M - je prodloužitelná.
  Z příkladu Schwarzschildovy geometrie (která je zjevně singulární) je vidět, že geodetická nekompletnost - tedy existence neúplných časových a izotropnich geodetik - je postačující podmínktou singulárnosti prostoročasu. Z fyzikálního hlediska však musíme považovat za singulární i takový prostoročas, který je sice geodeticky kompletní, ale ve kterém existují nekompletní časupodobné světočáry (ne-geodetiky). Fyzikální význam nekompletnosti vzhledem ke světočárám prostorového typu, po nichž se nemůže pohybovat žádný reálný objekt, není jasný a proto ji zde nebudeme uvažovat.
  Můžeme tedy konečně vyslovit obecnou definici prostoročasové singularity:

Podmínka "nerozšiřitelný" je v definici 3.9 proto, že každý rozšiřitelný prostoročas automaticky obsahuje nekompletní světočáry. Například vezmeme-li jen část rovinného (a samozřejmě regulárního) Minkowskiho prostoročasu, budou se zde vyskytovat neúplné geodetiky, které budou končit (nebo začínat) na "okraji" námi vymezené části tohoto prostoročasu. Tento jev by samozřejmě nebylo rozumné považovat za singularitu. První věta v definici 3.9 se dá též ekvivalentně říci takto:
    Prostoročas (M,g) se nazývá singulární, jestliže každá jeho extenze obsahuje nekompletní světočáry
    časového nebo izotropního typu.
  Podle definice 3.9 jsme tedy za příznak singularity prostoročasu zvolili přítomnost světočáry, která v nějakém místě končí za konečný vlastní čas a nemůže pokračovat dále. V příštím §3.7 bude ukázáno, za jakých předpokladů takto definované singularity v prostoročasech obecné teorie relativity vznikají.

Zbývá nám vyjasnit si fyzikální vlastnosti a strukturu singularit. Vybudovat "fyziku singularit" není nijak snadné, protože singularity jsou samy o sobě čímsi "nefyzikálním", co musí být vyloučeno z fyzikální variety M, aby tato zůstala varietou. Jedna z metod analýzy singularit byla navržena Gerochem [95] a Hawkingem [130] a dále zdokona Schmidtem [225]. Každé nekompletní světočáře se přiřadí příslušný "koncový bod", přičemž za totožné se považují ty koncové body, které přísluší takovým světočárám G₁ a G₂, že světočára G₂ vchází do prostoročasové oblasti vzniklé kolem svštočáry G₁ jejími malými variacemi, a tam již zůstává (obr.3.27). Takovým ztotožněním vznikají třídy ekvivalence koncových bodů nekompletních světočar a množina všech těchto tříd ekvivalence vytváří jistou hranici ¶M kolem singularity. Tato hranice je jednoznačně určena strukturou (M,g), tj. může být stanovena měřeními v nesingulárních bodech M.

Obr.3.27. Kolem singularity se sestrojí jistá hranice ¶M, sestávající z tříd ekvivalence "koncových bodů" nekompletních světočár v M. Za totožné (tj. patřící do stejné třídy ekvivalence) se přitom považují koncové body takových světočar G1 a G2, kde G2 vchází do čárkované oblasti vznikající kolem G1 malými variacemi a již z ní nevychází.

Že otázka definice a klasifikace prostoročasových singularit není nijak triviální, si můžeme ukázat na jednoduchém příkladě. Vezmeme-li v úvahu pouze relativistickou kinematiku, můžeme si představit raketu, která se v obyčejném Minkowskiho prostoročase tak urychluje, že její světočára se stává izotropní (raketa dosahuje rychlosti světla) natolik rychle, že celkový interval vlastního času pozorovatele v raketě bude konečný - světočára bude mít konečnou "délku". Po uplynutí konečného času již raketu nebude možno zobrazit žádným světobodem v daném Minkowskiho prostoročase. Tato situace je však fyzikálně neuskutečnitelná, protože raketa pohybující se po takové světočáře by musela mít nekonečné množství paliva. Geroch [96] ale zkonstruoval prostoročas, který je sice geodeticky kompletní, ale obsahuje neúplné světočáry časového typu s konečným zrychlením; z takového prostoročasu by se dalo "uletět" na raketě s konečnou zásobou paliva.
  Intuitivně očekáváme, že singularita souvisí s nekonečně velikou křivostí prostoročasu. Skutečně, definice 3.9 toto zahrnuje, protože jednou z příčin, proč nelze nějakou světočáru prodloužit za určitý její bod, může být neomezeně velká křivost prostoročasu v blízkosti tohoto místa. Neúplnost prostoročasu však nemusí být vždy způsobena singularitou křivosti. Byly zkonstruovány příklady, např. prostoročas Taubův, Newmanův, Tamburinův a Untiho [188],[127], který splňuje podmínky definice singularity 3.9 (obsahuje horizonty, za něž nelze některé geodetiky prodloužit), ale přitom má všude konečnou křivost. Neúplnost geodetik zde má spíše topologický než metrický charakter. Prostoročasy tohoto druhu jsou však čistě umělou konstrukcí a nemohou se uplatnit, pokud je v prostoročase nějaká hmota. Obecně lze očekávat, že ve fyzikálně reálných situacích budou singularity prostoročasu skutečně způsobeny nekonečně velkou křivostí, popř. její nespojitostí (stále však mějme na paměti výše uvedenou diskusi "Fyzikální nereálnost singularit"!).

3.6. Kerrova a Kerrova-Newmanova geometrie		3.8. Hawkingovy a Penroseovy teorémy o singularitách

Vojtěch Ullmann