Částice mikrosvěta, jejich získávání a aplikace ve
výzkumu a technologiích
1.
Jaderná a radiační fyzika
1.0. Fyzika - fundamentální
přírodní věda
1.1. Atomy a atomová
jádra
1.2. Radioaktivita
1.3. Jaderné reakce
1.4. Radionuklidy
1.5. Elementární
částice
1.6. Ionizující
záření
1.5.
Elementární částice a urychlovače
Při výkladu vlastností atomů v kap.1.1 jsme
poznali, že ani atom, ba dokonce ani jeho jádro nejsou
elementárními stavebními kameny hmoty, ale jsou složeny z
ještě menších částic - elektronů, protonů, neutronů.
Při studiu radioaktivity jsme poznali i některé další
částice - pozitrony, neutrina. Jsou tyto subatomární
částice již opravdu vnitřně "jednolité" -
elementární a fundamentální? Nebo mají svou vnitřní
strukturu, složenou z "ještě menších" částic? (podrobnější diskuse je níže v pasáži "Jsou elementární částice
skutečně elementární?").
V této kapitole se pokusíme o stručný, ale
systematický výlet do pestrého a podivuhodného světa
elementárních částic. Při výkladu budeme postupovat
induktivním způsobem. Po úvodních pasážích o
společných vlastnostech částic, jejich třídění a
zákonitostech interakcí, budeme postupovat od základních,
známých a hojně rozšířených částic a jejich
jednoduchých vlastností (přímočaře plynoucích z
experimentů), přes "exotičtější" částice a
složitější mechanismy interakcí, až k unitárním
symetriím a pokusům o vyjasnění vnitřní struktury
částic. Zmíníme i hypotetické a modelové částice,
z nichž některé nejsou dosud ani přímo objeveny, či jejich
úloha v přírodě zatím není zcela pochopena.
Nejdříve si nastíníme systematiku
elementárních částic a pak si rozebereme vlastnosti
a interakce jednotlivých konkrétních druhů
částic, včetně vzniku částic při
vysokoenergetických interakcích. A rovněž antičástic
- jejich vznik a anihilace, jejich role v přírodě, možnosti
využití. Zamyslíme se též nad tím, co mají jednotlivé
částice společné a jak jsme pokročili na cestě k
jednotnému pochopení fyziky částic a polí - k unitární
teorii pole. Nakonec si popíšeme, jakým způsobem
zkoumáme interakce částic při vysokých energiích na urychlovačích
částic.
Za vším tím množstvím získaných poznatků o
elementárních částicích je skryto obrovské úsilí a kolosální
objem práce tisíců fyziků, techniků a dělníků -
konstruktérů složitých urychlovacích systémů a
detekčních aparatur.
Předtím si ale učiníme několik obecných
poznámek a diskusí o částicích jako takových :
Terminologická poznámka -
elementární? :
Název "elementární" neboli "základní"
by měl znamenat, že se jedná o objekt dále nedělitelný,
bez vnitřní struktury; je to tedy nejjednodušší materiální
objekt chovající se jako samostatná fyzikální entita. V
průběhu přírodovědného poznání mikrosvěta se však
několikrát ukázalo, že částice dříve považované za
základní (elementární) mají vnitřní strukturu a skládají
se z ještě "menších", základnějších či
"elementárnějších" částic. Podle dřívějších
názorů nedělitelný atom (odtud jeho název) má složitou
strukturu elektronového obalu a atomového jádra. Protony a
neutrony v atomových jádrech byly též považovány za
nedělitelné, avšak novější výzkumy (ve standardním modelu
částic) ukázaly, že se skládají z kvarků (stejně jako
ostatní hadrony). Názory na "elementárnost" částic
se tak mohou měnit v závislosti na aktuálním stavu
fyzikálního poznání (podrobnější
diskuse je níže v pasáži "Jsou elementární částice skutečně
elementární?").
Jelikož tedy mnohé částice jsou
"složené", označení "elementární"
zde může být zavádějící. Jedná se však o vžitý název,
podobně jako název "atom", který již dávno
neznamená "nedělitelný". V posledních letech se
často slovo "elementární" vypouští a hovoří jen
o "částicích".
Existují
vůbec elementární částice ? "Kuličkový" model.
Naše představa existence - že
"něco existuje" - se odvíjí od
naší každodenní zkušenosti s pozorováním makrosvěta
okolní přírody. Existují např. kameny - můžeme je vidět,
ohmatat, potěžkat, příp. nimi hodit. Existují různé druhy
rostlin a živočichů se specifickým vzhledem a vlastnostmi.
Existují buňky v organismech, které můžeme pozorovat v
mikroskopu, včetně jejich vnitřní struktury (viz např. §5.2., část "Buňky - základní jednotky živých
organismů") a studovat jejich biochemické projevy. V mikrosvětě
subatomárních či dokonce subnukleárních rozměrů je to
však složitější. Částice mikrosvěta rozhodně nemůžeme
vidět ani sebesilnějším mikroskopem - jsou mnohem
menší než vlnová délka viditelného světla. Ani tehdy,
kdybykom se v myšlené sci-fi představě zmenšili na
"pidimužíky" velikosti pikometru a pozorovali pomocí
záření mnohem kratších vlnových délek, žádné
lokalizované částice bychom neviděli. Kvantové relace
neurčitosti "rozmazávají" stanovení rychlosti při
přesném měření polohy a měření rychlosti částice zase
rozmazává její polohu. Viděli bychom snad jen rozmazané
chomáčky fluktuujících polí. Z tohoto obvyklého pohledu
bychom mohli vyslovit "kacířské" tvrzení, že
"elementární částice neexistují"!
Při podrobnějším fyzikálním bádání však
dospíváme k poznání, že existuje "něco"
skrytého, co je nositelem fyzikálních sil, např.
elektrického náboje, něco co přenáší prostorem energii, co
způsobuje vzájemná působení - interakce -
hmotných těles. V klasické fyzice to jsou fyzikální pole, v
kvantové fyzice kvanta polí. To "něco"
nazýváme elementární částice (slůvko "elementární" bylo diskutováno
výše). Nedovedeme si to nijak konkrétně
představit a proto si je modelově
znázorňujeme jako malé kuličky - např.
elektrony kreslíme jako červené, protony jako modré, neutrony
jako šedé kuličky, neutrina jako třebas zelené; je to
otázka konvence. Tyto kuličky, mající určitou hmotnost,
náboj a další fyzikální charakteristiky, se podle obvyklých
zákonitostí (relativistické) mechaniky
prostorem pohybují určitou rychlostí a s ní
související kinetickou energií. S určitou pravděpodobností (viz níže "Účinný průřez") se mohou "srážet" - interagovat
- s jinými kuličkami (částicemi), přičemž z tohoto místa
vylétají další kuličky - částice stejných nebo jiných
vlastností. Během vlastního průběhu interakce se
"kuličkový model" však použít nedá, probíhají
tam často značně složité kvantově-polní procesy
(viz níže "Feynmanovy
diagramy").
Kuličkový model je velice úspěšný - v
koprodukci s fyzikálními mechanismy elektromagnetických,
silých a slabých interakcí dovede vysvětlit či znázornit
prakticky všechny jevy s částicemi mikrosvěta v atomové,
jaderné, radiační a částicové fyzice. Toto
"kuličkové znázornění", příp. doplněné o
vlnovou povahu, proto kreslíme ve většině obrázků našeho
pojednání "Jaderná fyzika a fyzika ionizujícího
záření".
Kdo si objednal
"exotické" částice?
Pro pochopení stavby hmoty, která je kolem nás, vystačíme s několika
málo shora zmíněnými částicemi (§1.1 a 1.2) -
fotony, elektrony, protony, neutrony (popř. ještě neutriny,
mesony, kvarky u a d). Přesto však při
interakcích částic (ať již uměle vyvolaných, nebo v
kosmickém záření) se setkáváme s mnoha dalšími
částicemi, které - jak se aspoň zdá - nemají
žádnou úlohu při stavbě hmoty. Nic z nich není složeno,
nejsou schopny vytvořit vázané struktury, většinou se po
svém vzniku okamžitě rozpadají. Vzniká metaforická otázka
"kdo si je objednal?" - jaký mají
smysl a úlohu ve fungování našeho světa? (poprve tuto otázku vyslovil I.I.Rabi v souvislosti s
objevem mionu). Odpověď na tuto otázku
se snaží najít unitární teorie pole a částicová fyzika v
koprodukci s astrofyzikou a kosmologií. Unitární teorie pole
se pokoušejí najít zákonitosti a mechanismy, které existenci
těchto částic umožňují nebo implikují - jako kvanta
excitovaných polí či geometrických struktur (§B.6 "Sjednocování
fundamentálních interakcí. Supergravitace. Superstruny." v knize "Gravitace, černé díry a fyzika
prostoročasu"). Astrofyzika a kosmologie ukazuje, že
všechny tyto částice patrně kdysi ve vesmíru byly
v nejranějších stádiích, svou úlohu při
"uvaření" hmoty již sehrály a pak zanikly
(viz např. §5.5 "Mikrofyzika a kosmologie. Inflační
vesmír." zmíněné knihy); bez
nich by vesmír nebyl takový jaký je, možná by vůbec
nevznikla hmota..?.. Některé tyto částice snad tvoří zatím
záhadnou "temnou hmotu" ve vesmíru (viz
např.§5.6 "Budoucnost vesmíru. Šipka času."). A my se nyní pokoušíme tyto částice znova
vytvořit a zkoumat, abychom pochopili raný vesmír a
mohli určitěji odpovědět na otázky, jak vznikla hmota a
jaké má vnitřní vlastnosti...
Nerozlišitelnost elementárních částic
Tělesa a částice v klasické mechanice při
svém pohybu neztrácejí svou "individualitu",
a to i tehdy, když se jedná o stejné částice se stejnými
fyzikálními vlastnostmi (z makroskopického hlediska). Takové
částice tvořící daný fyzikální systém můžeme v
určitém počátečním čase "označkovat" či
"očíslovat" a potom při sledování jejich pohybu
můžeme, aspoň v principu, v každém časovém okamžiku identifikovat
každou z částic v systému - částice jsou zde rozlišitelné.
Při analýze pohybu a chování částic v kvantové
mechanice je situace z tohoto hlediska úplně jiná. V
důsledku korpuskulárně-vlnového dualismu a principu
neurčitosti nemají částice, např. elektrony, žádné
trajektorie ve smyslu klasické kinematiky. Stanovíme-li polohu
částice v daném okamžiku, stává se neurčitou její
hybnost; pak v dalších následujících okamžicích není
možné stanovit žádné určité hodnoty souřadnic částice.
Kdybychom se tedy v určitém okamžiku pokusili lokalizovat
elektrony a pomyslně si je "očíslovat", pak v jiném
časovém okamžiku při lokalizaci elektronu v určitém bodě
prostoru již nemůžeme určit, který z uvažovaných
elektronů se dostal do tohoto bodu. V kvantové mechanice není
žádná možnost průběžně sledovat pohyb jednotlivých
částic a tím je rozlišovat. Mikročástice se projevují jen
svými interakcemi s jinými částicemi.
Stejné částice tedy v kvantové mechanice zcela ztrácejí
svou individualitu - jejich fyzikální vlastnosti jsou
identické, jsou vzájemně nerozlišitelné.
Spin, symetrie vlnové funkce a statistické
chování částic
Na tomto principu
nerozlišitelnosti částic je založeno kvantově-mechanické
chování souborů skládajících se ze
stejného druhu částic. Jelikož částice jsou stejné a
nerozlišitelné, musí být ekvivalentní i fyzikální stavy
soustavy získané záměnou (přehozením, transpozicí) dvou
částic "1" a "2"; z kvantového hlediska
musí hustota pravděpodobnosti úyú2 tohoto systému zůstat stejná při vzájemné
záměně částic: úy("1","2")ú2 = úy("2","1")ú2, tj. buď y("1","2") = y("2","1"),
nebo y("1","2")
= -y("2","1")
- vlnová funkce soustavy se může změnit jen o znaménko.
Existují tedy dvě možnosti: 1.Vlnová funkce je buď symetrická a
při libovolné permutaci částic se nemění; 2.
Nebo, vlnová funkce systému je antisymetrická
- při transpozici každé dvojice částic mění znaménko.
Která z těchto možností se realizuje, závisí na druhu
částic - souvisí to s jejich spinem (§1.1.,
pasáž "Spin"). Níže si podle
tohoto kritéria částice rozdělíme na bosony
se symetrickou vlnovou funkcí (celočíselný spin) a fermiony
s antisymetrickou vlnovou funkcí (poločíselný spin) - pasáž
"Fermiony-Bosony". Rozborem vlnových funkcí soustavy stejných
částic lze ukázat, že v souboru identických fermionů
se v tomtéž kvantovém stavu nemohou nacházet dvě částice
(nebo více částic) - platí tzv. Pauliho vylučovací
princip. Zatímco v souboru bosonů se v
tomtéž kvantovém stavu může nacházet neomezený počet
částic.
Analýza
vztahu mezi spinem částic a jejich statistickým chováním v
souboru částic se rozpadá na tři dílčí problémy :
1. Vztah mezi spinem a symetrií vlnové funkce
Spin je vnitřní moment hybnosti částic,
analogický rotačnímu momentu hybnosti při
rotaci částice kolem své osy (ale nedá se takto
kvantitativně vysvětlit!), spíše souvisí se symetriemi
vzhledem k prostorové rotaci (v rámci
kvantové mechaniky je spin popsán v §1.1., pasáž "Spin"). Z hlediska kvantové
teorie pole (druhotné kvantování)
se spin pole interpretuje jako míra symetrie v rovinné vlně příslušného pole: dané pole má spin s (spinové číslo s), jestliže jeho rovinná vlna je invariantní
vůči pootočení o úhel
2p/s kolem směru
šíření. Spin částice tedy udává rotační
symetrii vlnové funkce vůči rotaci v prostoru. Pro
částice s celočíselným spinem, nejčastěji s=1, jsou
vlnové funkce invariantní vůči pootočení o úhel
360o ;
vlnové funkce jsou symetrické vůči
transpozici. ..., částice se chovaji jako bosony.
Pro částice s poločíselným spinem 1/2 jsou vlnové funkce antisymetrické.
....... ......, částice se chovají jako fermiony.
Pozn.:
Toto je jen letmý heuristický nástin
vztahu mezi spinem částice a symetrií vlnové funkce. Při
podrobnějším odvození se používá analýza pomocí
relativistické kvantové teorie pole.
2. Vztah mezi symetrií vlnové funkce a
obsazováním kvantových stavů
Uvažujme dvě stejné částice a, b s vlnovými
funkcemi y(....... y(........ ......; vlnová funkce pro soustavu složenou
z těchto dvou částic pak bude Y(....... = ..... Pokud jsou
funkce y(.......
y(.... antisymetrické
vzhledem k transpozici částic y(....... = - y(...., bude
výsledná vlnová funkce Y(...... dvojice částic nacházejících se ve stejném
kvantovém stavu rovna nule - pravděpodobnost je zde
nulová. Dvě částice s antisymetrickou vlnovou funkcí se tedy
nemohou nacházet v témže kvantovém stavu, platí pro
ně tzv. Pauliho vylučovací princip.. Pro částice se
symetrickou vlnovou funkcí vůči transpozici, budou
všechny kombinace stavových funkcí mít pozitivní znaménka,
takže výsledná vlnová funkce Y bude též kladná a
nenulová - libovolný počet částic tohoto druhu
může být v tomtéž kvantovém stavu.
3. Vlastní statistické chování souborů
částic
Pod statistickým chováním (zkráceně "statistikou")
částic zde rozumíme průměrné rozdělení
(distribuci) jejich stavů - podle rychlostí, kinetických
energií - ve velkém souboru těchto částic. Touto
analýzou se zabývá speciální obor statistická
fyzika, v praxi většinou v součinnosti s termodynamikou.
V nejjednodušším případě dostatečně velkého souboru
neinteragujících částic v termodynamické rovnováze,
chovajících se podle zákonů klasické (nekvantové)
fyziky, analýza metodami statistické mechaniky
ukazuje, že průměrný (očekávaný) počet částic
<N(E)> s energií E je dán tzv. Maxwell-Boltzmannovým
rozdělením <N(E)> = 1 / e-E/kB.T, kde T je
absolutní teplota [oK] a kB je Boltzmannova konstanta (udávající
přepočetní koeficient mezi průměrnou kinetickou energií
částic v plynu a termodynamickou teplotou plynu kB=1.380649×10-23 J/oK).
V případě shora zmíněných kvantových
vlastností (bod 2.) bude rozdělovací funkce N(E) záviset na
obsazovacích pravidlech kvantových stavů. V kvantové
statistické fyzice se distribuční funkce podle
obsazovacích možností kvantových stavů částic upřesňuje
na tvar :
<N(E)> = 1 / (e-E/kB.T ± 1) ,
kde ve jmenovateli kladné znaménko "+" platí pro
fermiony - Fermi-Diracovo statistické rozdělení
a zápozné znaménko "-" pro bosony - Bose-Einsteinovo rozdělení.
Pozn.: V termodynamice plynů
tvořených atomy či molekulami s určitým chemickým
složením se ve jmenovateli distribučních funkcí vyskytuje
ještě tzv. chemický potenciál m : e-(E-m)/kB.T, vyjadřující
energetické změny při chemických reakcích, které mohou
nastávat při srážkách atomů. U elementárních částic by
analogie této situace mohla vzniknout, pokud by částice měly
dostatečnou kinetickou energii pro interakce s transmutacemi a
tvorbou nových částic.
Ve
Fermi-Diracově rozdělení částic splňujících Pauliho
vylučovací princip se vyskytují i situace, kdy některým
různým stavům odpovídá stejná energie - dochází k tzv. degeneraci
energetických hladin. V čitateli rozdělovacího zákona místo
"1" je pak faktor degenerace g, který udává
počet různých stavů odpovídajících určité stejné
energetické úrovni: <N(E)> = g / (e-E/kB.T + 1). Degenerace
energetických hladin vzniká především v důsledku nějakých
druhů symetrií v daném systému, jako je
pohyb v centrálně symetrickém poli .
Důležitou
vlastností Fermi-Diracova rozdělení částic v souboru
fermionů je možnost vzniku tzv. degenerované hmoty
či degenerovaného plynu. V souboru
neinteragujících fermionů - ideální Fermiho plyn -
mohou částice uzavřené v konečném objemu nabývat pouze
diskrétní hodnoty energií (kvantové stavy). Pauliho
vylučovací princip přitom zabraňuje identickým fermionům
obsadit stejné kvantové stavy. Při vysokých hustotách látky
jsou všechny energetické hladiny fermionů obsazeny
až do určité maximální energie, které odpovídá určitá
maximální hybnost; tomuto stavu se říká degenerace,
jedná se o degenerovaný fermionový plyn. Každý
další fermion v daném objemu musí zaujmout novou vyšší
energetickou hladinu a mít tím i vyšší hybnost. Tlak zde
proto roste podstatně rychleji než odpovídá stavové rovnici
ideálního plynu.
Statistické chování chování elektronů,
protonů a neutronů podle Fermi-Diracova rozdělení, se vznikem
degenerace, má velký význam ve stelární astrofyzice, kde
spoluurčuje rovnovážný stav hvězd proti působení
gravitace, porušení této rovnováhy a kolaps hvězdy
na bílého trpaslíka a neutronovou hvězdu (§4.1 "Úloha gravitace při vzniku a
evoluci hvězd" a §4.2
"Konečné fáze hvězdné evoluce. Gravitační
kolaps. Vznik černé díry."
v knize "Gravitace, černé díry a fyzika prostoročasu").
Nastíněnou
analýzu vztahů mezi spinem, symetrií vlnových funkcí a
statistickým chováním souborů částic, můžeme shrnout do výsledného
teorému :
| Spin => symetrie vlnové
funkce => statistické chování částic |
| Částice s poločíselným spinem (s=
1/2, 2/3, ....) mají vlnovou funkci antisymetrickou
vzhledem k transpozici částic, ve stejném kvantovém
stavu může být nanejvýš jedna tato částice
(Pauliho vylučovací princip) a v souboru částic se
řídí Fermi-Diracovou statistikou - jsou to fermiony. |
| Částice s celočíselným spinem (s=
0, 1, 2, ....) mají vlnovou funkci symetrickou vzhledem
k transpozici částic, ve stejném kvantovém stavu
může být neomezený počet těchto částic a v
souboru částic se řídí Bose-Einsteinovou statistikou
- jsou to bosony. |
Fyzikální parametry částic;
kvantová čísla
Vlastnosti elementárních částic se charakterizují vhodnými
fyzikálními parametry, z nichž některé jsou známé i z
klasické fyziky, jiné jsou čistě kvantové a nemají
klasickou analogii. Těmto parametrům elementárních částic,
které jsou většinou kvantovány, tj. nabývají diskrétních
hodnot, se říká kvantová čísla.
¨ Klidová
hmotnost, doba života
Jsou to základní nekvantované charakteristiky
částic. Klidová hmotnost částic se
vyjadřuje jen zřídka v gramech, ale nejčastěji v
energetických jednotkách elektronvoltech eV, keV, MeV
*) - v souvislosti s Einsteinovým vztahem E = m.c2 ekvivalence hmotnosti
a energie. Někdy se udává i v násobcích hmotnosti
elektronu. Doba života, resp. poločas
rozpadu částic se vyjadřuje v sekundách a
jejich dekadických zlomcích (10-xx sec.); u stabilních částic se považuje za Ą.
*) Přesněji řečeno, energetické
vyjádření hmotnosti je v MeV/c2, avšak c2 se často vynechává.
¨ Velikost, rozměry a tvar elementárních
částic ? -
problematické !
V běžném životě i ve fyzice makroskopických jevů má
velký význam prostorová velikost těles,
jejich tvar a jednotlivé rozměry. V mikrosvětě je toto však problematické.
U částic mikrosvěta totiž v důsledku vlnové povahy a
kvantových relací neučitosti pojem prostorové
"velikosti" ztrácí význam - nelze
jej definovat a změřit. Tyto částice nejsou nějaká drobná
"materiální tělíska" s pevným povrchem, jak je
známe z našich běžných zkušeností z makrosvěta, ale
spíše prostorově rozprostřené "zhuštěniny
polí" vlnové povahy. Nemají žádné určité
hranice. Lze u nich definovat pouze jakousi "efektivní
velikost" částice při interakcích
- pomocí dosahu působících sil a tzv. účinného
průřezu (viz níže část "Interakce
elementárních částic",
pasáž "Účinný průřez interakcí částic"). Z rozptylových experimentů při ostřelování
částic - při zjišťování jak "blízko k sobě"
částice pronikly. Taková "efektivní velikost" však
pro danou částici může být pokaždé jiná
při různých druzích interakcí. Tyto potíže s velikostí
částic se obcházejí fyzikální dohodou,
že elementární částice mikrosvěta se v zásadě budou
považovat za bodové s nulovou velikostí,
přičemž při interakcích se uvažují účinné průžezy...
Fyzikální snahy
o určení velikosti elementárních částic
V počátcích zkoumání mikrosvěta se atomoví a
jaderní fyzikové usilovně snažili stanovit velikost
("poloměr") nově objevených částic - elektronu a
protonu. U elektronu s hmotností me a
elementárním nábojem e se při analýze z různých
hledisek dospělo ke třem velmi odlišným hodnotám:
- Klasický
(nekvantový) neboli Thomsonův poloměr
elektronu vychází z modelu, že elektron je koule, na jejímž
povrchu je rovnoměrně rozložen elektrický náboj o hodnotě e.
Za poloměr elektronu re se bere
takový poloměr koule, aby elektrostatická potenciální
energie tohoto náboje odpovídala klidové hmotnosti elektronu me podle
relativistického vztahu ekvivalence hmoty a energie E = mec2. Vychází: re = e2/4peomec2 = 2,818.10-13cm.
Je to takový poloměr, aby veškerá klidová hmotnost
elektronu me měla elektrický
původ (byla tvořena elektostatickou
potenciální energií). Tento přístup je analyzován i
v §1.6, pasáži "Nelineární elektrodynamika"
monografie "Gravitace, černé díry a fyzika
prostoročasu".
- Bohrův
poloměr elektronu vychází ze skutečnosti, že
naprostá většina elektronů je vázána v atomech, takže
velikost elektronu by by bylo přirozené odvodit z rozměrů
atomu. Podle Bohrova kvantového modelu (§1.1,
část "Bohrův model
atomu") má
nejnižší (základní, neexcitovaná) orbita elektronu v atomu
vodíku poloměr r1 = 4peoh/mee2 = 0,529.10-8cm.
Tato hodnota se zde považuje za poloměr elektronu re.
- Comptonova
vlnová délka elektronu je nejmenší vzdálenost, na
kterou lze podle kvantových relací neurčitosti omezit
("stlačit") elektron: lc ~ h/mec » 10-9cm.
Pokud se elektron pokusíme stlačit do menší velikosti, pak
podle principu neurčitosti se jeho hybnost stane
natolik velkou, že jeho kinetická energie převýší klidovou energii elektronu mec2. V takovém
případě bude dostačující energie na vytvoření nového
elektron-pozitronového páru. Comptonova délka je tedy nejmenší
vzdálenost, na kterou k sobě dva elektrony mohou
proniknout, aniž dojde ke vzniku nových částic...
Z nynějšího pohledu mají
tyto hodnoty již jen modelový a historický význam a za
"skutečné" rozměry elektronu se nepovažují.
Pro elektrony se nakonec žádná věrohodná
hodnota "velikosti" nepodařila určit,
čím vyšší kinetická energie, tím hlouběji se při
interakci vzájemně přiblížují - jako by byly bodové
s nulovou velikostí (<10-16
cm)..?.. Podobné se to
předpokládá u ostatních leptonů *). Z hlediska
korpuskulárně-vlnového dualismu by efektivní
velikost elektronu, jeho "vlnová délka", závisela
na jeho rychlosti (§1.1, pasáž "Částicově-vlnový dualismus").
*) U neutrin, které vykazují
pouze slabou interakci, se efektivní "velikost"
předpokládá podstatně nižší než u elektronů, cca 10-16cm.
Žádná přímá měření zde nejsou uskutečnitelná.
U protonů a
neutronů byla jejich efektivní "velikost" pro silné
interakce stanovena na cca 1,6.10-13cm, podle změřeného dosahu
těchto jaderných sil (viz §1.1, pasáž
"Silná jaderná
interakce"), jakožto "zbytkového" projevu silné
interakce mezi kvarky uvnitř protonů a neutronů. Podobně pro
ostatní hadrony (piony, kaony, hyperony). Pro elektromagnetickou
interakci se "velikost" protonu měří
pomocí rozptylu urychlených elektronů. Další metodou je vodíková
spektrometrie: přesné měření energetických hladin (rozdílu v energiích mezi 2S1/2 a 2S1/2 orbitaly - hyperjemná struktura způsobená Lambovým
posunem v důsledku kvantových fluktuací virtuálních
elektron-pozitronových párů v elektrickém poli protonu); touto metodou se dospělo k hodnotě 0,88.10-13cm. Tato měření byla modifikována v
novém experimentu, kde atomy vodíku byly vystaveny svazku
nízkoenergetických mionů, přičemž některé miony se
zachytily a nahradily ve vodíkovém atomu elektrony. Takový
mion díky své vyšší hmotnosti (je cca
200-krát těžší než elektron) obíhá
podstatně blíže protonu, takže rozdíly v energetických
hladinách jsou "citlivější" na strukturu protonu.
Zde se dospělo k poněkud nižší hodnotě poloměru protonu 0,84.10-13cm. Protony, jakož i ostatní hadrony,
nejsou "elementární" částice, ale jsou složeny z kvarků,
takže k jejich struktuře a "velikosti" má co říci
tzv. kvantová chromodynamika (viz
níže "Uvězněné kvarky"), na fundamentální úrovni pak unitární teorie pole ("Sjednocování fundamentálních interakcí.
Supergravitace. Superstruny."
v monografii "Gravitace, řerné díry a fyzika
prostoročasu").
U fotonů, jakožto kvant
elektromagnetického vlnění, je jejich efektivní
"velikost" odvislá od vlnové délky záření.
Fotony záření gama mají efektivní rozměry jen pikometry,
fotony viditelného světla stovky nanometrů, u radiovln bychom
si mohli představit i mnohametrové rozměry "fotonů"
- zde se však fotony vůbec nedají prokázat...
¨ Elektrický
náboj
Mimořádně důležitým parametrem částic je jejich elektrický
náboj, který je kvantován a proto se, místo v
coulombech, vyjadřuje v násobcích velikosti elementárního
náboje elektronu |e| s uvedením znaménka *) -
elektron má pak náboj -1, proton +1, hyperon W náboj -2, neutron
a další nenabité částice samozřejmě 0. Antičástice k
nabitým částicím mají náboje opačného znaménka (a
stejné absolutní velikosti). Ve všech známých interakcích
je striktně splněn zákon zachování elektrického
náboje: součet nábojů částic před interakcí je
stejný jako součet nábojů částic vylétajících po
interakci.
*) Níže se setkáme i s nábojem 1/3e či 2/3e
u kvarků.
¨ Spin,
magnetický moment
Další důležitou kvantovou charakteristikou částic
je jejich spin neboli spinové číslo s,
vyjadřující vlastní moment hybnosti částice v násobcích
Planckovy konstanty h. Kromě nulového spinu
(vyskytujícího se u mezonů p a K) je nejmenším možným spinem hodnota s=1/2
(takový spin mají elektrony, protony, neutrony, neutrina,
miony). Spin s=1 mají fotony, s=3/2 těžké hyperony W, spin s=2
gravitony. Se spinem korpuskulárních částic úzce souvisí
jejich magnetický moment, udávaný v
násobcích elementárního Bohrova magnetonu e.h/4pme, popř. jaderného
magnetonu e.h/4pmp
(podrobněji je diskutováno v §1.1,
pasáž "Kvantový moment hybnosti,
spin, magnetický moment"). Spinové číslo částic dále určuje
kvantově-mechanické statistické chování v
souborech částic - viz níže "Bosony" a
"Fermiony".
Pozn.: Spin - rotace ?
Spin částic se podle klasické mechaniky obvykle interpetuje
jako jejich rotační moment hybnosti. Tato
vlastnost elementárních částic však má specificky kvantovou
povahu a nelze ji uspokojivě vysvětlit pomocí klasických
mechanických představ (spin nelze
kvantitativně vysvětlit např. rotací částice kolem vlastní
osy!).
¨ Parita
je kvantové číslo, charakterizující chování vlnové funkce
kvantově-mechanického objektu - jádra či elementární
částice - vzhledem k prostorovému zrcadlovému odrazu, tj.
transformaci souřadnic x®-x, y®-y, z®-z, t®t. Pokud se
přitom vlnová funkce popisující stav částice nezmění, je
parita kladná: P=1, či "+". Pokud při této
transformaci vlnová funkce systému změní znaménko, je parita
záporná: P= -1,
neboli "-". Dá se ukázat, že parita systému s
orbitálním momentem hybnosti l je (-1)l. Analýza interakcí
elementárních částic ukazuje, že parita protonu a neutronu
je kladná, zatímco parita fotonů a mesonů p+,-,o je záporná. Parita se někdy uvádí jako index
vpravo nahoře u kvantového čísla momentu hybnosti soustavy,
třebas jádra, JP: buď J+ nebo J-. U elementárních částic pak jako index u spinového
čísla: sP
- např. 0-, (1/2)+ a pod.
Parita P celkově není
příliš důležitým kvantovým číslem.
Svůj teoretický význam má však parita
v souvislosti s vlastnostmi symetrie a zákony zachování při
interakcích částic - viz níže pasáž "CPT symetrie interakcí" v části "Čtyři typy interakcí". Parita se zachovává při silných a
elektromagnetických interakcích, avšak při slabých
interakcích se nezachovává (diskusi a experimentální
ověření viz níže "CPT symetrie interakcí"; z nezachování parity vychází hypotéza tzv. zrcadlové
hmoty, diskutovaná níže v části "Hypotetické a
modelové částice", pasáž
"Stínová zrcadlová hmota - Katoptrony?").
¨ Leptonové
a baryonové číslo
Za účelem třídění elementárních
částic se částicím přiřazuje leptonové číslo
L, které pro leptony je L = ±1 (podle toho, zda se jedná o částici nebo
antičástici), pro ostatní částice L=0, a baryonové
číslo B, které pro baryony je B = ±1 (opět
"+" pro částice, "-" pro antičástice) a
pro jiné částice než baryony je B=0. Leptonové a baryonové
číslo se zachovává prakticky při všech
druzích interakcí *) - součet leptonů a baryonů (s
respektováním znamének) před interakcí a po interakci je
stejný.
*) Jediná výjimka se vyskytuje u gravitační
interakce s účastí černých děr: při
pohlcení částic pod horizont černé díry se ztrácejí
všechny jejich individuální charakteristiky kromě hmotnosti,
elektrického náboje a orbitálního momentu hybnosti ("černá
díra nemá vlasy"); částice jako by se
"rozpustila" v sumárním gravitačním poli černé
díry - viz §4.5 "Teorém "černá díra
nemá vlasy"" v
knize "Gravitace, černé díry a fyzika
prostoročasu". Leptonové a baryonové číslo se
nezachovává ani při kvantové evaporaci černé díry
- §4.7 "Kvantové vyzařování a termodynamika
černých děr" v téže
monografii.
¨ Další kvantová
čísla izospin, podivnost a hypernáboj
budou zavedena níže v souvislosti s mezony K, hyperony a s unitárními
symetriemi elementárních částic - viz pasáž "Unitární symetrie a multiplety částic".
Intermediální
a virtuální částice
Podle představ kvantové teorie pole probíhá
vzájemné silové působení dvou částic tak, že si tyto
částice vzájemně vyměňují (vysílají a
přijímají) tzv. intermediální částice,
jež jsou kvanty příslušného pole. Každá částice
podléhající interakci je obklopena "oblakem"
příslušných intermediálních částic, které mimo akt
interakce zůstávají virtuální.
K vysvětlení mechanismů interakcí a
vzájemných přeměn elementárních částic se používají
nejen pozorované "reálné" částice vstupující do
interakcí nebo vyzařované jako důsledek interakce, ale často
též určité "pomocné" částice,
zprostředkovávající určité etapy interakce, které přímo
pozorovány nejsou. Takovéto virtuální částice *)
"existují" pouze po velmi krátkou dobu,
která je kratší než čas nutný pro změření jejich energie
podle relací neurčitosti. V úloze virtuálních částic mohou
sloužit běžně známé a prokázané částice,
např. fotony, často se však používají i částice zatím
neznámé a neprokázané - modelové a hypotetické
částice (jsou zmíněny níže). Virtuální částice
nemohou být přímo detekovány, ale mohou se projevovat v
reálných měřitelných jevech, neboť interagují s reálnými
částicemi a poli; takové skryté interakce mohou vyvolat
např. spontánní emisi skutečných částic či anomálie v
závislosti účinných průřezů interakcí na energii.
Interakce pomocí intermediálních částic se znázorňují
pomocí tzv. Feynmanových diagramů.
*) Virtuální
= myšlený, zdánlivý, neskutečný, potenciální, fyzicky
nepřítomný. Původně pochází z lat. virtus = muž,
mužnost, ctnost, prošlo však výraznou etymologickou
proměnou.
"Teplota"
částic ?
V nauce o teple - kinetická teorie tepla, termika,
termodynamika - teplota úzce souvisí s rychlostí či
energií částic. Teplota běžného látkového prostředí je
dána rychlostí kmitavého či chaotického pohybu částic z
nichž je látka složena - atomů a molekul. Střední
kvadratická rychlost vk2 pohybu částic
souvisí s termodynamickou teplotou T[oK] vztahem
1/2 mo vk2 = 3/2 kB.T ,
kde kB=1,38.10-23J.K-1 je Boltzmannova
konstanta a mo je klidová hmotnost částic látky (v nejjednodušším případě ideálního
jednoatomového plynu). Tedy teplota je
úměrná střední kinetické energii částic Ek= (1/2).mo vk2 .
Tato kinetická koncepce teploty
se z látkového prostředí zobecňuje i na
prostředí složená z jiných částic než jsou molekuly a
atomy - na fyzikální soubory různých mikročástic a jejich
vázaných kombinací *). Kinetická energie částic Ek se zde pak měří v
elektronvoltech [eV] a Boltzmannova konstanta má hodnotu kB=8,617.10-5 eV.K-1 (nositelem kinetické energie v ionizované látce a
souborech částic jsou většinou elektrony). V zásadě tedy můžeme energetický stav souborů
částic ekvivalentně měřit buď střední kinetickou energií
Ek
částic v [elektronvoltech], nebo termodynamickou teplotou T ve
[stupních Kelvina].
*) Bylo by jistě zavádějící tvrdit že "částice má
teplotu xxx °K"; částice žádnou veličinu
"teplota" nemají. Přesnější je formulace
"daný soubor částic má termodynamickou teplotu xxx °K".
Teplotu v takových souborech částic již samozřejmě nelze
měřit běžným teploměrem vloženým do systému (s
dosažením teplotní rovnováhy), nýbrž na základě
radiačního vyzařování nebo přímo měřením energií
částic pomocí detektorů.
Pokojové teplotě T=cca300oK odpovídá
kinetická energie elektronů Ek=zhruba 26 milielektronvoltů. Vysokoteplotní
plasma potřebná pro účinnou termonukleární
fúzi deuteria a tritia se musí ohřát na teplotu cca
150 milonů stupňů (lhostejno zda Kelvina
či Celsia), což představuje kinetickou
energii částic cca 12 keV (viz §1.3,
část "Slučování atomových jader"). A u kvark-gluonové
plasmy se na kratičký okamžik dosahuje obrovské
termodynamické teploty vyšší než 1012
stupňů ( viz
níže pasáž "Kvark-gluonová
plasma - "5.skupenství hmoty""), kinetická energie
částic dosahuje řádově TeV.
Třídění
elementárních částic
Elementární částice se třídí a rozdělují do skupin podle
svých význačných vlastností, vyjádřených fyzikálními
parametry a kvantovými čísly. Nejzákladnější
charakteristikou každého předmětu *), a tedy i elementární
částice, je její hmotnost - přesněji
řečeno hmotnost klidová mo.
Podle speciální teorie relativity
totiž aktuální hmotnost m (setrvačná hmotnost,
charakterizující podle 2.Newtonova zákona F = m.a odpor
tělesa vůči zrychlování) závisí na rychlosti
pohybu tělesa v: m = mo/Ö(1-v2/c2), kde mo je klidová hmotnost, stanovená v inerciální
vztažné soustavě, v níž je těleso v klidu. Výsledná
hmotnost m je tím větší, čím rychleji
se částice pohybuje; pro v®c roste nade všechny meze. Proto žádná částice,
jejíž klidová hmotnost je nenulová, se nemůže pohybovat
rychlostí světla. Celková energie částice (součet klidové
a kinetické energie) je podle speciální teorie relativity
rovna E = (mo/Ö(1-v2/c2)).c2 = m.c2 - Einsteinova rovnice vyjadřující rovnocennost
hmotnosti a energie.
*) Další základní charakteristika objektů v makrosvětě -
prostorová velikost (rozměry, objem), nemá u
elementárních částic žádný význam! V
důsledku korpuskulárně-vlnového dualismu a principu
neurčitosti nelze částicím v mikrosvětě
přiřadit žádnou určitou velikost (podrobněji
bylo diskutováno výše v pasáži "Velikost,
rozměry a tvar elementárních částic ? - problematické !"). V modelových
představách však můžeme uvažovat o jakýchsi "efektivních"
velikostech částic, daných vlastnostmi interakce těchto
částic (např. proton má z hlediska silné interakce rozměr »1,6.10-13cm). Z těchto
představ vychází i tzv. účinný průřez
interakce částic (viz níže).
Podle klidové hmotnosti
rozdělujeme částice na čtyři skupiny :
- Částice s
nulovou klidovou hmotností
V atomové a jaderné fyzice jsou to především kvanta
elektromagnetického záření - fotony,
v subnukleární fyzice i modelové částice gluony
zprostředkovávající silnou interakci. V obecné
teorii relativity a kvantové gravitaci pak příp.
ještě kvanta gravitačního vlnění - gravitony
(gravitační vlny jsou v
astronomii prokázány jen nepřímo, první přímá
detekce se podařila teprve zcela nedávno - viz "První
přímá detekce gravitační vlny zařízením LIGO ! "; na experimentální prokázání
gravitonů není naděje v dohledné budoucnosti). Z hlediska kvantové teorie pole částice s
nulovou klidovou hmotností zprostředkovávají - jako výměnné
intermediální částice - interakce dlouhého
(neomezeného) dosahu (fotony
elektromagnetickou, gravitony gravitační interakci,
gluony silnou interakci mezi kvarky).
Pozn.: Může se zdát
paradoxní mluvit o "klidové hmotnosti" u
částic, které principiálně nikdy nemohou být v
klidu. Ve speciální teorii relativity je však klidová
hmotnost částice definována jako invariantní velikost
(4-rozměrná délka, nezávisející na vztažné
soustavě) 4-vektoru hybnosti částice - viz vztah
(1.101´) v §1.6 "Čtyřrozměrný prostoročas
a speciální teorie relativity"
knihy "Gravitace, černé díry a
fyzika prostoročasu".
Fotony mají nulovou klidovou hmotnost, avšak jejich
setrvačná (relativistická) hmotnost závisí na
frekvenci: m = h.n/c2. Při zabrzdění odevzdá foton veškerou svou
energii a zanikne, na rozdíl od částice s nenulovou
klidovou hmotností, která odevzdá jen svou kinetickou
energii a po zabrzdění i nadále existuje se svou
klidovou hmotností.
- Leptony - lehké částice s malou klidovou hmotností (řec. leptos = tenký, jemný,
slabý, útlý, hubený *)
Sem náleží především elektrony e-
a pozitrony e+ s klidovou hmotností me = 9,1.10-28g = 511 keV (v jaderné fyzice bývá zvykem
hmotnost vyjadřovat v souvislosti se vztahem E = m.c2 v
energetických jednotkách elektronvoltech). Dále jsou
to neutrina (elektronové ne, mionové nm,
tauonové nt)
a antineutrina s klidovou hmotností cca 2 eV.
Do kategorie leptonů se dnes zařazuje i mion
m- (označovaný jako "těžký
elektron"), který má hmotnost »206me a dokonce i tauon
t- s hmotností »3484me, označovaný
jako "supertěžký elektron"; a samozřejmě
jejich nábojově sdružené antičástice.
*) Původní označení leptony,
jakožto lehké částice, dnes již ztrácí svůj
původní doslovný význam, vzhledem k zařazení mionů
a tauonů. Úloha leptonů jako základních stavebních
částic hmoty, spolu s kvarky, bude nastíněna níže v
pasáži "Standardní model
elementárních částic".
Podle tohoto standardního modelu leptony (spolu se
svými antičásticemi) tvoří tzv. generace.
První generaci tvoří elektron s elektronovým
neutrinem. Do druhé generace patří mion se svým
mionovým neutrinem, do 3.generace tauon s tauonovým
neutrinem. Předpokládá se, že další generace,
tvořené ještě těžšími analogy elektronu,
neexistují. Analogické 3 generace se rozlišují u
kvarků.
Leptony podle dosavadních
poznatků nemají vnitřní strukturu,
standardní model je považuje za bodové
částice (jiný přístup se
uvažuje v teorii superstrun). Všechny leptony podléhají slabé interakci,
nabité pak i interakci elektromagnetické.
- Baryony - těžké částice
(řec. baryos = těžký)
Sem patří především proton p+ s hmotností
mp
= 1836me = 938 MeV/c2 a neutron no s o něco
větší hmotností mn = 1838me (a samozřejmě jejich antičástice). Protony
a neutrony se souhrnně označují jako nukleony
- stavební částice atomového jádra. Mezi baryony pak
patří ještě těžší částice - hyperony.
Ty vznikají při srážkách částic vysokých energií
a velmi rychle se rozpadají - jejich
doba života je řádově »10-10sekundy.
Známe hyperony Lo (hmotnost 2183me), S+,-,o
(hmotnost »2330me), Xo,- (hmotnost »2580me), W- (hmotnost »3273me).
Jedinými stabilními baryony jsou protony
(zatím zde pomíjíme hypotézu
rozpadu protonu), ve vazbě s
protony v atomových jádrech též neutrony.
Ostatní jsou nestabilní, rozpadají se na nukleony a
piony. Baryony jsou "vybaveny" všemi druhy
interakcí - silnou, slabou, elektromagnetickou (pokud
jsou el. nabité) - a samozřejmě
gravitační, kterou zde neuvažujeme. Z hlediska interakce patří mezi hadrony.
- Mezony - středně těžké částice (řec. mesos = střední, mezi
něčím - jejich hmotnost leží mezi elektronem a
protonem)
Nejlehčí z nich je mezon m- (mion *) s hmotností mm = 206me, dále
kladný mezon p+ a záporný p- s hmotností 273 me, neutrální pion po s
hmotností 264me. Nakonec jsou to K-mezony K+,- (hmotnost 966me) a Ko (hmotnost 974me).
*) Upozornění:
Miony m jsme zde sice podle jejich hmotnosti zařadili
mezi mezony, avšak podle vlastností svých interakcí a
struktury jsou nyní zařazovány mezi leptony! Vznikají
při procesech s účastí slabé interakce, jsou
nestabilní a rozpadají se na elektrony a neutrina (viz
níže).
Mezony p a K vznikají při
procesech s účastí silné interakce a jsou nestabilní
- rozpadají se slabou interakcí na miony a neutrina
(K-mezony i silnou interakcí na piony); způsoby rozpadu
a doby života jsou uvedeny níže. Podobně jako
baryony, i mezony p a K jsou hadrony, interagující
obecně všemi 4 druhy interakcí.
Původ klidových
hmotností částic
Výše zmíněné diametrálně odlišné klidové hmotnosti
různých druhů částic byly dříve čistě empirickou
záležitostí. Nyní se je standardní částicový model
pokouší vysvětlovat v zásadě dvěma mechanismy :
1. U základních, elementárních
bezstrukturních částic - fotonů, leptonů, kvarků,
intermediálních bosonů - jejich hmotnost závisí na
hodnotách vazbových konstant interakce příslušných
polí s všudypřítomným Higgsovým-Kibbleovým skalárním
polem (jehož kvanty jsou Higgsovy
bosony). Pro fermiony se tako
interakce nazývá též Yukawova vazba (modeluje se Yukawovým potenciálem s exponenciální
závislostí). Můžeme si to
zjednodušeně představit tak, že částice při svém pohybu s
sebou "táhne" i určitou část energie-hybnosti
Higgsova pole (podle velikosti vazbové
konstanty), čímž se efektivně jeví
hmotnější (podle 2.Newtonova
zákona), klade větší silový odpor
vůči urychlování, při stejné rychlosti nese vyšší
kinetickou energii.
Fotony a gluony neinteragují s
Higgsovým polem vůbec, mají proto nulovou klidovou hmotnost.
"Obyčejné" elektrony s Higgsovým
polem interagují jen poměrně slabě (vazbová konstanta g ~ 3.10-6), mají klidovou
hmotnost 511keV. Jim příbuzné leptony, miony
("těžké elektrony") interagují silněji (vazbová
konstanta ~ 6.10-4) a mají klidovou hmotnost 200-x větší, 105,6MeV. A tauony
("supertěžké elektrony") interagují s Higgsovým
polem velmi silně (vazbová konstanta ~ 1.10-2) a mají proto
klidovou hmotnost 1777 MeV, více než 3000-x větší než elektrony!
Kvarky "d" s vazbovou konstantou ~ 2,6.10-5 mají hmotnosti
4,6MeV, kvarky "s" s vazbovou konstantou ~ 5.10-4 mají hmotnosti
94,6MeV, kvarky "b" s vazbovou konstantou ~ 5.10-2 mají hmotnost
4,3GeV. Zvláště silnou interakci s Higgsovým polem mají bosony
W+,-, Z0 způsobující slabou interakci (vazbová konstanta g ~
1), což vede k jejich vysokým hmotnostem 80-90 GeV a velmi
krátkému dosahu slabé interakce.
Pozn.: I
tento přístup zůstává v zásadě fenomenologický:
empiricky změřené hmotnosti M částic se jen
transformují na hodnoty vazbové konstanty g s Higgsovým
polem podle jednoduchého vzorce M = g .Vv/21/2, kde Vv
je "očekávaná" hodnota potenciálu Higgsova
vakua Vv = (21/2. GF)-1/2 ~
246 GeV (GF je redukovaná Fermiho konstanta slabé
interakce). Standardní model zatím nedokáže předpovědět
konkrétní hodnoty hmotností či vazebných konstant.
Higgsův mechanismus se často dává do
souvislosti s poněkud málo intuitivní koncepcí "spontánního
narušení symetrie" - je podrobněji diskutováno v
§B.6 "Sjednocování fundamentálních interakcí.
Supergravirace. Superstruny.",
pasáž "Symetrie ve fyzice a jejich narušení"
knihy "Gravitace černé díry a fyzika prostoročasu".
2. U "složených"
částic, hadronů - protony, neutrony, hyperony, piony, kaony,
... - tvoří klidová hmotnost jejich stavebních složek -
kvarků - jen malou část celkové hmotnosti,
kolem 1 %. Většina hmotnosti hadronů pochází z kinetické
energie vnitřního pohybu jeho kvarkových komponent.
Např. proton má hmotnost 938MeV, zatímco klidová hmotnost
kvarku "u" je jen 2MeV a kvarku "d" 5MeV.
Spektrum klidových
hmotností částic - je omezené či nekonečné ?
Klidové hmotnosti různých druhů částic jsou velmi
rozdílné, jejich hodnoty tvoří široké
"spektrum". Od fotonů s nulovou či neutrin s
nepatrnou klidovou hmotností, přes lehké elektrony (cca
0,5MeV), mezony (kolem 140-500MeV), až po těžké baryony s
klidovými hmotnostmi 1-1,7GeV. Nejtěžšími známými
částicemi jsou bosony W+,-,Zo slabých interakcí o hmotnostech kolem 80-90GeV a
Higgsovy bosony s klidovou hmotností cca 120GeV. Vzniká
otázka, zda zde spektrum hmotností již končí, nebo existují
ještě těžší částice? V 60. a 70. letech se
diskutovala tzv. Hagedornova hypotéza o existenci nekonečného
množství částic o stále vyšších hmotnostech,
které by se mohly postupně objevovat, jak by se konstruovaly
stále výkonnější urychlovače. Současná
částicová fyzika je k tomu spíš skeptická, mohlo by se
příp. jednat jen o excitované stavy kvark-gluonových
kombinací..?.. - rozhodnout mohou jen budoucí experimenty.
Podle způsobu interakce mezi
elementárními částicemi se vyčleňuje zvláštní skupina :
- Hadrony - částice vykazující silnou
jadernou interakci (řec. hadros
= silný, těžký, tlustý, robustní)
Sem náleží protony, neutrony, mezony p a K,
hyperony. Původ silné (jaderné) interakce se klade do
modelových subnukleárních částic kvarků
(viz níže). Hadrony jsou tedy částice s kvarkovou
strukturou - baryony jsou složeny ze tří kvarků,
mezony ze dvou. Hadrony nejsou tedy v pravém
slova smyslu "elementární", avšak jejich
přímé rozložení na kvarky je značně problematické
- viz níže část "Kvarková struktura hadronů".
Pozn.: Název "hadron"
poprve zavedl L.B.Okun z Fyzikálního institutu v
Moskvě v r.1962.
Podle doby života můžeme
elementární částice dělit na :
- Stabilní
částice s nekonečně
dlouhou dobou života.
Sem patří elektron e-, pozitron e+, foton, proton p+ *), neutrina n (pomineme-li jev oscilace neutrin, který nelze
považovat za rozpad).
*) Podle některých tzv. grandunifikačních
teorií by proton nemusel být zcela stabilní
částicí, ale měl by se rozpadat s poločasem T1/2>»1033let. Tato
myšlenka je do značné míry spekulativní, neboť za
dosavadní existenci vesmíru se možná nestačil
rozpadnout ani jeden proton..?. Pouze v případě
otevřeného vesmíru s nekonečnou dobou evoluce by
rozpad protonů snad mohl v časových měřítcích »10100let
přispět k tzv. tepelné smrti vesmíru (viz např.§5.6 "Budoucnost vesmíru. Šipka času." v knize "Gravitace,
černé díry a fyzika prostoročasu")....
- Částice s
dlouhou dobou života.
Sem patří neutron no, který, pokud je volný (mimo atomové
jádro), se rozpadá b--přeměnou:
no
® p+ + e- + ne´ s
poločasem T1/2@13 minut. S
určitými výhradami zde můžeme zařadit i mion m- s dobou
života 2.10-6sec (rozpadá se na elektron a neutrina: m- ® e-
+ ne´+ nm).
- Částice s krátkou
dobou života.
To jsou všechny ostatní reálné částice, které na
krátký okamžik vznikají při interakcích částic o
vysokých energiích a vzápětí se rozpadají, jejich
doba života se pohybuje v rozmezí cca 10-8-10-20 sec.
Můžeme některé vyjmenovat: mezony p+ a p-
s dobou života 2,6.10-8sec, po
(»10-16sec), K+ (1,2.10-8sec), Ko (»10-10sec), hyperony Lo
(2,5.10-10sec), S+ (8.10-11sec), S- (1,5.10-10sec), So (»10-20sec),
skupina hyperonů Xo,- a W- s dobami života řádu 10-10sec.
- Částice s ultrakrátkou
dobou života - tzv. rezonance
Vznikají při některých interakcích
vysokoenergetických částic (jako je p+,-
+ p+ ® p+,- + p+, nebo interakce protonu s antiprotonem za
vzniku několika p-mezonů) a okamžitě se rozpadají, jejich doba života
činí asi 10-23 až 10-20 sekundy. Projevují se vlasně jen výrazným rezonančním
maximem v energetické závislosti účinného
průřezu dané interakce, nebo zhuštěninami a píky na
Dalitzově diagramu energií sekundárních
částic (viz níže pasáž "Analýza
dynamiky interakcí částic").
Rozeznáváme baryonové rezonance a mezonové
rezonance (jako je mezon r nebo některé
druhy mezonů K*). Rezonance se mnohdy ani za zvláštní
částice nepovažují, označují se jako kvazičástice.
Jsou to spíše jen dočasně excitované stavy dvou či
více baryonů nebo mezonů, které se rozpadají
okamžitě, jakmile vyletí za hranice oblasti silné
jaderné interakce, v níž vznikly. Vzhledem k
extrémně krátké době života nemají patrně
žádný význam pro stavbu a vlastnosti hmoty. Jejich
studium je však důležité pro lepší proniknutí do
subnukleární struktury hadronů, jejich kvarkové
struktury a pochopení vlastností silných interakcí v
rámci kvantové chromodynamiky (QCD).
Fermiony
- Bosony
V pasáži "Nerozlišitelnost částic"
- "Spin, symetrie vlnové funkce a statistické
chování částic" jsme si ukázali, jak spin částic určuje
statistické chování souborů částic.
Podle spinu, a v důsledku toho i podle
kvantově-mechanického statistického chování
v souborech částic, se tedy elementární částice dělí na
dvě velké skupiny :
- Fermiony - částice s "poločíselným"
spinem s = ±(1/2)h, ±(3/2)h, ....
Jsou to především všechny stavební
částice látky: proton, neutron,
elektron. Z leptonů jsou to dále miony
a všechny druhy neutrin. Z baryonů pak
dále hyperony. Všechny vyjmenované
fermiony mají spin 1/2, kromě hyperonu W který má
spin 3/2.
V kvantové mechanice se ukazuje, že soubory
částic s poločíselným spinem se řídí tzv. Fermi-Diracovou
statistikou, pro niž je charakteristické, že
dvě či více částic nemohou být ve stejném
kvantovém stavu (Pauliho vylučovací princip, jsou to
"nesnášenlivé" částice) - v daném
kvantovém stavu může být jej jeden fermion. Proto
jednotlivé elektrony v atomovém obalu zaujímají a
obsazují různé kvantové stavy a takto vzniklé
elektronové konfigurace hladin atomového obalu jsou
příčinou veškeré různorodosti chemického
slučování prvků i jejich dalších vlastností *). A
podobným způsobem i v atomovém jádře nukleony
obsazují různé energetické hladiny v poli silných
interakcí. Lze říci, že fermionům, které jsou
schopny tvořit různorodé struktrury, vděčíme za rozmanitost
přírody..!..
*) Kdyby všechny elektrony mohly
obsadit stejný (nejnižší) kvantový stav, měly by
atomy všech prvků stejné vlastnosti a náš svět by
byl velmi fádní. Naštěstí však elektrony díky své
"nesnášenlivosti" postupně obsazují různé
hladiny v atomovém obalu a různé prvky tím mají
různé vlastnosti a schopnosti slučování, dané
počtem elektronů připadajících na vnější
(valenční) vrstvu.
Fermionový
plyn
Pauliho vylučovací princip pro fermiony má dále
významné důsledky pro chování souboru volných
fermionů, tzv. "fermionového plynu".
Při silném stlačování takového "plynu"
obsadí fermiony všechny nižší možné energetické
stavy, takže takový plyn se pak velmi silně
"brání" dalšímu stlačování - vyšší
stavy jsou spojeny s velkou hybností a tedy vysokým
tlakem. A každý další fermion, který se dostane
dovnitř takto stlačené hmoty, nemůže při
srážkách s ostatními fermiony měnit svůj stav,
neboť všechny okolní kvantové stavy jsou již
obsazeny a žádný další fermion se tam nemůže
dostat; takový fermion se pak pohybuje jalko volný,
okolní prostředí nemůže měnit jeho hybnost. Látka
v takovém stavu se všemi obsazenými kvantovými stavy
se nazývá degenerovaný fermionový plyn
a hraje velkou úlohu v konečných stádiích evoluce
hvězd - bílých trpaslících a neutronových
hvězdách (podrobněji je rozebíráno v §4.2 "Konečné
fáze hvězdné evoluce. Gravitační kolaps" monografie "Gravitace,
černé díry a fyzika prostoročasu").
- Bosony - částice s "celočíselným"
spinem s = 0, ±1h, ±2h, ....
Sem patří především kvanta polí,
přenášející síly, jimiž na sebe částice
působí. Označují se též jako intermediální
částice zprostředkující jednotlivé
interakce. Bosony se spinem s=0 se označují jako skalární,
se spinem s=1 jako vektorové (označení "skalární" a
"vektorové" souvisí s matematickým
formalismem jejich teoretického popisu v kvantové
fyzice).
Nejdůležitějším bosonem je foton
(spin 1), dále p-mezony (spin 0), bosony W-, W+, Zo (spin 0), gluony (spin 1),
hypotetické gravitony (spin 2).
Bosony se neřídí Pauliho vylučovacím principem.
Soubory částic s celočíselným spinem se z
kvantově-mechanického hlediska řídí tzv. Bose-Einsteinovou
statistikou, v níž (na rozdíl od fermionů)
se v každém kvantovém stavu může nacházet
neomezený počet částic ("snášenlivé"
částice). Počet bosonů se v přírodě nezachovává.
Když např. rozsvítíme žárovku, okolní prostor
zaplaví miliardy nově vzniklých fotonů. A naopak,
spousta stávajících fotonů je absorbována ve hmotě
- zanikají při interakcích s atomy a molekulami
látky.
Při nízkých teplotách systému
má každý boson snahu zaujmout nejnižší energetický
stav - vzniká tzv. bosonový kondenzát,
který má supratekuté a příp. supravodivé (v
případě elektricky nabitých částic) vlastnosti.
Fermiony v úloze bosonů; Supravodivost
Za určitých okolností se i soubor fermionů, např.
elektronů, může efektivně chovat jako bosony. Snižujeme-li
teplotu vodivé látky, obsahující volné elektrony ve formě
"elektronového plynu", dochází při teplotách kolem
cca 4°K ke spojování elektronů do dvojic - tzv. Cooperových
párů, v nichž se poločíselné spiny elektronů
opačného směru sčítají na spiny nulové (singletní
spárování), tj. celočíselné. Vazbu mezi elektrony Cooperova
páru zprostředkuje jejich interakce s kmitající krystalovou
mřížkou. Takové dvojice se pak již chovají jako bosony,
které při nízké teplotě mají tendenci zaujmout nejnižší
energetický stav (Pauliho vylučovací princip jim to
nezakazuje, protože pro bosony neplatí). Vzniká tzv. bosonový
kondenzát v základním energetickém stavu, v němž
se spárované elektrony pohybují krystalovou mřížkou zcela
volně bez odporu - vzniká elektrická supravodivost.
Supravodivost
Supravodivost je tedy kvantově-elektrický jev, při němž
materiál neklade průchodu elektrického proudu žádný
ohmický odpor a v materiálu se neuvolňuje žádné teplo.
Objevil jej v r.1911 holandský fyzik H.K.Onnes, který na
přístroji vlastní konstrukce zkapalnil hélium a v dalších
experimentech měřil elektrický odpor kovů při nízkých
teplotách. S klesající teplotou měrný odpor kovů
obecně klesá (s pomaleji kmitajícími
atomy krystalové mřížky se elektrony méně často
srážejí, snadněji procházejí).
Extrapolací tohoto mírného téměř lineárního poklesu
odporu s teplotou k absolutní nule lze očekávat určitou malou
zbytkovou hodnotu odporu *).
*) Z klasického pohledu by se dala
očekávat i opačná situace: elektrony při zastavení svých
tepelných pohybů by se mohly spojit s ionty krystalové
mřížky, "zamrznout" a přestat se pohybovat - z
vodiče by se stal izolátor, který elektrický proud
nepropouští.
Když Onnes prováděl měření teplotní závislosti odporu
na vzorku vysoce čisté rtuti, s překvapením zjistil náhlý
spád odporu rtuti na nulu (neměřiteně
malou hodnotu) při teplotách kolem 4,2
°K. Supravodivost byla pak zjištěna u olova, cínu a řady
dalších materiálů a slitin. Mikroskopickou teorii nízkoteplotní
supravodivosti vypracovali v r.1957 J.Bardeen, L.Cooper
a J.R.Schriffer (BCS teorie) - podle ní vazba mezi
elektrony a kmity krystalové mřížky (fonony) může
efektivně vést k přitažlivé interakci mezi dvojicemi
elektronů: elektron při svém průchodu krystalovou mřížkou
vytváří kladnou "díru", kterou je přitahován
druhý elektron. Touto dynamickou vazbou se vytvářejí
efektivně vázané Cooperovy páry dvou elektronů,
které vytvářejí bosonový kondenzát s vysokým stupněm
korelovaného uspořádání elektronů. Teplota, při
které látka přechází z normálního do supravodivého stavu,
se nazývá kritická teplota.
Intenzívní výzkum supravodivosti objevil řadu materiálů s
touto vlastností, které lze rozdělit do dvou skupin:
- Supravodiče I.typu jsou některé
kovy, dosahující supravodivosti za nízkých teplot (kritická
teplota nižší než 30°K) a ztrácející supravodivé
vlastnosti v silnějších magnetických polích
(Meissnerův-Ochsenfeldův jev). Tuto supravodivost vysvětluje
BCS teorie.
- Supravodiče II.typu jsou některé
slitiny kovů (především mědi) a nekovových příměsí
(oxidů keramické povahy), které dosahují supravodivosti i
při vyšších kritických teplotách a zachovávají si tuto
vlastnost i v silných magnetických polích. Zvláště
zajímavé materiály tohoto druhu jsou kompozitní sloučeniny
ytria, barya, mědi a kyslíku Y1Ba2Cu3O7, nebo analogicky
lanthanu. Zde nastává supravodivost při kritické teplotě
90-100 °K - vysokoteplotní supravodivost, což
umožňuje použít ke chlazení kapalný dusík. Úplná
mikroskopická teorie vysokoteplotní supravodivosti dosud nebyla
vytvořena, avšak dosavadní výzkumy ukazují na mechanismus
vázání elektronů do Cooperových párů pomocí
elektron-spinových interakcí elektronů s excitacemi spinů
(anti)feromagnetických struktur v krystalové mřížce, která
má "šupinkovou" strukturu.
 |
Vlevo:
Supravodivý elektromagnet je tvořen cívkou, navinutou
ze supravodivého materiálu, umístěnou v kryostatu s
kapalným héliem (zkratující
bifilární vedení slouží k zapínání a vypínání
proudu v silných perzistentních elektromagnetech - viz
"Elektromagnety
v urychlovačích").
Vpravo: Závislost ohmického
odporu supravodivého materiálu Nb-Ti na teplotě (pro 1m drátu o0,3mm). |
Supravodivost již nyní nachází významné
uplatnění v řadě oblastí vědy, techniky, medicíny. Jsou to
především supravodivé elektromagnety: cívka
svinutá do velkého počtu závitů z vhodného supravodivého
materiálu se umístí do Dewarovy nádoby s chladicím médiem
(zatím převážně kapalné hélium), vzbudí se v ní silný
proud (stovky i tisíce ampér) a oba její konce se spojí.
Proud potom protéká neomezenou dobu bez spotřeby
elektrické energie a budí silné magnetické pole -
jednotky až desítky Tesla - viz níže
"Elektromagnety v urychlovačích", pasáž "Supravodivé
elektromagnety".
Podmínkou funkce je samozřejmě trvalé chlazení na teplotu
nižší než kritickou *). Takové supravodivé elektromagnety
se s výhodou používají v řadě oblastí - nukleární
magnetická rezonance,
kruhové urychlovače,
termonukleární tokamaky.
*) Toto trvalé chlazení
supravodivé cívky je potřeba pečlivě hlídat!
Pokud by vlivem odpařování hladina chladicího média poklesla
natolik, že část vinutí by se oteplila nad kritickou teplotu,
supravodivost by náhle zanikla. V tomto místě
vinutí by vznikl ohmický odpor, proud vinutím by rychle klesal
a magnetické pole zanikalo. To by mělo za následek
elektromagnetickou indukci velké elektromotorické síly ve
vinutí. Značná energie uložená v magnetickém poli by se
rychle přeměnila na indukovaný proud
vinutím, které by se ohmickým odporem silně zahřálo,
zbytek chladicího média by se uvedl do bouřlivého varu a
vinutí by se mohlo spálit!
Teplotní přechod z normálního do
supravodivého stavu v okolí kritické teploty Tc je velmi prudký - na křivce
závislosti odporu na teplotě je v tomto místě téměř kolmá
přechodová hrana supravodivosti. Tohoto jevu
se využívá ve velmi citlivých bolometrech pracujících na
hraně supravodivosti TES (Transition
Edge Sensor) - §2.5, pasáž "Mikrokalorimetrické
detektory".
Pokud by se podařilo uskutečnit opravdu vysokoteplotní
supravodivost - vyvinout materiály, které by byly
supravodivé i za pokojové teploty, vedlo by to patrně k revoluci
v elektronice slabo- i silnoproudé. Supravodivými
dráty by bylo možné vést elektrickou energii beze ztrát, bez
nutnosti transformace na vysoké napětí. Do supravodivých
elektromagnetů by bylo možno ukládat-akumulovat elektrickou
energii. V průmyslových aplikacích se pracuje na supravodivé
levitaci, při níž interakce indukovaných vířivých
proudů vede ke vzniku síly, díky níž se magnet může
vznášet nad supravodičem, nebo "viset" v
magnetickém poli. Uvažuje se především o magnetickém
závěsu místo ložisek a o využití v magneticky
levitujících rychlovlacích.
Supratekutost
Podobně atomy, složené z fermionů, se mohou efektivně
chovat jako bosony, pokud jejich celkový spin je celočíselný
(resp. nulový), popř. když dochází k singletnímu či
tripletnímu spárování atomů s poločíselným spinem na
výsledný spin celočíselný (0 nebo 1). I zde pak při
nízkých teplotách může vzniknout bosonový kondenzát,
jehož částice (či kvazičástice) se mohou v prostředí
pohybovat zcela volně bez třecího odporu. Na tomto principu je
založena supratekutost některých
zkapalněných plynů (především hélia) za nízkých teplot.
Za zajímavost stojí, že hélium nemá pevnou fázi,
zůstává kapalné až prakticky do absolutní nuly. Pod
teplotou 2,17°K se stává supratekutým - teče bez
vnitřního a povrchového tření a má velmi vysokou tepelnou
vodivost.
V souvislosti s určitými
"podivnými" nesymetriemi při produkci a rozpadu
některých částic (viz níže) se rozlišuje zvláštní
skupina:
- Podivné částice (Strange particles) - sem náleží mesony K a hyperony.
V rámci kvarkového modelu je nositelem podivnosti kvark
"s" (strange). Vlastnosti těchto částic
budou rozebírány v příslušných pasážích níže.
Antičástice,
antihmota, "antisvěty"
Ve světě elementárních částic obecně ke každé částici
existuje její "opačný" či "sdružený"
partner - antičástice, která má určité
fyzikální charakteristiky shodné s danou elementární
částicí, ale některé jiné fyzikální charakteristiky mají
opačné znaménko či směr. Antičástice má s částicí stejnou
hmotnost, spinové číslo, dobu života a izospin,
avšak její náboj a magnetický moment jsou opačné
(stejné co do velikosti, ale opačného znaménka); opačné
znaménko se připisuje i leptonovmu číslu, baryonovému
číslu a projekci izospinu. Jedná-li se o neutrální částice
bez elektromagnetických vlastností, mohou být sdruženy buď
samy k sobě (foton, po, graviton), takže
vlastně nemají antičástice, nebo mohou mít
částice a antičástice od sebe odlišné
(např. neutron, neutrina). V případě fermionů vznikají
částice a antičástice v párech a rovněž v
párech zanikají.
V naší přírodě (složené z hmoty) se
antihmota, resp. antičástice, vyskytují tam, kde dochází k
interakcím částic při vysokých energiích -
vyšších než dvojnásobek klidové hmotnosti elektronu či
pozitronu 2x511=1,022MeV; tehdy vznikají pozitrony.
Pozitrony jsou emitovány i při radioaktivitě beta+ (viz
§1.2, část "Radioaktivita b+"), kde vznikají při
transmutaci kvarků "u"-->"d" uvnitř
protonů v důsledku slabé iterakce (obr.1.2.5 dole). Těžší antičástice
(antiprotony, antineutrony, hyperony) pak mohou vznikat až při
značně vysokých energiích, 3 GeV a vyšších. To je doména
velkých urychlovačů (v nepatrné intenzitě i kosmického záření).
Poznámka
1 - Antisvět
Na řadě míst našeho pojednání o jaderné a radiační
fyzice používáme termín "antisvět"
- v alegorickém významu.
Antičástice vznikající při interakcích a radioaktivitě v
laboratořích jsou samozřejmě součástí "našeho"
světa. O "antisvětech" se někdy
uvažuje v astronomii jako o těch (hypotetických) útvarech
nebo částech vesmíru, které jsou složeny z antihmoty (srov.
též níže pasáž "Antiatomy"). Složitou otázkou je, proč pozorujeme
antičástic nesrovnatelně méně, než částic, které jsou
pro nás "normální a běžné"? Pokouší se na to
odpovědět kosmologické teorie v koprodukci s částicovou
fyzikou - viz níže odkaz v poznámce k pasáži "Antiatomy,
Antisvěty".
Poznámka 2 - Antičástice => Záporná
energie? Inverze času? - Ne
!
V počátcích vývoje kvantové fyziky se antičástice (jako je
pozitron) považovaly za částice se "zápornou
energií", nebo částice pohybující se "zpět v
čase" (formální transformace
souřadnic v Diracově rovnici to umožňují). Tyto koncepce sehrály svého času důležitou
heuristickou roli v rozvoji částicové fyziky. Nyní jsou tyto
zavádějící představy již opuštěné a částice i
antičástice mají "rovnoprávné" místo ve
standardním modelu, v aplikacích, jakož i v unitarizačních
schématech.
Diracovské
a Majoranovské částice
Podle vztahu ke svým antičásticím se elementární částice
někdy rozdělují na dvě skupiny :
¨ Diracovské
částice
mají odlišné antičástice. Patří sem
především všechny elektricky nabité částice, ale i
některé neutrální částice jako je neutron nebo neutrální
K-mezon.
¨ Majoranovské
částice
mají shodné částice a antičástice. Vedle
fotonu sem patří neutrální p-mezony (pion po); některé hypotézy uvažují i o neutrinech, není to zatím rozhodnuto.
Některé
význačné antičástice mají svůj vlastní název
či označení - antičástice k elektronu e- se nazývá pozitron
e+, nábojově sdružené antičástice se označují opačnými
znaménky nábojů, např. miony m-, m+, analogicky piony p-, p+ a další částice.
Řada antičástic se však označuje prostě předponou "anti"
a vlnovkou "~" nad symbolem částice *)- např. antiproton
p´, antineutron n´.
*) Ve fontech dostupných formátu
"html" však bohužel znaky s vlnovkou nahoře nejsou k
dispozici, takže v našich textech označujeme antičástice čárkou
( ´
) vpravo nahoře.
Anihilace antičástic s
částicemi
Při interakci antičástic se svými odpovídajícími
"protějšky", částicemi, mohou tyto dvojice
navzájem zaniknout *) - anihilovat - za vzniku
jiných (lehčích) částic či antičástic. Často to bývají
fotony (pozitrony anihilují s elektrony za
vzniku dvou fotonů gama vylétajících v protilehlých
směrech, pod úklem 180o, což se s výhodou využívá v
gamagrafickém zobrazení metodou pozitronové emisní
tomografie v nukleární medicíně po aplikaci
pozitronového beta+-radionuklidu, např. 18F - §4.3, část "Pozitronová emisní tomografie PET"). Jsou přitom splněny
zákony zachování energie a kvantových čísel (opačná
kvantová čísla se "vynulují"). Dochází k úplné
přeměně klidové hmotnosti (+kinetické energie) na
energie jiných částic a polí, přičemž původní částice zanikají.
Konkrétní procesy anihilace budou popsány níže pro
jednotlivé druhy částic.
*) Anihilace částic neznamená jejich
zničení, ani přeměnu hmoty v "čistou energii" !
O procesu anihilace antičástic s částicemi se dosud tradují
některé téměř mystické představy. Pocházejí z doby, kdy
se tyto procesy teprve objevovaly a připadaly fyzikům natolik
neobvyklé, že jim přisuzovali zvláštní filosofický
význam. Nyní víme dvě vzájemně související skutečnosti :
× Při anihilaci částic,
navzdory názvu (lat. nihil=nic; anihilace=zničení,
zmizení), nedochází k jejich zničení,
zániku či zmizení z tohoto světa "beze stopy", ale
k jejich přeměně na jiné částice
mikrosvěta, při splnění všech obvyklých zákonů
zachování (energie, hybnosti, náboje a dalších kvantových
charakteristik). Nic se přitom neztratilo ani nezískalo.
× Anihilace není
přeměna hmoty na energii, či látky na "čistou
energii", jak se někdy uvádí. Při anihilaci (jako
ostatně při každém známém přírodním procesu) je splněn
zákon zachování energie - ovšem celkové,
relativisticky chápané energie, včetně klidové energie
částic. Jde tedy jen o přeměnu jedné formy
hmoty na jinou formu.
Ostatně,
přeměna "částic hmoty" na pole (s kvanty nulové
klidové hmotnosti) nastává u obvyklých částic jen při
anihilaci elektronu s pozitronem. Antiprotony či antineutrony
"anihilují" za vzniku jiných masívních částic
(pionů - viz níže), takže o "přeměně hmoty v čistou
energii" nelze vůbec mluvit..!..
Největší
anihilace v historii našeho vesmíru
se odehrála na počátku jeho evoluce před více než 13
milardami let, v době cca 10-4s. po velkém třesku, na přechodu mezi hadronovou a
leptonovou érou, kdy vzájemně zanihilovaly baryony a
antibaryony a vzápětí na konci leptonové éry (cca
10s.), kdy zanihilovaly pozitrony s elektrony.
Výsledkem bylo záření (pozorované
nyní jako reliktní) a zůstal
malý přebytek hmoty (1:109) z baryonové asymetrie. Tyto
grandiózní události jsou podrobněji rozebírány v §5.4
"Standardní kosmologický model. Velký třesk.", pasáž "Baryonová asymetrie vesmíru" knihy "Gravitace, černé díry a fyzika
prostoročasu" (viz též níže pasáž "Proč je náš svět z hmoty a ne z
antihmoty?").
"Antiatomy",
"antisvěty"
Antičástice mají vzhledem k sobě úplně stejné
vlastnosti *) svých interakcí jako částice, takže
kolem antiprotonu může obíhat pozitron a vytvořit tak atom
"antivodíku". Podobně mohou antiprotony a
antineutrony vytvářet atomová "antijádra", kolem
nichž mohou obíhat pozitrony ve slupkách o stejných
energiích a podle stejných výběrových pravidel jak to známe
z naší atomové fyziky. Takovéto "antiatomy"
pak budou mít úplně stejné chemické i
spektroskopické vlastnosti jako atomy naší hmoty -
budou vytvářet prvky či sloučeniny antihmoty
se stejnými vlastnostmi jaké známe u naší hmoty.
*) Je antihmota úplně stejná jako hmota ?
Hmota a antihmota se nám v prakticky všech experimentech jeví
jako stejná - až na opačná znaménka el. nábojů a
některých dalších kvantových čísel má stejné
vlastnosti. Přesto však se antihmota od hmoty jemně
liší v chování - asymetrické produkci a rozpadech
některých "exotických" částic a antičástic (bylo experimentálně zjištěno především u K a B
mesonů). Tato skrytá rozdílnost mezi
hmotou a antihmotou, generovaná v nejranějších fázích
oddělování základních interakcí při vzniku vesmíru, mohla
nakonec spolupůsobit v hadronové éře ke vzniku baryonové
asymetrie ( §5.4 "Standardní
kosmologický model. Velký třesk.",
pasáž "Baryonová asymetrie
vesmíru" knihy
"Gravitace, černé díry a fyzika prostoročasu"). Proto je zde jen hmota a
jsme zde i my..!?..
Vzniká přirozeně otázka,
zda se někde ve vesmíru nachází tato antihmota? Aby mohla
dlouhodobě existovat, musí se antihmota nacházet odděleně
od hmoty, jinak by docházelo k masívní anihilaci. Otázka tedy
zní: jsou někde "antisvěty"?
Pomocí běžných spektrometrických metod to na dálku
nepoznáme - světlo z "antihvězd" či
"antigalaxií" by vzhledem k identickým vlastnostem
"antiatomů" mělo úplně stejná spektra jaká známe
u hvězd a galaxií. Jsou však dvě přesvědčivé indicie,
podle nichž se v nám dostupné části vesmíru žádná volná
antihmota nevyskytuje :
1. V primárním kosmickém záření
ze vzdáleného vesmíru se vyskytují pouze protony, nikoli
antiprotony (nepatrný podíl cca
10-4
antiprotonů pozorovaný v kosmickém záření jsou antiprotony sekundární;
vznikají při interakcích protonů vysokých energií s
mezihvězdným prostředím - s částicemi i fotony reliktního
záření; podobně pozitrony). V
kosmickém záření nebyla dosud zaznamenána žádná
složitější "antijádra" (složená z
antiprotonů a antineutronů) hélia či těžších prvků *).
Taková "antijádra" by přitom musela být ve velkém
množství emitována do vesmíru při každém výbuchu
případné "antihvězdy" jako supernovy, v
(anti)hvězdném větru, jakož i ve výtryscích z akrečních
disků antihmoty kolem černých děr. Kdyby kosmické záření
obsahovalo větší množství antiprotonů či složitějších
"antijader", mohli bychom je považovat za jakési
"vyslance" z antihvězd a antigalaxií. Ve skutečnosti
jich však pozorujeme jen velmi málo, právě tolik, kolik jich
průběžně vzniká interakcemi běžných vysokoenergetických
protonů kosmického záření s obyčejnou hmotou.
*) Případná detekce složitějších
"antijader" by byla pádným důkazem existence
velkého množství antihmoty - "antihvězd",
"antigalaxií" - někde ve vesmíru. Taková
složitější "antijádra" totiž nemohou vznikat
sekundárně žádnými vysokoenergetickými interakcemi
částic, ale mohly by mít svůj původ jedině v primárním
vzniku ve velkém množství antihmoty - v termonukleární
syntéze antičástic v "antihvězdách". Jsou
proto plánovány družicové "detektory antihmoty",
jako je AMS (Alpha Magnetic Spectrometer), které by byly schopny
zaznamenat "antihélium" (anti-alfa částice).
2. Pokud by některé hvězdy, galaxie nebo
oblaka plynů byly z antihmoty, na rozhraní hmoty a antihmoty by
docházelo k intenzívní anihilaci za vzniku
tvrdého záření g o energii 511keV. Žádná měření zatím takové
anihilační záření nezaznamenala.
Ve vesmíru se tedy buď žádné znatelné
množství antihmoty nevyskytuje, nebo se "antisvěty"
nacházejí v tak velkých vzdálenostech od nás => záření
je nesmírně slabé, takže je nejsme schopni našimi
přístroji registrovat.
Proč
je náš svět z hmoty a ne z antihmoty ? (nebo proč
není jenom ze záření?)
Zajímavá je otázka, proč dnes pozorujeme ve
vesmíru téměř výhradně "obyčejnou" hmotu a
téměř žádnou antihmotu? Či dokonce proč
je zde vůbec nějaká hmota a ne jenom záření?
Pro odpověď na tyto otázky bychom se museli vydat až k
samotným počátkům vesmíru. Podle současných
fyzikálníchch představ by na počátku vesmíru mělo
původně vzniknout stejné množství hmoty a antihmoty.
Veškeré experimenty jaderné fyziky totiž ukazují, že při
všech částicových interakcích dochází vždy ke sdružené
produkci částic a antičástic, v poměru 1:1.
Vlivem určitých specifických jevů - narušení
symetrie interakcí v počátečních okamžicích evoluce
vesmíru - množství hmoty nepatrně převážilo
nad antihmotou (cca 1:109),
došlo k mírné baryonové asymetrii vesmíru.
Víceméně náhodná kvantová fluktuace způsobila vítězství
hmoty nad antihmotou v našem velmi raném vesmíru. V
hypotetických jiných vesmírech tomu mohlo být opačně,
kvantová fluktuace ve vhodný okamžik nastala na druhou stranu
a takový vesmír by byl z antihmoty...

Tento nepatrný přebytek 1:109 způsobil, že pro
další vývoj vesmíru tato hmota zůstala *), zatímco všechna
ostatní hmota a antihmota vzájemně zanihilovala
již během hadronové a leptonové éry a nakonec se přeměnila
na záření (nyní pozorované jako reliktní záření).
Kdyby nedošlo k baryonové asymetrii v počátcích vesmíru,
veškeré částice by vzájemně zanihilovaly a vesmír by
sestával pouze ze záření (v takovém fádním vesmíru by nemohly vzniknout
hvězdy, planety, život...). Otázky
antihmoty a baryonové symetrie či asymetrie vesmíru jsou z
astrofyzikálního hlediska diskutovány v §5.4 "Standardní
kosmologický model. Velký třesk.",
pasáž "Baryonová
asymetrie vesmíru"
a §5.5 "Mikrofyzika a kosmologie. Inflační vesmír." knihy
"Gravitace, černé díry a fyzika prostoročasu".
*) Terminologie hmota-antihmota
je relativní. To, co zůstalo a z čeho je náš okolní svět,
jsme prostě nazvali hmota -
"obyčejná" hmota, zvaná někdy též koino-hmota
(řec. koinos = obvyklý, obyčejný. )A hypotetická
látka složená z opačných částic je pro nás antihmotou.
V myšleném vesmíru, kde by baryonová asymetrie převládla na
opačnou stranu, by tamní obyvatelé měli terminologii
opačnou, pro ně by běžná hmota bylo to, co my nazýváme
antihmotou...
Kombinované soustavy
částice-antičástice
Výsledkem interakcí antičástic s částicemi jsou procesy
anihilace, avšak tato anihilace nemusí nastat
okamžitě. Pokud mají částice a antičástice
opačná znaménka elektrického náboje (+ a -), mohou po
dostatečném zpomalení těsně před anihilací vytvořit vázanou
soustavu částice-antičástice. Nejznámější
vázanou soustavou tohoto druhu je pozitronium -
vázaná soustava elektronu a pozitronu, které podle modelové
představy obíhají kolem společného těžiště za
vyrovnání odstředivé síly oběhu a elektrické přitažlivé
síly (viz níže "Interakce nejdůležitějších
elementárních částic", pasáž "Pozitronium").
Podobně antiproton může být zachycen na oběžnou dráhu
kolem atomového jádra a nahratit tak elektron - vzniká antiprotonový
atom. Nejjednodušší antiprotonový atom je protonium,
které vzniká jako vázaná soustava protonu a antiprotonu
obíhajících kolem společného těžiště. Pozitronium i
protonium je nestabilní, během krátké doby (závisející
m.j. i na spinových orientacích) nakonec dojde k anihilaci
antičástice s částicí. Pozitronium a antiprotonium tedy nemají
obecnou důležitost (kromě speciálních případů a
aplikací).
Důležité jsou však vázané kombinace pozitronů
a antiprotonů (+ příp. i antineutronů), vytvářející antiatomy.
Jedině to může být reálná antihmota... Z hlediska
jaderné fyziky jsou pak důležité vlastnosti těchto
antiatomů. Především spektrometrické vlastnosti
(stručně zmíněné v pasáži "Umělá výroba antihmoty.
Antivodík.") a též gravitační
vlastnosti :
Antihmota:
gravituje nebo antigravituje ?
Nejobtížnější je měření gravitačních
vlastností antihmoty. Víme sice, že částice a antičástice
mají stejnou (klidovou) hmotnost, zbývá však ověřit, zda
antivodík "padá" v gravitaci úplně stejně jako
vodík? Pro běžnou hmotu složenou z atomů
tvořených elektrony, protony a neutrony, platí Newtonův
zákon všeobecné gravitace ("Newtonův
gravitační zákon"). V obecné teorii relativity - fyzice gravitace a
zakřiveného prostororočasu - platí velmi přesně ověřený princip
ekvivalence ("Univerzálnost
- základní vlastnost a klíč k pochopení podstaty gravitace") jehož důsledkem je, že působení
gravitace nezáleží na složení a struktuře hmoty.
Gravitační interakce mezi hmotou a antihmotou by měla být identická.
Objekt z antihmoty tak bude v gravitačným poli Země padat se
stejným zrychlením jako těleso z hmoty (zde
na povrchu Země bude jeho pád probíhat se známou hodnotou
gravitačního zrychlení 9,81 m/s2).
Logicky z toho usuzujeme, že to platí i pro
jednotlivé elementární částice - běžné (elektrony,
protony, neutrony), a pravděpodobně i pro exotické (neutrina,
mesony, hyperony, ...). Přímé experimentální ověření
gravitačních vlastností u jednotlivých izolovaných částic
je však prakticky nemožné, neboť tyto částice se pohybují
vysokými rychlostmi a vykazují elektromagnetické (a příp. silné) interakce s
okolím, podstatně silnější než gravitační - to naprosto
"přebije" nepatrnou gravitační sílu. Obecně však
lze říci, že běžná (koino)hmota gravituje,
vykazuje univerzální přitažlivé síly.
Jak je tomu ale u antičástic
(pozitrony, antiprotony, antineutrony), z nich složených "antiatomů"
a obecně u antihmoty? Z experimentů na
urychlovačích víme, že částice a antičástice mají stejnou
setrvačnou hmotnost. Bude však antihmota gravitovat
nebo antigravitovat? - působí mezi hmotou a
antihmotou přitažlivá nebo odpudivá gravitace? Některé nepodložené
hypotézy, jakož i názory laiků vsugerované názvem
"anti-", však zastávají názor o antigravitaci
antihmoty.
Z rozboru pravděpodobností krátkodobé
existence virtuálních elektron-pozitronových,
proton-antiprotonových a jiných dvojic částic
("polarizace vakua") plyne, že výsledky
Eötvösových, Dickeho a Braginského měření potvrzují
platnost principu ekvivalence pro běžné antičástice (jako je
pozitron a antiproton) s přesností ~ 10-5 až 10-6. Rozhodně tedy u antihmoty nelze očekávat "antigravitaci"
- žádné "padání nahoru"!
Antihmota bude normálně gravitovat (jen síla této gravitační interakce by teoreticky
mohla být zlehka odlišná - stručná diskuse je v §2.2,
část "Princip
ekvivalence" knihy
"Gravitace, černé díry a fyzika prostoročasu").
Jakým způsobem "padá" antiproton v
gravitačním poli, ve srovnání s běžným protonem? Měřit
gravitační účinky přímo na základních částicích
antihmoty - pozitronech a antiprotonech - není možné, neboť
jsou nabité a elektrické působení s okolím mnohonásobně
převyšuje hledanou sílu gravitační (je
to stejné jak bylo výše diskutováno u částic běžné
hmoty). Pro tento účel je potřeba
připravit antihmotu elektricky neutrální,
složenou z antiatomů. Optimální by bylo
vytvořit makroskopická tělesa z antihmoty- antiatomů. Ty
bychom potom pouštěli směrem dolů v zemském gravitačním
poli - tak jak to historicky dělal G.Galilei (snad ze šikmé nakloněná věže v Pize..?..). Tato tělesa by byla na začátku v klidu a jejich
okamžitá rychlost by byla dána pouze gravitačním
zrychlením. Případně bychom je pouštěli vodorovným vrhem s
definovanou počáteční rychlostí a sledovali jejich pohyb po
parabole.
Nic takového však s jednotlivými atomy
neumíme. Jsme schopni jen vytvořit plyn složený z antiatomů
vodíku, v němž se jednotlivé atomy pohybují chaoticky
různými rychlostmi v různých směrech, s rozložením
rychlostí podle "teploty", kterou bychom se snažili
minimalizovat. Tyto atomy pak na počátku nejsou v klidu, ale
mají různě velké počáteční rychlosti v různých
směrech. V gravitačním poli pak padají po parabolických
drahách, jejichž okamžité rychlosti v kolmém i podélném
směru by se skládaly s počátečními rychlostmi
antivodíkových atomů.
Jsou
však připravovány experimenty, které by byly schopny
eliminovat či korigovat tyto vlivy a přesně tak změřit
gravitační účinky přímo na atomech antivodíku -
je diskutováno v pasáži "Umělá
výroba antihmoty" -
"Experimentální měření atomů antivodíku - AEGIS" :
Umělá výroba
antihmoty. Antivodík.
Když se antihmota v dostupné části vesmíru nevyskytuje (nenáme žádné "doly" na antihmotu), bylo by možné si ji "vyrobit" uměle? V
urychlovačích produkujeme velké množství pozitronů a
obtížněji i antiprotonů a antineutronů (jsou
to však jen submikroskopická množství!),
takže by se zdálo, že nic nestojí v cestě umělému
"poskládání" těchto částic do
"antiatomů". Ve skutečnosti však je umělé
vytváření antihmoty neobyčejně obtížné!
Částice produkované v urychlovačích se totiž
pohybují vysokými rychlostmi blízkými
rychlosti světla - mají vysoké kinetické energie, o mnoho
řádů přesahující vazbové energie atomů. Pokud bychom
takto rychlé antiprotony a pozitrony pustili proti sobě,
proletěly by kolem sebe "bez povšimnutí" - téměř
bez interakce - a žádné antivodíkové atomy by nevznikly.
Aby se antiproton a pozitron mohly elektricky spojit do atomu
antivodíku, musejí být milionkrát zpomaleny!
Aby tedy mohl vzniknout atom antivodíku, musejí
být pozitrony a antiprotony z původních energií řádově MeV
zpomaleny na dostatečně malou vzájemnou
rychlost, aby antiproton mohl pozitron zachytit a udržet. To
není nijak snadné, takže se teprve nedávno (r.1995) na
urychlovači LEAR v laboratoři CERN podařilo vytvořit prvních
9 atomů antivodíku.
Antiprotony se zde nechaly
prolétat xenonem, čímž se brzdily a při interakci zároveň
vznikaly m.j. i páry elektronů a pozitronů. V uvedených
několika případech pak byl pozitron následně zachycen
prolétajícím antiprotonem za vzniku atomu antivodíku. Během
řádově 10-11 sec. pak při svém letu prostředím anihiloval s
normální hmotou a záblesk anihilačního záření prokázal
jeho kratičkou existenci. Při tak krátké době existence
nelze měřit žádné vlastnosti antiatomů.
Pro účinnější "výrobu antihmoty",
resp. atomů antivodíku, byl v CERN zkonstruován
elektromagnetický antiprotonový zpomalovač
- decelerátor. V elektromagnetickém poli (vytvářeném vysokofrekvenčním rezonátorem) se antiprotony ve svazku z urychlovače zpomalí z
původní energie cca 100MeV na jednotky MeV. To je stále
ještě příliš vysoká energie k účinné výrobě atomů
antivodíku i k dalším experimentům. Další zpomalení
antiprotonů se proto provádí průchodem přes tenké
hliníkové degradační fólie na cca 5 keV (výtěžnost je zde velmi nízká, jen cca 0,1%). Ve stadiu přípravy je však poslední účinný
decelerační stupeň ELENA (Extra Low
ENergy Antiproton ring), tvořený 30m hexagonálním
prstencem s radiofrekvenčními dutinami a elektronovým
chlazením. Zde dochází k dalšímu zpomalení antiprotonů
přijímaných z antioprotonového decelerátoru z 5MeV na
100keV. Stačí pak již jen menší zpomalení degradačními
fóliemi na cca 5keV, s podstatně menšími ztrátami než s
použitím pouze degradačních fólií; dosáhne se
dvojnásobného počtu antiprotonů. To vede k podstatně
efektivnější produkci většího počtu antivodíkových
atomů.
Zpomalené částice se pak vedou do chlazené
magnetické pasti, kde se oblak antiprotonů zachytí v
magnetickém poli a dále se v něm "ochlazuje" (zmenšuje se kinetická energie jejich pohybu). Pozitrony se jednoduše získávají
z beta+-radioaktivity, nejčastěji radioisotopu 22Na, nebo také reakcemi
pomocí lineárního urychlovače. Po základním zpomalení v
tenké fólii se vedou do magnetické pasti kde se dále
zpomalují ("ochlazují" podobně
jako antiprotony) a pak se pomalé
antiprotony a pozitrony současně vtřikují do
reakční komůrky s magnetickou pastí, kde již dochází k záchytu
pozitronů antiprotony za vzniku atomů antivodíku.
Při zpomalení a zachycení v magnetické pasti mají obě
částice dostatek času na své vzájemné navázání do atomů
antivodíku. Touto metodou se v první fázi podařilo detekovat
80 antiatomů vodíku, avšak po dalším zdokonalení -
zařízení ALPHA (Antihydrogen
Laser PHysics Apparatus) - se daří
produkovat desítky tisíc atomů antivodíku pro experimenty,
např. pro porovnání elektromagnetických spekter atomů
antivodíku a vodíku.
Pro produkci atomů
antivodíku je výhodné použít pozitrony ve formě pozitronia
- elektricky vázaného stavu elektronu a pozitronu (viz "Elektrony a
pozitrony"). Pozitrony z beta+-radioaktivity se nechají procházet porézním
terčíkem z křemičitého materiálu, v němž zachycují
elektrony a vzniká pozitronium e--e+.
Pomocí laserových paprsků se pak pozitronium excituje
do vyššího kvantového stavu (až n=25) a nasměruje se k
antiprotonům. Vysoce excitované pozitronium může poměrně
snadno předávat pozitron antiprotonu -
dochází k "nábojové výměně"
při níž antiproton zaujjímá v pozitroniu pozici elektronu:
(e--e+)* + p- --> H~* + e-, za vzniku excitovaného atomu antivodíku
H~*. Tento
proces má poměrně vysoký účinný průřez (závisí na 4.mocnině kvantového čísla n pozitronia). Další výhodou je nižší kinetická energie
vzniklého atomu antivodíku. Atomy antivodíku zde vznikají ve
vysoce excitovaném (Rydbergově) stavu, takže jsou citlivé na
gradienty elektrických a magnetických polí, což umožňuje s
nimi v experimentech manipulovat.
Kromě produkce vlastních
antiatomů je dalším velmi obtížným problémem jejich izolace
od okolní hmoty, aby se zabránilo okamžité anihilaci
s materiály reakční nádoby. K udržení nabitých
částic se běžně používá magnetické pole (především v tokamacích - viz §1.3, část
"Tokamak", či ve shora zmíněných magnetických
pastích). Atomy antivodíku jsou však
navenek elektricky neutrální. Mají ale magnetický
moment, takže reagují na magnetické pole (i když
slabě). Pomocí silných supravodivých elektromagnetů lze
vytvořit "magnetickou past", která
je schopna po určitou dobu antivodíkové atomy udržet v
magnetickém poli uvnitř reakční nádoby. Magnetické pole je
zde speciálně tvarované tak, že je nejsilnější na
okrajích a směrem ke středu se snižuje. Atomy jsou vtahovány
do "magnetické jámy" uprostřed, kde mohou zůstat
určitou dobu uvězněné. Pokud je tato doba dostatečně
dlouhá, antiatomy mají čas přejít do základního stavu, v
němž lze měřit jejich fyzikální vlastnosti. Otevírá se
tím cesta k přesnému testování předpokládané symetrie
hmoty a antihmoty (některé
nepatrné odlišnosti jsou diskutovány níže v pasáži "C P T symetrie interakcí"). Odhalení příp.
drobných rozdílů by mohlo pomoci objasnit, proč je náš
vesmír tvořen jen hmotou (srov. "Baryonová asymetrie vesmíru").
Experimentální měření atomů
antivodíku - AEGIS a GBAR
Pro přesné měření fyzikálních vlastností antivodíkových
atomů se v CERN buduje projekt AEGIS (Antihydrogen
Experiment: Gravity, Interferometry, Spectroscopy). Skládá
se z několika základních navazujících kroků :
1. Produkce
antiprotonů p- v protonovém synchrotronu. Svazek protonů p+
urychlených na energii 25GeV dopadá na iridiový terčík, kde
díky vysoké enegii vznikají spršky mnoha sekundárních
částic, mezi nimi i páry proton-antiproton. Antiprotony p- jsou
odseparovány pomocí magnetického pole. Mají vysoké energie,
rychlosti blízké c, široké energetické spektrum. Pro
vytváření antiatomů nejsou přímo použitelné, musejí se
zpomalit :
2. Antiprotonový
decelerátor, který na kruhové dráze v magnetickém
poli (vytvářeném elektromagnety) aplikuje silné elektrické
radiofrekvenční pole opačné polarity, funguje
"opačně" jako synchrotron. Má oválný tvar (průměru 60 m, na schématickém obrázku níže je
pro jednoduchost zakreslen jako kruhový),
po jeho obvodu jsou čtyři krátké rovné úseky s radiofrekvenčními
elektrodami, kde probíhá vlastní brzdění
antiprotonů. V AEGIS dochází ke zpomalení na 5,3 MeV,
což odpovídá cca 10% rychloti světla. Další zpomalení
antiprotonů se provádí průchodem přes tenké hliníkové
degradační fólie na cca 5 keV (výtěžnost
je zde velmi nízká, jen cca 0,1%; na schématu není
zakresleno).
3. Zachycení a
akumulace antiprotonů v elektromagnetické pasti (tzv.
Penning-Malmbergova past), komoře s magnetickým polem a sadou
kruhových elektrod. Provádí se zde též další zpomalování
antiprotonů kolizemi v oblaku pomalých elektronů.
4. Produkce pozitronů
e+ pomocí radioaktivity beta+ radionuklidu 22Na.
5. Vytváření
pozitronia Ps průchodem pozitronů přes
nanoporézní materiál. Využívá se otho-pozitronium, které
má delší životnost 142 ns (oproti
para-pozitroniu které má dobu života 1000-krát kratší). Excitace pozitronia do
Rydbergovského stavu Ps* s n=~25 pomocí ozařování UV a IR
lasery.
6. Vytváření atomů
antivodíku H*~ pomocí reakce nábojové
výměny antiprotonu p- s exitovaným pozitroniem Ps*. Takto vytvořené
pomalé antivodíkové atomy (s rychlostí
~ 25-80 m/s, odpovídá teplotě řádově 100 mK) se pak již vedou k experimentům pro měření jejich
vlastností.
7. Pro AEGIS vytvoření
pulsního horizontálního svazku atomů antivodíku
H*~ o konstantní rychlosti kolem 400
m/s. Využívá se zde účinek nehomogenního elektrického pole
na vysoce Rydbergovsky excitované atomy H*~ (umožňuje to manipulovat s nimi s využitím Starkova
efektu). Je to důležité pro další
analýzu parabolického pohybu atomů H~ v
gravitačním poli.

Rámcové zjednodušené schéma experimentálního studiia
fyzikálních vlastností atomů anti-vodíku - AEGIS a GBAR.
Při gravitačním experimentu
v AEGIS se odtud horizontální proud antivodíkových atomů
vede do systému dvou za sebou umístěných separačních
štěrbin (mřížek) *) s periodou mřížky 80mm, které
vytvářejí rovnoběžné svazky antivodíků. Následně se na
konci dráhy délky L tyto antivodíky anihilačně
detekují křemíkovým polohově citlivým detektorem s
prostorovým rozlišením 10mm. Analyzuje se struktura mřížky, která se na
polohově citlivém detektoru zobrazí jako řada maxim a minim v
různých výškách při detekci většího počtu antiprotonů.
Jejich vertikální polohy závisejí na poklesu (deflekci)
antivodíkových atomů v zemském gravitačním poli (cca 20mm). Koreluje se s
časy příletu antivodíkových atomů na detektor (které odpovídají jejich horizontálním rychlostem v). Vyhodnocuje se, nakolik výškový pokles h
antivodíků ve vzdálenosti L odpovídá zákonu
vodorovného vrhu rychlostí v v tíhovém poli Země s
gravitačním zrychlením g~ : h = 1/2.g~.(L/v)2. Jedná se o přímý laboratorní test platnosti
slabého principu ekvivalence v obecné teorii
relativity (viz §1.2, pasáž "Princip ekvivalence" v knize "Gravitace, černé díry ...") který říká, že trajektorie pohybu (zde pádu)
hmotného tělesa závisí pouze na jeho počáteční poloze a
rychlosti, nikoli na jeho struktuře a dalších vlastnostech - zda
platí přesně i pro antihmotu..?... Přesnost
stanovení g~ v experimentu AEGIS se očekává cca Dg~/g~ ~1%.
*) Toto uspořádání dvou nebo
tří mřížek ekvidistantně postavených za
sebou se v optice nazývá moiré-deflektometr
(franc. moiré = tkanina, jemná struktura, mřížka).
Poslední třetí mřížka je zde nahrazena pozičně citlivým
detektorem. Nevyužívá se zde v interferometrickém režimu
jako v optice, ale slouží pro přesné vymezení
horizontálních rovnoběžných trajektorií antivodíkových
atomů. Anihilující antivodíkové atomy vytvoří na detektoru
pásy - obrazce štěrbin mřížek, jejichž analýzou je možno
určit, o kolik klesly H~ při pohybu po parabole od
druhé mřížky do dopadu na detektor.
Vedle AEGIS se gravitačním měřením
antivodíku zabývá alternativní experiment GBAR
(Gravitational Behaviour of Anti
hydrogen at Rest), provozovaný u
téhož antiprotonového decelerátoru v CERN. K měření
gravitačního zrychlení antivodíkových atomů nepoužívá
horizontální pohyb s vyhodnocením pomocí
moiré-deflektometru, ale svislý volný pád
atomů antivodíku v měřicí komoře, s vyhodnocením
přesného času anihilace při dopadu antiatomů zhora na dno
komory. Trajektorie - výška h volně padajících atomů
H~ -
souvisí s časem vztahem h = 1/2.g~.(t2-t1)2,
kde t1 je
čas vstupu atomu do horního detektoru komory a t2 je čas dopadu a
anihilace atomu antivodíku na dně komory. V experimentu GBAR se
budou používat další stupně zpomalování antiproronů (ELENA)
a "chlazení" svazku p-, nakonec až na
energii 1 keV. Atomy antivodíku H~ se další reakcí
s pozitroniem připravují ve formě kladných antivodíkových
iontů H~+ - jeden antiproton a dva pozitrony (to vyžaduje vyšší tok pozitronů, které se zde
generují pomocí 9MeV lineárního urychlovače). Tyto H~+ se pak chladí pomocí Be+ iontů na teplotu
kolem 10mK. Pomocí laserováho pulsu se pak těsně před
měřením z H~+ odstraní nejvzdálenější pozitron a vytvoří se
neutrální atom antivodíku H~, jehož doba volného
pádu se měří ve svislé komoře s detektory. Díky měření
pádu velmi zpomalených antivodíkových atomů (s téměř
nulovou počáteční rychlostí, ~0,5m/s) lze očekávat
zlepšenou přesnost stanovení g~ cca Dg~/g~ ~10-3.
Při atomové
spektrometrii antivodíku se pomalý svazek antivodíků
vede do další magnetické pasti, kde se provádí jejich excitace
a měří se záření vyzařované nebo pohlcované při
přeskocích mezi jednotlivými energetickými hladinami.
Energetické hladiny v atomu jsou závislé na setrvačné
hmotnosti a náboji elektronu v atomu vodíku, či
pozitronu v antivodíku. Srovnáním energie elektronových
přechodů mezi vzbuzenou a základní hladinou u vodíku a
antivodíku můžeme ověřovat, zda jsou setrvačné hmotnosti a
náboje částic a antičástit přesně shodné, či je zde
nepatrný rozdíl. Pokud se setrvačná hmotnost částic a
antičástic liší, mohl by se příp. nepatrný rozdíl touto
spektrometrií změřit.
Výroba většího množství a těžší antihmoty ?
Přes všechny dílčí úspěchy ve shora zmíněných
náročných experimentech je bohužel nutno přiznat, že na
vytvoření většího množství antihmoty, ani
složitějších antiatomů než vodíku *),
zatím není naděje v blízké budoucnosti...
*) Na cílenou "výrobu" těžších
antijader opravdu není v dohledné době naděje. V nepatrném
počtu (s mizivou pravděpodobností) však mohou vznikat náhodně
při vysokoenergeticklých interakcích . Při srážkách
těžkých jader vzniká větší počet antiprotonů a
antineutronů. Pokud několik současně vzniklých antiprotonů
a antineutronů shodou okolností letí společným směrem
a s přibližně stejnou rychlostí, mohou se jadernými
silami "svázat" do těžšího antijádra -
anti-deuteria, anti-hélia. Jelikož tento proces má velmi malou
pravděpodobnost, je třeba uskutečnit mnoho miliard-trilionů
jaderých srážek, aby nějaké takové těžší antijádro
náhodně vzniklo. V r.2011 se takovým způsobem na urychlovači
těžkých iontů RHIC v Brookhavenu v experimentu STAR podařilo
identifikovat 18 vzniklých jader anti-helia-4 (během několika měsíců srážek), další úspěšné experimenty tohoto druhu
probíhají v CERN. Vznik ještě těžších antijader tímto
způsobem, vzhledem k téměř nulové pravděpodobnosti, se asi
nepodaří prokázat....
Antihmota - možný zdroj energie ?
V populárně-naučné a sci-fi literatuře se často uvádí,
že při anihilaci hmoty s antihmotou dochází
ke 100-% přeměně hmoty na energii, v souladu
s Einsteinovým vztahem E = m.c2. Mohla by tedy ve vzdálené budoucnosti být antihmota
nevyčerpatelným zdrojem energie, popř.
sloužit k pohonu mezihvězdných lodí
(fotonové rakety - viz níže) na rychlosti blízké rychlosti
světla? Bohužel to však není pravda, resp.
problém je mnohem složitější, vyskytují se překážky
nejen technického, ale i principiálního
fyzikálního charakteru.
Při anihilaci elektronu s pozitronem se skutečně veškerá
klidová hmotnost obou částic mění na elektromagnetické
záření: e+ + e- ® 2g. Není to však na světlo, ale na tvrdé záření
gama, které by se zrcadlem fotonové rakety neodráželo, ale
pohlcovalo. Při anihilaci protonů a neutronů s antiprotony a
antineutrony však nevzniká elektromagnetické záření (aspoň
ne přímo), nýbrž p-mezony, např. p'+p®2p++2p-+po ; ty se
pak rozpadají na miony a neutrina, např.: p- ® m- + n'm , p+ ® m+ + nm . Následuje rozpad mionů, např. m- ® e- + n'e+
nm , m+ ® e+ + ne+ n'm a
teprve potom by mohla nastávat anihilace elektronů s pozitrony
e+ + e- ® 2g (všechny tyto
interakce jsou podrobněji rozebírány níže). V hypotetickém
"anihilačním reaktoru" budoucnosti
by tedy muselo být dosaženo nejen účinné energetické
využití tvrdého záření g, ale i uzavření protonového, pionového, mionového
a elektronového (+ antičásticového) vysokoenergetického
"plasmatu" tak, aby sekundární částice mohly spolu
účinně anihilovat. Zatím není znám
žádný fyzikální mechanismus, který by to umožňoval. A už
vůbec není možné využít energii odnášenou neutriny....
Energetickému využití anihilace hmoty s
antihmotou brání i technické obtíže. Kdybychom např.
chtěli spojit dvě makroskopická tělesa, jedno z hmoty a
druhé z antihmoty, s cílem úplné anihilace, nebylo by to v
praxi příliš úspěšné vzhledem ke vzniku tzv. Leidenfrostovy
izolující bariéry *). Při dotyku povrchů obou těles
vznikne mohutný tok energie (záření a částic), který
ostatní hmotu těles od sebe odpudí, oddálí a izoluje tak,
že k účinné objemové anihilaci nedojde; reakce je spíše
plošná, než masívní objemová. Určitou možností by snad
bylo srazit obě tělesa vysokou rychlostí, aby kinetická
energie překonala tlak vzniklého záření. Nebo ještě lépe
uskutečňovat anihilaci postupně v proudu částic hmoty a
antihmoty (výše zmíněný "anihilační reaktor").
Nic z toho není v dohledné budoucnosti realizovatelné...
*) Podobný jev můžeme v běžném
životě pozorovat, když kápneme vodu na rozžhavenou plotnu
kamen. Kapičky vody se většinou nevypaří okamžitě
(expozívně), ale chvíli "poskakují" na rozpálené
plotně: při styku kapičky s plotnou vznikne pára, která na
chvíli vytváří plynný "polštář" izolující
kapičku od plotny.
Fotonová raketa ?
Kolimovaný zdroj elektromagnetického záření vykazuje efekt
"raketového tahu" (je to obrácený efekt ke světelnému tlaku, který
poprve pozoroval již Lebeděv). Je to
důsledkem zákona zachování hybnosti, neboli zákona akce a
reakce: elektromagnetické záření má tok hybnosti,
který je v klasické elektrodynamice popsán Poyntingovým
vektorem a z kvantového hlediska je dán hybností fotonů
(každý foton vlnění o frekvenci f má energii E=h.f a
hybnost p=h.f/c). Při vyzáření se tato hybnost předává
zdroji v opačném směru, přičemž předaná hybnost za
jednotku času udává působící sílu "tahu". Aby
tento "raketový efekt" byl znatelný, je třeba
neobyčejně vysoký tok záření, který není
dosažitelný stávajícími technickými prostředky. V projektu
fotonové rakety se počítá s anihilační
reakcí, popř. s termonukleární reakcí,
která by probíhala v ohnisku velkého polokulového či
parabolického zrcadla, které by odráželo
vznikající fotony a kolimovalo je směrem
"dozadu". Jak bylo již výše nastíněno, záření
vznikající při anihilační nebo termonukleární reakci není
světelné, ale vysokoenergetické g a korpuskulární
záření, pro které neplatí zákon odrazu; zrcadlo z
žádného známého materiálu by toto záření neodráželo,
ale převážně absorbovalo, což by vedlo k jeho tepelnému
zničení.
Pozn.: Místo
"fotonová raketa" je možno použít názvu "kvantová
raketa", neboť požadovaný efekt vzniká nejen
emisí fotonů, ale i jiných kvant-částic nesoucích hybnost.
Pro fotony je však nejpříznivější poměr [předaná hybnost®tah]/[potřebná
emitovaná hmotnost a energie].
Antihmota a antisvěty ve sci-fi
Tajemný nádech pojmu "antihmota" vedl ve
vědecko-fantastické literatuře ke vzniku představy "antisvětů", ve kterých je všechno
"opačně" a v nichž příp. žijí i naši
"dvojníci" - "antilidé". Tato sci-fi představa
nemá žádné astronomické opodstatnění (jak
bylo výše diskutováno v pasáži "Antiatomy,
antisvěty"), je to spíše hříčka pro naši
představivost ...
Uvažujme tedy hypotetickou
situaci, že někde ve zdáleném vesmíru se skutečně
nachází rozsáhlá oblast antihmoty, kde vzniklly (anti)galaxie
a v nich (anti)hvězdy včetně (anti)Slunce s planetární
soustavou, kolem něhož obíhá (anti)Země na které se vyvinul
úplně stejný život jako tady, včetně anti-lidí
:
 |
Představme si např. v
myšleném sci-fi experimentu, že by si "hmoťanka" zde ze Země pomocí
komunikace elektromagnetickým signálem domluvila s
"antihmoťanem" někde ze
vzdálené galaxie schůzku - "rande"- v
určitém místě ve vesmíru na poloviční cestě,
aniž by věděli že jsou vzájemně z antihmoty.
Zaparkovali by v raketách poblíž sebe, vystoupili do
volného prostoru a vydali se k sobě pozdravit se -
"Ahoj!"; zatím by se nic zvláštního
nedělo. Avšak v okamžiku, kdy by si podali ruce, by
došlo k masívní anihilaci
hmoty a antihmoty *) a oba partneři by byli
zničeni v mohutném atomově-částicovém výbuchu.
*) Vzhledem ke zniku výše
zmíněné Leidenfrostovy izolující bariéry nedojde
k celkové anihilaci obou těl, ale jen
povrchových částí dlaní rukou. I to by však
stačilo k záhubě a destrukci obou
partnerů!
Kdyby byli prozíraví, mohli by již na dálku
otestovat, zda jsou z hmoty stejné povahy. Nejsnadněji
tak, že by proti sobě vyslali slabý svazek elektronů
a měřili, zda po jejich dopadu nevzniká anihilační
gama záření 511keV. Pokud ano, nesměli by se k sobě
přiblížit - rychle by od sebe museli utéct, aby
nezahynuli..!.. |
Nezabýváme se zde představami antihmoty a
antisvětů založených na omylech a nedorozuměních,
kdy se předponě "anti"
mylně připisují jiné významy, např. filosofické,
obrácený tok času a pod. ..!..
Interakce
elementárních částic - obecné vlastnosti
Vzájemná působení - interakce
- různých objektů jsou základem veškerého dění v
přírodě. Při interakcích dochází k přenosu energie,
hybnosti, momentu hybnosti a nábojů mezi tělesy. Fyzika
dospěla k poznání, že podstatou veškerých vzájemných
působení a sil v přírodě jsou interakce mezi
elementárními částicemi hmoty. Vzájemná působení
částic popisujeme v zásadě třemi způsoby :
-> Mechanické
silové působení
Tělesa a částice při vzájemném přiblížení a kontaktu na
sebe prostě "působí silou" (o
jejíž původ a mikroskopickou podstatu se zde nezajímáme) a my vyšetřujeme "mechanické" důsledky
tohoto silového působení (v zásadě
podle 3 Newtonových zákonů mechaniky). S
tímto bezprostředním mechanickým silovým působením máme
největší zkušenost z každodenního života. Ve fyzice se tak
postupuje v klasické mechanice.
-> Fyzikální
pole - působení na dálku
Jedna částice v prostoru kolem sebe vytváří pole, které
silově působí na druhou částici, která se v něm nachází.
Tento velmi úspěšný popis je základem klasické
elektrodynamiky a gravitace.
Každému druhu vzájemného
působení přisuzujeme příslušné pole -
prostor v němž na částice působí určité síly. Velikost
působení pole v každém bodě prostoru se vyjadřuje pomocí intenzity
pole (síly působící na "jednotkovou testovací
částici") nebo pomocí jeho potenciálu
(práce spojené s přenosem částice do daného místa). V
klasické fyzice je to pole elektrické, magnetické,
gravitační. Změny - "rozruch" - v tomto poli se
šíří konečnou rychlostí od místa k místu, což je
doprovázeno přenosem energie, hybnosti a dalších
fyzikálních veličin.
Z hlediska klasické fyziky se veličiny, jako je
energie a hybnost, při změnách pole přenášejí spojitě.
V kvantové fyzice se ukazuje, že při změnách (rozruchu) v
poli se fyzikální veličiny přenášejí nespojitě
po určitých "porcích" - kvantech.
Kvantová teorie pole těmto kvantům přisuzuje určité částice
jako nositele interakce, což vede k následujícímu způsobu :
-> Výměna
částic v kvantové fyzice
Částice vysílají a přijímají určitá kvanta
polí, což vyvolává jejich vzájemné
působení. Tato výměnná kvanta si představujeme jako intermediální
částice - nositele interakcí. Tento popis je
charakteristický pro kvantovou teorii pole (základní
principy jsou nastíněny v §1.1, pasáž "Kvantová
teorie pole").
Ve standardním modelu částic jsou interakce
zprostředkovány výměnou intermediálních bosonů,
které jsou při této výměně ve virtuálním stavu -
existují tak krátce, že je díky kvantovému principu
neurčitosti nemůžeme přímo pozorovat. Pokud však při
interakci získá virtuální částice dostatečnou energii,
může se uvolnit a stát se rálnou částicí; to
běžně pozorujeme u fotonů, v experimentech na urychlovačích
se daří nepřímo pozorovat i těžké bosony W+,- a Z0.
Prostorový dosah
interakcí
V běžném životě a v okolní přírodě se
setkáváme se dvěma druhy interakcí: elektromagnetickou
a gravitační. Mají nekonečný dosah
- intenzita pole E(r) ve vzdálenosti r je dána zákonem
obrácených čtverců E(r) ~ k/r2 a potenciál f(r) ~ k/r. Zákon obrácených čtverců má geometrický
původ: kulová plocha poloměru r má povrch S=4pr2. Tuto závislost má
Coulombův zákon elektrostatiky a Newtonův zákon klasické
gravitace.
V
mikrosvětě se setkáváme s dalšími dvěma druhy sil, které
mají krátký dosah: tzv. silné
jaderné interakce (§1.1, pasáž
"Silná jaderná interakce") a slabé interakce (§1.2,
pasáž "Mechanismus beta.
Slabá interakce."). Pokud má pole-interakce krátký dosah,
závislost jeho potenciálu f(r) na vzdálenosti r se modeluje dodatečným exponenciálním
faktorem e-m.m.r: f(r) ~ k.e-m.m.r/r, kde m je hmotnost intermediální částice, m je škálovací
konstanta. Takováto závislost se nazývá Yukawův
potenciál (H.Yukawa jej zavedl v
r.1935 pro silné jaderné interakce; tam se to však později
ukázalo jinak...). Hodnota r ~ 1/(m.m) je efektivní dosah
interakce (vzdálenost, na které interakce
poklesne na hodnotu 1/e).
Prostorový
dosah interakcí v koncepci výměny částic
úzce souvisí s klidovou hmotností mo (neboli klidovou
energií Eo=mo.c2) výměnných
intermediálních částic. Nejjednodušeji se to dá ukázat
pomocí kvantové relace neurčitosti DE.Dt » h z níž plyne,
že u intermediální virtuální částice, která naruší
energii o hodnotu DE (rovnou její klidové energii Eo=mo.c2), může být maximální čas tohoto narušení Dt » h/DE = h/Eo. Za tu dobu může
tato částice rychlostí světla urazit dráhu Ds= c.Dt » c.h/Eo, což představuje
maximální či efektivní dosah interakce
zprostředkované touto intermediální částicí.
Elektromagnetická
interakce má nekonečný dosah,
zprostředkující částicí je foton o nulové
klidové hmotnosti (fotony mohou tedy
přenášet v limitě téměř nulovou energii, takže podle
relací neurčitosti mohou jako virtuální existovat téměř
nekonečnou dobu a limitně se dostat i na nekonečnou
vzdálenost). Rovněž gravitační
interakce má nekonečný dosah, je zprostředkována gravitony
s nulovou klidovou hmotností (zatím
hypotetické či modelové částice, které neumíme nijak
pozorovat).
Naproti
tomu slabé interakce jsou zprostředkovány
těžkými intermediálními bosony W+,- a Z0 o klidové energii 80
a 91 GeV/c2,
takže jejich dosah je velmi malý, řádově 10-15cm (viz níže pasáž "Bosony W+,-, Z0"). Proto i na
subnukleárních měřítcích je tato interakce velmi slabá (na ještě menších měřítcích však není slabší
než elektromagnetická).
Složitější
situace je u silné interakce. V atomových
jádrech (a obecně mezi hadrony) pozorujeme velmi krátký
dosah silné jaderné interakce cca 1,2×10-13 cm. Tato
skutečnost se dříve (provizorně,
nesprávně...) vysvětlovala pomocí
výměny intermediálních p-mesonů o klidové hmotnosti cca 135 a 140 MeV/c2. Po objasnění
kvarkové struktury hadronů se však tato koncepce opustila.
Poznalo se, že silná interakce primárně působí mezi kvarky
uvnitř hadronů a je zprostředkována gluony nulové
klidové hmotnosti, takže její dosah by měl být nekonečný.
Nyní se jaderné síly mezi nukleony chápou jako zbytkový
projev silné interakce mezi kvarky (podrobněji je diskutováno níže v části "Kvarková
struktura hadronů" a
"Čtyři
typy interakcí v přírodě",
též v §1.1, část "Silná
jaderná interakce").
Rozptylové experimenty
Základem zkoumání struktury mikrosvěta jsou tzv. rozptylové
experimenty *). Spočívají v tom, že studovaný
objekt ostřelujeme vhodnými částicemi -
elektrony, protony, a-částicemi a pod., a studujeme produkty
srážky (či dostatečného přiblížení)
nalétající částice s terčíkovým objektem (resp.s druhou
částicí). Jedná se buď o původní částice rozptýlené
(to je při nižších energiích), nebo jiné sekundární
částice, emitované při interakci (to nastává při
vyšších energiích). Analýzou energií, hybností, nábojů,
úhlů výletu a dalších parametrů sekundárních částic
můžeme získat důležité informace o struktuře zkoumaných
mikro-objektů a o mechanismech interakcí příslušných
částic. Interakce částic jsou důležité jednak při
zkoumání struktury hmoty, hlavně však sehrávají klíčovou
úlohu při formování hmoty ve vesmíru. Veškerá hmota která
zde je (a z níž jsme sami složeni) vznikla při interakcích
částic v počátečních stádiích vesmíru a později v nitru
hvězd ("Kosmická alchymie").
*) Nemáme prostě jinou možnost zkoumat
mikrostruktury tak malé, že nejsou přímo pozorovatelné
(ostatně, i běžné vizuální pozorování je do určité
míry jakýmsi "rozptylovým experimentem" s fotony
viditelného světla...). První důležitý rozptylový
experiment provedli již v r.1911 E.Rutheford spolu s H.Geigerem
a E.Marsdenem - vedl k objevu atomového jádra (viz §1.1, část "Stavba
atomů", obr.1.1.4).
Pod interakcemi elementárních částic
rozumíme procesy při vzájemných srážkách
dvou částic nebo srážkách částice s atomovým jádrem (zde se problematika částečně prolíná s jadernými
reakcemi rozebíranými v §1.3 "Jaderné reakce a jaderná energie"). Nejjednodušší
dvoučásticovou interakci primárních částic a
a b lze symbolicky zapsat jako a + b ® c + d - obr.1.5.1.A.
Výsledné sekundární částice c a d po
interakci mohou být buď tytéž jako a a b, nebo
částice jiné. Často však výsledkem interakce bývají jiné
částice než původní a též jiný jejich počet - zvláště
při vysokých energiích zpravidla vzniká vyšší
počet sekundárních částic (viz níže). Primární
částice a a b, vstupující do reakce, jsou již
"dopředu" známé (byly cíleně vytvořeny v
"iontovém zdroji" a urychleny v urychlovači, nebo
jedna z nich připravena v terčíku - viz níže
"Urychlovače"). Vylétající částice c, d,
popř. další sekundární částice, detekujeme a měříme
jejich vlastnosti pomocí detektorů. Procesy vlastní interakce
(srážky) se odehrávají v prostorové oblasti o
mikro-rozměrech řádu 10-8-10-15cm, takže nejsou dostupné přímému
pozorování. O jejich mechanismech si na
základě rekonstrukcí interakce vytváříme určité modelové
představy a teorie, které vysvětlují přechod od výchozího
stavu (a+b) k výslednému koncovému stavu (c+d+ příp. další částice).
Při interakcích částic mezi nimi působí tři *) základní
druhy sil (fyzikálních polí) :
- Silné interakce mezi
hadrony (mezony, baryony) mohou vyvolávat jednak
rozptyl, jednak jaderné reakce, při vysokých
energiích pak i procesy vzniku nových částic a
antičástic, jako jsou p-mezony, nukleony,
hyperony a jejich kombinace.
- Slabé interakce,
projevující se u leptonů, mezonů i baryonů, se při
srážkách většiny druhů částic uplatňují jen
poměrně okrajově. Výrazně se projevují u neutronů
(vzhledem k jejich rozpadu beta), neutrin (interakce
neutrin s nukleony - viz popis neutrinových experimentů
v §1.2, část "Neutrina") a vysokoenergetických procesů, kde
vznikají mezony p a K, hyperony a další částice rozpadající
se v důsledku slabé interakce.
- Elektromagnetické interakce
u nabitých částic způsobují Coulombovský rozptyl,
radiační procesy jako je brzdné záření, tvorbu
elektron-pozitronoých párů a jejich anihilaci,
fotojaderné reakce. Pro všechny tyto typy procesů je
charakteristické, že interakcí elektrických nábojů
s elektromagnetickým polem, v němž se náboje
nacházejí, vznikají kvanta záření - fotony,
většinou fotony gama-záření. Elektromagnetické
interakce jsou nejčastějšími procesy projevujícími
se při srážkách většiny částic.
*) Gravitační interakce u
elementárních částic je zcela zanedbatelná a dosud nebyla
nikdy zaznamenána. Mohla by se snad projevovat až při extrémně
vysokých energiích (»1019 GeV), o mnoho
řádů vyšších než dovedeme nyní dosáhnout. Nejednalo by
se však o nám běžně známé gravitační přitahování, ale
gravitace by byla součástí unitárního pole
(viz §B.6 "Sjednocování fundamentálních interakcí.
Supergravitace. Superstruny." v
knize "Gravitace, černé díry a fyzika
prostoročasu").
Při interakcích částic se obecně
uplatňuje zásada: "co je dovoleno, to se též
realizuje" - dochází ke všem druhům procesů
*), které jsou slučitelné se zákony zachování
energie, hybnosti, momentu hybnosti, elektrického náboje,
leptonového čísla. Je-li k dispozici dostatek energie,
realizuje se při srážkách částic celá řada procesů,
avšak s různou pravděpodobností. Tato pravděpodobnost je
dána vnitřními mechanismy interakce příslušných polí a
vztahem mezi příslušnými konfiguracemi výchozího a
koncového stavu. Pravděpodobnosti jednotlivých procesů
("kanálů" interakce) stanovuje kvantová teorie
pole pomocí tzv. maticových elementů (elementů matice rozptylu S, viz též níže "Feynmanovy
diagramy").
*) Jako kdyby všechna kvanta všech polí
byla potenciálně, skrytě a implicitně - virtuálně
- přítomna všude v prostoru, ve "vakuu". Z tohoto
"unitárního" pole se pak dodáním energie - excitací
pole - uvolňují příslušné částice, ať již
virtuální či skutečné.
Průběh a výsledek interakce částic závisí
především na dvou okolnostech :
¨ Na druhu
interagujících částic.
¨ Na kinetické
energii, s níž se částice srážejí (určující je zde energie v těžišťové
soustavě obou částic).
Pozn.: I při
srážkách stejných částic a při stejné energii však
zpravidla interakce proběhne pokaždé poněkud jiným způsobem
- různými "kanály" reakce. Můžeme si to vysvětlit
tak, že jednak srážka může proběhnout "čelně"
nebo "periferně" (tj. s různým impaktním faktorem a
vzájemným momentem hybnosti obou částic), jednak vlivem
stochastických zákonitostí kvantové fyziky se jednotlivé
možné konfigurační stavy realizují s různými
pravděpodobnostmi.
Feynmanovy diagramy
Pro přehledné grafické znázornění mechanismů interakcí
částic se často používají tzv. Feynmanovy diagramy
(R.Feynman je poprve zavedl v r.1948). Vycházejí z výměnného
popisu interakcí částic. Trajektorie
"látkových" částic, fermionů (elektron, proton,
...) jsou zde vyznačeny rovnými plnými čarami
s šipkami - částice mají šipku směřující vpravo,
antičástice vlevo. Výměnné intermediální částice (foton,
W-bosony, gluony...) jsou vyznačeny čárkovaně
nebo vlnovkami. Ve vodorovném směru je časová
orientace (používají se i jiné
konvence) - ovšem jen symbolická, tyto
diagramy neslouží ke konkrétnímu vyjádření časového
průběhu interakcí, ale jen k "topologickému"
znázornění jejich mechanismů; jsou určitou analogií
prostoročasových diagramů používaných v relativistické
fyzice. Základní Feynmanův diagram obecné blíže
nespecifikované interakce dvou částic a+b®c+d je na obr.1.5.1.A. Do
vzájemné blízkosti - interakční oblasti -
přilétají primární částice a a b, uvnitř
dochází k vlastním procesům interakce, načež z této
oblasti vylétají výsledné částice c a d.
Horní část obrázku 1.5.1.A znázorňuje obvyklý prostorový
nákres srážky obou částic, dolní část obrázku Feynmanovu
prezentaci této interakce.
Vlastní Feynmanovy diagramy pak specifikují a znázorňují
možné procesy uvnitř interakční oblasti pro
konkrétní druhy vstupujících a vystupujících částic.
Opět se skládají z vnějších čar s "volnými
konci", znázorňujících částice vstupující do
interakce a z ní vystupující. Vlastní interakční procesy
jsou zakresleny tzv. interakčními vrcholy -
body, v nichž se na výchozí vnější čáru částice
napojují vlnové nebo přerušované čáry, odpovídající
výměnným intermediálním částicím zprostředkujícím
interakci *). V interakčních vrcholech jsou splněny zákony
zachování energie, hybnosti, elektrického náboje,
leptonového čísla. Vnitřní čáry mezi interakčními
vrcholy vnějších čar odpovídají virtuálním
částicím, které neopouštějí interakční oblast a
mezi vstupujícími ani výslednými "fyzikálními"
částicemi v počátečním nebo koncovém stavu nejsou
přítomny; při vlastní interakci však působí a na výsledku
se podílejí. Z některých interakčních vrcholů mohou dále
vycházet i čáry s druhým volným koncem: ty odpovídají reálným
částicím (fotonům, W-bosonům, fermionům)
emitovaným při procesu.
*) V kvantové teorii pole
tyto čáry odpovídají tzv. propagátorům
(angl. propagation=šíření) - funkcím udávajícím
amplitudu pravděpodobosti (amplitudu "šíření
vlny") při pohybu částice s určitou energií a
hybností. Jedná se o fermionový (např. elektronový)
a bosonový (např. fotonový) propagátor. Propagátory
lze vyjádřit pomocí tzv. Greenových funkcí,
kteréjsou řešením vlnových rovnic příslušných částic
(buď nehomogenní Diracovy rovnice s d-funkcí souřadnic a času,
nebo d´Alembertovy rovnice pro potenciály elektromagnetického
pole). Vlastní interakční vrcholy odpovídají operátorům kreace
(vzniku) a anihilace (zániku, zničení)
příslušných částic.
Uvedeme si příklady Feynmanových diagramů pro některé
konkrétní typické interakce částic - obr.1.5.1. Z hlediska
jaderné, radiační a částicové fyziky jsou tyto interakce
podrobněji rozebírány na jiných příslušných místech
(§1.2, 1.3, 1.5, 1.6) našeho pojednání. Začněme interakcemi
při nízkých energiích. Nejjednodušším procesem s
částicemi je interakce dvou elektronů pod
vlivem elektromagnetické síly. Základním mechanismem,
působícím v interakční oblasti, je zde podle koncepce
kvantové elektrodynamiky výměna fotonů mezi
oběma elektrony - na Feynmanově diagramu jsou elektronové
čáry ve svých interakčních vrcholech spojeny fotonovou
čárou (obr.1.5.1.B) - jeden elektron vyzáří virtuální
foton g*,
druhý ho absorbuje, čímž se oba elektrony na svých drahách
vzájemně rozptýlí (pružný rozptyl).
Výsledným stavem jsou opět dva elektrony. Toto je však jen
jeden z možných procesů a navíc pouze v první aproximaci.
Již z klasické elektrodynamiky je známo, že při každém
zrychleném pohybu elektrických nábojů dochází k
vyzařování elektromagnetických vln. Emise fotonu brzdného
záření nastává i při rozptylu elektronů. Při vyšších
energiích se mohou realizovat i interakční vrcholy s
energetickými částicemi, které mohou generovat reálné
částice - linie s volnými konci odpovídající sekundárním
leptonům; při nejvyšších energiích i produkce těžkých
částic (viz níže).
Dalším jednoduchým procesem elektromagnetické interakce
je rozptyl fotonu na elektronu - Comptonův rozptyl
(je popsán v §1.6 "Ionizující záření", část
"Interakce záření
gama a X", obr.1.6.3). Na
Feynmanově diagramu v horní části obr.1.5.1C vidíme ve
vstupní oblasti plnou čáru elektronu a vlnovku fotonu. V
interakčním vrcholu vzniká virtuální elektron e* (který
jako by "pohltil" energii fotonu), který se v druhém
vrcholu opět mění na vylétající elektron a foton. Interakce
pozitronu s elektronem může při nízkých
energiích proběhnout opět buď jako Coulombický pružný
rozptyl (Feynmanův diagram je zcela analogický obr.1.5.1.B),
nebo jako proces anihilace za vzniku fotonů
gama - dolní část obr.1.5.1.C. Při vyšších energiích je v
obou těchto procesech opět více možností za vzniku dalších
sekundárních částic. Při nejvyšších energiích je řada
možností produkce i těžkých částic, včetně Higgsových
bosonů. Dvě takové možnosti "elektro-slabé
produkce" Higgsova bosonu jsou na obr.1.5.1.D: přímá
interakce e++e-®Z*®Z+H (H-vyzáření)
a sdružená produkce W nebo Z a jejich následná fúze
na H. Higgsovy bosony jsou vysoce nestabilní částice a
okamžitě se rozpadají buď na dva vysokoenergetické fotony,
nebo na čtyři leptony (přes intermediální bosony W či Z),
příp. dalšími zůsoby (vlastnosti
Higgsových bosonů jsou popsány níže v části "Hypotetické a modelové částice").

Obr.1.5.1. Příklady Feynmanových diagramů některých
význačných interakcí částic.
Pozn.: Symbolické obrázky protonů, neutronů a p-mesonů nejsou
součástí standardních Feynmanových diagramů; jsou zde
zakresleny jen pro názornost.
Slabé interakce
jsou zprostředkovány výměnými intermediálními bosony W
(popř. Z). Na obr.1.5.1.F je diagram důležitého procesu transmutace
kvarku d na u při b--radioaktivní přeměně neutronu na proton, elektron a
(anti)neutrino: no ® p+ + e- + n'e.
Tento proces, stejně jako analogický proces b+, odpovídá obrázku 1.2.5 v §1.2 "Radioaktivita", část "Radioaktivita
beta". Další důležité
procesy, probíhající vlivem slabé (resp. elektroslabé)
interakce, jsou rozpady pionů na miony a
neutrina, např. p- ® m- + n'm (analogicky probíhá rozpad p+) a mionů na elektrony a neutrina,
např. m- ® e- + n'e+ nm (analogicky pro m+) -
zachycují to Feynmanovy diagramy na obr.1.5.1.G.
Silné interakce jsou zprostředkovány
"výměnou" gluonů mezi kvarky, obsaženými
uvnitř hadronů - mesonů (především p a K) a baryonů
(protonů, neutronů, hyperonů). Nelinearita kvantové
chromodynamiky silné interakce spolu s ideou asymptotické
volnosti (viz níže "Uvězněné
kvarky", nebo "Sjednocování
fundamentálních interakcí. Supergravitace. Superstruny.") umožňuje Feynmanovy
diagramy (a poruchový přístup) používat jen v procesech, kde
je kvarkům předávána vysoká hybnost. "Klidové"
interakce kvarků v hadronech, silnou interakci nukleonů v
jádrech a "hadronizaci" kvark-gluonové plasmy takto
analyzovat nelze. Zato však lze dobře popsat vysokoenergetické
interakce mezi hadrony. Na obr.1.5.1.E je znázorněn Feynmanův
diagram produkce pionu při srážce dvou
protonů p+p®p+p+po; je to
jeden z možných procesů, alternativně může vznikat i
proton, neutron a p+, nebo
dva neutrony a p-.
Při vysokoenergetických interakcích (viz
níže), kdy je k dispozici dostatek energie, se může
realizovat široké spektrum různých vnitřních procesů.
Především, intermediální W-bosony či gluony, napojené v
interakčních vrcholech, mohou získat natolik vysokou energii,
že mohou generovat velmi těžké částice - Higgsovy
bosony H a těžké kvarky t, ve sdružené
produkci částice-antičástice. Ty se pak vzápětí rozpadají
za účinku intermediálních bosonů W na elektrony,
miony, tauony, neutrina a jejich antičástice. Higgsovy bosony
se též mohou rozpadat na dvojici vysokoenergetických fotonů g. Dále,
opakovanými procesy s intermediálními částicemi může při
jedné srážce vznikat více částic -
včetně kvarků, které vzápětí hadronizují. Na
obr.1.5.1.H je příklad vysokoenergetické srážky dvou
protonů při energii stovky GeV, kdy interakcemi s výměnnými
gluony mohou vznikat i těžké t-kvarky, b-kvarky,
pak W-bosony a nakonec leptony (elektrony e±, miony
m±, tauony t, neutrina n), které
vylétají z interakční oblasti a mohou být detekovány. Při
ještě vyšší energii desítky TeV (zatím nedosaženo...) je
jednou z více možností i vznik Higgsova bosonu
("silná produkce" H výměnnou interakcí
energetických kvarků s gluony nebo W-bosony) a série
následujících rozpadů na W-bosony a nakonec opět leptony či
kvarky - obr.1.5.1.I. A samozřejmě je to doprovázeno hadronizací
energetických kvarků. Na obr.1.5.1.I je znázorněn vznik
Higgsova bosonu tzv. gluonovou fúzí; dalšími
možnostmi je W nebo Z fúze (analogické jako na obr.D dole, jen místo elektronů
jsou kvarky), popř. sdružená
produkce s W nebo s t-t'-párem.
V těchto vysokoenergetických srážkách do interakční
oblasti vstupují i ostatní kvarky srážejících se protonů -
interakcí s gluony zde pak může vzniknout tzv. kvark-gluonová
plasma (viz níže pasáž
"Kvark-gluonová plasma -
"5.skupenství hmoty", " a v §1.3 pasáž
"Vysokoenergetické
srážky těžších jader. Kvark-gluonová plasma."), jejíž hadronizací
vznikají další sekundární hadrony
(především piony, nukleony), vylétající z interakční
oblasti. Na obr.1.5.1.H,I jsou vyznačeny dvě interakční
oblasti. První - "asymptoticky volná"
- odpovídá vysokoenergetickým interakcím, při nichž se i
kvarky chovají jako volné a jejich interakce může být
popsána Feynmanovými diagramy; je analogická interakčním
oblastem na ostatních diagramech. Druhá interakční oblast
odpovídá hadronizaci kvarků, které
nemohou vyletět samostatně, ale v gluonovém poli díky své
energii generují další dvojice kvarků-antikvarků, které se
spojují do dvojic a trojic - vylétají jako hardony - mesony p a K, protony,
neutrony, hyperony. Tyto částice vylétají často v úzce
směrovaných sprškách, zvaných jety, v
malém úhlu kolem směru letu původních energetických
kvarků.
V kvantové
teorii pole (v jejím tzv. poruchovém přístupu)
se Feynmanovy diagramy používají jako vodítko pro započtení
příspěvků od různých druhů možných procesů s
intermediálními kvanty do tzv. maticových elementů
(prvků S-matice rozptylu), udávajících
pravděpodobnosti kvantových přechodů mezi stavy daného
systému - zde mezi stavem před interakcí a po interakci
částic.
Nejprve se sestaví příslušné
Feynmanovy diagramy, jejichž vnější linie odpovídají
vstupujícím částicím počátečního stavu a vystupujícím
částicím koncového stavu. Vyšetřuje se postupně
1.aproximace (diagram s 2 interakčními vrcholy), 2.aproximace
(4 vrcholy), ..., N-aproximace (počet vrcholů 2N). Pro každou
z těchto aproximací se kreslí všechny rozdílné (topologicky
neekvivalentní) diagramy se stejnými vnějšími liniemi a
počty vrcholů. V každém takovém diagramu se pro jednotlivé
jeho části - vnější linie, vnitřní linie, vrcholy -
stanovují specifické členy (koeficienty), obsahující
(4-)hybnosti a vazbovou konstantu g příslušné interakce. Pak
se provede integrace přes všechny hybnosti. Příspěvky všech
diagramů se nakonec sečtou.
..............přijde doplnit.................
Vznik
nových částic při interakcích
Specifickým jevem při vysokoenergetických interakcích
částic je vznik nových částic - emise
dalších částic, které nebyly předtím přítomny. Mohou to
být buď částice stejného druhu jako vstupovaly do interakce,
nebo částice jiného druhu. Tento jev si vysvětlujeme pomocí
Diracovy kvantové koncepce vakua *), které
není "prázdným prostorem", ale je zaplněno virtuálními
částicemi, resp. dvojicemi částic a antičástic.
Jestliže při interakci v určitém místě vznikne dostatečně
velký gradient určitého pole - je předána dostatečně
velká energie - přemění se tyto virtuální
částice na částice reálné; to pozorujeme
jako emisi nových částic. Dochází přitom ke sdružené
produkci dvojic částic-antičástic. Nutnou podmínkou
pro vznik nových částic je dosažení dostatečně vysoké
energie interakce - prahové energie, vyšší
než Smo.c2, kde Smo je úhrnná klidová
hmotnost vznikajících částic.
*) Mechanismy vzniku částic se podrobně
zabývá kvantová teorie pole a unitární
teorie. K jejich grafickému znázornění se používají i
výše zmíněné Feynmanovy diagramy.
Vícenásobné
interakce - kaskády interakcí a spršky částic
Při interakci vysokoenergetických částic v dostatečně
objemném látkovém prostředí dochází k efektu vícenásobné
interakce. Sekundární částice, uvolněné při
první interakci dopadající primární částice, způsobují další
interakce, při nichž se produkují další
(terciální) částice, které činí totéž. Z jedné
dopadající částice tak v kaskádě interakcí vzniká celá sprška
sekundárních částic. Jak rozvíjející se sprška
proniká do hloubky materiálu, počet sekundárních částic
roste a jejich průměrná energie klesá. Jakmile tato energie
poklesne pod určitou prahovou mez, multiplikační proces se
zastaví a energie částic se bude dissipovat ionizací a
excitací; počet částic ve spršce bude klesat, až sprška
nakonec zanikne. V praxi rozlišujeme dva druhy kaskádních
interakcí:
¨ Elektromagnetické
spršky
vznikající při interakcích vysokoenergetických fotonů nebo
elektronů s atomy látky. Sekundární elektrony a fotony,
emitované při primární interakci, vlivem párové e-e+ produkce, Comptonova rozptylu, fotoefektu a brzdného
záření, vyvolávají další elektrony (+pozitrony) a fotony;
atd.
¨ Hadronové
spršky
vznikající v důsledu nepružných interakcí
vysokoenergetických hadronů s atomovými jádry materiálu.
Dochází ke vzniku jaderných fragmentů a k produkci nových
sekundárních částic - p, n, p, K. Počet těchto
sekundárních částic je přibližně úměrný logaritmu
energie n ~ lnE.
V řadě případů v praxi tato sprška není čistě
hadronová nebo elektromagnetická, ale smíšená.
Součástí hadronové spršky jsou piony, které se
vzápětí rozpadají: p+,-®m+,-+nm, po®g+g; vede to ke
vzniku elektromagnetické elektron-foton-mionové spršky,
která doprovází hadronovou kaskádu. Každá hadronová
sprška má tedy i elektromagnetickou složku. A při interakci
vysokoenergetických fotonů nebo elektronů dochází při fotojaderných
reakcích k emisi protonů a neutronů, které mohou
elektromagnetickou spršku obohacovat o hadronovou
složku. Kaskády interakcí a spršky sekundárních
částic pozorujeme u kosmického záření (viz obrázek
1.6.7 v §1.6, část "Kosmické záření") a
při interakcích částic na urychlovačích (v bublinových
komorách, trackerech a kalorimetrech).
Účinný
průřez interakcí částic. Impaktní parametr.
Podobně jako u chemických a jaderných reakcí, i interakce
elementárních částic probíhají různě "ochotně"
- s různou účinností či pravděpodobností, v závislosti na
druhu interakce a energii částic. Pravděpodobnost interakcí
částic lze názorně vyjádřit geometrickým způsobem pomocí
tzv. účinného průřezu reakce. Účinný
průřez (angl. cross section) vyjadřuje pravděpodobnost,
že ostřelující částice bude daným konkrétním způsobem
interagovat s terčovou částicí.
Koncepce účinného průřezu vychází z názorné
představy, že terčová částice se vzhledem k nalétající
částici chová jako "absorbující tělísko" o
poloměru r (na obr. černý kotouč), které částice
buď zasáhne a dojde k požadované interakci, nebo je
nezasáhne (mine je, proletí kolem) a k interakci nedojde. Čím
větší je poloměr tohoto tělíska, resp. jeho efektivní
ploška s = p.r2 - účinný průřez, tím větší je
pravděpodobnost interakce (pravděpodobnost, že částice se
"trefí").
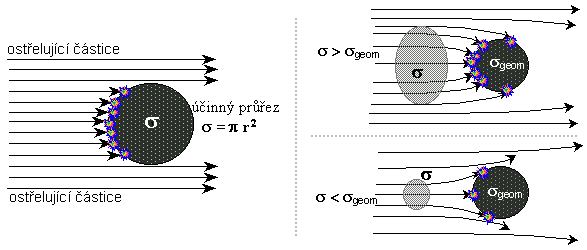
Vyjádření pravděpodobnosti interakce ostřelující částice
s terčíkovou částicí pomocí účinného průřezu
Účinný průřez může, ale nemusí, přímo
souviset s "geometrickým průměrem" terčové
částice rgeom, či jejím "geometrickým průřezem" sgeom = p.r2geom. Pro "přitahující se" částice je s > sgeom, pro odpuzující se částice je s < sgeom. Kromě toho stejná ostřelující částice může na
téže terčové částici způsobit různé
interakce, jejichž různé pravděpodobnosti popíšeme
různými parciálními účinnými průřezy. Tyto účinné
průřezy nemají již nic společného s geometrickými rozměry
částic - jsou důsledkem vnitřních mechanismů konkrétních
druhů interakcí (o geometrických
rozměrech částic bylo diskutováno výše v pasáži "Velikost
elementárních částic ...").
Jednotkou účinného průřezu v soustavě SI by byl m2, který je však
neadekvátně velký a proto se v jaderné fyzice používá
jednotka barn (bn): 1 bn = 10-28m2,
která má řádově velikost geometrického průřezu protonu
vzhledem k silné interakci.
Účinný průřez interakce velmi
těsně souvisí s koeficientem absorbce, tzv. lineárním
součinitelem zeslabení m, v exponenciálním
zákoně absorbce ionizujícího záření v látkách. Tato
souvislost bude vyjasněna v následujícím §1.6
"Ionizující záření", pasáž "Absorbce
záření v látkách".
Pro průběh konkrétní interakce je důležitý tzv. impaktní
parametr b: je to geometrická vzdálenost
středů efektivních "disků" interagujících
částic, v níž kolem sebe prolétají nebo se protínají. V
případě malého impaktního parametru b<<rgeom se jedná o centrální
srážku, při větších hodnotách b o srážku
periferní. Pokud je impaktní parametr větší
než rgeom,
resp. větší než součet efektivních poloměrů obou částic
(terčové a nalétající), nedochází již k přímé
interakci základním mechanismem (silnou krátkodosahovou
interakcí), ale částice mohou interagovat prostřednitvím
svých elektrických polí, pokud jsou nabité (taková srážka
se někdy nazývá ultraperiferní).
Závislost
účinného průřezu na energii
Při daném druhu částic a interakcí je účinný průřez
poměrně složitou funkcí energie
nalétající částice. Energetická závislost účinného
průřezu má často rezonanční charakter:
měníme-li spojitě energii interagující částice, objevují
se na křivce závislosti účinného průřezu výrazná
maxima kolem určitých konkrétních hodnot energie.
Tyto závislosti svým tvarem připomínají rezonanční křivky
závislost proudu, napětí či impedance u elektrických obvodů
RLC (obsahujících ohmický odpor R, indukčnost L a kapacitu
C), na frekvenci f střídavého elektrického signálu
kolem frekvence frez= 1/[2pÖ(LC)]. Pro účinný průřez tohoto druhu interakcí
byl již v r.1936 odvozen důležitý Breit-Wignerův
vztah *)
s = (l/2p)2.g.G2.1/[(E-Er)2 + (G/2)2] ,
kde Er je rezonanční energie, G představuje šířku
excitované hladiny intermediálního stavu při interakci, l je vlnová délka
částice, faktor g je funkcí poměru spinů výchozího a
konečného stavu.
*) Breit a Wigner odvodili tento vztah pro
speciální případ elastického rozptylu
nalétající částice v potenciálovém poli částice
terčíkové. S určitými modifikacemi však tento vzorec platí
pro všechny druhy interakcí vykazující rezonanční maxima
účinného průřezu.
Přítomnost rezonančních maxim v energetické závislosti
účinného průřezu svědčí pro existenci určitých dynamických
procesů při interakci - vznik vázaných systémů,
diskrétních excitovaných stavů či intermediálních
částic.
Interakce částic vysokých
energií
V §1.3 a 1.6 jsou rozebírány interakce především při
nižších a středních energiích, které vedou k
charakteristickým jevům excitace a ionizace atomů, popř. k
jaderným reakcím spojeným s transmutací atomových jader a
emisí jaderných částic. Při nízkých energiích (menších
než cca 1MeV) se celkový počet elementárních částic před
a po interakci nemění, vznikají příp. jen fotony
odnášející energii při deexcitaci vzbuzených stavů. Pokud
energie interagujících částic (včetně fotonů gama)
překročí prahovou hodnotu 2.me.c2 = 1,022MeV, mohou při reakci vznikat nové
(sekundární) částice - dvojice elektron e- a
pozitron e+.
Pod interakcí částic vysokých energií
se rozumí reakce vyvolané částicemi s energií, která leží
nad prahem produkce mezonů p, neboli nad energií »140MeV v těžišťové
soustavě. Se stoupající energií se při takových
interakcích může produkovat postupně více nových
sekundárních částic (většinou p-mezonů) a dále též
částice s vyšší klidovou hmotností - mezony K, nukleony a
antinukleony, hyperony, bosony W a Z (při
nejvyšších energiích mnoha TeV a více se očekávají i
produkce Higgsových bosonů, supersymetrických částic,
leptokvarků a dalších "exotických" dosud
neprokázaných částic).
Jsou-li částicemi vysokých energií (např. protony)
ostřelována atomová jádra, dochází k vyrážení několika
nukleonů a "odštěpků" - k "tříštění"
či fragmentaci jader.
Při nejvyšších energiích (řádově 100GeV a vyšších)
jsou interakce již značně složité a různorodé, dochází k
produkci velkého počtu sekundárních částic.
V laboratorní (terčíkové) soustavě vzniká úzký svazek
sekundárních částic, předenším pionů p, kolimovaných
dopředu ve směru pohybu primární částice - jakási tryska
či sprška částic. Dále vzniká širší
kužel těžších částic a také kvant gama. Při těchto
reakcích se plně projevují kinematické a dynamické efekty
speciální teorie relativity - označují se někdy jako ulrarelativistické.
Při vysokoenergetických srážkách těžkých částic
(protonů a zvláště těžších atomových jader) může na
kratičký okamžik vzniknout vzniknout zvláštní směsice
lokálně volných kvarků a gluonů - tzv. kvark-gluonová
plasma (podrobněji rozebíraná
níže v části "Kvarková struktura hadronů",
pasáž "Kvark-gluonová plasma - 5.skupenství
hmoty").
Studium interakcí částic při vysokých
energiích má velký význam pro poznání struktury
elementárních částic a podstaty sil, které
mezi nimi působí. Během srážky při vysoké energii
částice vzájemně proniknou "hluboko do svých
niter" a výsledek interakce může leccos vypovědět o
jejich stavbě. Vlivem kvantových procesů v polích silných,
slabých a elektromagnetických interakcí vznikají při
vysokoenergetických srážkách nové sekundární částice,
které jsou jednak zajímavé samy o sobě, jednak nesou
důležité informace o charakteru fundamentálních
přírodních sil, včetně možností jejich jednotného
chápání v rámci unitární teorie pole. Srážky částic
při vysokých energiích jsou jakousi "sondou"
do nejhlubšího nitra hmoty *) - a zároveň i
do procesů vzniku vesmíru (viz §5.5 "Mikrofyzika a kosmologie.
Inflační vesmír."
knihy "Gravitace, černé díry a fyzika
prostoročasu"). Konkrétní způsoby
interakcí částic budou popsány níže pro jednotlivé druhy
elementárních částic.
*) Srovnejme též s též levou částí obr.1.0.1 v §1.0. "Fyzika - fundamentální přírodní
věda".
Analýza dynamiky interakcí částic
Vysokoenergetické interakce
elementárních částic se studují pomocí velkých urychlovačů
(viz níže část "Urychlovače nabitých částic"). Na vlastní urychlovač navazují velmi
komplikované a precizní detekční aparatury a
systémy *), které analyzují sekundární částice a
záření, vzniklé při interakci vysokoenergetických
primárních částic s materiálem terčíku či vzájemně ve
vstřícných svazcích. Obsahují velký počet jednotlivých
detektorů různých druhů (scintilační, polovodičové,
ionizační), umístěných v silných a speciálně
konfigurovaných magnetických polích (pro analýzu hybnosti
nabitých částic). Analýzou druhu, náboje a hmotnosti těchto
vyletujících částic, jejich energií, hybností a úhlů
emise z místa interakce, lze rekonstruovat řadu parametrů
interakcí, k nimž dochází. Z toho lze usuzovat na strukturu
elementárních částic, vlastnosti působících polí a
interakcí, na existenci nových dosud neznámých kvant a
částic.
*) Pro tento účel se dříve používaly
velké bublinkové komory (viz §2.2, část
"Detektory stop částic"). Nyní jsou nahrazovány rozsáhlými a
složitými elektronickými detekčními systémy
(§2.1, část "Uspořádání a konfigurace
detektorů záření"),
obsahujícími mimo jiné tzv. trackery (angl. track
= stopa, dráha) - elektronické detektory drah částic.
Používají především multidetektorové polovodičové
systémy (§2.5 "Polovodičové
detektory"), popř. soustavy
speciálních ionizačních komor a scintilačních detektorů.
I tehdy, když se určitá intermediální částice rozpadne
hned v místě interakce (a nemůže být tedy detekována
přímo), nesou produkty jejího rozpadu určité informace o
jejích vlastnostech. Ze změřených energií a hybností lze
stanovit hmotnost původní částice. Vyneseme-li na vodorovnou
osu změřenou energii detekovaného souboru částic
odpovídajícího příslušnému "kanálu" rozpadu -
sekundárních částic, na které by se hledaná intermediální
částice měla rozpadat - a na svislou osu vyneseme
registrovaný počet případů (příp. normalizovaný na
jednotku energie primárních srážejících se částic, např.
protonů), může se na jinak plynulé křivce objevit drobný
"hrbolek", svědčící pro existenci krátkožijící
částice o příslušné klidové hmotnosti, odpovídající
energii na vodorovné ose.
Na základě kvantové relace neurčitosti mezi dobou života t částice a
neurčitostí stanovení její klidové energie E = mc2 (t.DE » h) lze ze
stastistického "rozmazání" stanovených hodnot
klidové hmotnosti určit dobu života t intermediální částice.
Dalitzův
diagram
Na výstupu detekčních systémů, obklopujících místo
interakce, se objevuje velké množství impulsů
různých velikostí, tvarů, časových a úhlových korelací,
nesoucích informace o energiích, hybnostech a dalších
parametrech sekundárních částic. Orientovat se v tak velkém
množství dat není nikterak snadné. Pro přehledné zobrazení
a kinematickou analýzu produktů interakcí
částic se často používají tzv. Dalitzovy diagramy
(diagramy tohoto typu poprve zavedl R.H.Dalitz v r.1953 při
studiu rozpadů K-mezonů). Ze zákonů zachování energie a
hybnosti vyplývá, že kinematiku interakce lze vhodně
parametrizovat druhou mocninou energie částic. Na osách
diagramu se vynášejí (v energetických jednotkách GeV2) druhé mocniny
efektivních hmotností»energií dvojic dceřinných částic (produktů
interakce*), většinou p-mezonů.
*) Jestliže např. při interakci dvou
primárních částic P1 a P2: P1+P2®A+B+C vzniknou
tři sekundární částice A,B,C, na osu X vynášíme m2AB a na osu
Y hodnoty m2BC. Tyto kvadráty hmotností jsou rovné druhým
mocninám součtů 4-hybností částic: m2AB = (pA+pB)2,
analogicky mBC.
Pokud studovaný
druh interakce probíhá přímo, bez
ovlivnění dynamickými procesy intermediálních částic či
rezonančních stavů (což je z určitého
pohledu totéž...), jsou výsledné
částice náhodně rozděleny a distribuce příslušných
měřených bodů na Dalitzově diagramu je přibližně homogenní,
vyplňující trojúhelníkovou oblast pod diagonálou danou
použitou energií. Pokud však při interaci vzniká nějaká
krátkožijící intermediální částice
(resp. rezonanční proces), jejímiž produkty rozpadu jsou
detekované sekundární částice, je distribuce měřených
bodů na Dalitzově diagramu nehomogenní -
objevují se lokální zhuštěniny (v profilu
diagramem pak píky) v oblastech kolem hmotnosti intermediální
částice.
Analýzy tohoto
druhu se dříve prováděly manuálně s vykreslením bodů na
papír. Nyní se provádějí pomocí výkonné počítačové
techniky, diagramy jsou digitalizované a zobrazují se pomocí
počítačové grafiky, někdy i s barevnou modulací obrazu.
Zavádějí se též Fourierovy transformace pro analýzu vztahu
mezi časovým a energetickým spektrem u krátkožijícího
stavu intermediální částice či rezonance. Všechny tyto
metodické přístupy jsou užitečné nejen při analýze
interakcí částic, ale všude tam, kde potřebujeme odlišit
kinematické efekty od dynamických, prokázat existenci
nějakého krátkožijícího vázaného stavu, který není
přímo pozorovatelný.
Energetická
závislost účinného průřezu
Tento postup se
vhodně kombinuje s analýzou energetické závislosti účinných
průřezů interakce, jejíž případný rezonanční
charakter se vyjadřuje pomocí shora zmíněného Breit-Wignerova
vztahu. Vyskytují-li se v energetické závislosti
účinného průřezu interakce rezonanční vrcholy a zároveň
na Dalitzově diagramu energetické distribuce sekundárních
částic jsou patrné lokální zhuštěniny a píky, je téměř
jisté, že při interakci dochází k dynamickým
procesům vzniku excitovaných stavů či
intermediálních částic.
Chybějící
energie
Pokud je
studovaná interakce doprovázena vznikem neutrálních slabě
interagujících částic, nelze tyto normálním způsobem
detekovat. Zde je určitou možností rozbor energetické
bilance: určíme energie a hybnosti ostatních částic
a na základě zákona zachování energie a hybnosti určíme
hodnoty energie a hybnosti, které neznámá částice odnáší.
Z nich pak můžeme určit klidovou hmotnost neznámé částice.
.?..doplnit-další druhy
diagramů+obrázky..?...
Vlastnosti
a interakce nejdůležitějších elementárních částic
V tomto odstavci si stručně přiblížíme jednotlivé
nejvýznačnější částice mikrosvěta, jejich původ a vznik
při interakcích částic, jejich vlastnosti a hlavní způsoby,
jak interagují mezi sebou a s dalšími částicemi. Při tomto
stručném popisu vlastností elementárních částic se
nebudeme držet výše nastíněné systematiky, ale budeme
postupovat od známých, rozšířených a v praxi využívaných
částic k "exotičtějším", méně známým a
skrytějším částicím, jejichž význam pro stavbu a
vlastnosti hmoty někdy ani není znám.
 Fotony
Fotony 
jsou kvanta elektromagnetického záření. Mají nulovou
klidovou hmotnost, pohybují se rychlostí světla *), jsou
nositeli energie E = h.n, kde h je Planckova konstanta a n je frekvence
elektromagnetické vlny o vlnové délce l = c/n. Jsou bosony se spinovým
číslem 1. Podle zákonitostí elektrodynamiky fotony
obecně vznikají při všech zrychlených
pohybech elektricky nabitých částic (např. brzdné
záření). Emitují se při deeexcitacích v
atomových obalech (viditelné a UV
záření, charakteristické X-záření - §1.1., pasáž "Záření atomů") a atomových jádrech (záření gama - §1.2, část "Záření gama"), kde odnášejí příslušný energetický rozdíl
excitovaných stavů. Fotony záření gama dále vznikají při anihilacích
pozitronů s elektrony e++e-®2g (§1.6, část "Interakce nabitých částic -
přímo ionizující záření",
obr.1.6.1 dole, pasáž "Interakce
pozitronového (beta+)
záření"), jakož i v řadě dalších interakcí elementárních
částic. Zde budeme uvažovat většinou fotony vyšších
energií - záření g.
*) Viz však teoretickou poznámku o
možném vlivu kvantových fluktuací prostoročasu na rychlost
tvrdého záření g v §1.6: "Pohybuje
se vysokoenergetické g-záření
pomaleji než světlo?".
Interakce fotonů středních energií s látkou
jsou popsány v §1.6, část "Interakce záření gama a X", jedná se především o fotoefekt, Comptonův
rozptyl, tvorbu e-e+-párů.
Fotony vysokých energií (>10MeV) mohou svými interakcemi vyvolávat tzv. fotojaderné
reakce, při nichž jsou z jader vyráženy neutrony,
protony, popř. více nukleonů, deuterony, a-částice. Nad prahovou
energií záření gama asi 140MeV pak při interakci vznikají
další částice, např. p-mesony: g + p ® n + p+, g + p ® p + po, a pod. Při velmi vysokých energiích fotonů gama (>300MeV) může být
generována řada dalších částic, včetně těžkých (srov. výše "Interakce částic
vysokých energií").
Fotony, jakožto kvanta
elektromagnetického vlnění, fakticky zavedl A.Einstein v
r.1905 při studiu fotoefektu (§1.1 "Atomy a atomová
jádra", obr.1.1.1); vlastní název "foton"
později navrhl americký chemik G.N.Lewis.
 Elektrony a pozitrony
Elektrony a pozitrony 
 Elektrony e-
Elektrony e-
jsou základními, skutečně elementárními, stabilními
částicemi hmoty, které tvoří elektronový obal atomů.
Elektron je nositelem záporného elementárního náboje e =
1,60219.10-19C, jeho klidová hmotnost je me = 9,1095.10-31kg (=511keV/c2), řadí se mezi leptony, je fermionem se spinem
(1/2)h. Magnetický moment elektronu je e.h/4pme - tzv. Bohrův
magneton. Podle představ současné kosmologie elektrony
vznikly v nejranějších fázích vývoje vesmíru po velkém
třesku, při oddělování elektromagnetické a slabé
interakce. Kromě toho elektrony vznikají při řadě procesů a
interakcí jiných elementárních částic, např. při b--radioaktivitě no ® p+ + e- + ne´ a při mnoha
dalších procesech, jak je vidět z níže popsaných interakcí
ostatních částic. Kromě atomové a jaderné fyziky hrají
elektrony klíčovou roli v jevech elektromagnetických, jejichž
převážná většina je založena na pohybu elektronů,
vytvářejících elektrický proud.

r. 1895: J.J.Thomson - objev elektronů
=> první model atomu
Elektron byl, jakožto vůbec první elementární
částice stavby hmoty, objeven v r.1895 J.J.Thomsonem při
studiu elektrických výbojů v plynech v katodové trubici.
 Pozitron e+
Pozitron e+
je antičásticí k elektronu, má tudíž stejnou hmotnost a
spin, elektrický náboj je stejné velikosti, ale opačného
(kladného) znaménka. Ve vakuu je pozitron stabilní
částicí, stejně jako elektron. Jakmile se však nachází v
látkovém prostředí zaplněném atomy a tudíž i elektrony,
zaniká v anihilační interakci s elektrony: e+ + e- ® 2g (§1.6, část "Interakce nabitých částic -
přímo ionizující záření",
obr.1.6.1 dole, pasáž "Interakce
pozitronového (beta+)
záření"), přičemž vznikají dvě kvanta záření gama o
energiích 511keV, rozlétající se v protilehlých směrech
(pod úhlem 180°). Tato dokonalá úhlová korelace se s
výhodou využívá v gamagrafickém zobrazení metodou pozitronové
emisní tomografie v nukleární medicíně po aplikaci
pozitronového beta+-radionuklidu, např. 18F (§4.3, část "Pozitronová emisní tomografie PET").
Pozn.: Tyto
zákonitosti platí přesně jen v těžišťové
vztažné soustavě pozitronu a elektronu. Energie fotonů 2x511keV je důsledkem
zákona zachování energie (klidová energie
elektronu i pozitronu je m0e.c2 = 511keV), protilehlý směr 180° je důsledkem zákona
zachování hybnosti. Při srážkách pozitronů a
elektronů vyšších energií by se úhel rozletu anihilačních
fotonů lišil od 180°. V látkovém prostředí však pozitron
a elektron mají v okamžiku, kdy dojde k anihilaci, již
poměrně malé rychlosti, takže emitovaná kvanta vylétají
skutečně téměř opačným směrem.
Pozitronium
Těsně před vlastní anihilací elektron e- a pozitron e+
mohou na chviličku kolem sebe obíhat
(obíhají kolem společného těžiště) - utvoří zvláštní
vázaný systém (podobný atomu vodíku) zvaný
positronium (Ps). Rozměr "atomu"
pozitronia je dvojnásobek atomu vodíku, vazbová energie
pozitronia je 6,8 eV. Podle vzájemné
orientace spinů elektronu a pozitronu může být pozitronium
buď v singletním stavu 1S0 s opačně orientovanými spiny -
tzv. parapozitronium p-Ps (1/4 případů), nebo v
tripletním stavu 3S1 se souhlasně orientovanými spiny -
tzv. orthopozitronium o-Ps (3/4 případů).
Tento systém pozitronia je však nestabilní,
obě částice se za vyzařování elektromagnetických vln k
sobě po spirále přibližují; u p-Ps za cca 120ps na sebe
"dopadnou" a dojde k vlastní anihilaci na dva
fotony g, každý o energii
511keV. V případě o-Ps je anihilace na dva fotony zakázána
kvantovými výběrovými pravidly (souvisí se zákonem
zachování spinového momentu hybnosti - každý z fotonů má
spin 1), takže o-Ps by se ve vakuu rozpadalo s poměrně dlouhou
dobou života cca 140ns emisí 3 fotonů se spojitým
energetickým spektrem (celkovou energii 1022keV si
fotony rozdělí stochastickým způsobem). V látce však
pozitron vázaný v o-Ps daleko dříve stačí anihilovat s
některým "cizím" elektronem z okolního prostředí,
který má opačnou orientaci spinu - vznikají opět dva
fotony g o energiích 511keV.
Při anihilaci pozitronu s elektronem
vznikají v naprosté většině případů 2 fotony gama, jak
bylo výše uvedeno. Někdy jich však může vzniknout i více,
avšak s velmi malou pravděpodobností (pravděpodobnost, že
při e-e+-anihilaci
vznikne 2+n fotonů je úměrná a-n, kde a=1/137
je konstanta jemné struktury). Pokud pozitron interaguje s
elektronem vázaným v atomovém obalu, může být zánik
takového páru doprovázen i vysláním pouze jediného
fotonu, přičemž část energie a příslušná hybnost mohou
být předány buď atomovému jádru nebo některému z
ostatních elektronů; pravděpodobnost tohoto procesu je však
velice malá a v praxi se neuplatňuje.
Doba života pozitronů
v látkách činí řádově stovky pikosekund. Přesná hodnota
však záleží na lokálních elektronových hustotách a
konfiguracích, čehož se využívá ve spektroskopické metodě
PLS (Positron Lifetime Spectroscopy ....).
Zkoumaný materiál se lokálně ozařuje b+- g zářičem (nejčastěji 22Na),
přičemž doba života pozitronů se stanovuje na základě
měření zpožděných koincidencí mezi detekcí fotonu
záření g z ozařujícího
radionuklidu (u 22Na je to g 1274 keV) a detekcí anihilačního fotonu
g 511 keV.
V pozemské přírodě se tudíž pozitrony za
normálních okolností trvale nevyskytují, vznikají jen na
kratičkou dobu při určitých interakcích elementárních
částic a vzápětí (za cca 10-10-10-7s) opět anihilují s elektrony. Nejobvyklejším
procesem, při němž vznikají pozitrony, je b+-radioaktivita způsobená přeměnou
protonu p+
v jádře na neutron no, pozitron e+ a neutrino: p+ ® no + e+ + ne (§1.2,
část "Radioaktivita b+"). Pozitrony jsou dále
poměrně častými produkty při interakcí částic při
vysokých energiích (bude níže
několikrát ukázáno) a při rozpadech
mionů a pionů (viz níže "Miony m a tauony t"); takto se vyskytují v sekundárním
kosmickém záření (viz pasáž
"Kosmické záření" v §1.6). Pozitrony mohou
vznikat i za pomoci záření gama: pokud má záření gama
vyšší energii než 1022 keV, jedním ze způsobů jeho interakce s látkou je
tvorba elektron-pozitronových párů (§1.6, část "Interakce záření gama a X", pasáž "Tvorba
elektron-pozitronových párů").
Pro úplnost se zmíníme o jednom
"exotickém", v praxi zatím neuskutečněném,
způsobu vzniku pozitronů :
Breit-Wheelerův
proces produkce e+e- párů
Podle kvantové elektrodynamiky by dvojice
elektron-pozitron teoreticky mohly vznikat i při srážce
dvou fotonů g1+g2 ® e++e- ; je to
inverzní proces k výše uvedené anihilaci pozitronu s
elektronem: e++e-®2g (G.Breit a J.A.Wheeler ho navrhli již v r.1934). Tento dvoufotonový proces má však velmi malou
pravděpodobnost (nepatrný účinný průřez), k jeho
prokázání by bylo potřeba extrémně intenzívní kolimované
svazeky fotonů gama o energii vyšší než 511keV; při detekci
by pak hledaný efekt byl mnohonásobně překryt daleko
silnějším sekundárním zářením - zatím se nepodařilo...
Další možností fotoprodukce by mohl být tzv. multifotonový
Breit-Wheelerův proces (...), při němž vysokoenergetické
fotony při průchodu přes velmi silné elektromagnetické pole
by se mohly rozpadat na elektron-pozitronové páry. Zde je
určitá možnost realizace v blízké budoucnosti pomocí vysoce
výkonných laserových systémů...
Pozitron
poprve pozoroval v r.1932 C.D.Anderson v kosmickém záření
detekovaném pomocí Wilsonovy mlžné komory umístěné v
magnetickém poli, kde se objevila stopa částice stejných
ionizačních vlastností jako elektron, ale s opačným směrem
stáčení v magnetickém poli, tedy "kladný"
elektron.
 Protony a neutrony
Protony a neutrony 
Protony a neutrony, souhrnně nazývané nukleony,
jsou stavebními částicemi atomových jader. Jedná se o
těžké částice ze skupiny baryonů,
vykazují silnou interakci což je řadí mezi hadrony
- jsou složeny ze 3 kvarků. Jsou přírodního původu
- vznikly v "ohnivé peci" velkého třesku na
počátku tzv. hadronové éry, v první miliontině sekundy
existence vesmíru. Kromě toho vznikají při řadě procesů a
interakcí jiných elementárních částic; při radioaktivních
přeměnách b-,+ dochází k vzájemným přeměnám neutronů a
protonů (§1.2, pasáž "Mechanismus rozpadu
b. Slabé interakce.").
Protony, jakožto jádra vodíku, byly
objeveny při studiu elektrických výbojů v plynech zhruba ve
stejné době jako elektrony (koncem 19.stol.). Neutrony byly
objeveny až v r.1932 J.Chadwickem při ostřelování jader
berylia částicemi alfa (§1.1 "Atomy a atomová
jádra", část "Stavba atomového jádra").
 Proton p+
Proton p+
nese kladný elementární elektrický náboj stejné absolutní
velikosti e jako elektron, jeho klidová hmotnost je mp = 1,6726.10-27kg = 1836,151 me = 938,256MeV/c2. Magnetický moment
protonu je e.h/4pmp
- tzv. jaderný magneton, který je 1836-krát menší
než Bohrův magneton (zjednodušeně si to
můžeme představit tak, že při stejném spinu a náboji
těžký proton "rotuje pomaleji", než lehký
elektron). Proton je stabilní
částice (pomineme zde některé spekulace o možném rozpadu
protonu *). Počet protonů v jádře (protonové číslo Z)
určuje zároveň i počet elektronů a jejich energetické
hladiny v obalu - a tudíž i "velikost" atomu a jeho
chemické vlastnosti při slučování s dalšími atomy.
Samotný proton tvoří jádro nejjednoduššího prvku - vodíku
1H1. S volnými protony
se setkáváme v ionizované vodíkové plasmě a při jaderných
reakcích, do nichž urychlené protony vstupují, nebo jsou
jejich produkty. Protony jsou nejčastějším částicemi,
které se pro účely jaderné fyziky urychlují v
urychlovačích (viz níže kapitolu "Urychlovače
nabitých částic"). Počet protonů v atomovém jádře udává protonové
(atomové) číslo Z, které zároveň určuje počet
elektronů v atomovém obalu a tím i chemické vlastnosti atomu
- pozici prvku v Mendělejevově periodické tabulce.
*) Tzv. grandunifikační teorie připouštějí nestabilitu
protonu, který
by se měl rozpadat na miony či pozitrony a na jeden neutrální
či dva nabité piony [p+ ® (m+ nebo e+) + (po nebo p++p-)]
s dobou života řádově tp»1030-1033 roků. Tento rozpad by byl
způsoben přeměnou kvarku na lepton prostřednictvím bosonu X
a vzhledem k obrovské hmotnosti bosonu X je jeho
pravděpodobnost nesmírně malá. Experimenty zatím dávají
odhady tp>1030 let. Tyto pokusy o pozorování rozpadu protonu se
provádějí hluboko pod zemí (z důvodu odstínění
kosmického záření), kde jsou umístěny velké nádrže s
vodou, opatřené mnoha fotonásobiči, které by mohly
zaregistrovat slabé záblesky způsobené průchodem rychlých
částic vzniklých jako produkty rozpadu protonu.
Nejdokonalejším zařízením tohoto druhu je Superkamioka-NDE
v Japonsku, které sice nezaznamenalo žádný rozpad protonu,
ale bylo velice úspěšné při detekci a spektrometrii neutrin
(viz pasáž "Neutrina"
v §1.2 "Radioaktivita").
Pozn.: Jiným
hypoteticým a značně kuriózním mechanismem by mohl být
rozpad protonu přes virtuální černou díru
(§4.8 "Astrofyzikální význam černých děr" v monografii "Gravitace, černé díry a
fyzika prostoročasu"). Černé minidíry vyzařují
kvantovým Hawkingovým mechanismem částice, které jsou
obecně jiné, než ty které černá díra pohltila; porušuje
se zákon zachování baryonového čísla (§4.7 "Kvantové
vyzařování a termodynamika černých děr" v téže knize). Pokud tedy dva kvarky v protonu
spadnou do virtuální černé mikrodíry, je možné zpětné
vyzáření např. antikvarku a leptonu, čímž se proton
přemění na mion či elektron a pion.
 Neutron no
Neutron no
je elektricky neutrální, jeho klidová hmotnost mn = 1,6748.10-27kg = 1838,65 me = 939,55MeV/c2 je o něco vyšší
než u protonu. Ve stabilních atomových jádrech jsou neutrony
stabilní, volný neutron (ve vakuu) se rozpadá
s poločasem cca 13 minut b--rozpadem
no ® p+ + e- + n'e na proton, elektron a
antineutrino. Rozdíl v hmotnosti neutronu a protonu činí asi
2,5-x hmotnost elektronu (tento rozdíl pochází z rozdílu hmotnosti kvarků
"u" a "d" a z rozdílu vazebné energie). Avšak intermediální boson W, který přeměnu
kvarků zprostředkovává, je asi 80-x hmotnější než proton
nebo neutron, takže je zde vysoká potenciálová bariéra.
Neutron se tedy, navzdory drobnému energetickému přebytku,
nerozpadá okamžitě na proton, ale tunelové překonání této
bariéry mu v průměru trvá těch 13 minut.
S
volnými neutrony se v pozemské přírodě běžně
nesetkáváme, v horních vrstvách atmosféry jich menší
množství vzniká při interakcích kosmického záření (§1.6, část "Kosmické záření"). Jsou však běžnými produkty jaderných
reakcí a do jaderných reakcí též ochotně vstupují
(§1.3, pasáž "Reakce vyvolané
neutrony"). Intenzívními zdroji
neutronů jsou jaderné reaktory, ať již štěpné (),
nebo zatím pokusné fúzní termonukleární (§1.3, část "Štěpení
atomových jader" a "Slučování
atomových jader"). Jako laboratorní zdroje neutronů se konstruují
specifické malé urychlovače nabitých částic (většinou
deuteronů, s tritiovým terčíkem) zvané neutronové
generátory (viz níže
"Urychlovače nabitých částic", pasáž "Neutronové
generátory"), nebo radioisotopové
zdroje tvořené směsí a-zářiče s lehkým prvkem (jako je směs americia s
beryliem, dochází k reakci a,n), či těžkým transuranovým radionuklidem
(nejčastěji kalifornium 252), při jehož spontánním
štěpení se uvolňují neutrony (§1.3,
"Transurany").
Původ hmotnosti protonů a
neutronů
Protony a neutrony jsou mnohem těžší, než činí součet
hmotností jejich kvarků. Např. proton má hmotnost 938MeV,
zatímco hmotnost kvarku "u" je 2MeV a kvarku
"d" 5MeV. Většina hmotnosti protonu proto pochází z
kinetické energie vnitřního pohybu jeho
kvarkových komponent. Vysvětluje se to na základě kvantových
relací neurčitosti, podle nichž součin neurčitosti v
poloze a hybnosti částice je větší než Planckova konstanta.
Kvarky jsou v protonu či neutronu uzavřeny
("uvězněny") v prostorové oblasti o průměru cca 10-13cm; tato vnuceně
velmi malá neurčitost v poloze kvantově implikuje značnou
hybnost a tím i kinetickou energii každého z kvarků,
nejméně cca 200MeV. Bilance kinetické energie takových tří
intenzívně kmitajících kvarků je přibližně ekvivalentní
hmotnosti protonu.
Kdyby všechny kvarky měly stejné hmotnosti, dalo by se
čekat, že proton bude poněkud hmotnější než neutron,
protože elektrický náboj protonu (který neutron nemá)
přispívá k jeho vnitřní energii. Rozdíl v hmotnosti kvarků
"u" a "d" (který se v
unitárních teoriích polí a částic vysvětluje interakcí s
Higgsovým polem - viz níže) však
způsobuje, že neutron (u,u,d) je poněkud "těžší"
než proton (u,d,d). Tento rozdíl hmotnosti způsobuje
nestabilitu volného neutronu, jeho b-rozpad na proton, elektron
a neutrino působením slabé interakce.
Antičástice k protonům a
neutronům
Antiproton p'- se od protonu liší jen svým záporným nábojem a
opačným směrem magnetického momentu, ve vakuu je rovněž
stabilní částicí. Antineutron n'o je neutrální
částicí jako neutron, od něhož se liší jen opačnou
orientací magnetického momentu, poločas jeho rozpadu ve vakuu
je stejný jako u neutronu, rozpadá se podle schématu n'o ® p'- + e+ + ne na antiproton, pozitron a neutrino.
Antiprotony a antineutrony se v pozemské přírodě
běžně nevyskytují, vznikají při interakci částic
vysokých energií a zase pak zanikají interakcemi s nukleony.
Vzhledem k zákonu zachování baryonového čísla mohou být
antinukleony produkovány pouze v párech společně s nukleony.
Nejobvyklejší způsob produkce antiprotonů p' je v reakcích
p + p ®
2p + p + p' , resp. p + n ® 2p + n + p' ,
přičemž prahová kinetická energie ostřelujícího protonu
(v laboratorní terčíkové soustavě) činí asi 5,6GeV, resp.
3,6GeV; pokud však tato interakce probíhá při ostřelování
jádra, může být prahová energie produkce antiprotonů i
nižší (kolem 3GeV). Antineutrony vznikají v podobných
reakcích p + p ® 2p + n + n' , resp. p + n ® p + 2n + n', dále pak v
reakcích antiprotonů p' + p ® n + n', p' + n ® n + n' + p-.
Při interakcích antinukleonů jsou nejdůležitěší
interakce (p',p) antiprotonů s protony. Při vysokých
energiích zde mohou vznikat i další těžké částice jako
jsou hyperony, což bude zmíněno níže. Při nízkých
energiích antiprotonů nebo při jejich zastavení (viz níže)
dochází k zániku nukleonových párů s
produkcí mezonů, kvant gama, popř. dochází k reakci p'+p®n+n'
("výměna náboje"). Zánik párů (p',p) je silnou
interakcí, při níž nejčastěji vznikají mezony p *) (jen v malém procentu mezony K);
nejmenší počet vzniklých mezonů vzhledem k zákonu
zachování hybnosti jsou 2 mezony p, většinou jich však
vniká více, nejčastěji 5 mezonů - typická interakce tohoto
druhu je: p' + p ® 2p+ + 2p-
+ po .
*) Vznik mesonů p při anihilaci antiprotonu
s protonem je důsledkem kvarkové struktury:
antikvarky v antiprotonu a kvarky v protonu se spojují do dvojic
kvart-antikvark, což jsou mesony.
Při vniknutí antiprotonu do látky dochází
vlivem elektromagnetické interakce k ionizaci atomů, podobně
jako u každé jiné nabité částice, čímž se antiproton
brzdí a zpomaluje. Během tohoto zpomalování může antiproton
zaniknout při interakci s jádrem, avšak může se zpomalit
(či téměř zastavit) natolik, že může být zachycen
protonem (vodíkovým jádrem) - vzniká nový "exotický
atom", zvaný protonium, sestávající z
protonu a antiprotonu obíhajících kolem společného
těžiště. Podobně může být zachycen i jiným těžším
jádrem na některé vyšší dráze (odkud vyrazil elektron) a
při svém oběhu pak přechází na nižší dráhy, což je
doprovázeno emisí buď fotonů X-záření, nebo Augerových
elektronů. Nakonec je pohlcen jádrem a zanikne intrakcí s
protonem či neutronem za vzniku pionů.
Antihmota
Antiproton, kolem něhož obíhá pozitron, tvoří atom "antivodíku",
který má analogické vlastnosti jako obyčejný vodík.
Antiprotony a antineutrony mohou vytvářet "anti-atomová
jádra", kolem nichž mohou obíhat pozitrony v úplně
stejných konfiguracích jako je tomu u příslušných
obyčejných atomů - jedná se o "antiatomy",
které by v rámci "antisvěta" měly
úplně stejné chemické i spektroskopické vlastnosti jako
naše atomy - tvořily by antihmotu - (bylo diskutováno výše, pasáž "Antičástice,
antihmota, antisvěty").
Antiproton byl objeven v r.1955 na
urychlovači v Berkeley při ostřelování měděného terčíku
protony urychlenými na 6,2GeV. V r.1956 byl objeven antineutron
na témže urychlovači: se stejnou energií byl protony
ostřelován beryliový terčík a vzniklé antiprotony byly
vedeny do soustavy scintilátorů a Čerenkovova detektoru
zapojených v antikoincidenci, kde reakcí p'+p®n+n' s
vodíkovými jádry vznikaly antineutrony, které při interakci
s nukleony v Čerenkovově detektoru byly registrovány jako
intenzívní záblesky.
 Neutrina a antineutrina
Neutrina a antineutrina  (podrobněji viz odkaz "Neutrina
- "duchové" mezi částicemi")
(podrobněji viz odkaz "Neutrina
- "duchové" mezi částicemi")
Jsou to všudypřítomné, avšak téměř nepolapitelné
částice. Neutrina n a antineutrina n' jsou nejlehčí a nejslaběji interagující ze všech
známých druhů elementárních částic - náleží mezi
leptony. Jsou to fermiony se spinovým číslem 1/2, nenesou
elektrický náboj, nevykazují silnou interakci, ale pouze slabou
interakci (a univerzální
gravitační interakci, která nás zde z hlediska fyziky
elementárních částic nezajímá, může však mít určité kosmologické
důsledky).
Rozeznáváme tři druhy neutrin: neutrino elektronové
ne, mionové nm a tauonové nt, které se však mohou spontánně vzájemně
přeměňovat při tzv. oscilaci neutrin.
Neutrino jako takové je mixáží vlastních stavů
ektronového, mionového a tauonového neutrina a proto
dochází k periodické přeměně jednoho neutrina na druhé.
Elektronová neutrina vznikají typicky při vzájemných
přeměnách neutronů a protonů b-,+-rozpadem: no ® p+ + e- + n'e,
p+ ® no + e+ + ne, mionová a tauonová neutrina pak při rozpadu mionů
a tauonů: m- ® e- + n'e+ nm, t- ® nt
+ e- + n'e, t- ® nt + m- + n'e,
...... Neutrina kromě toho vznikají v řadě vzájemných
interakcí elementárních částic, v nichž se uplatňují
slabé interakce. Velké množství neutrin vzniká při
termojaderných reakcích v nitru Slunce a hvězd, odkud díky
své velmi slabé interakci snadno pronikají ven a jsou
vyzařovány do okolního prostoru. Zvláště silný
"záblesk" neutrinového záření vzniká při
výbuchu supernovy - viz §4.2 "Konečné
fáze hvězdné evoluce. Gravitační kolaps" knihy "Gravitace, černé díry a fyzika
prostoročasu". Ve vesmíru se
nachází i obrovské množství tzv. reliktních neutrin
pocházejících z leptonové éry vesmíru těsně po velkém
třesku. Neutrina patří, spolu s fotony, mezi nejhojnější
částice ve vesmíru. Vlastnosti neutrin, jejich vznik,
metody detekce a příp. kosmologický význam neutrin, jsou
podrobněji popsány v §1.2 "Radioaktivita", část
"Neutrina - "duchové" mezi částicemi".
Neutrina byla jako hypotetické
částice zavedena W.Paulim r.1930 při studiu energetické
bilance b-rozpadu (viz §1.2, část "Radioaktivita
beta", obr.1.2.3), jejich název a
specifikace vlastností pocházejí od E.Fermiho.
Experimentálně byla neutrina prokázána až v r.1956
experimenty nastíněnými ve zmíněném odkazu "Neutrina".
 Miony m a tauony t
Miony m a tauony t 
 Miony m- a m+
Miony m- a m+
(jsou to vzájemně antičástice), označované též jako
"těžké elektrony", jsou středně těžké částice
s hmotností mm = 206 me, nesou záporný nebo kladný elektrický náboj
stejné velikosti jako je elementární náboj elektronu;
neexistují neutrální miony bez elektrického náboje. Miony
jsou nestabilní částice, které se s
poločasem »2.10-6s rozpadají na elektron, resp. pozitron, a dvě
neutrina: m- ® e- + n'e+ nm , m+ ® e+ + ne+ n'm. Tento rozpad má charakter slabé interakce a je
podobný radioaktivnímu rozpadu beta; rovněž energetické
spektrum vznikajících elektronů nebo pozitronů je zde
spojité, maximální energie činí »53MeV.
Miony se v pozemské přírodě
vyskytují v sekundárním kosmickém záření (viz pasáž "Kosmické záření" v §1.6). Vznikají ve
vyšších vrstvách atmosféry (nad 10km) při srážkách
protonů a dalších částic primárního kosmického záření
s protony a neutrony jader dusíku a kyslíku v atmosféře. V
těchto primárních srážkách vznikají nejdříve p-mezony, které se
během cca 2,5.10-8s rozpadnou na miony, které se s kinetickou energií
cca 4MeV pohybují relativistickou rychlostí. Vzhledem ke své
době života »2.10-6sekundy by podle klasické mechaniky mion uletěl jen
zhruba 500metrů a pak se rozpadl - na povrch Země by tedy
prakticky žádné miony neměly dopadnout. Díky relativistické
dilataci času však mion z hlediska
pozorovatele na Zemi "žije déle" a má dost času,
aby dopadl na povrch Země. Tento experimentální fakt, že mion
uletí dráhu 20-krát delší než by v klasické mechanice
odpovídalo jeho době života, je přesvědčivým důkazem
efektu zpomalování toku času podle
speciální teorie relativity.
Nejčastější způsob vzniku mionů je při rozpadu p-mezonů: p- ® m- + n'm , p+ ® m+ + nm (viz následující pasáž
"Mezony p a K").
Interakce mionů s nukleony probíhají podle schématu: m- + p ® n + nm , m+ + n ® p + nm , .....
Vnikne-li záporný mion m- do
látky, může být (po svém zpomalení ionizací) zachycen
Coulombovým polem jádra a vytvořit svéráznou vázanou
soustavu podobnou atomu - tzv. mionový atom
nebo mezoatom. Kladný mion m+ prolétající látkovým prostředím může zase
zachytit elektron a vytvořit nestabilní vázanou soustavu mionu
m+ a obíhajícího
elektronu e-, zvanou mionium; je to soustava
analogická pozitroniu a má strukturu podobnou vodíkovému
atomu.
Mion m byl objeven v r.1936
C.D.Andersonem a S.H.Neddermeyerem při studiu kosmického
záření ve Wilsonově mlžné komoře (podobně jako pozitron).
Pozn. :
Z hlediska standardního modelu částicové fyziky stojí za
zajímavost gyromagnetický moment mionů,
který má ..... anomální ......... (je diskutováno níže v
pasáži "g-2 experiment").
 Tauony t- a t+
Tauony t- a t+
(jsou to vzájemně antičástice), označované též jako
"supertěžké elektrony", jsou velmi těžké
částice s hmotností mt
»
3484me » 1177MeV/c2, nesou záporný nebo
kladný elektrický náboj stejné velikosti jako je
elementární náboj elektronu. Tauony jsou vysoce nestabilní
částice, které se s poločasem »3.10-13s rozpadají na elektron nebo mion a dvě neutrina: t- ® e- + n'e+
nt , t- ® m- + n'm+ nm. Vzhledem ke své vysoké klidové hmotnosti jsou však
tauony schopné rozpadat se i na hadrony, především piony p-, p+, po a taunová neutrina, např. t- ® p- +nt , t- ® p- + po + nt , t- ® p- + p+ + p- +nt , etc.
.
Tauon t byl objeven v letech
1974-77 týmem pod vedením M.Perla při experimentech s
vysokoenergetickými srážkami pozitronů a elektronů ve
vstřícných svazcích urychlovače ve Stanfordu. Při
srážkách elektronů s pozitrony docházelo ke vzniku dvojic t+ a t-, které
se rozlétly jen na krátkou vzdálenost (cca 1mm) a vzápětí
se rozpadaly na elektrony, miony a neutrina. Vznik tauonů byl
prokázán na základě detekce nabitých částic, analýzou
jejich energií a úhlového rozložení (metodikou zmíněnou
výše "Analýza dynamiky interakcí částic").
 Mesony p a K
Mesony p a K 
 p-mesony
(nazývané též piony)
p-mesony
(nazývané též piony)
jsou nejčastějším druhem nových sekundárních částic,
vznikajících částicovými interakcemi při vysokých
energiích převyšujících cca 300MeV; při ještě vyšších
energiích (nad »1GeV) pak vznikají i K-mesony a hyperony.
Mesony p a K mají následující společné vlastnosti: jsou to
středně těžké částice se spinem 0 (patří tedy mezi
bosony), vykazují silné interakce (jsou hadrony) a jsou nestabilní.
Podle standardního modelu částic jsou tvořeny vázaným
kvarkem a antikvarkem.
Nabité mesony p-
a p+, které jsou vzájemně antičásticemi, nesou
záporný či kladný elementární náboj stejné velikosti jako
elektron, mají klidovou hmotnost »2,4898.10-25g » 273me » 140MeV/c2 a s poločasem »2,55.10-8s se rozpadají
(slabou interakcí) na miony a neutrina: p- ® m- + n'm , p+ ® m+ + nm (miony se pak dále rozpadají na
elektrony a neutrina). Při tomto rozpadu
se uvolňuje kinetická energie (mp-mm).c2 » 34MeV, z čehož mion m odnáší menší část
cca 4,2MeV a zbytek kinetické energie necelých 30MeV získává
mionové neutrino nm.
Vedle částicových interakcí v
urychlovačích vznikají piony na kratičký okamžik v horních
vrstvách atmosféry při interakcích vysokoenergetických
protonů z primárního kosmického záření s nukleony v
jádrech dusíku, kyslíku a uhlíku; vzápětí se rozpadají na
miony (viz pasáž "Kosmické záření" v §1.6).
Neutrální meson po
má klidovou hmotnost »264me » 135MeV/c2 a s velmi krátkým poločasem »0,9.10-16s se rozpadá (elektromagnetickou interakcí) na dvě
kvanta gama: po ® g + g.
Pozn. : Z
hlediska vnitřní struktury jsou mesony vázaným systémem kvark-antikvark.
Tento systém je však nestabilní a jeho rozpad můžeme
zjednodušeně chápat jako proces "anihilace"
kvark-antikvarkové dvojice; buď slabou interakcí přes
intermediální boson W±, nebo elektromagneticky přímo na kvanta g (srov.
příslušný Feynmanův diagram na obr.1.5.1). Je to trochu
analogické jako u výše zmíněného pozitronia,
které je též nestabilním vázaným stavem dvojice
částice-antičástice (e--e+),
které anihilují na kvanta g.
p-mesony
sehrály pestrou a zajímavou úlohu v historii jaderné
fyziky. Dlouhou dobu (40.-70.léta) byly považovány za
výměnné částice, zprostředkovávající
silné jaderné interakce krátkého dosahu protonů a neutronů
v jádrech atomů (pochází od H:Yukawy). Zdála se tomu
nasvědčovat i skutečnost, že při vysokoenergetických
srážkách protonů a neutronů pravidelně vznikají piony.
Idea p-mezonů
jako nositelů silné intrakce se však nakonec neosvědčila.
Ukázalo se, že podstata silné interakce leží hlouběji -
tkví ve vnitřní kvarkové struktuře protonů a neutronů.
Při interakcích protonů a neutronů vznikají piony nikoli
jako výměnné částice, ale proto, že p-mesony jsou lehčí a
jednodušší částice složené rovněž z kvarků (a jejich
antičástic), stejně jako nukleony. Přesto však jsou p-mesony nejdůležitější
ze všech nestabilních "exotických" částic; mohou
mít dokonce praktické využití, viz např.
§3.6, část "Hadronová
radioterapie".
 Mesony K,
Mesony K,
zvané též kaony, jsou více než 3-krát
těžší než p-mesony.
Nabité mesony K+
a K-, které jsou vzájemně antičásticemi, nesou kladný
či záporný elektrický náboj stejné velikosti jako elektron,
mají klidovou hmotnost »966,6me » 494MeV/c2 a s poločasem »1,24.10-8s se rozpadají na p-mesony, miony a neutrina: K+®p++po, K+®m++n, K+®p++p++p-, K+®p++po+po, K+®po+m++n, K+®po+e++n; analogicky (sdruženě) i K-.
Neutrální meson Ko
má hmotnost »974,2me » 498MeV/c2 a velmi rychle se rozpadá na p-mesony a též na miony,
elektrony a neutrina dvěma druhy rozpadů:
dvoučásticové rozpady: Ko®p++p-, Ko®po+po, -
(poločas »0,9.10-10s);
tříčásticové rozpady: Ko®po+po+po, Ko®p++p-+po, Ko®p+,-+m-,++n, Ko®p-,++e+,-+n, - (poločas »5,7.10-8s).
To, že se meson Ko rozpadá s
dvěma různými poločasy a různými pochody, lze vysvětlit
předpokladem, že meson Ko je kvantovou "směsí" dvou neutrálních
částic KoL ("Long") a KoS ("Short"), které mají různé doby života a různá schémata
rozpadu. Tyto skutečnosti se interpretují tak, že pozorovaný
meson Ko je vnitřně "směsí" či superpozicí Ko a jeho
antičástice K'o. Mezi těmito dvěma stavy neutrální kaon spontánně
"osciluje".
Interakce mesonů p
a K
Mesony p- a p+
interagují při nízkých energiích s nukleony především
reakcemi: p- + p ® n + g, p+ + n ® p + g, při vysokých energiích pionů pak dochází i ke
sdružené produkci kaonů, hyperonů a antihyperonů, např. p- + p ® K+ + K- + n, p- + p ® L + Ko, a pod.
- další reakce viz níže v odstavci o hyperonech.
Při interakci s látkou mohou být p--mesony (po příslušné zabrzdění ionizačními
ztrátami energie) zachycovány na orbitě kolem
jádra (podobně jako elektrony v atomu), takže na na velmi
krátkou dobu se vytvoří mesoatom s pionem p-, který je pak pohlcen jádrem a tam se sloučí s
protonem (p-+p®n+g).
Vznik mesonů p a
K
p-mesony
vznikají především jako nové sekundární částice
při interakcích protonů s nukleony, pokud kinetická energie v
laboratorní (terčíkové) soustavě je vyšší než 2.mp.c2 » 300MeV. Reakcí tohoto
typu může být několik:
p+p ® p+n+p+, p+p ® p+p+po, p+n ® n+n+p+, p+n ® p+p+p-,
p+n ® p+n+po, n+n ® n+p+p-, n+n ® n+n+po , ....,
přičemž tyto reakce mohou probíhat jak na volných
nukleonech, tak na nukleonech vázaných v jádře. Piony mohou
být také produkovány fotojadernými reakcemi tvrdého
záření gama: g+p ® n+p+, g+p ® p+po, jejichž prahová energie záření gama činí zhruba
mp.c2 » 140MeV.
Mesony K vznikají tzv. asociovanou produkcí
ve dvojicích buď spolu, nebo ve dvojicích s hyperony, a to
buď při vzájemných interakcích nukleonů, nebo p-mesonů s
nukleony. Příklady takových interakcí jsou: p+p ® L+K++p, p-+p ® K++K-+n, p-+p ® L+Ko, atd.;
další kombinace s hyperony jsou uvedeny v následujícím
odstavci.
Podivnost
částic
Uvedené mezony K, jakož i níže zmíněné hyperony,
mají některé zvláštní - "podivné"
- vlastnosti, s nimiž se nesetkáváme u ostatních částic.
Jedná se o nesymetrie při produkci a rozpadu
těchto částic. Tyto částice vznikají ve
vysokoenergetických hadronových srážkách s vysokou
pravděpodobností - párová produkce silnou interakcí.
Jejich rozpad však většinou probíhá poměrně pomaleji
(řádově 10-10s) pomocí slabé interakce. K vysvětlení
této situace byla zavedena nová veličina či (aditivní)
kvantové číslo nazvané podivnost S (Strange
- pro běžné částice je S=0, podivné částice mají S=±1,±2, hyperon W dokonce S=-3),
které se zachovává při silných interakcích, ale při
slabých interakcích se nezachovává. Je tím vysvětleno, že
při silných interakcích běžných částic vznikají podivné
částice ve dvojicích, jejichž součet podivnosti je nulový,
avšak slabou interakcí se podivné částice mohou rozpadat i
na částice bez podivnosti.
Pro vysvětlení v rámci kvarkového modelu hadronů byl
zaveden nový kvark "s" (strange),
který je nositelem podivnosti; s má podivnost S=-1,
antikvark s' má S=1, ostatní kvarky S=0. Přítomnost
kvarku "s" v dvoukvarkové kombinaci je
charakteristická pro podivné mezony K, pokud
se "s" vyskytuje v tříkvarkové kombinaci, jedná se
o hyperony - obr.1.5.3.
 Hyperony
Hyperony 
Nejtěžší dosud známé částice (kromě
tauonů), vznikající při částicových
interakcích za vysokých energií, jsou hyperony.
Všechny hyperony jsou fermiony, většinou se
spinem 1/2, s výjimkou W- který
má spin 3/2. Všechny hyperony jsou dále hadrony
vykazující silnou interakci a jsou to částice vysoce nestabilní
s velmi krátkou dobou života. Známe 7 druhů hyperonů (+
jejich antičástice), které zde stručně vyjmenujeme :
Hyperon Lo je elektricky nenabitý,
má hmotnost »2183me » 1116MeV/c2, dobu života »2,5.10-5s a rozpadá se podle schémat: L ® p + p- (66%), L ® n + po (34%).
Hyperon S+ s kladným elementárním nábojem má hmotnost »2327me » 1189MeV a s poločasem »0,8.10-10s se rozpadá na
nukleony a piony: S+ ® p + po, S+ ® n + p+.
Hyperon S- se záporným elementárním nábojem má hmotnost »2340me » 1197MeV a s poločasem »1,65.10-10s se rozpadá na
neutron a pion: S- ® n + p-.
Hyperon So bez elektrického náboje má hmotnost »2332me » 1193MeV a s velmi
krátkým poločasem blízkým
10-20s se rozpadá na hyperon lambda a foton gama: So ® L + g.
Hyperon X- se záporným nábojem má hmotnost »2585me » 1321MeV a s poločasem »1,7.10-10s se rozpadá na
hyperon lambda a pion: X- ® L + p-.
Hyperon Xo bez elektrického náboje má hmotnost »2566me » 1315MeV a s poločasem »3.10-10s se rozpadá na
hyperon lambda a pion: Xo ® L + po.
Hyperon W- se záporným nábojem má hmotnost »3405me » 1675MeV/c2 a s poločasem »1,5.10-10s se rozpadá na
hyperony a mesony: W- ® Xo,- + p-,o, W- ® L + K-.
Pozn.: Ve velmi
malém procentu případů byly pozorovány i další možnosti
rozpadu hyperonů, např. L®p+e-+n, S+®p+g, Xo®p+p-, a řada dalších.
Hyperjádra
Hyperony vykazují silné interakce, takže mohou vstupovat
do jader a být tam navázány jadernými silami - vznikne tzv. hyperjádro
či hyperfragment. V typickém hyperjádře je jeden z
neutronů nahrazen hyperonem Lo;
takové hyperjádro se pak značí NAL. Např. v jaderných emulzích ozařovaných mesony K- z
urychlovače byla pozorována hyperjádra 9BeL. Hyperjádra jsou nestabilní útvary,
které se rozpadají dvojím způsobem: mesonovým rozpadem nebo
nukleonovým rozpadem. Při mesonovém způsobu
se hyperon L uvniř jádra rozpadne podle schématu L®p+p-, nebo L®n+po, takže
např. hyperjádro 9BeL se rozpadne na meson p-, proton p+ a jádro 8Be4 (které se pak v tomto případě rozpadá na dvě
alfa-částice 4He2). Při nukleonovém rozpadu dochází
k reakcím L+p®p+n, nebo L+n®n+n, takže např. zmíněné hyperjádro 9BeL by se
rozpadlo způsobem: 9BeL®4He+3He+n.
Antihyperony
Podobně jako k nukleonům existují antinukleony, i ke každému
z uvedených hyperonů existuje příslušný antihyperon
(všechny tyto hyperony jsou samostatné, nejsou vzájemně
antičásticemi jako je to kupř. u mesonů p- a p+ či m- a m+). Podle
principu nábojové symetrie mají antihyperony stejné
hmotnosti, spin a dobu života jako hyperony, avšak opačná
znaménka el. náboje, baryonového čísla a magnetického
momentu. Rozpadová schémata antihyperonů jsou rovněž
nábojově sdružená s rozpadovými schématy hyperonů a
rovněž i reakce částic, při nichž antihyperony vznikají,
jsou analogické jako u hyperonů (dochází často k
"asociované" produkci hyperonů a antihyperonů či
mesonů - viz níže). Je třeba mít na paměti, že
antihyperony k nabitým hyperonům mají opačná znaménka el.
náboje, např. antihyperon S'- má kladný jednotkový náboj, takže přesněji
bychom jej mohli označit jako (S'-)+.
Hyperony vznikají při interakcích protonů, antiprotonů, p a K mesonů s
nukleony při vysokých energiích (>»5GeV), přičemž
v silných interakcích typu (nukleon+nukleon) nebo (p+nukleon) vznikají
současně dvě částice ze skupiny mesonů a hyperonů
(meson+meson, meson+hyperon, hyperon+antihyperon) - dochází ke sdružené
či asociované produkci hyperonů,
antihyperonů a mesonů, např.:
p + p ®
2p + L
+ L' ,
p + p ®
p + L +
K+ ,
............
.............
.............
K- + p ® W- + K-+ Ko ,
Dráhy hyperonů, resp. jejich
rozpadových produktů, jsou pozorovány ve Wilsonových
mlžných komorách, jaderných fotoemulzích a bublinových
komorách. Již v r.1947 pozorovali G.D.Rochester a C.C.Butler
při studiu kosmického záření ve Wilsonově mlžné komoře
dráhy dvou částic vylétajících z jednoho bodu - další
výzkumy ukázaly, že šlo o meson Ko rozpadající se na mesony p- a p+ a o
hyperon L rozpadající se na proton p+ a meson p-. Když pak urychlovače s dostatečně velkou energií
umožnily vytvářet svazky protonů a mesonů p, byly při studiu
jejich interakce v bublinových komorách a fotoemulzích
objeveny všechny další hyperony a zákonitosti jejich
asociované produkce s mesony K.
 Rezonance
Rezonance
Vznikají při některých interakcích vysokoenergetických
částic (jako je p+,- + p+ ® p+,- + p+, nebo interakce protonu s antiprotonem za vzniku
několika p-mezonů) a okamžitě
se rozpadají, jejich doba života činí asi 10-23 až 10-20 sekundy. Projevují
se vlasně jen výrazným rezonančním maximem v
energetické závislosti účinného průřezu dané interakce,
nebo zhuštěninami a píky na Dalitzově diagramu
energií sekundárních částic, které naznačují vznik
nějakého dočasně vázaného stavu. Rozeznáváme baryonové
rezonance a mezonové rezonance (jako je mezon r nebo některé
druhy mezonů *K). Rezonance se mnohdy ani za zvláštní
částice nepovažují, označují se jako kvazičástice.
Jsou to spíše jen dočasně excitované stavy vzniklé při
interakci dvou či více baryonů nebo mezonů, které se
rozpadají okamžitě, jakmile vyletí za hranice oblasti silné
jaderné interakce, v níž vznikly. Vzhledem k extrémně
krátké době života nemají patrně žádný význam pro
stavbu a vlastnosti hmoty. Jejich studium je však důležité
pro lepší proniknutí do subnukleární struktury hadronů,
jejich kvarkové struktury a pochopení vlastností silných
interakcí v rámci kvantové chromodynamiky (QCD). Některé
mezonové a baryonové rezonance jsou vyznačeny níže na
kvarkovém diagramu na obr.1.5.3.
 Bosony W-, W+, Z0
Bosony W-, W+, Z0 
Tyto bosony jsou intermediální částice zprostředkující slabou
interakci (Weak int.) v rámci
Weinbergova-Salamova modelu sjednocení elektromagnetické a
slabé interakce.
W-
a W+ nesou záporný a kladný elementární náboj stejné
velikosti jako elektron, mají hmotnost »82GeV/c2, jsou vzájemně
svými antičásticemi. W-bosony zprostředkovávají vzájemné b-přeměny
neutronů a protonů (podle schématu na obr.1.2.5 v §1.2 "Radioaktivita", pasáž "Mechanismus
rozpadu b. Slabá interakce."). Při této radioaktivitě beta- a beta+ způsobují W-,+
-bosony vzájemné přeměny kvarků "u" a
"d" uvnitř nukleonů, přičemž samotné W
zůstávají virtuální - okamžitě se rozpadají na
výsledný kvark, elektron či pozitron a neutrino.
Neutrální Z0
boson má hmotnost »93GeV, je svou vlatní antičásticí. Má menší
důležitost než W, v pozemské přírodě ani v
nynějším vesmíru se příliš neprojevuje. Patrně se však
významněji uplatňoval ve vysoenergetických procesech v
extrémních podmínkách velmi raného vesmíru (příp. i při výbuchu supernov..?..) - může zprostředkovávat vzájemné interakce
mezi neutriny (§1.2, pasáž "Interakce neutrin s částicemi a hmotou").
Pokud W či Z vzniknou při
vysokoenergetické interakci částic jakožto "reálné
částice", jsou vysoce nestabilní (s
dobou života cca 3x10-25 sec.)*) a vzápětí
se rozpadají na leptony a neutrina; typicky: W-® e- + n', W+® e+ + n, Zo® m+ + m- (nebo e+ + e-). Nebo
na kvarky a antikvarky. Při velmi vysokých
energiích je řada dalších možností jejich interakcí,
včetně produkce těžkých částic jako jsou Higgsovy bosony.
Feynmanovy diagramy některých důležitých interakcí bosonů
W±,Z0 jsou zakresleny na obrázcích 1.5.1.D,F,G,H,I. Částicové interakce způsobené výměnou nabitých
intermediálních bosonů W+,- se někdy označují jako "slabé nabité
proudy", reakce způsobené nenabitým Zo bosonem jako "slabé
neutrální proudy".
*) Částice s tak krátkou
dobou života nemohou být nijak přímo
experimentálně detekovány (rozpadnou se dříve než stihnou
vyletět z místa interakce, do žádného detektoru
nedoletí...). Mohou být detekovány pouze zplodiny jejich
rozpadu. Neutrina naše detektory u urychlovačů nejsou schopny
zaznamenat vůbec (nemají elektrický
náboj a téměř s ničím neinteragují),
mohou být jen nepřímo prokázány tím že změříme v
celkové bilanci energie a hybnosti určitou hodnotu chybějící
energie nebo hybnosti.
Intermediální bosony W-,W+,Zo byly nepřímo
experimentálně prokázány v r.1983 při interakcích ve
vstřícných proton-antiprotonových svazcích 270GeV«270GeV Super
Proton Synchrotronu v CERN.
 Hypotetické
a modelové částice
Hypotetické
a modelové částice 
Nakonec zde letmo zmíníme i některé "exotické"
částice, které by měly existovat podle určitých více či
méně ověřených teorií a modelů,
avšak nebyly dosud přímo experimentálně prokázané -
zůstávají částicemi hypotetickými.
Modelové částice
 Kvarky
Kvarky
jsou modelové "stavební" částice hadronů (jak je nastíněno níže - "Kvarková
struktura hadronů"). Kvarky jsou fermiony se spinem 1/2 a nesou třetinový
elektrický náboj -(1/3)e, +(2/3)e. Bylo zavedeno celkem 6
druhů kvarků, každý má svou antičástici - antikvark.
Jednotlivé kvarky a kvarkový model hadronů je stručně
popsán níže. Kvarky jsou primárními nositeli silné
interakce, zprostředkované gluony. Zároveň
však mohou podléhat vzájemným vnitřním transmutacím
za působení slabé interakce, zprostředkované
intermediálními bosony W-,W+,Zo (hlavním projevem této
transmutace kvarků je radioaktivita b, viz obr.1.2.5). Volné kvarky nebyly nikdy
pozorovány - viz následující odstavec "Gluony"
a níže pasáž "Kvark-gluonová plasma".
 Gluony (angl. glue=klih, lepidlo
- drží kvarky "slepeny" pohromadě v hadronech)
Gluony (angl. glue=klih, lepidlo
- drží kvarky "slepeny" pohromadě v hadronech)
jsou částice, které zprostředkovávají silné
interakce mezi kvarky (a svými "zbytkovými
projevy" i jaderné interakce mezi nukleony). Jsou to bosony
se spinem 1, mají nulovou klidovou hmotnost, nemají elektrický
náboj, nesou však tzv. "barevný náboj" *),
charakterizující různé druhy kvarků. Podobně jako foton,
nemá gluon antičástici (je svou vlastní antičásticí).
Gluonová interakce kvarků má zvláštní vlastnosti. Pokud
mají kvarky vysokou energii a jsou blízko u sebe, gluonová
interakce téměř nepůsobí a kvarky se chovají jako volné
částice - tzv. asymptotická volnost. Avšak
když se kvarky od sebe vzdálí na cca 10-13cm, začnou gluonové interakce intenzívně působit a
silně svazují kvarky k sobě - dochází k
"uvěznění" kvarků v hadronech. Další diskuse je
níže v pasáži "Kvark-gluonová plasma".
*) Foton, který zprostředkovává
elektromagnetickou interakci, sám nenese náboj této interakce
(elektrický náboj); fotony mezi sebou neinteragují. Gluony
však nesou "barvu" - náboj silné interakce, takže
mohou mezi sebou interagovat. Mohly by teoreticky vytvářet i
vázané systémy - tzv. gluonium.
Preony - jsou hypotetické sub-kvarkové
částice, z nichž by se mohly skládat kvarky (viz níže
pasáž "Preonová hypotéza").
 Gravitony
Gravitony
jsou kvanta gravitačního vlnění. Gravitační vlny
předpovídá obecná teorie relativity jakožto fyzika gravitace
a prostoročasu; jsou řešením Einsteinových rovnic
gravitačnho pole, podobně jako z Maxwellových rovnic
elektrodynamiky plyne existence elektromagnetických vln.
Gravitační vlny se od elektromagnetických liší jednak svým
velmi nepatrným působením na látku, jednak svým tzv. kvadrupólovým
charakterem. Hypotetický graviton má nulovou klidovou hmotnost,
pohybuje se rychlostí světla, jeho spinové číslo je 2.
Gravitační vlny se již podařilo
přímo detekovat, i když je to na hranicích současné
experimentální techniky. Na experimentální prokázání
gravitonů není naděje v dohledné budoucnosti. O
gravitačních vlnách pojednává podrobně §2.7 "Gravitační vlny" v knize "Gravitace,
černé díry a fyzika prostoročasu".
Skeptická poznámka k reálnosti existence gravitonů je tam v
pasáži "Gravitony - kvanta gravitačního
vlnění?".
 Higgsovy bosony
Higgsovy bosony
- jsou to kvanta tzv. Higgsova-Kibleova *) skalárního
pole, které se v kalibračních unitárních teoriích pole
zavádí do lagrangiánu za účelem tzv. spontánního
narušení symetrie elektroslabé interakce (viz
např. §B.6 "Sjednocování fundamentálních inetrakcí" v knize "Gravitace, černé díry a fyzika
prostoročasu"). Toto pole vede též
k tomu, že některé intermediální bozony získají
hmotnost (klidovou) a příslušné interakce se stanou
silami krátkého dosahu - jsou to především
W a Z bosony (elektro)slabé interakce. V tomto Higgsově
mechanismu klidová hmotnost částic vzniká interakcí s
všude přítomným Higgsovým polem, které proniká celým
vesmírem; čím je interakce dané částice s tímto polem
silnější, tím má větší hmotnost. Některá kvanta, jako
fotony, toto pole neovlivňuje a proto nemají žádnou klidovou
hmotnost, další částice Higgsovo pole přitahuje a dodává
jim hmotnost. Dalo by se tím vysvětlit, proč jsou některé
intermediální bosony tak těžké, zatímco jiné částice,
např. elektrony, jsou velmi lehké. Zjednodušeně řečeno,
Higgsovy bosony by měly být součástí neviditelného
kvantového pole, které vyplňuje vakuum ve vesmíru a
způsobuje, že ve vesmíru jsou hmotné částice
vytvářející látkové struktury; bez nich by neexistoval
svět v podobě, jak jej známe. Pokud by některé základní
stavební částice hmotnost nezískaly, vesmír by vypadal zcela
jinak: Částice bez klidové hmotnosti by volně létaly
vesmírem rychlostí světla a nikdy by nevytvořily atomy, z
nichž pak vznikaly hvězdy, planety a život...
*) Tuto hypotézu poprve zavedli v r.1964 ve svých pracech
autoři P.Higgs, F.Englert a R.Brout, G.Guralnik, C.Hagen a
T.Kibble. Higgsovo pole v r.1967 využili S.Weiberg, A.Salam a
S.Glashow při vybudování teorie elektroslabé interakce
s těžkými intermediálními bosony W±,Z°.
Samotný Higgsův boson H má
vysokou klidovou hmotnost, řádově stovky GeV *). Higgsovy
bosony by mohly vznikat silnou interakcí při
vysokoenergetických srážkách protonů
výměnnou interakcí energetických kvarků s gluony či
W-bosony (tzv. gluonová fúze,
obr.1.5.1.I, W nebo Z fúze, popř. sdružená produkce
s W nebo s t-t' párem), nebo
elektro-slabou interakcí při srážkách elektronů
např. interakcí e++e-®Z*®Z+H (H-vyzáření), nebo
opět W či Z fúzí - viz obr.1.5.1.D. Higgsovy bosony jsou
vysoce nestabilní částice s dobou života
pouhých cca 10-22s. Nemohou být tedy detekovány přímo, ale jen na
základě analýzy sekundárních částic vznikajících při
jejich rozpadu - jejich rozpadových produktů.
Pokud Higgsův boson vznikne při vysokoenergetické interakci
částic, předpokládá se, že se velmi rychle rozpadne na
jiné energetické částice. Nejjednodušší rozpad H ® g + g na dva fotony
gama by mohl nastávat již při nižších hmotnostech kolem
100GeV. Pokud má Higgsův boson hmotnost vyšší než 160GeV,
může se rozpadat i na dva W-bosony: H ® W + W, které se
vzápětí rozpadají na dva leptony a dvě neutrina (jak bylo zmíněno výše v pasáži "Bosony
W-,W+,Zo"). Při hmotnosti H
vyšší než cca 180GeV může rozpad vést na dva Z-bosony: H ® Z + Z, které se
rozpadají na 4 leptony - po dvojicích mionů m++m- nebo elektronů e++e-. V
případě, že Higgsův boson je těžší než cca 500GeV,
mohou nastávat i další způsoby jeho rozpadu, např. H ® b+b', nebo H ® t++t- , další mohou, ale nemusí jít přes intermediální
Z-bosony; nakonec mohou vyústit v produkci kvarků, jejichž
hadronizací by vznikaly spršky (výtrysky - jety)
částic. Feynmanovy diagramy některých možností vzniku
Higgsových bosonů a jejich rozpadu jsou uvedeny výše v
pasáži "Feynmanovy diagramy " (na obrázku 1.5.1.D,I).
*) Srážkové experimenty (na
urychlovačích Tevatron a LEP - viz níže "Velké
urychlovače") dávaly pouze dolní hranici pro hmotnost
Higgsova bosonu cca 170GeV/c2. Ostatně, podle supersymetrických modelů by mohlo
existovat několik druhů Higgsových bosonů:
lehké skalární ho, těžké skalární Ho, kladně a záporně
nabité H±.
Objev Higgsova bosonu
Na konferenci ICHEP2012 v australském Melbourne 4.července 2012
byl na základě dat z experimentů ATLAS a CMS v CERN oznámen
objev nového bosonu, jehož vlastnosti jsou konsistentní s
Higgsovým bosonem. Pečlivou analýzou asi 60 tisíc případů
detekce dvojic fotonů (pocházejících ze srážek
vysokoenergetických protonů) se na křivce závislosti počtu
fotonů na energii podařilo najít malý (ale
signifikantní, asi 160 dvojic fotonů) pík
v oblasti energie kolem 126GeV. Tento pík by měl patrně
pocházet z 2-fotonového rozpadu Higgsových bosonů.
Úroveň spolehlivosti prokázání nové částice detekcí
jejích rozpadových produktů je 5s. Je třeba provést další
experimenty, aby bylo jisté, že jde o Higgsův boson a nikoli
jinou dosud neznámou částici. Za tento objev byla v r.2013
udělena Nobelova cena P.Higgsovi a F.Englertovi.
 Zdroj:
CERN-LHC
Zdroj:
CERN-LHC
Objev Higgsova bosonu na velkém urychlovači LHC detekcí
produktů jeho rozpadu - zde dvou opačných fotonů gama se
specifickými energiemi na detekčním systému ATLAS.
Higgsův boson - "božská"
částice ?
V popularizační literatuře se často uvádí novinářský
bonmot, že Higgsův boson je jakousi "božskou
částicí", která dává vesmíru hmotnost. Není to
tak docela pravda. Více než 99% běžné
("zářivé") hmoty, z níž je složen vesmír,
běžná látka i naše těla, je tvořeno protony a neutrony. Ty
se skládají z kvarků, jejichž hmotnost, související s
Higgsovým mechanismem, představuje jen cca 5% hmotnosti
protonů a neutronů. S Higgsovým polem podstatně souvisí
hmotnost jen bosonů W a Z, kvarků a hmotnosti leptonů; ty
však představují jen malou část hmotnosti Vesmíru.
Důležitost Higgsova bosonu spočívá v tom, že to byla
poslední dosud neobjevená částice standardního modelu,
jejíž objev potvrzuje (jinak nezjistitelné) Higgsovo pole, bez
kterého by standardní model neuměl vysvětlit experimentálně
naměřené hmotnosti leptonů, kvarků a intermediálních
bosonů - nosičů sil. Bez Higgsova mechanismu by kvarky byly
bez hmotnosti a nevytvářely by protony a neutrony, atomární
hmota by neexistovala...
Hypotetické
částice
 Supersymetrické částice
Supersymetrické částice 
V supersymetrických unitárních teoriích
elementárních částic je ke každé základní částici
přiřazen její tzv. superpartner - každý
boson má svého fermionového superpartnera a fermion má naopak
svůj bosonový protějšek. Tyto "partnerské"
částice nebyly zatím pozorovány. Vysvětluje se to tím, že
boson-fermionová supersymetrie je narušená; vede to k tomu,
že hmotnost superpartnerů není stejná, ale supersymetričtí
partneři ke známým částicím mají hmotnost daleko vyšší,
takže při nám dostupných energiích je nemůžeme pozorovat.
Názvy těchto částic se vytvářejí příponou "ino"
(u bosonů zprostředkujících interakce), nebo předponou
"s-" (u fermionů) k názvu
výchozí částice. Nejčastěji diskutované supersymetrické
částice jsou gravitina, fotina, příp. neutralina:
Gravitina
jsou kvanta kalibračního pole v supergravitační unitární
teorii pole (superpartner gravitonu), mají spin 3/2 nebo 5/2.
Fotina
jsou slabě interagující hmotné částice se spinem 1/2,
zaváděné jako supersymetrický partner fotonu.
s - částice
Někdy se diskutují i supersymetrické částice k dalším
fermionům: s-leptony jako superpatneři k leptonům, např. s-elektron,
s-mion, s-neutrino (zvané též neutralino - mělo by mít vysokou hmotnost desítky či stovky
GeV); či kvarkům - s-kvarky.
Higgsino - supersymetrický fermion k Higgsovu bosonu.
 Další hypotetické částice:
Další hypotetické částice: 
 Axiony
Axiony
jsou velmi lehké (klidová hmotnost cca 10-5-1 eV/c2)
hypotetické částice se spinem 0, které by s okolím měly
interagovat slabou a gravitační interakcí.
V rámci kvantové chromodynamiky byly
axiony postulovány při řešení CP-problému narušení
kombinace nábojové symetrie a parity v teorii kvarků. CP symetrie, která je narušena
u slabých interakcí, by z teoretického hlediska měla být
narušena i pro silnou interakci. Jelikož se toto
experimentálně nepozoruje, byla do kvantové chromodynamiky
zavedena dodatečná symetrie (která je spontánně narušena),
kvanta příslušného pole jsou nový typ částic nazvaných axiony
(jejich supersymetričtí partneři se
nazývají axina).
Reliktní axiony snad mohly
vznikat ve velmi raném vesmíru krátce po velkém třesku, v
leptonové éře nebo ještě dříve. Předpokládá se, že by
též v nepatrném procentu mohly vznikat při rozptylu fotonů
na elektronech, takže jejich intenzívním zdrojem by mohlo být
i nitro Slunce. Velké množství axionů by mělo vznikat při
výbuchu supernovy (spolu s neutriny).
Pokud mají axiony velmi
nízkou hmotnost, budou stabilní, neboť neexistují
žádné lehčí částice na které by se mohly rozpadnout (axiony s vysokou hmotností by dlouhodobě nepřetrvaly
ve vesmíru do nynější doby). Vesmír by
tak mohl být naplněn velkým množstvím primordiálních
axionů (jejich velmi chladným
Bose-Einsteinovým kondenzátem). Axiony
jsou proto považovány za možné částicové kandidáty
temné hmoty ve vesmíru.
Pro axiony byla navržena 2-fotonová
interakce v silném magnetickém poli (Primakoff
efekt): 1. Axion
interaguje s elektromagnetickým polem za vzniku fotonů. 2.
Inverzní proces, ve kterém se foton v přítomnosti silného
magnetického pole přemění pomocí virtuálního fotonu na
axion. Část vysoce energetických fotonů při rozptylu na
elektrických nábojích se tím může přeměňovat na axiony.
Kuriozní průchod
světla zdí za pomoci axionů ?
Proces konverze fotonů na axiony a
obráceně axionů na fotony by mohl snad fungovat v
následujícím pokusu: Intenzivní svazek
fotonů z výkonného laseru pustíme přes komoru se silným
magnetickým polem proti neprůhledné překážce (zeď, kovová
deska a pod.). Na druhou stranu desky umístíme též komoru se
silným magnetickým polem a za ni detektor fotonů. Pokud se
nějaká malá část fotonů při průletu magnetickým polem
zkonvertuje na axiony, tyto axiony snadno projdou
překážkou, neboť interagují jen slabě. Na
druhou stranu desky umístíme též komoru se silným
magnetickým polem a za ni detektor fotonů. V magnetickém poli
by pak některé prošlé axiony mohly být přeměněny
zpět na fotony a svazek laseru tak nepatrně obnoven. Takže by
se mohlo zdát, že část světla mohla projít přes
neprůhlednou desku..?..
Diskutují se některé možnosti, jak by snad
bylo možno axiony detekovat. Interakce axionu s elektrony či s
velmi silným magnetickým polem by mohla vést k produkci kvanta
elektromagnetického záření - mikrovlnného fotonu, který by
se dal detekovat. Fotony tohoto původu by mohly být
registrovány při výbuchu blízké supernovy. Zkoušejí se i
experimenty s laboratorní produkcí axionů pomocí
interakcí intenzívních fotonových svazků z výkonných
laserů s elektrony v silném magnetickém poli, s následnou
detekcí při zpětné konverzi axionů na fotony, opět v
silném magnetickém poli. Všechno zatím bezúspěšně...
 WIMP
WIMP
Výše uvedené (zatím hypotetické) částice - gravitina,
fotina, axiony - se někdy souhrnně označují jako "slabě
interagující hmotné částice" - zkratka WIMP
(Weak Interacting Mass
Particle). S okolím interagují slabě a
gravitačně. Předpovídá je supersymetrické rozšíření
standardního modelu. Mohly by tvořit podstatnou složku tzv. temné
hmoty ve vesmíru (viz např. §5.6 "Budoucnost
vesmíru. Šipka času. Skrytá hmota."
v knize "Gravitace, černé díry a fyzika
prostoročasu"). Zatím se je nepodařilo detekovat...
 Magnetické monopóly
Magnetické monopóly
- hypotetické částice duální vůči elektrickému náboji.
Magnetický monopól vzniká při záměně elektrických a
magnetických veličin v Maxwellových rovnicích a následné
aplikaci kvantové teorie pole.
Klasická teorie elektromagnetického pole
magnetické monopóly nepřipouští: jedna z
Maxwellových rovnic div B = 0 říká, že
magnetické pole je nezřídlové s uzavřenými siločárami,
tj. magnetické monopóly neexistují (viz např. §1.5 "Elektromagnetické
pole. Maxwellovy rovnice" v knize
"Gravitace, černé díry a fyzika prostoročasu").
Magnetické monopóly byly zavedeny jako pokus o (aspoň
hypotetické) formální zrovnoprávnění, či nastolení
symetrie, elektřiny a magnetismu. Nebyly nikdy detekovány, v
naší přírodě neexistují, jejich
hypotetická přítomnost těsně po velkém třesku byla
anulována inflační expanzí raného vesmíru (§5.5 "Mikrofyzika a kosmologie.
Inflační vesmír.").
 Leptokvarky X, Y
Leptokvarky X, Y
- hypotetické vektorové bosony X a Y (zvané leptokvarky,
protože způsobují přechody mezi kvarky a leptony) se
zavádějí v tzv. grandunifikačních teoriích GUT (již zmíněný §B.6 "Sjednocování
fundamentálních inetrakcí"
v knize "Gravitace, černé díry a fyzika
prostoročasu"). Měly by mít velmi
vysoké hmotnosti řádově
mX,Y ~1015 GeV/c2,
zatím mimo možnosti experimentálního prokázání ve velkých
urychlovačích...
 Superstruny
Superstruny
jsou hypotetické (modelové) jednorozměrné elementární
útvary délky řádu 10-33cm (Planckova délka), jejichž různě excitované
vibrační stavy a vzájemná propojení by podle tzv. teorie
superstrun měly být základem veškerých částic a
polí - základem unitární teorie pole
sjednocující všechny 4 interakce v přírodě. Struny mohou
být otevřené nebo uzavřené. Podle způsobu kmitání strun
vzniká různá hmotnost, náboj, spin a pod. Takovéto struny by
pak mohly tvořit základní částice (fermiony - kvarky,
elektrony, ... a bosony - fotony, gluony, ...) standarního
modelu.
Zobecněním
superstrun jsou tzv. p-brány, které mohou mít více (p) prostorových dimenzí a
vyvíjejí se ve vícerozměrném (většinou 11-rozměrném)
prostoročase. O teorii superstrun je
stručně pojednáno v závěrečné části §B.6 "Sjednocování
fundamentálních inetrakcí"
knihy "Gravitace, černé díry a fyzika prostoročasu".
 Tachyony (řec. tachyos=rychlý)
Tachyony (řec. tachyos=rychlý)
jsou ryze spekulativní částice, které se mohou pohybovat
pouze nadsvětelnou rychlostí a mají (v
souvislosti se známým vztahem závislosti hmotnosti na
rychlosti m = mo/Ö(1-v2/c2) ve speciální teorii relativity) imaginární
hmotnost. Motivací pro zavedení tachyonů je pouze
spekulace o jakési symetrii vzhledem k rychlosti světla,
nesvědčí pro ně žádné fyzikální argumenty; spíše by
vyvolávaly vážné problémy s principem kauzality. Z hlediska
teorie relativity jsou tachyony stručně diskutovány v pasáži
"Tachyony" §1.6 "Čtyřrozměrný
prostoročas a speciální teorie relativity" zmíněné knihy "Gravitace,
černé díry a fyzika prostoročasu".
 "Stínová"
či zrcadlová hmota - Katoptrony ?
"Stínová"
či zrcadlová hmota - Katoptrony ?
Na závěr našeho letmého přehledu "zoologie"
hypotetických částic zmíníme ještě poněkud nejasnou
představu o tzv. zrcadlové hmotě, která by
snad mohla skrytě existovat vedle "naší obyčejné"
hmoty. Hypotéza vychází z experimentálně zjištěného nezachování
parity při slabých interakcích částic (je diskutováno
níže - "CPT symetrie interakcí"). Vznikla myšlenka, že zrcadlová symetrie by
mohla být obnovena, kdyby ke každé "naší"
pozorované fundamentální částici existoval skrytý,
"stínový" partner ("dvojče") - zrcadlová
částice, při jejíž interakci dochází k opačnému
porušení parity. Naše běžné částice jsou
"levotočivé", zrcadlové částice
"pravotočivé", celkově je paritní symetrie
zachována. Parita pak může být spontánně narušena Higsovým
mechanismem; v případě nenarušené paritní symetrie
jsou hmotnosti částic a jejich zrcadlových partnerů stejné,
při narušení parity jsou hmotnosti zrcadlových partnerů
odlišné. Zrcadlové částice se někdy označují souhrnným
názvem katoptrony (řec. katoptro = zrcadlo).
Zrcadlová hmota, pokud existuje, jen velmi slabě
interaguje s běžnou hmotou. Síly mezi zrcadlovými
částicemi jsou totiž zprostředkovány zrcadlovými
bosony, které jsou obecně jiné, než intermediální
bosony "naší" hmoty. Zrcadlová hmota je proto
prakticky nepozorovatelná *), aspoň ne
přímými metodami, opticky. Výjimkou jsou gravitony,
takže zrcadlová hmota by měla vykazovat gravitační
účinky - mohla by být proto kandidátem na zatím
záhadnou temnou hmotu ve Vesmíru (podrobněji
rozebíranou v §5.6 "Budoucnost vesmíru. Šipka
času. Skrytá hmota."
monografie "Gravitace, černé díry a fyzika
prostoročasu").
*) V rámci superstrunových teorií se zrcadlové
částice dokonce někdy umisťují nikoli do "našeho"
3-rozměrného prostoru, ale do tří jiných "extradimenzí".
Unitární
symetrie a multiplety částic
Velký počet elementárních částic, které byly objeveny při
vysokoenergetických interakcích, přirozeně vedl nukleární
fyziky ke snahám o jejich systematiku a
zavedení unitarizačních schémat - k
vytvoření jakési periodické tabulky částic,
analogicky k Mendělejevově periodické tabulce prvků (§1.1, část "Bohrův model atomu" a "Interakce atomů", pasáž "Periodické chemické
vlastnosti atomů").
Především, každému baryonu a leptonu je přiřazeno baryonové
číslo B a leptonové číslo L
(částice +1, antičástice -1), které se zachovávají při
všech interakcích. Byly zjištěny výrazné podobnosti
a symetrie mezi některými elementárními
částicemi, především hadrony.
Odhlédneme-li od elektrického náboje, lze např. protony a
neutrony považovat za dva stavy (dublet) jedné částice -
nukleonu. Podobně piony p+,po,p- tvoří triplet
podobných částic. Při studiu samotných silných interakcí,
které jsou nábojově nezávislé, můžeme od náboje
odhlédnout. Pro popis těchto podobností a symetrií byla
zavedena nová veličina izotopický spin neboli
izospin T *). Nukleony mají izospin T = 1/2,
přičemž projekce izospinu T = +1/2 odpovídá protonu a T =
-1/2 neutronu. Pionům se připsal izospin T = 1, s projekcemi
-1,0,+1 pro p-,po,p+. V soustavě
interagujících nukleonů a pionů pak platí zákon zachování
izospinu.
*) Vyšlo se z formální analogie s
obyčejným spinem, kde částice se spinem 1/2 se vyskytuje ve
dvou stavech s průmětem spinu -1/2, +1/2 a částice se spinem
1 ve třech stavech s průměty spinu -1,0,+1. Izospin T
je vektorem v myšleném (pomocném) "izotopickém
prostoru". Obecně částice s izospinem T se může
vyskytovat v (2 T +
1) stavech s projekcemi izospinu na vztažnou osu: -T, (-T+1),
(-T+2), ..., -1, 0, 1, ..., (T-2), (T-1), T.
Dalším důležitým krokem byl objev některých
"podivných" (nečekaných) vlastností interakcí
mesonů K a hyperonů při jejich sdružené párové produkci,
které vedly k zavedení pojmu podivnosti,
popsaného kvantovým číslem S ("Strange").
Později bylo zavedeno obecnější kvantové číslo zvané hypernáboj
Y = B + S, dané součtem baryonového čísla B a
podivnosti S. Ukázalo se, že při silných interakcích
se zachovává jak izospin T, tak hypernáboj Y. Tato
rozšířená symetrie vedla k sestavení multipletu baryonů -
dekupletu (3/2+), v němž však v té době chybělo jedno místo; byl
tak předpovězem hyperon W, který byl zanedlouho skutečně objeven.
Jednotlivé hadrony se zakreslovaly do speciálních
diagramů, kde na vodorovné ose se vynášela projekce izospinu
Tz, na svislé ose
hypernáboj Y a na šikmé ose elektrický náboj Q. Spojnice
takto vyznačených multipletů částic tvořily pravidelné
geometrické obrazce - trojúhelníky, šestiúhelníky a jejich
kombinace, viz níže obr.1.5.3. Takováto analýza unitární
symetrie (kterou nalezli v r.1964 M.Gell-Mann a
Y.Ne'eman) ukázala, že systematiku hadronů lze velmi dobře
vysvětlit hypotézou, že hadrony jsou složeny ze subčástic
nazvaných kvarky - baryony z tripletu
kvarků, mezony z dvojice kvarků, jak bude nastíněno v
následující pasáži.
Jsou elementární částice skutečně
elementární ?
Pokusme se nyní podívat, jak je to s "elementárností"
a vnitřní strukturou základních stavebních
částic hmoty. Důležitým vodítkem pro posouzení
"elementárnosti" ("fundamentálnosti")
částic nám může sloužit to, zda se daná částice
samovolně rozpadá (přeměňuje) či nerozpadá
na jiné druhy částic. Za opravdu vnitřně
"jednolité", kompaktní elementární částice bez
vnitřní struktury, můžeme podle dosavadních poznatků
považovat foton a elektron,
které vznikají či zanikají vždy jako celek a nepřeměňují
se na jiné druhy částic. Neutron a proton se mohou vzájemně
přeměňovat za účasti elektronů, pozitronů a neutrin;
nemohou být tedy v pravém slova smyslu
"elementární". Totéž se týká p-mezonů a
hyperonů. Tedy obecně hadronů...
Pozn.: Jelikož mnohé
částice jsou složené, označení "elementární" je
zde zavádějící. Jedná se však o vžitý název, podobně
jako název "atom", který již dávno neznamená
"nedělitelný". V posledních letech se ale často
slovo "elementární" vypouští a hovoří jen o
"částicích".
Bootstrap model
hadronových interakcí
"Předchůdkyní" kvarkového modelu byla tzv. bootstrapová
hypotéza interakcí hadronů, kterou v 60.letech vypracoval
G.F.Chew. Nehledaly se zde žádné fundamentálnější
částice, které stojí za vlastnostmi interakcí, ale
předpokládalo se, že jsou to v podstatě "ty samé"
hadrony (včetně hadronových rezonancí), působící v jakési
zpětné vazbě (bootstrap =
samozaváděcí, zpětnovazební). V
částicové fyzice je tato koncepce nyní již jen okrajová a
není obecně přijímaná...
Kvarková
struktura hadronů
Výše naznačená systematika
hadronů ukazuje, že v jejich vlastnostech se dají nalézt
výrazné tzv. unitární symetrie. Na základě
těchto symetrií byl v r.1964 (autoři
M.Gell-Mann a Y.Ne'eman) sestaven tzv. kvarkový
model hadronů, podle něhož jsou všechny hadrony
složeny z ještě "elementárnějších pračástic" -
kvarků.
Slovo "quark", které nemá
žádný jazykový význam, převzali autoři kvarkového modelu
s notnou dávkou recese ze hry spisovatele Jamese Joyse.
Kvarky jsou fermiony se
spinem 1/2 a s třetinovým elektrickým nábojem:
-(1/3)e, +(2/3)e, každý kvark má svou antičástici - antikvark´.
Pro vysvětlení systematiky hadronů pomocí aditivního
kvarkového modelu bylo postupně zavedeno celkem 6 druhů
kvarků, z nichž nejdůležitější jsou dva: "u"
(up), "d" (down) - jsou z nich složeny nukleony.
Třetí kvark "s" (strange) je nositelem
"podivnosti". Kvark "b" (bottom) se podílí
na porušení symetrie CP. Charakteristiky všech kvarků jsou
uvedeny níže v přehledné tabulce v části "Standardní
model - jednotné chápání elementárních částic".
Mezony
jsou složeny z dvou kvarků - kombinace
kvark-antikvark (q q´).
V případě opačné orientace spinů obou kvarků dostáváme
tzv. skalární mezony se spinem s=0, např. p+ = (u d´), p- = (d u´), po = (u u´) +
(d d´). Je-li
jedním z kvarků "s", jedná se podivné
mezony K+,-,0 ............ Při paralelní orientaci spinů v dvojici
kvark-antikvark vznikají tzv. vektorové mezony se
spinem s=1, které pozorujeme jen jako mezonové rezonance
s velmi krátkou dobou života (cca 10-23s) - mezon r+,-,0 nebo *K+,-,0.
Baryony
jsou složeny ze tří kvarků, přičemž spiny
těchto kvarků mohou být orientovány tak, že výsledný spin
baryonu je s=1/2, nebo s=3/2. Např. proton p = (u u d) a neutron n = (d d u) se
spinem 1/2, či hyperon Lo se spinem 3/2.
Baryony obsahující kvark "s" se nazývají hyperony
(vlastnosti hyperonů byly popsány výše). Systematika mezonů a baryonů z hlediska kvarkové
struktury je schématicky znázorněna diagramy na
následujícím obr.1.5.3 :

Obr.1.5.3. Schématické znázornění unitární symetrie a
kvarkové stavby hadronů.
Pozn.1: Z důvodu
souladu s textem, kde nejsou k dispozici fonty s vlnovkou, jsou
antičástice označeny čárkovaně ( ' ).
Pozn.2: Stejné kvarkové kombinace, lišící se
vyšším spinem, odpovídají buď samostatné částici (např.
r, D),
nebo jsou označeny stejným symbolem jako známá částice s
antipralelními spiny těchže kvarků a indexem "*"
(např. *K, *S).
Vedle těchto základních multipletů lze
vytvořit i řadu dalších kombinací z "exotických"
kvarků c, b, t *), ať již (pseudo)skalární, nebo vektorové;
některé z nich byly již experimentálně prokázány. Např.:
D-mesony - obsahují c-kvarky: D+ (c,d'), Do (c,u'), podivný Ds (c,s'), charmonium
(c,c')
B-mesony - obsahují b-kvarky: B+ (u,b'), Bo (d,b'), podivný Bs (s,b'), Bc (c,b'), ypsilonium
(b,b')
B-mesony (zvláště neutrální Bo) se produkují v párech částice-antičástice na
velkém urychlovači LHC (experiment LHCb zmíněný níže) z
důvodu výzkumu jejich asymetrické produkce a rozpadů s
porušením CP symetrie.
Všechny tyto kombinace se chovají jen jako rezonanční
stavy s velmi krátkou dobou života (kratší než cca 10-13sec). Vznikají na
kratičký okamžik při vysokoenergetických interakcích
elektronů, protonů a dalších částic. Rozpadají se řadou
různých způsobů (leptonových i hadronových) na elektrony e±,
fotony g,
miony m±, neutrina ne,m,t,
kaony K±,0, částečně i piony p±,0.
*) Top kvark t, který je nejtěžší (cca
170MeV/c2),
se po svém vzniku natolik rychle rozpadá (typicky na b-kvark a
W-boson), že nestačí vytvořit hadronové vázané stavy,
nenastává u něj hadronizace a vznik jetů.
Původ hmotnosti hadronů
Hadrony jsou mnohem těžší, než činí součet hmotností
jejich kvarků. Např. proton má hmotnost 938MeV, zatímco
hmotnost kvarku "u" je 2MeV a kvarku "d"
5MeV. Většina hmotnosti protonu proto pochází z kinetické
energie vnitřního pohybu jeho kvarkových komponent.
Vysvětluje se to na základě kvantových relací
neurčitosti, podle nichž součin neurčitosti v poloze a
hybnosti částice je větší než Planckova konstanta. Kvarky
jsou v protonu či neutronu uzavřeny ("uvězněny") v
prostorové oblasti o průměru cca 10-13cm; tato vnuceně velmi malá neurčitost v poloze
kvantově implikuje značnou hybnost a tím i kinetickou energii
každého z kvarků, nejméně cca 200MeV. Bilance kinetické
energie takových tří intenzívně kmitajících kvarků je
přibližně ekvivalentní hmotnosti protonu.
Rozdíl v hmotnosti kvarků "u", "d",
"s" (který se v unitárních
teoriích polí a částic vysvětluje interakcí s Higgsovým
polem) však způsobuje rozdíly v
hmotnostech mezonů p a K, jakož i baryonů - protonů, neutronů a
různých druhů hyperonů.
Virtuální "moře
kvarků" ?
Základní představa vysvětluje hadrony jakožto složené ze
dvou nebo tří "valenčních" kvarků,
vázaných silnou interakcí gluonového pole. Podle koncepce
kvantové teorie pole se však očekává, že kromě
"reálných, valenčních" kvarků by v hadronech měly
být přítomné i virtuální páry kvark-antikvark,
spontánně vznikající a vzápětí anihilující. Mohly by
tvořit jakési virtuální "moře kvarků"
uvnitř hadronů, které by se při vysokoenergetických
interakcích mohlo "materializovat" a podílet se na
mechanismech vzniku emitovaných částic, kvark-gluonové plasmy
a její hadronizaci ..?..
Uvězněné kvarky.
Jety. Hadronizace kvarků
Úspěšnost kvarkového modelu přirozeně vedla k intenzívním
snahám nalézt jednotlivé kvarky experimentálně.
Ani v laboratořích vysokých energií na urychlovačích, ani v
kosmickém záření se však žádné částice, které by měly
třetinový elektrický náboj, nepodařilo nalézt.
Pokud kvarky vůbec existují, musejí být v nukleonech velmi
silně vázány *), nelze je uvolnit. Kvarky tedy
zůstávají částicemi hypotetickými, resp. modelovými,
které sice velmi elegantně vysvětlují vlastnosti hadronů,
ale jejichž existence nebyla přímo prokázána.
*) Nemožnost
získat volné kvarky
Velmi silná vazba znemožňuje získat volné
kvarky z následujícího důvodu: Při snaze odtrhnout kvarky v
hadronu od sebe tím, že dodáváme stále více energie
(třebas nepružnými interakcemi ostřelujících částic,
obr.1.5.4), bude nakonec tato energie tak vysoká, že
převýší prahovou energii pro vznik nového páru
kvark-antikvark. Tyto nově vzniklé kvarky se pak v gluonovém
poli okamžitě spojí do dvojic nebo do trojic
s kvarky původními. Původní hadron jsme tím sice
"rozbili", ale nezískáme přitom volné kvarky, ale
zase jen vázané systémy dvou či tří
kvarků, tj. hadrony.
Analogická situace je známa z klasického magnetismu
při dělení permanentního tyčového magnetu, majícího
severní a jižní magnetický pól. Pokud rozlomíme magnet na
dvě části, ve snaze oddělit jižní a severní pól, dojde k
rekonfiguraci magnetických domén za vzniku dvou magnetů,
každý opět se severním a jižním pólem. Nelze tedy takto
odseparovat a vyrobit magnetický "monopól" jižní
či severní, analogicky jako se nedaří odseparovat a uvolnit
jednotlivé kvarky z hadronu...
O asymptotické volnosti kvarků a jejich
hadronizaci je zmínka ještě níže.
Nepřímo byl však kvarkový model podpořen
výsledky experimentů s rozptylem elektronů na
protonech, při nichž se měřily úhly a energie
rozptýlených elektronů a protonů. Při nižších energiích
(do cca 1GeV) se proton chová jako kompaktní
"kulička" o poloměru » 1 fm (=10-15m). Při vysokých energiích je však chování
protonů zcela jiné; poprvé byl takový experiment s rozptylem
vysokoenergetických elektronů (o energiiích vyšších než 1010 eV) na nukleonech
proveden na urychlovači SLAC ve Stanfordu (r.1960-70
- J.I.Friedman, R.E.Taylor, H.W.Kendall a kol.). Při takovém "tvrdém ostřelování" se
nukleon nechoval jako kompaktní částice s rovnoměrným
rozložením náboje, ale jako soustava tří velmi malých
rozptylových center (o rozměru cca 10-16
cm), v nichž je koncentrován
elektrický náboj. Tyto částice uvnitř protonů R.Feynman
nazval partony. Přímému ztotožnění kvarků
a partonů však bránil rozpor - na jedné straně se při
experimentech partony v nukleonech chovaly jako volné, na druhé
straně kvarky jsou tak silně vázány, že je nelze z nukleonů
uvolnit.
Pro pochopení
specifických vlastností kvarkové struktury hadronů byla v
70.letech vytvořena tzv. kvantová chromodynamika
(QCD, řec. chromos = barva), což je polní teorie
silné interakce. V rámci QCD byla vytyčena koncepce tzv. asymptotické
volnosti kvarků (vazbový potenciál kvarků se
blíží nule při velmi malých vzdálenostech » 1 fm) a
dále byla vyslovena hypotéza dokonalého uvěznění
kvarků v hadronech, podle níž kvarky nemohou
existovat jako volné částice, ale pouze vázané v hadronech -
vazbový potenciál rychle roste se vzdáleností, k úplnému
uvolnění kvarků by byla potřebná nekonečně velká energie (přesvědčivější důvod je diskutován výše v
poznámce "Nemožnost získat volné kvarky".). Silná interakce mezi kvarky je v QCD
zprostředkována vektorovým kalibračním polem, jehož kvanta
s nulovou klidovou hmotností, zvaná gluony,
zde hrají podobnou úlohu jako fotony v kvantové
elektrodynamice, kde zprostředkovávají elektromagnetické
působení mezi nabitými částicemi.
Podle některých hypotéz by kvarky mohly
být složeny z ještě "menších" částic,
nazvaných preony - viz níže část "Standardní
model -
jednotné chápání elementárních částic", pasáž "Preonová hypotéza".

Obr.1.5.4. Schématické
znázornění mechanismu interakce vysokoenergetického elektronu
s protonem.
Za velmi vysokých energií při tvrdých a
hluboce nepružných srážkách elektronů s protony vzniká
řada sekundárních částic, které vylétají neizotropně
v jakýchsi směrovaných "výtryscích" - jetech.
Detailní analýza úhlového rozdělení a energie částic v
jetech ukázala následující mechanismus interakce, který lze
rozdělit do dvou etap (obr.1.5.4): Během 1.etapy
vysokoenergetický elektron při interakci s protonem předá
část své kinetické energie jednomu z kvarků, který se po
tomto rozptylu po určitou kratičkou dobu pohybuje prakticky
volně (asymptotická volnost) uvnitř protonu; podobně i zbytek
protonu tvořený dvěma zbývajícími kvarky. Nedojde však k
uvolnění kvarků z protonu. Jakmile vzdálenost mezi
urychleným kvarkem a zbytkem protonu přesáhne zhruba 1fm (10-15m), nastává
2.etapa: síly mezi nimi začnou prudce narůstat a v
kvark-gluonovém poli dojde k produkci kvarků a antikvarků,
které se zformují do mesonů a baryonů - dojde k tzv. "hadronizaci"
kvark-gluonového plasmatu *). Výsledkem je vyzáření dvou
úhlově kolimovaných spršek částic - jetů,
které vylétají přibližně ve směrech letu incidenčního
kvarku a zbytku protonu v první etapě. Tyto jety jsou vlastně stopami
po kvarcích. Kvarková struktura hadronů se projevuje
při řadě vysokoenergetických interakcí.
*) Můžeme si zjednodušeně představit,
že kvarky v hadronech jsou spojeny jakýmisi
"strunami" (gluonovými trubicemi), které je drží
pohromadě jako "gumová vlákna". Při "pokusu o
únik" kvarků, tj. při růstu vzdálenosti mezi kvarky, se
tato struna "trhá" na kratší struny délky cca 1fm,
odpovídající mesonům a baryonům (volné konce struny vedou
ke vzniku nové dvojice kvarku a antikvarku). Tato starší
představa se často používala začátkem 70.let.
Přesvědčivější důvod byl diskutován výše v poznámce
"Nemožnost získat volné kvarky".
Kvark-gluonová plasma - "5.skupenství hmoty"
Za normálních okolností nemohou být kvarky volné, jsou vždy
vázány silnou interakcí do hadronů. Když se hadronová hmota
zahřeje na extrémně vysokou teplotu vyšší
než 1012 °K,
tehdy hustota kinetické energie mnohonásobně převyšuje
hustotu energie v jádře, střední volná dráha kvarků je
menší než poloměr jádra. Při těchto velmi vysokých
teplotách a hustotách jsou hadrony natlačeny tak blízko na
sebe, že se vzájemně "prolínají" svou kvarkovou
strukturou a ztrácejí svoji "identitu". V prostoru
mezi kvarky je takové množství gluonů, že jejich vzájemné
silové působení "odstiňuje" přitažlivost mezi
kvarky. Hmota v tomto stavu je na kratičký okamžik tvořena
rovnovážnou směsicí (asymptoticky) volných
kvarků a gluonů. Tento vysoce "exotický" stav hmoty
se nazývá kvark-gluonová plasma.
Kvark-hluonová plasma se někdy považuje za
jakési "páté skupenství" hmoty:
tři běžně známá skupenství jsou pevné, kapalné a
plynné; za vysokých teplot, nebo působením silných
elektrických polí, výbojů či záření, vzniká ionizovaný
plyn - plasma sestávající z volných
elektronů a kladných iontů či atomových jader - označovaná
jako 4.skupenství; a jaderná kvark-glunová plasma je
5.skupenství. V souvislosti s touto analogií a s představou
asymptorické volnosti kvarků v gluonovém poli by se dalo
očekávat, že kvark-gluonová plasma bude mít charakter
ideálního plynu jen slabě interagujících kvarků.
Složité experimenty na urychlovačích, ve spojení s
důkladnou analýzou dat z detektorů částic však ukázaly,
že se spíše chová jako silně interagující téměř
ideální kvark-gluonová kapalina,
jevící vlastnosti supratekutosti. V této plasmě se
patrně projevují zbytkové interakce, jejichž
relativní síla je srovnatelná s van der Waalsovými
silami pozorovanými u klasických kapalin.
Kvark-gluonová plasma vzniká jen na nepatrný
okamžik při srážkách vysokoenergetických částic
- hadronů a zvláště těžších atomových jader - na
urychlovačích (kde se pomocí složitých
systémů detektorů monitorují vznikající spršky
sekundárních částic - baryonů, pionů, kaonů, viz níže
"Velké
urychlovače"), či v kosmickém záření. V kontextu jaderných
reakcí je kvark-gluonová plasma rozebíraná v §1.3, pasáž
"Vysokoenergetické srážky
težších atomových jader".
Nepůsobí-li další síly, za kratičký
okamžik cca 10-22sec. dochází k opětnému uvěznění kvarků a
gluonů z kvark-gluonové plasmy do hadronů - kvarky začnou
tzv. hadronizovat po dvojicích (vznikají mezony p a K)
a trojicích (vznikají baryony
- většinou protony a neutrony, v menším množství mohou
vznikat i hyperony, viz níže drobnou pasáž "Podivná
kvarková hmota?").
Kvark-gluonová plasma zaniká, z místa zániku
vylétá množství částic...
Předpokládá se, že právě taková
kvark-gluonová plasma tvořila hmotu vesmíru v
jeho počátečních stádiích - tzv. hadronové éře
- několik mikrosekund po velkém třesku (podrobněji
je rozebíráno v §5.4 "Standardní kosmologický
model. Velký třesk. Formování struktury vesmíru." monografie "Gravitace,
černé díry a fyzika prostoročasu"). Vznik kvark-gluonové plasmy při vysokoenergetických
srážkách v urychlovačích se proto někdy označuje jako
jakýsi laboratorní "malý třesk",
či "malý velký třesk" (little Big Bang).
Jediné místo ve vesmíru, kde by se snad ve velkém množství
mohla trvale vyskytovat stabilizovaná
kvark-gluonová plasma, jsou centrální oblasti neutronových
hvězd (§4.2, pasáž "Vnitřní struktura neutronových
hvězd" téže knihy; tam
se však na ni jaksi nepodíváme...,
budeme trvale odkázáni na studium jejího vysoce nestabilního
stavu při srážkách v urachlovačích).
Podivná kvarková
hmota ?
Byla však vyslovena hypotéza (E.Witten, r.1984), že pokud by
byl v kvark-gluonové plasmě obsažen dostatečný počet
"podivných" s-kvarků (vedle obvyklých
kvarků u a d tvořících
nukleony), může to zabránit hadronizaci a takováto "podivná
kvarková hmota" může být stabilní. Za tituace,
kdy jsou kvarky velmi "natlačeny" blízko sebe a
všechny nižší fermionové stavy jsou obsazeny, se kvarky s
prakticky nemohou přeměňovat na kvarky u,
neboť pro takto nově vzniklé kvarky u již
není volné kvantové místo. Opačné přeměny mohou
nastávat, takže se ustaví rovnovážná konfigurace kvarků u,d,s
ve fermionovém plynu, která je energeticky výhodnější než
hadronizace. Výsledný útvar by pak mohl být stabilní,
držený pohromadě silnou interakcí. Podivná kvarková hmota
je schopna pohlcovat neutrony, rozkládat je na kvarky a
vytvářet další podivnou kvarkovou hmotu. Předpokládá se,
že menší fragmenty podivné kvarkové hmoty by mohly
přežívat z hadronové éry na počátku evoluce vesmíru, nebo
by mohly vznikat při výbuchu supernovy. Žádné
experimentální důkazy pro takový exotický stav hmoty zatím
nejsou. Některé astrofyzikální aspekty jsou zmíněny v §4.2
"Konečné fáze hvězdné evoluce. Gravitační
kolaps" již zmíněné
knihy "Gravitace, černé díry a fyzika
prostoročasu").
Stabilita a nestabilita kvarků,
hadronů, nukleonů
Časová stabilita či nestabilita
částic je obecně dána složitou souhrou silných,
elektromagnetických a slabých interakcí,
determinujících kvantové procesy mechanismů přeměn
a energetické poměry mezi částicemi, které
jsou "ve hře". U hadronů jsou těmito základními
částicemi kvarky. V nukleonech tvořících
atomomová jádra v naší přírodě jsou to kvarky
"u" a "d".
Jejich stabilita, či vzájemné přeměny, implikují stabilitu
nebo nestabilitu protonů, neutronů a dalších hadronů. U
neutronů a protonů jsou tyto přeměny způsobeny slabou
interalcí :

Schématické znázornění
mechanismu b--rozpadu neutronu (nahoře) a b+-přeměny
protonu (dole) transmutací kvarků v rámci standardního modelu
elementárních částic.
Z energetického hlediska o
možnostech těchto přeměn rozhodují rozdíly
hmotnosti kvarku "u" a "d". Pokud
jsou rozdíly hmotnosti mezi kvarky "u" a "d"
příliš velké, může docházet k samovolné přeměně
protonů či neutronů uvnitř jader.
K rozpadu neutronů v jádře A, vedoucí k
radioakivitě beta-, NAZ
--> NBZ+1 + p + e- + n , nemůže
docházet, když je splněna hmotnostně-energetická nerovnost
md < mu
+ me + EDem + EB ,
kde md a mu jsou hmotnosti
kvarků "u" a "d", EDem= 1,7 MeV je elektromagnetický příspěvek k
rozdílu hmotnosti mezi protonem a neutronem a EB je vazebná energie
neutronu uvnitř jádra. Podobně k beta+ přeměnám
protonů, NAZ --> NBZ-1 + n + e+ + n, v jádrech nemůže
docházet, když je splněna hmotnostně-energetická nerovnost
mu < md
+ me - EDem + EB .
Při dané hmotnosti kvarků md a mu a protonů a neutronů o radioaktivitě beta- či
beta+ tedy v podstatě rozhoduje vazbová
energie EB neutronu či protonu v jádře podle slupkového
modelu. Vazbová energie protonů a neutronů v jádrech se
detailně liší pro různá jádra, pro středně těžká a
těžká jádra v průměru činí EB= 8MeV - viz graf na obr.1.3.3 v §1.3., část "Štěpení a slučování
atomových jader. Jaderná energie". Vlastnosti radioaktivních přeměn beta jsou
podrobněji analyzovány v §1.2, části "Radioaktivita
beta".
Aby mohl existovat volný samostatný stabilní
proton - jádro vodíku, pro zabránění jeho
spontánní přeměny p --> n + e+ + n na neutron a
pozitron, musí být splněna nerovnost
md > mu - me + EDem .
A aby mohl existovat stabilní atom vodíku,
který by se nemohl spontánně přeměnit na neutron reakcí elektronového
záchytu p + e- --> n + n, musí být splněna podmínka
md > mu
+ me + EDem .
Co
udržuje svět pohromadě? - aneb: 4 typy
interakcí v přírodě
Veškeré výsledky dosavadního
fyzikálního a přírodovědeckého bádání ukazují, že
všechny struktury a jevy v přírodě jsou podmíněny
působením jen čtyř základních druhů interakcí :
- 1. Gravitační
interakce
Gravitační interakce je nejrozšířenějším druhem
interakce v přírodě. Působí mezi všemi
tělesy, poli a částicemi - má univerzální
povahu. Má dlouhý dosah
(neomezený) a je vždy přitažlivá
*), má "kumulativní" charakter. Je to síla
"držící svět pohromadě":
váže pozemská tělesa, vodu i atmosféru k Zemi,
udržuje Zemi a ostatní planety na oběžných drahách
kolem Slunce, udržuje Slunce a ostatní hvězdy ve
funkci citlivě regulovaného termonukleárního
reaktoru, váže hvězdy v galaxiích, řídí vývoj
Vesmíru jako celku.
*) Pouze pro některé
"exotické" a hypotetické druhy hmoty (či
spíše konfigurace fyzikálních polí, např. tzv.
"falešného vakua") může mít gravitace odpudivý
charakter. Týká se to především
hypotetických fázových přechodů na samém počátku
vývoje vesmíru během tzv. inflační expanze
vesmíru. Nyní se spekuluje o přítomnosti tzv. temné
energie ve vesmíru, která by mohla způsobovat
zrychlování expanze vesmíru i v současné době. Zde
můžeme jen odkázat např. k příslušné Kapitole
5 v knize "Gravitace,
černé díry a fyzika prostoročasu"; viz též
"Antropický princip aneb kosmický Bůh".
Na klasické úrovni (pro
slabá pole) je gravitace popsána Newtonovým
zákonem všeobecné gravitace, v obecné a
exaktní formě pak Einsteinovými rovnicemi
gravitačního pole v rámci obecné teorie
relativity - gravitace je zde vyjádřena jako zakřivený
prostoročas. Při zrychleném pohybu
gravitujících těles se budí časově proměnné
gravitační pole, přičemž podle Einsteinových rovnic
vznikají gravitační vlny, které se
šíří do prostoru a odnášejí část energie (a
hybnosti) zdroje (Gravitační vlny). Kvanty těchto gravitačních vln jsou
hypotetické gravitony.
I když je gravitace nejslabší silou,
díky své univerzálnosti má
kumulativní charakter a při velkém nahromadění hmoty
ve vesmírných tělesech může zesílit
natolik, že překoná všechny ostatní síly. Může
pak vést ke katastrofickým jevům jako
je gravitační kolaps a vznik černých
děr (Konečné fáze
hvězdné evoluce. Gravitační kolaps. Vznik černé
díry.). V
kosmologickém měřítku pak gravitace rozhoduje o osudu
celého vesmíru - jeho vzniku, vývoji a
příp. zániku (§5.4 "Standardní
kosmologický model. Velký třesk." knihy "Gravitace, černé díry a
fyzika prostoročasu"). Jedna z možností je dokonce gravitační
zhroucení celého vesmíru do "ohnivé pece
velkého krachu"; i když pro náš vesmír toto asi
nehrozí, neboť podle současných astronomických
pozorování se vesmír neustále akceleračně
rozpíná (§5.6, pasáž "Akcelerovaná
expanze vesmíru? Temná energie?").
Při běžném studiu interakcí
elementárních částic nemá gravitace díky své
slabosti žádný vliv, i když
tušíme, že v nejmenších mikroměřítcích řádu 10-33cm (Planckova délka) může
i zde hrát rozhodující úlohu v
geometricko-topologické struktuře prostoročasu..?..
- 2.
Elektromagnetická interakce
Tato druhá nejrozšířenější interakce nepůsobí
mezi všemi druhy částic, ale jen mezi těmi
částicemi, o nichž říkáme, že mají elektrický
náboj. Elektrické síly jsou přitažlivé i
odpudivé, což interpretujeme pomocí dvou druhů
(znamének) elektrického náboje - kladného
a záporného, přičemž stejnojmenné
náboje se odpuzují a opačné náboje se přitahují.
Elektrický náboj je kvantován -
existuje nejmenší (elementární) možné množství
náboje e = 1,602.10-19 C. Základním nositelem záporného
elementárního náboje je elektron,
kladného elementárního náboje proton.
Přitažlivé elektrické síly mezi protony v jádře a
elektrony v obalu především udržují pohromadě
strukturu atomů (kap.1.1, obr.1.1.3), následně k sobě
vážou atomy v molekulách a v krystalových
mřížkách. Elektrické síly jsou tak zodpovědné za
veškerou různorodost tvarů i chemického
složení našeho světa.
Běžná hmota většinou obsahuje v
průměru stejný počet protonů a elektronů, takže je
navenek elektricky neutrální. Porušení této rovnosti
v zastoupení protonů a elektronů je základem
veškerých jevů elektrických. Elektrické náboje
kolem sebe budí elektrické pole.
Důležitou vlastností elektromagnetismu je to, že
pohybem elektrických nábojů vzniká magnetické
pole (působící na pohybující se náboje
Lorentzovou silou) a časovou proměnností magnetického
pole zase vzniká (indukuje se) pole elektrické.
Elektromagnetická interakce je tak základem veškerých
jevů elektřiny a magnetismu, včetně jejich širokých
technických aplikací.
Elektromagnetické pole je fyzikálně popsáno tzv. Maxwellovými
rovnicemi elektrodynamiky, které v obecné
formě odrážejí všechny zákonitosti buzení pole,
vzájemných indukčních přeměn mezi elektrickým a
magnetickým polem, jakož i dynamiku šíření změn v
poli. Zrychleným pohybem elektrických nábojů vzniká
časově proměnné elektromagnetické pole a dochází k
buzení elektromagnetických vln, které
se odpoutávají od svých zdrojů, šíří se
rychlostí světla a odnášejí do prostoru část
energie (a hybnosti) zdrojové soustavy. Vyzařování
elektromagnetických vln je kvantováno - děje se ve
formě fotonů. Deexcitace energeticky
vzbuzených stavů a hladin v atomech a atomových
jádrech se děje většinou vyzářením kvanta
elektromagnetického záření - fotonů světla,
X-záření, g-záření.
Kromě elektronů a protonů vykazují
elektromagnetickou interakci a nesou elektrický náboj i
mnohé další elementární částice - např. mezony p-,p+, K,
miony m-,
hyperony S-,S+, též hypotetické kvarky či intermediální
bosony W-,W+ atd. Elektromagnetická síla tak hraje
důležitou úlohu při většině vzájemných
interakcí (srážek) elementárních částic.
- 3. Silná
interakce
Jak již samotný název říká, jedná se v praxi o
nejsilnější interakci, která však působí jen mezi
některými druhy těžších částic, které souhrnně
nazýváme hadrony. Jsou to především
protony a neutrony, dále pak p-mezony, K-mezony a
hyperony. Význačnou vlastností silných interakcí
mezi hadrony je jejich krátký dosah -
působí efektivně jen do vzdálenosti řádu 10-13 cm, při
větších vzdálenostech velmi rychle slábnou a
stávají se zanedbatelnými.
Největší význam silných interakcí
spočívá v tom, že drží pohromadě jádra
atomů vůči elektrickým odpudivým silám
mezi protony. Kromě toho se silná interakce podílí na
řadě procesů s elementárními částicemi, zvláště
při vysokých energiích.
V praxi se silná
interakce většinou ztotožňuje s jadernou
interakcí krátkého dosahu, neboť s jejími
projevy se fyzika setkala poprve v atomovém jádře a
jsou v přírodě nejdůležitější. Z dnešního
teoretického pohledu, podle modelu kvarkové struktury
hadronů, je však základní a primární
fyzikální interakcí silná interakce mezi
kvarky, která je dlouhého dosahu!
Příslušná zprostředkující kvanta silné interakce
mezi kvarky se nazývají gluony.
Pozorované "silné interakce" mezi hadrony, a
tedy i jaderné síly, vznikají až sekundárně jako
jakýsi "zbytkový projev" této primární
silné interakce mezi kvarky uvnitř hadronů.
Mechanismus "zbytkového projevu" způsobuje krátkodosahovost
pozorovaných interakcí mezi hadrony (§1.1, část "Silná jaderná interakce"). Situace je zde
poněkud analogická jako u chemické vazby, kde
krátkodosahové vazbové síly v molekulách rovněž
vznikají jako "zbytkový projev" patřičně
odstíněné dlouhodosahové elektromagnetické interakce
mezi atomy (na dálku elektricky neutrálními) v
molekule, která je podstatou chemické vazby. Podobně
je tomu u krátkého dosahu Van der Waalsovy síly
(viz §1.1, část "Interakce atomů").
- 4. Slabá
interakce
Posledním druhem "skrytých", typicky
mikroskopických sil krátkého dosahu, jsou tzv. slabé
interakce, které však působí mezi širší
třídou elementárních částic, než interakce silné;
slabá interakce se projevuje u všech typů
elementárních částic mimo fotonů a gravitonů. Na
rozdíl od ostatních třech druhů interakcí slabé
interakce nevytvářejí vázané stabilní
systémy částic - je to způsobeno tím, že
mají velmi krátký dosah (řádově 10-16 cm), takže
i v subnukleárních měřítcích mají velmi slabou
intenzitu. Projevují se pouze rozpadem
některých elementárních částic *). Hlavní význam
slabých interakcí pro nás spočívá v tom, že
způsobují radioaktivitu beta -
vzájemnou přeměnu neutronů a protonů, doprovázenou
emisí elektronu b-,
pozitronu b+,
či pohlcením elektronu z obalu (elektronový záchyt).
Slabá interakce je totiž schopna uvnitř hadronů přeměňovat
kvarky d na u a naopak, za
působení zprostředkujících intermediálních bosonů
W- a W+ (§1.2, část "Radioaktivita
beta", obr.1.2.5). Společným doprovodným jevem všech těchto
přeměn je emise neutrina n.
Slabá interakce se projevuje i při dalších procesech
v mikrosvětě, především při interakcích a
přeměnách mionů m, mesonů p a K.
*) Neznamená to však, že by
slabá interakce v přírodě a vesmíru hrála pouze
rozkladnou úlohu! Spolupodílí se na nukleosyntéze
složitějších prvků z jednodušších v nitru hvězd
(přeměna protonu na neutron při p-p reakci i CNO
cyklu). A v závěrečném stádiu masívních hvězd,
při výbuchu supernovy, je radioaktivita b-, spolu s
neutronovou fúzí, hybnou silou syntézy
těžších prvků až po transurany (opakovaná
neutronová fúze + přeměna neutronu na proton ® nové
jádro s vyšším protonovým číslem). Viz např.
"Kosmická alchymie", nebo "Úloha gravitace při vzniku a
evoluci hvězd").
Vliv slabých
interakcí na stavbu jader
Slabá interakce hraje důležitou
úlohu i při stavbě atomových jader, při jejich
stabilitě. Kdyby v mikrosvětě existovala jen silná
interakce (a elektromagnetická), mohly by existovat i
"mononukleonová" jádra složená jen z
protonů nebo jen z neutronů (mononeutronová
jádra by neměla elektronový obal).
Mohly by vznikat i jaderná "monstra" složená
i z tisíců neutronů. Nic takového však v přírodě
nepozorujeme, neexistují stabilní jádra ani ze dvou
samotných protonů nebo ze dvou neutronů; i samotný
neutron je nestabilní. V přírodě totiž působí
další druh sil - slabá interakce, která radioaktivitou
beta (- nebo +) nemilosrdně přemění
každé jádro, u něhož je porušen určitý poměr
mezi počtem protonů a neutronů. Mechanismy těchto
procesů jsou rozebírány v §1.2, část "Radioaktivita
beta", viz též "Stabilita
a nestabilita jader".
Ukazuje se zajímavé pravidlo hierarchie
interakcí: částice, která podléhá některé ze 4
základních interakcí, automaticky podléhá i všem slabším
interakcím.
Symetrie interakcí (C P
T)
Důležitou úlohu v chápání interakce částic hrají vlastnosti
symetrie - zda a jakým způsobem se změní chování
fyzikálního systému při určité (myšlené či skutečné) transformaci
souřadnic či jiných parametrů částic. Pod symetrií rozumíme
takové transformace veličin popisujících daný fyzikální
systém, které ponechávají tvar pohybových zákonů tohoto
systému beze změn (obecný fyzikálně-matematický rozbor
symetrií a zákonů zachování v teorii pole viz v §B.6 "Sjednocování
fundamentálních interakcí. Supergravitace. Superstruny.", pasáž "Symetrie
ve fyzice" knihy
"Gravitace, černé díry a fyzika prostoročasu"). Zde
se stručně zmíníme o třech základních druzích symetrie
při interakcích částic, o jejich kombinacích
a jejich narušení.
¨ C-symetrie,
nábojové sdružení (angl. Charge = náboj)
- spočívá v záměně všech částic v systému za jejich antičástice
s opačnými náboji. Pokud se takový systém bude chovat
stejně jako s původními částicemi, označíme jej jako
C-invariantní. Základní zákonitosti světa a antisvěta jsou
skutečně stejné. Existence pouze levotočivých neutrin a
provotočivých antineutrin však naznačuje, že při slabých
interakcích může být C-symetrie porušena.
¨ P-symetrie,
zrcadlové obrácení - paritní symetrie
- spočívá v zrcadlovém obrácení všech poloh a orientací
částic v systému, včetně záměny levotočivých a
pravotočivých momentů hybnosti. V makrosvětě i pro většinu
procesů v mikrosvětě (silné a elektromagnetické interakce)
je P-symetrie zachována. U rozpadů K-mezonů vlivem slabé
interakce, jakož i u b-rozpadu jader (např. 60Co) však byly pozorovány určité asymetrie,
narušující pravo-levou symetrii - porušení zákona
zachování parity *).
*) Do poloviny padesátých let se
předpokládalo, že parita se zachovává při všech
interakcích částic (podobně jako v makrosvětě) - že platí
zákon zachování parity. V r.1956 T.D.Lee a Ch.N.Yang
začali zkoumat platnost zachování parity při slabých
interakcích, připustili její narušení a navrhli
příslušné experimenty. Rozhodující experiment provedla v
r.1957 čínsko-americká fyzička Ch.-S.Wu (s
kolektivem spolupracovníků - E.Ambler, R.W.Hayward, D.D.Hoppes,
R.P.Hudson) na b-rozpadu
jader kobaltu 60Co. Vzorek 60Co, ochlazený na velmi nízkou teplotu (0,01°K pomocí
adiabatické demagnetizace - aby tepelné pohyby nerušily
orientaci jader) byl vložen do silného magnetického pole,
které zorientovalo magnetické momenty a spiny jader do přesně
definovaného směru. Pomocí scintilačních detektorů pak bylo
měřeno úhlové rozložení vylétajících elektronů beta
vzhledem ke směru orientace momentu hybnosti (spinu) jádra. Pro
vlastní měření elektronů b byl použit antracenový scintilátor, další dva
scintilační detektory NaI(Tl), umístěné kolmo k sobě,
registrovaly anizotropii doprovodného záření g pro monitorování
dosaženého stupně orientace kobaltových jader. Byly provedeny
dvě série měření pro dva opačné směry vektoru
magnetického pole B v závislosti na teplotě.
Asymetrie v úhlovém rozložení záření b byla sledována relativním
počtem impulsů v antracenovém scintilátoru v závislosti na
teplotě: pro nízké teploty (vysoká orientace jader) byla
pozorovaná asi 20% asymetrie, při vyšších teplotách (s
ubýváním stupně orientace kobaltových jader) ubýval stupeň
úhlové asymetrie v emisi elektronů; se zánikem orientace
jader též vymizela i asymetrie v úhlovém rozložení
emitovaných elektronů. V případě platnosti P-symetrie by
počet elektronů vyletujících pod určitým úhlem f měl být stejný
jako počet elektronů vylétajících v protilehlém směru
180°-f.
Byla však spolehlivě zjištěna asymetrie v úhlovém
rozložení elektronů b, svědčící o porušení P-symetrie - nezachování
parity.
Vedle radioaktivity b se nezachování
parity ve slabých interakcích projevuje i u rozpadů
mezonů K (kaonů) na mesony p (piony), které byly
popsány výše v části "Vlastnosti a interakce
nejdůležitějších částic",
pasáž "Mezony p a
K". Mezony K i p mají zápornou paritu. Při rozpadu nabitého K na
tři nabité piony (např. K+®p++p++p-) je parita před i po rozpadu záporná. Nastává
však i rozpad nabitého K (se zápornou paritou) na jeden
nabitý a jeden neutrální mezon p, např. K+®p++po; tato
výsledná soustava dvou mezonů p má celkovou paritu kladnou
- parita se nezachovává. Když byly v r.1953 objeveny tyto dvě
možnosti 2- a 3-pionových rozpadů nově objeveného mezonu do
stavů s různou paritou, bylo to považováno za rozpady dvou
různých částic, označovaných jako částice J a t. Další měření
však ukázala, že tyto domnělé dvě částice mají hmotnost,
náboj a dobu života stejné - že částice J a t jsou jedinou
částicí, která dostala název K a která se může rozpadat
dvěma (či několika) způsoby, z nichž některé
nezachovávají paritu.
¨ T-symetrie
- inverze času
- spočívá v obrácení směru toku času, v prozkoumání, zda
všechny procesy v systému mohou probíhat v obráceném
pořadí. Z mechanického hlediska zaměníme počáteční a
koncové stavy částic a obrátíme vektory jejich pohybových
rychlostí. Základní zákony elektrodynamiky a gravitace se
nemění při obrácení směru času. Pro velké statistické
soubory částic jsou sice časově obrácené procesy na
mikroskopické úrovni principiálně možné, avšak jejich
pravděpodobnost je velmi malá - v souladu s 2.zákonem
termodynamiky výsledné makroskopické procesy jsou
fakticky nevratné (k tomu viz např. "Determinismus -
náhoda
- chaos ?" v §3.3 knihy "Gravitace,
černé díry a fyzika prostoročasu"). Ukázalo se navíc,
že T-symetrie zcela neplatí ani na úrovni srážek dvou
částic, je narušena působením slabé interakce.
Kombinované symetrie
Jelikož tedy samotné C, P i T symetrie mohou být narušené,
přinejmenším při procesech s účastí slabých interakcí,
bylo prozkoumáno, zda se symetrie neobnoví při kombinaci
příslušných transformací:
¨ CP -
symetrie
vznikne nahrazením levého pravým a zároveň výměnou
částic za antičástice. I zde se ukazuje, že některé
rozpady K0-mezonů
na piony *) asi v 0,2% případů narušují CP-symetrii.
*) Jedná se o kvantově smíšený stav
mezonu K0
a anti-K0,
při němž vznikají dva různé stavy označované KL (s delší dobou
života cca 10-8s) se zápornou hodnotou kombinované CP a KS (s kratší dobou
života cca 5.10-10s) s kladnou hodnotou CP. Oba tyto stavy se rozpadají
slabou interakcí dvěma různými způsoby. Krátce žijící
mezon KS
se rozpadá dvoučásticově na dva p-mezony, déle žijící KL pak zpravidla na tři
piony, nebo pion a mion či elektron a neutrino. V experimentech
na urychlovači v Brookhavenu v r.1964 byla však u KL pozorována i malá
"příměs" rozpadu na dva mezony p, představující stav s
kladnou hodnotou CP. Hodnota CP se tak změnila ze záporné na
kladnou - bylo prokázáno narušení CP symetrie.
Narušení CP symetrie nastává i při rozpadech K0 na piony a leptony: KL®p++e-+n', KL®p-+e++n, při nichž je
rozpad za vzniku pozitronů o cca 0,2% častější než
elektronů.
¨ CPT -
symetrie
vznikne tak, že: zaměníme částice za antičástice +
zaměníme levé za pravé + obrátíme chod času. V rámci
relativistické kvantové teorie pole v r.1957 W.Pauli
zformuloval CPT-teorém o zachování kombinované CPT
symetrie. Zde se ukazuje, že zatím žádný experiment
neodporuje této symetrii - předpokládá se platnost
CPT-symetrie.
Narušení symetrie
Kdyby vždy a všude panovala absolutní a dokonalá
symetrie, byl by svět velice fádní a nevyznačoval by se
pozorovanou pestrostí; dokonce by nevznikla látka v obvyklém
smyslu, nebyly by atomy, vesmír by sestával z rozptýlených
částic a záření. Narušení C či CP symetrie
v mikrosvětě mělo pravděpodobně velmi důležité důsledky
v nejranějších fázích po vzniku vesmíru: vedlo k mírnému
převládnutí hmoty nad antihmotou - k baryonové
asymetrii vesmíru. V období před velkým sjednocením
interakcí způsobovaly částice X a Y, tzv. leptokvarky,
přechody mezi kvarky a leptony. Vlivem narušení CP symetrie
probíhaly tyto procesy mírně nesymetricky - na cca 108 vzájemných přeměn
proběhlo o jednu přeměnu více směrem k hmotě, než k
antihmotě. Při následné anihilaci látky a antilátky na
konci hadronové éry tak zbyla určitá malá převaha
částic, tvořících hmotu z níž nyní sestává
vesmír. Další podrobnosti viz v §5.4 "Standardní
kosmologický model. Velký třesk. Formování struktury
vesmíru." a v §B.6
"Sjednocování fundamentálních interakcí.
Supergravitace. Superstruny."
knihy "Gravitace, černé díry a fyzika
prostoročasu".
Úloha
interakcí při fungování světa
Význam a úlohu jednotlivých druhů interakcí v přírodě si
můžeme názorně (i když snad příliš
populárně a zjednodušeně, za což se kolegům omlouvám ...) přiblížit v následujícím myšlenkovém pokusu.
Představme si, že existuje Bůh, který je absolutně
všemohoucí a který se rozhodne prakticky "otestovat"
důležitost jednotlivých interakcí pro stavbu a fungování
vesmíru ("není snad některá z nich zbytečná?").
Za tím účelem bude pokusně "vypínat" či
"rušit" jednotlivé druhy interakcí a pozorovat, co
to "se světem udělá":
¨ Řekne: "Tak,
a od teďka ruším gravitaci!".
Co by se stalo? Okamžitě nastane beztížný stav, budeme se
vznášet, což by se nám mohlo chvíli líbit. Odhlédneme-li
od katastrofických událostí zde na Zemi (pokles
atmosférického tlaku na nulu, vylití vody z oceánů, únik
atmosféry do vesmíru, puknutí zemské kůry a vulkanická
katastrofa), napadne nás ihned, že Země opustí svou oběžnou
dráhu a odletí od Slunce do vesmíru. Ve skutečnosti to však
nestihne! Mezitím by totiž Slunce explodovalo jako gigantická
termonukleární bomba a během cca 20 minut by Zemi dostihla
obrovská vlna žhavé plasmy, v níž by se celá Země
vypařila. Tak by skončily všechny hvězdy, takže vesmír by
se zaplnil horkou plasmou a posléze chladnoucím plynem,
všechny struktury by se rozplynuly a nakonec zanikly v
"tepelné smrti" vesmíru. Tedy ne zrovna veselý
konec.
¨ Pokud by Bůh řekl: "Nyní
ruším elektromagnetickou interakci!",
okamžitě by se rozpadly všechny atomy na jádra a oddělené
elektrony - všechny struktury by opět zanikly a proměnily se v
plasmu.
¨ Kdyby Bůh zrušil
silnou interakci,
rozpadla by se okamžitě všechna atomová jádra (elektricky by
explodovala) a tím i atomy; existovat by mohl nadále jen vodík
1H1.
¨ Zrušení
slabé interakce
by mělo poněkud složitější a méně přímočaré
důsledky, neboť slabá interakce nevytváří žádné vázané
systémy (typu atomů a jejich jader). Kromě zastavení b-rozpadu by patrně
vyhasly termonukleární reakce v nitru Slunce *). Bez slabé
interakce by nedošlo ke zhroucení masívních hvězd na
neutronovou hvězdu, ale hvězda by patrně zůstala ve stádiu
degenerovaného elektronového plynu. Pokud by však zrušení
slabé interakce nastalo již v počátečních fázích vývoje
vesmíru, nevznikla by baryonová asymetrie a převaha hmoty nad
antihmotou. Nedošlo by k vesmírné nukleosyntéze (ani k
primordiální, ani k hvězdné) a celý vesmír by sestával
pouze z částic a záření. Pokud by k hypotetickému zrušení
slabé interakce došlo v leptonové éře, byl by stejný počet
protonů a stabilních neutronů; v primordiální a hvězdné
nukleosyntéze by vznikala nejenom dnes známá stabilní jádra,
ale všechny isotopy by byly stabilní - vznikala by i jaderná
"monstra" s velkým počtem neutronů nebo složená
jen z neutronů, lehká jádra složená jen z protonů a pod.
Chemické složení vesmíru by bylo úplně jiné než
pozorujeme (a každopádně nevhodné pro
vznik života).
*) Termonukleární syntéza ve hvězdách
začíná fúzí dvou protonů p+, při níž
vzniká deuteron 2H a je emitován pozitron a neutrino: p+ + p+ ® 2H1
+ e+ + ne. Vlastní vazba
protonu a neutronu v deuteronu je dílem silné interakce,
avšak nutná přeměna jednoho z protonů na neutron (vázaný
stav dvou protonů neexistuje) v procesu p+ ® no + e+ + ne je dílem slabé interakce. Bez
slabých interakcí by tedy fúze neproběhla, Slunce a
hvězdy by nesvítily!
Vidíme tedy, že
žádná z fundamentálních interakcí není zbytečná,
všechny jsou "životně důležité"!
K tomu, aby svět vypadal a fungoval stávajícím způsobem je
dokonce třeba, aby poměry sil jednotlivých interakcí
(vazbové konstanty) měly přesně ty hodnoty, které pozorujeme
- podrobnější diskuse viz §5.7 "Antropický
princip a existence více vesmírů"
knihy "Gravitace, černé díry a fyzika
prostoročasu", nebo práci "Antropický princip aneb kosmický Bůh".
Standardní
model -
jednotné chápání elementárních částic
Obrovské množství experimentálních poznatků o vlastnostech
a interakcích elementárních částic, získané v rozmezí
50.-80.let, zpracovaných a sjednocených v duchu řady
kvantově-teoretických koncepcí, vyústilo v tzv. standardní
model elementárních částic a jejich interakcí,
který zde můžeme stručně a zjednodušeně shrnout takto:
Základními
"stavebními kameny" hmoty jsou fundamentální
fermiony - kvarky a leptony:
¨ Kvarky:
u, d, c, s,
t, b
¨ Leptony:
elektron e, mion m, tauon t;
neutrina - elektronové ne,
mionové nm , taunové nt.
Tyto fundamentální leptony a kvarky se rozdělují do tří
generací (viz 3 sloupce v tabulce). Každá generace je
složena ze dvou leptonů a dvou kvarků, přičemž sobě
odpovídající částice různých generací se výrazně liší
pouze svými hmotnostmi; ostatní
charakteristiky jsou stejné.
Pozn.: Důvod,
proč dochází k takovému opakování struktur
částic ve velkých hmotnostních škálách, zatím neznáme -
je to jedna z důležitých otázek současné částicové
fyziky a zřejmě též unitární teorie pole. Podrobnější
diskuse je uvedena níže v pasáži "Preonová
hypotéza".

Systém základních částic látky a kvant polí, tvořící
základ nynějšího standardního modelu částic.
Velikost náboje q je uvedena v násobcích náboje elektronu
(e), klidová hmotnost m částic v MeV, pokud není
uvedeno jinak.
Mezi těmito fundamentálními kvarky a
leptony působí fundamentální interakce -
síly gravitační, elektromagnetické, silné a slabé. Tyto
síly lze v rámci kvantové teorie pole popsat
pomocí výměny zprostředkujících částic - intermediálních
bosonů. Pomineme-li gravitaci, která v mikrosvětě
nehraje prakticky žádnou úlohu *), mají tyto intermediální
bosony spin 1 (označují
se jako vektorové, v souvislosti s matematickým
formalismem jejich teoretického popisu):
¨ Foton
- kvantum elektromagnetického pole, zprostředkovává
elektromagnetickou interakci (bývá zvykem jej značit g).
¨ W+,W-,Z
- těžké bosony zprostředkovávající slabou interakci,
např. přeměny kvarků uvnitř hadronů (obr.1.2.5).
¨ Gluony g
- nositelé silné interakce mezi kvarky.
*) Úloha gravitace v
mikrosvětě je permanentním námětem diskusí fyziků,
zvláště v souvislosti s unitární teorií pole,
viz §B.6 "Sjednocování fundamentálních inetrakcí" knihy "Gravitace, černé díry...".
Gravitony mají spin 2.
Vlivem elektromagnetické
interakce se při srážkách nabitých částic v
proměnném elektromagnetickém poli generují fotony záření g, rodí se a
anihilují elektrony a pozitrony.
Vlivem slabé
interakce dochází rovněž k tvorbě elektronů a
pozitronů spolu s neutriny (z
intermediálních bosonů W), k vzájemné
přeměně jednotlivých druhů kvarků uvnitř hadronů - a tím
k přeměnám neutronů a protonů (radioaktivita b), mesonů i
hyperonů. Slabá interakce, v důsledku
své vlastnosti porušovat invarianci vůči kombinované
prostorové a nábojové inverzi CP, patrně způsobila i baryonovou
asymetrii vesmíru - převahu hmoty nad antihmotou.
Silná
interakce, která dokonale váže kvarky uvnitř
hadronů, svým "zbytkovým projevem" váže nukleony v
atomových jádrech; kromě toho způsobuje řadu interakcí mezi
elementárními částicemi, při nichž v kvarkově-gluonovém
poli v procesu "hadronizace" vznikají nové mesony a
baryony.
Všechny
tyto procesy mezi několika málo druhy leptonů a
kvarků způsobují veškerou pestrost
a různorodost našeho světa. Standardní
model, který shrnuje prakticky všechny naše poznatky
o elementárních částicích, je na jedné straně velkým
triumfem fyziky mikrosvěta, neboť s velkou přesností
vysvětluje chování různých jevů mezi částicemi. Na druhé
straně je jasné, že standardní model nemůže být úplnou a
definitivní teorií mikrosvěta, neboť je neúplný.
Jednak vůbec nezahrnuje gravitační působení a sjednocení
gravitace (obecné teorie relativity) s kvantovou teorií. Dále
má v některých aspektech příliš fenomenologický charakter
- obsahuje mnoho volných parametrů jako jsou
některé hmotnosti částic a vazbové konstanty interakcí,
které standardní model neumí předpovědět a musejí se
zjišťovat experimentálně. Skutečně úplná teorie by měla
být schopna tyto parametry stanovit i číselně - např. jaká
by měla být hodnota elektrického náboje elektronu a jeho
hmotnost, podobně protonu a dalších částic, jaká je síla
(resp. poměry sil - vazbové konstanty) jednotlivých interakcí
a pod.
Stavební částice
kvarků a leptonů - Preony ?
Podle standardního modelu elementárních částic jsou tedy
základními "stavebními kameny" hmoty fundamentální
fermiony - kvarky a leptony. Vzniká otázka, zda tímto
je hierarchie struktury hmoty konečná? Nebo je každá
"elementární" částice tvořena dalšími, ještě
"elementárnějšími" částicemi? Výše uvedená
tabulka rozdělení kvarků a leptonů na 3 generace m.j.
ukazuje, že dochází k opakování vlastností
částic ve velkých hmotnostních škálách. To navozuje (podle
analogie s periodickou tabulkou prvků *) možnost, že rozdíly
mezi generacemi pramení z uspořádání ještě
menších stavebních prvků hmoty v leptonech a
kvarcích. Tyto hypotetické stavební "kameny" kvarků
a leptonů byly nazvány preony (řec. pre=před).
*) D.I.Mendělejev sestavil periodickou
tabulku prvků když si všiml, že určité chemické
vlastnosti prvků se opakují. Atomová fyzika to později
vysvětlila jako důsledek stavby atomů. Podobně by tomu mohlo
být i v částicové fyzice. I 12 známých fundamentálních
částic má některé opakující se vlastnosti.
To může naznačovat, že ve skutečnosti nejsou základní a
elementární, ale že jsou uvnitř složeny z
ještě menších částic, jejichž uspořádání určuje
jejich osobité vlastnosti.
Na základě některých (značně neurčitých)
výsledků rozptylových experimentů byla vyslovena hypotéza,
že kvarky (a snad i leptony) by mohly být složeny z ještě
"menších" částic, nazvaných preony.
Každý kvark by mohl být tvořen třemi preony. Podle modelu
Salama a Pati jsou to somony určující generaci (3
druhy, nulový náboj), flavony určující
"vůni" (2 druhy, náboj 1/2) a chromony
určující "barvu" (4 druhy, náboj 1/6).
Alternativní model, který navrhli Harrari, Shupe a Seidberg,
považuje kvarky a leptony za kombinace tří preonů (tzv. rishonů)
dvojího typu, jeden s elektrickým nábojem +1/3 a druhý s
nulovým nábojem, přičemž každý z nich má své
antičástice s opačným elektrickým nábojem -1/3 a 0.
Elektron by byl kombinací preonů "---", pozitron
"+++", kvark "u" by sestával z
"++0", elektronové neutrino z "000" atd.
"Silonosné" hmotné bosony by sestávaly z kombinací
6 preonů, např. W+="+++000", foton by byl
dvojicí preonu a antipreonu "+-". Excitované
stavy systému preonů by mohly odpovídat jednotlivým
generacím částic. Na další úrovni hypotézy by mohly být i
pre-preony, pre-pre-preony a pod., podle toho,
kolik neobjevených úrovní v hmotě ještě existuje...
Vzniklo několik preonových modelů, snažících se
vysvětlit různé kvarky a leptony kombinací různého počtu
specifických druhů preonů. Zatím je to všechno jen pouhá
spekulace a numerologie (tou byl ostatně ve
svých počátcích i kvarkový model protonů, neutronů a
dalších hadronů). Jakékoli experimentální potvrzení
preonové hypotézy zatím chybí. Mohly bi ji
podpořit experimenty se srážkami částic při nejvyšších
energiích, pokud by ukázaly, že kvarky a leptony mají
nenulovou velikost (dosavadní experimenty ukazují spíše na
bodový charakter kvarků a leptonů). Naráží se zde i na
některé teoretické problémy souvisejícími s velmi malými
rozměry (menšími než cca 10-15cm) preonů a jejich lokalizací, které by podle
kvantového principu neurčitosti měly implikovat nepřípustně
velké efektivní hybnosti a tím i hmotnosti, o mnoho řádů
vyšší vyšší než odpovídá skutečným hmotnostem - hmotnostní
paradox.
Z čeho jsme složeni
My lidé, okolní příroda a všechny předměty s nimiž
přicházíme do styku, jsou složeny z kvarků
"u" a "d" a z elektronů.
Mezi nimi působí pole - elektromagnetické,
silných a slabých interakcí. Další druhy kvarků a leptonů
se uplatňují pouze ve vysokoenergetických procesech interakcí
částic v urychlovačích a kosmickém záření, jakož i v
některých bouřlivých astrofyzikálních procesech. V naší
pozemské přírodě se s nimi nesetkáváme.
Problémy a možnosti
rozšíření standardního částicového modelu ?
Po objevu Higgsova bosonu byl standardní model žístic
prakticky uzavřen, neměl žádné chybějící prvky, v
zásadě vysvětluje všechna pozorovaná experimentální fakta.
Přesto je zde však řada nejasností. U těch teoretických se
vkládají naděje do budoucích unitárních teorií pole.
Chybí zde však vysvětlení temné hmoty ve vesmíru, které je
hmotnostně pětkrát více než nám známé hmoty, popsané
standardním modelem (§5.6 "Budoucnost
vesmíru. Šipka času. Temná hmota. Temná energie." v knize "Gravitace, černé díry ....). ..... ................... ..................
Existují
nové dosud neobjevené částice ?
Interakce částic se v běžných experimentech projevují
většinou přímo, explicitně při srážkách buď rozptylem
nebo reakcemi, s příp. zánikem a vznikem nových částic. To
je detailně prozkoumáno. V kvantové fyzice však probíhají i
skryté - virtuální, vakuové - interakce. Vakuum je podle
kvantové teorie pole zaplněno virtuálními páry částic a
antičástic, které neustále vznikají a vzápětí zanikají.
Pokud se tak stane v bezprostřední blízkosti
"reálné" částice, i za ten kratičký okamžik své
virtuální existence mohou s reálnou částicí stačit
nepatrně interagovat, což poněkud změní její fyzikální
parametry. Jedním z takových parametrů, který může být
ovlivněn interakcemi s virtuálními částicemi ve vakuu, je magnetický
moment částice (§1.1, pasáž
"Kvantový moment hybnosti. Spin.
Magnetický moment.").
Anomální magnetický moment mionu.
Experiment g-2.
Magnetický moment elektronu je e.h/4pme - tzv. Bohrův magneton (§1.1, pasáž "Kvantový
moment hybnosti. Spin. Magnetický moment."). Pro buzení magnetického pole rotačním
pohybem částic se zavádí tzv. gyromagnetický poměr
g, což
je poměr buzeného magnetického momentu a mechanického momentu
hybnosti rotující částice, zde spinu. Pro elektron a mion se
spinem 1/2 by tento koeficient měl být g=2.
Ale v 50.letech bylo změřeno, že hodnota g elektronu je o něco větší
než 2 (.........). Bylo to přisouzeno vlivu interakcí s
virtuálními částicemi vakua - mírně zvýšená hodnota
g
vzniká příspěvky z interakcí virtuálních dvojic všech
elementárních částic které existují.
Skutečná změřená hodnota gyromagnetického
poměru g
fermionů - elektronů, mionů - respektive její rozdílnost od
2, v sobě nese informaci o tom, jaké všechny elementární
částice v přírodě existují a účastní se vakuových
virtuálních interakcí. Miony jsou 207-x hmotnější než elektrony,
takže vakuové virtuální částice na ně působí mnohem
silněji a rozdíl mezi skutečným g a výchozí hodnotou 2 je
zde větší. Měření rozdílu g-2 pro mion tak může poskytnout nezávislou představu
o tom, zda k němu přispěly pouze stávající částice
standardního modelu, nebo zvýšená hodnota je indicií pro
existenci dalších dosud neobjevených částic..?.. Náročná
měření tohoto druhu se proto nazývají "mionové experimenty
g-2"
(g minus dvě).
Ve vakuových virtuálních interakcích by se
měly uplatňovat všechny v přírodě existující částice a
kvantová pole - známé i příp. i ty další dosud neobjevené
(vakuum "o nich ví", virtuálně je
obsahuje...). Experimenty typu g-2 je nám mohou
dopředu prozradit, bez nutnosti jejich "fyzické
výroby". Neposkytují nám však žádné informace o
jejich vlastnostech, ani zda se jedná o jednu novou částici,
nebo je jich několik. K tomu je musíme na okamžik fyzicky
vytvořit při srážkových experimentech a z detekce jejich
rozpadových produktů odvodit jejich vlastnosti. To bude úkolem
nových větších urychlovačů...
Experiment začíná svazkem velkého počtu
protonů (cca 1012 /s.) z urychlovače, z nichž při dopadu na terčík
vzniká mimo jiné částice i velké množství pionů, která
se rychle rozpadají na miony. Paprsek mionů+ se pak vede do
magnetického prstence. Vlastní měření g-2 se provádí v magnetickém prstenci s velmi
homogenním magnetickým polem, v němž v kruhu pod vlivem
silného magnetického pole obíhá velký počet mionů
rychlostí blízkou rychlosti světla. Při tomto kruhovém letu
dochází k precesi spinu a magnetického momentu mionů kolem
vektoru magnetického pole. Přitom se miony neustále rozpadají
na pozitrony a neutrina. Neutrina odlétají bez interakce pryč.
Pozitrony, které se pohybují stejným směrem jako miony před
rozpadem, se detekují řadou detektorů rozmístěných na
vnitřní straně magnetického prstence. Jsou to jednak
scintilační detektory PbF2 a dále řada trackerů na bázi ionizačních komor,
které registrují trajektorii pozitronů z rozpadu mionů.
Měří se energie, čas a lokalizace příchodu rozpadových
pozitronů. Frekvence precese závisí na hodnotě magnetického
momentu, tedy na gyromagnetickém poměru g.
První experiment tohoto uspořádání proběhl v
letech 1997-2001 v Brookhavenu, další měření za
modernějších a přesnějších podmínek pokračuje od r.2018
ve Fermilabu. Výsledkem experimentu je zatím hodnota g = 2,00233184110(82). Vypočtená
teoretická hodnota podle standardního modelu přitom je g = 2,00233183620(86). Experimentální a
teoretické hodnoty se tedy jen nepatrně liší - od osmého
desetinného místa. Kdyby experimenty g-2 potvrdily anomálii naznačující existenci neznámých
elementárních částic - existenci částicové fyziky nad
rámec standardního modelu, byl by to velký stimul pro
konstrukci nových větších urychlovačů.
Je zde ale i další možnost: Co když v
současné variantě standardního modelu byla anomální hodnota
magnetického momentu mionu nepřesně spočítána? Konečné
objektivní výsledky těchto náročných studií se snad
podaří získat až za řadu let...
Sjednocování interakcí - unitární
teorie pole a elementárních částic
I když redukce
obrovské různorodosti jevů a struktur v přírodě na pouhé 4
základní typy interakcí, působících mezi několika málo
druhy základních částic (vlastně kvarky a leptony), je
impozantním příspěvkem fyziky k jednotnému
chápání světa, fyzikům to přesto nestačí. Mají
ještě vyšší ambice: vytvořit definitivní finální
teorii či jednotnou teorii všeho (TOE -Theory Of
Everything) - sjednotit
stávající čtyři druhy interakcí do interakce
jediné, popsané unitárním polem,
jehož kvantové vlastnosti by pak popisovaly všechny druhy
elementárních částic.
Unitární teorie pole tvoří velmi speciální část
teoretické fyziky s vazbami na jadernou a částicovou fyziku,
jakož i na teorii relativity, astrofyziku a kosmologii. Leží
tak již mimo rámec našeho pojednání o jaderné a radiční
fyzice. K dalším podrobnostem můžeme odkázat na speciální
literaturu, na těchto stránkách např. na kapitolu B "Unitární
teorie pole a kvantová gravitace" v knize "Gravitace,
černé díry a fyzika prostoročasu".
Urychlovače
nabitých částic
Pro studium vlastností, struktury a interakcí
elementárních částic, výrobu umělých radionuklidů, jakož
i pro aplikace v různých oblastech vědy a techniky (včetně
medicíny), je potřeba použít částic urychlených na
vysoké kinetické energie. Jelikož přírodní
radioaktivní látky poskytují omezenou intenzitu a hlavně
energii emitovaných částic, je nutno se obrátit k umělému
urychlování částic. Uměle urychlit dovedeme pouze stabilní
*) elektricky nabité částice - elektrony e-,
pozitrony e+ , protony p+, deuterony d+, jádra hélia He++=a-částice a jádra (ionty) těžších prvků.
Vysokoenergetické částice bez náboje (jako jsou fotony g, neutrony no, neutrální piony,
...) a krátkožijící částice (p-mezony, hyperony, ...) lze
pak získat sekundárně - interakcemi
urychlených nabitých částic s dalšími částicemi ve
vhodném terčíku.
*) Jedinými nestabilními
částicemi které lze v zásadě urychlovat jsou miony m±,
jejichž doba života 2,2 mikrosekundy, v koprodukcí s
relativistickou dilatací času, umožňuje mnohonásobný pohyb
po kruhové dráze v urychlovači po dobu cca 0,1 s. dostatečnou na účinné
urychlení. Mionové urychlovače - collidery -
mohou být perspektivní pro získání vysokých energií díky
minimálnímu synchrotronovému vyzařováním a k realizaci
"čistých" srážek, při nichž je všechna energie k
dispozici pro tvorbu nových sekundárních částic (je diskutováno na konci této kapitoly v pasáži
"Mionové urychlovače?").
Přístroje,
které působením silných elektrických a magnetických polí
urychlují nabité částice, se nazývají urychlovače.
Vlastní urychlování nabitých částic
způsobuje elektrické pole (elektrická složka
elektromagnetického pole intenzity E) svým
silovým působením na náboj Fe = q.E, magnetické
pole se využívá ke změně dráhy
nabitých částic*). Popř. proměnné magnetické pole indukuje
pole elektrické, které způsobuje urychlovací efekt.
*) Magnetické pole samotné nemůže urychlovat,
protože Lorentzova síla Fm = q.[v´B] působí v magnetickém poli intenzity B
kolmo ke směru pohybu nabité částice rychlostí v,
takže nevykonává žádnou práci. Pouze
mění směr, zakřivuje dráhu nabité částice, bez změny
rychlosti.
Pozn.:
Za nejjednodušší urychlovač částic lze
považovat již rentgenku (§3.2 "Rentgenová diagnostika") - je to lineární elektrostatický urychlovač
elektronů, jejichž zdrojem je žhavená katoda, (vnitřním)
terčíkem je anoda, ven vychází brzdné (+charakteristické)
X-záření. První skutečný urychlovač sestavil v r.1931
R.J.van de Graff s použitím elektro-mechanického
generátoru vysokého napětí (nazývaným jeho jménem), v
r.1932 pak J.D.Cockcroft a E.T.S.Walton s použitím kaskádového
násobiče napětí (soustava usměrňovacích diod s
vhodně zapojenými kondenzátory). Bylo dosaženo energie
urychlených protonů asi 0,5MeV, s níž byla pozorována první
jaderná transmutace vyvolaná uměle urychlenými částicemi.
První kruhový urychlovač (cyklotron) zkonstruoval E.O.Lawrenc
rovněž v r.1932. Tím začala éra používání urychlovačů
v jaderné fyzice.
Kosmické
urychlovače
Procesy urychlování stavebních částic hmoty probíhají i v
přírodě, a to často v mnohem větším měřítku a
intenzitě, než to my dokážeme uměle. V bouřlivých
procesech ve hvězdách a galaxiích dochází k
procesům, které fungují jako "kosmické
urychlovače" částic. Jsou diskutovány především tři
mechanismy urychlování částic ve vesmíru:
¨ Fermiho
mechanismus plynulého difuzního urychlování při
opakované interakci částic s pohybujícími se rozlehlými
oblaky ionizovaného plynu, za spolupůsobení magnetického a
elektrického pole.
¨ Výbuch
supernovy, při němž se vnější části hvězdy
rozpínají rychlostí blízkou rychlosti světla, přičemž ve
vzniklé rázové vlně mohou být v prudce expandující
ionizované hmotě protony urychlovány na energie až stovky
TeV.
¨ Pohlcování
hmoty černou dírou, kdy velké množství hmoty,
přitahované černou dírou, vytvoří kolem ní tzv. akreční
disk, v jehož nejnižší centrální oblasti dochází k
extrémně silnému ohřevu pohlcované látky klesající po
spirále do černé díry. Podél osy symetrie tohoto tlustého
rotujícího disku pak "trychtýři" z vnitřní
části uniká proud částic a záření - tzv. jet
neboli výtrysk, který obsahuje částice urychlené na
velmi vysoké relativistické energie.
Těmito
mechanismy (a možná i dalšími dosud neznámými) vzniká
vysoce energetické kosmické záření -
podrobnosti z hlediska radiační fyziky viz v §1.6
"Ionizující záření", část "Kosmické záření", z hlediska astrofyziky a kosmologie pak v kap.4
"Černé díry" v knize "Gravitace,
černé díry a fyzika prostoročasu".
Základní
rozdělení urychlovačů
Z hlediska účelu a použití lze urychlovače
rozdělit do dvou skupin:
¨ Malé
urychlovače pro průmyslové a medicínské využití,
kde nejsou potřeba extrémně vysoké energie (většinou
stačí jednotky až desítky MeV), ale bývá často žádoucí
dosáhnout poměrně vysokého toku (fluence)
částic, aby požadovaný technologický, analytický či
terapeutický efekt byl dostatečně účinný. Jedná se o
relativně malé přístroje s rozměry urychlovací komory
řádu desítek centimetrů až několika metrů. Takovéto
urychlovače jsou nejrozšířenější, často jsou vyráběny i
sériově.
¨ Velké
urychlovače pro výzkum ve fyzice elementárních částic,
kde je většinou rozhodující dosáhnout co
nejvyšších energií urychlených částic; vysokých
efektivních energií interakcí řádu TeV a vyšších lze
dosáhnout jen s použitím metody vstřícných svazků
(collider), jak je diskutováno níže. Pro studium
interakcí s nízkým účinným průřezem je zároveň potřeba
dosáhnout i vysokého toku vysokoenergetických
částic (často jen jedna interakce z několika miliard je
"ta pravá"). Toto jsou unikátní zařízení o
velkých rozměrech (desítky a stovky metrů, ty největší až
několik kilometrů!); jsou součástí komplexních
laboratorních systémů se složitými detekčními aparaturami.
Stavba takových zařízení trvá řadu let a je finančně
velmi náročná - až miliardy dolarů. Problematika velkých
urychlovačů bude stručně diskutována níže - pasáž "Velké
urychlovače".
Čím
menší struktury zkoumáme, tím větší potřebujeme
zařízení
Při zkoumání mikrosvěta se projevuje zajímavá, na první
pohled paradoxní zákonitost: čím menší objekt zkoumáme
nebo ovlivňujeme, tím větší - mohutnější a výkonnější
- zařízení potřebujeme. Tento trend není nový a projevoval se vlastně již v
optické oblasti. Pro pozorování milimetrových objektů
vystačíme s obyčejnou lupou, pro studium buněk potřebujeme
již složitější a větší mikroskop, pro zkoumání procesů
v buněčném jádře se již neobejdeme bez poměrně velkého a
složitého elektronového mikroskopu. Obecně zde platí, že k
pozorování daného objektu potřebujeme záření o kratší
vlnové délce, než jsou efektivní rozměry objektu.
Ještě
složitější je situace u studia nejmenších
"elementárních" částic hmoty, kde přicházejí ke
slovu specifické vlastnosti jejich interakcí. Odpudivé síly
mezi částicemi mohou zabránit požadované interakci, při
stejných podmínkách mohou probíhat různé druhy procesů,
vznikají nové částice často s krátkou dobou života. Pro
poznání struktury elementárních částic a podstaty
sil, které mezi nimi působí, je nutné realizovat
srážky částic při co největších energiích. Při
takových kolizích částice vzájemně proniknou "hluboko
do svých niter" a výsledek interakce může leccos
vypovědět o jejich stavbě. Vlivem kvantových procesů v
polích silných, slabých a elektromagnetických interakcí
vznikají při vysokoenergetických srážkách nové
sekundární částice, které jsou jednak zajímavé samy o
sobě, jednak nesou důležité informace o charakteru
fundamentálních přírodních sil, včetně možností jejich
jednotného chápání v rámci unitární teorie pole. Srážky
částic při vysokých energiích jsou jakousi "sondou"
do nejhlubšího nitra hmoty - a zároveň i do procesů
vzniku vesmíru (viz §5.5 "Mikrofyzika
a kosmologie. Inflační vesmír." knihy "Gravitace, černé díry a fyzika
prostoročasu"). Lze říci, že
velké urychlovače jsou nejvýkonnějšími
"mikroskopy"*) do nitra hmoty a s trochou
nadsázky zároveň i největšími "teleskopy",
které umožňují "dohlédnout" až k velmi raným
fázím vývoje vesmíru, kam již žádné obvyklé
astronomické dalekohledy dohlédnout nemohou. Nejedná se
samozřejmě o přímé fyzické pozorování jevů v počátku
vesmíru, ale o jejich pokud možno věrnou experimentální
simulaci.
*) Ve spektru "nástrojů
zkoumání" na obr.1.0.1 leží na levém okraji (§1.0. ,
část "Metody a nástroje zkoumání
přírody").
Co se týče druhu
urychlovaných částic, některé typy urychlovačů
jsou "univerzální" a mohou v principu fungovat pro
různé druhy částic, pokud je poskytuje iontový zdroj; tuto
vlastnost mají lineární urychlovače nebo synchrotrony. Jiné
typy jsou schopné urychlovat pouze určité druhy částic,
např. betatron pouze elektrony. V praxi jsou však urychlovače
svým konstrukčním uspořádáním většinou
"specializované" a dělí se na urychlovače elektronů,
protonů a těžších iontů.
Luminozita
urychlovačů
Intenzita (četnost), s jakou probíhají interakce urychlených
částic, závisí na hustotě jejich toku. Charakterizuje se
pomocí veličiny zvané luminosita urychlovače
L [cm-2s-1], což je počet částic na cm2 za sekundu (jakási "svítivost",
"světelnost"). Na velkých colliderech dosahuje
luminosita L»1031-1033cm-2s-1, u urychlovačů pracujících s pevným terčíkem pak
bývá až L»1035cm-2s-1.
Podle způsobu technické realizace a tvaru
dráhy, na níž urychlování částic probíhá,
rozdělujeme urychlovače na dva základní typy: lineární (LINAC) a kruhové (cyklické) - oba typy budou podrobněji popsány
níže. Zmíníme předtím ještě jeden zajímavý a možná
perspektivní typ urychlovačů (patří do
kategorie lineárních, avšak svým principem se zásadně
liší), který je zatím ve stádiu
výzkumu a vývoje :
Laserové
plasmové urychlovače LWFA
Novou zajímavou a perspektivní metodou urychlování nabitých
částic (především elektronů) je využití velmi
intenzívních elektromagnetických paprsků z vysokovýkonových
laserů. Při průchodu intenzivního světelnho
paprsku z laseru plynným prostředím dochází k ionizaci
plynu, vzniká plasma. Ozáříme-li plynné
prostředí velmi intenzívním krátkým pulzem laserového
světla, vzniká v prostředí plasmová stopa,
která za sebou strhává uvolněné elektrony. Při průchodu
plasmou laserový impuls ponderomotorickou silou
vytlačuje elektrony z oblastí svého vf. impulzu, takže za
ním v plasmě vzniká vlna či brázda vychýlených
elektronů. Elektrony se pohybují v prostředí
kladných iontů a za působení Coulombovy elektrické síly se
budou vracet zpět ke svým rovnovážným polohám (které "překmitnou"),
přičemž může docházet k periodickému vychylování souboru
elektronů vůči souboru iontů (které se
ve vysokofrekvenčním poli díky své podstatně větší
hmotnosti téměř nestačí rozpohybovat)
- k oscilacím elektronů v Coulombickém poli,
doprovázeným periodicky proměnným elektrickým polem. Vzniká
jakási stopa vlnící se koncentrace elektronů a intenzity
elektrického pole - plasmová vlna či "brázdové
pole" (wakefield), podobná vlnící se
stopě či brázdě, kterou za sebou zanechává loď rychle
plující po vodní hladině. Frekvence oscilací elektronů v
plasmové vlně (plasmová frekvence) je wp = Ö[rp.e2/(eome)],
kde me
hmotnost elektronu, e náboj elektronu, rp hustota plasmy (počet částic na m3), eo permitivita vakua. Při oscilacích elektronů v
plasmové vlně vzniká střídavé elektrické pole o amplitudě
intenzity Emax = me.wp.c/e. Urychlující
elektrický gradient v lineární plasmové vlně tedy může
dosahovat maximální hodnoty E = c.Ö(me.rp/eo), úměrné odmocnině hustoty plasmy. Pro hustoru
plasmy rp» 1018částic/cm3 dosahuje
urychlující gradient hodnot E»1GeV/cm, což je o 2-3
řády vyšší než v lineárních urychlovačích.

Podélná složka
oscilujícího elektrického pole v této plasmové vlně může
za určitých okolností (synchronizované energie a hybnosti) urychlovat
elektrony, které jsou neseny na vlně elektrického
pole (podobně jako je tomu u vysokofrekvenčních lineárních
urychlovačů popsaných níže). Při použití laseru s
fokusovanými pikosekundovými pulsy vysoké intenzity (cca 1018W/cm2) vzniká velmi
intenzívní podélné urychlovací pole, které může elektrony
urychlit na energii asi 50MeV (ve
špičkových laboratorních experimentech se podařilo
dosáhnout i energie řádově GeV, elektronový výtěžek je
však zatím velmi malý). Pokusné
urychlovače na tomto principu dostaly název LWFA
(Laser Wake Field Accelerator -
laserové urychlovače brázdovým polem, angl.
wake = stopa za lodí, brázda),
na obrázku vlevo. Jejich výhodou jsou velmi malé
rozměry *). Rychlý pokrok laserové techniky slibuje
možnosti efektivního urychlování, řízeného několika
sekvenčními laserovými pulzy (jeden
impuls vybudí brázdové pole, druhý následný impuls do něho
uvolní, "injektuje", elektrony).
Podaří-li se tuto technologii dotáhnout do stádia praktické
použitelnosti, pak takový maličký "stolní" LINAC,
urychlující v laserem vzbuzené plasmové vlně na
centimetrové dráze elektrony na energie desítky a stovky MeV,
by našel široké uplatnění ve výzkumu, průmyslu i
medicíně.
*) U plasmových urychlovačů
totiž může mít akcelerační pole mnohem větší
gradient než u klasických elektrostatických či
radiofrekvenčních urychlovačů (lineárních a kruhových,
popsaných níže). U klasických elektronických urychlovačů
je intenzita urychlujícího pole limitována
elektrickou pevností izolátorů a koronovými výboji v
urychlovací trubici. Tato limitovaná hodnota urychlujícího
gradientu vyžaduje pro získání vysokých energií dlouhé
urychlovací trubice. Gradienty polí v plasmě jsou o
2-3 řády silnější než v klasických radiofrekvenčních
urychlovačích, což vede k mnohem menším délkám
urychlovací dráhy.
Laserové
urychlování protonů
Dělají se experimenty i s laserovým
urychlováním protonů. Přímé laserové
urychlování protonů nefunguje, těžké protony nestačí
reagovat na rychle proměnné pole v brázdové vlně. Je třeba
použít dvoustupňový způsob,
schématicky znázorněný v pravé části obrázku :
1. Krátké vysoce výkonné
laserové impulsy nejprve metodou LWFA
urychlují elektrony na vysoké energie řádu
GeV.
2. Tyto vysokoenergetické elektrony pak
prolétají proton-elektronovou urychlovací trubicí,
do níž se současně (synchronizovaně) injektují
protony, předurychlené v malém
urychlovači na energii cca MeV (je to pro lepší synchronizaci a účinnější
předávání energie mezi elektrony a protony). Mezi
skupinami elektronů a protonů působí přitažlivé
Coulombovské síly, čímž se elektrony zpomalují a protony
urychlují (obr. vpravo).
Vysokoenergetické elektrony tak svým elektromagnetickým polem
protonům předávají energii, "vlečou" je za sebou a
urychlují protony na energie řádu 100MeV. Na
výstupu z trubice se pak pomocí elektromagnetu oddělí
elektronový a protonový svazek.
Pokud se tuto technologii podaří
dotáhnout do praktického použití, nahradily by se velké
cyklotrony a složitý rozvod protonů do ozařoven v protonové
terapii (§3.6 "Radioterapie",
část "Hadronová radioterapie") malými kompaktními
laserovými urychlovači, které by se daly bez problémů
namontovat do gantry jednotlivých ozařovacích přístrojů ve
stávajících radioterapeutických místnostech...
Kombinace
více urychlovačů
Pro některé speciální experimentální a technické aplikace
se kombinují dva či více lineárních nebo
kruhových urychlovačů do jednoho většího systému. Je to
především pro získání velmi vysokých energií
částic, které jsou nejdříve předurychleny v
menších urychlovačích a pak se injektují do velkého
urychlovače k finálnímu urychlení (viz níže "Velké urychlovače"). Některé nově vyvíjené systémy pro protonovou
radioterapii (§3.6
"Radioterapie", část "Hadronová
radioterapie") kombinují předurychlení protonů v menším
cyklotronu s definitivním urychlením v lineárním urychlovači
za účelem lepších možností elektronické regulace energií
protonů pro zacílení Braggova maxima hloubkové dávky do
oblasti tumoru.
Primární
a sekundární záření z urychlovačů
Urychlené nabité částice tvoří tzv. primární
svazek, který může být využit dvojím způsobem:
¨ Přímé
využití primárního svazku,
který po dopadu na vhodný terčík (či v
interakci vstřícných svazků) vyvolává požadovanou interakci
pro studium elementárních částic, výrobu radionuklidů,
radioterapii nebo pro jiný radiační analytický či
technologický proces. Terčíkem zde může být ozařovaný
technologický materiál, nebo i tělo pacienta - nádorová
tkáň ("Radioterapie").
¨ Využití
sekundárního záření,
které vzniká při dopadu a interakci
primárních urychlených částic s terčíkem.
Druh a vlastnosti tohoto sekundárního záření závisí
především na druhu a energii primárních částic a dále na
materiálu a provedení terčíku. U urychlených elektronů je
to především brzdné záření g
(spojité spektrum podobně jako u X-záření, ale podstatně
vyšší energie). Urychlené protony mohou při interakci s
terčíkovými jádry poskytovat sekundární neutrony,
p- a K-mezony, antiprotony,
hyperony atd., v závislosti na energii.
Sekundární záření může být vyváděno v tzv. sekundárních
svazcích k vlastnímu použití. V medicínské oblasti je
nejčastější použití brzdného g-záření z elektronového
urychlovače v radioterapii (viz §3.6 "Radioterapie", ve stádiu experimentů je terapie p--mezony či antiprotony).
Svazek vysokoenergetických částic, ať již primárních
či sekundárních, může být k příslušným interakcím
využíván buď uvnitř urychlovače, kde
vzniká (je instalován vnitřní terčík), nebo může
být pomocí vhodných elektromagnetických polí směrován a vyveden
ven z urychlovače. Pomocí vakuových transportních trubic je
pak veden do prostoru laboratoře, k interaci s atomy a jádry vnějšího
terčíku (viz též níže pasáž "Terčík").
Zmíníme na tomto místě tři specifické způsoby využití
sekundárního záření, produkovaného urychlovači, které
mají praktické využití i mimo vlastní jadernou fyziku:
Urychlovače
jako generátory brzdného g-záření
Jsou-li urychlovanými částicemi elektrony,
pak při jejich dopadu na terčík z těžkého
materiálu, nejčastěji wolframu, vzniká brzdné
elektromagnetické záření se spojitým spektrem. Jeho
maximální energie se téměř rovná kinetické energii
urychlených dopadajících elektronů. Toto je velmi častý
způsob produkce tvrdého fotonového záření pro použití v
jaderné fyzice, analytických metodách (§3.4 "Radiační analytické metody materiálů") a především v radioterapii (§3.6 "Radioterapie"). Jako
urychlovače elektronů se používá buď betatron,
nebo častěji lineární urychlovač (oba způsoby jsou
popsány níže, viz též §3.6, část "Isocentrická
radioterapie", obr.3.6.1).
Urychlovače jako neutronové
generátory
Urychlovače ve speciálním uspořádání mohou sloužit jako elektronické
zdroje neutronového záření - tzv. neutronové
generátory. Neutrony vznikají nebo se uvolňují v
řadě částicových a jaderných reakcí. Z hlediska snadné a
účinné produkce neutronů jsou nejvýhodnější reakce jader
tritia a deuteria. Stačí, abychom urychlili deuterony na
energii cca 100-200keV a nechali je dopadat na terčík
obsahující tritium, aby docházelo k jaderné reakci 2D1 + 3T1
® 1n0 + 4He2 (+17,6MeV), při níž se uvolňují neutrony.
K tomu stačí docela malý "stolní" lineární
urychlovač. Analogická reakce D + D ® 1n0
+ 3He
(+3,3MeV) je méně výhodná, neboť má nižší účinný
průřez a deuterony musejí být urychleny na vyšší energii,
cca 1MeV. Základní uspořádání takového neutronového
generátoru sestává ze tří hlavních částí:
iontového zdroje, urychlovacího a fokusačního systému a
terčíku. Do iontového zdroje se napouští zředěné
deuterium, které se elektrickým výbojem ionizuje. Ionizované
atomy deuteria - deuterony - se z této plasmy
elektrickým polem přivádějí mezi elektrody urychlovacího a
fokusačního systému. Urychleným svazkem deuteronů se
bombarduje tritiový terčík; tritium je vázano ve formě hydridu
v tenké povrchové vrstvě absorbátoru, nejčastěji titanu,
zirkonu či skandia, podkladový materiál terčíku se chladí,
pro vysoké výkony se používá diskovitý rotující terčík (svazek pak zasahuje každé jeho místo pouze velmi
krátký časový okamžik, během kterého se exponované místo
nepřehřeje a teplo se stačí odvést - podobně jako v
rentgence s rotující anodou). Jaderná
reakce deuteria s tritiem je exotermická a vylétají při ní
téměř monoenergetické neutrony s energií asi 14MeV *) (z
terčíku vylétají prakticky izotropně do celého
prostorového úhlu). Při energii deuteronů 200keV a intenzitě
jejich svazku 1mA se dosahuje výtěžek cca 2.106 neutronů/sekundu. Při snaze o dosažení vysokých
výtěžků neutronů, vyšších než cca 2.1011 n.s-1, se tritiový
terčík rychle vyčerpává. Byly proto vyvinuty speciální
uzavřené urychlovací systémy - tzv. neutronové
trubice, plněné zředěnou směsí deuteria D a
tritia T (regulovaně doplňovanou,
s odvodem hélia). Oba tyto druhy iontů,
D+T vytvářené výbojem v iontovém zdroji, se současně
urychlují a bombarduje se jimi terčík, v jehož povrchové
vrstvě se ustálí stejná koncentrace atomů D a T;
požadovaná reakce pak nastává nárazy urychleného D
na T v terčíku, i při nárazech urychleného T
na terčíkové D. V poslední době jsou konstruovány i miniaturní
neutronové generátory (laboratorní,
"stolní"), používající vysokofrekvenční
urychlování iontů D a T. Schématický nákres
principu neutronových generátorů bude doplněn... (zatím viz
náznakové vyobrazení na konci §4.3, část "Neutrony stimulovaná
emisní počítačová tomografie NSECT").
*) Přímé použití těchto vysokoenergetických neutronů je
vhodné u neutrony stimulované jaderné
gama-spektrometrické analýzy. Pro neutronovou
aktivační analýzu je zapotřebí tyto neutrony
zpomalit v moderátoru.
Neutronové záření nachází uplatnění při
neutronové aktivační analýze (§3.4, část
"Neutronová
aktivační analýza"), v některých
radiačních technologiích, zkouší se i v radioterapii
(§3.6, část "Hadronová
radioterapie").
Urychlovače jako generátory
synchrotronového záření
Zcela speciální způsob využití sekundárního záření z
urychlovače spočívá ve využití synchrotronového
záření *). Je to elektromagnetické záření, které
vyzařuje nabitá částice při pohybu po zakřivené dráze. Z
hlediska funkce kruhových urychlovačů je to jev
"parazitní" a nepříznivý, který
"užírá" kinetickou energii urychlovaných částic a
brání dosahovat vysokých energií, zvláště u elektronů.
Avšak UV a rtg složka synchrotronového záření může být
použita v některých aplikacích při analýze materiálů i v
biologii a medicínské diagnostice. Proto se konstruují
speciální urychlovače pro produkci synchrotronového
záření, jak je níže stručně popsáno.
*) Název vznikl z toho, že toto záření
(ve viditelné části spektra) bylo poprve pozorováno v r.1947
na synchrotronu GE v New Yorku při
urychlování elektronů na kruhové dráze. Intenzívní
synchrotronové záření vzniká ve vesmíru
při rychlém pohybu elektronů v silném magnetickém poli kolem
kompaktních objektů, především neutronových hvězd,
které jsou pozorovány jako pulsary -
podrobněji §4.2. "Konečné fáze hvězdné
evoluce. Gravitační kolaps",
část "Pulsary", obr.4.3, knihy "Gravitace,
černé díry a fyzika prostoročasu". Zde se však budeme
zabývat umělou výrobou synchrotronového záření na
urychlovačích.
Částice s klidovou hmotností mo a nábojem e,
pohybující se s kinetickou energií E po dráze o
poloměru zakřivení R, podle zákonů elektrodynamiky (viz §1.5 "Elektromagnetické
pole. Maxwellovy rovnice."
monografie "Gravitace, černé díry a fyzika prostoročasu"; plyne z Larmorova vzorce (1.61')) vyzařuje elektromagnetické vlny o
výkonu P = (2/3).(e2.c/R2).[E/moc2]4. Z tohoto vztahu je
vidět, že vyzařování je podstatné pouze pro lehké
nabité částice, elektrony či pozitrony, pohybující
se s vysokou energií, tj. s relativistickou rychlostí, po
silně zakřivené dráze. Při pomalém pohybu
(nerelativistickou rychlostí) se obíhající částice jeví
jako oscilující elektrický dipól, vyzařující slabé
monochromatické záření s frekvencí danou periodou oběhu
(podobně jako vysílací anténa), prakticky do všech směrů (s vyzařovacím diagramem podle obr.1.4 zmíněného
odkazu). Při pohybu částice
relativistickou rychlostí je však elektromagnetické záření
vysíláno v úzkém kuželu, jehož osou je tečna k
orbitě částice v daném bodě. Úhel otevření tohoto kužele
je přibližně rovný moc2/E.
Vnější pozorovatel uvidí záření jen během doby, kdy tento
kužel protíná jeho stanoviště ("majákový
efekt"). Při pohybu částice po kruhové dráze bude tedy
pevný pozorovatel či detektor registrovat pulzy
záření, jejichž frekvence je dána dobou oběhu částice
T=L/c, kde L je délka orbity. Spektrum vlastního
synchrotronového záření S se skládá z řady
harmonických složek, které jsou v důsledku průběžného
pohybu po orbitě natolik "rozmazané", že se
výsledné spektrum jeví jako spojité, s maximem
energie kolem ESmax[keV] » 2400.Ee3[GeV]/R[m] » 0,6.B[T].Ee2[GeV] (pohyb elektronu s kinetickou energií Ee po dráze s
poloměrem zakřivení R, pod vlivem magnetického pole o
intenzitě-indukci B). V oblasti vyšších energií než
ESmax
spektrální intenzita záření rychle klesá.
Experimenty se synchrotronovým zářením se
dříve prováděly na synchrotronech určených k urychlování
elektronů ("parazitní"
využití). Později však byly
konstruovány speciální jednoúčelové urychlovače, optimalizované
pro produkci synchrotronového záření (2.generace).
Neobsahují žádný terčík, ani se z nich žádné částice
nevyvádějí. Elektrony jsou urychlovány v akumulačním
prstenci - evakuované trubici tvaru mnohoúhelníku, v
jehož zaoblených vrcholech jsou umístěny ohybové magnety.
Do jedné z přímých sekcí se vstřikují elektrony, v druhé
jsou urychlující elektrody (vysokofrekvenční rezonátor).
Částicím se dodává jen tolik energie, kolik se jí
elektromagneticky vyzáří, takže elektrony mohou v trubici
cirkulovat dlouhou dobu (elektrony, které
vypadnou z cirkulace v důsledku srážky s atomy zbytkového
plynu v trubici, jsou doplňovány z injektoru). Synchrotronové záření se odebírá ze
zakřivených drah v ohybových vrcholech. U
některých typů (3.generace) jsou do dráhy svazku v přímých
sekcích trubice vložena speciální magnetická zařízení,
tvořená sérií magnetů s periodickým střídáním směru.
Jejich úkolem je horizontálně či vertikálně zvlnit dráhu
elektronů. Jsou to tzv. undulátory ("zvlňovače") se
slabším polem a viglegy (angl. wiggle=třepotat, třást se) se silným magnetickým polem (cca 10T). V undulátoru
je dráha elektronů zvlněna jen slabě, což vede k
vyzařování harmonicky modulovaného signálu, téměř
monochromatické vlny, jejíž vlnová délka je dána tzv. undulátorovou
rovnicí: l = [lU/2(1-v2/c2) ]. (l + K2/2)
s undulátorovým parametrem K = e.Bo.lU/2pmec. V těchto
rovnicích lU je undulátorová
perioda (prostorová vzdálenost opačné polarity
elektromagnetů undulátoru), e je náboj elektronu a me jeho klidová
hmotnost, Bo maximální hodnota magnetického pole, c
rychlost světla. Změnou energie (rychlosti) elektronů, nebo
intenzity magnetického pole lze tedy v širokém rozsahu měnit
vlnovou délku výstupního záření. V silných magnetech
vigleru se dráhy elektronů prudce periodicky zakřivují, což
vede k intenzívnímu vyzařovaní synchrotronového záření
kratších vlnových délek.
Pro produkci synchrotronového záření se
začínají používat i lineární urychlovače
elektronů (4.generace zdrojů), jejichž zhuštěný
oblak (bunch) při průchodu dlouhým undulátorem
interaguje s buzenou elektromagnetickou vlnou, kterou sám
vytvořil. Elektrony jsou v něm mírně zpomalovány nebo
zrychlovány (podle toho, zda jsou ve fázi nebo protifázi) tzv.
ponderomotorickou sílou, čímž vzniká uvnitř
elektronových obláčků redistribuce elektronové hustoty s
jemnou podélnou strukturou o prostorové periodě
odpovídající přibližně vlnové délce záření - nastává
tzv. mikrobunching. V této pravidelné
"mikroobláčkové" struktuře lze dosáhnout
synchronizace a koherentního skládání elektromagnetického
záření z jednotlivých mikro-shluků elektronů. Pokud
elektrony vyzařují synchronně se shodnou fází, výstupní
záření dosahuje mnohonásobně vyšší intenzity a značného
stupně koherence. Toto spontánní "samozesílení"
záření z periodicky "samo"-modulovaného
elektronového oblaku v undulátoru je analogické vzniku
záření v laserech - jedná se zde o jakýsi "laser"
s volnými elektrony (FEL - Free Electron
Laser). Elektrony opouštějící undulátor jsou pomocí
magnetického pole odchylovány a vedeny pryč (do absorbátoru
nebo k příp. dalšímu použití), aby nekontaminovaly
výstupní svazek fotonového záření. Systémy FEL se zatím
experimentálně zkoušejí na velkých lineárních
urychlovačích elektronů (nejvyšší
dosud použitá energie elektronů byla 14GeV na urychlovači
SLAC ve Stanfordu, kde délka undulátoru činila 112m s 33
segmenty o magnetickém poli 1,25T; výstupní koherentní
X-záření dosahovalo energie 8,25keV a fluence 1012 fotonů v pulzu
délky 0,07ps).
Při energiích urychlovaných elektronů Ee»2-10GeV je tak možno získat širokou škálu vlnových
délek i v rentgenové oblasti. Hlavní
předností těchto specializovaných zdrojů synchrotronového
záření, označovaných též někdy jako "fotonové
továrny", je vysoká intenzita záření,
jeho úzká úhlová kolimace, pulzní charakter, dobrá
definovatelnost, stabilita a nastavitelnost parametrů.
Základní
části urychlovačů
Než se budeme zabývat jednotlivými typy urychlovačů,
zmíníme se o čtyšech základních součástech, které mají
všechny urychlovače :
¨ Zdroj
urychlovaných částic (iontový zdroj)
emituje do "startovacího" místa urychlovacího
systému požadovaný druh částic, jako jsou elektrony, protony
či těžší ionty. V nejjednodušším případě se jedná o ionizační
trubici obsahující příslušný zředěný plyn
(např. vodík H), kde v doutnavém výboji mezi katodou a anodou
(při napětí cca stovky voltů až desítky kV) vznikají ionty
(u vodíku jsou to protony p+) a ty jsou pomocí
tenké kapiláry vedeny "odsávací" elektrodou do
urychlovacího systému. Pro získání těžších jader
(iontů) se používá výboj ve zředěném plynu (obsahujícím
příslušný prvek) při dostatečně vysokém napětí, aby
docházelo k ionizaci i na K slupce. Vznikají přitom ionty s
různým stupněm ionizace, z nichž je potřeba požadovaná
jádra (ionty s nejvyšším stupněm ionizace) odseparovat
pomocí elektrického a magnetického pole a zavést je do
urychlovacího systému.
Pro urychlovače elektronů je zdrojem
prostá žhavená katoda (termoemise elektronů)
opatřená vhodnými urychlujícími a fokusujícími anodami -
"elektronovým dělem" - podobně jako u obrazovky.
Popř. může být katoda opatřena mřížkou pro
elektronickou regulaci toku elektronů.
V poslední době se vyvíjejí i laserové zdroje,
v nichž je emise částic generována vysokou koncentrací
energie z krátkých a velmi intenzívních laserových pulzů,
dopadajících na vhodný terčík. Vznikají tak prvotní oblaky
(bunch) částic, elektronů nebo iontů, které jsou
pak urychlovány v pulsním vysokofrekvenčním režimu v
urychlovačích, nebo v laserové "brázdové vlně" (výše uvedené "Laserové plasmové
urychlovače LWFA").
Složitěji se pro urychlení získávají antičástice. Pozitrony
se získávají ostřelováním terčíku z materiálu s vysokým
protonovým číslem Z (např. wolframu) urychlenými elektrony,
přičemž elektromagnetickou interakcí v poli jader vznikají
m.j. pozitrony e+. Podobně antiprotony p' je nutno
získávat ostřelováním vhodného terčíku protony
urychlenými na energie vyšší než 3GeV, kdy dochází m.j. k
reakcím p + p ® 2p + p + p'.
U velkých urychlovačů vysokých energií se jako zdroje
částic k urychlení někdy používají injektory
- do hlavní komory jsou "předurychlené" částice
vstřikovány pomocným lineárním či kruhovým urychlovačem
(s energií jednotky až desítky MeV, popř. GeV) a následně
urychlovány na požadovanou vysokou energii (GeV či TeV).
¨ Urychlovací
komora, trubice
Prostor, v němž se částice pohybují a dochází k jejich
urychlování, má různý tvar a velikost, podle typu
urychlovače. Může to být užší nebo širší, kratší či
delší trubice přímkového nebo kruhového tvaru,
plochá válcová komora. Musí zde být vysoké vakuum,
aby nedochízelo k rušivým srážkám částic s atomy plynu.
¨ Urychlovací
elektrody, elektromagnetické pole
V evakuované urychlovací komoře či trubici je umístěn urychlovací
systém elektrod či vlnových rezonátorů, kde při
synchronizovaném působení elektromagnetického pole na
prolétající nabité částice vzniká urychlovací
síla. Urychlovací systém je napájen ze zdroje
elektrického napětí - viz níže pasáž
"Elektrické napájení urychlovačů".
¨ Terčík,
na nějž dopadá svazek urychlených částic, je buď vnitřní
- je umístěn uvnitř urychlovacího systému, nebo vnější
- svazek částic je vyveden ven z urychlovací trubice. Terčík
může dále být pevný, nebo místo něj
může být interakční oblast, kde se
částice střetávají ve vstřícných svazcích
(viz níže "Vstřícné
svazky - collidery"). Rovněž sekundární částice, produkované na
vnitřním terčíku (jako jsou p nebo K mesony), se
působením magnetického a elektrického pole vyvádějí ve
formě svazku do prostoru laboratoře, kde jsou umístěny
měřící aparatury (detekční přístroje, bublinové komory
atd.). Při dopadu urychlených částic na (pevný) terčík se
většina kinetické energie částic mění na teplo -
ostřelovaný terčík se zahřívá. Aby
nedošlo k jeho tepelnému poškození či odpaření
terčíkové látky, je nutno toto ztrátové teplo (může činit i stovky wattů)
odvádět - terčík se fixuje na masívní kovovou podložku s
dutinou, chlazenou protékající vodou (podobně jako anody výkonových rentgenových trubic). Terčík ani interakční oblast nemají speciální
urychlovače pro produkci synchrotronového záření, zmíněné
výše.
Terčík či obecně místo, kde
dochází k interakcím urychlených částic, bývá opatřen detektorem
sekundárních částic. V jednodušších případech
slouží k monitorování vznikajících
jaderných reakcí. U velkých urychlovačů pro výzkum
interakcí částic je tvořený často celým složitým detekčním
systémem, umožňujícím podrobnou analýzu drah,
energií, hybností a dalších charakteristik sekundárních
částic vznikajících při vysokoenergetických interakcích -
viz §2.1, pasáž "Uspořádání a konfigurace detektorů
záření".
Vstřícné svazky - collidery
Dopadá-li urychlená částice na (pevný, nepohyblivý)
terčík a tam se srazí s další částicí nebo jádrem,
spotřebuje se na vlastní interakci ve skutečnosti jen malá
část kinetické energie nalétající částice, neboť podle
zákona akce a reakce se část energie dopadající částice
přemění na kinetickou energii odražené částice a nově
vzniklých částic. Pro výsledek interakce je důležitá
kinetická energie v těžišťové soustavě
(CMS) obou částic - jen ta se skutečně
"spotřebuje" na vlastní interakci *). Podstatného
zvýšení efektivní energie interakce můžeme dosáhnout tím,
že nalétající a terčíková částice se budou pohybovat proti
sobě se srovnatelně vysokými kinetickými energiemi
(resp. hybnostmi). Obě takové částice se pak po srážce
prakticky zastaví a skoro celá jejich kinetická energie se
může využít na vlastní interakci a tvorbu nových částic.
V tom spočívá metoda vstřícných svazků
bez použití klasického terčíku: obě částice, jejichž
interakce chceme zkoumat, se urychlí na vysoké energie a ve
vstřícných svazcích se pouštějí proti sobě tak, aby se
vzájemně čelně srážely a interagovaly. Oba svazky se
urychlují buď v jedné trubici (např. elektron-pozitronové
svazky), nebo ve dvou různých trubicích. V daném místě
urychlovacího prstence se oba svazky urychlených částic,
letících opačným směrem proti sobě, působením
magnetického pole fokusují a navedou se tak, aby se čelně
srážely. Přístroje tohoto druhu se nazývají collidery
("srážeče") a umožňují studovat interakce
částic při podstatně vyšších efektivních energiích než
je tomu u klasických urychlovačů s pevnými terčíky - v
současné době se dosahuje až TeV. Místo, kde dochází k
interakcím vstřícných svazků, interakční oblast,
je obklopeno složitým detekčním systémem (jak bylo výše zmíněno, viz též pasáž "Velké
urychlovače, LHC") pro detailní studium sekundárních částic.
Collidery se používají pouze pro badatelský výzkum
interakcí částic při velmi vysokých energiích, za
vzniku nových "exotických" částic.
*) Vztah mezi energií interakce v
laboratorní a těžišťové vztažné soustavě je dán
dynamickou analýzou srážky za použití zákona zachování
energie a hybnosti. Při nárazu částice klidové hmotnosti mo, pohybující se s
kinetickou energií E, na stejnou částici v klidu, je
efektivní energie interakce Eef= E1/2.(moc2)1/2. Srazí-li se
např. proton s kinetickou energií 400GeV s terčíkovým
protonem v klidu, pro interakční produkci nových částic
zůstane pouze energie 28GeV. S rostoucí energií energetická
účinnost interakce prudce klesá. Např. pro dosažení
efektivní energie Eef=6TeV bychom při pevném terčíku museli ozařovat
protony s kinetickou energií asi 2.104TeV (k čemuž by i za použití výkonných
elektromagnetů s B=7T byl potřeba kruhový urychlovač protonů
s obvodem cca 105km - větší než obvod Země!). Při vstřícné
srážce stejných částic, které se proti sobě pohybují se
stejnou kinetickou energií E, je však pro interakci k dispozici
celá energie Eef=2.E - je to tedy jediný prakticky použitelný způsob
dosažení velmi vysokých efektivních energií interakcí.
Aby vstřícné srážky byly dostatečně časté, je třeba
zajistit značně vysokou intenzitu obou svazků
(luminozitu). Proto se na některých urychlovačích
používají speciální akumulační prstence,
v nichž se v silném magnetickém poli hromadí urychlené
částice (např. protony a antiprotony) z několika dávek a
teprve po dosažení dostatečné intenzity se realizuje srážka
ve vstřícných svazcích.
Lineární
urychlovače
Lineární urychlovače urychlují nabité částice
působením elektrického pole během jejich pohybu po lineární
přímkové dráze. Lineární urychlovač se
často zkráceně nazývá Linac (Linear
accelerator). Můžeme je rozdělit
na elektrostatické (vysokonapěťové) a vysokofrekvenční.
Obr.1.5.5. Zjednodušené
schéma lineárního urychlovače elektrostatického (vlevo) a
vysokofrekvenčního (vpravo).
Základní schéma elektrostatického
lineárního urychlovače je na obr.1.5.5 vlevo. Z iontového
zdroje vstupují požadované částice (elektrony, protony,
deuterony a pod.) do urychlovacího systému, tvořeného
několika souosými kovovými válcovými elektrodami V1, V2, ...,Vn,
mezi nimiž je rozloženo postupně vzrůstající vysoké
napětí U1,
U2, U3, ....,Un. Elektrostatickým polem jsou nabité částice s
nábojem q na lineární dráze urychlovány na energii E = q .
(U1+U2+U3+ ...+Un)
danou součtem napětí na jednotlivých elektrodách. Mezera
mezi dvěma po sobě následujícími válcovými elektrodami
působí na letící částice jako "elektrická
čočka" (je to podobné jako v
obrazovce), fokusující proud částic do
úzkého svazku, který nakonec dopadá na terčík. Urychlovací
elektrody jsou napájeny vysokým napětím buď z
elektronického kaskádního násobiče (soustava
vhodně zapojených diod a kondenzátorů), nebo z
elektrostaticko-mechanického Van de Graffova generátoru.
Používá se napětí od několika stovek kilovoltů až asi do
5MV; vyšších napětí je obtížné dosáhnout pro vznik
korónových a jiskrových výbojů *).
*) Tyto problémy s elektrickými
výboji vznikají v látkových prostředích - ve
vzduchu, dielektrikách, izolátorech. Pro zajímavost si
můžeme uvést drobnou diskusi, jak je tomu ve vakuu? :
Jaké nejsilnější
může být elektrické pole?
V rámci klasické (nekvantové) fyziky může být elektrické
pole ve vakuu libovolně silné, až téměř k nekonečnu (v látkovém prostředí je to však omezeno
elektrickou pevností dielektrika). Z
hlediska kvantové elektrodynamiky však i ve vakuu
existuje principiální omezení, způsobené existencí
vzájemných antičástic elektronu a pozitronu:
nelze vytvořit elektrické pole o intenzitě silnější než Ee-e+ = me2c3/e.h = 1,32.1016 V/cm, kde me je klidová hmotnost
elektronu či pozitronu. Při překročení této intenzity je
totiž gradient potenciálu vyšší než prahová energie 2mec2 a dochází ke vzniku dvojice elektronu a
pozitronu, která intenzitu elektrického pole
automaticky zredukuje. Tak silné elektrické pole se zatím
nepodařilo vytvořit, klasickou elektronikou to není možné;
určitou možností v budoucnosti by mohly být silné impulsy z
extrémně výkoných laserů...
..............doplnit ....
tandemové urychlovače?
Efektivnější
způsob, jak na lineární dráze urychlit nabité částice na
značně vysokou energii bez použití extrémně vysokého
napětí, je realizován ve vysokofrekvenčním
lineárním urychlovači, jehož nejjednodušší
schéma je na obr.1.5.5 vpravo. Nabité částice z iontového
zdroje Z vstupují do urychlovacího systému válcových
elektrod V1, V2, V3, ...,Vn,
které jsou připojeny ke střídavému elektrickému
napětí U(t) = Uo.cos(w.t) =Uo.cos(2pf.t) o amplitudě
Uo a frekvenci f.
Liché válce jsou připojeny k jednomu pólu, sudé válce k
druhému pólu vysokofrekvenčního zdroje vysokého
elektrického napětí. Přijde-li kladná částice s nábojem q
a hmotností m ze zdroje Z ve fázi, kdy první
válcová elektroda V1
má záporný potenciál -Uo, pak získá energii E1 = q.Uo a
rychlost v1 = Ö(2qUo/m), takže délku l1 uvnitř válce V1 proletí za čas t1 = l1/v1. Je-li
frekvence f střídavého napětí volena tak, aby
urychlená částice vstoupila do mezery mezi válci V1 a V2 v
čase, kdy se polarita obrátí a válec V1 má kladný a V2
záporný potenciál, je částice znovu urychlena o energii q.Uo, t.j. má již energii 2.q.Uo. Je-li synchronizace
mezi frekvencí f, napětím Uo a délkami elektrod lk *) volena
tak, aby se vždy během průchodu mezi jednotlivými válcovými
elektrodami Vk
obrátila polarita střídavého napětí, budou se tyto
"synchronní" částice při průchodu každou
elektrodou znovu a znovu urychlovat.
*) Jak je vidět z obr.1.5.5 vpravo, k dosažení synchronizace
se musí délka válcových elektrod Vk postupně zvyšovat, jak narůstá rychlost částic.
Toto již neplatí při dosažení rychlosti blízké rychlosti
světla, kdy se při urychlování již rychlost částice
prakticky nezvyšuje; s kinetickou energií roste jen relativistická
hmotnost částice.
Stojí též za zmínku, že k vlastnímu elektrickému
urychlení částice dochází v mezerách mezi
elektrodami, zatímco uvnitř kovového válce, kde je gradient
elektrického pole blízký nule (elektrické pole je
odstíněno), prolétají částice setrvačností (to platí i u
elektrostatického urychlovače v levé části obrázku).
Vývoj těchto
urychlovačů postupoval tak, že frekvence f se
zvyšovala, přičemž místo válcových elektrod se
používají dutinové rezonátory. Novější
lineární urychlovače užívají pro vytvoření
urychlujícího pole vlnovodu, rozděleného
vhodnými diskovými výběžky na řadu rezonančních dutin a
napájeného frekvencí několika GHz (nejčastěji kolem 3GHz) z
klystronového nebo magnetronového generátoru
(stručně popsaných níže). Ve vlnovodu se vytváří
vysokofrekvenční střídavé elektromagnetické pole ve formě
postupné nebo stojaté elektromagnetické vlny.
Pokud se v poli této nosné vlny urychlovaná
nabitá částice pohybuje synchronizovaně, na
částici působí stálá urychlující síla daná elektrickou
složkou E elektromagnetické vlny. Částice k
urychlení se do urychlovacího systému dutinových rezonátorů
či vlnovodů vstřikují z iontového zdroje, či elektronové
trysky v případě elektronů, ve formě "shluků" (bunch)
v pulzním režimu, v přesné elektronické
synchronizaci *) s urychlujícím vysokofrekvenčním polem.
*) Aby ve vysokofrekvenčním poli na
částici působila stálá urychlující elektrická síla,
musí do vlnovodného urychlovacího systému vstoupit ve vhodné
fázi a s rychlostí blízkou fázové rychlosti vlny - musí
být splněna synchronizační podmínka.
Pulzní režim iontového zdroje (resp. elektronové trysky) a
vysokofrekvenčního generátoru je řízen elektronickým
obvodem osazeným speciálními výkonovými spínacími
součástkami - je to buď speciální elektronka thyratron
nebo polovodičový tyristor. Urychlovací vlnovodný
systém je tvořen několika speciálně tvarovanými kovovými
(měděnými) rezonančními dutinami,
řazenými za sebou. Elektrony jsou v pulzních dávkách do
urychlovacího systému vstřikovány z elektronové trysky
("děla") s energiíí cca 30-50keV, protony z
iontového zdroje s energií podstatně vyšší. Rezonanční
dutiny na počátku urychlovacího systému mají kratší délku
a vzdálenosti mezi sebou, další se prodlužují tak, aby se
fázová rychlost elektrického pole shodovala s narůstající
rychlostí částice. Celý systém je trochu podobný obr.1.5.5
vpravo, avšak místo válcových elektrod je větší počet
rezonančních dutin a místo vodičů, přivádějících
střídavé napětí, vede do počáteční části trubice
vlnovod z magnetronu nebo klystronu.
Malé lineární
urychlovače elektronů jsou nyní velmi často používány v radioterapii
- viz §3.6 "Radioterapie" (kde postupně vytlačily dříve používané
betatrony), především jako zdroj tvrdého brzdného
záření gama o energiích cca 5-40MeV. Velké
vysokofrekvenční lineární urychlovače s nosnou vlnou se
používají pro energie až desítky GeV, projektovány jsou i
pro oblast několika TeV. Používají se buď jako samostatné
základní přístroje, nebo mohou sloužit k předurychlení
částic - jako injektory pro velké synchrotrony (viz níže, obr.1.5.6 vpravo nahoře). Na rozdíl od kruhových urychlovačů, kde jedním
urychlovacím systémem jsou částice opakovaně mnohokrát
urychlovány, v lineárním urychlovači dochází k postupnému
urychlování v mnoha urychlovacích systémech řazených
přímkově za sebou. I při použití vysokých gradientů (až
100MV/m) a vysokých frekvencí (až 30GHz) pro dosažení
vysokých energií (řádově až TeV) činí délka
největších lineárních urychlovačů i několik kilometrů!
Kruhové
urychlovače
(cyklické)
Velmi efektivním způsobem, jak urychlit nabité
částice na vysoké energie, je jejich mnohonásobné
urychlení v elektrickém poli, kam jsou částice
opakovaně vraceny po kruhové dráze
působením magnetického pole *). Na částici
s nábojem q je zde aplikována nejen elektrická urychlující
síla Fe = q.E, ale i Lorentzova síla Fm = q.[v ´ B] působící v
magnetickém poli intenzity B kolmo ke směru
pohybu nabité částice rychlostí v. Tato
magnetická síla způsobuje, že nabitá částice se bude
pohybovat po kruhové dráze o poloměru R =
m.v.c/(q.B). Je-li ve vhodných místech této kruhové dráhy
synchronně aplikováno elektrické urychlující pole (v
tečném směru), budou částice periodicky urychlovány
při každém svém oběhu.
*) Toto magnetické pole je generováno elektromagnety
- cívkami, jejichž závity prochází silný elektrický proud.
V poslední době se často používají supravodivé elektromagnety,
což podstatně snižuje spotřebu elektrické energie
(fyzikální principy supravodivosti jsou stručně rozebírány
výše v pasáži "Fermiony v úloze bosonů;
Supravodivost").
C y k l o t r o n
Základním typem kruhového urychlovače je cyklotron
(první cyklotron zkonstruoval E.O.Lawrenc
již v r.1932), jehož princip je
schématicky znázorněn v levé části obr.1.5.6 :
Obr.1.5.6. Vlevo: Schématické
znázornění cyklotronu. Vpravo:
Schématické znázornění synchrotronu.
Mezi póly silného elektromagnetu jsou v
ploché kruhové vakuové komoře upevněny dva duté kovové
poloválce tvaru písmena D, tzv. duanty poloměru R, mezi
nimiž je urychlovací mezera. Duanty jsou
zhotoveny z vodivého neferomagnetického materiálu, jako je
měď nebo mosaz. Duanty D1 a D2 jsou připojeny ke zdroji střídavého napětí
U = Uo.cos(2pf.t) o frekvenci f
(závisí na síle magnetického pole a
hmotnosti urychlovaných částic - protony, deuterony či
těžší jádra; bývá kolem 20MHz),
takže v mezeře mezi duanty je střídavé elektrické pole.
Nabité částice vstupují do středu urychlovací mezery z
iontového zdroje ].
Následkem síly, kterou elektrické pole v mezeře působí na
částici s nábojem q a hmotností m, je částice
vtažena do jednoho z duantů (který má právě opačnou
polaritu) s určitou rychlostí v1. Uvnitř duantu, kde je elektrické pole odstíněno,
působením silného magnetického pole B opíše
částice půlkružnici o poloměru r1 = m.v1/(q.B) (tento poloměr je dán
rovnováhou mezi odstředivou silou a Lorentzovou magnetickou
silou: m.v12/r1 = q.B.v1). Doba, za kterou projde
částice tuto půlkružnici, je T = pr1/v1 = pm/(q.B) - vidíme, že tato doba (půl-perioda) oběhu
částice nezávisí na její rychlosti v1 ani na jejím poloměru dráhy r1; frekvence kruhového oběhu částice tedy je f =
q.B/(2pm)
a je konstantní *), protože m, q a B
jsou v daném uspořádání konstanty. Jestliže jsou duanty
napájeny střídavým napětím právě o této frekvenci f
(je splněna podmínka rezonance či synchronizace),
pak v okamžiku kdy částice opíše půlkružnici v prvním
duantu a ocitne se opět v urychlovací mezeře, je polarita
duantů již opačná a částice bude opět urychlena
elektrickým polem, takže do druhého duantu vletí s větší
rychlostí v2>v1. V druhém duantu se
bude pohybovat opět po kružnici, nyní však o poloměru r2 = m.v2/(q.B), který je
větší než byl r1, ale se stejnou periodou a frekvencí kruhového
pohybu. Stejným způsobem je pak částice při každém svém průchodu
mezerou mezi duanty znovu a znovu urychlována,
přičemž se pohybuje po kružnicích s rostoucím poloměrem r,
tedy po spirále (obr.1.5.6). Z poslední své
dráhy o maximálním poloměru (blízkém
poloměru duantů R) je urychlená
částice elektrostaticky nebo magneticky vychýlena a vyvedena
do prostoru terčíku, na nějž narazí a
vyvolá tam patřičné jaderné procesy.
*) Jedná se o tzv. isochronní
cyklotron (řec. isos=stejný, chronos=čas) -
rovnoměrný v čase, pravidelný, s konstantní
frekvencí. Technické řešení pro zachování
isochronní funkce cyklotronu i pro vysoké - relativistické
- energie urychlovaných částic bude nastíněno níže v
pasáži "Izochronní cyklotron".
Pohyb a urychlování
částic v cyklotronu
Pro objasnění
zákonitostí cyklotronového urychlování budeme analyzovat
pohyb částice s nábojem q a hmotností m v magnetickém
poli intenzity (indukce) B v cyklotronu o poloměru R,
na jehož duanty je přivedeno střídavé napětí amplitudy Uo a frekvence f.
Při pohybu částice rychlostí v ve směru kolmém na
magnetické pole na ni bude působit Lorentzova síla
F = q.B.v ve směru kolmém k vektoru magnetické indukce B
a k rychlosti pohybu v. Její dráha se tím
zakřiví do kružnice, přičemž vznikne odstředivá
síla. Pohyb částice bude pak dán rovnováhou mezi
magnetickou a odstředivou silou: q.B.v = m.v2/r . Poloměr
r kružnice, po níž se částice pohybuje, tedy bude r =
m.v/q.B. Perioda T oběhu částice po
kružnici je rovna obvodu kružnice 2pr dělenému rychlostí
částice: T = 2pr/v = 2pm/q.B. Perioda oběhu T částice tedy nezávisí
na její rychlosti (ani energii). Doba mezi jednotlivými
průlety částice urychlovací mezerou mezi duanty je tedy v
průběhu urychlování pořád stejná. Aby cyklotron urychloval
částici při každém jejím průletu urychlovací mezerou mezi
duanty, musí být frekvence 1/T, se kterou částice obíká v
magnetickém poli, rovna frekvenci f zdroje napětí: f =
q.B/2pm.
Částice vstupuje z iontového zdroje do středu
r=0 cyklotronu s téměř nulovou kinetickou energií. Při
každém průchodu mezerou mezi duanty získá při urychlení
napětím Uo kinetickou energii DEk
= q.Uo.
Když proletí mezi duanty n-krát, získá kinetickou energii Ek a rychlost v:
Ek = n.q.Uo = 1/2 m.v2, => v = Ö(2 Ek/m). Bude se pohybovat po kružnici poloměru r =
m.v/q.B = [Ö(2m Ek)]/q.B. Máme-li tedy cyklotron poloměru R s
magnetickým polem B, bude maximální energie
urychlených částic Emax = R2.q.B/2m, přičemž počet oběhů mezi duanty bude n =
Emax/Uo.q.
Praktický příklad: Cyklotron
poloměru 38cm s magnetickým polem 1,5T bude urychlovat protony
při frekvenci 22MHz na maximální energii 15MeV. Při
napájecím napětí (amplitudě) mezi duanty 50kV oběhnou
protony cca 300-krát než dosáhnou maximální energii.
Poznámka :
Maximální energie urychlených částic (daného
druhu s nábojem q a hmotností m) v
cyklotronu závisí pouze na poloměru R a velikosti
magnetického pole B, nikoli na napájecím napětí
duantů. Mohl by tím vzniknout dojem, že k urychlování i na
vysoké energie by mohlo stačit napájet duanty nízkým
napětím cca 10V a částice by po několika milionech oběhů
získaly požadovanou energii např. desítek MeV. Toto by snad v
principu bylo možné pro jednotlivé částice. Při
urychlování svazku mnoha částic se však
projevují vzájemné odpudivé síly rozptylující svazek,
fluktuace a turbulence - při příliš dlouhé dráze by
většina částic vůbec nedospěla do maximálního poloměru,
skončila by na stěnách duantů. Pro účinné urychlování je
proto žádoucí použít k napájení duantů cyklotronu pokud
možno vysoké napětí (amplitudu) desítek kV,
aby počet oběhů byl max. několik stovek.
Synchrocyklotron
- relativistický
Shora nastíněný princip činnosti cyklotronu bude při
konstantní frekvenci fungovat jen do té doby, kdy hmotnost
urychlované částice můžeme považovat za konstantní, tj.
pouze v nerelativistické oblasti. Chceme-li
použít cyklotron k urychlování částic na vyšší energie,
kdy rychlost částic je již srovnatelná s rychlostí světla,
přestává být setrvačná hmotnost částice m
konstantní, ale zvyšuje se s rostoucí rychlostí: m = mo/Ö(1-v2/c2). Ve stejném tempu se zvyšuje poloměr R = mo.v/[q.B.Ö(1-v2/c2)] a snižuje
frekvence oběhu částic v konstantním magnetickém
poli: f = [q.B/(pmo)].Ö(1-v2/c2). Aby mohla být
částice nadále urychlována i v této relativistické
oblasti, je potřeba modulovat frekvenci
urychlovacího napětí tak, aby byla stále v rezonanci s
frekvencí oběhu částice; nebo zesilovat magnetické
pole. Takto upravený cyklotron se "synchronizací" se
nazývá synchrocyklotron nebo relativistický
cyklotron (ve starší literatuře se
vyskytuje i název "fázotron"). Tyto přístroje pracují v pulsním režimu,
přičemž kmitočet urychlovacího napětí na duantech je
modulován a mění se cca 50-krát za vteřinu z hodnot cca
25MHz na začátku cyklu na cca 12MHz na konci cyklu (závisí na síle magnetického pole a hmotnosti
urychlovaných částic). Synchrocyklotrony se používají
pro urychlování protonů na energie do asi 1GeV.
Izochronní
cyklotron -
relativistický
Alternativní možností k synchrocyklotronu je tzv. izochronní
cyklotron, který pracuje při konstantní
frekvenci a časově konstantním magnetickém poli,
avšak intenzita magnetického pole se zvyšuje s
poloměrem; dosahuje se toho speciálním tvarováním
pólových nástavců elektromagnetu *). To vede k většímu
zakřivení vzdálenější dráhy urychlované částice, kompenzaci
vyšší setrvačné hmotnosti částice a zachování
cyklotronové rezonance při konstantní frekvenci (a bez nutnosti časové modulace intenzity
magnetického pole). Izochronní cyklotrony
se používají pro energie protonů do cca 500MeV, přičemž
jsou v kontinuálním režimu schopny produkovat
podstatně vyšší tok urychlených částic
než synchrocyklotrony v pulsním režimu.
*) Tento radiální gradient magnetického
pole však má rozbíhavý účinek na obíhající svazek
částic v příčném směru. To je třeba kompenzovat tzv. magnetickou
fokusací: pólové nástavce elektromagnetu jsou
rozděleny na několik segmentů (většinou 8, je schématicky znázorněno na obr.1.5.6
nahoře) v nichž se v azimutálním směru
střídají magnetické gradienty silnějšího
a slabšího pole (modelované výstupky -
segmenty - na povrchu nástavců), které
mají na svazek pohybujících se částic fokusační účinek.
Pro dokonalejší fokusaci se segmenty pólových nástavců
často tvarují do spirály (obr.1.5.6
nahoře). Izochronní cyklotron se proto
též někdy nazývá AVF (Azimutal Varying
Field) cyklotron.
Urychlování
záporných iontů
V cyklotronu se standardně urychlují těžké kladně
nabité částice - protony, deuterony, alfa částice,
příp. těžší jádra jako je uhlík 12C. Ve speciálních aplikacích se však pro zvýšení
"efektivního výkonu" cyklotronu používá
zajímavá modifikace: urychování záporných iontů.
Atomům vodíku nebo deuteria se v iontovém zdroji v
elektrickém výboji dodají dva elektrony, čímž vzniknou
záporné ionty H-
či D- vodíku se dvěma elektrony. Ty se potom urychlují v
cyklotronu. Technologie urychlování záporných iontů v
cyklotronu přináší dvě výhody :
--> Možnost produkce více externích radiačních
svazků s různými energiemi
Do cesty urychlovaných záporných iontů se v příslušné
dráze vloží tenká fólie, která "strippováním"
odstraní jejich dva elektrony - vzniknou požadované p+ či d+. Tím se obrátí
směr jejich zakřivení v magnetickém poli, což způsobí
jejich rychlé vyvedení z pole cyklotronu do
externího svazku příslušné energie. Tato technika tak
umožňuje současnou produkci několika externích svazků o
různých energiích, které se dají nezávisle využívat.
--> Možnost zvýšení fluenčního výkonu
vnějšího svazku z cyklotronu
U malých cyklotronů používaných pro výrobu
radioisotopů (§1.4, pasáž
"Výroba umělých radioisotopů") je důležitým
požadavkem vysoká intenzita - fluenční
výkon - protonových či deuteronových svazků. Při energiích
kolem 40MeV se daří dosahovat poměrně značného proudu ve
vnitřním paprsku cca 2-5 mA. Tento maximální výkon lze však
plně využít jen při ozařování interního terčíku,
instalovaného uvnitř vakuové urychlovací trubice. Pro
rutinní výrobu radionuklidů je ale výhodnější vyvedení
částicového svazku k ozařování vnějších
terčíků. V klasických cyklotronech urychlujících
kladné částice se výsledný paprsek extrahuje elektrostatickým
deflektorem. Na přepážce tohoto deflektoru vzniká
značné disipativní teplo, které je omezujícím
faktorem pro dosažení vysokého fluenčního výkonu
extrahovaného svazku.
Tyto
nevýhody do značné míry odstraňuje technologie urychlování
záporných iontů. Po potřebném urychlení
záporných iontů probíhá účinná extrakce protonů
strippováním H- v tenké uhlíkové fólii, která zadrží oba
elektrony a propustí těžké kladné vodíkové jádro p+ či D+, s minimální
tepelnou disipací. Dosahuje se tím podstatně vyšších
výkonů produkce radionuklidů ve vnějším terčíku.
To je důležité především pro výrobu větších aktivit
krátkodobých radioisotopů pro scintigrafickou diagnostiku (§4.8 "Radionuklidy a radiofarmaka pro
scintigrafii") a biologicky cílenou radionuklidovou terapii (§3.6 "Radioisotopová terapie") v nukleární medicíně.
S y n ch r o t r o n
Pro urychlování částic na velmi
vysoké energie vychází v kruhovém urychlovači
příliš velký poloměr jejich orbit, takže
cyklotronový způsob se spirálovým pohybem částic v ploché
vakuové komoře již není prakticky použitelný. Aby dokonale
vakuový prostor nebyl enormně velký, stejně jako
elektromagnety, je nutno použít kruhové urychlovače s pevnou
kruhovou dráhou. Aby se nabitá částice urychlovala a
udržela se na pevné kruhové dráze o poloměru R, je potřeba
aby s rostoucí rychlostí v(t) urychlovaných částic se s
časem synchronně zvyšovala jak frekvence
f(t) urychlovacího napětí, tak intenzita magnetického
pole B(t), která již nemůže být konstantní, ale je
rovněž funkcí času. Takto synchronně pracující urychlovač
s pevnou kruhovou dráhou se nazývá synchrotron
(ve starší literatuře se vyskytoval i
název "synchrofázotron", "bevatron",
"kosmotron").
Schématické znázornění jeho principu je v pravé
části obr.1.5.6. Částice jsou urychlovány ve vakuové
trubici o průměru cca 3-8cm (většinou eliptického
průřezu), stočené do kruhu o průměru stovek metrů až
několika kilometrů(!). Trubice je obklopená velkým
množstvím segmentů dipólových elektromagnetů
(u velkých přístrojů i více než 1000 segmentů), který
budí magnetické pole udržující částice na kruhové
orbitě. Synchrotron urychluje již předběžně
urychlené částice, které se do urychlovací komory
vstřikují z vhodného injektoru, kterým
bývá lineární nebo kruhový urychlovač s energií cca
20-100MeV *). Spolu s magnety jsou ve vhodných místech kruhové
dráhy umístěny urychlovací elektrody
napájené střídavým vysokým napětím, jehož frekvence f
je synchronně modulována tak, aby částice mezi elektrody
přišla v době, kdy polarita zajistí vždy další a další
urychlení částice. Současně s frekencí je zvyšována i
intenzita B (z historických
důvodů nazývaná magnetickou indukcí) magnetického pole.
*) U velkých přístrojů je potřeba i vícestupňové
předurychlení - nejdříve lineární urychlovač, pak
menší synchrotron, který injektuje částice do hlavního
urychlovače (synchrotronu); pro nejvyšší energie i kaskáda
několika synchrotronů za sebou - viz níže "Velké
urychlovače", LHC.
Synchrotron pracuje v pulsním režimu,
kdy protony vstupující v pravidelných dávkách z injektoru do
urychlovací trubice při energiích řádově 100MeV, vykonají
během urychlovacího cyklu, trvajícího cca
3-5 sekund, několik milionů oběhů, přičemž se urychlí na
řádově 100GeV až několik TeV; magnetické pole v průběhu
urychlovacího cyklu vzroste z hodnoty desetin Tesla na několik
T. Urychlovací cyklus se periodicky opakuje cca 5-10-krát za
minutu.
Po skončení urychlovacího cyklu dopadají částice buď
na vnitřní terčík, nebo jsou vyvedeny
elektromagnetickým polem na vnější terčík,
popř. jsou vedeny do akumulačního prstence pro realizaci
interakcí částic ve vstřícných svazcích.
Při nárazu svazku např. protonů na terčík vzniká
množství částic nejrůznějších druhů, z nichž můžeme
soustavou elektrických a magnetických polí
"odseparovat" částice požadovaného druhu, fokusací
je zformovat ve svazek a zamířit je na další terčík.
Získáváme tak sekundární svazky např.
antiprotonů, pionů, mionů, kaonů, hyperonů. K separaci
částic se používá proměnných elektrických a magnetických
polí, k fokusaci svazků se používá magnetických
čoček, většinou v kvadrupólovém uspořádání,
kde se kříží dvě magnetická pole, jejichž gradienty
postupně fokusují svazek ve vertikálním i horizontálním
směru.
Při velkých hodnotách poloměru R,
který pro dosažení vysokých energií řádově stovky GeV
musí dosahovat několika kilometrů, je potřeba, aby průřez
urychlovací trubice byl co nejmenší - aby bylo možno
dosáhnout potřebného vysokého vakua (<10-6mm Hg) a aby náklady na výrobu elektromagnetů, jakož
i nároky na jejich elektrický příkon, nebyly enormně
vysoké. Částice po vstřiku do urychlovací trubice konají
radiální a vertikální kmity kolem své základní kruhové
dráhy. Kromě toho mají částice ve svazku tendenci rozbíhat
se do všech stran, neboť jsou souhlasně nabité a proto se
odpuzují. Nemá-li dojít k dopadu částic na stěny trubice,
je třeba udržet urychlované částice na jejich orbitě s
vysokou přesností, takže je třeba udržet amplitudu
radiálních a vertikálních kmitů co nejnižší, stejně jako
rozptyl částic. Jinými slovy, je potřeba provádět silnou
fokusaci, při níž se shluk vstřiknutých částic
během urychlování koncentruje a formuje do intenzívního úzkého
svazku prudce letících částic. Tato silná
magnetická fokusace je realizována tak, že elektromagnet
synchrotronu je sestaven z velkého počtu vhodně tvarovaných segmentů,
které mají střídavě kladný a záporný gradient intenzity
magnetického pole. Tyto gradienty magnetického pole působí v
radiálním a vertikálním směru střídavě jako spojné a
rozptylné magnetické čočky, které v
konečném důsledku vedou k dvojité fokusaci
svazku v obou směrech. U novějších velkých urychlovačů
bývají cívky elektromagnetů často supravodivé.
Velké
synchrotrony jsou velmi nákladná unikátní zařízení,
budovaná ve velkých světových centrech výzkumu v oblasti
jaderné fyziky a elementárních částic, většinou v široké
mezinárodní spolupráci (náklady na
vybudování dosahují několika miliard dolarů). Na vlastní urychlovač navazují velmi komplikované
a precizní detekční aparatury a systémy *),
které analyzují sekundární částice a záření, vzniklé
při ultrarelativistických interakcích vysokoenergetických
primárních částic s materiálem terčíku či vzájemně ve
vstřícných svazcích. Analýzou druhu, náboje a hmotnosti
těchto částic, jejich energií, hybností a úhlů emise z
místa interakce, lze rekonstruovat řadu parametrů interakcí,
k nimž dochází. Z toho lze usuzovat na strukturu
elementárních částic, vlastnosti působících polí a
interakcí, na existenci nových dosud neznámých kvant a
částic - viz výše "Analýza dynamiky
interakcí částic". Problematika velkých urychlovačů bude stručně
diskutována níže - pasáž "Velké urychlovače".
*) O metodice detekce záření viz kap.2
"Detekce
a spektrometrie záření",
detekční systémy vysokoenergetických interakcí částic jsou
obecně nastíněny v §2.1, pasáž "Uspořádání a konfigurace detektorů
záření".
B e t a t r o n
Kruhový indukční urychlovač elektronů se nazývá betatron
(vyrábí totiž "umělé záření b-", což jsou rychlé elektrony, známé jinak z
radioaktivity beta). Princip betatronu je schématicky
znázorněn na obr.1.5.7 vlevo.
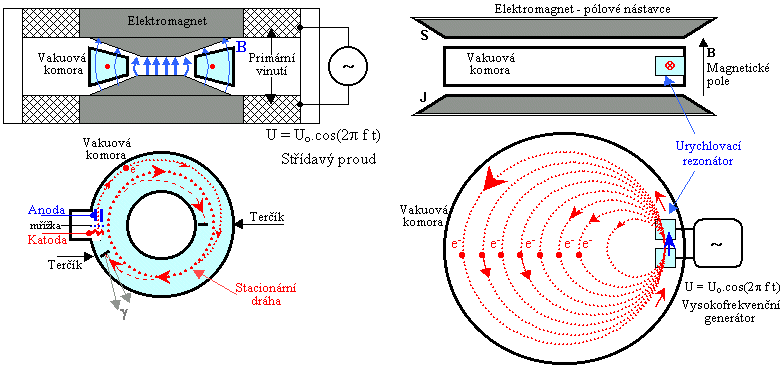
Obr.1.5.7. Vlevo:
Schématické znázornění betatronu. Vpravo: Schématické
znázornění mikrotronu.
Urychlovací trubice betatronu má tvar
prstence (toroidu) zhotoveného z elektricky nevodivého
materiálu (sklo, porcelán) s vysokým vakuem uvnitř. Trubice
je umístěna ("navléknuta") mezi pólovými nástavci
elektromagnetu, napájeného střídavým proudem.
Elektrony jsou ve vhodném okamžiku (vhodné fázi periody
střídavého proudu) vstřikovány do urychlovací trubice elektronovou
tryskou, tvořenou žhavenou katodou,
mřížkou a urychlující a fokusující anodou - je to pobobné
"elektronové dělo" jako je u obrazovky. Časově
proměnné magnetické pole indukuje v trubici vířivé
elektrické pole, jehož elektromotorická síla,
směřující podél kruhové dráhy, tyto elektrony urychluje.
Z elektronického hlediska je betatron vlastně
"transformátorem", jehož primární vinutí je
napájeno střídavým proudem a jehož "sekundárním
vinutím" (o jednom "závitu") je urychlovací
trubice, v níž se ve vakuu (místo v drátech vinutí)
pohybují elektrony urychlované indukovanou elektromotorickou
silou. Na kruhové dráze jsou elektrony udržovány magnetickým
polem. K urychlování elektronů dochází jen v první
čtvrtině sinusového průběhu střídavého napětí
v elektromagnetu. Ve vhodném okamžiku vzestupné části
sinusovky jsou injektovány elektrony, které jsou urychlovány,
magnetické pole narůstá, elektrony se po spirále stáčejí
dovnitř a po určitou dobu obíhají po stacionární dráze, na
níž jsou neustále urychlovány. Po dosažení vrcholu
čtvrtperiody slábne vířivé elektrické pole, obrací svůj
směr a elektrony by posléze byly naopak brzděny. Zároveň
však dochází k zeslabení magnetického pole a elektrony se
začnou pohybovat po spirále k zevnímu okraji trubice, kde
narazí na terčík nebo jsou vyvedeny k zevnímu použití.
Některé typy betatronů mají radiální gradient magnetického
pole a urychlovací fázi nastaveny tak, že pohyb elektronů na
konci urychlovacího cyklu probíhá po spirále směrem dovnitř
a trerčík je umístěn při vnitřním okraji urychlovací
trubice.
Elektro-mechanický rozbor trajektorie elektronu při
urychlování indukovaným elektrickým polem E po
kruhové dráze poloměru R (při němž se kombinuje
Faradayův zákon elektromagnetické indukce u = -dF/dt = 2p.R.c.E s
urychlující elektrickou silou podél kruhové dráhy q.E,
kolmou Lorentzovou magnetickou silou q.[v ´ B] = q.v.B a
odstředivou silou m.v2/R) vede k podmínce rovnovážného urychlování
elektronu na dráze poloměru R: 2pR2.B = F, neboli magnetický tok F plochou pR2 dráhy elektronu se
musí rovnat dvojnásobku toku, který by dráhou protékal,
kdyby na celé ploše bylo homogenní magnetické pole s
intenzitou B. Tato "betatronová podmínka" je
zajištěna vhodným tvarováním pólových nástavců
elektromagnetu.
Elektromagnet menších betatronů
bývá často napájen střídavým proudem z normální
elektrické sítě 220V s frekvencí 50Hz, příkon činí
jednotky až desítky kW. Poloměr kruhové dráhy bývá
desítky centimetrů. Během urychlovacího cyklu, který trvá
cca 5milisekund, vykonají elektrony cca 2miliony oběhů,
přičemž se indukovanou elektromotorickou silou urychlí na cca
desítky MeV. Pak dopadají buď na vnitřní terčík
(přičemž budí brzdné záření gama), nebo jsou ve svazku
vyvedeny ven - slouží pak k elektronovému ozařovaní, např.
pro technické či lékařské účely. Stejné využití má i
tvrdé brzdné záření gama.
Betatrony se používají pro energie elektronů do cca
300MeV. Při velkých energiích je však potřeba (podobně jako
u cyklotronu) provádět synchronizaci vzhledem
k růstu hmotnosti elektronů s jejich energií. Spojením
principu betatronu a synchrotronu vzniká betasynchrotron,
který urychluje elektrony na kruhové orbitě uvnitř
vakuovaného prstence nejprve na betatronovém principu pomocí
elektromagnetů napájených střídavým proudem, načež takto
předurychlené elektrony jsou dále urychlovány mezi
elektrodami, na něž se zapojí vysokofrekvenční urychlovací
napětí se synchronizovanou frekvencí, přičemž
odpovídajícím způsobem vzrůstá magnetické pole.
Menší betatrony se v 60.-80.letech hojně používaly v radioterapii
(viz §3.6 "Radioterapie"), hlavně jako zdroj tvrdého brzdného záření
gama o energiích do cca 40MeV. V posledních letech byly však
betatrony prakticky vytlačeny lineárními urychlovači
elektronů, které mají výhodu menších rozměrů, vyšší
intenzity toku elektronů a snadnější možnosti modulace
svazku.
Mikrotron
Speciálním, zřídka užívaným, typem kruhového urychlovače
elektronů je mikrotron, označovaný též
někdy jako "elektronový cyklotron".
Jeho činnost je schématicky znázorněna v pravé části
obr.1.5.7. V magnetickém poli mezi pólovými nástavci silného
elektromagnetu je umístěna plochá válcová komora
s vysokým vakuem, podobně jako u cyklotronu, avšak místo
duantů je u okraje komory namontován elektrický urychlovací
systém - dutinový rezonátor, napájený
vysokofrekvenčním napětím z magnetronového či
klystronového generátoru (frekvence f činí několik
GHz). Elektrony prolétají mnohokrát tímto rezonátorem, kam
jsou po kruhové dráze vraceny magnetickým polem, přičemž
při každém průletu jsou urychlovány na vyšší a vyšší
energii. Vzhledem ke zvýšené kinetické energii je poloměr
dráhy elektronu po každém průletu rezonátorem vždy větší
a větší. Aby elektron přišel mezi elektrody rezonátoru ve
správné fázi periody vysokofrekvenčního napětí a mohl být
znovu urychlen, je třeba splnit frekvenční podmínku rezonance
2p.f =
k. e.B/(mo.c), podle
níž kruhová frekvence urychlovacího napětí musí být
celočíselným k-násobkem uvedeného podílu, kde e je
náboj elektronu, B magnetická indukce, mo klidová hmotnost elektronu.
Elektrony pro urychlování se vstřikují elektronovým
dělem, popř. se získávají emisí ze stěn rezonátoru.
Mikrotrony se občas používají pro urychlování elektronů na
energie několika MeV, jejich předností je dosažení vysokých
intenzit toku urychlených elektronů ve svazku. Z
jednotlivých drah lze vyextrahovat monoenergetické svazky
elektronů, z menších drah nižší energie, z největší
dráhy při okraji urychlovací komory pak elektrony o
maximální energii.
Elektrické napájení urychlovačů
Svou vysokou kinetickou energii
získávají částice v urychlovačích působením
elektromagnetických polí, t.j. přeměnou části elektrické
energie, kterou musí být urychlovače napájeny. Tak složité
přístroje, jakými obecně urychlovače jsou, musejí být
opatřeny složitou elektronickou aparaturou, obsahující
několik typů a zdrojů elektrického napájení :
n Napájení
urychlovacích elektrod
je tím základním elektrickým napájením, dodávajícím
vlastní elektrickou energii pro urychlování nabitých
částic. U rentgenek a elektrostatických lineárních
urychlovačů se jedná o vysoké stejnosměrné napětí
- desítky kilovoltů, až několik megavoltů. U
vysokofrekvenčních lineárních urychlovačů a kruhových
urychlovačů jsou urychlovací elektrody napájeny vysokofrekvenčním
střídavým napětím o frekvenci řádově MHz až
několika GHz (elektronické obvody
produkující toto vf napětí jsou stručně popsány níže v
pasáži "Vysokofrekvenční generátory
elektrického napětí").
n Napájení
iontového zdroje
Vlastní částice k urychlení jsou v iontovém zdroji
získávány rovněž elektricky. Nejjednodušší je to u
elektronů, získávaných termoemisí ze žhavené katody,
která je napájena žhavicím proudem ze
žhavicího transformátoru (220V se
transformuje na 6-24V, žhavicí proud cca 2A-20A). Protony a těžší ionty se získávají v elektrickém
výboji, napájeném stejnosměrným napětím řádově
stovky až několik tisíc voltů.
n Napájení
cívek elektromagnetů
Pro tvarování dráhy urychlených nabitých částic se
používají silné elektromagnety, tvořené cívkami
napájenými elektrickým proudem mnoha desítek až několika
tisíc ampér. U klasických elektromagnetů je to energeticky
náročné, vzniká teplo, elektromagnety se musejí chladit.
Největší část elektrické energie pro napájení
urychlovačů většinou spotřebovávají právě
elektromagnety. U novějších velkých urychlovačů se v
elektromagnetech používají často supravodivé
cívky.
Problematika elektromagnetů v
urychlovačích je podrobněji rozebírána níže v pasáži
"Elektromagnety v urychlovačích".
n Napájení
vakuového a chladicího systému
Pro zajištění vysokého vakua v
urychlovacích trubicích se používá výkonných vývěv.
K udržení vysokého vakua může přispět i chlazení trubice
(spolu se supravodivými elektromagnety) na nízké teploty, při
nichž případné zbytky vzduchu vymrzají na stěnách trubice.
V řadě elektricky napájených součástí se značná část
elektrické energie mění v teplo, které je
potřeba odvádět pomocí vzduchotechniky či jiných chladicích
systémů. U supravodivých elektromagnetů se sice
teplo přímo nevyvíjí, avšak chladicí hélium je třeba
recyklovat ve zkapalňovacích přístrojích. Všechno toto
technické "zázemí" urychlovače obsahuje řadu
elektromotorů, které jsou napájeny buď přímo ze střídavé
sítě (220V), nebo jsou řízeny elektronicky.
n Napájení
řídící a regulační elektroniky
Činnost urychlovačů je zcela podmíněna přesnou
časovou a intenzitní souhrou mezi elektrickými a
magnetickými poli v různých částech urychlovacího systému.
Toto musejí zajišťovat složité elektronické obvody,
řízené v současné době digitální počítačovou
technikou.
Pozn.: Pro
nejjednodušší "urychlovač", kterým je rentgenka,
je schéma elektrického napájení nakresleno na obr.3.2.2B v
§3.2.2 "X-záření - rentgenová diagnostika", část
"Zdroje X-záření - rentgenky".
Vysokofrekvenční
generátory elektrického napětí
Urychlovací elektrody většiny typů urychlovačů jsou
napájeny střídavým vysokofrekvenčním napětím
či vf elektromagnetickým vlněním. Frekvence jednotky až
stovky MHz lze připravit v klasických oscilátorech s
indukčně-kapacitními LC obvody, osazených elektronkami či
nověji polovodičovými tranzistory. Velmi vysoké frekvence
(potřebné např. pro lineární vysokofrekvenční
urychlovače, mikrotron a pod.) vznikají ve vysofrekvenčních
generátorech, které jsou osazeny speciálními elektronkami - magnetrony
a klystrony, které mohou pracovat jako vysokofrekvenční
oscilátory o velmi vysokých frekvencích (vf)
řádově GHz. Pro nejvyšší frekvence slouží gyrotrony.
Magnetron
je válcová dioda, jejímž středem vede
žhavená katoda, kolem níž je koaxiální anoda. Mezi katodu a
anodu je přivedeno elektrické napětí. Dioda je kromě toho
vložena do longitudinálního magnetického pole
(mezi pólové nástavce elektromagnetu, pro jednodušší
aplikace stačí i permanentní magnet), jehož směr je
rovnoběžný s katodou - obr.1.5.8 vlevo dole. Na elektrony
emitované z katody tak působí kombinované zkřížené
pole - radiální elektrické pole mezi katodou a anodou
a podélné magnetické pole vnějšího magnetu. Elektrony
emitované katodou jsou přitahovány k válcové anodě, avšak
Lorentzovou magnetickou silou se dráhy elektronů zakřivují
tak, že při určité hodnotě anodového napětí a intenzitě
magnetického pole již elektrony nedopadají přímo na anodu,
ale vytvoří oblak kroužící v prostoru mezi
katodou a anodou. Anoda magnetronu není jednoduchý válec, ale
je tvořena kovovým blokem obsahujícím několik (většinou 8)
obvodových dutinových rezonátorů - obr.1.5.8
vlevo nahoře. Elektrony během svého kruhového pohybu při
průletu kolem rezonančních dutin odevzdávají část své
energie a vzbuzují elektromagnetické oscilace
v dutinách. Nejúčinnější předávání energie
elektromagnetickému poli v rezonátorech nastává při takové
rychlosti pohybu elektronu, kdy se během jeho přechodu od
jedné obvodové štěrbiny k druhé změní polarita pole ve
štěrbině na opačnou; pak je elektron u každé štěrbiny
brzděn a odevzdává energii poli v rezonátoru. Tato synchronizace
(nazývaná p-mód) se dosahuje vhodnou volbou anodového napětí.
Celkově je pohyb elektronů značně složitý. Kmitající
elektromagnetické pole hustotně moduluje rotující
elektronový oblak - dochází ke shlukování elektronů
do ohnutých paprsků tvaru "kola s loukotěmi" (počet
loukotí je poloviční než počet obvodových rezonátorů
anody), které se otáčejí kolem osy; je to jen symbolicky
nakresleno na obr.1.5.8 vlevo nahoře. Lze říci, že celý
systém magnetronu je uveden do stavu intenzívních
vysokofrekvenčních oscilací (jejichž frekvence je
dána mechanickými rozměry rezonátorů), při nichž je
elektrická energie protékajícího anodového proudu s vysokou
účinností přeměňována na energii kmitajícího
pole. Vzniklý vysokofrekvenční signál pak anténami či
vlnovody vychází k vnějšímu použití.
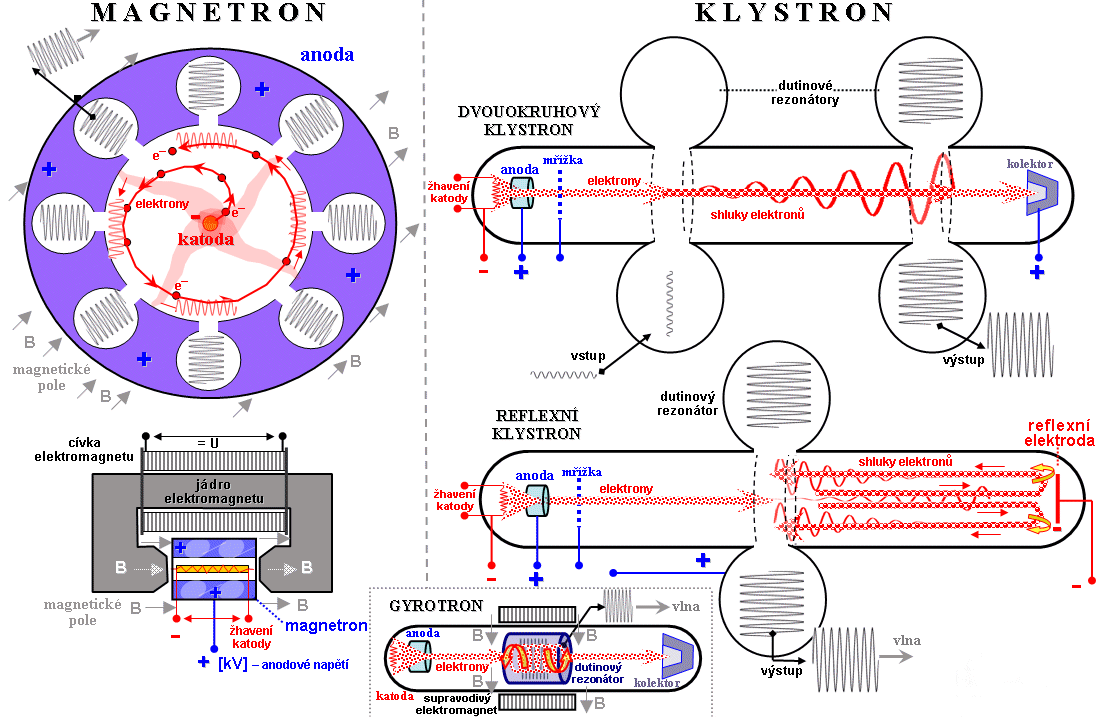
Obr.1.5.8. Fyzikálně-elektronický princip činnosti
magnetronu, klystronu a gyrotronu.
Vlevo nahoře: Příčný řez magnetronem s
naznačeným pohybem elektronů mezi katodou a anodou ve
zkříženém elektrickém a magnetickém poli. Vlevo
dole: Zapojení a umístění magnetronu do
magnetického pole - podélný řez. Vpravo nahoře:
Dvouokruhový klystron jako zesilovač vf signálu. Vpravo
dole: Reflexní jednookruhový klystron jako oscilátor
a generátor vf signálu. Dole uprostřed:
Gyrotron s naznačenýnm spirálním pohybem elektronů v silném
magnetickém poli a vznikem elektromag. oscilací v dutinovém
rezonátoru.
Klystron (řec. klys=příboj, vlny
narážející do pobřeží)
je rovněž vakuová trubice, v níž elektrony emitované
žhavenou katodou jsou urychlovány a fokusovány do úzkého
lineárního svazku dutou anodou připojenou na
kladné napětí. Kinetická energie elektronového svazku
(shluků elektronů) se převádí na elektromagnetické kmity v
rezonančních dutinách. Klystrony se rozdělují na dva
základní typy:
¨ Dvouokruhový klystron,
kde elektrony z katody na své cestě k anodě procházejí
nejprve jedním rezonátorem, který je rychlostně
moduluje, načež vzniklé shluky elektronů
procházejí druhým dutinovým rezonátorem, v němž v
případě dosažení rezonance vzbuzují oscilace
- obr.1.5.8 vpravo nahoře. V oblasti mezi oběma rezonátory je
někdy kolem trubice umístěn magnet pro udržení a fokusaci
elektronového paprsku ve středu trubice. Elektrony, které již
předaly svou kinetickou energii, jsou zachycovány v kolektoru
(zbytek jejich energie se tam přemění v
teplo; u velkých přístrojů jsou příp. tyto elektrony pro
zvýšení účinnosti navraceny zpět do prostoru před
rezonátory). Napájíme-li první
(vstupní) rezonátor vnějším vf signálem, pak oscilace
vzbuzené v druhém (výstupním) rezonátoru mají větší
amplitudu než kmity přiváděné do vstupního
rezonátoru - na obr.1.5.8 vpravo je to
sybmolicky naznačeno zesilující se vlnovkou. Tento druh klystronu slouží jako zesilovač
vf signálu. Zavedením zpětné vazby
(elektrickým propojením dutin obou rezonátorů dvouokruhového
klystronu) je možno sestrojit generátor
samobuzených kmitů o vysokém výkonu, podobně jako u níže
uvedeného klystronu reflexního. Pro speciální účely vf
techniky se konstruují i klystrony s větším počtem
rezonančních dutin - dosahuje se tím většího zesílení a
možnosti ladění v širším frekvenčním rozsahu.
¨ Reflexní klystron,
v němž po urychlení a fokusaci elektronů anodou do
lineárního paprsku jsou tyto elektrony na opačném konci
trubice odráženy zápornou reflexní elektrodou
(repeller - odpuzovač) a navraceny zpět do pracovního
prostoru elektronky. Rychlost elektronů uvnitř klystronu je modulována
jejich interakcí s dutinovým rezonátorem, v
němž prolétající elektrony vzbuzují elektromagnetické
oscilace. Každý elektron projde rezonátorem dvakrát. V
přímém směru je tok elektronů rychlostně modulován, shluky
elektronů pokračují směrem k reflexní elektrodě,
kde se zastaví, obrátí se a v opačně orientovaném poli se
urychleně pohybují zpět k rezonátoru, do něhož tyto shluky
elektronů vstupují a rezonátor budí. Při správném
nastavení napětí na reflexní elektrodě vzhledem ke
geometrickým rozměrům vstupují shluky elektronů do
rezonátoru vždy v okamžiku, kdy vf pole má maximální
hodnotu opačné polarity a odevzdávají mu energii - je
dosaženo rezonance a oscilace se trvale
udržují (obr.1.5.8 vpravo dole). Z dutinového rezonátoru je
elektromagnetický vf signál odváděn anténou či vlnovodem.
Magnetron
dosahuje poměrně vysoké účinnosti cca 60-70% převodu
napájecí elektrické energie na vysokofrekvenční signál.
Klystron, jehož účinnost je poněkud nižší (cca 30-40%),
zato generuje vf kmity se stabilnější frekvencí, s možností
jejího přesného ladění a modulace. Magnetrony a klystrony
mají široké použití ve vysokofrekvenční technice
- v UHF televizním vysílání, satelitním spojení, radarové
technice, mikrovlnném ohřevu (např. v mikrovlnných troubách
jsou mikrovlny buzeny magnetrony); pro nás je důležité jejich
použití v urychlovačích částic. Pracují
často v pulzním režimu, přičemž dosahují
úctyhodných výkonů až stovky megawatů! V oblasti nižších
výkonů jsou magnetrony a klystrony v poslední době
nahrazovány polovodičovými součástkami.
Gyrotron
Pro oblasti nejvyšších frekvencí byly zkonstruovány tzv. gyrotrony
(řec. gyros = otáčení, kroužení,
soustružení; též otáčivý gril), obr.1.5.8 uprostřed dole. Jsou to vakuové
elektronky, v nichž elektrony emitované z katody jsou
urychlené v "elektronovém děle" napětím desítky
až stovky kV a soustředěny do lineárního paprsku. V
pracovním prostoru gyrotronu se nachází dutinový
rezonátor a je zde aplikováno velmi silné
magnetické pole (cca 3-8T), buzené většinou
supravodivým elektromagnetem. Při pohybu v tomto silném
magnetickém poli elektrony krouží po spirále
s Larmorovou frekvencí f = e.B/(2pme) závisející
na intenzitě B magnetického pole. Při průchodu této
elektronové spirály dutinovým rezonátorem - pokud dojde k cyklotronové
rezonanci - se v něm vzbuzují intenzívní
elektromagnetické kmity vysokých frekvencí »20-250GHz (k
rezonanci může docházet na základní frekvenci dané rozměry
rezonátoru, nebo na vyšších harmonických). Po průchodu
rezonátorem jsou elektrony, které již předaly většinu své
energie, absorbovány v kolektoru. Elektromagnetické
vlny jsou vlnovodem odváděny k vnějšímu použití. Kromě
mikrovlnné vf elektroniky se gyrotrony zatím ojediněle
používají pro vf ohřev plasmy v nejnáročnějších
aplikacích, např. v oblasti termonukleární fúze v
tokamacích (§1.3, část "Slučování
atomových jader"; v
budovaném tokamaku ITER je plánováno více jak 20 výkonných
gyrotronů pro ohřev deuterium-tritové plasmy v pracovní
toroidní trubici).
Pozn.:
Vznik elektromagnetických kmitů v dutinových rezonátorech
magnetronu a klystronu se z elektronického hlediska někdy
zjednodušeně vysvětluje takto: Jednotlivé komory či
dutinové rezonátory si můžeme představit jako malé oscilační
obvody - paralelně zapojené LC. Štěrbina mezi okraji
komůrek se chová jako malý "kondenzátor" C
(kapacity jednotek pF), vodivý vnitřní plášť rezonátoru
představuje "cívku" L. Elektrony při průchodu kolem
komory nabíjejí štěrbinu ("kondenzátor"), čímž
začne okamžitě procházet proud kolem komory
("cívkou"). Vzniklé magnetické pole indukuje
opačný proud, nabíjející "kondenzátor" na
opačnou polaritu ...atd... - v komoře vzniká střídavý proud
vysoké frekvence f=1/L.C podobně jako v oscilačním obvodu LC.
Toto přirovnání je sice názorné, avšak pro přesnou
analýzu se příliš nehodí, tam je nutno použít metody
vlnového chování elektromagnetického pole.
Elektromagnety v urychlovačích a dalších nukleárních přístrojích
Důležitou součástí většiny urychlovačů jsou elektromagnety,
které obecně slouží pro tvarování dráhy
urychlených nabitých částic působením Lorentzovy síly
kolmé k rychlosti pohybu. Pro základní zakřivování dráhy
jsou to dipólové elektromagnety, pro fokusaci
jednotlivých částic do vymezeného svazku kvadrupólové
elektromagnety, někdy se používají i složitější tvary
pólových nástavců. V klasickém provedení jsou
elektromagnety tvořeny cívkami, navinutými s
potřebným počtem závitů izolovaným drátem z dobrého
vodiče, většinou mědi, na vhodném feromagnetickém jádře
(tvořícím "pólové nástavce"). Síla
buzeného magnetického pole (magnetická indukce) je
úměrná elektrickému proudu přes cívku. Přivádí se buď
stejnosměrný proud - permanentní elektromagnet, nebo
proměnný či střídavý proud - budí se časově
proměnné či střídavé magnetické pole.
"Pomocné" cívky pro fokusaci svazku, jeho korekce,
vyvádění či separaci, mají u všech urychlovačů toto
klasické provedení. U menších a starších přístrojů se
klasické elektromagnety používají i pro základní
zakřivování svazku částic v kruhových
urychlovačích - cyklotronech a synchrotronech.
U velkých vysokoenergetických cyklotronů a
synchrotronů je pro udržování částic na kruhových drahách
potřeba značně silné magnetické pole, pro
jehož buzení musí cívkami protékat elektrický proud mnoha
desítek až několika tisíc ampér. Při použití klasických
elektromagnetů je to energeticky náročné, vzniká teplo,
elektromagnety se musejí chladit. U novějších velkých
urychlovačů se proto v silných elektromagnetech používají
často supravodivé cívky :
Supravodivé
elektromagnety
Fyzikální principy supravodivosti byly stručně rozebírány
výše v pasáži "Fermiony v úloze bosonů.
Supravodivost.".
Připomeňme si zde jen základní skutečnost, že při ochlazení
některých vodičů na dostatečně nízkou teplotu - nižší
než je tzv. kritická teplota Tc - jejich měrný elektrický odpor klesne na
nulu (prakticky na nulu klesne ohmický
odpor pro stejnosměrný proud; induktivní složka
odporu, impedance, pro střídavý proud zůstane nezměněna). Za této situace i silný elektrický proud protéká
supravodičem absolutně bez tepelných ztrát.
Nejpoužívaným supravodivým materiálem pro
elektromagnety je slitina niob(53%)-titan(47%) pracující do 9
Tesla, příp. Nb3Sn, použitelný i nad 9 T. Byly vyvinuty i tzv. vysokoteplotní
supravodiče, které mají kritickou teplotu vyšší než
-196°C a místo kapalného hélia mohou pracovat i při
použití kapalného dusíku. Pro silné elektromagnety se ale
zatím nehodí, nedaří se z nich vytvořit dlouhé tenké
dráty.
Materiálová poznámka :
Je zajímavé, že jako vhodný izolační materiál
pro supravodivé vinutí může sloužit měď,
která je za normální teploty jedním z nejlepších
elektrických vodičů! V oblastech jednotek stupňů Kelvina
však měď nepřechází do supravodivého stavu, má měrný
odpor mnoho-miliardkrát větší než supravodivý Nb-Ti, takže
se vzhledem k supravodiči chová jako izolant.
Supravodivé dráty bývají tvořeny větším počtem (min.
několik desítek, někdy ale i několik tisíc) tenkých vláken
NbTi uložených v měděné matrix (příp. vhodné slitiny
mědi, niklu).
Navineme-li tedy cívku ze supravodivého
materiálu, při průchodu elektrického proudu jejími závity
je buzeno magnetické pole bez tepelných ztrát ve vinutí -
vzniká supravodivý elektromagnet. Může
pracovat ve dvou režimech:
l Kontinuální
režim napájení z vnějšího
zdroje proudu - konstantního či časově proměnného,
analogicky jako u běžných cívek. Výhodou však je možnost
dosažení velmi silného magnetického pole při nízké
elektrické spotřebě. Silný proud vzniká i při velmi
nízkém napětí zdroje, bez tepelných ztrát. Kontinuální
režim se používá především tam, kde je potřeba
operativně měnit intenzitu magnetického pole
- např. v synchrotronu či tokamaku.
l Perzistentní
režim - v uzavřeném
supravodivém vinutí se elektrický proud jednou vybudí a pak
se samovolně trvale udržuje, vzhledem k
absenci ztrát ve vinutí v podobě produkce tepla. Bezstrátově
cirkulující proud ve vinutí se nemůže zmenšovat ani
narůstat, není-li z vnějšku dodávána nebo odebírána
elektromagnetická energie. Udržuje se tím samozřejmě i
silné magnetické pole - jedná se o perzistentní
supravodivý elektromagnet s nakrátko uzavřeným
vinutím ve velmi stabilním proudovém a energetickém stavu.
Pro supravodivost je však vinutí nutno trvale udržovat na
nízké podkritické teplotě cca 3°K v kryostatu pomocí
kapalného hélia *). Elektrická energie je tak potřeba pouze k
pohonu chladicího systému. Pro vytvoření magnetického pole
cca 3 Tesla je typicky potřeba supravodivá cívka s cca 20 000
závity (o indukčnosti několika desítek Henry) s proudem cca
500 Ampér. Perzistentní režim se používá tam, kde
potřebujeme dlouhodobě stabilní magnetické
pole, např. v zobrazovací nukleární magnetické rezonanci MRI.
*) Toto trvalé chlazení
supravodivé cívky je potřeba pečlivě hlídat!
Pokud by vlivem odpařování hladina chladicího média poklesla
natolik, že část vinutí by se oteplila nad kritickou teplotu,
supravodivost by náhle zanikla - tzv. quench
("zhasnutí" - viz níže). V tomto místě vinutí by
vznikl ohmický odpor, proud vinutím by rychle klesal a
magnetické pole zanikalo. To by mělo za následek
elektromagnetickou indukci velké elektromotorické síly ve
vinutí. Značná energie uložená v magnetickém poli by se
rychle přeměnila na indukovaný proud
vinutím, které by se ohmickým odporem silně zahřálo,
zbytek chladicího média by se uvedl do bouřlivého varu a
vinutí by se mohlo spálit!
 |
Obr.1.5.9. Vlevo:
Supravodivý elektromagnet je tvořen cívkou, navinutou
ze supravodivého materiálu, umístěnou v kryostatu s
kapalným héliem. Při vybuzení a
utlumení supravodivého proudu v silných
perzistentních elektromagnetech lze s výhodou použit
zkratování teplotně ovládaným supravodivým klíčem
(bifilární vinutí + vyhřívací drátek).
Vpravo: Závislost ohmického
odporu supravodivého materiálu Nb-Ti na teplotě (pro 1m drátu o0,3mm). |
"Zapnutí"
(vybuzení či nabití) a
"vypnutí" (utlumení či vybití)
silného elektrického proudu v supravodivém vinutí velkého perzistentního
elektromagnetu je delikátní záležitost! V silném
magnetickém poli je uložena značná energie, takže v
důsledku elektromagnetické indukce ve vinutí supravodivý
proud jeví značnou časovou setrvačnost.
Zapnutí a vypnutí supravodivého proudu zde proto nelze
uskutečnit naráz nějakým jednoduchým vypínačem, jak jsme
zvyklí v běžných elektrických obvodech (vedlo
by to k indukci vysokonapěťových špiček a proudů
působících proti náhlé změně, které by mohly vést k
porušení supravodivosti), ale musí být
prováděno postupně - plynule. Supravodivá
vinutí "nesnášejí" prudké změny proudu, které
navíc též mohou indukovat silné vířivé proudy v měděné
matrix kolem supravodivých drátů, nebo napěťové špičky v
dalších součástkách. Vybuzení proudu v uzavřeném vinutí
supravodivé cívky vyžaduje specifický postup.
Vybuzení proudu se standardně
provádí připojením vnějšího zdroje o
nízkém napětí cca 10V (postačujícím
k "protlačení" nárustu proudu několika ampér/min.
proti induktivnímu odporu cívky), který
je schopen dodávat požadovaný nominální proud (např. 500A).
Indukčnost supravodivého vinutí klade nárustu proudu odpor,
nabíjení trvá cca 50min. při řízeném nárustu proudu cca
10A/min. Po dosažení požadovaného proudu (magnetické
indukce) je nutno vývody cívky uvnitř kryostatu supravodivě
"zkratovat"; vnější zdroj proudu je
pak možné odpojit (specifickým
způsobem popsaným níže) a proud cívkou
pak již teče samovolně "navěky" *).
*) Je to jen přibližně, věčný tok
konstantního supravodivého proudu je idealizací! Ve
skutečnosti i supravodivý proud, a tím i magnetické pole B,
bude s časem velmi pozvolna klesat podle
obvyklého exponenciálního vztahu B(t) = B(0).e-(R/L).t, s časovou konstantou R/L, kde R
je zbytkový odpor způsobený elektrickými
spoji a vlivy magnetického pole na tok elektronů v
supravodiči. V některých přístrojích, jako je nukleární
magnetická rezonance, se na tento pozvolný pokles zavádí
příslušná korekce (např. drobná změna
rezonanční frekvence).
Odpojení vnějšího
zdroje po supravodivém zkratování cívky je rovněž nutno
provádět plynule. Bezprostředně po
zkratování bude totiž supravodivým zkratem procházet
poměrně malý proud, který bude navíc opačného směru, než
je potřeba vytvořit v uzavřeném obvodu supravodivé cívky.
Náhlé odpojení vnějšího zdroje v této fázi by vedlo ke
skokovému nárustu proudu ve zkratovém vedení, který by mohl
porušit jeho supravodivé vlastnosti. Proud, který dosud tekl
do supravodivé cívky z připojeného vnějšího zdroje, je
potřeba řízeně a plynule "přesměrovat" tak, aby
začal protékat supravodivým zkratem. Po dobu několika minut
je proto nutno snižovat proud tekoucí
vnějším zdrojem (který se přepne do
režimu řízeného zdroje proudu s nízkým vnitřním
odporem - již není potřeba napětí působící proti
induktivnímu odporu cívky) z nominální
hodnoty na nulu. Indukčnost hlavního vinutí zachovává proud,
takže supravodivým zkratem postupně narůstá proud (který měl těsně po zkratování menší hodnotu a
původně opačný směr!) až na
nominální hodnotu; teprve pak vnější zdroj odpojíme.
Pro vypnutí
či vybití supravodivého proudu se postupuje opačně: k
vnějším vývodům se připojí externí zdroj nastavený na
nominální proud (např.500A), přeruší se supravodivé
zkratování cívky a proud ve zdroji se elektronickou regulací
pozvolna snižuje (cca -50A/min.); po cca 10min. je supravodivý
elektromagnet "vybitý", za intenzívního chlazení
zdroje.
Supravodivé zkratování či rozpojení -
"klíčování" - přívodů
cívky se dříve provádělo elektro-mechanicky. Nyní se časo
používá teplotně ovládaný supravodivý klíč:
k vývodům hlavní cívky uvnitř kryostatu je paralelně
připojen delší supravodič (bifilárně
svinutý aby nevznikalo nežádoucí magnetické pole) s kouskem odporového topného drátku. Pokud je - při
nabíjení či vybíjení - topení zapnuto, je zkratující
supravodič převeden do normálního (odporového) stavu - zkrat
je vyřazen (rozpojen). Po vypnutí topení se
bifilární vinutí zchladí, čímž se obnoví
supravodivý zkrat a uzavřeným obvodem může trvale
procházet supravodivý proud, bez vnějšího zdroje (obr.1.5.9
vlevo).
Poděkování:
Rád bych poděkoval kolegovi Ing. Jiřímu Vítovcovi
z Kliniky zobrazovacích metod FN Plzeň za důležité údaje o
elektronickém režimu 3T perzistentního supravodivého
elektromagnetu v hybridním zobrazovacím přístroji PET/MRI.
Odkaz: ......
Quench supravodivého
magnetu
Neplánovaný a neřízený náhlý zánik supravodivosti,
zvaný quench ("zhasnutí"),
je nepříjemnou událostí pro supravodivý magnet pracující
ve vysokointenzívním režimu. Může nastat v zásadě v
důsledku 5 příčin:
× Porucha chlazení
- hladina chladicího média poklesne natolik, že část vinutí
se oteplí nad kritickou teplotu Tc a přejde do normálního rezistivního režimu
(bylo již zmíněno výše)....
× Porucha
supravodivého propojení elektrického obvodu - vadou
materiálu nebo nedokonale provedeným spojem. V tomto místě
dojde k silnému elektrickému výboji (oblouku) s prudkým
zahřátím a roztavením komponentů. K nejtěžší havárii
tohoto typu došlo v r.2008 na velkém urychlovači LHC v
CERN.....
× Příliš silný
elektrický proud - dojde k překročení kritické
hustoty proudu Ic (cca 1000-4000 A/mm2), nad kterou již použitý materiál ztrácí
supravodivé vlastnosti.
× Příliš silné
magnetické pole - dojde k překročení kritické
hodnoty magnetické indukce Bc, nad kterou již použitý materiál ztrácí
supravodivé vlastnosti a přejde do běžného rezistivního
režimu.
× Příliš velká
rychlost změny magnetického pole - indukované
vířivé proudy v nosné měděné matrix mohou svými
tepelnými účinky v některém místě zahřát část vinutí
nad kritickou teplotu.
Pokud by z některé z těchto příčin došlo
ke ztrátě supravodivosti, byť jen v malém
okrsku elektromagnetu, v tomto místě vinutí by vznikl ohmický
odpor, proud vinutím by rychle klesal a magnetické pole
zanikalo. To by mělo za následek elektromagnetickou indukci
velké elektromotorické síly ve vinutí. Značná energie
uložená v magnetickém poli by se rychle přeměnila na indukovaný
proud vinutím, které by se Jouleovým teplem silně
zahřálo. Ztráta supravodivosti během několika
sekund a silné ohřátí elektromagnetu má nevratný charakter řetězové
reakce, při níž se většina chladicího média vypaří
bouřlivým varem. Je to velmi nebezpečné pro pracovníky v
blízkosti elektromagnetu, který se může i trvale
poškodit..!..
Silné
elektromagnety, často supravodivé, se vedle
urychlovačů používají i v jiných přístrojích atomové a
jaderné fyziky, v průmyslu, medicíně. Nejmohutější
elektromagnety se používají v tokamacích na
magnetické udržení vysokoteplotní plasmy pro termonukleární
fúzi (§1.3, část "Tokamak"). Středně velké supravodivé elektromagnety (cca 1-5
T) se rutinně používají v nukleární magnetické
rezonanci pro dosažení základní orientace
magnetických momentů jader (§3.4, část
"Nukleární magnetická rezonance").
Velké
urychlovače
Pro výzkum v oblasti fyziky
(elementárních) částic jsou budovány velké unikátní
urychlovače se snahou dosáhnout co nejvyšších
energií urychlených částic. Jejich úkolem je
detailní zkoumání vlastností interakcí částic -
upřesňování mechanismů interakcí již známých částic a hledání
částic nových. Velké urychlovače (především
synchrotrony) byly vybudovány např. ve FermiLabu u Chicaga, v
Brookhavenu u New Yorku, v CERNu, v Dubně či Serpuchovu. Na
každém z těchto urychlovačů byly získány nové objevné
výsledky, nebo se takové výsledky očekávají. V poslední
době se používají většinou interakce urychlených částic
ve vstřícných svazcích (collidery). Uvedeme zde v
tabulce jen heslovitě několik největších urychlovačů z
posledních let:
| Název urychlovače |
Laboratoř |
Částice |
Energie [GeV] |
Rok |
| SLAC (Stanford Linear Accelerator
Center ) |
Stanford |
e-
- e+ |
50 |
1966 |
| Tevatron |
Fermilab |
p+
- p- |
980 |
1987 |
| LEP (Large Electron-Positron collider)
|
CERN |
e-
- e+ |
100 |
1989 |
| RHIC (Relativistic Heavy Ion Collider
) |
Brookhaven |
p-p, Au-Au, ... |
200 |
2000 |
| LHC (Large Hadron Collider) |
CERN |
p-p, Pb-Pb, ... |
7000 |
2008 |
| VLHC
(Very Large Hadron Collider) - budoucnost ?? |
p-p, ..... |
? >>LHC ? |
? >2030 ? |
| CLIC (Compact LInear Collider) - budoucnost ?? |
e- - e+ |
3000 |
?? |
Large
Hadron Collider (LHC)
Zatím největší urychlovač byl v současné době
vybudován v ústřední evropské jaderné laboratoři CERN
(Centre Europeen pour Recherche Nucleaire) *) na Švýcarsko-Francouzském
pomezí pod názvem LHC - Large Hadron
Collider (velký hadronový "srážeč") v r.2008.
*) Název "nukleární výzkum",
vytyčený při založení ústavu v r.1954, nyní již není
zcela výstižný. Původní oblast jaderného výzkumu se již
dávno transformovala. Hlavním zaměřením CERN je již
několik desetiletí výzkum v hluboce subnukleární
oblasti a hlavně v částicové fyzice,
často bez přímé souvislosti s atomovámi jádry. I název
"evropský" byl již rozšířen, na mnoha
projektech spolupracují i odborníci z mimoevropských zemí.
LHC je synchrotron
(princip činnosti byl popsán výše, obr.6.6.5 vpravo), jehož
prstenec se nachází v tunelu po předchozím elektronovém
urychlovači LEP asi 100m pod zemí (50-150m pod terénem), jeho
obvod je dlouhý 26,66 km. Systém magnetů podél dráhy
urychlovače je velmi složitý. Kruhovou dráhu urychlovaných
částic s vysokou přesností zajišťuje více než 1200
supravodivých dipólových elektromagnetů po obvodu
trubice. Dále je tam umístěno téměř 900 magnetů kvadrupólových
i složitějších tvarů, pro fokusaci svazku urychlovaných
částic, korekce a modifikace tvaru dráhy. Vodiče
supravodivých elektromagnetů jsou zhotoveny z niobo-titanové
slitiny a pracují při teplotě 1,9°K. K vlastnímu
urychlování protonů nebo těžších iontů dochází v
jednoum segmentu prstence, kde je unístěn systém
radiofrekvenčních rezonančních dutin,
napájených intenzivním vysokofrekvenčním napětím o
frekvenci 400MHz. Magnetické pole zakřivuje dráhy nabitých
částic přesně podél centrálního obvodu tunelu a vrací je
periodicky do urychlovacích dutin. Při jednom oběhu se
kinetická energie protonu zvýší o 480keV.
LHC, jakožto synchrotron, potřebuje ke své
činnosti částice již předurychlené (viz obr.1.6.5 vpravo).
V případě tak vysokých energií jsou protony dokonce 4-stupňově
předurychlené, k čemuž se využívají již dříve
zkonstruované urychlovače v CERN, zařazené v sérii podle
velikosti dosahovaných energií. Protony, získávané ionizací
vodíku, jsou nejdříve urychlené v lineárním urychlovači
(LINAC) na energii 50MeV, odtud jsou vedeny do kruhového
urychlovače PS "booster", kde získají energii
1,4GeV. Pak jsou směrovány do prstence protonového
synchrotronu PSR (Proton Synchrotron Ring) s
výstupní energií 25GeV a nakonec do dalšího synchrotronu SPS
(Super Proton Synchrotron), který jim udělí
výstupní energii 450GeV. S touto výchozí energií jsou
injektovány k finálnímu urychlení do prstence hlavního
urychlovače LHC, kde budou během mnoha oběhů urychleny na
výstupní energii 7TeV, přičemž magnetické pole v segmentech
elektromagnetů se během každého cyklu mění z počáteční
hodnoty 0,5T (při 450GeV) až na 8,3T (při 7TeV), proud v
dipólových elektromagnetech dosahuje více než 10000A. Nárust
kinetické energie v LHC z počátečních 450GeV na 7TeV trvá
zhruba 30 minut. Jelikož synchrotron pracuje v pulsním režimu,
urychlují se protony ve skupinách či shlucích (angl.
bunches). Protony se urychlují ve dvou trubicích
(prstencích) v opačných směrech pro
interakce ve vstřícných svazcích. Při rychlosti blížící
se rychlosti světla (99,999995%c) udělá proton v LHC více
než 11000 oběhů/sekundu. Ve vstřícných svazcích se
produkuje 1 srážka na 10 miliard částic, při plném výkonu
dochází k více než 30 milionům srážek za sekundu. Celková
energie protonového svazku dosahuje až 350 MJ. Kromě protonů
může LHC urychlovat i těžší jádra,
především jádra olova (pro experiment ALICE, zmíněný
níže).
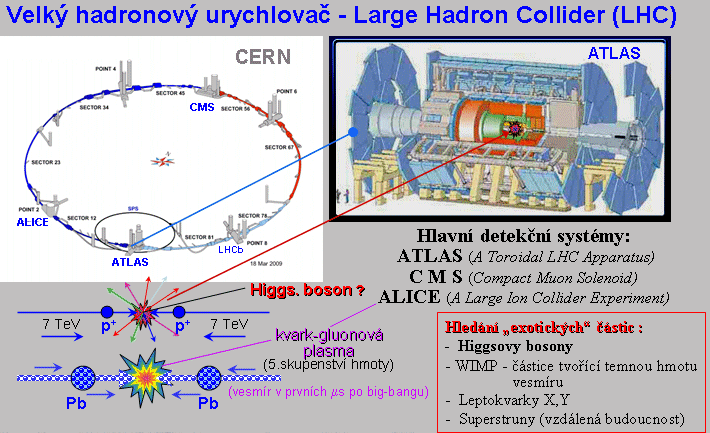
Po obvodu urychlovače LHC jsou čtyři místa,
kde se trubice propojují a protisměrné svazky částic se
kříži - zde probíhají interakce ve vstřícných
svazcích. Tato místa jsou obklopena velkými a složitými
detekčními systémy (srov. §2.1, pasáž "Uspořádání a konfigurace detektorů
záření"), pomocí
nichž se provádá šest hlavních experimentů :
¨ ATLAS (A
Toroidal LHC Apparatus)
je největším detekčním systémem (váží asi 7000tun),
hlavním nosným programem LHC. Komplexně měří a analyzuje
částice vznikající při srážkách protonů o energii 14TeV.
Detekční systém ATLAS (a též níže uvedený CMS,
částečně i ALICE) má válcové koaxiální
uspořádání podobné, jako je na modelovém obrázku
2.1.2 v §2.1, pasáž "Uspořádání a konfigurace detektorů
záření"), avšak
mnohem složitější; je to nejsložitější a
nenákladnější detekční zařízení v dosavadní historii!
Vnitřní část detektoru, která zaznamenává dráhy
nabitých částic vylétajících z místa srážky, se skládá
ze tří souosých vrstev ("slupek") dráhových
detektorů (trackerů): nejníže jsou
pixelové polovodičové detektory, pak stripové detektory a
detektory přechodového záření. Celý systém je umístěn v
silném podélném magnetickém poli 2Tesla supravodivého solenoidního
elektromagnetu; ze zakřivení drah částic v magnetickém
poli lze určit náboj a hybnost částic.
Další vrstvu detekčního systému tvoří spektrometr,
nazývaný "kalorimetr",
jehož úkolem je absorbovat energii vylétajících částic a
kvantifikovat ji (její "vzorek") pomocí výstupních
elektrických impulsů. Skládá se ze dvou částí: elektromagnetický
kalorimetr pro měření energie fotonů a elektronů a hadronový
kalorimetr ...........
Poslední, vnější vrstva detektoru ATLAS je tvořena mionovým
spektrometrem, určeným pro detekci
vysokoenergetických mionů, které jsou schopny projít vrstvou
kalorimetru. Analýzou drah mionů, zakřivených silným toroidálním
magnetickým polem, lze určit jejich hybnosti a znaménka
elektrických nábojů. K detekci drah mionů se používají
driftové trubicové a mnohodrátové ionizační komory.
¨ Detektor CMS
(Compact Muon Solenoid),
optimalizovaný pro detailní analýzu mionů,
spolupracuje se systémem ATLAS při komplexní analýze
vysokoenergetických interakcí. Jeho struktura je podobná jako
u ATLASu. Pro analýzu trajektorií rychlých mionů je
součástí detekčního systému velký elektromagnet
válcového tvaru (solenoid), vytvářejícím
magnetické pole o síle 4Tesla.
Na detekčních
sytémech ATLAS a CMS se analyzují nové částice, především
Higgsovy bosony (podrobněji je
diskutováno výše v části "Hypotetické
a modelové částice").
Pokud by jeho rozpad šel elektromagnetickým způsobem přímo
na vysokoenergetické dvojice g, nebo (přes W-bosony) na elektrony a pozitrony, byly
by tyto sekundární částice zachyceny v elektromagnetickém
kalorimetru ATLASu nebo CMS. Při rozpadu na miony (přes
Z-bosony) by přišla ke slovu hlavně mionová detekční část
CMS. A všechny nabité částice mohou zanechávat své stopy ve
vmitřních dráhových detektorech (trackerech) obou
systémů.
¨ ALICE (A
Large Ion Collider Experiment)
je dalším experimentálním systémem, jehož úkolem je
studium srážek jader ("těžkých
iontů"), především olova, při těžišťových
energiích až 5GeV/nukleon a zkoumání vlastností vznikající
kvark-gluonové plasmy (viz
výše "Kvark-gluonová plasma"). Podobně jako ATLAS a
CMS, má i ALICE válcové koaxiální uspořádání velkého
počtu detektorů, určených k registraci a rekonstrukci
parametrů především nabitých částic vznikajících při
srážkách jader. Slouží ke studiu extrémních stavů hmoty
(jaderné, hadronové) při podobných podmínkách, jaké byly
ve vesmíru na počátku hadronové éry, v prvních
mikrosekundách existence vesmíru (viz
§5.4 "Standardní kosmologický model. Velký třesk.
Formování struktury vesmíru."
knihy "Gravitace, černé díry a fyzika
prostoročasu", část "Etapy vývoje vesmíru -
Hadronová éra").
¨ TOTEM (Total Cross
Section, Elastic Scattering and Diffraction Dissociation)
slouží k přesnému měření efektivních
rozměrů protonů - účinných průřezů - pro různé druhy
interakcí. Je též používán ke kalibračním měřením
vlastností LHC (jako je "luminosita" -
účinnost produkce srážek v urychlovači). Je tvořen 8
detektory, umístěnými velmi blízko srážejících se svazků
u detektoru CMS.
¨ LHCb (Large
Hadron Collider beauty)
má za úkol studovat narušení CP symetrie při rozpadech
B-mesonů obsahujících těžký (druhý nejtěžší) b-kvark.
Při vysokoenergetických srážkách protonů v LHC vzniká m.j.
i velký počet párů b-b' kvarků-antikvarků a jejich
hadronizací pak B-mesony i baryony. Způsob rozpadu těchto
částic je citlivý na narušení CP symetrií - jestli se hmota
chová nepatrně odlišně než anihmota. Částice jsou nejprve
lokalizovány detektorem VELO (VErtex Locator),
umístěným blízko místa srážky. Identifikace částic před
a po průchodu dipólovým magnetickým polem je prováděna
pomocí dvou prstencových zobrazovacích Čerenkovových
detektorů RICH (Ring Imaging Cherenkov detectors) - viz §1.6, pasáž "Čerenkovovo záření" a
§2.4, pasáž "Čerenkovovy detektory". Komora RICH1 se nachází hned za detektorem VELO, za
magnetem je detektor stop částic, následuje komora RICH2 pro
identifikaci částic s velkou hybností. Dále jsou zařazeny
elektromagnetické a hadronové kalorimetry pro měření
energií částic. Nakonec jsou umístěny mionové komory . Tyto
výsledky by mohly být zajímavé z hlediska vzniku nerovnováhy
hmoty a antihmoty (baryonové asymetrie) v počátečních
fázích vývoje vesmíru - proč vznikl přebytek hmoty nad
antihmotou (§5.4 "Standardní
kosmologický model. Velký třesk.",
pasáž "Baryonová asymetrie
vesmíru" knihy
"Gravitace, černé díry a fyzika prostoročasu").
¨ LHCf (Large
Hadron Collider forward)
studuje vysokoenergetické částice generované
"dopředu" ve směru protonového svazku. Spektrometr
(kalorimetr) LHCf se zaměřuje především na neutrální
energetické částice (fotony g, neutrální piony,
neutrony) emitované pod malými úhly; nabité částice mohou
být registrovány trackery v ATLAS a CMS, částice emitované
pod velkými úhly pak navíc kalorimetry a mionovými
spektrometry obou systémů. Těmito komplexními měřeními je simulováno
kosmické záření a studovány kaskády částic,
vznikající při jeho interakcích (srov. obr.1.6.7 v pasáži
"Kosmické
záření", §1.6).
Již při
plánování a výstavbě si fyzikové od tohoto velkého
urychlovače mimo jiné slibovali, že energie srážek v LHC by
mohla být dostatečná k experimentálnímu nalezení tzv Higgsových
bosonů, zatím hypotetických modelových částic,
generujících hmotnosti některých elementárních částic -
kvant polí, především bosonů W a Z elektroslabé interakce (byly zmíněny výše v pasáži "Hypotetické
a modelové částice";
viz též §B.6 "Sjednocování
fundamentálních interakcí. Supergravitace. Superstruny" knihy "Gravitace, černé díry a fyzika
prostoročasu", část "Globální a lokální
symetrie; Kalibrační pole"). To se
skutečně splnilo!
Rovněž nejlehčí
supersymetrické částice (LSP - Lightest
Supersymmetric Particle) by při těchto interakcích snad
mohly být prokázány. Diskutuje se i možnosti získání
nepřímých důkazů pro extra-dimenze předpokládané
některými unitárními teoriemi pole (viz o pár řádků
výše uvedený odkaz §B.6) - to se dosud
nesplnilo...
Objev Higgsova bosonu
Na konferenci ICHEP2012 v australském Melbourne 4.července 2012
byl na základě dat z experimentů ATLAS a CMS v CERN oznámen
objev nového bosonu, jehož vlastnosti jsou konsistentní s
Higgsovým bosonem. Pečlivou analýzou asi 60 tisíc případů
detekce dvojic fotonů (pocházejících ze srážek
vysokoenergetických protonů) se na křivce závislosti počtu
fotonů na energii podařilo najít malý (ale
signifikantní, asi 160 dvojic fotonů) pík
v oblasti energie kolem 126GeV. Tento pík by měl patrně
pocházet z 2-fotonového rozpadu Higgsových bosonů.
Úroveň spolehlivosti prokázání nové částice detekcí
jejích rozpadových produktů je 5s. Je třeba provést další
experimenty, aby bylo jisté, že jde o Higgsův boson a nikoli
jinou dosud neznámou částici. Za tento objev byla v r.2013
udělena Nobelova cena P.Higgsovi a F.Englertovi.
 Source:
CERN-LHC
Source:
CERN-LHC
Objev Higgsova bosonu na velkém urychlovači LHC detekcí
produktů jeho rozpadu - zde dvou opačných fotonů gama se
specifickými energiemi na detekčním systému ATLAS.
Impozantní systém urychlovače LHC a
detekčních aparatur je nejsložitějším a
nejdůmyslnějším dílem, jaké lidstvo vytvořilo ve
své dosavadní historii! Podrobnosti o konstrukci, průběhu
výstavby a výsledcích experimentů na LHC jsou uvedeny na
oficiálních www-stránkách CERN: http://lhc.web.cern.ch/lhc/.
Nebezpečí
z velkých urychlovačů?
V souvislosti s konstrukcí a provozem velkých urychlovačů se
občas v masmédiích objevují spekulace a poplašné zprávy,
že energie srážejících se částic je tak velká, že při
interakci může vzniknout "černá díra" či dokonce
nový "velký třesk", což by nás údajně mohlo ohrozit,
nebo dokonce pohltit a zničit Zemi i celý vesmír!!
Tyto spekulace pramení z nepochopení problematiky, jsou z
fyzikálního hlediska zcela nepodložené a chybné,
přinejmenším ze dvou důvodů:.
1.
I kdyby při vysokoenergetické interakci vznikla černá díra
(což by ostatně bylo velmi zajímavé), vzhledem k malé
celkové energii by to byla mikroskopická černá díra,
která by se okamžitě kvantově vypařila a
zanikla - za vyslání energetických částic (o menší
celkové energii než měly původní částice). Taková černá
mikrodíra tedy nic nepohlcuje (není toho schopna, srov. §4.7 "Kvantové
vyzařování a termodynamika černých děr" výše zmíněné knihy
"Gravitace....."), může být
jen virtuální; bylo by velmi těžké ji
vůbec prokázat.
2.
Částice o mnohem vyšších energiích (dokonce o 9 řádů
vyšších!) se běžně vyskytují v kosmickém
záření (viz §1.6
"Ionizující záření", část "Kosmické záření"), interagují a srážejí
se s ostatními částicemi ve vesmíru i v zemské atmosféře
již po miliardy let, aniž se něco "katastrofického"
stane.
Koncepční perspektivy
velkých urychlovačů
Kruhové
či lineární urychlovače ?
Jakkoli je princip kruhového urychlování nabitých částic
velmi úspěšný a efektivní, zdá se, že kruhové
urychlovače se v pozemských podmínkách již přiblížily k
hranicím svých možností. Pokud bychom chtěli nabité
částice urychlovat na ještě podstatně vyšší energie při
reálně dostupných průměrech kruhové dráhy (t.j.
průměrech urychlovacích trubic), čím dál více by se
uplatňoval jev vzniku synchrotronového záření*),
které by odnášelo značnou část kinetické energie částic
a nakonec by znemožnilo další urychlení. Zdá se tedy, že
budoucí urychlovače pro nejvyšší energie v pozemských
podmínkách budou muset být lineární. Délka
lineárních urychlovačů pro dosažení vysokých energií
činí mnoho kilometrů. To je v pozemských podmínkách
rovněž limitující faktor.
*) Synchrotronové záření vzniká jako
brzdné záření v důsledku nerovnoměrného pohybu elektricky
nabitých částic při kruhovém oběhu. Podle známého
Larmorova vzorce elektrodynamiky je intenzita tohoto
vyzařování úměrná elektrickému náboji a druhé mocnině
zrychlení pohybu částice, zde se jedná o dostředivé
zrychlení kruhového pohybu. Při dané kinetické energii
je tedy intenzita synchrotronového záření nepřímo úměrná
kvadrátu hmotnosti částice. Tento jev se proto uplatňuje
především při kruhovém urychlování lehkých částic, elektronů,
které se při dosažení vysokých kinetických energií
pohybují vysokými rychlostmi a s vysokými radiálními
zrychleními. U protonů vzhledem k jejich vysoké hmotnosti je
synchrotronové vyzařování milionkrát menší.
Lineární collidery mají další nevýhodu:
zatímco u kruhových colliderů se urychlené částice
magneticky opakovaně vracejí do interakčního místa a tam se
jejich dráhy mnohokrát protínají, u lineárních colliderů
se urychlený shluk částic se svým protiběžným shlukem
setká pouze jedenkrát a většina částic
uletí pryč - jejich energie je ztracena. Uvažuje se proto o
určité "rekuperaci" energie nesené svazkem
částic prošlých interakční oblastí: tyto částice by po
průletu interakční oblastí mohly postupně předávat svou
energii urychlovací struktuře v protilehlém lineárním
urychlovači. Další možností je využití částic, které
bez interakce proletěly interakční oblastí, k experimentům
na pevných terčících.
Protonové
nebo elektronové urychlovače ?
Protony a elektrony (vč.
pozitronů) jsou z hlediska svých vlastností a struktury velmi
odlišné částice, což se projevuje odlišnými mechanismy
interakcí. Protony mají složitou vnitřní
strukturu kvarků interagujících prostřednictvím gluonového
pole. Při jejich vysokoenergetické srážce neinteragují jako
celek, ale energie interakce se rozdělí na
jednotlivé kvarky, přičemž v gluonovém poli dochází k
produkci většího množství dalších částic - dvou a
tříkvarkových kombinací, mezonů a baryonů. Tyto procesy
jsou sice důležité z hlediska studia silných interakcí a
vlastností hadronů, avšak energie interakce se
"rozmělní" na velký počet sekundárních částic;
nelze dosáhnout koncentrace energie na malý počet částic.
Zhruba 1/2 hybnosti protonu je nesena gluony, v protonu jsou
vázány 3 kvarky. Na každý kvark tak připadá cca 1/6
hybnosti protonu, takže efektivní energie
kvarkových interakcí je Eef»E/6. (při
eletron-protonové kolizi je to zhruba Eef»E/Ö6). Při
protonových srážkách vstupují do interakcí všechny kvarky,
které "zamoří" detekční prostor kolem místa
interakce množstvím sekundárních částic (obr.1.5.1G,H). V
tomto "balastu" je značně obtížné
"najít" (odseparovat) vzácné případy požadované
interakce jedné z dvojic kvarků.
Elektron je naproti tomu částice prakticky
bodová bez vnitřní struktury (aspoň v nám známých a
dostupných prostorových měřítcích). Při vysokoenergetické
srážce proto elektrony interagují jako celek
(Eef=E),
vzniká podstatně méně sekundárních částic, na které se koncentruje
podstatně větší část energie. Pro hledání nových
masivních částic jsou proto interakce urychlených
kompaktních elektronů výhodnější, než složitě
strukturovaných protonů. Zjednodušeně se dá říci, že při
vysokých energiích jsou srážky elektronů
"tvrdší" než srážky protonů. Elektronové
srážky jsou podstatně "čistší" než protonové,
vzniká při nich mnohem méně sekundárních částic
(srovnejme příslušné Feynmanovy diagramy na obr.1.5.1).
Výhodou je proto nižší radiační pozadí nezajímavých
částic, mezi nimiž se snadněji hledají požadované masivní
částice. Zdá se tedy, že pro dosažení nejvyšších
faktických koncentrací energií při interakcích budou výhodnější
velké urychlovače elektronů - vstřícné
elektron-pozitronové srážky.
Pozn.:
Konstruktéři z LHC v CERN již projektují stavbu velkého elektron-pozitronového
collideru pod názvem CLIC (Compact
LInear Collider) s energií 3TeV.
Mionové
urychlovače ?
Pro dosažení co nejvyšší energie, která by při srážce
byla k dispozici pro tvorbu nových částic, mají tedy
protonové a elektronové urychlovače určitá omezení.
Kruhové urychlovače elektronů mají při technicky
dosažitelném průměru omezení v důsledku synchrotronového
záření. Lineární urychlovače mají zase omezení v
technicky dosažitelné délce urychlovací dráhy. U protonů a
antiprotonů se synchrotronové záření téměř neuplatňuje,
takže je můžeme urychlit na podstatně vyšší energie.
Protony a antiprotony však nejsou základní kompaktní
částice, ale složené částice s kvark-gluonovou strukturou.
Při kolizi se nesrážejí "celé protony", ale vždy
pouze jedna základní částice uvnitř každého protonu;
ostatní prolétnou bez přímé žádoucí interakce. Při
srážce je zde pro tvorbu nových částic k dispozici jen
zlomek energie urychleného protonu. Z místa srážky vyletí
velké množství částic, z nichž většina nenese informaci o
přímé srážce dvou kvarků.
Určitou potenciální možností, jak do značné
míry obejít tato omezení a získat vhodné elementární (bezstrukturní) částice
urychlené na velmi vysokou energii, která při srážce bude
celá k dispozici pro tvorbu nových částic, je urychlování mionů
m±. Miony (výše uvedené v pasáži "Miony m a tauony t ")
jsou částice do značné míry podobné elektronům a
pozitronům e±. Mají stejný elektrický náboj,
jsou elementární a chovají se jako bodové částice. Od
elektronu se mion liší hmotností - je 206-krát těžší
než elektron - a je nestabilní - s dobou života 2,2
mikrosekundy se rozpadá na elektron a dvě neutrina.
Nestabilita mionů T1/2=2,2 ms není tak extrémní (na
rozdíl od pionů), aby zcela znemožňovala možnost jejich
urychlení. V koprodukcí s relativistickou dilatací času
speciální teorie relativity, umožňuje mnohonásobný pohyb
rychlostí blízkou rychlosti světla po kruhové dráze v
urychlovači po dobu cca 0,1 s., dostatečnou na účinné urychlení. Velkou
výhodou mionů je jejich relativně vysoká klidová
hmotnost 206-x větší než u elektronů. To umožňuje urychlovat
miony v kruhovém urychlovači na velmi vysoké energie (podobné protonům) téměř bez
nežádoucího efektu ztráty energie synchrotronovým
zářením.
K vytvoření svazku urychlených mionů je
potřeba několika kroků :
=> Urychlit protony na vysoké
energie vyšší než cca 300 MeV. => Nechat
je dopadnout na terčík (kovový či
plastový). => Vznikne
tím sprška částic obsahující rychlé nabité piony. =>
Piony se pak rychle rozpadnou na miony a anti-miony. =>
Ty se vedou do protiběžných urychlovacích prstenců
synchrotronu - collideru, kde se urychlí na vysoké energie a
pak se nechají srazit.
Výsledkem by byly čisté srážky při
vysokých energiích mezi bodovými částicemi, kde 100% jejich
energie je k dispozici pro tvorbu nových částic. Z místa
srážky by do detektorů přicházel relativně
"čistý" signál, bez nadměrné kontaminace
parazitními interakcemi. Očekávanou nevýhodou tohoto
technologicky složitého procesu vytváření, shromažďování
a kolimace mionů a antimionů, bude podstatně menší
četnost srážek (cca 10-5-x ve srovnání s
elektron-pozitronovým nebo proton-protonovým colliderem), takže bude obtížné nashromáždit potřebnou
statistiku pro prokázání objevu nových druhů částic..?..
Mionové urychlovače - collidery
- mohou být perspektivní pro získání vysokých energií
díky minimálnímu synchrotronovému vyzařováním a k
realizaci "čistých" srážek, při nichž je všechna
energie k dispozici pro tvorbu nových sekundárních částic.
Vesmírné
urychlovače ?
Technické problémy a omezení u velkých urychlovačů jsou
povětšinou dány pozemskými podmínkami, v nichž se
urychlovače konstruují a provozují. Mnohé z těchto
problémů by automaticky odpadly, kdybychom urychlovače
instalovali mimo prostor naší Země.
Konstrukce urychlovačů ve vesmíru má několik
principiálních výhod :
¨ Dostatek volného
prostoru
pro instalaci i těch nejrozsáhlejších urychlovacích
systémů.
¨ Beztížný stav
Odpadá nutnost robustních konstrukcí zajišťujících
mechanickou pevnost. Lze též snadno, bez konstrukčních
zásahů, provést změny polohy a rekonfiguraci jednotlivých
částí urychlovacího systému v prostoru.
¨ Vysoké vakuum,
které je k dispozici všude, v celém prostoru, a to
"zadarmo". Odpadá tedy nutnost konstruovat
urychlovací trubice, v nichž v pozemských podmínkách jen
obtížně udržujeme potřebné vakuum. Urychlované částice
se mohou pohybovat ve volném prostoru po drahách, přesně
určených a tvarovaných magnetickým polem.
¨ Nízká teplota
(při odstínění slunečního záření,
nebo ve vzdáleném vesmíru), která u
vhodných materiálů automaticky zajišťuje supravodivost.
Cívky elektromagnetů tedy není nutno chladit,
jednou vzbuzený proud se bude trvale udržovat a budit
permanentní magnetické pole k potřebnému zakřivování drah
urychlovaných nabitých částic. I elektromagnety s časově
proměnným magnetickým polem budou pracovat bez energetických
ztrát teplem.
Reálnému
využití těchto principiálních předností však za
současného stavu naší techniky brání zatím velmi
obtížně řešitelné technické problémy. Je
to především vynesení konstrukčního materiálu o vysoké
váze (statisíců tun) ze zemského povrchu, proti gravitaci, na
oběžnou dráhu kolem Země, nebo dokonce do vzdáleného
vesmírného prostoru. Na to zatím technické prostředky
nemáme, současné rakety jsou příliš slabé, pomalé a
neefektivní. Dále je to otázka dálkového napájení
elektrickou energií a též zajišťování přesné polohy
jednotlivých částí urychlovacího systému se submilimetrovou
přesností. Pouze oblast přenosu měřených dat z interakcí
částic by byla řešitelná i prostředky naší současné
elektroniky (která v posledních desítiletích - jako jediná z
technických disciplin - udělala zásadní kvalitativní
pokrok!).
V budoucnu lze očekávat, že experimenty s částicemi
urychlenými na nejvyšší energie ze z pozemského
prostoru přesunou do vesmíru...
Vojtěch Ullmann







 Zdroj:
CERN-LHC
Zdroj:
CERN-LHC









