 |
|
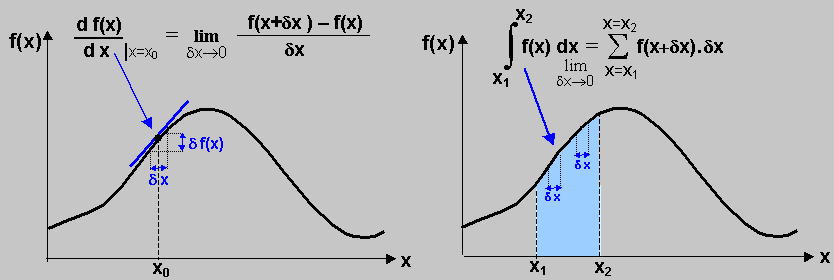
| Derivace funkce f(x) v bodě x=x0 | (určitý)Integrál funkce f'(x) v rozmezí x1-x2 |
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | Gravitace, černé díry a fyzika |
Kapitola 1
GRAVITACE A JEJÍ MÍSTO VE FYZICE
1.1. Vývoj poznatků o přírodě,
vesmíru, gravitaci
1.2. Newtonův gravitační zákon
1.3. Mechanická LeSageova
hypothéza podstaty gravitace
1.4. Analogie mezi gravitací a
elektrostatikou
1.5. Elektřina a magnetismus. Maxwellovy rovnice.
Elektromagnetické vlny.
1.6. Čtyřrozměrný prostoročas
a speciální teorie relativity
1.5. Elektřina a magnetismus. Maxwellovy rovnice. Elektromagnetické vlny.
Nejvýznamější silou,
která určuje veškerou vnitřní strukturu a chování
přírodních objektů, od subnukleárních, atomových a
molekulárních měřítek, až k makroskopickým rozměrům
okolní přírody (včetně nás samých) a měřítek Země a
ostatních planet, je elektromagnetická
interakce.
Nositelé elektrických sil jsou základní stavební
částice atomů - elektrony nesoucí záporný elementární elektrický náboj a protony nesoucí kladný náboj (kladná
a záporná znaménka se vyvinula na základě konvence). Elektrické síly mezi protony
a elektrony, v koprodukci s kvantovými zákonitostmi, určují strukturu atomů, a tím chemické a fyzikální vlastnosti látek
(... "Interakce atomů "...).
Každý elektrický náboj (nabité
těleso) kolem sebe budí elektrické
pole podle Coulombova zákona (1.20b) o
intenzitě úměrné velikosti náboje a nepřímo úměrné
druhé mocnině vzdálenosti; pokud se náboj nepohybuje (v dané vztažné soustavě),
jedná se o pole elektrostatické. Elektrické pole
působi silovými účinky na každé jiné nabité
těleso které se do tohoto prostoru dostane. Jestliže se náboj
pohybuje (jedná se o elektrický
proud), budí kolem sebe kromě
elektrického pole ještě pole magnetické
podle Biot-Savart-Laplaceova zákona (1.33a).
Magnetické pole vykazuje silové účinky na každé elektricky
nabité těleso které se pohybuje kolmo na
směr vektoru magnetického pole (Lorentzova síla).
Sloučení obou polí představuje elektromagnetické
pole.
Jestliže se elektrické náboje pohybují proměnnou
rychlostí (se zrychlením či
zpomalením), vytvářejí kolem sebe časově
proměnné elektromagnetické pole, což vede ke vzniku elektromagnetických
vln, které se odpoutávají od svého zdroje a
odnášejí s sebou do prostoru část jeho energie. Při pohybu
nebo časových změnách v magnetickém poli vzniká podle
Faradayova zákona elektromagnetické indukce
pole elektrické; a časové změny pole elektrického
vyvolávají zase pole magnetické. Toto pole se řídí Maxwellovými
rovnicemi elektromagnetického pole, které vznikly
sloučením a zobecněním všech zákonitostí elektřiny a
magnetismu. Sloučená nauka o elektřině a magnetismu,
zahrnující dynamiku pohybů nábojů a časové proměnnosti
polí, se nazývá elektrodynamika. Toto bude
hlavní náplní stávajícího §1.5.
V předchozím §1.4 jsme
viděli, že analogie mezi Newtonovou gravistatikou a Coulombovou
elektrostatikou je velmi těsná. Elektrostatické pole je však
speciálním případem obecného pole elektromagnetického, které panuje v okolí
pohybujících se elektrických nábojů. Je proto užitečné
všimnout si vlastností elektromagnetického pole a pokusit se
nalézt případné analogie s obecným
"gravidynamickým" polem v okolí pohybujících se
těles. Elektrodynamika je nejdokonalejší a
nejúspěšnější teorií klasické fyziky, která si
zachovává svou plnou platnost i v moderní relativistické
fyzice. Lze říci, že elektrodynamika je jedním ze základních kamenů celé fyziky a sehrála klíčovou úlohu
při formování speciální a obecné teorie relativity, jakož
i kvantové fyziky.
Pozn.: Historický vývoj poznatků o
elektřině a magnetismu je stručně nastíněn v §1.1 v
pasáži "Elektrodynamika,
atomová fyzika, teorie relativity, kvantová fyzika". O relativistickém pohledu na vztah elektického
a magnetického pole je krátce diskutováno níže v pasáži
"Relativistický elektromagnetismus", podrobněji pak v tam uvedených odkazech.
Linearita
elektromagnetismu
:
Elektrické a magnetické působení ve vakuu je lineární ve zdrojích (elektrických nábojích
různých velikostí) i v hodnotách polí buzených
přímo či indukcí. Platí zde přesně princip
superpozice. Hodnoty intenzit elektrického a
magnetického pole z různých zdrojů se jednoduše sčítají
(vektorově). Neplatí to již zcela v látkovém prostředí,
kde se uplatňují efekty interakcí elektrických a
magnetických polí s konfiguracemi atomů v látkách.
Níže uvidíme, že to může nastávat při buzení
elektrického pole náboji v nehomogenních dielektrikách, na
jejich rozhraních, a hlavně při buzení magnetického pole ve
feromagnetických látkách, kde se projevuje i stav nasycení a
hysterese.
V kvantové teorii pole se vyskytují efekty vyšších
řádů, kdy fotony interagují prostřednictvím smyček
fermionů. Necháváme zde stranou hypotézu nelinearity
elektrodynamiky při supersilnývh intenzitách polí ("Nelineární elektrodynamika")...
Fyzikální názvy a
jednotky v elektřině a magnetismu
Během dlouhodobého vývoje fyziky a
přírodovědy se nejen získávaly stále nové poznatky, ale
zaváděly se i různé fyzikální veličiny a jednotky pro
jejich kvantifikaci. Badatelé objevující nové věci navrhují
slova a symboly aby je popsali. Navzdory výborné erudici
badatelů, tyto prvotní autorské návrhy někdy nejsou
dobré, neboť ještě není dostatečně známa podstata
jevů a jejich souvislosti s dalšími procesy (příp. i ještě neobjeveými).
Z důvodu školometského konzervatismu však některé starší
názvy přetrvávají. Obzvlášť dynamický vývoj a hojnost
různých jednotek se odehrával v oblasti elektřiny a
magnetismu v průběhu konce 18. až první poloviny 20.století..
Systematické práce na vytvoření jednotné a
racionální soustavy fyzikálních jednotek začaly v
r.1862 z iniciativy Britské asociace pro rozvoj vědy. Vznikl
tak "absolutní" systém CGS
založený na třech základních jednotkách Centimetr,
Gram, Sekunda. Byla ustavena Mezinárodní
konference pro váhy a míry a realizovány etalony
pro metr a kilogram. Existovalo však mnoho různých jednotek
elektrických a magnetických, často založených na
sekundárních empirických poznatcích (např. jednotka Ampér
na základě vylučování stříbra elektrickým proudem při
elektrolýze, nebo Ohm pomocí elektrického odporu sloupce
rtuti). Z hlediska podstaty a souvislosti jevů se ve
fundamentální (teoretické) fyzice často používá systém CGSE
(navržený C.F.Gaussem), který pokládá koeficienty e0 a m0 rovny 1 - zahrnuje je
do veličin intemzit elektrického E a
magnetického B pole. Vede to k stručným a
výstižným zápisům rovnic mezi eleltromagnetickými
veličinami. Budeme je při teoretických analýzách většinou
používat. Důležité výsledné vzorce a praktické aplikace
však uvedeme i v jednotkách SI.
Mezinárodní systém jednotek SI se
vyvíjel především v první polovině 20.století. Tři
základní mechanické jednotky metr, kilogram a sekunda
byly v r.1950 doplněny o elektrickou jednotku ampér -
vznikla tím soustava MKSA. V r.1960 pak Mezinárodní
konference pro míry a váhy systém založený na metru,
kilogramu, sekundě, ampérech, kelvinech a kandelách pojmenovla
"Systeme international d'unités"
(Mezinárodní systém jednotek) se zkratkou SI.
Pro technické aplikace je nyní soustava SI
nejpraktičtější a téměř výhradně používaná, protože
její jednotky většinou mají velikost srovnatelnou s rozměry
a intenzitami v běžné přírodě; a též proto, že všechny
současné měřící přístroje jsou kalibrovány v těchto
jednotkách.
Poznámka: Chybná či nelogická definice
základních jednotek elektromagnetismu !
Historický vývoj poznávání základních fyzikálních
zákonitosti se někdy ubíral docela spletitými cestami. Spolu
s tím se utvářely i definice fyzikálních veličin a
jejich jednotek, které byly poplatné dobovým
představám.
Nešťastné bylo zavedení elektrického proudu
jako základní veličiny a jeho SI jednotky Ampér (pomocí
"magnetického silového působení dvou nekonečných
rovnoběžných vodičů..."). Fyzikálně primární
je přitom elektrický náboj, od kterého by
měl být odvozený elektrický proud jako množství
náboje prošlého za jednotku času (Coulomb/sekundu). Nebo v
magnetismu terminologická nelogičnost názvů "intenzita
magnetického pole" a "magnetická indukce"
- mělo by to být obráceně! - (u elektrického pole je to
přitom v pořádku). Je stručně diskutováno níže v pasáži
"Intenzita<->Indukce v elektromagnetismu".
Toto nešťastné "zkřížení" názvů "intenzita-indukce"
vzniklo během historického vývoje nauky o elektřině a
magnetismu, kdy magnetismus byl mylně vysvětlován fluidovou
teorií, analogicky jako elektrostatika. A bohužel to tak
již zůstalo i v nynější soustavě SI ...
Integrální
a diferenciální formulace fyzikálních rovnic
Elektrodynamika je fyzikální obor, kde se v matematických
vzorcích nejvíce ze všech používají derivace a integrály
vektorových polí, často sjednocených do formalismu
diferenciálních operátorů. Kolegové fyzikové jsou jistě s
těmito technikami dobře obeznámeni, ale pro příp. zájemce z
jiných oborů bych se zde pokusil napsat pár poznámek o jejich
podstatě a přínosu. Fyzikální pole jsou vyjádřeny
hodnotami f sil-intenzit a energií-potenciálů
v různých místech v prostoru. Jsou to tedy funkce místa
- prostorových souřadnic x,y,z a času t - f(x,y,z,t).
Ukážeme si to nejdříve na funkcích jedné proměnné f(x) a
jejich grafickém znázornění.
Soustředíme se na aspekty mající fyzikální
význam - na funkce spojité, pro které existují
derivace a integrály. Složitější matematické závislosti a
konstrukce budeme diskutovat v kapitole 3 "Geometrie
a topologie prostoročasu",
kde se budeme zabývat i problematikou divergencí,
nekonečna a singularit.
Derivace a integrál jako
čísla
Pro analýzu přírodních dějů za různých situací
potřebujene často zjistit, jak rychle (jak prudce, s
jakým gradientem) se mění jeden parametr ve vztahu k jinému
parametru. Toto kvantifikuje matematická operace derivace
jednoho parametru podle druhého parametru - zapisuje se
d f(x)/dx| x=x0
v bodě x0,
značí se též f '(x). Je to strmost změny
hodnoty této funkce vzhledem k infinitezimílní změně její
nezávisle proměnné. V mechanice vyjadřuje derivace polohy
podle času rychlost pohybu tělesa. Pro funkci jedné
proměnné f(x) derivace určuje směrnici tečny (tangens úhlu) křivky jejího
grafu v daném bodě x0. Pro funkce více proměnných f(x,y,z,t) se
zavádějí parciální derivace ¶f/¶x, ¶f/¶z, ¶f/¶z, ¶f/¶t - částečné gradienty
ve směru jednotlivých souřadnicových směrů x,y,z a času t.
Za proměnnou se zde bere jen ta, podle které se derivuje,
přičemž ostatní proměnné se považují za konstantní.
 |
|
| Derivace funkce f(x) v bodě x=x0 | (určitý)Integrál funkce f'(x) v rozmezí x1-x2 |
Často též potřebujeme sčítat-sumovat
místní okamžité hodnoty určité veličiny do výsledné kumulované
hodnoty, která může determinovat funkžní chování
dalších veličin. Pokud jsou to neměnné hodnoty, je to
prostý aritmetický úkon "+" sčítání. Při
proměnných hodnotách funkce f(x) se však toto sčítání
musí provádět postupně, lokálně jakožto integrování.
Zapisuje se x1ňx2f(x) dx : jedná se o určitý integrál - v určitém
rozmezí x1-x2 hodnot nezávisle proměnné x. Znak integrálu ň
je svisle prodloužené pásmeno "S", zkratka pro sumaci.
Integrované rozmezí x1÷x2 se rozdělí na infinitesimílní úseky dx a postupně se
sčítají elementární součiny f(x1+n.dx).dx až po dosažení x2. Určitý integrál funkce f(x) udává plochu
pod její křivkou mezi hodnotami x1 a x2.
Ve dvojrozměrném zobecnění, pro funkce dvou
proměnných f(x,y), se integruje pomocí infinitezimálních
plošných rovnoběžníků a počítají se plošné
integrály Sňňf(x,y) dS buďto skalárních veličin (jako je hmotnost nebo náboj pomocí jejich plošné
hustoty), nebo tok vektorového pole přes
určitou zadanou plochu S. Dále se počítají křivkové
integrály podél určité parametrizované křivky ve
2-D rovině. Plošné integrály vektorových funkcí lze
převést na objemové integrály pomocí Gaussova vzorce o
divergenci, nebo na křivkové integrály pomocí Stokesova
vzorce o rotaci - viz obrázek níže.
Derivování a integrování
funkcí
Shora jsme si pro funkci f(x) nastínili její derivaci v
konkrétním bodě x0 a její integrál v určitém rozmezí x1-x2. Výsledkem je zde
určité lokální číslo. Pro úplnější analýzu
chování funkcí však může být důležité provést operace
derivování a integrování ve všech místech funkce
f(x) - pro všechny hodnoty proměnné x (v daném definičním oboru).
Výsledkem tohoto procesu je pak nová funkce
f '(x) nebo F(x), která ukazuje diferenciální nebo
kumulativní trend původní funkce f(x).
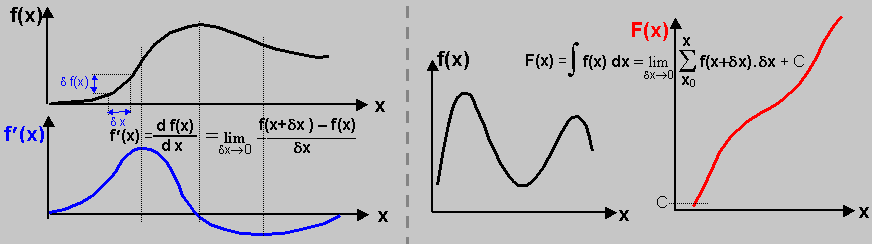
Zderivováním funkce f(x) vznikne funkce f '(x),
která v každém místě kvantifikuje proměnnost
původní funkce f(x) při změnách nezávisle proměnné x.
V místech kde je funkce f(x) rostoucí je zderivovaná funkce f '(x)
kladná a její hodnota je úměrná strmosti růstu, v
klesajících oblastech f(x) jde derivace do záporných hodnot.
V místech kde je f(x) konstantní, nebo má lokální maxima či
minima, je derivace f '(x) nulová.
Integrál ňf(x) dx = F(x) se nazývá neurčitý integrál,
neboť nemá stanovená žádná rozmezí nezávisle proměnné x,
integruje se průběžně v celém definičním oboru funkce
f(x). Pokud je funkce f(x) nezáporná, je její integrál F(x)
monotóně rostoucí funkcí. Jde-li funkce f(x) i do záporných
hodnot, mohou i v integrované funkci F(x) převládnout
záporné hodnoty.
 |
|
| Derivováním funkce f(x) vznikne funkce f '(x) | Integrováním funkce f(x) vznikne funkce F(x) |
Derivování a integrování funkcí jsou
vzájemně opačné procesy - z derivované fukkce f ´(x)
můžeme získat původní funkci f(x) integrováním, s
použitím počáteční podminky. A naopak z funkce F(x)
můžeme zderivováním získat původní funkci f(x). Funkce
F(x) se někdy nazývá "primitivní funkce" k funkci
f(x).
Diferenciální operátory
Derivace funkcí vektorových
polí (zde intenzit elektrických a magnetických polí) se pro
lepší přehlednost kombinují-sjednocují do
formalismu tzv. diferenciálních operátorů :
Nabla N: Základním
diferenciálním operátorem je zde "nabla N":
NF = ¶F/¶x + ¶F/¶y + ¶F/¶z . Od operátoru N jsou pak odvozeny další derivační kombinace :
Gradient: grad F = NF = [¶F/¶x, ¶F/¶y, ¶F/¶z] kvantifikuje prudkost-strmost změn
skalárního pole F v různých místech. V elektrodynamice se
jedná o gradient potenciálu f.
Divergence vektorové funkce F: div F = N . F
= ¶Fx/¶x + ¶Fy/¶y + ¶Fz/¶z. Kvantifikuje
lokální tok - rozbíhavost, sbíhavost - vektorového pole F.
V elektrostatice vyjadřuje způsob, jakým distribuce
elektrických nábojů vytváří elektrické pole E
- (1.32b).
Laplaceův operátor: D f = div grad
f = N2 f = ¶2f/¶x2 + ¶2f/¶y2 + ¶2f/¶z2 . Kvantifikuje dynamiku změny
pole F v prostoru. Ve 4-rozměrné formulaci x,y,z, c.t
speciální teorie relativity se používá d'Alembertův
diferenciální operátor š f = ¶2f/¶x2 + ¶2f/¶y2 + ¶2f/¶z2 -
(1/c2)¶2f/¶t2.
Rotace či curl je vektorový součin operátoru nabla
N a zkoumané vektorové funkce F: rot
F = N × F
= [(¶Fz/¶y - ¶Fy/¶z)+(¶Fx/¶z - ¶Fz/¶x) + (¶Fy/¶x - ¶Fz/¶z)]. Kvantifikuje lokální
rotaci - cirkulaci - otáčení - vektorového pole,
změn směru vektoru F ve vektorovém
poli. Vyjadřují to rozdíly parciálních derivací Fx,y,z mezi
souřadnicemi x,y,z. Velmi dobře se hodí pro modelování
magnetického pole B, které má kolem
budících pohybujících se nábojů či proudlů kruhový-spirální
tvar - (1.33)-(1.37).
Důležité jsou zde souvislosti mezi diferenciálními
vztahy a integrálními závislostmi fyzikálních
veličin, zde intenzit a potenciálů pole. Pro diferenciální
operátory "div" a "rot"
platí dvě důležité integrální rovnice :
--» Gauss-Ostrogradského
vzorec o divergenci ukazuje, že plošný integrál
vektového pole F(x,y,z) přes uzavřenou plochu
S je roven objemovému integrálu divergence pole div F
přes objem V uvnitř této uzavřené plochy. Znamená
to, že tok vektorového pole F přes uzavřenou
plochu S se rovná objemovému integrálu z divergence
pole div F, t.j. lokálních přírustků a
úbytků pole F, ve vnitřní oblasti uzavřené
plochou S.
--» Stokesův
integrální vzorec o rotaci ukazuje,
že tok vektoru rot F plochou S v
prostoru je roven křivkovému integrálu citkulace vektoru F
podél křivky C , která tuto plochu ohraničuje.
Můžeme si to představit tak, že lokální rotace vektorového
pole F na ploše S se sčítají
do výsledné citkulace vektorového pole F
podél celkové křivky C ohraničující plochu S.
Pro vektor magnetické intenzity B viz.
(1.34.b), (1.37.b).
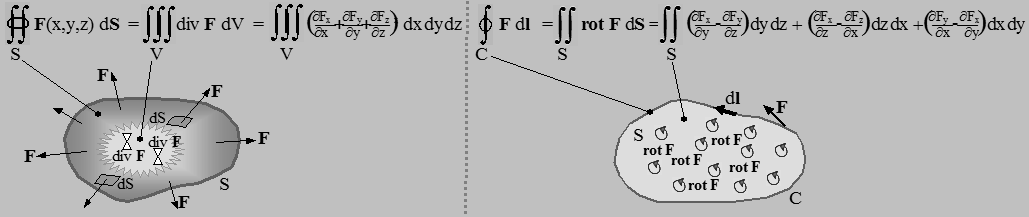 |
|
| Gauss-Ostrogradského vzorec o divergenci | Stokesův integrální vzorec o rotaci |
Elektrický náboj
Název "elektrický náboj" Q se v elektrodynamice
používá ve dvou významech :
1. Těleso nebo částice která vykazuje
silové elektrické působení. Říkáme též že je nosičem
elektrického náboje nebo že je elektricky nabité.
Primárně jsou to
elektrony a protony a dále ionty a tělesa která mají
vzájemný přebytek počtu elektronů nebo protonů.
V mikrosvětě jsou i další nabité
částice - miony, piony, hyperony (§1.5 "Elementární
částice a urychlovače", část "Elementární částice a jejich vlastnosti"), které jsou však velmi nestabilní, v naší
přírodě se nevyskytují a pro nauku o elektřině nemají
význam.
2. Fyzikální veličina kvantikující
velikost - míru elektrického náboje Q. Základní jednotkou
náboje v soustavě SI je 1 Coulomb. V atomové a jaderné fyzice
se též často jako jednotka používá náboj elektronu 1 e =
1,602×10-19 Coulombu.
Rozložení elektrických
nábojů se v teorii pole vyjadřuje pomocí hustoty náboje r(x,y,z,t), která je obecně funkcí
místa a času, takže celkový náboj obsažený v prostorové
oblasti V je Q = Vňňň r dV.
V elektromagnetickém poli
působí na zkušební částici s nábojem q pohybující se
rychlostí v celková síla (Lorentzova
síla)
| F = q . E
+ q . [ v x B ] , elektrická síla magnetická síla |
(1.30) |
kde E je intenzita elektrického pole a B je intenzita magnetického pole (z historických důvodů nazývaná magnetická indukce), "x" znamená vektorový součin. Níže si nejdříve probereme zvlášť vznik a vlastnosti elektrického a magnetického pole a pak jejich vzájemné souvislosti a dynamické chování v elektromagnetickém poli.
Pohyb elektrických
nábojů - elektrický proud
V nauce o elektřině se pohyb elektrických nábojů obecně
nazývá elektrický proud. Zvláštní význam má uspořádaný pohyb nábojů, především ve vodičích. V
užším významu se proto elektrickým proudem nazývá uspořádaný pohyb nosičů elektrického náboje. Kvantifikuje se veličinou elektrický proud I, což je elektrický náboj q
procházející průřezem vodiče za jednotku času: I = dq/dt.
Jednotkou v soustavě SI je 1 Ampér, což je náboj jednoho
Coulombu prošlý za 1 sekundu (nešikovná
technická definice 1A pomocí "silového magnetického
působení dvou nekonečných rovnoběžných vodičů..."
pro nás není důležitá).
Podle druhu a pohybu nosičů náboje se elektrický
proud rozděluje na dvě základní skupiny :
-> Kondukční - vodivý proud je
uspořádaný tok volných nosičů náboje v látkovém
prostředí působením elektrického pole. Především je to
pohyb volných elektronů v kovových vodičích, pohyb iontů v
elektrolytech nebo v plynech při elektrických výbojích. Částice nesoucí elektrický
náboj se při svém pohybu v prostředí srážejí s atomy
látky, čímž jim předávají část své kinetické energie a
rozkmitávají je. Dochází tím ke ztrátám energie
elektrického proudu a k zahřívání prostředí. Vodivé
prostředí klade elektrickému proudu určitý odpor (minimalizace či
téměř anulování odporu je diskutována v §, pasáži
"....").
-> Konvekční - proudivý elektrický
proud způsobený mechanickým pohybem nosičů náboje
v prostředí, bez momentálního působení elektrického pole (nosiče náboje jsou buď unášeny proudícím
látkovým prostředím, nebo se pohybují setrvačností ve
vakuu). Důležitým příkladem
konvekčního proudu je pohyb nabitých částic v
urychlovačích. U konvekčního proudu ve vakuu nedochází k
srážkám nabitých částic s částicemi prostředí, takže
zde nevznikají tepelné účinky, ale jen elektrické a
magnetické.
Z hlediska časového průběhu a
směru toku nábojů se setkáváme se dvěma druhy elektrického
proudu :
-> Stejnosměrný proud, v němž
elektrické náboje v čase nemění směr svého toku.
Velikost proudu může být buď časově konstantní (během sledovací doby funkce),
nebo proměnná - rostoucí, klesající, pulzující
(při zachování stejného směru). Zdrojem stejnosměrného
proudu jsou např. elektro-chemické galvanické články a
akumulátory, termočlánky, fotovoltaické články. Častými
elektronickými zdroji jsou usměrňovače, které
získávají stejnosměrný proud ze střídavého.
-> Střídavý proud, který s časem periodicky
mění směr svého toku. Periodický průběh může být
různý, např. obdélníkový (prosté
střídání "+" a "-"), pilovitý, ale nejčastější je sinusový -
harmonický: I(t) = Imax . sin(w.t + j), kde Imax je amplituda, w je úhlová
frekvence související s frekvencí f vztahem w = 2p.f a j (0÷360°) je
fázový posun začátku časové souřadnice t (nebo fázový posun mezi napětím a proudem). Frekvence f udává počet kmitů za
jednotku času; jednotka 1 Hz značí jeden kmit za 1 sekundu (název je podle jednoho z průkopníků
elektromagnetismu H.Hertze). Názory na to
co je nízkofrekvenční či vysokofrekvenční se liší, v
závislosti na oboru v němž se střídavý proud používá. V
běžném životě a v elektroakustice se jako hranice většinou
bere 20 kHz. V radiotechnice bývá tato hranice posunuta nahoru,
do MHz oblasti...
Máme v zásadě dva typy zdrojů střídavého proudu :
--» Alternátory jsou rotační výkonové
elektro-mechanické zdroje střídavého proudu pro energetické potřeby. Zdrojem mechanické energie je rotující turbina - parní v tepelných a jaderných
elektrárnách, nebo vodní v hydroelektrárnách (příp. vrtule ve větrném zdroji). Turbina pohání zmagnetovaný rotor alternátoru, který tím vytváří točivé magnetické pole. V cívkách statoru se pak indukuje střídavé napětí o frekvenci danou otáčkami/s.
Alternátory v elektrárnách mají ve svém statoru navinuté tři cívky úhlově posunuté o 120°, čímž
vytvářejí 3-fázový proud. V globálně propojené
elektrické síti všechny alternátory pracují synchronně s
frekvencí 50 Hz, v USA s frekvencí 60 Hz.
Malé a podstatně jednodušší 1-fázové
alternátory na napětí cca 14V se používají v automobilech
se spalovacím motorem, který je pohání a ony nabíjejí
akumulátor a napájejí zapalování, reflektory a ostatní
elektrickou výbavu..
--» Oscilátory jsou elektronické obvody, v
nichž dochází k periodickému kmitání
elektrického napětí a proudu s frekvencí závislou na
parametrech součástek (kondenzátorů,
cívek, rezistorů, tranzistorů) a často je lze ladit. Většinou se
vytvářejí harmonické sinusové
kmity (vyjímečně obdélníkové nebo pilovité v multivibrátorech) pro použití v radiotechnice nebo přístrojové technice (podrobněji níže "Vysílání a přijímání
elektromagnetických radiovln").
Elektrické součástky a
obvody v elektronice
Při praktickém
využití elektřiny, elektrického proudu a napětí, se
používají elektrotechnické
součástky
(prvky, elementy) různých požadovaných vlastností. Z
hlediska dodávání či spotřeby elektrické energie můžeme
tyto součástky rozdělit do dvou kategorií :
-> Aktivní -
zdrojové, které
do obvodu dodávají elektrickou energii. V silnoproudé
energetice to jsou elektro-mechanické generátory
(alternátory, dynama), které pomocí rotačních turbin či
vrtulí přeměňují mechanickou energií páry, vody či větru
na elektrickou energii. Dále fotovoltaické články a
galvanické články. Na obrázku je vlevo schématicky
znázorněna výroba elektrické energie v elektrárně (zde
jaderné), transformace napětí z 6 kV na 220-400 kV, uprostřed
dálkové vedení do oblasti spotřeby. Pro dálkový přenos
energie je výhodné transformovat na
vysoké napětí,
kde pak stačí relativně malý proud, čímž se minimalizují
ohmické ztráty ve vedení a stačí též
tenčí dráty (používají se většinou
lana Al-Fe průřezu cca 300mm2). Při
příliš vysokém napětí, cca >500kV, se však zase
zvyšují ztráty ionizací vzduchu a drobnými koronovými
výboji. Vpravo je na obrázku schématicky zakreslena
transformace na 22 kV v trafostanici a nakonec na 220 V pro
napájení běžných elektrospotřebičů u odběratelů :
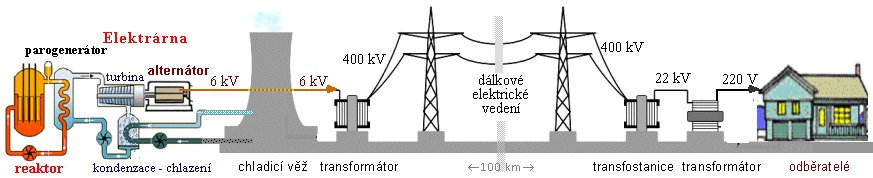
Výroba a rozvod elektrické energie
Kromě těchto základních primárních zdrojů jsou to sekundární elektronické zdroje, které
touto primárně vytvořenou elektřinou napájejí výsledné
elektrické obvody v domácích spotřebičích, průmyslových
strojích a laboratorních přístrojích - transformátory,
usměrňovače, měniče :
| Napájení elektrických obvodů | |||||||||
 |
|||||||||
| Alternátor v elektrárně Výkonový transformátor Přístrojový transformátor Malý transformátor Galvanická baterie Pojistky, jističe, přepínače |
-> Pasivní součásrtky, které odebírají
elektrickou energii a přeměňují ji na jiné druhy energie
(tepelné, světelné, mechanické, zvukové,
elektromagnetické...). Zmíníme několik nejčastějších
elektronických součástek :
=» Rezistory zvané též odpory, jejichž úkolem je klást elektrickému
proudu určitý zvýšený odpor, čímž se elektrický proud snižuje a na odporu vzniká určitý úbytek napětí. Při průchodu
silnějšího proudu (např. několika Ampér) rezistortem
vzniká značné teplo, takže rezistory se mohou používat i
jako topné články. Jednotkou elektrického odporu je
1 Ohm [W]:
Rezistor má odpor 1W, když při napětí 1 V jím protéká proud 1 A. Rezistory se vyrábějí z vodivých
materiálů se zvýšeným měrným odporem, jako jsou slitiny
železa, niklu a chromu, či mědi a niklu, pro větší odpory grafit. Buď ve formě kovových odporových
drátků, nebo tenkých vrstev grafitu či metalických nebo
metaloxidových vrstev, nanesených na izolujících (většinou keramických) nosičích s vyfrézovanými drážkami
pro zvýšení délky vrstvy a tím zvýšením odporu. Rezistor
s regulovatelně nastavitelným odporem pomocí třetí
elektrody, mechanicky posunované podél odporové vrstvy, se
nazývá reostat nebo potenciometr (název
pochází z toho že je to odporový dělič napětí, dříve
používaný v přístrojích pro měření
elektrického potenciálu, napětí).
=» Kondenzátory zvané někdy též kapacitory. Základní konstrukce kondenzátoru
spočívá ve dvou vodivých deskách (elektrodách),
oddělených mezi sebou izolační vrstvou
dielektrika.
Když se na každou z desek přivedou elektrické náboje
opačné polarity které se přitahují, izolační dielektrikum
mezi nimi nedovolí, aby se nosiče nábojů dostaly do kontaktu.
Desky zůstanou nabité i po odpojení elektrického zdroje.
Základní vlastností kondenzátoru je shromažďovat
elektrický náboj Q. Tato schopnost se kvantifikuje,
ve vztahu s elektrickým potenciálem - napětím U,
veličinou zvanou kapacita C = DQ/DU. Obecně elektrickou kapacitu má
každé vodivé těleso. Jednotkou kapacity v soustavě SI je 1 Farad: Těleso má kapacitu 1 Farad, když
dodáním náboje 1 Coulomb se jeho napětí zvýší o 1 Volt.
Farad je značně velká jednotka, proto se používají její
dekadické zlomky mikrofarad 1µF = 10-6 F, nanofarad 10-9 F, pikofarad 10-12 F. Běžná
osamocená tělesa mají velmi malou kapacitu cca jednotek až
desítek pikofaradů (kapacita lidského
těla je cca 30pF).
U kondenzátorů je jejich zvýšená kapacita způsobena velkou
plochou desek umístěných v těsné blízkosti vedle sebe, kde
jsou opačné elektrické náboje k sobě silně přitahovány.
Kapacita kondenzátoru je dána velikostí-plochou desek S,
jejich vzájemnou vzdáleností d a permitivitou e izolující dielektrické vrstvy : C = e. S/d . Klasické technické provedení je svitkový kondenzátor jehož elektrody jsou delší tenké
hliníkové pásy, mezi nimiž je papírová nebo plastická
fólie, namotány do válečku. Vyrábějí se v kapacitách cca
desetiny až desítky mikrofaradů. Pro vyšší kapacity
desítky, stovky a tisíce mikrofaradů se používají elektrolytické kondenzátory, kde v hermeticky zapoudřeném
válečku je vodný roztok elektrolytu (většinou
borité kyseliny),
ve kterém je ponořena hliníková elektroda. Vysoké kapacity
je zde dosahováno velmi tenkou dielekltrickou vrstvou oxidu a
vysokou permitivitou elektrolytu. Naopak pro velmi malé kapacity jednotek a desítek pF jsou jednoduše
používány malé kovové destičky ve
vzduchu. Jsou
to i kondenzátory s proměnnou -
laděnou - kapacitou, kde se plechové elektrody rotačním
pohybem zasouvají mezi sebe. Používají se ve frekvenčních
ladicích obvodech (viz níže "Cílené
vysílání a přijímání radiovln"). ...... varikapy ......
=» Indukční
cívky
navinuté z vodivého drátu, nejčastěji měděného.
Elektrický proud procházející vinutím vytváří uvnitř
magnetické pole. Každý vodič při průchodu proudu kolem sebe
vytváří magnetické pole podle Biot-Savartova zákona (1.33b)
buzení magnetického pole elektrickým proudem. Při časové
změně procházejícího proudu je toto proměnné magnetické
pole doprovázeno elektromagnetickou indukcí napětí podle
Faradayova zákona, přičemž toto indukované napětí působí
proti napájecímu napětí. Indukčnost L vodiče je jeho schopnost
indukovat v sobě napětí v důsledku změn
proudu, který
jím protéká. Jednotkou (vlastní *) indukčnosti vodiče v
soustavě SI je 1 Henry (podle
J.Henryho, který byl vedle Faradaye a Maxwella též
průkopníkem elektromagnetismu). Vodič nebo cívka má indukčnost 1
Henry, když při změně proudu o 1 Ampér za sekundu se na něm
indukuje napětí 1 Volt. Vlastní indukčnost drátu nebo cívky
můžeme zjednodušeně považovat za jakousi "elektrickou setrvačnost": odolává, klade odpor, změnám
v proudu který jím protéká, indukcí opačného napětí.
*) Pokud
se v blízkosti tohoto vodiče nachází další vodič, bude v
něm v důsledku proměnného proudu sousedního vodiče též
indukováno určité napětí. Zde hovoříme o vzájemné
indukčnosti.
I jednoduchý přímý vodič vykazuje určitou malou
vlastní indukčnost, která závisí na délce drátu a jeho
tloušťce (delší a tenčí dráty mají
větší indukčnost L analogicky jako u odporu R;
tyto závislosti zde však nejsou lineární, neboť závisejí
na prostorovém průběhu magnetického pole v okolí vodiče). Pro přímý drát kruhového průřezu je jeho
vlastní indukčnost L [nanoHenry] dána semiempirickým vzorcem L[nH] = µ . l . [ln ( 2.l/r
) - 1], kde l je délka drátu a r jeho poloměr (tloušťka/2) v metrech, m je
relativní permeabilita. Např. drát délky 1 metr a tloušťky 1 milimetr má indukčnost cca 1,5 mH.
V případě střídavého proudu
se vytváří proměnné střídavé magnetické pole, které
zpětně indukuje elektrické napětí - samoindukce.
To se skládá s
procházejícím, působí proti, způsobuje fázový posun mezi
napětím a proudem. Cívka klade střídavému proudu určitý
odpor - impedanci - závislou na frekvenci (viz
níže). Cívky bývají navinuty buď "vzdušně" bez
jádra, nebo kolem feromagnetického jádra. Tvar osy cívky je
buď přímý - tzv. solenoid, nebo kruhový toroidní. Prostá cívka tvaru solenoidu má
indukčnost L = µ.N2 .S/l , kde S je plocha průřezu cívky, µ
je permeabilita prostředí, N je počet závitů cívky, l je
délka cívky. Pokud je navinuta na feromagnetickém jádře,
její indukčnost se zvýší v poměru relativní permeability µr materiálu
jádra. Toroidně navinuté cívky se vyznačují vysokou
indukčností a nízkým rozptylem magnetického pole do okolí.
=» Transformátory jsou soustavy magneticky
vázaných cívek, které pomocí elektromagnetické indukce
mohou přeměňovat (transformovat) střídavý proud určitého
napětí na vyšší nebo nižší napětí a přitom umožňují
galvanické oddělení obou elektrických obvodů. Skládá se ze
dvou či několika cívek (vinutí) od sebe elektricky
izolovaných, ale sdílejících společné magnetické pole :
- Primární vinutí se nazývá to, do kterého se přivádí
výchozí (napájecí) střídavý elektrický proud nebo signál
o napětí U1. Vzbuzuje se tím střídavé
magnetické pole.
- V
sekundárním vinutí toto proměnné magnetické pole
elektromagneticky indukuje střídavé napětí U2,
které se odtud odebírá do dalšího obvodu nebo spotřebiče.
Magnetická vazba obou vinutí je
realizována tím, že obě cívky jsou umístěny těsně vedle
sebe nebo jedna uvnitř druhé, nejčastěji jsou navinuty na
společném feromagnetickém jádře. V magnetické vazbě obou
cívek se snažíme dosáhnout, aby co nejvíce magnetických
siločar procházelo společně primárním i sekundárním
vinutím. Optimální magnetická vazba primárního a
sekundárního vinutí závisí na řadě okolností. Pro velmi
vysoké frekvence, vyšší než cca 300MHz, nejsou použitelná
materiálová jádra, cívky jsou "vzdušné" a magnetická vazba je
dána pouze těsným geometrickým uspořádáním obou vinutí.
Pro středně vysoké frekvence 1 kHz - 300 MHz se používají
jádra z feritu (směsné oxidy železa s niklem, zinkem nebo manganem,
vytvářené lisováním), který má vysoký měrný odpor, což
snižuje ztráty vířivými proudy. Pro nízké frekvence
desítky a stovky Hz, nejčastěji pro síťovou frekvenci 50 Hz,
se materiál a provedení jádra volí podle druhu
transformátoru. Malé přístrojové transformátory nízkého
výkonu mají jádra sestavena nejčastěji z vrstvy několika
desítek na sebe poskládaných plechů tloušťky cca 0,5-1 mm z
feromagnetických slitin železa, niklu, kobaltu, molybdenu.
Většinou se používá slitina permalloy (20% Fe, 80% Ni). Pro výkonové transformátory, kde je
požadována vysoká účinnost transformace a nízké
energetické ztráty, se pro plechy transformátorového jádra
používá speciální křemíková
ocel nebo amorfní kovy vytvořené rychlým ochlazením
roztavených slitin železa, niklu, kobaltu a dalších kovů.
Tyto materiály mají vysokou magnetickou permeabilitu a nízké
ztráty hysteresí a vířivými proudy.
V primárním vinutí
procházející střídavý proud I1 vytváří střídavý
magnetický tok F1
= N1.I1.µ.S/l, který je magnetickou vazbou veden k
sekundárnímu vinutí, poněkud zeslabený na F2. V sekundární cívce tento
střídavý magnetický tok F2 podle Faradayova zákona elektromagneticky
indukuje elektrické napětí U2(t). = N2.dF2/dt.
V případě ideálního
transformátoru,
kde magnetický tok je identický pro obě vinutí (F1=F2) a nedochází k ohmickým
ztrátám ve vinutí ani k hysteresním ztrátám ve
feromagnetickém materiálu jádra, je U1.I1 = U2.I2 a převodní
koeficient transformátoru K = U1/U2 = I2/I1 = N1/N2 je dám poměrem počtu závitů
N1 v primárním a N2 v sekundárním vinutí. Když
má sekundární vinutí menší počet závitů než primární,
dochází k transformaci dolů k nižšímu napětí (snižující transformátor), při vyšším počtu závitů v
sekundáru než v primáru nastává transformace nahoru (zvyšující transformátor).
Sekundárních vinutí v
transformátorech bývá i několik s různýn počtem závitů,
pro získání více různých napětí pro jednotlivé části
složitějších obvodů (např. primár na
220 V a sekundáry na 6, 12, 24, 120 V, ...). Někdy se používají i tzv. autotransformátory, u kterých se pro primár i sekundár
používá společné vinutí s odbočkami pro různá napětí.
V elektronických laboratořích se někdy používají i variabilní autotransformátory, kde po obvodu toroidního
vinutí se posunuje otáčivý kontakt, který z různých
závitů může snímat plynule nastavitelné napětí (po určitých malých krocích v závislosti na počtu
závitů).

-------------------------------------- Malé přístrojové transformátory
----------------------------------------------------------- --------- Velké energetické transformátory --------
Pečlivě konstruované transformátory jsou energeticky
velmi účinné a mají ohmické a feromagnetické ztráty často
menší než 1%. Malé nízkovýkonové transformátory se
zahřivají většinou jen mírně a stačí jejich chlazení
okolním vzduchem, v některých přístrojích jsou instalovány
malé ventilátory. U výkonových transformátorů v energetice,
které transformují výkony řádu megawatů, může však
vznikat jouleovské zahřívání mnoho kilowatů. Je zde proto
potřeba zajistit jejich účinné chlazení. Jsou zapouzdřeny
ve velkých kovových nádobách s chladicím
"transformátorovým" olejem, který kromě chlazení
zajišťuje i lepší izolační vlastnosti jednotlivých vinutí
proti elektrickým výbojům vysokého napětí, které by
nastávaly ve vzduchu. Olej je veden přes vnější chladicí
systém s ventilátory a po ochlazení pak zase zpět k
transformátoru (na obrázku vpravo).
=» Světelé
zdroje které
při průchodu elektrického proudu přeměňují část
elektrické energie na elektromagnetické záření optického
spektra - na světlo. Klasické zdroje světla - žárovky sestávají z tenkého kovového drátku,
většinou z wolframu (často stočeního do spirálky)
umístěného v evakuované baňce, který se průchodem
elektrického proudu zahřívá na vysokou teplotu cca 1500-2000 oC, což vede k tepelné emisi světla. Novějšími světelnými
zdroji jsou polovodičové LED diody.
=» Diody
a tranzistory (dříve se
používaly elektronky) jsou polovodičové součástky
obsahující přechody P-N mezi polovodiči typu P a
typu N. V diodách tento přechod způsobuje jednosměrnou vodivost, fungují jako usměrňovače. V tranzistorech, kde jsou 3
elektrody s přechody P-N, kolektor, báze a emitor, mohou m.j.
fungovat jako zesilovače elektrického
signálu.
Slabý signál přivedený na bázi může způsobit
nmohonásobně větší změnu proudu mezi emitorem a kolektorem.
=» Elektromotory
které
provádějí přeměnu elektrické energie na mechanickou,
většinou rotační. Mají dva systémy cívek: nehybný stator a otáčející se rotor. V motorech na střídavý proud
speciílně navinuté cívky statoru vytvářejí točivé magnetické pole, které přes další indukované pole v
rotoru vytváří silové působení, způsobující mechanické
otáčení rotoru. Motory na stejnosměrný proud mají buď
rotor tvořený permanentními magnety, nebo rotor obsahuje
drážky s komutátorem, na který je připojeno vinutí.
=» Spínače či přepínače, které umožňují buď zapnutí a vypnutí elektrického obvodu, nebo přepínání
proudu mezi různými částmi složitějšího obvodu (jsou uvedeny vpravo na obrázku nahoře).
=» Jističe,
pojistky,
které při nepřípustné hodnotě proudu trvale rozpojí obvod,
čímž chrání jeho součástky před poškozením ("spálením"
např. při zkratu).
Pojistky mohou být tavné (roztavení
tenkého drátku a přerušení obvodu), nebo elektromagnetické
jističe s
cívkou, jejíž magnetické pole svým
silovým působením mechanicky rozpojí elektrický kontakt.
Vedle těchto jednotlivých
"diskrétních" součástek novější
elektrické obvody mohou obsahovat i tzv. integrované
obvody
zvané též mikročipy, které ve společném pouzdře obsahují
větší množství jednotlivých elementů, většinou
polovodičových, někdy i mnoho tisíc. Nejvyšší hustotu
integrace mají mikroprocesory a paměťové obvody.
| Nejčastější součástky v elektrických obvodech | |||||||||
 |
| Rezistory a potenciometry Kondenzátory Indukční cívka solenoidní a toroidní Žárovky a LED diody Tranzistory Integr. obvody Elektromotory |
Elektrické obvody
Poznámka :
U základních elektronických součástek odporů-rezistorů,
kondemzátorů a cívek budeme při analýze vlastností
elektrických obvodů předpokládat, že se jedná o ideální součástky - rezistory s odporem R,
kondenzátory s kapacitou C a indukční cívky s
indukčností L.
Abychom mohli využít vlastností těchto
elektronických součástek, musíme je vzájemně vodivě
spojit do elektrického obvodu, aby přes
ně mohl procházet elektrický proud. Pokud je vodivá dráha
elektrickým obvodem uzavřená - nepřerušená, jedná se o uzavřený
elektrický obvod. Je-li tato vodivá dráha v
některém místě přerušena, jedná se o otevřený
elektrický obvod. Nejjednodušší způsob je zde
elektro-mechanický spínač jehož kontakty mohou být
zapnuty-spojeny či vypnuty-rozpojeny. Používají se i
složitější elektronické způsoby uzavření a otevření
elektrických obvodů a jejich částí.
Základním parametrem elektrického obvodu (a každé
elektrické součástky) je jeho volt-ampérová
charakteristika - závislost proudu I na
napájecím napětí U. V nejjdnodušších situacích v
praxi je tato závislost lineární podle Ohmova
zákona I = U/R, kde R je celkový odpor, který
jednotlivé součástky v obvodu kladou elektrickému proudu.
Jedná se zde o odpor, který klade vodič protékajícém
elektronům. Jednotka elektrického odporu je 1 Ohm [W]. Obvodem či elementem o
odporu 1W při
napětí 1 V protéká proud 1 A. Při sériovém zapojení se
hodnoty jednotlivých odporů jednoduše aritmeticky sčítají,
při paralelním zapojení se sčítají jejich převrácené
hodnoty. Pro polovodičové součástky - diody, tranzistory -
Ohmův zákon ale již přesně neplatí, volt-ampérová
charakteristika je složitější, nelineární.
Nejčastěji používané elektrické propojení
součástek v elektrických obvodech je pomocí kovových
drátů často opatřených plastovou izolací, nebo
tenkých měděných plíšků na destičkách plošných spojů.
Tyto vodiče však samy o sobě kladou určitý malý odpor (delší a tenčí dráty mají větší odpor). Odpor vodiče (drátu) délky l o průřezu S
je R = rR .l/S , kde rR je měrný
elektrický odpor materiálu vodiče (pro
měď je rR=1,7×10-8 W.m). Nejčastěji
používané kovové vodiče, jako je měděný drát tloušťky
kolem 1mm, mají velmi malý odpor cca 0,02
W/metr, takže v praktické
elektronice se většinou zanedbává (odpor 1W by měl takový
drát až při délce cca 50m). Skutečně téměř
nulový odpor mají supravodivé materiály (viz pasáž "Supravodivost" v §1.5 knihy "Jaderná
fyzika a fyzika záření"). Látky nevodivé - dielektrika,
neobsahující volné nosiče náboje mají naopak specifický
odpor téměř nekonečný (řádově
rR
>1014 W.m).
Složitější situace je u elektrických obvodů se střídavým
proudem, většinou s harmonickým sinusovým průběhem v
čase t o frekvenci f : I = I0 .sin (2p.f.t). Běžné rezistory (odpory) se chovají téměř
stejně jako při stejnosměrném proudu, jejich ohmický odpor
nezávisí na frekvenci. Naprosto odlišně se však chovají kondenzátory
a cívky. Ve stejnosměrném obvodu se paralelně
zapojený kondenzátor může jednorázově nabít. Pokud je
zapojený sériově, též se jednorázově nabije, avšak jeho
dielektrická mezera je nevodivá a obvod se chová jako
rozpojený, žádný proud již neprochází. Elektrická
cívka se ve stejnosměrném obvodě naopak chová jako vodič.
Při střídavém napětí se však elektrody
kondenzátoru střídavě nabíjejí, vybíjejí a znavu
nabíjejí opačnou polaritou, což způsobuje že kondenzátory
jsou efektivně pro střídavý proud vodivé (izolační mezeru kondenzátoru překonává tzv. Maxwelův
posuvný proud, diskutovaný níže, vzorec (1.35)). Efektivní odpor kondenzátoru (kapacitance) vůči střídavému napětí je nepřímo úměrný
kapacitě C kondenzátoru a nepřímo úměrný frekvenci f
: XC = 1/2p f .
C . V elektrické cívce
střídavý proud vytváří proměnné magnetické pole, které
zpětně indukuje elektrické napětí, které půdobí proti napájecímu napětí - dochází k samoindukci. Efektivní odpor indukční
cívky (induktance) vůči střídavému napětí je přímo úměrný
índukčnosti L cívky a přímo úměrný frekvenci f
: XL =L.2p.f .
Efektivní odpor kondenzátoru XC a indukčnosti XL vůči střídavému napětí se nazývá impedance
(lat. impedire = bránit, být v
cestě, zadržovat, překážet, značí se většinou X). Též "jalový" odpor nebo "reaktance",
zatímco odpor rezistoru R se nazývá "činný
odpor". Ohmické odpory + kapacitance a induktance se
pak skládají ve výslednou impedanci obvodu Z.
Při kvantifikaci impedancí se spíše než frekvence f
častěji používá kruhová frekvence w = 2p f . Kapacitní
impedance XC = 1/w . C , induktivní impedance XL = w . L a činný odpor R rezistoru se však v
elektrickém obvodu spolu nesčítají aritmeticky (jak je to u
rezistorů), ale "geometricky". Celková impedance sériového
zapojení rezistoru R s kondenzátorem C je Z = Ö[R2 - 1/(w.C)2], pro paralelní zapojení rezistoru s
kondenzátorem je výsledná impedance Z = Ö(R2+w2C2R4)/(w2 C.R2 + 1) .
Při průchodu střídavého proudu rezistorem jsou
sinusovky napětí U=U0 .sin (w.t) a proudu I=I0 .sin (w.t) vzájemně ve fázi, napětí a proud dosahují
svého minima a maxima ve stejných časových okamžicích. Při
průchodu střídavého proudu kondenzátory či indukčnostmi
však dochází mezi napětím a proudem k fázovému posunu
j - napětí a proud dosahují
svého maxima či minima v různých okamžicích.
Přiřadíme-li jedné celé periodě úhel 360°, pak na
kondenzátoru se napětí spožďuje o 90° za proudem -
je to způsobeno procesem střídavého nabíjení kondenzátoru.
Na indukční cívce naopak napětí předbíhá o 90°
proud - v důsledku samoindukce.
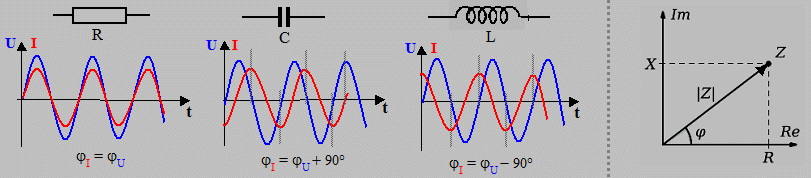 |
| Vztah fáze střídavého napětí U a proudu I u rezistoru, kondenzátoru a indukční cívky. | Fázový diagram impedance rezistoru R a reaktance X |
Pokud jsou v obvodu zapojeny rezistory,
kondenzátory i indukčnosti, bude celkový fázový posun mezi
napětím a proudem různý v závislosti na poměru hodnot R,
C a L těchto součástek. U sériově
zapojeného RLC obvodu "ideálních" součástek
rezistoru, kondenzátoru a cívky mohou nastat 3 význačné
případy :
1. Pokud je XL < XC , na
indukční cívce bude menší napětí než na kondenzátoru a
obvor RLC bude mít kapacitní charakter - napětí se
bude spožďovat za proudem o 0<j<-90°.
2. Když je XL
> XC , na
indukční cívce bude větší napětí než na kondenzátoru a
obvor RLC bude mít indukční charakter - napětí bude
předbíhat proud o 0<j<90°.
3. Ve speciálním případě XL = XC na
indukční cívce bude stejné napětí jako na kondenzátoru a
obvor RLC bude mít jen odporový charakter, celkový
fázový posun bude j = 0. K tomuto speciálnímu stavu dochází při zcela
určité rezonanční frekvenci f = 1/2p.Ö(L.C) .
Celková efektivní impedance obvodu je Z = Ö[R2 + (w . L)2 -
1/(w.C)2] a
fázový posun mezi celkovým napětím U a proudem I
je j = arccos R/Ö[R2+(XL-XC)2]
.
Při rotačním pohybu bodu po kružnici poloměru r
jeho vodorovné a svislé souřadnice x,y nabývají hodnot x =
r.cos j a y = r.sin j , kde
j je
úhel mezi spojnicí počátku souřadnic (0,0) a polohou (x,y)
bodu na kružnici. Proto se střídavé napětí/proud U/I = U0/I0.sin 2pf.t často znázorňuje
pomocí kruhově rotujícího vektoru U/I (0,U0/I0) délky |U0/I0| rotujícího
úhlovou rychlostí j(t) = 2pf.t = w.t. Tento vektor se někdy nazývá "fázor",
neboť jeho natočení j
udává okamžitou fázi střídavého
napětí.
Impedance se někdy vyjadřuje v komplexním (imaginárním) formalismu.
Komplexní vyjádření impedance v algebraickém tvaru je Z = R
+ i.X, kde R je "činný" odpor, X je
impedance a "i" je imaginární jednotka. Tato dvě
čísla R a X se mohou graficky zakreslit jako bod
(R,X) do dvojrozměrné roviny komplexních čísel, kde na
vodorovné ose jsou reálné souřadnice R a na svislé
ose imaginární souřadnice X. Každé komplexní číslo
pak můžeme znázornit pomocí vektoru v této rovině,
začínajícím v počátku (0,0) a končícím v bodu (R,X).
Tento vektor lze vyjádřit i pomocí jeho délky |Z| = Ö(R2 + X2) a hodnoty úhlu j = artang(X/R), který svírá s
vodorovnou osou. Je to tedy komplexně vyjádřený
"fázor". Vzniká tak fázový diagram
znázorňující komplexní impedanci Z zakreslenou jako
vektor v komplexní rovině, která má jako vodorovnou
souřadnicí reálnou složku impedance a jako svislou
souřadnici má imaginární složku impedance. Impedanci pak
můžeme vyjádřit v goniometrickém tvaru komplexního
čísla Z = |Z| . (cos j + i . sin j), který se někdy zapisuje i v exponenciálním
tvaru Z = |Z| . e i .
j.
Tento formalismus má výhodu v tom, že pro
"sčítání" impedancí platí stejné výsledné
vztahy jako pro sčítání stejnosměrných odporů. Určitou
nevýhodou je však menší intuitivní srozumitelnost, neboť
imaginární čísla jsou jen modelová a umělá, v reálné
přírodě se nevyskytují. Komplexní formalismus pro impedanci
je používán spíše odborníky v elektronice při návrhu a
analýze složitějších RLC obvodů.
Favorizované
sinusovky
!
Funkční průběh časové závislosti elektromagnetických signálů
může být v zásadě velmi různý. Avšak když sledujeme
elektrické signály v různých obvodech, střídavé napětí,
vyzařování elektromagnetických vln a jejich přijímání,
pozorujeme v naprosté většině harmonický
sinusový
průběh, přesný nebo alespoň přibližný. Může být
zajímavé diskutovat, co takto favorizuje
sinusovky
oproti jiným matematickým funkcím..?..
Z matematického hlediska má
funkce sinus či kosinus "dar obzvláštní odolnosti":
když ji zderivujeme d sin(x)/dx = cos(x) dostaneme
kosinus, což je zase sinus s fázovým posunem 90°. I po zintegrování ňsin(x)dx = -cos(x) je to jen záporný
kosinus. Vynásobením sinusovky konstantou to bude zase
sinusovka. Projekce kruhového pohybu poloměru r do
souřadnic x a y kmitají harmonicky jako x(t) =
r . cos w.t , y(t) = r
. sin w.t , kde w je
úhlová frekvence.
Všechny oscilační pohyby
způsobené silou F která je úměrná výchylce x od
rovnovážého stavu F = -k.x - pohyb klasického kyvadla,
vlny na vodní hladině, pružné kmity částic v látkovém
prostředí, elektrické kmity v LC oscilátoru - probíhají s
výslednou výchylkou tvaru x(t) = r . sin w.t . Z elektronického hlediska,
sinusový signál je jediný tvar, který nezmění svůj
charakter když projde elektrickým obvodem obsahujícím
kapacity, indukčnosti a rezistory. A každou
konfiguraci elektrického signálu či elektromagnetického
vlnění lze pomocí Fourierovy analýzy rozložit na superpozici
menšího či většího počtu harmonických sinusových
signálů či vln různých frekvencí a amplitud..!.. Případná nelinearita v
elektrickém obvodu zkreslí čistý sinusový průběh, což se
manifestuje objevením se signálů tzv. vyšších
harmonických,
chovajících se opět jako sinusovky odlišných frekvencí.
Sinusové kmity a vlny
přirozeně produkuje příroda v oblasti mechaniky a
elektrodynamiky; podobně jako v oblasti gravitace ve vesmíru
přirozeně vznikají eliptické dráhy pohybu planet kolem
hvězd, oběhů měsíců kolem planet, nebo vzájemných oběhů
hvězd v binárních a vícenásobných stelárních systémech. Sinusoidy a kosinusoidy jsou tedy přirozenými
funkcemi, kterými lze modelovat a kvantifikovat řadu
přírodních dějů pomocí jednoduchých harmonických
oscilátorů.
Naprostá většina elektrické energie pro světovou ekonomiku a spotřebu v
našich domácnostech se vyrábí v alternátorech, kde točivé
magnetické pole indukuje v cívkách střídavý
proud přesně sinusového průběhu frekvence 50 či 60 Hz.
Jak rychlá je
elektřina ?
Co se týče
rychlosti, u elektřiny se setkáváme se dvěma extrémy:
rychlost šíření elektromagnetického pole a rychlost pohybu
elektronů ve vodičích. Notoricky známá je zkušenost, že
když zapneme vypinač, žárovky vzdálené mnoho metrů (i kilometrů - městské osvětlení) se okamžitě rozsvítí. Nebo
telefonické spojení i na velké vzdálenosti se okamžitě
naváže (neuvažeme zde složité
retranslační spoje).
Takže někdo by z toho mohl vyvodit závěr, že elektrony se ve
vodiči pohybují vysokou rychlostí. Tento závěr by byl zcela
mylný.
Elektrony se sice ve vodiči, i
bez zapnutého elektrického obvodu, pohybují za pokojové
teploty značně vysokými rychlostmi řádově tisíce km/s.,
avšak jsou to jen mikroskopické zcela chaotické tepelné
pohyby, které v celkovém součtu nevytvářejí žádný
elektrický proud. Když na vodič přiložíme napětí, kromě
svého chaotického pohybu se začnou pomalu posunovat jedním
směrem, ke kladnému napětí - tzv. driftový pohyb. Rychlost
tohoto pohybu je však velmi malá, řádově milimetry/sekundu.
Jak to, že se tedy vzdálená žárovka okamžitě rozsvítí?
Při zapnutí vypinače se totiž téměř okamžitě začnou
posouvat elektrony po celé délce spojovacího vodiče a
žárovka se tím okamžitě rozsvítí. Ten prakticky okamžitý
efekt je způsoben rychlostí šíření elektromagnetického
pole podél vodiče, která je blízká rychlosti světla (viz
níže "Rychlost šíření
elektromagnetického signálu"). Tedy "hlemýždi
aktivovaní rychlostí světla"....
Pohyb elektrických nábojů v
prostoru a čase se v teorii pole obecně popisuje pomocí
hustoty proudu j(x,y,z,t) ş r.v, kde v je okamžitá rychlost pohybu
nábojů v daném místě (x,y,z); elektrický proud
protékající danou plochou S pak je I = Sňň
j
dS. Zákon zachování
elektrického náboje pak říká, že změna náboje
obsaženého v každé dané prostorové oblasti V
musí být rovna množství náboje, které projde uzavřenou
plochou S = ¶V obklopující tuto oblast :
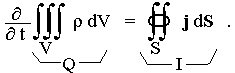 |
(1.31a) |
Použitím Gaussovy věty odtud plyne známá rovnice kontinuity
| div j + ¶r / ¶t = 0 , | (1.31b) |
vyjadřující zákon zachování elektrického náboje v diferenciálním tvaru.
Coulombův zákon buzení
elektrického pole náboji
Fundamentálním zákonem elektřiny je Coulombův
zákon
buzení elektrického pole elektrickými náboji (v předchozím §1.4 jsme jej uvedli pod číslem
(1.20b)) :
| q l . q 2 Fel = - k . ------------ . r° , r2 |
(1.20b) |
| Fel = - k . q1 .q2 /r2 . r° , | (1.20b) |
který vyjadřuje
vzájemné silové působení dvou (bodových) elektrických nábojů q1 a q2 umístěných ve vakuu ve
vzdálenosti r od sebe (r° je jednotkový polohový vektor
obou nábojů vůči sobě). Znaménko "-" vyjadřuje
skutečnost, že stejnojménné náboje (stejné polarity) se
odpuzují. Hodnota konstanty k závisí na použité soustavě
jednotek. Ve fundamentální fyzice se pokládá k=1 (čímž se přirozeně definuje jednotka elektrického
náboje pomocí jeho silového působení na jednotkovou
vzdálenost *), v soustavě SI je k = ~8,988×109 N m2 C-2 a jednotkou elektrického
náboje je 1 Coulomb (C).
*) Historický vývoj fyziky však bohužel
vedl k tomu, že v soustavě jednotek SI není náboj primárně
kvantifikován pomocí svých elektrických silových účinků,
ale až zprostředkovaně pomocí magnetických účinků
elektrického proudu (jednotka proudu Ampér; jeden Coulomb
je pak definován jako 1A/1s).
V soustavě SI se Coulombův zákon zapisuje ve
tvaru s koeficientem k = 1/4pe0 :
| Fel = - 1/4pe0 . q1 .q2 /r2 . r° , | (1.20b) | S I |
kde e0 je permitivita
vakua e0 = ~8,854×10-12 F .
m-1 . Permitivita látkových prostředí bude diskutována
níže - "Coulombův zákon v látkovém prostředí".
Etymolog: Lat. permittere
= přeposlat, povolit - nakolik látkové prostředí
umožní proniknout elektrickým silám.
Pro silové působení v prostoru
"na dálku" se ve fyzice zavádí
pojem fyzikální pole, což je prostor, v němž na (zkušební)
částice působí síly daného druhu. V elektřině je
to elektrické pole buzené elektrickými náboji (a též elektromagnetickou indukcí). Pokud se elektrické náboje
nepohybují, jedná se o elektrostatické
pole které kvantifikujeme
vektorem elektrické intenzity Eel, což je síla působící na jednotkový
zkušební náboj q, tj.
| Fel = q . Eel . |
Elektrická síla a
intenzita Eel je obecně funkcí
místa - souřadnic ve studovaném prostoru. Pro stručnost
zápisu budeme místo jednotlivých souřadnic x,y,z používat polohový vektor r (radiusvektor) - spojnici počátku soustavy
souřadnic a vyšetřovaného bodu, kde se nachází např.
náboj nebo tam stanovujeme intenzity E(r) a potenciály j(r) polí.
Vedle intenzity Eel se v elektrickém poli zavádí i elektrický potenciál j(r). Je to skalární veličina popisující
potenciální energii elektrického náboje v
elektrickém poli - množství práce potřebné k přenesení
jednotkového elektrického náboje z referenčního
(vztažného) místa, kde se potenciál pokládá za nulový, do
daného místa r v elektrickém poli. Za
referenční bod s nulovým potenciálem se obvykle bere místo
nekonečně vzdálené od soustavy nábojů, kde již nepůsobí
žádné elektrické pole (aspoň limitně); v praxi
se bere povrch Země (uzemnění). Potenciál j elektrického pole souvisí s jeho
intenzitou E vztahem
| Eel = - grad j(r) , |
kde grad f = [¶f/¶x, ¶f/¶y, ¶f/¶z] je vektorový diferenciální
operátor kvantifikující "prudkost spádu" - gradient - skalárního pole f ve směru souřadnic x,y,z.
Rozdíl potenciálů dvou bodů
udává elektrické napětí U mezi těmito dvěma místy,
jehož jednotkou je 1 volt [V]. Napětí 1
Volt je takové, že
k jeho překonání bodovým nábojem 1 Coulombu je potřeba vykonat (nebo se uvolní - v závislosti na polaritě) práci 1 Joulu. Napětí U
mezi dvěma místy r1 a r2 v elektrickém poli o intenziě E(r) je dáno rozdílem
| Ur1,r2 = j(r2) - j(r1) = r1ňr2 E(r) . dl |
(integruje se podél spojnice "l"
mezi oběma místy).
Elektrické napětí se v praxi kvantifikuje ani ne tak pro
různá místa v prostoru, ale mezi elektrodami na něž je přivedeno z
určitého zdroje. Při přemístění náboje q
mezi místy s rozdílem napětí U se vykoná (či uvolní) práce
W = q . U.
Coulombův zákon je pak možno
vyjádřit prostřednictvím intenzity elektrického pole Eel (index "el" budeme v dalším již
vynechávat) buzeného v prostoru kolem
bodového elektrického náboje Q :
| E (r) = k . Q / r2 . r° . | (1.20c) |
Buzený elektrický potenciál zde pak je
| j (r) = k . Q / | r | . | (1.20d) |
Potenciál závisí jen na vzdálenosti |r|, nikoli
na směru vzhledem k budicímu náboji Q.
V praxi se elektrické pole nechává budit většinou
nikoli náhodně rozmístěnými elektrickými náboji, ale elektrodami
na něž je přivedeno elektrické napětí [V] z vhodného
zdroje, kterým může být galvanický článek,
elektro-mechanický generátor, elektronický obvod či jiné
konfigurace přístrojové nebo materiální.
Elektrické
pole v látkovém prostředí
Coulombův zákon ve tvaru (1.20b,c,d)
platí nejen ve vakuu, ale i v elektricky homogenním a izotropním látkovém prostředí, v izolantu často zvaném dielektrikum :
| Fel = - 1/4pe . q1 .q2 /r2 . r° , | (1.20b´) | S I |
přičemž konstanta
úměrnosti k se vyjadřuje ve tvaru k = 1/4pe, kde e je permitivita
(dielektrická
konstanta) daného látkového prostředí.
Permitivita vakua je e0 = ~8,854×10-12 F .
m-1 .
Název
"izolant" a "dielektrikum" se někdy
terminologicky rozlišuje (dielektrikum je izolant v němž
dochází k polarizaci částic). Vzhledem k atomové struktuře
všech známých látek vždy dochází k polarizaci atomů a
molekul, takže z fyzikálního hlediska je terminologický
rozdíl bezpředmětný.
Jsou v zásadě dva druhy dielektrik. Buď je látka
složena z polárních atomů či molekul -
permanentních dipólů, které se vlivem vnějšího
elektrického pole natáčejí do směru pole. Nebo je látka
složena z původně nepolárních částic, které jsou ale polarizovatelné
vlivem vnějšího pole. V obou případech při vložení do
elektrického pole dojde k polarizaci, přičemž polarizované
dipóly působí proti vnějšímu poli a polarizace snižuje
výslednou intenzitu E elektrického pole v
dielektriku ve srovnání s polem ve vakuu.
Způsob, jakým vzniká elektrická polarizace a
magnetizace atomů a molekul látkového prostředí a jak se
projevuje na intenzitách výsledného elektrického a
magnetického pole, je názorně ukázán v §1.1, psáži "Elektromagnetické a optické vlastnosti látek" monografie "Jaderná
fyzika a fyzika ionizujícího záření".
Permitivita látek e se často kvantifikuje pomocí relativní
permitivity er = e/e0 vzhledem k vakuu, zvané též dielektrická
konstanta. Udává, kolikrát se elektrická síla mezi
náboji zmenší, když jsou místo vakua umístěny v daném
prostředí (zároveň udává, kolikrát
se zvýší kapacita kondenzátoru, když se mezi deskové
elektrody vloží dielektrikum). Pro vakuum
je samozřejmě er = 1, pro vzduch a
jiné zředěné plyny je též blízká 1. Pro dřevo a
lisovaný papír je er ~2-2,5 , plexisklo cca 3,5 , vodní led 4,8 , diamant 5,5 , pro vodu er =80 (je to polární sloučenina).
Pro naši teoretickou analýzu podstaty elektrických
jevů zde nepotřebujeme zavádět veličinu D =e . E
zvanou elektrická indukce. Použijeme ji jen níže pro
formulaci Maxwellových rovnic v látkovém prostředí
(1.38´-41´).
Ve vakuu je závislost mezi velikostí elektrických
nábojů a buzeným elektrickým polem přesně lineární
(přímá úměrnost) s koeficientem 1/4pe0
až do kolosálně vysokých intenzit cca 1012
Volt/mikrometr.
Je omezena až na kvantové úrovni (stručná
diskuse "Jaké nejsilnější může být elektrické pole?"). V
dielektrickém látkovém prostředí za běžných situací je
tato linearita zachována též, jen s poněkud nižším
koeficientem 1/4pe. Linearita zde může být
narušena až pro velmi silné elektrické pole, kdy se může
projevit fenomén elektrické
pevnosti dielektrika :
Při vysoké hodnotě intenzity elektrického pole
může nastat porušení izolačních schopnosti dielektrika - dojít k elektrickému průrazu
a lavinovitému průchodu velkého množství nabitých
částic (většinou elektronů), k přeskoku jiskry
mezi elektrodami opačné polariry. Působením silného
elektrického pole se uvolňují původně vázané elektrony a
mohou se urychlit natolik, že při srážkách s neutrálními
atomy a molekulami jsou vyráženy další a další elektrony,
čímž během řádově nanosekund vznikne lavinovitý proud,
elektrický průraz. Pokud jsou elektrody napájeny z
"tvrdšího" elektrického zdroje většího výkonu,
může v místě průrazu vzniknout trvalejší výboj -
elektrický oblouk, s tepelnými účinky roztavení či
vznícení materiálu. Hodnota průrazného napětí
[kV/mm] záleží především na druhu izolačního
(dielektrického) materiálu, ale i na konfiguraci elektrod, na
případném obsahu nečistot, mikroskopických dislokací a
volných elektronů či iontů, které bývají i v izolantech ve
stopovém množství obsaženy. Pro vzduch činí cca 2-3 kV/mm,
pro sklo a porcelán cca 10-30, pro PVC 30-50, polyetylen cca
100, pro polyester až 180 kV/mm.
Vedle klasických dielektrik, u nichž dochází k
polarizaci vlivem vnějšího elektrického pole a po jeho
anulování polarizace vymizí, se ojediněle vyskytuje několik
materiálů, které mohou být trvale polarizované i po
odstranění vnějšího elektrického pole - tzv. elektrety,
elektrické analogie permanentních magnetů. Základní způsob
vzniku elektretu spočívá ve třech krocích: 1.
Roztavení vhodné dielektrické látky, např. parafinu
nebo pryskyřice. 2. Vložení roztavené látky
do silného elektrického pole - mezi elektrody na něž
se připojí vysoké napětí několik kilovoltů/cm. Zde dojde k
polarizaci atomů či molekul uvnitř roztavené látky. 3.
Nechat v tomto elektrickém poli ochladit a ztuhnout
roztavenou látku. Zpolarizované molekuly ve ztuhnuté látce
ztratí pohyblivost ("zamrznou") a zachovají si svou polarizaci i po vypnutí
elektrického pole. V okolí elektretu pak bude trvale působit
elektrostatické pole. Slabé elektrety se přirozeně vyskytují
i v přírodě, především v různých formách oxidu
křemíku. Pro uměle vyráběné elektrety jsou vhodné
některé snadno tavitelné dielektrické materiály jako je
parafin (vosk), pryskyřice, polymerované plastické hmoty jako
jsou fluoropolymery, polypropylen, PET, PTFE, dále síra, ......
Vedle termálního způsobu se elektrety nověji
připravují i koronovým výbojem, ozařováním
tenkých vrstev měkkým X-zářením, injektováním
elektronů pomocí urychlovače. Elektrety se používají
elektromechanicky v malých elektretových mikrofonech, ve
snímačích senzorů v monitorech pohybů a deformací,
filtračních médiích vzduchu, xerografii, paměťových
přístrojích, integrálních detektorech ionizujícího
záření (zvláště při měření
koncentrace radonu)...
Z hlediska teorie pole Coulombův
zákon lze vyjádřit ve tvaru Gaussovy
věty elektrostatiky (obr.1.3a)
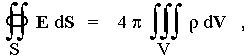 |
(1.32a) |
odkud plyne diferenciální rovnice
| div E = 4p r . | (1.32b) |
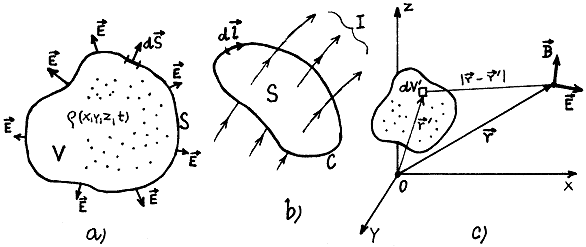
Obr.1.3. Buzení elektrického a magnetického pole elektrickými
náboji a proudy.
a) Celkový
elektrický náboj Q obsažený v prostoru uvnitř libovolné
uzavřené plochy S je
podle Gaussovy věty dán tokem vektoru intenzity elektrického
pole E přes tuto
uzavřenou plochu S.
b) Cirkulace vektoru magnetické indukce B kolem uzavřené křivky C
je úměrná celkovému elektrickému proudu I
protékajícímu plochou S
ohraničenou křivkou C.
c)
Elektromagnetické pole buzené soustavou pohybujících se
elektrických nábojů je dáno rozložením nábojů a proudů, retardovaným vždy o čas potřebný
poli k překonání vzdálenosti r - r' z jednotlivých míst dV' soustavy do
vyšetřovaného místa r.
V přírodě i v elektronických aplikacích
mohou vznikat silná elektrická pole pod napětím mnoha
milionů voltů. Pro zajímavost si můžeme uvést drobnou
diskusi, jaké nejsilnější elektrické pole může být
dosaženo? :
Jaké
nejsilnější může být elektrické pole ?
V rámci klasické (nekvantové) fyziky může být elektrické
pole ve vakuu libovolně silné, až téměř k nekonečnu (v látkovém prostředí je to však omezeno
elektrickou pevností dielektrika). Z
hlediska kvantové elektrodynamiky však i ve vakuu
existuje principiální omezení, způsobené existencí
vzájemných antičástic elektronu a pozitronu:
nelze vytvořit elektrické pole o intenzitě silnější než Ee-e+ = me2c3/e.h = 1,32.1016 V/cm, kde me je klidová hmotnost
elektronu či pozitronu. Při překročení této intenzity je
totiž gradient potenciálu vyšší než prahová energie 2mec2 a dochází ke vzniku dvojice elektronu a
pozitronu, která intenzitu elektrického pole
automaticky zredukuje. Tak silné elektrické pole se zatím
nepodařilo vytvořit, klasickou elektronikou to není možné;
určitou možností v budoucnosti by mohly být silné impulsy z
extrémně výkoných laserů...
Na konci §1.6, v pasáži "Nelineární elektrodynamika", bude diskutován ryze teoretický model
klasické relativistické nelineární elektrodynamiky.
Buzení magnetického pole
Vedle elektrických sil působících i mezi
nepohybujícími se náboji, existují v oblasti elektřiny i magnetické
síly působící jen mezi pohybujícími se
náboji. Prostor ve kterém tyto síly působí se nazývá magnetické
pole. Pohybuje-li se v tomto prostoru elektrický náboj
q rychlostí v, působí na něj
síla
| Fmag = q . [ v x B ] , | (1.30b) |
kde B je intenzita
magnetického pole (z historických důvodů
nazývaná magnetická indukce) v daném místě; "x" znamená vektorový součin.
Nazývá se Lorentzova síla. Tato síla je kolmá ke směru rychlosti v částice. Jednotkou magnetické
indukce B v soustavě SI je 1
Tesla: V
homogenním magnetickém poli o intenzitě (indukci) 1 Tesla
působí na lineární vodič délky 1 metr, natažený kolmo k
magnetickým siločárám a protékaný konstantním proudem 1
Ampér, síla 1 Newton. V systému CGS je jednotkou magnetické
indukce l Gauss = 10-4
Tesla.
Magnetické pole B je buzeno pohybujícími
se elektrickými náboji, tj. elektrickým proudem,
podle Biotova-Savartova-Laplaceova zákona. Základní
tvar pro bodový elektrický náboj Q, pohybující se
rychlostí v udává, jak silné
magnetické pole B bude budit ve vzdálenosti r
- v místě s polohovým vektorem r = r . r0 :
| B (r) = k . Q . [v x r0] / r 2 . | (1.33a) |
Biot-Savartův zákon se většinou formuluje v diferenciálním tvaru pro elektrický proud protékající lineárním vodičem :
| d B = k . I . [dl x r0] / r 2 , | (1.33b) |
kde dl je element délky vodiče jímž protéká stacionární elektrický proud I , r vzdálenost měřeného místa a r° je jednotkový polohový vektor směřující od tohoto proudového elementu do vyšetřovaného místa ("x" je vektorový součin). Hodnota konstanty k závisí na použité soustavě jednotek. Ve fundamentální fyzice se pokládá k=1, v soustavě SI je k= m0/4p, kde koeficient m0 je permeabilita vakua, v jednotkách SI je m0 = ~1,257×10-6 N . A-1 :
| B (r) = m0/4p . Q . [v x r0] / r 2 . | (1.33a) | S I |
| d B = m0/4p . I . [dl x r0] / r 2 , | (1.33b) | S I |
Etymolog.: Lat. permeare
= procházet, propouštět - zde vlastnost látky propouštět či
zesilovat magnetické pole.
Permitivita e0 a permeabilita m0 souvisejí s rychlostí světla c ve vakuu vztahem c = 1/Ö(e0.m0), jak bude ukázáno v části
"Elektromagnetické vlny". Ze srovnání vztahů
(1.30b) s (1.33a,b) vidíme, že magnetismus je nerozlučně
svázán s dynamikou pohybu
elektrických nábojů: Magnetické pole silově působí na
pohybující se náboje a zároveň je vytvářeno pohybem
nábojů. Ze vztahu (1.34a,b) je pak vidět, že magnetické pole
může vznikat i časově proměnným
elektrickým polem.
Magnetické pole v látkovém
prostředí
Biot-Savart-Laplaceův zákon buzení
magnetického pole ve tvaru (1.33a,b) platí nejen ve vakuu, ale
i v homogenním a
izotropním látkovém prostředí,
přičemž permeabilita vakua m0 je nahrazena
magnetickou permeabilitou daného materiálu
m.
Většina látek (plyny, voda, dia- a paramagnetické kovy jako jsou
měď, hliník, zlato, .... ) mají permeabilitu m téměř rovnou m0; pouze
feromagnetické kovy železo, kobalt, nikl a jejich slitiny mají
permeabilitu řádově 100× až 100000-krát vyšší.
Pro materiály se zavádí relativní permeabilita mr = m / m0 ve srovnání s vakuem, podle jejíž
hodnoty se materiály rozdělují do 3 kategorií :
-> Diamagnetické mr < 1, které magnetické pole
mírně zeslabují. Vnitřní slupky v atomovém obalu jsou plně
obsazeny elektrony, orbitální a spinové momenty jsou zcela
vykompenzovány, výsledné magnetické momenty atomů jsou
nulové. Při vzbuzení magnetického pole se v materiálu
indukuje slabý magnetický moment působící proti vnějšímu magnetickému poli. Jsou to
některé kovy jako je měď, stříbro, zlato, rtuť, většina
organických látek, voda, inertní plyny.
-> Paramagnetické mr > 1, které magnetické pole
mírně zesilují. Vnitřní slupky v atomovém obalu nejsou
plně obsazeny elektrony, magnetické momenty atomů nejsou
nulové, ale jsou nepravidelně orientované všemi směry. Po
vybuzení vnějšího magnetického pole se momenty atomů
orientují do směru vnějšího pole, což mírně zesílí výsledné magnetické pole. Jsou to
např. kovy hliník, hořčík, chrom, platina ...
-> Feromagnetické mr >> 1, které magnetické pole
výrazně zesilují. Je to způsobeno tím, že v těchto
látkách jsou přítomny spontánně vznikající magnetické domény velikosti ~10-4-10-2 cm obsahující cca 1012-1018 atomů, které mají uvnitř
své magnetické momenty shodně orientované. Bez přítomnosti
vnějšího magnetického pole jsou směry jednotlivých domén
chaoticky orientované, takže výsledný magnetický moment je
nulový (výjiimkou jsou permanentní
magnety). Stačí
však vybudit poměrně slabé magnetické pole, aby se
magnetické momenty domén částečně zorientovaly do směru
vnějšího pole, což vede ke značnému
zesílení
vnějšího magnetického pole. Feromagnetismus vykazuje
především železo, kobalt, nikl, gadolinium, rutenium a jejich
slitiny (jako je permalloy 20% Fe,
80% Ni - mr~100 000; suprrmalloy
20% Fe, 75% Ni, 5% Mo - mr~800 000). Feromagnetické vlastnosti
fungují jen při doatatečně nízkých teplotách. Při
teplotách vyšších než tzv. Curieův
bod magnetické
domény zanikají a materiál přechází z feromagnetického do
paramagnetického stavu. Pro železo je Curieova teplota 1040 oC, pro
neodymové magnety jen cca 70-120 oC.
Při velmi silných vnějších
magnetických polích však jsou již téměř všechny
magnetické domény natočeny do směru pole a další
zvyšování jeho intenzity již vede jen k mírnějšímu
paramagnetickému zesilování. Feromagnetické zesilování mr vnějšího pole je tedy závislé na intenzitě vnějšího pole, jeví stav nasycení.
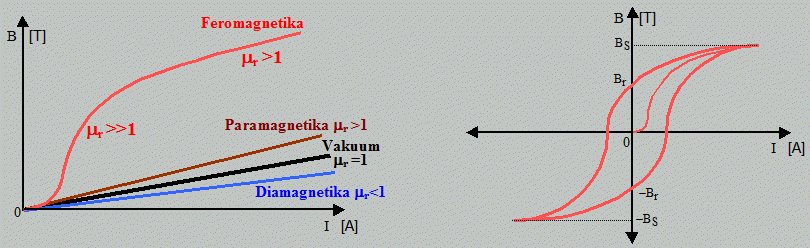 |
| Vlevo: Magnetizační závislosti pro základní kategorie látek. Vpravo: Hysteresní smyčka feromagnetika. |
Magnetizační charakteristiky -
závislosti výsledné magnetické indukce na intenzitě buzení
- jsou pro dia- a paramagnetické materiály lineární
přímky, protože jejich mr je konstantní. Pro feromagnetické materiály to již
není přímka, neboť jejich mr se v průběhu
magnetizace mění v závislosti na intenzitě magnetického
pole. Manifestuje se zde složitější nelineární
magnetizační charakteristika, vykazující stav nasycení
BS.
U řady feromagnetických materiálů se navíc
projevuje zvláštní dynamické "paměťové"
chování tzv. hysterese - nevratnost
magnetizačních procesů . Když vybudíme dostatečně silnou
magnetizaci, při opětovném snižování buzeného
magnetického pole se pak výsledná křivka magnetizace nevrací
po stejné funkční závislosti jako předtím při
zvyšování, ale má poněkud vyšší hodnoty než předtím.
Když intenzita magnetického buzení klesne na nulu, zůstane
určitá nenulová remanentní magnetická indukce Br,
kterou si materiál podrží (cca 0,1-1 T). Část magnetických
domén zůstává orientovaná. Ke zrušení remanentní
magnetizace je potřeba aplikovat určitou koercitivní
magnetizaci opačného směru, jejíž další zvyšování pak
vede k magnetizační křivce opačné polarity, vykazující
rovněž stav nasycení -BS. Při střídavé
magnetizací v opačných polaritách vzniká uzavřená křivka,
zvaná hysteresní smyčka.
Podle šířky hysteresní smyčky se feromagnetické
materiály dělí na dvě kategorie :
--» Magneticky měkké mají úzkou hysteresní
křivku s nízkou hodnotou Br , takže po
zrušení vnějšího magnetického pole jejich vlastní
magnetické pole také prakticky zaniká. Tuto
vlastnost má čisté železo (s nízkým
obsahem uhlíku <0,1%), permalloy.... ..
......
--» Magneticky
tvrdé s
širokou hysteresní smyčkou a velkou hodnotu Br . Po zrušení vnějšího
magnetického pole zůstávají nadále zmagnetovány a chovají
se jako permanentní magnet. Jejich magnetické pole lze
zrušit pomocí vnějšího magnetického pole opačné polarity.
Takto se chová železo-ocel s velkým obsahem uhlíku, ocel
wolframová, chromová a kobaltová. Nejsilnější permanentní
magnety se připravují z prvků vzácných zemin samaria
(Sm-Co-5, Sm-2-Co-17) a neodymu (Fe-Nd-B). Dosahují vysokých
hodnot remanence Br ~ 0,8-1,4
Tesla.
Pro naši teoretickou analýzu podstaty magnetických
jevů zde nepotřebujeme zavádět veličinu H =
e . B
zvanou magnetická intenzita. Použijeme ji jen níže
pro formulaci Maxwellových rovnic v látkovém prostředí
(1.38´-41´).
Z Biotova-Savartova zákona
(1.33b) plyne Ampérův zákon
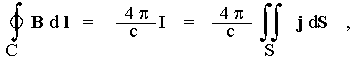 |
(1.33c) |
podle něhož křivkový integrál (cirkulace) vektoru magnetické indukce po libovolné uzavřené křivce C je úměrný celkovému proudu protékajícímu plochou S, kterou tato křivka obepíná (obr.1.3b).
Integrál na levé straně Ampérova zákona závisí jen na křivce C = ¶S, takže aby rovnice (1.33b) mohla obecně platit, je třeba aby plošný integrál na pravé straně byl stejný pro všechny plochy S mající za konturu danou křivku C. S pomocí Gaussovy věty lze snadno ukázat, že toto je splněno jen tehdy, když div j = 0, tj. když se jedná o stacionární elektrický proud, který nezpůsobuje změny v rozložení elektrického náboje v okolí křivky C. Pro obecné nestacionární proudy je proto třeba rovnici (1.33b) zobecnit, aby byla slučitelná s rovnicí kontinuity. Dosazením v rovnici kontinuity (1.31b), která platí i pro nestacionární proudy, za r z rovnice (1.32b), dostaneme
div [ j + (1/4p) ¶E/¶t ] = 0 .
Tím je nalezen vektor j + 1/4p¶E/¶t, jehož divergence je vždy rovna nule a který ve stacionárním případě splývá s běžnou hustotou "vodivého" proudu j. Člen jMaxw = (1/4p) ¶E/¶t se nazývá Maxwellův posuvný proud a může existovat i ve vakuu bez přítomnosti skutečných elektrických nábojů. Maxwell navrhl v případě nestacionárního pole v rovnici (1.33b) proudovou hustotu j nahradit právě vektorem j + (1/4p) ¶E/¶t , neboli vyslovil hypothézu, že posuvný proud vykazuje stejné magnetické účinky jako běžný "vodivý" proud skutečných elektrických nábojů :
| (1.34a) |
Magnetické pole je tedy buzeno celkovým efektivním proudem
| Ief = ňň j dS
+ ňň (1/4p) ¶E/¶t dS . vodivý proud Maxwellův posuvný proud |
(1.35) |
Maxwellova hypothéza se ukázala být velmi správná a plně
odpovídá všem zkušenostem s elektromagnetickými jevy.
Maxwellův posuvný proud je např. tím proudem, který
"překonává" izolační vrstvu kondenzátorů a
způsobuje jejich "vodivost" pro střídavé proudy.
Máme-li totiž rovinný kondenzátor s
plochou desek S, pak mezi intenzitou homogenního
elektrického pole v mezeře a nábojem kondenzátoru q platí
vztah E = 4pq/S, takže okamžitý proud
protékající kondenzátorem I = ¶q/¶t = S.(1/4p) ¶E/¶t = S.jMaxw je dán
Maxwellovým proudem.
Posuvný proud, který - i když není
tvořen pohybem skutečných elektrických nábojů - má
normální magnetické účinky, nachází svou analogii i v
gravitačním poli, kde i ve vakuu bez skutečných
materiálních těles existuje efektivní Isaacsonova
energie a hybnost gravitačních vln, která má
gravitační účinky (zakřivuje prostoročas) jako každá
jiná hmota (viz §2.7 a 2.8).
Převedením integrálu podél křivky C pomocí Stokesovy věty na integrál přes plochu S, obepínanou touto křivkou, dostáváme rovnici buzení magnetického pole elektrickým proudem (vodivým a posuvným) v diferenciálním tvaru
| rot B = (4p/c) j + (1/c) ¶E/¶t . | (1.34.b) |
Z této rovnice je jasně vidět, že
magnetické pole může vznikat nejen pohybem (proudem)
elektrických nábojů, ale též časově
proměnným elektrickým polem.
Pozn.: Všimněme si
koeficientu 1/c = 3,33×10-9
s/m ve
všech vztazích (1.33)-(1.34) mezi intenzitou magnetického pole
B, proudem I, j a elektrickým
polem E. Velmi nízká hodnota tohoto
koeficientu je odrazem skutečnosti, že magnetické pole
vznikajíci pohybem nábojů či elektromagnetickou indukcí je
obecně velmi slabé ve srovnání s
polem elektrickým (buzeným
stejnojmennými náboji). Pro
elektromagnetické vlny je tato skutečnost letmo diskutována
níže v pasáži "Méně známé vlastnosti
elektromagnetických vln".
Silné magnetické pole desítky Tesla
lze laboratorně vytvořit při průchodu silného proudu
několik tisíc Ampér elektromagnetickými cívkami, většinou
supravodivými (§1.5, část "Elektromagnety v urychlovačích" a §1.3, část "Tokamak"). Ve vesmíru vznikají mohutná magnetická pole
při gravitačním smršťování a kolapsu kompaktních
stelárních objektů bílých trpaslíků a neutronovývh
hvězd, kdy zrychlováním rotace při zákonu
zachování momentu hybnosti se enormně zahustí magnetické
siločáry a magnetické pole může vzrůst na obrovské hodnoty
až ~108-1012 Tesla (§4.2, část
"Astrofyzikální význam supernov").
Dalším základním zákonem elektromagnetismu je poznatek, že magnetické siločáry jsou spojité a uzavřené křivky. Jinými slovy, magnetické pole je nezřídlové, neexistují magnetické "náboje" (monopóly)*) z nichž by vycházely nebo do nichž by vstupovaly magnetické siločáry (na rozdíl od elektrických nábojů na nichž začínají a končí elektrické siločáry). Proto z uzavřené plochy S musí vycházet právě tolik magnetických siločar, kolik jich do ní vchází, tj. magnetický tok z uzavřené plochy se rovná nule :
 |
(1.36a) |
Převedením plošného integrálu na objemový pomocí Gaussovy věty dostáváme rovnici
| div B = 0 , | (1.36b) |
která je matematickým
vyjádřením principu kontinuity magnetických siločar v
diferenciálním tvaru.
---------------------------
*) Necháváme zde stranou
Diracovu hypothézu magnetických monopólů, vycházející z formálního požadavku
symetrie rovnic elektrodynamiky. Experimenty snažící se
nalézt magnetické monopóly zatím nevedly k žádným
výsledkům. Magnetické monopóly se však uvažují v
kvantových unitárních teoriích pole a diskutuje se i jejich
případný význam pro kosmologii velmi raného vesmíru (§5.5
"Mikrofyzika a kosmologie. Inflační vesmír.").
Elektromagnetická indukce
Generace elektrického pole časově proměnným magnetickým
polem je vyjádřena Faradayovým zákonem elektromagnetické
indukce
 |
(1.37a) |
podle něhož elektromotorická síla (elektrické napětí) U ş ˇňC E dl indukovaná podél uzavřené křivky C je úměrná rychlosti, s jakou se mění magnetický tok F ş ňňSB dS plochou S obepínanou touto křivkou C. V integrálu na pravé straně nezáleží na volbě plochy S obepínané danou křivkou C, protože magnetické pole je nezřídlové (div B = 0). Převedením křivkového integrálu na levé straně pomocí Stokesovy věty na plošný integrál dostaneme zákon elektromagnetické indukce vyjádřený v diferenciálním tvaru :
| rot E = - (1/c) ¶B/¶t . | (1.37b) |
Maxwellovy
rovnice
Nastíněnou aplikaci matematického aparátu diferenciálního a
integrálního počtu na empiricky zjištěné zákonitosti
elektromagnetismu (tj. na poznatky Coulombovy, Ampérovy,
Faradayovy, Biotovy, Savartovy aj.) a jejich zobecnění provedl
J.C.Maxwell, který dospěl k úplné
soustavě základních rovnic elektromagnetického pole a shrnul
jednotlivé poznatky do ucelené teorie. Své veledůležité
rovnice J.C.Maxwell zformuloval v r. 1865 nejpve v souřadnicovém tvaru složek x,y,z elektrického E a
magnetického B pole a proudové hustoty j. Vznikla tím
značně složitá soustava více nečž 20 rovnic (někdy se zmiňuje i složitější tzv. tetrádový
formalismus, který byl však záhy opuštěn). Do kompaktního vektorového tvaru (1.38)-(1.41) je v r. 1884
přeformuloval O.Heaviside.
Tyto Maxwellovy
rovnice (1.31b)
až (1.37b), které jsme si výše postupně odvodili, můžeme v
diferenciálním tvaru přehledně shrnout takto :
| Maxwellovy rovnice elektromagnetického pole |
 |
(1.38) |
| (1.39) | |
| (1.40) | |
| (1.41) |
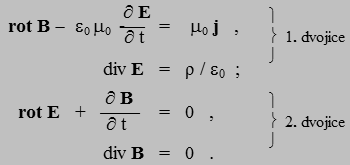 |
(1.38) | S I |
| (1.39) | ||
| (1.40) | ||
| (1.41) |
Tyto rovnice určují
elektrické E a magnetické B pole buzené daným rozložením
nábojů r a proudů j.
1.dvojice Maxwellových rovnic popisuje generaci
elektrického a magnetického pole materiálními zdroji, tj.
hustotou elektrického náboje r a proudu j
vystupujícími na pravé straně. 2.dvojice vyjadřuje další
vnitřní vlastnosti pole. Z rovnic (1.38) a (1.40) je vidět,
že elektrické E a magnetické B pole mohou svou časovou
proměnností vzájemně generovat
jedno druhé --> elektrodynamika.
Lagrangián
pro elektromagnetické pole
Maxwellovy rovnice elektromagnetického pole jsme si zde
odvodili fyzikálně - induktivním způsobem z
Coulombova, Biot-Savartova, Ampérova, Faradayova zákona. V
teoretické fyzice se pohybové zákony a rovnice pole často
odvozují deduktivním způsobem pomocí variačního
principu nejmenší akce [165]. Klasický fyzikální
systém se popisuje integrálem akce S
| S = ň L(q1,q2, ...qn,, q.1,q.2,.........q.n) d t.... |
kde L je tzv. Lagrangeova funkce - Lagrangián,
popisující všechny dynamické charakteristiky qi daného systému a
jejich časové derivace q.i, n je počet
stupňů volnosti. Variační
princip nejmenší akce dS = 0 pak vede k
Lagrangeovým rovnicím, z nichž plynou pohybové rovnice či rovnice
pole studovaného systému (podrobněji
v závěru §2.5, pasáž "Variační odvození rovnic
gravitačního pole").
Pro elektromagnetické pole má Lagrangián tvar :
| L = 1/8p (E2-B2) + j.A - r.j . | (1.42) |
Z variačního principu nejmenší akce s lagrangiánrm (1.42) lze odvodit Maxwellovy rovnice (1.38-41).
Elektromagnetické pole v
látkovém prostředí - elektrodynamika kontinua
V našem teoretickém rozboru uvažujeme
elektromagnetické pole především ve vakuu,
které je pro fundamentální fyziku výchozím přirozeným
prostředím. Jen pro úplnost zde letmo nastíníme, jak se
elektromagnetické pole chová v látkových
prostředích (látkovém "kontinuu").
Interakcí elektrického a magnetického pole s atomy a
molekulami látky dochází k jejich elektrické polarizaci
a magnetizaci, což se zpětně projevuje na
vektorech intenzity elektrického a magnetického pole. Způsob,
jakým vzniká elektrická polarizace a magnetizace atomů a
molekul látkového prostředí a jak se projevuje na
intenzitách výsledného elektrického a magnetického pole, je
názorně ukázán v §1.1, psáži "Elektromagnetické a optické vlastnosti látek" monografie "Jaderná
fyzika a fyzika ionizujícího záření".
Pro
kvantifikaci tohoto vlivu látkového prostředí na intenzity
elektrického a magnetického pole se zavádějí dva nové
vektory: indukce elektrického pole D
a intenzita magnetického pole H
(historicky vzniklý zmatek v terminologii
je diskutován níže v poznámce "Intenzita<-->indukce v elektromagnetismu?"). Se základními elektrickými veličinami veličinami E
a B ve vakuu souvisejí vztahy :
| D = e . E , B = m . H , |
kde e je elektrická permitivita látky (zvaná též dielektrická konstanta) popisující zeslabení elektrického pole vlivem
polarizace látky, m je magnetická permeabilita
udávající zesilující či zeslabující efekt magnetizace
látky na magnetické pole.
Maxwellovy
rovnice elektromagnetického pole v látkovém prostředí (elektricky nevodivém) se pak
dají zapsat ve stejném tvaru (1.38-41) jako ve vakuu, ve
kterých jsou však "vakuové" intenzity E
a B na patřičných místech nahrazeny
"látkovými" vektory D a H
-> elektrodynamika kontinua :
 |
(1.38´-41´) |
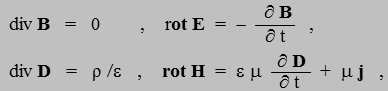 |
(1.38´-41´) | S I |
kde vztahy mezi E a D=E/e , B
a H=B/m obsahují materiálové
koeficienty elektrické permitivity e a
magnetické permeability m. Zahrnují i příp. nehomogenity a nelinearity
polarizace a magnetizace - koeficienty e a m mohou
nabývat proměnných hodnot (na rozdíl od konstant e0 a m0 ve vakuu). V
některých materiálových prostředích a při vysokých
intenzitách polí se proto může projevovat nelineární
elektrodynamika (nemáme zde na
mysli hypotetickou možnost nelineární elektrodynamiky i ve
vakuu pro extrémně silné elektromagnetické pole "Nelineární elektrodynamika").
Zákony
elektrodynamiky kontinua, shrnuté v
Maxwellových rovnicích (1.38´-41´), popisují všechny
elektromagnetické jevy probíhající v látkových
prostředích (viz již zmíněnou
pasáž "Elektromagnetické a optické
vlastnosti látek"). Vlivem interakcí elektrických a magnetických polí
s atomy a molekulami látky se časové změny v polích (viz níže "Retardované potenciály") a elektromagnetické vlny v
látkových prostředích šíří rychlostí c´
nižší než ve vakuu: c´ = 1/Ö(e.m) < c = 1/Ö(eo.mo) = 2,998.108m/s @ 300 000 km/s (u světla to vede ke známým optickým jevům lomu
světelných paprsků při přechodu mezi látkami s různou
"optickou hustotou" - různým indexem lomu
způsobeným různou rychlostí c´).
Terminologická
poznámka: Intenzita <-- > indukce v
elektromagnetismu ?
Pojem intenzita v přírodovědě (i v běžném vyjadřování)
charakterizuje stupeň síly, mohutnosti,
vydatnosti nějakého děje, jevu - zde tedy síly pole.
Intenzita elektrického pole E opravdu
vyjadřuje elektrickou sílu působící v tomto
poli na částici s jednotkovým elektrickým nábojem (ve vhodných jednotkách).
"Intenzita" magnetického pole B by
analogicky měla vyjadřovat magnetickou Lorentzovu sílu (druhý člen v (1.30)) působící
v tomto poli na částici s jednotkovým nábojem, při kolmém
pohybu jednotkovou rychlostí. Veličina B,
popisující skutečně působící magnetickou sílu, se však v
magnetismu nazývá nikoli intenzita, ale magnetická indukce!
A "intenzitou" magnetického pole se nazývá odvozená
veličina H (=B/m)
"korigovaná" na magnetickou permeabilu látkového
prostředí. Přitom v elektrostatice je elektrická indukce
D (=E/e) odvozená veličina
charakterizující elektrické pole s odpočtením vlivu
dielektrické polarizace. Je to tedy opačně...
Toto nešťastné "zkřížení" názvů
"intenzita-indukce" vzniklo během historického
vývoje nauky o elektřině a magnetismu, kdy
magnetismus byl vysvětlován fluidovou teorií,
analogicky jako elektrostatika. A bohužel to tak již
zůstalo... V našich pojednáních budeme proto pod "intenzitou
magnetického pole" často rozumět vektor B
(konvenčně nazývaný magnetická indukce).
Pozn.: Slovo
"indukce" zde charakterizuje
elektrické a magnetické změny v látkách, vyvolané při
jejich vložení do elektromag. polí. Neplést s
elektromagnetickou indukcí (1.37)..!..
Vlastnosti
Maxwellových rovnic
Všimněme si stručně některých obecných vlastností
soustavy Maxwellových rovnic (ve vakuu). Především, z
1.dvojice Maxwellových rovnic dostaneme (aplikací operace
"div" na rovnici (1.38), operace "¶/¶t" na rovnici (1.39) a
jejich sečtením) rovnici kontinuity div j + ¶r/¶t = 0. Rozložení a pohyb elektrických
nábojů nemůže být tedy zadán zcela libovolně; aby byly
Maxwellovy rovnice splnitelné, musí být vyhověno rovnici
kontinuity. Jinými slovy, elektrické náboje kolem sebe budí
elektrické a magnetické pole tak, aby se samy zachovávaly -
rovnice kontinuity je důsledkem
rovnic pole.
Rovnice (1.39) a (1.41) neobsahují
časové derivace a mají proto charakter okrajových podmínek;
zbývající dvě rovnice (1.38) a (1.40), které lze (s
použitím operace "div" na obě strany) upravit na
tvar
¶/¶t (div E - 4pr) = - 4p (div j + ¶r/¶t) = 0 , (rovnice kontinuity)
¶/¶t div B = -c div rot E ş 0 ,
pak zaručují, že jsou-li tyto počáteční podmínky div E = 4pr a div B = 0 splněny v nějakém čase t=0, zůstávají splněny neustále ve všech časech.
Potenciály pole
V teorii pole je výhodné kromě vektorů intenzit daného pole
zavést též potenciály pole, což jsou veličiny
jejichž derivace (diferenciální formy) udávají příslušné
intenzity. V elektrostatice lze intenzitu elektrického pole E vyjádřit jako gradient elektrického potenciálu j (E = -grad j), čímž je identicky splněna rovnice rot E = 0. V magnetismu platí rovnice div
B = 0, takže
musí existovat veličina (vektorové pole) A, taková, že B = rot A. Z druhé dvojice Maxwellových rovnic plyne, že vektory
E a B v případě obecného elektromagnetického
pole lze vyjádřit pomocí veličin j a A ve tvaru
| E = - grad j - (1/c) ¶A/¶t , | (1.43a) |
| B = rot A . | (1.43b) |
Zavedením takového elektrického
potenciálu j a magnetického vektorového potenciálu A jsou obě poslední Maxwellovy
rovnice splněny identicky.
Jelikož intenzity polí závisejí pouze
na derivacích potenciálů, nejsou tyto potenciály určeny
jednoznačně, daným polím E a B mohou odpovídat různé hodnoty
potenciálů. Např. k A lze přičíst libovolný
konstantní vektor a k j libovolnou konstantu, aniž se
změní hodnoty intenzit E a B. Obecně, magnetické pole B = rot A se nezmění, jestliže k A
přičteme gradient libovolné funkce f (rot
grad f ş 0); aby se přitom nezměnilo ani
elektrické pole E (1.43a), je zároveň třeba k
potenciálu j přidat člen -(1/c).¶f/¶t. Provedeme-li tedy tzv. cejchovací (kalibrační) transformaci potenciálů *)
| A ® A' = A + grad f , j ® j' = j - (1/c)¶f/¶t , | (1.44) |
kde f(r,t) je libovolná skalární funkce místa
a času, příslušné elektromagnetické pole se nezmění (E®E'=E, B®B'=B). Tato určitá "svoboda"
ve volbě potenciálů umožňuje vybrat tvar potenciálů
(provést jejich "kalibraci") tak, aby to bylo co
možná nejvýhodnější pro daný problém.
*) Procedura kalibrační
transformace v teorii pole je obecně diskutována v
§B.6, pasáži "Kalibrační (cejchovací)
transformace; kalibrační pole".
Retardované potenciály
Maxwellovy rovnice (1.38) a (1.39), vyjádřené dosazením z
(1.43a,b) pomocí potenciálů, mají obecně značně složitý
tvar
![]()
Tyto rovnice se značně zjednoduší, předepíše-li se pro potenciály tzv. Lorentzova kalibrační podmínka:
| grad A + (1/c) ¶j/¶t = 0 | (1.45) |
(tato podmínka může být splněna transformací (1.44) s funkcí f splňující rovnici Df - (1/c2).¶2f/¶t2 = div A + (1/c).¶j/¶t). Při této kalibraci nabývají Maxwellovy rovnice, vyjádřené pomocí potenciálů, separovaný a symetrický tvar d'Alembertových rovnic
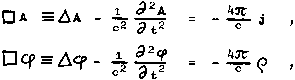 |
(1.46a) (1.46b) |
kde o ş ¶2/¶x2 + ¶2/¶y2 + ¶2/¶z2 - (1/c2)¶2/¶t2 je d'Alembertův diferenciální operátor. V matematické fyzice se ukazuje, že obecné řešení těchto rovnic má tvar *)
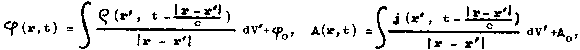 |
(1.47a,b) |
kde r = (x,y,z) je polohový vektor bodu v
němž stanovujeme potenciály, r'= (x',y',z') je polohový vektor
objemového elementu dV'= dx'dy'dz' při integraci hustoty
náboje a proudu, jo
a Ao popisují vnější pole
působící na soustavu (resp. integrační konstanty). Vztahy
(1.47a,b) ukazují, že v daném místě r a v daném časovém okamžiku t je
pole dáno nikoliv okamžitým rozložením náboje a proudu v
celém prostoru, ale rozložením retardovaným (zpožděným do minulosti)
vždy o čas |r - r'|/c, který je potřeba k tomu,
aby se rychlostí c překonala vzdálenost R = |r - r'| z jednotlivých bodů (x',y',z')
zdrojové soustavy do vyšetřovaného místa (x,y,z) - viz
obr.1.3c. Řešení (1.47) se proto nazývá retardované potenciály. Změna (rozruch) v elektromagnetickém
poli (vyvolaná např. změnou v rozložení nábojů) se tedy šíří konečnou rychlostí rovnou
rychlosti světla c.
*) Pozn.: V předchozím §1.4 a v první polovině
tohoto §1.5 jsme plošné a objemové integrály značili
dvojnými a trojnými integrály: ňňSf(...)dS a ňňňVf(...)dV. V dalším však pro
stručnost budeme používat jen jedno integrační znamení: ňSf(...)dS a ňVf(...)dV s uvedením plochy S a
objemu V.
Relativistický elektromagnetismus
V klasické elektrodynamice jsou elektrické a magnetické pole
samostatná oddělená pole, vzájemně související jen
zákonitostmi buzení a indukce, shrnutými v Maxwellových rovnicích. Ve speciální
teorii relativity (pojednané v
následujícím §1.6 "Čtyřrozměrný
prostoročas a speciální teorie relativity"),
vytvořené A.Einsteinem na základě pečlivé analýzy
elektromagnetismu však uvidíme, že rozdělení
elektromagnetických sil na samostatné elektrické a magnetické
není fundamentální, ale může být závislé na vztažné
soustavě. Zjednodušeně řečeno, to co se jeví pozorovateli v
jedné vztažné soustavě s klidovým rozmístěním
elektrických nábojů jako čistě elektrická síla, bude se
pohybujícímu pozorovateli v jiné vztažné soustavě jevit
jako magnetická síla, resp. kombinace elektrických a
magnetických sil.
Je magnetické pole relativistickým
projevem pole elektrického ?
Akcentováním vztahů mezi elektrickým a magnetickým polem a
pohybem nábojů někteří autoři dospěli k názoru, že
magnetické pole jako takové neexistuje samostatně, ale lze ho
považovat za relativistický
projev elektrického pole. Máme-li v jedné vztažné soustavě
systém statických elektrických nábojů, bude zde působit jen
elektrické pole, nebudeme pozorovat žádné magnetické pole.
Avšak pohybující se pozorovatel v jiné vztažné soustavě,
který se bude dívat na tentýž systém nábojů, bude vidět proud nábojů, podle elektrodynamiky budící
magnetické pole - vzniká magnetické pole spojené s pohybem
nábojů - s elektrickým proudem - podle
Biot-Savartova-Laplaceova zákona. Avšak z hlediska STR se
magnetické pole zde objevuje jako "relativistický
produkt" při Lorentzových
transformacích
souřadnic za přítomnosti klidového elektrického pole? Takto
to však lze interpretovat jen v nejjednoduších speciálních
situacích rozložení elektrických nábojů a při
translačném pohybu, jako je pohyb elektronů v lineárním
vodiči. Neplatí to pro rotační pohyby, pro magnetická pole
permanentních magnetů ani pro indukovaná magnetická pole.
Všechny tyto souvislosti jsou však založeny na vzájemném
vztahu elektrického a magnetického pole, vyjádřenému v
Maxwellových rovnicích. Objektivně zde máme elektrické pole produkující sílu nezávislou na pohybu
nábojů a magnetické pole vytvářející sílu v
závislosti na rychlosti pohybu náboje, které spolu koexistují
a vzájemně se ovlivňují a obě jsou nezbytná pro
elektromagnetické působení v přírodě. Obecně tedy magnetické pole nelze vysvětlit jako
relativistický projev pole elektrického !
Relativistická kombinace
elektrických a magnetických sil bude podrobněji analyzována v
§1.6, část "Čtyřrozměrná elektrodynamika", kde elektrické a magnetické pole bude
zkombinováno do 4-tenzoru elektromagnetického pole
2.řádu. Uvidíme, že změnou inerciální vztažné soustavy
se jeho elektrické a magnetické komponenty mísí
- podobně jako speciální teorie relativity mísí prostorové
a časové součadnice v prostororočasu. To je teoretickým
základem relativistického elektromagnetismu.
Elektromagnetické
vlny
Obecné zákonitosti vzniku a
šíření vln v přírodě jsou diskutovány v §2.7, pasáži
"Šíření vln - obecný přírodní
fenomén". Zde si ukážeme vznik
a vlastnosti vlnění v elektromagnetickém poli.
Základní mechanismus vzniku elektromagnetických
vln pomocí pohybu elektrických nábojů byl nastíněn již na
začátku této kapitoly :
Jestliže se elektrické náboje pohybují proměnnou
rychlostí (nerovnoměrně, se
zrychlením či zpomalením), vytvářejí
kolem sebe časově proměnné
elektromagnetické pole, což vede ke vzniku elektromagnetických
vln, které se odpoutávají od svého zdroje a
odnášejí s sebou do prostoru část jeho energie. Při pohybu
nebo časových změnách v magnetickém poli vzniká podle
Faradayova zákona elektromagnetické indukce pole
elektrické; a časové změny pole elektrického vyvolávají
zase pole magnetické. Tak se jedno druhým vzájemně indukují (níže však uvidíme, že toto tvrzení je
zavádějící).
Nerovnoměrným - kmitavým
- pohybem elektrických nábojů (souvisejícím
příp. se střídavým napětím ~U) se
generuje kmitavé elektromagnetické pole, které se šíří do
okolního prostoru rychlostí světla c. Amplituda
kmitání v takto vzniklé elektromagnetické vlně se
vzdáleností kvadraticky klesá. Vlna při svém šíření
obsahuje vzájemně spřaženou a vektorově navzájem kolmou
elektrickou E a magnetickou B
složkou, které jsou zároveň kolmé ke směru šíření
rychlostí světla c :

Pozn.: Často se uvádí, že
podle Maxwellových rovnic (1.38) a (1.40) se ve vlně
elektrické E a magnetické B
pole vzájemně indukují dynamikou jejich proměnnosti
při kmitání. Níže však uvidíme že toto často uváděné
tvrzení je zavádějící. Někdy se můžeme setkat dokonce s
tvrzením, že vzájemné indukování elektrické a magnetické
složky v elektromagnetické vlně způsobuje jejich
šíření prostorem. Není tomu tak - šíření
vlny je způsobeno konečnou rychlostí c šíření
elektromagnetické interakce v prostoru, retardovanými
potenciály (1.47). Vzájemné indukování elektrické a
magnetické složky může jen případně zajišťovat neustále
stejnou strukturu vlny během jejího šíření prostorem. Na
obrázku uprostřed jsme elektrickou E a
magnetickou B složku ve vlně pro názornost
zakreslili se stejnou amplitudou. Ve skutečnosti je však
magnetická složka nesrovnatelně menší než
elektrická - elektromagnetické vlny jsou v praxi vlny
elektrické - je diskutováno níže v pasáži "Méně
známé vlastnosti elektromagnetických vln". Proto "vzájemné indukování" E
a B nemůže ve skutečnosti probíhat...
Když se elektromagnetická
vlna setká s elektrickými náboji, začne je rozkmitávat
v rytmu své frekvence (na obrázku vpravo), slaběji či silněji v závislosti na své amplitudě
(snížené úměrně se vzdáleností od
místa svého vzniku). Na tom je založen
účinek elektromagnetických vln na látkové prostředí,
jakož i jejich laboratorní detekce a radiotechnické
přijímání pro přenos zvukové, obrazové a
digitální-datové informace.
Základní vlastnosti elektromagnetických vln
plynou z Maxwellových rovnic elektromagnetického pole.
Napíšeme-li tedy Maxwellovy rovnice (1.38) a (1.40) pro
vakuovou prostorovou oblast, kde j = 0 a r = 0, pak jejich parciální
derivací podle času a dosazením ze zbývajících dvou
Maxwellových rovnic dostaneme d'Alembertovy
rovnice
| D E - (1/c2) ¶2E/¶t2 = 0 , D B - (1/c2) ¶2B/¶t2 = 0 | (1.48) |
analogické rovnicím (1.46) pro potenciály, avšak bez přítomnosti elektrických nábojů. Jelikož tyto rovnice mají nenulová řešení, může elektromagnetické pole existovat i samostatně, bez přímé vazby na elektrické náboje a proudy. Budeme-li hledat partikulární řešení závislá pouze na jedné souřadnici, např. na. x, a na čase t, zjednoduší se rovnice (1.48) na
¶2E/¶x2 - (1/c2) ¶2E/¶t2 = 0 (a analogicky pro B)
a řešením bude každá funkce tvaru
E = E(x, t - x/c) , B = B(x, t - x/c) .
Stejná hodnota pole E a B jako je v bodě o souřadnici xo
v časovém okamžiku to bude ve všech místech,
jejichž souřadnice a čas splňují rovnici x - xo = c.(t - to). Jedná se tedy o příčné vlnění šířící se ve směru
osy X fázovou rychlostí c,
nezávisle na vlnové délce či frekvenci (to
platí ve vakuu; v látkovém prostředí je rychlost šíření
nižší a bývá poněkud proměnná pro různé frekvence -
efekt disperze světla). Elektromagnetické
pole se ve vlně mění jako funkce vzdálenosti a času.
Z Maxwellových rovnic tak plyne existence elektromagnetických
vln, které se
šíří rychlostí rovnou rychlosti
světla (z obecně-fyzikálního hlediska je rychlost světla
diskutována v §1.1, pasáž "Rychlost světla").
Tento poznatek přivedl Maxwella k názoru, že světlo je zřejmě elektromagnetické vlnění o
velmi krátké vlnové délce. Tím se Maxwellovi podařilo
sjednotit do ucelené teorie nejen jevy elektrické a
magnetické, ale zahrnout tam i jevy optické.
Pozn.: O vzniku a
vlastnostech různých druhů elektromagnetického záření
(radiovlny, infračervené záření, viditelné světlo, UV a
X-záření, záření g) je podrobněji pojednáno např. v §1.1 "Atomy a atomová jádra" , pasáž "Elektromagnetické
pole a záření " pojednání "Jaderná
fyzika a fyzika ionizujícího záření".
Subtilní
vlastnosti elektromagnetických vln
Z dokonale prozkoumaných a ověřených zákonitostí
elektrodynamiky (shrnutých v Maxwellových
rovnicích) jednoznačně vyplývají jen
tři základní vlastnosti elektromagnetických vln:
1.Jsou to příčné vlny (kmitají
kolmo ke směru svého šíření); 2.Vektory
elektrické E a magnetické B
intenzity kmitají neustále kolmo k sobě; 3.Ve
vakuu se šíří rychlostí světla c. Další
"subtinější" vlastnosti již mohou být různé,
v závislosti především na konkrétním způsobu jejich vzniku
a na interakcích s hmotným prostředím. Zmíníme zde
některé subtilnější vlastnosti elektromagnetických
vln (na které se někdy objevují
odlišné názory).
-> Vztah mezi velikostí elektrické E a
magnetické B složky ve vlnách.
V různých ilustracích, obrázcích a diagramech se elektrická
a magnetická složka většinou znázorňuje ve zhruba stejné
velikosti. Ve skutečnosti je to ale úplně jinak. Ze vztahů
(1.33)-(1.34) o buzení magnetického pole náboji a indukcí
plyne, že vlnu o elektrické amplitudě E doprovází
magnetické pole o amplitudě B = E/c. Poměr amplitud
elektrického a magnetického pole ve vlně tedy je
E[V/m] /B[Tesla] = c = 3 × 108
[m/s] .
I značně silné elektromagnetické vlny jsou tedy
doprovázeny jen velmi slabými magnetickými poli (např. poměrně silná vlna o elektrické amplitudě E
~1000 V/m bude doprovázena jen velmi slabým magnetickým polem
B ~3,3×10-6 T, podstatně
slabším než magnetické pole Země).
Elektromagnetické vlny jsou tedy prakticky v zásadě elektrické
vlny ! Číselné velkosti E a B však
závisejí na použité soustavě jednotek.
Pozn.: Výše uvedený poměr
E/B = c a níže uvedená rovnice (1.56) distribuce hustoty
elektrické a magnetické energie platí pouze pro rovinné
monochromatické vlny emitované kmitajícím elektrickým
dipólem.
-> Relativní fáze elektrické a magnetické
složky.
Kmitají tyto složky ve fázi, nebo s fázovým
posunem? Ve většině diagramů v literatuře se kreslí ve
stejné fázi. Avšak při generování elektromagnetických vln
klasickým elektrickým LC oscilátorem kmitajícím frekvencí f
= 1/[2pÖ(LC)] je v induktivní zóně elektrická složka
vyjádřena kosinusovou časovou závislostí E = Eo.
cos(2p.t) a magnetická složka
sinusovou závislostí B = Bmax. sin(2p.t). Je zde tedy
fázový rozdíl 90°. Není znám způsob, kterým by se
později ve vlnové zóně tento fázový rozdíl anuloval. Ve
světle výše zmíněné skutečnosti o zcela nepatrném
zastoupení magnetické složky však toto asi nemá žádný
praktický význam..?..
Z tohoto důvodu i často uváděné tvrzení, že
v elektromagnetické vlně se elektrická a magnetická pole vzájemně
indukují jedno druhým, ztrácí opodstatnění. Změny
elektrického pole sice indukují velmi slabé magnetické pole,
které však efektivně rozhodně není schopno zpětně
indukovat elektrické pole o příslušné intenzitě.
-> Generují se v elektromagnetické vlně
elektrická a magnetická složka navzájem ?
Často se uvádí, že v elektromagnetické vlně změna
elektrického pole způsobí magnetické pole, jehož změna pak
indukuje proměnné elektrické pole a tak dále - neustále
dokola, a to je důvodem šíření vlny. Prostorově se
měnící elektrická a magnetická pole sice mohou způsobit
jejich vzájemnou změnu v čase, ale Maxwellovy rovnice a jejich
řešení obecně neimplikují kauzální vazbu mezi
elektrickými a magnetickými poli. Elektrická a magnetická
složka je současně a nezávisle vytvářena jejich
společnými zdroji - časově proměnnou distribucí
elektrických nábojů a proudů. Zrychlení nabitých částic
takto generuje elektromagnetické pole, které se šíří do
okolního prostoru a poté ve větší vzdálenosti se stane
nezávislým na zdroji elektrického pole které je vytvořilo;
šíří se jako EM vlny. Názory na kauzální vztah mezi
elektrickou a magnetickou složkou v elektromagnetických vlnách
se různí, je to možná otázka interpretace..?..
-> Jsou všechny elektromagnetické vlny sinusové
?
Elektromagnetické vlny se graficky znázorňují téměř vždy
jako sinusoidy. Takový nebo podobný tvar se očekává
vzhledem k tomu, že EM vlny nejčastěji vznikají
vibračním-kmitavým pohybem elektrických nábojů, který má harmonický
"sin-cos" průběh. Všechny oscilační pohyby způsobené
silou F která je přímo úměrná výchylce x od
rovnovážého stavu F = -k.x, probíhají s výslednou
výchylkou kmitavého tvaru x(t) = r . sin 2p.f.t s frekvencí f = Ö(k/m), kde m je hmotnost částice.
Když se podíváme na vlny
v materiálním prostředí v přírodě, mají tendenci být sinusovými
vlnami. Natáhneme-li strunu na kytaře v určitém bodě o
kousek z původního přímého směru, nabude mírně
trojúhelnikový tvar. Když ji pustíme, vrátí se a překmitne
do opačného tvaru a zase zpět, ale po několika oscilacích
již bude kmitat sinusově na základní frekvenci dané délkou
a napětím struny. Ve struně působí podélné elastické
síly které rozředí nepravidelné oscilace a převedou je na
harmonické. Podobné síly působí ve všech pružných
látkových prostředích. Ve vakuu však žádné takové síly
nejsou, takže příp. kmitání polí zde může být velmi různého
tvaru.
Obecně tedy závislost kmitání E
a B na čase a poloze může být různého
tvaru, v závislosti na pohybu elektrických nábojů, či
průběhu střídavého napětí na anténě, kterými je buzeno.
Elektromagnetické vlny tedy rozhodně nemusí být
sinusové. Nesinusově proměnná elektrická a
magnetická pole budou generovat nesinusové elektromagnetické
vlny. Pokud bychom např. do vysílací antény pustili z
multivibrátoru střídavé napětí obdélníkového nebo
pilovitého průběhu, byly by emitovány vlny s tímto
průběhem E a B, jehož
charakter by se zachovával během šíření prostorem;
a když by takové vlny byly detekovány jinou - přijímací -
anténou, obdržel by se signál původního tvaru. Pouze v
případě harmonického sinusového průběhu ve zdroji je
vyzařována sinusová vlna. Každou konfiguraci elektromag.
vlnění však lze pomocí Fourierovy analýzy rozložit
na superpozici menšího či většího počtu
harmonických sinusových vln různých frekvencí a amplitud.
Přesně sinusová vlna je jen matematickou idealizací, reálné
vlny se od tohoto tvaru vždy více či méně odlišují. Ať
již je to v důsledku fluktuací ve zdroji - modulací ve
vysílači radiovln, nebo interakcí s látkovým prostředím,
kde se jejich rychlost a chování mohou měnit (a to i v závislosti na frekvenci).
Sinusoidy jsou tedy jen matematicky výhodnou sadou funkcí,
kterými lze modelovat řadu přírodních dějů pomocí
jednoduchých harmonických oscilátorů. Je
diskutováno výše v pasáži "Favorizované sinusovky".
-> Ojediněle se diskutuje i otázka, zda kromě příčných
elektromagnetických vln by se mohly vyskytovat i podélné
elmag. vlny. Pokud se jedná o vlny ve vakuu, tam jiné než
příčné vznikat nemohou, protože zde není žádné
médium, jehož částice by se rozkmitávaly a interakcemi s
dalšími částicemi přenášely kmitání dále a dopředu. V
homogenních a izotropních dielektrických látkových
prostředích jsou elmag. vlny rovněž příčné. V
nehomogenních prostředích na rozhraní materiálů s výrazně
rozdílnými permitivitami a permeabilitami, jakož i ve
dvojlomných dielektrikách, mohou elektromagnetické vlny
efektivně (zdánlivě?) vykazovat slabou podélnou složku. Specifická situace
je v plasmatickém prostředí, kde běžně vznikají podélné
plasmové vlny. Zde se však nejedná o elektromagnetické
vlny, ale o vlny hustoty nabitých částic (elektronů a iontů), které
mohou sekundárně vytvářet elektromagnetické pole vibrující
podélně a postupující rychlostí podstatně nižší než c
.
Obecnější otázka :
-> Může elektrické a magnetické pole existovat
každé zvlášť ?
Za statických podmínek, neměnících se s ohledem na
čas, může existovat jedno bez druhého.
Např. supravodivá cívka se stálým stejnosměrným proudem
má magnetické pole, ale nemá žádné elektrické pole. A
naopak, nabitý kondenzátor odpojený od elektrického zdroje
má elektrické pole bez magnetického pole. Neuvažujeme zde mikroskopické kvantové kmitání a
magnetické momenty elektronů a protonů.
Za dynamických podmínek časové
proměnnosti však elektrické a magnetické pole nemůže
existovat samostatně. Podle Maxwellových rovnic (1.38) a (1.41)
svou proměnností generují vzájemně jedno druhé. Pokud je
jedno pole časově proměnlivé, druhé musí být nenulové a
též časově proměnné.
Cílené vysílání a
přijímání elektromagnetických radiovln
Nerovnoměrný pohyb elektrických nábojů představuje jen
základní ideový mechanismus vzniku vln. Pro cílené
vytváření dostatečně silných elektromagnetických vln k
aplikacím ve sdělovací technice, průmyslu a vědeckém
výzkumu je potřeba toto vlnění účinně generovat
elektronickými metodami. Je potřeba vytvářet intenzivně vibrující
soustavy velkého množství nábojů v elektrických
obvodech - střídavé elektrické napětí a
proud. Základní metodiku vysílání a přijímání
elektromagnetických vln si přiblížíme pro klasickou
radiotechniku v oblasti nižších a středně velkých
frekvencí cca 300 kHz - 3 MHz (vlnové délky 1000 m až 100 m -
střední vlny), pro pásmo 3 - 30 MHz (vlnové délky 100 až 10
metrů) a velmi krátkých radiovln frekvencí 30 - 300 MHz.
Vyšší frekvence pak zmíníme v následující pasáži "Elektromagnetické
vlny velmi vysokých frekvencí".
Elektrický
oscilátor
Základním výchozím elektronickým obvodem je elektrický
oscilátor. V nejjednodušším provedení je tvořem
kondenzátorem o vhodné kapacitě C a cívkou o vhodné
indukčnosti L zapojené paralelně, ve spojení s
aktivním elementem (většinou
tranzistorem) vytvářejícím zpětnou
vazbu a dodávku elektrické energie U.
Jestliže kondenzátor C
nabitý na napěrí U připojíme paralelně k cívce L, začne
se kondenzátor přes cívku vybíjet, cívkou začíná
protékat proud a kolem ní se bude vytvářet magnetické pole.
Po vybití kondenzátoru proud ustane, ale v cívce se
nahromaděným magnetickým polem začne indukovat napětí
opačného směru, kterým se zpětně začne nabíjet
kondenzátor. A po jeho nabití se vybíjecí děj bude opakovat.
Kondenzátor s cívkou si nazájem budou periodicky vyměňovat
energii s frekvencí f = 1/[2p.Ö(L.C)]. Jelikož v obvodu jsou vždy ohmické a
radiační ztráty, amplituda kmitů by exponenciálně klesala,
kmity by byly tlumené. Pokud tyto ztráty průběžně
elektronicky nahradíme zesilovačem ve zpětné vazbě, nebude
amplituda klesat, vznikne stabilní zdroj střídavého napětí.
V tomto rezonančním obvodu
LC střídavým nabíjením a vybíjením kondenzátoru
přes indukčnost cívky budou tedy vznikat sinusové
elektrické kmity o frekvenci f = 1/2p.Ö(L.C) a periodě T = 2p.Ö(L.C), které budou
udržovány zpětnou vazbou a pak je bude možno zesílit a dále
zpracovat. Změnou hodnot L nebo C se reguluje
frekvence - provádí se ladění; většinou se
ladění provádí změnou kapacity C pomocí proměnného
ladicího kondenzátoru (otočného nebo
elektronického). Místo laděného obvodu
se v oscilátorech někdy používá krystalový piezoelektrický
rezonátor (umožňuje vysokou přesnost a
stabilitu frekvence).
Ve vysilačích se nyní
již nepoužívá jednoduchý Thomsonův LC oscilátor,
ale byly vyvinuty složitější elektronické oscilátory. .... ....... .........
Jednoduchý LC
rezonanční obvod se používá v přijímačích,
nejčastěji v superhetech. Ladění se provádí změnou kapacity C
pomocí proměnného ladicího kondenzátoru. Dříve se
používal mechanický otočný kondenzátor (na obrázku vlevo nahoře), v
pásmu středních a krátkých rozhlasových vln se nejčastěji
používal otočný ladicí kondenzátor v rozsahu 0÷500 pF a
indukční cívka cca 0,1 mH (cca 50 závitů ve vzduchu bez
jádra, pro vyšší frekvence s příslušně nižším počtem
závitů). Místo otočného kondenzátoru se nyní používá
elektronický varikap.
Pro potřeby přenosu
informace - zvuku, hudby, obrazu, digitálních dat - se
základní sinusové vysokofrekvenční napětí moduluje
amplitudově nebo frekvenčně. V rytmu potřebného
přenášeného signálu se lehce zvyšuje či snižuje jeho
amplituda nebo frekvence. Základní vysokofrekvenční
harmonický signál se nazývá nosný signál, který
se pak lehce modifikuje modulačním signálem.
Výsledný modulovaný signál se pak zesiluje ve výkonovém
výstupním obvodu koncového zesilovače, který je osazen
výkonovými elektronkami nebo výkonovými tranzistory. Při
vyšších výkonech je instalováno i účinné chlazení.
Anténa
Když máme hotový takový vysokofrekvenční zdroj
střídavého napětí, je potřeba jej přivést k
vnějšímu vodiči, který bude kolem sebe vytvářet střídavé
elektrické a sekundárně magnetické pole, které se bude
pak šířit do prostoru. Takový vodič se nazývá (vysílací)
anténa. V nejjednodušším případě to
může být obyčejný kus drátu nebo kovová tyč; druhým
pólem elektrického obvodu je zde země - uzemění (z elektronického hlediska se anténa modeluje tzv. elektrickým
dipólem).
Antény jsou radiotechnické systémy vodičů,
které jsou schopny vyzařovat elektromagnetické
vlnění do volného prostoru (vysílací antény), nebo naopak z
volného prostoru toto vlnění přijímat a měnit je
na elektrické signály (přijímací antény). Když je
vysílací anténa napájena střídavým napětím frekvence f,
přeměňuje část dodávané elektrické energie na emisi
elektromagnetických vln délky l = c/f. Antény se
charakterizují několika základními parametry :
-> Vysílací účinnost antény, či citlivost
přijímací antény. Optimalizuje se vhodnými rozměry antény
a geometrickým uspořádáním jednotlivých vodičů; její
délka by měla být nejméně l/2 .
-> Směrová selektivita - antény vysílají či
přijímají v určitých směrech lépe než v jiných. Tato
vlastnost se kvantifikuje směrovou vyzařovací
charakteristikou antény.
-> Frekvenční selektivita, kdy antény mají
různou účinnost pro různé frekvence f či vlnové
délky l. Pro kratší vlnové délky se
může uplatňovat i polarizační selektivita -
geometrická konstrukce a natočení antényv prostoru
ovlivňuje, jak účinně přijímá vlny různé polarizace.
-> Impedance antény. Z elektronického hlediska
je anténa součástí elektrického obvodu se střídavým
signálem - vysílací anténa je posledním (výstupním) prvkem
vysílače, přijímací anténa vstupním prvkem. Proto
záleží na tom, jak se v tomto obvodu elektricky chová, t.j.
jaký má odpor, v tomto případě impedanci Z = U/I.
Je to poměr napětí U a proudu I na konektoru
antény. Např. anténa typu půlvlnného
dipólu má impedanci 75 ?, anténa typu Yagi má Z=300 ?. . .......
.....obrázek vyzařovací charakteristiky
různých druhů antén ....???
Každý elementární úsek antény vyzařuje vlny
do všech směrů, přičemž v každém místě antény
protéká jiný proud. Takže z každého úseku jsou
vyzařovány vlny s jinou intenzitou. Vyzařování celé antény
je potom dáno součtem z jednotlivých elementárních úseků.
Obecně tedy platí, že všechny vyzařovací
charakteristiky silně závisí na geometrii antény a na
poměru její velikosti a vlnové délky.
Elektromagnetické pole mění svůj charakter v
různých vzdálenostech od vysílací antény. Pro
anténu velikosti D, která vysílá na vlnové délce l,
rozlišujeme podle vzdálenosti (poloměru) R od antény tři význačné zóny :
-» Nejbližší
oblast, někdy nazývaná reaktivní, je v těsné
blízkosti od antény 0<R<l, do vzdálenosti menší
než je vlnová délka. V tomto bezprostředním okolí
vysílací antény vznikají elektromagnetická pole složitého
průběhu, která ještě nemají transverzální charakter
elektromagnetických vln. Elektrické pole má kromě příčné
i podélnou složku šíření. Dochází k neustálým
spontánním "reakcím" - výměnám energie mezi
proměnnými poli a zdrojem, sousední anténou. Probíhá
kmitání "tam a zpátky", nesouvisející s
vyzařováním.
-» V induktivní
zóně, nazývané též blízká zóna, ve
vzdálenosti v rozmezí l < R
< 2.D2/l má elektromagnetické pole již transversální vlnový
charakter, ale přetrváná zde ještě induktivní zpětná
vazba s anténou. Vyzařovaný výkon zde do určité míry
závisí na přítomnosti "přijímače" emitovaných
vln (umístěním přijímače do
induktivní zóny se poněkud zvýší elektrický příkon
vysílací antény).
-» Ve vlnové
zóně, zvané též vzdálená zóna, ve
vzdálenosti cca R > 2.D2/l , v praxi typicky od
několika desítek vlnových délek, se již ustaví
kolmý průběh kmitajícího elektrického a magnetického pole
ve vlně s lokálně rovinnou vlnoplochou (ve
velkých oblastech prostoru má vlna kulovou vlnoplochu) a energie vln je nevratně vyzařována do volného
prostoru, nezávisle na přítomnosti nějakého
"přijímače". Není zde již žádná zpětná vazba
s vysílající anténou.
Pro dosažení dalekého dosahu bývají antény
výkonných vysilačů robustní konstrukce umístěné ve
výšce na stožárech. Vysokofrekvenční signál se k anténám
přivádí pomocí koaxiálních kabelů. Vysílací
výkon velkých profesionálních vysilačů bývá i několik
desítek kW až megawaty. V oblasti středních a krátkých vln
lze pro daleký dosah vysílání/přijímání použít i odrazu
vln v ionosféře.
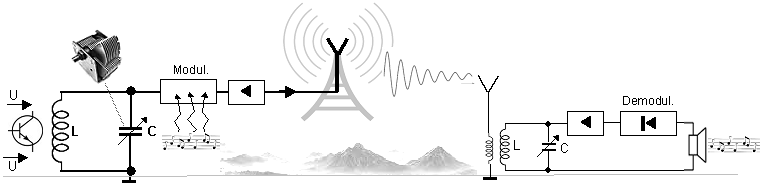
Přijímací anténa může být
podobného provedení jako vysílací, ale v zásadě bývá
daleko menší. Elektromagnetické vlny v ní indukují velmi
slabý signál stejné frekvence a průběhu jako byl vyslaný.
Přijímaná frekvence se opět naladí v rezonančním LC
obvodu. Vybraný signál se pak musí mnohonásobně zesílit a
pak jej lze demodulovat - vyextrahovat signál nesený
změnami amplitudy nebo frekvence - a použít jej ke
sdělovacím nebo výzkumným účelům.
Superheterodynní
radiopřijímač
Jednoduché přijímače s přímým zesílením vf
signálu z přijímací antény (jako je na
obrázku vpravo) měly nízkou citlivost a
nedostatečnou frekvenční selektivitu. Bylo proto vyvinuto
podstatně složitější elektronické zpracování
přijímaného signálu. Tzv. superheterodynní
přijímač (název vznikl složením superpozice
a řec. hetero=různý, dyn=moc, síla.....), zkáceně nazývaný superhet, superponuje
přijímanou frekvenci signálu s laditelnou frekvencí
místního oscilátoru do rozdílové mezifrekvence,
která se pak zesiluje a demoduluje. Místní LC oscilátor se
ladí pomocí dvojitého otočného kondenzátoru nebo varikapu,
synchronně s přijímacím LC rezonančním obvodem. Smíšením
přijímaného signálu s frekvencí místního oscilátoru
vzniká součtová nebo rozdílová frekvence. Během desítek
let se vyninula norma, že pro frekvenční rozsah přijímaného
signálu cca 100kHz-30MHz (střední, dlouhé a krátké vlny) se
používá mezifrekvence většinou 455kHz, pro VKV frekvence cca
30-300 MHz pak mezifrekvence 10,7MHz. Mezifrekvenční signál se
pak zesiluje, frekvenčně selektuje pomocí úzkých
mezifrekvenčních filtrů a pak demoduluje na výsledný
zvukový nebo obrazový signál. Superhet tím dosahuje vysokou
citlivost, odstup signál-šum a vysokou frekvenční
selektivitu.
Omluva autora
:
Pasáž o vysílání a přijímání radiovln jsem zde napsal
poněkud více technicky zaměřenou, než je potřeba pro
fyzikální výklad elektrodynamiky, gravitace, vesmírné
astrofyziky. Je to pro mne jakási reminiscence na moje školní
a gymnaziální roky, kdy mi učarovala elektřina a
radiotechnika. Již v 8. a 9. třídě ZŠ jsem si vlastnoručně
zkonstruoval dvě vysilačky: pro oblasti cca 0,5 - 30 MHz a
další kolem 70 - 100 MHz, osazené elektronkami EF22 a PL36. A
jako radioamatér jsem se snažil přijímat vzdálené stanice -
DX (Distanční příjem na X-vzdálenost,
co největší; podařilo se i z Číny).
Omlouvám se případným čtenářům (jinak orientovaným) za
tuto subjektivní atypii a děkuji za pochopení...
Elektromagnetické
vlny velmi vysokých frekvencí
Pro generování elektromagnetického záření velmi vysokých
frekvencí řádu GHz (např. 3-30 GHz) a tedy krátkých vlnových délek řádu centimetrů (např. 10cm - 1cm), již nelze
používat klasické LC oscilátory, ale nástroje
vysokofrekvenční elektroniky. Oscilátory pro
tyto vysoké frekvence jsou v zásadě dvojího typu :
-> Speciální elektronky magnetrony a klystrony
s rezonančními dutinami (podrobněji
popsané v §1.5 , pasáži "Elektrické napájení urychlovačů"). Používají se hlavně
pro velké vysokofrekvenční výkony řádově kilowatů až MW.
-> Speciální polovodičové součástky se záporným
diferenciálním odporem, jako jsou Gunnovy diody, tunelové
diody, IMPATT diody (nárazová ionizační
lavinovitá dioda). Pokud je takový
element integrován do obvodu mikrovlnné rezonanční dutiny a
je aplikováno stejnosměrné napětí U (cca 9V u Gunn diody) pro
dosažení oblasti záporného odporu, začnou vznikat
spontánní oscilace (na obrázku vlevo). Frekvence pak závisí na velikosti rezonanční
dutiny.
Pro vedení ultra-VF oscilujícího napětí z oscilátoru do
antény již nejsou optimální koaxiálmí kabely (kde jsou vysoké ztráty), ale
používají se často vlnovody - kovové
trubice obdélníkového nebo kruhového průřezu. Když
elektromagnetická vlna dopadá šikmo na vodivé stěny trubice,
zcela se od nich odráží. Postupnými odrazy se šíří v
podélném směru vlnovodem. Superpozicí
dopadajících a odražených vln vzniká ve vlnovodu složitý
průběh který má složku postupné vlny v podélném směru a
stojaté vlny v příčném směru.
Vysilací antény pro
centimetrové radiovlny mohou být v nejjednodušším případě
opět obyčejné dráty či tyčové antény s všesměrovým
účinkem. Vzhledem ke krátkým vlnovým délkám je zde však
možnost úzce směrových antén ve tvaru
trychtýřů nebo paraboloidů :
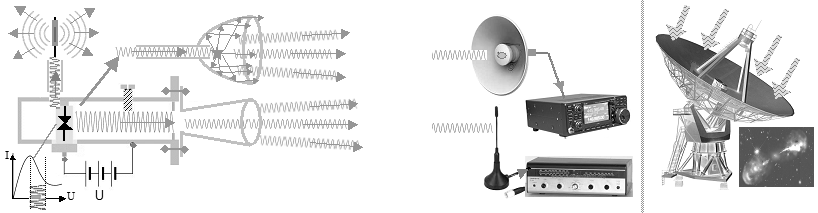
Tyto velmi krátké vlny se šíří přímočaře
- pouze v přímé vizuální viditelnosti bez překážek,
nedochází k ohybu ani k odrazu od ionosféry. Přijímací
antény mohou být opět drátové (prutové) bez
směrového účinku, nebo směrové parabolické.
Pro náš astrofyzikální obor jsou zde
důležité radioteleskopy (na obrázku vpravo)
a detekce mikrovlnného kosmického záření (§5.4, pasáž "Mikrovlnné reliktní záření -
posel zpráv o raném vesmíru").
Pro ještě vyšší frekvence, v oblasti infračerveného,
viditelného a UV záření, již nefungují
žádné elektronické oscilátory a antény, ale toto záření
vzniká vibracemi excitovaných atomů a molekul v látkách.
Používají se zde speciální techniky kombinující
elektronické metody atomové fyziky (včetně
laserových), s fotonásobiči a
polovodičovými fotodiodami pro detekci a spektrometrii
tohoto záření. A nejvyšší frekvence a energie X
a gama záření jsou již doménou jaderné a
radiační fyziky (podrobné
pojednání "Jaderná fyzika a fyzika
ionizujícího záření").
Elektromagnetické vlny jsou velmi důležité v astrofyzice,
neboť vznikají při řadě různých procesů ve vesmíru (v zásadě téměř při všech, dokonce i v okolí
černých děr). A umožňují nám zkoumat
a nepřímo "nahlédnout" do těchto často nesmírně
vzdálených procesů v hlubinách vesmíru - je diskutováno v
§1.1, pasáži "Elektromagnetické záření -
základní zdroj informací o vesmíru".
Rovinné
elektromagnetické vlny
V rovinné vlně šířící se ve směru osy X jsou všechny
veličiny funkcemi pouze t-x/c. Je-li E
= E(t-x/c), pak z Maxwellových rovnic (1.38) a (1.40) pro
r = 0, j
=0, plyne ¶B/¶t = -rot E = (n°/c) ´ (dE/d(t-x/c))
= n° ´ ¶E/¶t, takže vztah mezi elektrickým a
magnetickým polem v elektromagnetické vlně je
| B = n° ´ E / c , | (1.49) |
kde n° je jednotkový vektor ve směru šíření vlny ("´" značí vektorový součin). To znamená, že vektory elektrického a magnetického pole E a B jsou neustále kolmé jak navzájem, tak i k vektoru n° směru šíření vlny - elektromagnetické vlny jsou příčné. Protože B = rot A, stačí pro popis rovinné vlny pouze vektorový potenciál A, pomocí něhož se pole E a B stanoví vztahy
| E = A. ´ n° , B = (1/c) [(A. ´ n°) ´ n°] | (1.49') |
(tečka nad A
znamená derivaci podle času: A.
ş ¶A/¶t).
Nejjednodušší případ
elektromagnetické vlny je vlna monochromatická s konstantní
frekvencí f, v níž pole je v každém daném bodě
jednoduchou harmonickou funkcí času: A(t)r =const.= Ao(r).cos(wt + a), a = a(r), kde w = 2p.f = 2p/T je kruhová frekvence
vlny, a
je konstantní fázový posun. Veličina l= 2pc/w pak
představuje vlnovou délku, tj. vzdálenost kterou vlna
urazí za jednu periodu T (vzdálenost dvou nejbližších míst
se stejnou fází). V rovinné monochromatické vlně bude pole
harmonickou funkcí argumentu t-x/c
A = Ao cos [w.(t - x/c) + a] ,
kde Ao ani a nezávisí na t ani na x. Zavedením vlnového vektoru
| k =def (w/c) . n° | (1.50) |
lze rovinnou vlnu vyjádřit ve tvaru
| A(r,t) = Ao cos (wt - k.r + a) | (1.51) |
platném pro libovolný směr šíření vlny (analogicky pro B a E). Tento výraz pro monochromatickou rovinnou vlnu se často zapisuje v komplexním tvaru
| A = Re [Âo . e i(k.r - wt)] , | (1.51') |
kde Âo = A . eia je konstantní komplexní vektor; podobně lze vyjádřit i pole E a B.
Rychlost
šíření elektromagnetického signálu
Rozruch - signál - v elektromagnetickém poli
se tedy v prostoru šíří konečnou rychlostí c,
plynoucí z retardovaných potenciálů (1.47a,b), které jsou
řešením Maxwellových rovnic. Rychlost šíření
elektromagnetických signálů můžeme měřit v zásadě ve
třech prostředích :
-> Ve vakuu, kde je to rychlost světla
ve vakuu c = 299 792,458 km/s. - maximální možná
rychlost šíření interakcí v přírodě (§1.1, pasáž "Rychlost světla").
-> V dielektrickém látkovém prostředí,
kde je tato rychlost c´= 1/Öem poněkud menší než
c=1/Öeomo ve vakuu (§1.2, pasáž "Elektromagnetické a optické vlastnosti látek"). Ve vzduchu (za normálního tlaku) je to
0,9997 c = 299 702
km/s, ve vodě asi 0,75 c = 225 000 km/s, v diamantu jen 0,413 c = 123 800 km/s .
-> V kovových vodičích - elektrických
drátech - měříme rychlost pohybu elektrického
signálu podél vodiče (nehovoříme
již většinou o elektromagnetických vlnách, které dovnitř
vodiče neproniknou), která je dána,
kromě rychlosti světla v daném prostředí kolem vodiče,
též vlastní specifickou indukčností a kapacitou
vodiče. Pro přímý měděný drát (kabel
tloušťky ~ 1 mm) bylo naměřeno cca 0,65 c ~ 195 000 km/s. Stojí za
zajímavost, že rychlost šíření elektromagnetického
signálu ve vodičích poněkud závisí na tom, zda se jedná o
"holý" drát bez izolace, či o izolovaný kabel,
příp. koaxiální.
V elektronických obvodech a sítích je důležité časové
zpoždění signálu, dané vydělením délky kabelu
hodnotou rychlosti pohybu signálu. Limituje minimální šířku
či maximální frekvenci impulsů, kterou jsou sítě a obvody
schopny přenášet a zpracovávat. Ve vysokofrekvenční
elektronice dále dochází ve vodičích k fázovým posunům
mezi napětím a proudem a k nežádoucím odrazům a interferencím
signálů. Tyto efekty odrazů a interference signálů též
mohou výrazně ovlivnit elektronická měření rychlosti
signálu ve vodičích.
V
důsledku těchto efektů se vyskytují především
arteficiálně vyšší - nadsvětelné - naměřené
rychlostii šíření signálu v elektrických kabelech, z
čehož se někdy vyvozují poněkud bombastická tvrzení typu
"Naměřil jsem nadsvětelnou rychlost šíření
signálu v elektrickém kabelu - a tím jsem vyvrátil teorii
relativity!"...
Vnitřní
moment hybnosti - spin - elektromagnetické vlny
Při pootočení souřadnicové soustavy o úhel J kolem směru šíření n°
rovinné elektromagnetické vlny se pole ve vlně bude
transformovat podle zákona ®Â'= eiJ.Â; elektromagnetická vlna je invariantní vzhledem k pootočení o
úhel 360° kolem směru šíření. Vlastnosti symetrie rovinných vln vůči rotaci kolem směru
šíření jsou důležité v kvantové fyzice, kde určují spin
příslušných částic vznikajících kvantováním daného
pole. Na klasické úrovni je spin s
definován jako
s = 360°/(úhel symetrie rovinné vlny vůči pootočení kolem směru šíření) ;
spin elektromagnetických vln a jejich kvant - fotonů je tedy roven s = 1.
Orbitální moment
hybnosti elektromagnetické vlny. Spirálovitě polarizované
záření.
Hybnost p je veličina kvantifikující
"intenzitu pohybu" nějakého objektu
hmotnosti m pohybujícího se rychlostí v: p = m.v. Moment hybnosti L je pak veličina popisující jak je
tento pohyb orientován vzhledem k prostoru - ke vztažným
bodům, většinou k počátku souřadnic: L = r
x p, kde r je vektor aktuální
vzdálenosti částice od počátku souřadnic.
Když přichází svazek elektromagnetického záření, kromě
energie má zpravidla i určitý moment hybnosti vzhledem k
počátku souřadnicové soustavy. Při interakci je spolu s
energií předáván (celý nebo jeho část) dané částici
nebo soustavě....
Jsou-li elektromagnetické vlny
vyzařovány rotujícím zdrojem, zanechá tato rotace
specifické stopy na struktuře emitovaných vln. Při vzniku
vlny se maximum a minimum E a B při rotaci zdroje vůči sobě
periodicky časově posouvají, takže fáze vlny - střídání
maxima a minima - se budou posunovat při šíření vlny
rychlostí c . Vlnoplocha nabývá šroubovnicový
tvar spirály. Vzniká jakési "rotující,
stáčející se či spirálové záření" se
specifickými vlastnostmi polarizace. Dopadá-li na nabité
částice, způsobí m.j. jejich rotaci kolem směru šíření
paprsku, což lze považovat jako projev momentu hybnosti
tohoto záření. Chová se tedy jako vlnění s orbitálním
momentem hybnosti.
V §4.4 , pasáži "Šíření
světla v poli rotující černé díry" je diskutováno, že
podobná situace může nastávat u rotujících černých děr,
kde záření z akrečního disku může být takto spirálně
polarizováno vlivem rotační deformace prostoročasu.
Pozn.: V
laboratorních optických experimentech se toto světlo s
helikálně rotující polarizací generuje speciálními
rotujícími zdroji, válcovými čočkami, lasery, hologramy, a
měří se pomocí prostorových modulátorů světla. U radiovln
lze helikální polarizace dosáhnout speciální prostorovou
konfigurací antén napájených fázově posunovanými
střídavými signály, u zvukových vln analogicky pomocí
systémů reproduktorů. Gravitační vlny vznikající v
rotujících systémech černých děr nebo neutronových hvězd
by rovněž měly mít složku helikální rotující polarizace
(jejich měření je však komplikované, zatím se nepodařilo).
Obecné zákonitosti vzniku a šíření vln v přírodě jsou diskutovány v §2.7, pasáži "Šíření vln - obecný přírodní fenomén".
Energie
elektromagnetického pole
V elektrostatice lze jednoduchými úvahami (o práci potřebné
k rozmístění nábojů do dané
konfigurace) ukázat,
že elektrostatickou energii soustavy N nabitých těles
ee = (1/2)a=1SNqa.ja = (1/2) ňr.j dV = (1/8p) ň E2 dV
lze vyjádřit pomocí integrálu intenzity jejich společného elektrického pole, takže elektrickému poli lze přisoudit energii rozloženou s hustotou We = (1/8p) E2 v prostoru. Podobně úvahy o práci potřebné ke vzniku elektrických proudů v soustavě elektrických obvodů (proti indukovaným elektromotorickým silám vznikajícím nárustem magnetického pole) ukazují, že energie soustavy takových vodičů
em = (1/2)a=1SNIa.Fa = (1/2) ňA.j dV = (1/8p) ň B2 dV
je dána objemovým integrálem vektoru indukce B buzeného magnetického pole a můžeme ji považovat za energii tohoto magnetického pole rozloženou v prostoru s hustotou Wm = (1/8p) B2. Hustota energie v elektromagnetickém poli se pak rovná součtu hustot odpovídajících elektrické a magnetické složce :
| Welmag = (1/8p) ( E2 + B2 ) . | (1.52) |
Je jasné, že takové přisouzení energie poli je v rámci Coulombova, Ampérova a Faradayova zákona čistě formální, protože se jedná jen o jiný popis interakční energie při představě okamžitého silového působení nábojů a proudů na dálku. Fyzikální ospravedlnění mu však dává skutečnost, že rozruch v elektromagnetickém poli se šíří konečnou rychlostí. Tato konečná rychlost šíření změn v poli vede k závěru (abychom se neopakovali, viz argumentaci v úvodu §2.8 "...."), že elektromagnetické pole samotné musí skutečně obsahovat energii (a hybnost), která může proudit z jednoho místa na druhé a konat práci na elektrických nábojích a proudech (měnit se na jiné formy energie). Elektromagnetické pole není tedy jen prostor v němž působí elektrické a magnetické síly, ale je samostatnou fyzikální realitou - specifickou formou hmoty.
Skalárním vynásobením Maxwellovy rovnice (1.38) polem E a rovnice (1.40) polem B a jejich sečtením dostaneme po úpravě rovnici
| ¶ [(E2 + B2)/8] / ¶t = - div [(c/4p).(E ´ B)] - j . E . | (1.53) |
Integrace přes nějakou zvolenou prostorovou oblast V po aplikaci Gaussovy věty pak dává
| |
(1.54) |
Levá strana představuje změnu energie elektromagnetického pole eelmag obsažené uvnitř oblasti V za jednotku času. První integrál na pravé straně udává práci, kterou elektrické síly vykonají s náboji za jednotku času, neboli změnu kinetické energie ekin nábojů za jednotku času (magnetické síly s náboji žádnou práci nekonají a nemění tedy jejich kinetickou energii). Rovnice (1.54) tedy vyjadřuje zákon zachování energie v elektromagnetickém poli: elektromagnetická energie obsažená v prostorové oblasti V se zmenšuje jednak o mechanickou práci vykonanou elektrickými silami s náboji uvnitř oblasti V, jednak o energii přenesenou (vyzářenou) polem z oblasti V přes ohraničující plochu S = ¶V do vnějšího prostoru. Rovnici (1.54) je možno napsat též ve tvaru
| |
(1.54') |
podle něhož úbytek celkové energie elektromagnetického pole a nabitých částic v objemu V za jednotku času je roven toku vektoru (c/4p).(E´B) plochou S obklopující oblast V. Proto vektor
| P = (c/4p) . ( E ´ B ) | (1.55) |
nazývaný Poyntingův vektor představuje
energii procházející jednotkou plochy za jednotku času, neboli je to vektor hustoty toku elektromagnetické
energie v
prostoru. Při integraci v (1.54) přes celý prostor, kdy
ohraničujicí plocha S je nekonečně vzdálena a pole
je na ní rovno nule, vyjadřuje rovnice (1.54), resp. (1.54'),
prostě zákon zachování součtu celkové energie
elektromagnetického pole a kinetické energie všech nábojů.
Podobně lze ukázat, že
elektromagnetické pole má hybnost p danou
integrálem
| p = ň (1/4pc) . ( E ´ B ) dV , |
takže hybnost objemové
jednotky elektromagnetického pole je rovna P/c2.
Energie přenášená elektromagnetickými
vlnami
Elektromagnetické vlny odnášejí určitou část energie ze
zdrojové soustavy do okolního prostoru. V dostatečně velké
vzdálenosti - ve vlnové zóně - již existují samostatně, bez vazby na původní zdroj, který
již pak nijak není ovlivněn tím, zda vlna někde předala
svou energii. V samotné elektromagnetické vlně je obsažena
energie bez ohledu na to, zda je absorbována nebo ne. Když se
vlna setká se systémem elektrických nábojů, její
kmitající elektrické a magnetické pole může vyvíjet síly
a pohybovat těmito náboji - vykonávat práci, předávat energii. Větší či menší část energie vlny
je tím absorbována, intenzita se sníží a příp. zbylá
část putuje dál.
Čím větší je intenzita
elektrického E a magnetického B pole - amplituda vlny - tím větší nese vlna
energii a tím větší účinek může způsobit na
elektrických nábojích. Hustota
proudu energie
v rovinné elektromagnetické vlně je vzhledem k (1.49) rovna
| P = (c/4p) ( E x B ) = (c/4p) E2.n° = (c/4p) B2.n° , |
což vzhledem k (1.52)
souvisí s hustotou energie Welmag vztahem P
= c . Welmag . n°,
z něhož je rovněž vidět, že pole i energie se ve vlně
šíří rychlostí světla.
Hustota elektrické energie v elektrickém
poli je We = (1/2)eo E2. Hustota magnetické energie v
magnetickém poli je Wm = B2/(2mo).
Energie v každém místě a čase v elektromagnetickm poli je
dána součtem energií elektrického a magnetického pole, tedy
pro hustoty :
Welmag = We + Wm = 1/2 eo E2 + 1/2mo.B2 .
V elektromagnetické vlně E a B souvisejí vztahem E = c.B, rychlost světla ve vakuu je c = 1/Ö(e0.m0). Takže v elektromagnetické vlně spolu souvisí hustota elektrické a magnetické energie :
| We = 1/2 eo E2 = 1/2 eo B2 c2 = 1/2 eo B2 /(e0.m0) = 1/2mo.B2 = Wm , | (1.56) - SI |
t.j. hustota magnetické energie Wm a hustota elektrické energie We jsou zde stejné, navzdory skutečnosti, že proměnné elektrické pole obecně vytváří jen slabé magnetické pole. Celková energie vlny je pak W = We + Wm = eo E2 . Intenzita elektromagnetické vlny, což je energie procházející jednotkou plochy (kolmé na směr šíření) za jednotky času pak je IW = c.eo.E2 .
Elektromagnetické
vyzařování energie
Mějme soustavu pohybujících se elektrických nábojů
soustředěnou v nějaké omezené prostorové oblasti (obr.1.4).
Umístíme-li počátek souřadnic někam dovnitř této soustavy
nábojů, pak při studiu pole ve velkých vzdálenostech
R>>L, kde L je charakteristický rozměr
soustavy, budou všechna místa zdrojové soustavy přibližně
ve stejné vzdálenosti R jako je počátek souřadnic.
Vzdálenosti |R- r|
jednotlivých míst r' zdroje od vyšetřovaného vzdáleného
bodu R je přibližně rovna |R- r'| @ R - R°. r', kde R° je jednotkový vektor
směřující od počátku O do vyšetřovaného bodu, takže
retardované potenciály lze pro velké
vzdálenosti napsat ve tvaru
j(R,t) = (1/R). ň r(r', t - R/c + R°.r'/c) dV' , A(R,t) = (1/R). ň j(r', t - R/c + R°.r'/c) dV' .
Retardační čas se
tedy skládá ze dvou různých částí. První část R/c
určuje vnější retardaci, tj. dobu potřebnou k tomu, aby
změny v elektromagnetickém poli překonaly vzdálenost od
počátku souřadnic, neboli od zdrojové soustavy, do
vzdáleného pozorovacího místa. Druhá část rovná -R°.r'/c charakterizuje vnitřní retardaci,
tj. dobu šíření rozruchu v poli v rámci zdrojové soustavy.
V případě, že rozložení náboje v
soustavě se mění dostatečně pomalu, lze vnitřní retardaci
zanedbat. K tomu stačí, aby charakteristická doba T,
za kterou se rozložení náboje znatelně změní, splňovala
podmínku T>> L/c. Jelikož c.T je vlnová délka l elektromagnetické vlny vyzařované
soustavou, lze podmínku zanedbatelnosti vnitřní retardace
napsat též ve tvaru L << l, tj.
rozměry soustavy musejí být malé ve srovnání s délkou
vyzařovaných vln. Charakteristická doba změny rozložení
nábojů T souvisí s průměrnou rychlostí v
nábojů vztahem T » L/v, takže k zanedbání
retardace je třeba, aby platilo v«c, tj. rychlosti pohybu
nábojů musejí být malé oproti rychlosti světla. Při
zanedbání vnitřní retardace jsou potenciály ve velkých
vzdálenostech od zdrojové soustavy rovny
j(R,t) = (1/R). ň r(r', t - R/c) dV' , A(R,t) = (1/R). ň j(r', t - R/c) dV' .
V těchto vzdálenostech velkých ve srovnání jak s rozměry zdrojové soustavy, tak s délkou vyzařovaných vln - ve vlnové zóně - je možno v rámci malých oblastí prostoru proměnnou složku pole považovat za rovinnou vlnu. Stačí zde tedy stanovit vektorový potenciál A = (1/cR). ň r.v dV' = (1/cR)a=1SNqava = (1/cR) (d/dt)a=1SNqar'a , tj.
| A(R,t) = (1/cR) . d.(t-R/c) , | (1.58) |
kde d ş Sqara je elektrický dipólový moment soustavy, jaký byl v čase t-R/c. Elektrické a magnetické pole je pak podle (1.49) rovno
| E(R,t) = (1/c2R) [ (d.. ´ R°) ´ R°] , B(R,t) = (1/c2R) (d.. ´ R°) , | (1.59) |
kde dipólový moment d se opět bere v okamžiku t-R/c (tečky nad d znamenají derivaci podle času).
Tok elektromagnetické energie ve vlnové zóně, tj. intenzita elektromagnetického záření, je vyjádřena Poyntingovým vektorem podle (1.57)
| P = (c/4p) (E´B) = (1/4pc3R2) (d..´R°)2 = (d.. 2/4pc3R2) sin2J . R° , | (1.60) |
kde J je úhel mezi směry vektorů d.. a R (použijeme-li polárních souřadnic - obr.1.4b). Úhlové rozdělení intenzity záření elektrického dipólu je dáno koeficientem sin2J, příslušný směrový diagram je na obr.1.4c. Celková energie vyzařovaná soustavou za jednotku času (tj. vyzařovaný výkon) I = dE/dt je pak dána tokem energie přes celou sférickou plochu R=const. :
 |
(1.61) |
V případě, že zdrojová soustava sestává pouze z jednoho zrychleně se pohybujícího náboje q, je d.. = q.r.. = q.a, a vyzařovaný výkon je roven
| I ş dE/dt = (2.q2/3c3) . a2 . | (1.61') |
Tento vyzařovací zákon odvodil v r.1899 irský fyzik J.Larmor. V soustavě jednotek SI je navíc přítomem koeficient k = 1/(4peo) vystupující v Coulombově zákoně.

Obr.1.4. Elektromagnetické pole ostrovní soustavy
pohybujících se elektrických nábojů.
a) Pole buzené
soustavou pohybujících se elektrických nábojů je dáno
nikoliv okamžitým, ale retardovaným rozložením a pohybem
nábojů.
b) Ve velké
vzdálenosti od zdrojové soustavy (ve vlnové zóně) je
proměnná složka pole dána druhou časovou derivací
dipólového momentu soustavy d..
a má charakter elektromagnetických vln odnášejících
pohybovou energii zdroje do prostoru.
c) Směrový diagram
vyzařování elektrického dipólu.
Vztahy (1.58) až (1.61) pro pole a záření ostrovní soustavy elektrických nábojů ve vlnové zóně byly získány v aproximaci prvního řádu v poměru L/l (členy vyšších řádů byly zanedbány), což vedlo k uplatnění pouze dipólového momentu soustavy. V obecném případě je však třeba vzít v úvahu i další členy v rozvoji potenciálu podle mocnin L/l, což vede k tomu, že celková intenzita elektromagnetického záření soustavy pohybujících se nábojů je dána časovými derivacemi jednotlivých multipólových momentů rozložení náboje. Kromě dipólového momentu se na záření obvykle nejvíce podílí kvadrupólový moment Kab = ň r.(3xaxb - dab.r2) dV a popř. magnetický dipólový moment m = (1/2c) ň r.(r´v)dV, které k záření přispívají podle známého vztahu (viz např. [166])
| (1.62) |
Jestliže vlastnosti zdrojové soustavy jsou takové, že d.. = 0 (tak je tomu např. v soustavě složené z těles se stejným specifickým nábojem q/m), dipólové záření nevzniká. V takových případech se uplatní pouze záření způsobené dalšími členy v rozvoji potenciálu podle mocnin L/l, tj. záření vyšších multipólů.
Elektrodynamika tak dospívá k obecnému závěru, že při každém
zrychleném (nerovnoměrném) pohybu elektrických nábojů se vyzařují
elektromagnetické vlny, které odnášejí část jejich
kinetické energie do prostoru*). V §2.7 uvidíme, že v
podstatě ke stejnému závěru - vyzařování gravitačních
vln při zrychleném pohybu gravitujících těles - dospívá i
obecná teorie relativity, i když vlastnosti gravitačních vln
se od vlastností vln elektromagnetických v některých
aspektech liší (gravitační vlny jsou především
nesrovnatelně slabší).
*) Tento jev hraje důležitou úlohu v atomové fyzice
pro strukturu atomového obalu a vznik záření při jeho
deexcitacích (viz §1.1 "Atomy a atomová jádra" knihy "Jaderná fyzika a fyzika ionizujícího
záření"). Dále pak v jaderné
fyzice a fyzice ionizujícího záření. Zvláště rychle
letící elektrony jsou při interakci s
látkovým prostředím prudce brzděny, takže
podle vztahu (1.61´) vyzařují poměrně intenzívní
elektromagnetické záření - tzv. brzdné záření.
Brzdné záření nachází významné využití při buzení X-záření
dopadem elektricky urychlených elektronů na anodu v
rentgenkách - viz §3.2 "Rentgenová diagnostika", nebo při buzení tvrdého g-záření
dopadem vysokoenergetických elektronů z betatronu či
lineárního urychlovače na vhodný terčík (viz §1.5
"Elementární částice", část "Urychlovače
nabitých částic" v
téže publikaci).
Proměnná elektromagnetická pole buzená soustavou pohybujících se nábojů jsme vyšetřovali ve vlnové zóně, tj. v dostateěně velkých vzdálenostech od zdrojové soustavy, a vyzařovanou energii jsme počítali pomocí Poyntingova vektoru. Analýza elektromagnetického pole v malých vzdálenostech pak ukazuje, že uvnitř a v blízkosti zdrojové soustavy se vytváří určitá malá proměnná složka elektrického pole s fází odlišnou od hlavní proměnné složky. V aproximaci třetího řádu je tento člen rovný
Ere = (2/3c3) d... .
Ve zdrojové soustavě tedy bude na každý náboj q působit určitá dodatečná síla "reakce" fre = q.Ere konající za jednotku času práci fre.v, takže celková práce vykonaná tímto polem se všemi naboji soustavy vychází A re = (2/3c3) d... Sqava = (2/3c3) d....d, což při zprůměrování podle času (přes několik period T) dává
A re = - (2/3c3) d..2 .
Je vidět, že tato
přídavná složka pole způsobuje příslušné brzdění pohybů
nábojů ve zdroji zpětnou reakcí vyzařovaných vln, a to v
plné energetické shodě se vzorcem (1.61) získaným analýzou
pole ve vzdálené vlnové zóně. Takovýto rozbor má svou
velkou důležitost u gravitačních vln, kde výpočet energie
ve vlnové zóně není zdaleka tak jasný a jednoznačný jako
je tomu v elektrodynamice - to uvidíme v §2.8 "Specifické
vlastnosti gravitační energie".
Rovnici pohybu m.v
= q.E + (q/c).(v
´ B) nabité částice v elektromagnetickém
poli pod vlivem Lorentzovy síly (1.30) je tedy třeba doplnit o brzdící účinek elektromagnetického vyzařování:
| m .v = q.E + (q/c) (v ´ B) + (2q2/3c3) v.. ; | (1.63) |
tato rovnice je
použitelná tehdy, když rychlost částice je malá oproti
rychlosti světla a brzdící síla je podstatně menší než
Lorentzova síla působící na náboj od vnějšího pole E a B.
Další
podrobnosti o vlastnostech elektromagnetického pole a o jejich
aplikacích lze nalézt v příslušné literatuře; z
přehledových momografií uveďme např. [235],[264],[206].
É
t e r
Elektromagnetická pole byla v minulosti považována za projev
určitých druhů pohybu éteru *). Některá (elektricky nabitá)
tělesa uvádějí tento éter do pohybu, který se v něm
šíří konečnou rychlostí a předává se jiným tělesům.
Takový éter by však musel mít velmi neobvyklé fyzikální
vlastnosti. Aby se v něm mohly šířit elektromagnetické vlny,
které jsou příčné, musel by mít některé vlastnosti
pevného tělesa. A už vůbec není mechanický model éteru
slučitelný s experimentálně zjištěnou konstantností
rychlosti světla ve všech inerciálních soustavách. Snahy
uvést tuto skutečnost do souladu s modelem éteru nevedly k
úspěchu (např. předpoklad
"strhávání éteru" pohybem Země neobstál při
konfrontaci s pozorovanou aberací světla ze stálic). Proto byla představa éteru opuštěna a dospělo se k poznání, že nositelem
elektromagnetického pole je samotný
prostor. A.Einstein pak ve speciální teorii relativity završil tuto
koncepci vývodem, že stálost rychlosti světla je odrazem
souvislosti prostoru a času. Elektromagnetismus tak sehrál
významnou heuristickou úlohu při odhalování hlubších a
obecnějších zákonitostí přírody -
zákonitostí relativistické fyziky.
*) Éter
Podle antických řeckých filosofů a přírodozpytců (zejména
Aristotela) byl "nebeský" prostor - vesmír - zaplněn
hypotetickou všudypřítomnou neviditelnou jemnou substancí
zvanou éter (řec. aithér,
lat. aether = jasné světlo, nebe,
vrchní vrstvy vzduchu). Éter si představovali jako
pružnou průhlednou tekutinu, dokonale prostupnou bez tření,
nevažitelnou, nezničitelnou. Spolu s ostatními živly
"země, voda, vzduch, oheň" jako "pátý
živel", který nepůsobí na zemském povrchu, ale v
nebesklých sférách. Z éteru jsou vytvořena všechna nebeská
tělesa, hvězdy, planety, Slunce. Éter přenáší světlo a
teplo ze Slunce a světlo od hvězd a planet.
Pozn.: V
chemii se éter nazývá prchavé organické
rozpouštědlo (lat. aether).
Fyzika 19.stol. považovala za samozřejmé, že
každé vlnění se může šířit jen v tom pružném hmotném
(látkovém) prostředí, jehož kmitavým pohybem vzniká.
Těžko si lze představit mořské vlny bez vody nebo zvuk bez
vzduchu (či jiného pružného akustického prostředí plynné,
kapalné nebo pevné fáze - viz známý elementární pokus s
budíkem nebo zvonkem pod recipientem vývěvy). Když se
zjistilo, že světlo a ostatní elektromagnetické vlny se
šíří nejen ve vzduchu a dalších optických látkových
prostředích, ale i ve vakuu, vyvstal problém prostředí
či média, v němž se šíří elektromagnetické vlny. Tak se
znovu oživila představa éteru - univerzální
vše prostupující "látky", vyplňující veškerý
prostor a pronikající veškerou hmotou (podobně jako voda
proniká oky rybářské sítě tažené za lodí). Tento éter
vytváří prostředí pro šíření světla, tepla a jiných
elektromagnetických vlnění; je rovněž nositelem gravitace.
Jelikož se éter neprojevoval v žádných jiných fyzikálních
a chemických jevech, soudilo se, že je průsvitný,
nevažitelný, dokonale prostupný bez tření, nemá žádné
chemické vlastnosti. Látka s takovými rozpornými vlastnostmi
byla experimentálně prakticky neprokazatelná.
Dalo se pouze zkoumat, jak průnik éterem
působí na rychlost světla za různých
konfigurací pohybového stavu zdroje světla a pozorovatele.
Již sám Maxwell navrhl experiment s využitím pohybu Země:
světlo při pohybu éterem ve stejném směru jako obíhá Země
na své dráze kolem Slunce musí mít poněkud jinou rychlost
než světlo které se šíří kolmo k tomuto pohybu nebo ve
směru opačném, přičemž rozdíl rychlosti světla by měl
být cca 10-7. Maxwell se již výsledku tohoto experimentu
nedočkal; až 8 let po jeho úmrtí, v r.1887 A.Michelson a
E.Morley provedli toto měření pomocí interference paprsků
monochromatického světla odražených dvěma zrcadly ve
vodorovném a svislém směru, přičemž se celé
interferenční zařízení na plovoucí desce dalo otáčet.
Výsledek, že v rychlosti světla v obou směrech nebyl
naměřen žádný rozdíl, se v té době jevil
neočekávaným a paradoxním. Negativní výsledek tohoto pokusu
byl však potvrzen i dalšími měřeními. Žádné hypotézy ad
hoc, jako je strhávání éteru (éter je tažen spolu se
zemským povrchem, takže se jeho postavení vůči
interferometru nemění) se nepotvrdily. Naproti tomu se
negativní výsledek Michessonova a Morleyova pokusu dařilo
vysvětlit Lorentzovou kontrakční hypotézou,
podle níž se rozměry všech těles ve směru jejich rychlosti v
zkracují v poměru 1/Ö(1-v2/c2). Definitivní a univerzální vysvětlení pak podal
Einstein ve své speciální teorii relativity,
podle níž je rychlost světla (ve vakuu) za všech pohybových
podmínek a ve všech směrech stejná. Představa éteru tak
byla s konečnou platností opuštěna,
nahradily ho vlastnosti samotného prázdného prostoru,
spojeného s časem do jednotného prostoročasového
kontinua. Přesto se však dosud v oblasti
radiotechnických aplikací elektromagnetických vln často
používají výrazy "vysílat do éteru"
či "přijímat z éteru".
Po vytvoření obecné teorie
relativity však Einstein uznal, že roli dřívějšího
statického éteru má ekvivalentně časoprostorové kontinuum,
které je dynamické a je popsáno polem metrického tenzoru gik .
Nelineární
elektrodynamika ?
Při všech intenzitách, které pozorujeme v přírodě i
laboratoři, se nám elektické a magnetické pole ve vakuu jeví
jako lineární - pro hodnoty intenzit E
a B, jakož i pro potenciály, přesně platí princip
superpozice.
Na konci následujícího §1.6 "Čtyřrozměrný prostoročas a speciální
teorie relativity", pasáži
"Nelineární elektrodynamika", budou diskutovány hypotetické možnosti, jak
by se extrémně silné elektromagnetické pole i ve vakuu mohlo
chovat nelineárním způsobem..?..
| 1.4. Analogie mezi
gravitací a elektrostatikou |
1.6. Čtyřrozměrný
prostoročas a speciální teorie relativity |
| Gravitace, černé díry a fyzika prostoročasu : | ||
| Gravitace ve fyzice | Obecná teorie relativity | Geometrie a topologie |
| Černé díry | Relativistická kosmologie | Unitární teorie pole |
| Antropický princip aneb kosmický Bůh | ||
| Jaderná fyzika a fyzika ionizujícího záření | ||
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | ||