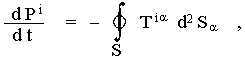 |
(2.86) |
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | Gravitace, černé díry a fyzika |
Kapitola 2
OBECNÁ TEORIE
RELATIVTITY
- FYZIKA GRAVITACE
2.1. Zrychlení a gravitace z hlediska
speciální teorie relativity
2.2. Univerzálnost - základní
vlastnost a klíč k pochopení podstaty gravitace
2.3. Lokální princip ekvivalence
a jeho důsledky
2.4. Fyzikální zákony v
zakřiveném prostoročase
2.5. Einsteinovy rovnice
gravitačního pole
2.6. Deviace a fokusace geodetik
2.7. Gravitační vlny
2.8. Specifické vlastnosti gravitační energie
2.9.Geometrodynamická soustava
jednotek
2.10. Experimentální
ověřování teorie relativity a gravitace
2.8. Specifické vlastnosti gravitační energie
Energie je důležitá
fyzikální veličina při dynamických prosesech ve
fyzikálních systémech (v relativistické
fyzice zde figuruje i klidová energie-hmotnost částic). Podle klasické ("školské") definice je energie skalární veličina,
která vyjadřuje schopnost hmoty (těles, látky, pole) konat
práci (řec. energeia - energeia
= síla, snaha, schopnost k činům). Může mít různé formy, v klasické
mechanice se rozlišuje především kinetická
energie
(pohybová) daná známým vzorečkem Ekin= 1/2
m.v2
a potenciální energie (polohová, konfigurační) Ep
způsobená přitahováním či odpuzováním částic a těles
gravitací či elektromagnetismem. V relativistické fyzice je
důležitá i tzv. klidová energie objektů, částic, s nenulovou
klidovou hmotností. Hmotnost a energie jsou podle STR
ekvivalentní podle známého Einsteinova vztahu E = m.c2
(§1.6, část "Relativistická dynamika").
Energie se může přeměňovat z jednohu
druhu na jiný, avšak v izolované soustavě její celkové
množství zůstává stejné, nelze ji vytvořit ani zničit -
platí zákon zachování energie. To je spolehlivě dokazováno
experimentálně. Z hlediska teoretické fyziky je zákon
zachování energie, jakož i dalších veličin (integrálů
pohybu), hybnosti, momentu hybnosti, matematicky formulován v teorému E.Noetherové, podle něhož zákony zachování jsou
důsledkem symetrie (invariance) daného fyzikálního systému
vůči transformacím proměnných veličin které jej popisují (je podrobněji rozebíráno v souvislosti s
unitárními teoriemi pole v GravitaceB-6.htm#Symetrie). Zákon zachování energie je
důsledkem homogenity času - nezávislost na
posunu v čase.
Gravitační
vazbová energie
V oblasti gravitace se s energií setkáváme v běžném
životě, jakož i v astronomii planet a hvězd. Je to potenciální energie Ep těles v gravitačním poli a s
ní související gravitační vazbová
energie,
při pohybu těles pak jejich kinetická
energie Ekin.
Máme-li v klidové soustavě hmotných
těles nebo částic jednotlivé objekty od sebe velmi vzdálené
(teoreticky v nekonečné vzdálenosti), takže vzájemná gravitace
mezi nimi nepůsobí, je jejich hmotnost-energie dána součtem
klidových hmotností jednotlivých částic a je poněkud
větší, než když tyto objekty k sobě přiblížíme na
kratší vzdálenost, kde výrazně působí gravitační síly.
Při tomto přibližování (např. kontrakci plynoprachového
oblaku do protohvězdy, viz §4.1) se uvolňuje vazbová
gravitační energie (gravitační síla vykonává práci po
dráze přibližování), takže výsledná hmotnost-energie
vázaného systému je poněkud nižší, než je součet výchozích
hmotností a energií jednotlivých částic. Naopak při
vzdalování těles (např. start rakety ze
Země do Vesmíru)
musíme působit silou a vykonávat mechanickou práci prototi
gravitačním přitažlivýn silám. Vazbová gravitační
energie je záporná, projevuje se určitý
gravitační "hmotnostní defekt" u gravitačně vázaných
systémů *). Pro běžná makroskopická tělesa je tento defekt
zcela nepatrný a neměřitelný, menší než cca 10-30, pro velké planety je řádu 10-8, pro hvězdy cca 10-6.
*) Analogická situace je i u elektrické
vazbové energie atomů a jaderné vazbové energie. Na
čerpání vazbové energie atomů v poli přitažlivých
Coulombických sil je založena kinetika chemických
reakcí. Uvolňování části vazbové energie
nukleonů v potenciálovém poli přitažlivých silných
interakcí je zdrojem jaderné energetiky. U
atomových jader je hmotnostní defekt poměrně vysoký, takže
štěpením těžkých jader uranu lze získat asi 0,1% a
slučováním lehkých jader cca 1% energie z ideálního limitu
E=mc2. V
§4.8 "Astrofyzikální význam černých děr" uvidíme, že u gravitačně zhroucených
kompaktních útvarů, především černých děr, může být
dosaženo ještě podstatně větší účinnosti
"ždímání" energie z hmoty.
Ve všech těchto případech makroskopických těles, planet a hvězd pro stanovení gravitační vazbové energie Ep vystačíme s klasickou Newtonovou mechanikou a naukou o gravitaci (§1.2 "Newtonův gravitační zákon", případně §1.4 u elektřiny): pro každou částici či hmotnostní element Dm stanovíme její součin j.Dm s gravitačním potenciálem j v daném místě (vypočteném pomocí vztahu (1.26b)) a integrujeme přes všechny elementy soustavy. Pro nejobvyklejší případ kulového tělesa poloměru R s hustotou látky r(r) můžeme využít centrální symetrie a rozdělit si těleso na kulové slupky poloměru r a tloušťky Dr, jejichž hmotnost Dm=4pr2.r.Dr vždy vynásobíme gravitačním potenciálem j(r)=m(r)/r, daným celkovou hmotností m(r)=p.0ň rr2.r dr obsaženou uvnitř koule poloměru r. Pak integrujeme pak od 0 do R: Ep = 0ňR[m(r)/r]dr. Pro zjednodušený modelový příklad homogenního kulového tělesa hmotnosti M a poloměru R (r= M/[(4/3)pR3] = const.) vychází gravitační potenciální vazbová energie :
Ep = G . M2 / R .
Pro nehomogenní kouli
můžeme použít modifikovaný vztah Ep
= [G.M2/R].f, kde koeficient f závisí
na rozdělení hustoty v tělese. Pokud je hustota hmoty ve vnitřní
části větší než v periferních částech (jak tomu bývá u
hvězd), je f>1 - vazbová gravitační energie je poněkud
vyšší.
Pouze u masivních gravitačně velmi silně vázaných
kompaktních útvarů jako jsou bílí trpaslíci, především
však neutronové hvězdy a černé díry, je třeba pro analýzu
energetických procesů použít zákonitostí obecné teorie
relativity. Gravitační hmotnostní defekt je zde již velmi
významný.
Interakční či
konfigurační vazbová gravitační energie je velmi důležitá
pro řadu astrofyzikálních procesů, převším vznik hvězd a
planetárních systémů (§4.1 "Úloha
gravitace při vzniku a evoluci hvězd"), formování
velkorozměrové struktury vesmíru (§5.4
"Standardní kosmologický model. Velký třesk.
Formování struktury vesmíru."), galaxií, hvězdokup, dynamiku akrečních disků
kolem černých děr (§4.8 "Astrofyzikální
význam černých děr"). V této kapitole se však budeme zabývat
problematikou energie samotného gravitačního pole.
Energie gravitačního pole -> Má
gravitační pole energii ?
V předchozím §2.7 bylo ukázáno, že rozruch v gravitačním
poli se šíří konečnou
rychlostí
(rovnou rychlosti světla). Tato skutečnost logicky vede k
závěru, že gravitační pole musí
mít energii a hybnost. Jestliže totiž jeden hmotný systém
způsobí rozruch v gravitačním poli, který se rozšíří k
druhému systému a předá mu určitou energii, vynoří se
otázka: kde je energie a hybnost v časovém intervalu mezi
jejím "vysláním" jedním tělesem (systémem)
a jejím "přijetím" druhým systémem? Jedinou
uspokojivou odpovědí je, že pole samotné musí mít ty
zachovávající se charakteristiky hmoty (integrály pohybu),
jejichž přenos zprostředkovává - energii, hybnost, moment
hybnosti -
stejně jako běžná tělesa a látková prostředí.
Jak bylo vysvětleno v §1.6, distribuce energie a hybnosti ve fyzikální soustavě se ve STR vyjadřuje pomocí tenzoru energie-hybnosti Tik (1.107). Celková energie E, hybnost P = (Pa) (a= 1,2,3) a z nich složená čtyřhybnost Pi ş (E,Pa) je pak dána objemovými integrály
| E = xo=const.ňT°° d3x , Pa = xo=const.ňT°a d3x , P i = xo=const.ňT i° d3x . | (2.84) |
Zákon zachování energie a hybnosti má potom diferenciální tvar
| ¶ T ik T ik,k ş ----------- = 0 , ¶ x k |
(2.85) |
který v trojrozměrném přepisu je analogický rovnici kontinuity jk,k ş ¶r/¶t + div j = 0 v elektrodynamice, kde jk ş (r, j) je čtyřproud, r ş j° je hustota náboje a j je hustota proudu.
Jestliže obklopíme sledovanou soustavu myšlenou uzavřenou plochou S, přechodem od objemových integrálů (2.84) k plošným integrálům s použitím Gaussovy věty a diferenciálního zákona (2.85) dostaneme zákony zachování energie a hybnosti v integrálním tvaru
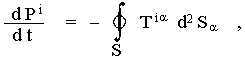 |
(2.86) |
kde d2Sa jsou složky (normálového) vektoru elementu plochy. Tento zákon říká, že rychlost změny energie a hybnosti v nějaké prostorové oblasti je rovna celkovému proudu energie a hybnosti přes uzavřenou plochu S ohraničující tento objem. Analogický zákon platí i pro moment hybnosti. Pro izolovanou soustavu je na pravé straně (2.86) nula, takže Pi = const. - energie a hybnost se s časem nemění.
Zobecněním výše zmíněného lokálního zákona zachování (2.85) energie a hybnosti na přítomnost gravitačního pole (zakřivený prostoročas) je podle principu ekvivalence tenzorový vztah (viz §2.4)
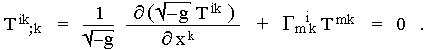 |
(2.87) |
V takovém tvaru však
již tato rovnice nevyjadřuje žádný lokální zákon
zachování, protože vlivem přítomnosti druhého členu v
(2.87) neumožňuje přechod mezi plošnými integrálními toky
a objemovými integrály s použitím Gaussovy věty (tak jak to
bylo možné mezi diferenciálním (2.85) a integrálním (2.86)
zákonem zachování). V zakřiveném prostoročase obecné
teorie relativity tedy obecně neplatí zákony zachování energie a
hybnosti hmotných soustav! Souvisí to s tím, že se musí
zachovávat energie a hybnost nejen samotných zdrojů, ale
včetně energie a hybnosti gravitačního pole, která však
není zahrnuta do Tik *). Křivost prostoročasu je
určitým specifickým přispěvkem k energii a hybnosti, který
musí být započítán abychom získali správný (přesný)
zákon zachování. Z rovnice Tik;k = 0 lze obecně získat pouze
přibližný integrální zákon zachování energie a hybnosti
zdroje, jestliže jej budeme integrovat přes oblast o rozměrech
malých ve srovnání se složkami tenzoru křivosti Riklm; pak lze zavést vektorovou bázi, která
bude v této oblasti téměř kovariantně konstantní a obdržet
přibližný integrální zákon zachování energie a hybnosti.
*) Podobně jako se v Newtonovské
mechanice obecně nezachovává samotná kinetická energie,
nýbrž pouze součet kinetické energie a potenciální energie
soustavy v příslušném silovém poli.
Z čistě teoretického hlediska není porušení zákonů zachování energie a hybnosti v obecné teorii relativity tak "tragické", jak by se mohlo na první pohled zdát. Každou úlohu v OTR lze totiž v principu řešit pomocí Einsteinových rovnic bez nutnosti použití zákonů zachování. Přesto však jsou energie a hybnost natolik důležité a pro praxi užitečné pojmy fyziky, že jejich ztráta by byla velmi nepříjemná. Můžeme to srovnat s jinými oblastmi fyziky, např. s klasickou teorií srážek pružných těles. I bez použití zákonů zachování lze pomocí detailního rozboru deformací kolidujících těles v principu vypočítat jejich pohyby. Takový výpočet je však složitý a jsou pro něj třeba konkrétní údaje o vlastnostech materiálu jednotlivých těles. Výhody použití zákonů zachování energie a hybnosti jsou zde evidentní. Stejně tak je i v obecné teorii relativity rozumné pokusit se zavést zákony zachování veličin interpretovatelných jako energie a hybnost vyšetřovaných soustav.
Pseudotenzor
energie-hybnosti
Pro získání zakonů zachování by bylo užitečné
"překážející" člen v (2.87) vyjádřit jako
obyčejnou čtyřdivergenci nějaké veličiny, kterou označíme
tik:
Gimk Tmk = ¶ t ik /¶ xk .
Je jasné, že veličina tik nemůže mít tenzorové transformační vlastnosti; jako tenzor se chová pouze při lineárních transformacích - nazývá se pseudotenzor. Za Tmk můžeme dosadit z Einsteinových rovnic, takže bude
¶ t ik /¶ xk = 1/8p Gimk G mk .
Řešení rovnice (2.88) není jednoznačné, existuje mnoho různých veličin tik splňujících tuto rovnici (k tomu viz níže).
Tenzorový zákon (2.87) lze tedy upravit na tvar
| ( T ik + t ik ),k = 0 , | (2.89) |
kde v tik je použito Einsteinových rovnic tak, aby v tomto tik vystupovaly jen gravitační proměnné gik. Vztah (2.89), který obsahuje (za cenu ztráty tenzorového charakteru) již běžné parciální derivace, umožňuje přechod mezi objemovými a plošnými integrály a vyjadřuje proto zákon zachování součtu tenzoru energie-hybnosti Tik těles a negravitačních polí a tzv. pseudotenzoru energie-hybnosti gravitačního pole tik, který by měl určovat hustotu a tok energie a hybnosti samotného gravitačního pole. Integrací rovnice (2.89) dostaneme
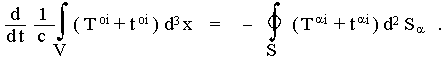 |
(2.90) |
Veličiny Pi = (1/c)ň(Toi + toi)d3x, které v situaci bez gravitačního pole v inerciální soustavě (tik =0) přecházejí v běžnou 4-hybnost ňToidV soustavy, lze interpretovat jako celkovou čtyřhybnost soustavy zahrnující jak zdroj, tak gravitační pole. Komponenty Tai + tai pak vyjadřují příslušný proud energie a hybnosti. Platí tedy integrální zákon zachování čtyřvektoru
| P i = (1/c) Sň ( T ik + t ik ) dSk | (2.91a) |
celkové energie a hybnosti soustavy včetně gravitačního pole. Integruje se zde přes celou hyperplochu S prostorového typu; pokud je to hyperplocha xo=const., bude
| P i = (1/c) Vň ( T io + t io ) dV . | (2.91b) |
Pozici a úlohu pseudotenzoru energie-hybnosti gravitačního pole tik v Einsteinových rovnicích je možno ujasnit (a zároveň získat jednu z variant jeho konstrukce) tím, že budeme uvažovat metriku opět ve tvaru (2.63)
gik = hik + hik
bez nároku na to, aby hik byly všude malé. Einsteinovy rovnice je pak možno přepsat ve tvaru
| Rik(1) - 1/2 hikR(1) = (8pG/c4) (Tik + tik) , | (2.92) |
kde Rik(1) = 1/2 (hli;kl - h;ik - hik;ll + hlk;il) je část Ricciho tenzoru křivosti Rik lineární v hik a
| t ik = (c4/8pG)(Rik - 1/2 gikR - Rik(1) + 1/2 hikR(1) . | (2.93) |
Jelikož pro veličiny Rik(1) platí linearizovaná varianta Bianchiho identit (Rik(1) - 1/2 hikR(1)),k = 0 , plyne z rovnic pole (2.92) diferenciální zákon zachování pro Tik + tik ş hilhkm(Tlm + tlm) :
| ( T ik + t ik ),k = 0 . |
Z rovnice (2.92) je vidět, že zdrojem pole hik jsou veličiny Tik+ tik, pro něž platí diferenciální zákon zachování (2.89); tik určené vztahem (2.93) je tedy pseudotenzorem energie-hybnosti gravitačního pole.
Diferenciální zákon zachování tvaru (2.89) bude identicky splněn tehdy, když Tik+ tik může být vyjádřeno jako čtyřdivergence
| ( T ik + t ik ) = U ikl,l | (2.94) |
tzv. superpotenciálu Uikl = -Uilk antisymetrického v posledních dvou indexech. Vyjádření (2.94) umožňuje objemové integrály v (2.91) pro veličiny Pi převést pomocí Gaussovy věty na plošné integrály přes uzavřenou plochu S obklopující vyšetřovanou soustavu:
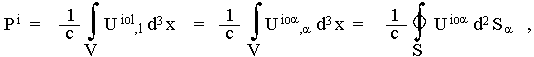 |
(2.95) |
kde dSa = nar2dW je element "vyřezaný" na uzavřené ploše S prostorovým úhlem dW = sinJdJdj s vrcholem v počátku souřadnic, na= xa/r je vnější normálový vektor k plošce dSa. Při konstrukci pseudotenzoru tik podle (2.92) a (2.93) je příslušný superpotenciál dán rovnicí
| R(1)ik - 1/2 hikR(1) = (c4/8pG) ¶ U ikl /¶ xl , |
která je splněna při
Uikl = hmm,k hil - hmm,i hkl - h,mmk hil + h,mmi hkl + hkl,i - hmli,k .
Pro celkovou energii soustavy uvnitř uzavřené plochy S pak ze vztahu (2.95) plyne
| E ş P° = (c4/8pG) Sň( hab,a - haa,b ) dSb , | (2.96a) |
což vyjádřeno pomocí gik = hik + hik dává
| P° = (c4/8pG) Sň( gab,a - gaa,b ) dSb . | (2.96a) |
Pro stanovení celkové energie, hybnosti a momentu hybnosti každé konečné soustavy stačí tedy znát asymptotické chování metriky ve velkých vzdálenostech. Pokud je tik, a tedy i Tik+ tik symetrické, platí diferenciální zákon zachování momentu hybnosti
| ¶Jmik/¶xm = 0 , Jmik ş xi(Tkm + tkm) - xk(Tim + tim) , | (2.97) |
podle něhož celkový 4-moment hybnosti
| Jik ş ň(xidPk - xkdPi) = (1/c) Sň[xi(Tkm + tkm) - xk(Tim + tim)] dSm = = (1/c) Vň[xi(Tko + tko) - xk(Tio + tio)] dV |
(2.98) |
se zachovává, tj. je konstantní pokud veličiny Jaik jsou rovny nule na ploše S ohraničující integrovaný objem V. Veličiny Joik popisují tedy hustotu a Jaik proud momentu hybnosti. Za pomoci superpotenciálu lze celkový moment hybnosti (jehož nejdůležitější komponenty J23=J1, J31=J2, J12=J3 tvoří obvyklý vektor J ş (J1,J2,J3) momentu hybnosti vzhledem k "těžišti" T soustavy xaT =ňxa(T°°+t°°)dV/ň(T°°+t°°)dV) vyjádřit též pomocí plošných integrálů přes vzdálenou uzavřenou plochu obklopující celou soustavu (podobně jako vztahy (2.96)).
Takovýto popis gravitační energie v zásadě provedl již před více než 50 lety sám Einstein. Brzy se však ukázalo, že fyzikální význam Einsteinova pseudotenzoru je poněkud pochybný. Bylo zjištěno, že při jeho použití např. i v rovném prostoru bez gravitace je možno pouhým přechodem ke sférickým souřadnicím dosáhnout nenulové hustoty energie a nekonečné celkové energie (neexistujícího) gravitačního pole. Tento absurdní výsledek se někdy nazývá Bauerův paradox. Kromě toho čtyři rovnice (2.88) pro 16 složek tik neurčují zdaleka jednoznačně funkční závislost tik na složkách metrického tenzoru gik a jeho derivacích. Stejně tak existuje nekonečně mnoho superpotenciálů, protože každý jiný soubor veličin U'ikl, které v asymptoticky rovinné oblasti jsou rovny složkám superpotenciálu Uikl, dávají tytéž hodnoty pro plošné integrály Pi (2.96).
V padesátých a šedesátých letech byla zkonstruována řada různých výrazů pro hustotu gravitační energie - jmenujme aspoň pseudotenzor Landaua a Lifšice [166] (který je symetrický a obsahuje jen první derivace gik) nebo pseudotenzor z r.1958 Mickeviče a Mollera [177]. Existuje a je možno vytvořit mnoho různých výrazů pro hustotu gravitační energie (při nichž by celkový tenzor energie-hybnosti při integraci přes dV dával zachovávající se veličiny a při vymizení gravitačního pole by přecházel v Tik) a není jasné, kterému z nich dát přednost - který (a zda vůbec některý) je správný. V souvislostí s uvedenými a některými dalšími problémy se odborníci v oblasti relativity a gravitace v padesátých a šedesátých letech rozdělili na tři skupiny: první věřili, že energii gravitačního pole lze lokalizovat a je třeba jen nalézt "magickou" formuli pro hustotu gravitační energie, která by vyhovovala po všech stránkách; druzí že sice gravitační pole má energii, ale ta je principiálně nelokalizovatelná; třetí konečně pochybovali o existenci gravitační energie vůbec - považovali gravitační pole za čistě geometrický projev. Rozebereme si tyto tři rozdílné názory.
Nejdříve můžeme být hotovi s třetím názorem (popírajícím gravitační energii): tento názor je jednoznačné nesprávný a vznikl následkem chybné interpretace při rozboru vlastností komponent některých výrazů pro pseudotenzory energie-hybnosti gravitačního pole [241]. Pro existenci energie gravitačního pole svědčí velmi pádné fyzikální argumenty. Gravitační energie může být studována pomocí metod, které nevyžadují aplikaci pseudotenzorů (nebo aspoň ne jejich explicitního tvaru) - přímé použití Einsteinových rovnic, které vedou k retardovaným potenciálům (2.65) a odtud ke konečné rychlosti (rovné rychlosti světla) šíření změn v gravitačním poli a k existenci gravitačních vln, které se odpoutávají od zdroje a odnášejí s sebou část jeho energie, hybnosti a momentu hybnosti i bez přítomnosti nějakého "přijímače" těchto vln (viz níže). Protože šíření změn v gravitačním poli je spojeno s předáváním energie, ukazuje konečná rychlost tohoto šíření na to, že gravitační pole samotné je nositelem energie (viz argumentaci v úvodu tohoto odstavce). Ještě sugestivněji ukazují existenci gravitační energie některé experimentální aspekty zmíněné v závěru tohoto odstavce.
O existenci gravitační energie tedy nemůže být pochyb, zbývá pouze vyjasnit, v čem se koncepce energie v obecné teorii relativity shoduje a v čem se liší od vlastností energie v negravitační fyzice. Velké zásluhy v oblasti výzkumu gravitační energie má C.Moller (jež dlouhou dobu zastával první názor o lokalizovatelnosti gravitační energie), který zkonstruoval řadu výrazů pro gravitační energii [182],[177] a zformuloval pět požadavků, kterým by měl vyhovovat správný pseudotenzor energie-hybnosti gravitačního pole:
Moller dále ukázal, že při použití složek metrického tenzoru jako potenciálů pole nelze všem těmto podmínkám současně vyhovět, a proto se používá např. tetrádový formalismus [182],[177]. Souvisí to též s potížemi při důsledně kovariantním popisu gravitačního pole pomocí složek metrického tenzoru jako potenciálů, protože metrické pole je kovariantně konstantní a nemá tedy smysl vyšetřovat závislost veličin na kovariantních derivacích potenciálů, které slouží zároveň jako základ metrické struktury.
Nelokalizovatelnost gravitační
energie
Snahy najít vyhovující vztahy pro hustotu lokální
gravitační energie nevedly k jednoznačným výsledkům. V
jakkoli silném gravitačním poli lze v každém bodě
použitím lokálně inerciální vztažné soustavy, kde Gikl=0, anulovat všechny tik; a naopak, i v plochém prostoročase bez
gravitace lze použitím vhodných křivočarých souřadnic
dostat nenulové hodnoty tik (shora zmíněný Bauerův
paradox). Je tedy principiálně nemožné zavést hustotu
energie gravitačního pole nezávislou na volbě souřadnicové
soustavy, a to i v případě, kdy celková energie je
definována jednoznačně. Proto nemá smysl mluvit o nějaké
určité lokalizaci energie gravitačního pole v prostoru, tj. o
tom, zda v daném místě je nebo není gravitační energie (a
jak velká).
V současné době je nejvíce rozšířen názor, podle něhož lokalizace gravitační energie není možná, energie gravitačního pole je jevem globálním, nikoliv lokálním a fyzikální význam mají (a to ještě ne vždy!) pouze integrální hodnoty energie, hybnosti a momentu hybnosti. Tento názor je v plné shodě s univerzálností gravitační interakce, tj. s principem ekvivalence, podle něhož v libovolném místě lze zavést lokálně inerciální vztažnou soustavu - lokálně "zlikvidovat" gravitační pole a tím i lokální gravitační energii. Lokální gravitační energie nefiguruje jako zdroj na pravé straně Einsteinových rovnic, nezakřivuje tedy prostoročas, nemá "váhu" a není měřitelná. Rozumné fyzikální vlastnosti má gravitační energie pouze v nelokálním smyslu.

Obr.2.13. K analogii mezi nelokalizovatelností energie
gravitačního pole
a nelokalizovatelností krásy malby po ploše obrazu.
Pro lepší pochopení nelokalizovatelnosti gravitační energie bude užitečné použít analogie se zcela jinou oblastí - s výtvarným uměním. Vezměme nějaký hezký umělecký obraz (třebas "Monu Lisu" od Leonarda da Vinci - obr.2.13) a vyšetřujme jeho krásu. Krása obrazu je sice pojem značně vágní a subjektivní, ale většina lidí se jistě shodne, že toto vrcholné dílo velkého renezančního mistra je krásné. Začneme-li však studovat "hustotu" s jakou je krása malby rozložena po ploše obrazu, začnou potíže. Když si rozdělíme plochu obrazu na poměrně velké oblasti (řekněme o rozměrech desítek centimetrů), lze ještě jakž takž říci, že v některých polích je soustředěno více krásy než v jiných. Např. v oblasti A1 (kde je tvář Giocondy) je soustředěno určitě více krásy než v oblasti A2 (ze zamlženého, byť mistrovsky pojatého pozadí - obr.2.13 vpravo nahoře). Zjemňujeme-li však rozdělení, brzy přestává být takové hodnocení možné. Vezmeme-li např. oblasti B1 a B2 (s rozměry asi 3x3 cm), nepoznáme na nich ani odkud pocházejí a o jejich kráse se již nedá vůbec mluvit ( zvětšeně je vidíme na obr.2.13 vpravo dole) - budou na nich fakticky vidět jen detaily nanášení a zasychání barvy. Vidíme tedy, že nemá smysl vyšetřovat hustotu, s jakou je krása malby rozložena po plátně obrazu: krása obrazu je veličina globální, nikoliv lokální, je to vlastnost kompozice celého obrazu. A podobně jako je krásný obraz soustavou ošklivých skvrn, je energetické gravitační pole soustavou lokálních oblastí bez gravitace a bez energie.
Zákony zachování energie, hybnosti a momentu hybnosti jsou důsledkem homogenity času, homogenity a izotropie prostoru. V tomto smyslu tedy pojmy energie, hybnost a moment hybnosti souvisejí se strukturou (symetriemi) prostoročasu. Za přítomnosti gravitace prostoročas v obecném případě nemá žádnou symetrii, takže lze očekávat vážné potíže se zákony zachování. Zákon zachování energie a hybnosti si ponechává platnost pouze v lokálně inerciální vztažné soustavě. Nelokalizovatelnost gravitační energie pak odpovídá nelokálnímu charakteru gravitace jako takové. Koncepce gravitační energie, stejně jako gravitační síly, jsou jen způsobem interpretace křivosti prostoročasu pomocí pojmů, na něž jsme zvyklí v rovinném prostoročase negravitační fyziky.
S lokálními symetriemi prostoročasu, a tím i s lokalizací gravitační energie, se v obecné teorii relativity musíme rozloučit. Existují však případy, kdy je můžeme nahradit symetriemi globálními a zachovat tak alespoň pojem celkové energie. Má-li prostoročas určité vlastnosti symetrie (např. sférickou, axiální nebo rovinnou symetrii) vyjádřené existencí příslušných Killingových vektorů xk (zavedených v §2.4), potom lze setrojit vektor Pi = Tikxk, pro který díky Killingovým rovnicím platí vztah Pi;i = Tikxk;i = (1/2)Tik(xk;i + xi;k) = 0 vyjadřující zákon zachování Pi. Podle toho zda je Killingův vektor xk časového nebo prostorového typu to lze interpretovat jako zákon zachování energie nebo hybnosti.
Gravitační
vyzařování ostrovní soustavy
Nejdůležitějším případem fyzikální soustavy, schopné
vyzařovat gravitační vlny, je ostrovní
fyzikální soustava *) v asymptoticky rovinném
prostoročase, tj. situace kdy vyšetřovaná soustava je
prostorově omezená (nachází se stále
poblíž počátku souřadnic) a v dostatečně velké vzdálenosti se
prostoročas stává rovinným. Zde můžeme celkovou energii
a hybnost soustavy dát do souvislosti s invariancí vůči
časovým a prostorovým posuvům vzhledem k pozorovateli v
nekonečnu (asymptotické symetrie).
*) Nejdůležitějšími ostrovními soustavami tohoto druhu jsou
dvojhvězdy či vícenásobné hvězdné systémy.
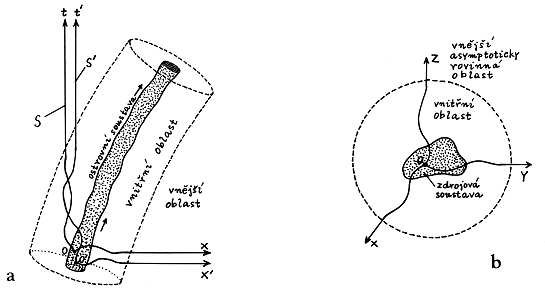
Obr.2.14. Prostoročas (a) a prostor (b)
kolem ostrovní fyzikální soustavy si můžeme rozdělit na
tři části:
l. Oblast vlastního zdroje (tečkovaně), kde kromě silných
gravitačních polí je Tik ą 0.
2. Blízká (ale vakuová) "vnitřní" oblast, kde
gravitační pole a zakřivení prostoročasu může být ještě
silné.
3. Vzdálená asymptoticky rovinná vnější oblast, kde
gravitační pole je velmi slabé (prostoročas téměř plochý)
a kde lze zavést asymptoticky inerciální vztažnou soustavu.
Použijeme-li v ostrovní soustavě asymptoticky Galileovské
vztažné soustavy, dostaneme jednoznačný výraz pro celkovou
energii-hybnost Pi soustavy, který se zachovává, je
nezávislý na volbě souřadnicové soustavy ve vnitřní
oblasti a chová se jako čtyřvektor vzhledem k asymptoticky
Lorentzovým transformacím.
Skutečně,
i přes nejednoznačnost výrazů pro pseudotenzor
energie-hybnosti gravitačního pole lze z nich získat jednoznačný výraz
pro celkový čtyřvektor energie a hybnosti
Pi = (1/c).ň(Toi +toi)dV takové ostrovní soustavy,
který má dobré fyzikalní vlastnosti ve smyslu Mollerova požadavku č.3,4,5. V
asymptoticky plochém prostoru můžeme kolem ostrovní zdrojové
soustavy vymezit natolik velkou prostorovou oblast, aby vně ní
gravitační pole bylo zanedbatelné (obr.2.14). Pro výpočet
energie a hybnosti pole je pak třeba vzít souřadnicovou
soustavu (s počátkem uvnitř nebo někde blízko zdroje)
takovou, aby ve vnější asymptotické oblasti (kde
podle předpokladu pole není) přecházela v Galileovskou
soustavu v níž r®Ąlim gik(x) ® hik + O(1/r), tj. gik(Ą) = hik a všechny složky tik zde vymizely. Ve vnitřní oblasti
(blízké zdroji) může být souřadná soustava zvolena
libovolně aniž to ovlivní hodnoty Pi. I když veličiny Tik+tik netvoří obecně tenzor a Pi
není tedy obecně vektor, je celková energie a hybnost
invariantní vůči takovým transformacím souřadnic xi ® x'i = xi + ei(x) , které
jsou asymptoticky identické, tj. r®Ąlim ei(x)= 0.
Plyne to snadno ze zákona zachování pro Pi. Vezmeme dvě souřadnicové
soustavy S a S' rozdílné ve vnitřní oblasti, avšak
přecházející asymptoticky v tutéž
Galileiho soustavu S. Pro porovnání hodnot Pi
a P'i v těchto dvou soustavách v určitých
časových okamžicích t a t' si lze představit další
(myšlenou) pomocnou "proměnnou" souřadnicovou
soustavu S", která ve vnitřní oblasti v okamžiku t
splývá se soustavou S a v okamžiku t'se soustavou S';
ve vnější oblasti se nemění a splývá stále s toutéž S.
Protože díky zákonu zachování dPi/dt = 0 jsou veličiny Pi
v každé vztažné soustavě konstantní a nezávislé na čase,
platí to i pro soustavu S'', takže Pi(t) = P''i(t') = P''i(t') = P'i(t'). Tato invariance je ostatně
též přímo vidět z plošného integrálu (2.96) aplikovaného
na uzavřenou plochu ležící v asymptotické oblasti, protože
žádné transformace měnící souřadnice pouze uvnitř
ohraničené prostorové oblasti nemohou ovlivnit globální hodnoty
těchto integrálů přes vzdálené plochy. Celková energie a
hybnost ostrovní soustavy se tak nejen zachovává, ale je i
nezávislá, na volbě souřadné soustavy, pokud tato
asymptoticky přechází v danou Galileovskou soustavu. Protože
tik jsou tenzorem vzhledem k
lineárím transformacím, tvoří složky Pi čtyřvektor vzhledem k
lineárním transformacím, tedy i vůči lineárním
transformacím převádějícím jednu asymptoticky Galileovskou
vztažnou soustavu na druhou.
V dostatečně velkých vzdálenostech od statické ostrovní soustavy se vliv detailů rozložení hmoty na gravitační pole postupně stírá a pole tam lze považovat za sféricky symetrické, dané přesným Schwarzschildovým řešením (3.13). Pro r®Ą má toto řešení asymptotický tvar (2.56c)
![]()
kde M je celková hmotnost soustavy. Dosazením
příslušných komponent metrického tenzoru do vztahu (2.96) a
integrací přes sféru poloměru r dostaneme P° = Mc2.
Mollerův požadavek č.5 je tedy rovněž
splněn.
Abychom si ukázali reálnou existenci energie gravitačního pole a zároveň hlouběji pronikli do specifické povahy gravitační energie, vraťme se k otázce vyzařování a přenosu energie gravitačními vlnami, jak jsme to slíbili v předchozím odstavci. Podle Newtonovy teorie izolovaná soustava budící časově proměnné gravitační pole, např. rotující tyč nebo binární systém podle obr.2.10, nebude gravitačně ztrácet žádnou energii - obě tělesa by věčně s konstantní periodou obíhala kolem společného těžiště. Možností, jak z takové soustavy extrahovat prostřednictvím gravitace energii, je např. umístit poblíž vhodné nepružné těleso; měnící se gravitační pole v něm způsobí časově proměnné slapové deformace, které se přemění na teplo zahřívající těleso (tepelná energie může být odváděna nebo se vyzařuje do prostoru infračerveným zářením). Toto se však odehrává v indukční zóně soustavy. V obecné teorii relativity však i v izolované soustavě vzájemný pohyb gravitujících těles vyvolává gravitační vlny odnášející ze soustavy energii - ve vlnové zóně.
Standartní (a do konce
šedesátých let vlastně jediná) metoda jak vypočítat
energii přenášenou gravitačním zářením, tj. množství
energie odnášené od daného zdroje gravitačními vlnami, je
stanovení proudu energie přes myšlenou uzavřenou plochu
obklopující zdroj dostatečně daleko ve vlnové zóně, s
použitím pseudotenzoru energie-hybnosti tik vlnícího se
gravitačního pole. Přitom se předpokládá, že energie
zdroje se zmenšuje se stejnou rychlostí, s jakou je takto
vypočtená energie gravitačními vlnami odnášena.
Obklopíme tedy zdrojovou
soustavu myšlenou uzavřenou
plochou S ležící v dostatečné vzdálenosti (a
tedy ve vlnové zóně). Množství energie odnášené od zdroje
gravitačními vlnami je podle (2.90) dáno proudem gravitační
energie přes tuto uzavřenou plochu S
(na ploše S
předpokládáme vakuum, tj. Tik=0) :
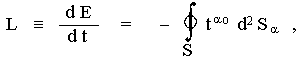
Pro výpočet proudu energie ta° je třeba určit gravitační pole ve vlnové zóně, tj. ve vzdálenostech R>>cT, velkých ve srovnání s délkou vyzařovaných vln. Vyjdeme z obecného řešení (2.65)
 |
(2.65) |
popisujícího metrické koeficienty, retardované t-R/c z jednotlivých míst zdrojové soustavy. Budeme předpokládat, že rychlosti těles ve zdrojové soustavě jsou dostatečně malé tak, aby délka vln byla mnohem větší než rozměry zdroje. K retardovaným integrálům (2.65) pak budou podstatně přispívat jen oblasti ležící uvnitř a v bezprostřední blízkosti zdroje. Umístíme-li počátek souřadnic někam dovnitř zároje, pak z hlediska každého dostatečně vzdáleného bodu budou všechna místa efektivní zóny zdroje přibližně ve stejné vzdálenosti R jako je počátek souřadnic. Retardované potenciály ve vlnové zóně lze tedy vyjádřit ve tvaru
| y ik = (4G/c4R) Vň ( T ik + t ik )(t-R/c,x'a) dV . |
Pro daný účel jsou potřeba jen prostorové složky yab dané distribucí celkového tenzoru napětí Tab+ tab. Použitím zákonů zachování (2.90), které jsou vlastně pohybovými rovnicemi zdroje, však lze veličiny yab vyjádřit pomocí integrálů distribuce hmoty-energie T°°+t°°, protože platí
| Vň ( T ab + t ab ) dV = (1/2) d2/dt2 Vň ( T oo + t oo ) dV . |
Pokud má zdroj nerelativistickou (tj. téměř Newtonovskou) povahu, lze gravitační příspěvek k celkové energii zanedbat (t°°<< T°°), takže dostaneme
| yab = (2G/c4R) d2/dt2 K ab(t-R/c,x'a) . | (2.99) |
kde
| K ab = Vň T oo(t,x) xa xb dV = c2 Vň r(t,x) xa xb dV . | (2.100) |
je kvadrupólový
moment
rozložení hmoty zdroje. Vztah (2.99) je proslulá kvadrupólová formule, udávající amplitudu gravitačních vln ve vzdálenosti R od
zdroje s časově proměnným kvadrupólovým rozložením hmoty (retardační proměná t-R/c v praxi nemá význam).
Pozn.: Alternativní
odvození kvadrupólového formule spočívá v rozložení Tik(t-R/c,xa) ve
vzorci (2.65) v mocninnou řadu, s ponecháním
členů do 2.řádu a substitucí vzorce pro kvadrupólový
moment.
Nyní již můžeme vypočítat
pseudotenzor t°a a vlnovou gravitační energii.
Ve velkých vzdálenostech od zdroje lze gravitační vlny
považovat (v ne příliš velkých
oblastech prostoru)
za prakticky rovinné, v nichž se pole mění pouze podél
jednoho (radiálního) směru v prostoru. Orientujeme-li zde
souřadnicovou soustavu tak, že tento směr šíření bude osou
xl, bude gravitační vlna určena pouze
komponentami h23 a h22=-h33 a nenulová složka pseudotenzoru bude pouze t01, pro kterou z definice tik vychází
| t 01 = (c2/16pG) [.h23 + 1/4 (.h22 - .h33 )2 ] | (2.101) |
(všechny veličiny jsou funkcí pouze (t-xl/c)). Dosazením za h23= y23, h22= y22 a h33= y33 z (2.99) dostaneme pro energii vyzařovanou za jednotku času přes jednotkovou plochu kolmou k ose xl vztah
| c. t 01 = (G/32pR2) [...K23 + 1/4 (...K22 -...K33 )2 ] , | (2.102) |
z něhož plyne výše
uvedený kvadrupólový vzorec (2.79) pro intenzitu
gravitačního záření v obecném směru n. Ztráta energie soustavy za
jednotku času, daná celkovým gravitačním zářením do
všech směrů protékajícím sférou poloměru R,
pak vychází
dE/dt = - (G/45c2) ...Kab2 ,
což je důležitá kvadrupólová
formule
(2.77) pro gravitačně vyzařovaný výkon. Důležitost těchto vzorců je
ukázána v §2.7 "Gravitační
vlny",
pasáž "Zdroje gravitačních vln ve
vesmíru".
Energie gravitačních vln
Vzhledem k (oprávněným) výhradám k fyzikálnímu významu
pseudotenzorů energie-hybnosti gravitačního pole však takový
výpočet sám o sobě nemusí být zcela přesvědčivý. Např.
skutečnost, že vhodnou volbou soudadné soustavy lze tik anulovat v každém bodě prostoru [241],
byla někdy interpretována tak, že gravitační vlny
nepřenášejí energii a reálně ani neexistují. I když proti
těmto námitkám lze argumentovat tím, že celková vyzařovaná energie
nezávisí na souřadnicové soustavě ani na použitém
pseudotenzoru, je třeba správnost standartního postupu
výpočtu vyzařované gravitační energie podložit metodami
nevyžadujícími přímé použití pseudotenzorů. A
skutečně, byly nalezeny hned dvě takové cesty. V
prvé řadě, Isaacson [140] zkostruoval tenzor (nikoliv
pseudotenzor) energie-hybnosti gravitačních vln šířících
se na pozadí zakřiveného prostoročasu, přičemž tento Isaacsonův tenzor (2.76) se ukázal být roven
pseudotenzoru tik zprůměrovanému přes několik
vln. Tím byla prokázána správnost výsledků získaných
standartní metodou s použitím pseudotenzoru pro energii
gravitačních vln. Dále, Thorne [249], Burke [36],
Chandrasekhar a Esposito [47] přímými výpočty ukázali, že
brzdění pohybů ve zdrojové soustavě vlivem zpětné
reakce buzeného proměnného pole přesně odpovídá energii odnášené gravitačními vlnami a počítané standartními
metodami s použitím pseudotenzorů. Stručně se o obou
metodách zmíníme.
Pro lepší názornost si zde znovu uvedeme obr.2.9 ukazující Isaacsonovu metodu analýzy energie gravitačních vln zprůměrováním přes několik vlnových délek :
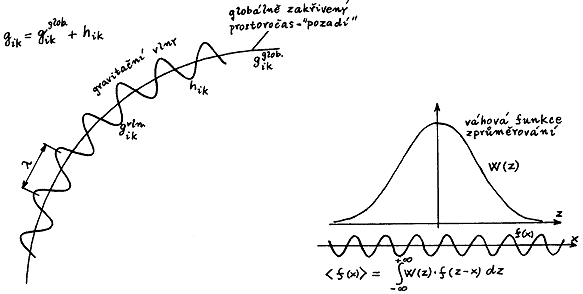
Obr.2.9. V Isaacsonově krátkovlnné aproximaci lze odlišit
globální zakřivení prostoročasu ("pozadí") od
lokálních fluktuací gravitačních vln, pokud je vlnová
délka mnohem menší než charakteristický poloměr křivosti
prostoročasu. Tato separace se provádí pomocí
zprůměrování přes oblast o několika vlnových délkách za
použití vhodné normované váhové funkce W(z) konvergující
k nule s rostoucí vzdáleností.
V gravitační vlně nelze lokalizovat energii a hybnost do oblasti menší než délka vlny - nedá se tedy určit, jakou část energie přenáší vrchol, dolina nebo "sklon" vlny. Je však možno říci, že určité dobře definované množství energie (a hybnosti) je obsaženo v dané dostatečně velké oblasti s rozměry několika vlnových délek. Plyne to z Isaacsonova formalismu (stručně vyloženého v předchozím odstavci), který pomocí rozdělení metriky na rychle a pomalu se měnící části umožňuje nejen vyšetřovat gravitační vlny v zakřiveném prostoročase (tj. jejich pohyb v poli gravitujících těles nebo na globálním pozadí zakřiveného vesmíru v kosmologii), ale zachycuje i obrácené působení, tj. zakřivování prostoročasu účinkem energie obsažené v gravitačních vlnách. Toto zakřivování prostoročasu gravitačními vlnami popisují rovnice (2.75)
| Rikglob
- 1/2Rglob gikglob
= |
mající tvar normálních Einsteinových rovnic, kde zdroj na pravé straně je Isaacsonův tenzor efektivní rozprostřené energie-hybnosti definovaný vztahem (2.76)
| T ikvln ş - (c4/8pG) (<Rikvln> - 1/2 gikglob . <Rvln>) . |
Navíc se ukazuje, že tento Isaacsonův tenzor je roven prostoročasovému průměru přes několik vlnových délek pseudotenzoru energie-hybnosti tik gravitačního pole ve vlně :
| T ikvln = < t ikvln > | (2.103) |
(konkrétně byl výpočet proveden pro pseudotenzor ve formě Landaua a Lifšice [166]). Pokud nejsme ve vakuu a kromě gravitačních vln jsou přítomna tělesa a další negravitační pole popsaná sumárním tenzorem energie-hybnosti TikH, budou rovnice (2.75) mít tvar
| G
ikglob
ş Rikglob - 1/2Rglob
gikglob = |
(2.104) |
Při zprůměrování
pseudotenzoru tik přes několik vlnových délek
tedy dostáváme tenzor energie a hybnosti Tvlnik gravitačních vln, který má
zcela dobrý fyzikální význam (ovšem v nelokálním smyslu).
Podle (2.75) a (2.104) může tento tenzor mimo jiné sloužit
jako rovnoprávný zdroj (spolu s tenzorem energie-hybnosti
těles a negravitačních polí) na pravé straně
Einsteinových gravitačních rovnic, a tedy přispívá ke
globálnímu zakřivení prostoročasu. V principu je možno
dokonce dosáhnout takového zkoncentrování gravitačních vln,
že vlivem jejich "samogravitace" část gravitační
energie podlehne gravitačnímu kolapsu a vytvoří
černou díru; taková "čistě gravitační" černá
díra bude mít díky teorému "černá díra nemá
vlasy" úplně stejné vlastnosti jako černá díra
vzniklá kolapsem běžné hmoty, třebas hvězdy - viz §4.5.
Jiným příkladem čistě gravitačního objektu *) je
Wheelerův gravitačni geon - hypotetický metastabilní útvar z
gravitačních vln udržující se pohromadě vlastní gravitací
(§B.3 "", pasáž "").
*) V rovinné gravitační
vlně energie a hybnost spolu souvisejí vztahem p= p = E/c -
rychlost gravitačních vln je rovna rychlosti světla, klidová
hmotnost gravitonů je nulová. Při setkání dvou vln různého
směru se jejich hybnosti p = p1+p2 sčítají vektorově,
zatímco energie E = E1+E2 se sčítají skalárně, takže E/c
> p - superpozice vln různého směru má efektivně
nenulovou klidovou hmotnost.
Isaacsonovým formalismem je tedy
potvrzena správnost globálních výsledků výpočtu energie a
hybnosti gravitačních vln standartními metodami s použitím
pseudotenzorů. Pro stanovení energie gravitačních vln lze
též poněkud oslabit základní požadavek asymptotické
Eukleidovosti metriky, protože stačí vyšetřovat konečný
objem o rozměrech podstatně převyšujících délku vln.
Při studiu gravitačního záření se automaticky předpokládá, že zdroj ztrácí energii (a moment hybnosti) přesně s toutéž rychlostí, s jakou je energie odnášena gravitačními vlnami. Avšak metody výpočtu energie gravitačnich vln ani zákony zachování, na nichž je tento předpoklad založen, nejsou v obecné teorii relativity vždy tak jednoznačné jako v klasické fyzice. Proto je zvláště cenné, že ztrátu energie zdroje je možno stanovit i přímými výpočty vlivu buzeného pole v blízkosti zdroje - analýzou zpětné reakce gravitačního pole na vyzařující soustavu. Tento rozbor vede k závěru, že uvnitř a v blízkosti zdroje se vytváří určitá malá proměnná složka prostoročasové křivosti (gravitačního pole) s fází odlišnou od hlavní proměnné složky; tento člen způsobuje ve zdroji brzdící síly.
Výpočty (založené opět na vztahu (2.65), resp. (2.99)) ukazují, že hlavní část této přídavné složky "re" způsobující brzdění lze při vhodné kalibraci vyjádřit ve tvaru
| hoore = (2G/15c5) (d5/dt5 K ab) xa xb , |
takže příslušné brzdění zpětnou reakcí vyzařovaných vln lze dokonce v hlavních rysech popsat pomocí modifikace Newtonova potenciálu :
| j = j New + j re , j re ş - 1/2 hoore = (2G/15c5) (d5K ab/dt5 )xa xb , | (2.99) |
kde jNew je Newtonův potenciál a j re je potenciál brzdné síly způsobené reakcí záření. Zrychlení každé testovací částice v tomto potenciálu j bude aaş d2xa/dt2 = - j,a = - j New,a- j re,a a brzdná síla působící na částici hmotnosti m bude rovna m.j re,a. Tato brzdná síla povede uvnitř zdroje ke ztrátě energie
d E / d t = Vň r . aa va dV = - Vň r . j re,a va dV ,
kde va je rychlost příslušného elementu rdV (složka jNew se zde neuplatňuje, protože v Newtonově teorii se energie zdroje zachovává a změna může být způsobena jen částí odpovídající j re). Průměrná rychlost, se kterou se vlivem brzdění zpětnou reakcí záření zmenšuje energie soustavy
< d E / d t > = - Vň r . j re,a va dV = (G/45c5) < (d3Kab/dt3)2>
vychází stejná jako rychlost, s níž je energie odnášena gravitačními vlnami podle kvadrupólového vzorce (2.77). Tento výsledek je zde však získán nezávislým způsobem, nijak nesouvisejícím s energií obsaženou v gravitačních vlnách!
Přeměny gravitační energie
Dosud jsme rozbor
vlastností gravitačni energie (a
zdůvodňování její existence) prováděli na teoretické úrovni.
Druhý směr argumentace ve prospěch existence energie
gravitačního pole se obrací k experimentu - ke studiu podmínek, za nichž
mohou gravitační síly konat práci a docházet k přeměně gravitační energie na jiné druhy
energie.
Za jeden z takových "gravitačních motorů" můžeme považovat např.
mořský příliv, který přeměňuje
prostřednictvím gravitačního působení část kinetické
energie obíhajícího Měsíce na teplo a mechanickou energii na
povrchu Země. Celý proces však probíhá hluboko uvnitř
"induktivní" zóny soustavy (prakticky
v jejím středu),
takže veškeré efekty retardace a konečné rychlosti
gravitačního působení se vzhledem k promalé oběžné
periodě nijak neprojeví - přenos energie zde lze popsat i v
rámci Newtonovy teorie.
Co se týče gravitačních vln, navrhl již v padesátých letech H.Bondi [21] velmi jednoduchý a názorný myšlený experiment, jehož uspořádání je na obr.2.15. Na hladké tyči se mohou téměř volně, s dostatečně malým třením, pohybovat dva hmotné prstence. Gyroskopy na koncích tyče zamezují její (lokální) rotaci. Celý systém se pohybuje volně v prostoru (těžiště po geodetice) a gravitační vlny v důsledku deviace geodetik posunují prstence od sebe a k sobě. Vlivem tření o tyč se takto část energie gravitačních vln přeměňuje na teplo, které můžeme od tyče odebírat. Popř. kdyby byly prstence přes páky a vhodné převodové ústrojí spojeny s dynamem, měnila by se energie gravitačních vln na elektrickou energii. Z energetického hlediska můžeme detektory gravitačních vln (stručně popsané v minulém odstavci) s trochou nadsázky považovat za jakési "mikroelektrárny" s nepatrným výkonem využívající energie gravitačních vln. Nemůže snad být přesvědčivějšího argumentu, že gravitační vlny mají energii, než to, že pomocí vhodného uspořádání lze v principu tuto energii odebírat a přeměňovat ji na jiný druh energie..!..
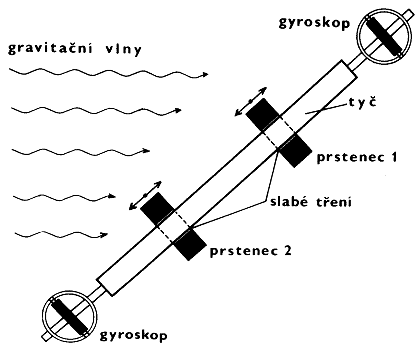 |
Obr.2.15. Jednoduché modelové uspořádání pro přeměnu energie gravitačních vln na teplo. |
Z obecné teorie relativity tedy jednoznačně plyne existence gravitačních vln, které se odpoutávají od zdroje a odnášejí s sebou do prostoru část jeho energie, hybnosti a momentu hybnosti i bez přítomnosti nějakého "přijímače" těchto vln. Integrální zákon zachování (2.86) energie a hybnosti přechází při zahrnutí gravitačního záření na tvar
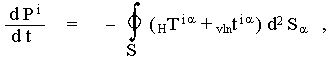 |
(2.106) |
kde plocha S leží v asymptoticky rovinném prostoročase (a tedy ve vlnové zóně soustavy). Tyto rovnice v asymptoticky rovinném prostoročase obklopujícím vyšetřovaný systém, které již neobsahují žádné netenzorové veličiny říkají, že rychlost změny energie a hybnosti soustavy je rovna proudu, kterým je přes uzavřenou plochu obklopující soustavu přenášena energie a hybnost látkovým prostředím (tělesa, plyn, částice a pod.) + negravitačními poli (např. elektromagnetickým zářením) - "H", a gravitačními vlnami - "vln". Vidíme tedy, že při analýze chování každé fyzikální soustavy v asymptoticky rovinném prostoročase můžeme s výhodou použít běžných zákonů zachování energie, hybnosti a momentu hybnosti (gravitačně měřených), přičemž ovšem musíme započítat i energii odnášenou (popř. pohlcovanou) gravitačními vlnami.
V průběhu výzkumu zůstávala dlouhou dobu otevřená otázka o znaménku gravitační energie a celkové energie fyzikální soustavy vůbec. V Newtonovské fyzice je celková energie hmotné soustavy a gravitačního pole dána integrálem
E = Vň [ r . v2/2 - (grad j)2/(8pG) ] d V ,
přičemž hustota energie samotného gravitačního pole w = -(grad j)2/(8pG) je zde záporná. Příslušný výpočet s použitím Einsteinova pseudotenzoru dává kladnou hustotu energie gravitačního pole; při použití některých jiných výrazů pro pseudotenzor tik (např. Landauův-Lifšicův pseudotenzor) vychází hustota gravitační energie záporná. Hustota energie gravitačních vln (zprůměrovaná) je kladná. Tyto rozpory, které vznikají různým rozdělením celkové energie na energii zdroje, energii gravitačního pole a interakční energii, však vzhledem k nelokalizovatelnosti gravitační energie nejsou důležité. Fundamentální význam však má znaménko celkové energie, které souvisí se stabilitou systému. V relativistické teorii negravitačních polí vychází výraz pro energii pole explicitně kladný. Výrazy pro energii gravitačního pole ani pro celkovou energii fyzikální soustavy v OTR však již tuto vlastnost nemají, o číselné hodnotě a znaménku celkové energie lze rozhodnout až pomocí analýzy rovnic pole. Taková analýza byla provedena v pracech Schoena a Yau [230],[231] a Wittena [282], kteří dokázali, že celková energie gravitačního pole a zdrojové soustavy (s kladným tenzorem energie-hybnosti) je kladná, jak to odpovídá základním fyzikálním požadavkům.
Na shora diskutovanou otázku, zda "Má gravitační pole energii?" můžeme tedy odpovědět kladně v závěrečném shrnutí o specifických vlastnostech gravitační energie v obecné teorii relativity :
| Teorém 2.6 (gravitační energie) |
|
Ve srovnání s klasickou fyzikou dochází v obecné teorii relativity k určité degradaci pojmu energie. Nejen že hustota energie ztrácí lokální význam (takže názorná představa energie jako určité "substance" spojitě a jednoznačně rozložené v prostoru již nemá opodstatnění), ale i celková energie může být definována jen při splnění speciálních geometrických a topologických předpokladů. Pouze v asymptoticky rovinném prostoročase s Eukleidovskou topologií mají veličiny globální energie a hybnosti ostrovní fyzikální soustavy dobře definovaný význam. Pokud neexistuje asymptoticky plochá oblast prostoročasu, neexistuje ani invariance vzhledem k prostoročasovým posuvům, k níž by bylo možno vztáhnout energii a hybnost. Obrazně lze říci že neexistuje rozumná "plošina" na niž by se dalo postavit a "zvážit" daný systém. Taková situace zřejmě nastává pro vesmír jako celek, jak ukazuje současná kosmologie (kap.5, §5.2). Energie, jež je v klasické fyzice fundamentálním pojmem a základním atributem hmoty, se tak stává řadovou veličinou (obecně bez názorného fyzikálního významu), která za určitých situací (díky svému zákonu zachování) popisuje některé vlastnosti hmoty. Ve světle souvislostí mezi zákony zachování a symetriemi prostoročasu nás však toto nemusí příliš překvapovat. Degradace pojmu energie úzce souvisí s revizí pojmů prostoru a času v obecné teorii relativity, které byly svrženy z trůnu absolutnosti a něměnnosti a staly se dynamickými prvky těsně souvisejícími s rozložením a pohybem hmoty.
| Gravitace, černé díry a fyzika prostoročasu : | ||
| Gravitace ve fyzice | Obecná teorie relativity | Geometrie a topologie |
| Černé díry | Relativistická kosmologie | Unitární teorie pole |
| Antropický princip aneb kosmický Bůh | ||
| Jaderná fyzika a fyzika ionizujícího záření | ||
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | ||