| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | Gravitace, černé díry a fyzika |
Kapitola 2
OBECNÁ TEORIE
RELATIVTITY
- FYZIKA GRAVITACE
2.1. Zrychlení a gravitace z hlediska
speciální teorie relativity
2.2. Univerzálnost - základní
vlastnost a klíč k pochopení podstaty gravitace
2.3. Lokální princip ekvivalence
a jeho důsledky
2.4. Fyzikální zákony v
zakřiveném prostoročase
2.5. Einsteinovy rovnice
gravitačního pole
2.6. Deviace a fokusace geodetik
2.7. Gravitační vlny
2.8. Specifické vlastnosti
gravitační energie
2.9.Geometrodynamická soustava
jednotek
2.10. Experimentální
ověřování teorie relativity a gravitace
2.6.
Deviace a fokusace geodetik
Nyní,
když již máme k dispozici Einsteinovy rovnice gravitačního
pole, se ještě na chvíli vrátíme k otázce vlivu
gravitačního pole na pohyb těles, kterou jsme načali v §2.4.
Homogenní gravitační pole lze v celém prostoru
"odfiltrovat" přechodem ke globální inerciální
soustavě. I v nehomogenním gravitačním poli lze podle
principu ekvivalence zavést lokální inerciální soustavu, v
níž budou všechny fyzikální děje probíhat (lokálně)
podle zákonů speciální teorie relativity. Protože tedy
gravitační pole lokálně neexistuje, vzniká otázka, jakým
způsobem vlastně skutečné (nehomogenní) gravitační pole
působí na fyzikální děje? Neboli
jinak: jak se na fyzikálních zákonech projevuje zakřivení prostoročasu?
Jak vůbec rozlišíme efekty gravitace od vlivu vztažné
soustavy? Je jasné, že lokálně nijak. Proto je třeba ke
studiu vlivu gravitace použít nelokální přístup.
Např. místo jedné testovací částice (kterou je možno vždy
považovat za lokálně volnou a která nám tedy nic neřekne o
zakřivení prostoročasu) budeme sledovat rozdílnost chování dvou
testovacích částic.
Gradienty
gravitačních sil, deviace geodetik
Mějme dvě testovací částice, z nichž jedna je umístěna v
bodě x i (tu budeme považovat za vztažnou) a
druhá v blízkém bodě x i + e i, kde e i je čtyřvektor prostoročasové
"odlehlosti" těchto dvou testovacích částic.
Jestliže obě blízké testovací částice necháme volně
spolu "padat" v gravitačním poli (obr.2.17), budou se
pohybovat po světočárách x i (l) a x i (l) + e i(l)
(čtyřvektor ei(l) spojuje body obou trajektorií se
stejným l), které jsou geodetikami :
![]()
Jestliže tyto rovnice od sebe odečteme a vypustíme členy vyššího řádu v ei (máme na mysli limitní přechod ei ® 0), dostaneme
![]()
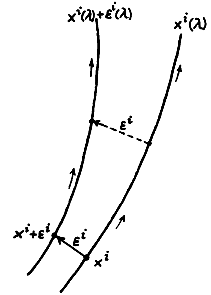 |
Obr.2.7. Dvě blízké testovací částice volně vedle sebe "padající" v gravitačním poli (zakřiveném prostoročase) se budou pohybovat po geodetikách které nebudou zcela paralelní, ale budou se vzájemně odchylovat (deviace geodetik). |
Zajímá nás rozdílnost pohybu obou testovacích částic (deviace obou geodetik), tedy kovariantní derivace jejich odchylky ei. S použitím vztahu (2.15) pro kovariantní (absolutní) derivaci vektoru podél křivky dostaneme konečný výsledek
| D2 e i
dxk
dxm -------- - Riklm ----- ----- el = 0 , dl2 dl dl |
(2.57) |
což je tzv. rovnice deviace geodetik. Podle ní dvě tělesa volně padající vedle sebe v nehomogenním gravitačním poli se budou vůči sobě vzájemně přibližovat nebo oddalovat (jejich geodetiky se budou vůči sobě odchylovat), přičemž vzájemné zrychlení obou částic D2ei/dl2 je úměrné tenzoru křivosti Riklm. Složky tenzoru křivosti tedy popisují gradienty gravitačních sil (slapové síly). V rovinném prostoročase jsou všechny složky tenzoru křivosti rovny nule - nedochází k deviaci geodetik.
Pro získání úplnějšího obrazu o vlivu gravitace na pohyb hmoty přejděme nyní od dvojice blízkých geodetik k celé kongruenci takových geodetik. Můžeme si to představit tak, že v každém bodě prostoru je umístěna bodová testovací částice a jejich světočáry tvoří v prostoročase tuto kongruenci geodetik - každým bodem (událostí) prostoročasu prochází určitá geodetika. Stanovíme-li pro každou geodetiku v každém jejím bodě jednotkový tečný vektor Vi, dostáváme pro kongruenci geodetik celé pole tečných vektorů Vi(xk). Rozbíhavost" (divergence), resp. "sbíhavost" (konvergence) C geodetik v dané kongruenci je určena kovariantni čtyřdivergencí vektorového pole Vi :
| C =def V i;i . | (2.58) |
Konvergence kongruence geodetik časového typu se řídí důležitou Raychaudhuriho diferenciální rovnici [127],[203]
| d C / d s = Rik Vi Vk + 2 s2 + (1/3) C2 | (2.59a) |
kde s popisuje vzájemný "skluz" geodetik (neuvažujeme zde rotaci; pokud by kongruence geodetik rotovala, byl by na pravé straně ještě člen -2w2). Analogická rovnice platí i pro konvergenci světelných (nulových) geodetik:
| d C / d l = Rik Vi Vk + 2 s2 + 1/2 C2 | (2.59b) |
kde V i jsou izotropní tečné vektory.
Energetické
podmínky
Všimněme si nyní některých obecných vlastností rovnic
(2.59a,b). Poslední dva členy na pravých stranách obou rovnic
jsou nezáporné, takže o výsledném znaménku změn
konvergence rozhoduje člen RikViVk. Aby i tento člen byl
nezáporný, musí být podle Einsteinových rovnic (2.50b)
gravitační pole buzeno tenzorem
energie-hybnosti splňujícím nerovnost
| (Tik - 1/2 T gik ) Vi Vk ł 0 | (2.60a) |
pro všechny vektory Vi časového typu, resp. nerovnost
| Tik Vi Vk ł 0 | (2.60b) |
pro izotropní vektory Vi (pro něž je gikViVk = 0). Pro tenzor energie-hybnosti tvaru ideální kapaliny (1.108) je to splněno tehdy, když hustota a tlak splňují relace
| r ł 0 , r + pa ł 0 , resp. r ł 0 , r + a=1S3pa ł 0 . | (2.61a,b) |
Tato tzv. slabá energetická podmínka (2.60) je splněna pro všechny
dosud pozororované formy hmoty, protože
hustota energie je zde nezáporná a k narušení energetické podmínky by bylo třeba velkého
záporného tlaku p *) .
*) Slabá energetická
podmínka by však nebyla splněna např. pro hypotetické C-pole ve "steady-state" modelu
vesmíru (zmíněném v kap.5), které má zápornou
hustotu energie Too, nebo pro
pole "falešného vakua" při inflační expanzi vesmíru (viz
§5.5). A rovněž ne pro hypotetickou tzv. exotickou
hmotu, používanou pro antigravitační
"vystužení" traverzabilních červích děr
(.......).
V praxi je zřejmě splněna ještě o
něco silnější podmínka tzv. energodominantnosti: pro každý vektor Vi
časového typu je TikViVk
ł 0 a vektor TikVk je časového nebo izotropního typu, tj.
lokální hustota energie je nezáporná a navíc lokální proud
energie se děje jen uvnitř nebo na plášti světelného
kuželu. Platí tedy T°° >= |Tik|, tj. energie "dominuje" nad ostatními složkami
tenzoru energie-hybnosti. Pro nejobvyklejší typ tenzoru
energie-hybnosti (1.108) je to splněno tehdy, když r ł 0, -r Ł paŁ
r (a= 1,2,3), tj. když tlak
nepřevyšuje hustotu energie, rychlost "zvuku" nepřevyšuje
rychlost světla.
Pozn.: V literatuře jsou někdy
diskutovány celkem 4 energetické podmínky (....., .... , ).
Pro naši analýzu geometrie prostoročasu v okolí černých
děr, jakož i globální kosmologické geometrie, však
vystačíme se slabou energetickou podmínkou a podmínkou
energodominantnosti.
Fokusace geodetik
Vidíme tedy, že člen RikViVk v rovnicích (2.59a,b) je při
splnění rozumných energetických podmínek (2.60) rovněž
nezáporný, takže pro rychlost změny konvergence geodetik
platí nerovnost
| d C / d s ł 1/3 C2 ł 0 , | (2.62) |
podle které konvergence monotónně roste podél kongruence geodetik. Můžeme tak vyslovit tvrzení:
| Teorém 2.5 (fokusace geodetik) |
| Jestliže jsou splněny
energetické podmínky (nerovnosti) pro tenzor
energie-hybnosti takové, aby podle Einsteinovych rovnic
bylo RikViVk ł 0 pro každý vektor Vi časového resp. izotropního typu, má gravitace přitažlivý charakter a na geodetiky časového resp. izotropního typu fokusující účinek. |
Tvrzení o fokusaci geodetik má velký význam pro geometricko-topologickou strukturu prostoročasu - používá se např. při důkazu 2.zákona dynamiky černých děr (§4.6) nebo při důkazu teorémů o existenci singularit prostoročasu (§3.8).
| Gravitace, černé díry a fyzika prostoročasu : | ||
| Gravitace ve fyzice | Obecná teorie relativity | Geometrie a topologie |
| Černé díry | Relativistická kosmologie | Unitární teorie pole |
| Antropický princip aneb kosmický Bůh | ||
| Jaderná fyzika a fyzika ionizujícího záření | ||
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | ||