Radioaktivita, radionuklidy, záření

1. Jaderná a radiační fyzika
1.0. Fyzika - fundamentální přírodní věda
1.1. Atomy a atomová jádra
1.2. Radioaktivita
1.3. Jaderné reakce
1.4. Radionuklidy
1.5. Elementární částice
1.6. Ionizující záření

1.2. Radioaktivita

Zkušenosti s látkou z níž je složen okolní svět ukazují, že většina látek je časově poměrně stálá a mění se jen v delších časových měřítcích. Tyto změny jsou však většinou povahy chemické, samotné atomy běžně se vyskytujících prvků jsou téměř vždy stabilní. Prakticky až do konce 19.stol. byli fyzikové a chemici pevně přesvědčeni, že atomy jsou neměnné a věčné.
Objev radioaktivity 
Na přelomu 19. a 20.stol. však byly objeveny jevy, kdy některé látky vysílaly neviditelné pronikavé záření. Již v r.1896 při pokusech s luminiscencí minerálů a krystalů zpozoroval H.Becquerel, že i bez ozáření vnějším světlem některé minerály (uranové sloučeniny) vysílají zvláštní neviditelné záření (Becquerel je zpočátku nazval "uranové záření"), které proniká i světlotěsným obalem fotografických desek a způsobuje jejich zčernání.
Henry Becquerel prováděl v Paříži pokusy s luminiscencí různých nerostů, včetně uranových minerálů které měl od svého otce. Vystavoval nerosty slunečním paprskům a pomocí zčernání fotografických desek posuzoval jejich luminiscenci. Jednoho dne, když měl již nachystány minerály k expozici, se obloha zatáhla a Becquerel zklamaně položil nerosty do zásuvky na zabalenou fotografickou desku. Po několika dnech fotografickou desku vyvolal (náhodně, snad pro srovnání či kontrolu jakosti desky, popř. zda nerosty nepůsobí na fotografickou desku třebas chemicky..?..) a s překvapením na desce uviděl černý obraz nerostu. Žádné vnější světlo nebo nějaká luminiscence nemohla tento obraz způsobit, neboť deska byla stále zabalena v černém papíře a nerost na slunečním světle nebyl, byl stále v temnotě zásuvky. Po dalších pokusech usoudil, že přímo z nitra některých minerálů vychází jakési neviditelné záření, které proniká krycím papírem a exponuje fotografické desky.
Pozn.: Krátké zamyšlení nad tím, nakolik objev radioaktivity byl dílem náhody či metodického postupu, je uvedeno v §1.0 "Fyzika - fundamentální přírodní věda", pasáž "Významné přírodovědecké objevy - náhoda nebo metoda?".

Tímto jevem se pak zabývali M.Sklodowská-Curieová, její manžel P.Curie a G.Bémont, kteří nalezli v uranové rudě i další "zářící" prvky, polonium a radium. Tento jev byl nazván radioaktivita (tyto látky "aktivně vysílaly radiaci"). Později se zjistilo, že radioaktivní prvky při vysílání tohoto záření mění svou chemickou povahu - radioaktivita je doprovázena přeměnou (transmutací) jader atomů jednoho prvku na prvek jiný. V r.1899 se vlastnostmi radioaktivního ("uranového") záření zabýval E.Rutheford, který v tomto záření nalezl dvě rozdílné složky :
- měkkou složku, kterou pohltí i list papíru a jejíž dolet ve vzduchu je pouze několik centimetrů; nazval ji paprsky a.
- tvrdší složku, asi 100-krát pronikavější než a, která prochází i tenkým hliníkovým plechem; tu nazval záření b.
Zakrátko v r.1900 zjistil P.Villard, že radium emituje ještě podstatně pronikavější záření, které je schopno proniknout i desítkami centimetrů betonu; nazval je záření g. Později se ukázalo, že jde o elektromagnetické záření s velmi krátkou vlnovou délkou, kratší než rentgenové záření.
   Dále v této době manželé Curieovi a A.Becquerel zjistili, že paprsky b mají záporný elektrický náboj, jehož měrná hodnota je blízká elektronu (tyto výsledky pak v r.1902 zpřesnil W.Kaufmann) - ukázalo se, že záření b je proudem elektronů. V letech 1903-1908 prováděl E.Rutheford řadu pokusů s průchodem radioaktivního záření v poli silných magnetů. Zjistil, že odchylka paprsků a v příčném magnetickém poli je podstatně menší a směřuje na opačnou stranu než u záporně nabitého záření b. Nakonec ukázal, že záření a je proudem dvojnásobně ionizovaných atomů hélia, tedy proudem heliových jader. U záření g zjistil, že se v magnetickém poli neodklání.
   V r.1908 E.Rutheford se svými spolupracovníky zjistili pomocí spektroskopie, že v uzavřené trubičce se vzorkem radia (chloridu RaCl₂) se objevily dva nové plyny, které tam dříve nebyly: jeden měl spektrální čáry hélia, druhý byl tehdy neznámý a byl nazván radiová emanace, nyní radon. Ukázalo se tak, že radioaktivita je samovolný rozpad atomového jádra, při němž se výchozí prvek mění v jiný - dochází k transmutaci prvku. V r.1919 tentýž Rutheford poprve dosáhl umělé transmutace neradioaktivního jádra: ostřelováním dusíku částicemi a z radioaktivního zdroje (radia) způsobil reakci ¹⁴N₇ + ⁴He₂ ® ¹⁷O₈ + ¹H₁, kterou nejdříve sledoval v komoře, naplněné různými plyny, pomocí fluorescenčního stínítka zaznamenávajícího vylétající protony ¹H₁. Přeměna dusíkového jádra po dopadu částice a byla v r.1923 potvrzena Ruthefordovým spolupracovníkem P.M.S.Blackettem ve Wilsonově mlžné komoře naplněné dusíkem, kde mezi velkým počtem "volných" drah částic a v dusíku byly nalezeny případy, kdy dráha částice a končila "rozvětvením" na dvě nové stopy: dlouhá a úzká dráha protonu a široká krátká stopa patřící jádru kyslíku.
Umělá radioaktivita 
   Všechny tyto základní poznatky byly učiněny na radioaktivitě přírodní, pozorované převážně u nejtěžších prvků. V r.1934 manželé F.Joliot-Curie a I.Joliot-Curieová poprve vytvořili radioaktivitu uměle vyvolanou.
Došlo k tomu, když ozařovali hliník paprsky a. Pozorovali, že takto ozářený hliník vysílá záření i tehdy, když ozařování paprsky a bylo zastaveno, přičemž intenzita záření postupně slábne. Jadernou reakcí s částicemi a se hliník měnil na radioaktivní fosfor ³⁰P, který se za vyslání pozitronu e⁺ rozpadá na křemík:
      a + ²⁷Al₁₃® ³⁰P₁₅ + n ; ³⁰P₁₅®(b⁺;2,5min)® ³⁰Si₁₄ + e⁺.
Pozitronové záření pozorovali J.-Curieovi v ionizační komoře. Jaderným reakcím je věnován §1.3 "Jaderné reakce".
   U některých uměle vytvořených radioaktivních látek (např. hned u první ³⁰P) pak pozorovali nový druh radioaktivity b⁺, kdy místo záporných elektronů jsou emitovány kladně nabité pozitrony. Postupně byla vytvořena celá řada umělých radioisotopů, které vykazovaly všechny druhy radioaktivity - b^-,+, g, a. V r.1940 G.N.Flerov a K.A.Petržak zjistili, že uran se kromě radioaktivity a v určitém velmi malém počtu případů rozpadá také samovolným štěpením na dvojice středně těžkých jader, přičemž se uvolňují neutrony; toto samovolné štěpení je charakteristické pro všechny transurany, kde se uplatňuje ještě výrazněji.
   Podobně jak tomu bylo i v jiných fyzikálních oborech, terminologie, veličiny a jednotky související s radioaktivitou a radioaktivním zářením prošly dlouhým a spletitým vývojem, který zanechal některé nelogičnosti a nejednoznačnosti - bude upřesněno níže.
   Nebudeme zde již podrobněji popisovat historický vývoj poznatků o radioaktivitě (a heroické úsilí badatelů) a vstoupíme přímo do současných fyzikálních poznatků o těchto jevech.

Obecné zákonitosti přeměny atomových jader
Jadernou přeměnou se rozumí změna složení nebo energetického stavu jádra. V této kapitole nás bude zajímat samovolný přechod jader do stabilnějšího stavu s nižší energií. Nejprve si podáme stručnou definici radioaktivity :

Při tomto procesu se uvolní část vazebné energie jádra ve formě kinetické energie produktů rozpadu (a často též ve formě elektromagnetického záření) - emituje se vysokoenergetické (ionizující) záření. Dochází buď k přeměně jader jednoho prvku na jádra jiného prvku - transmutaci (u radioaktivity a a b), nebo k energetické deexcitaci hladin téhož jádra (radioaktivita g - izomerní přechod). Radioaktivní přeměna se též nazývá radioaktivní rozpad (radioactive decay). Vedle názvu radionuklidy se často používá název radioisotopy (jedná se o určité konkrétní isotopy jader, vykazující radioaktivitu). Látky a předměty obsahující radionuklidy se označují jako radioaktivní zářiče. Vlastnostem konkrétních radionuklidů je věnován §1.4 "Radionuklidy", vznikající záření je pak podrobně rozebíráno v §1.3 "Ionizující záření".

Obr.1.2.1. Základní obecné schéma radioaktivní přeměny a exponenciální zákon radioaktivní přeměny.

Nejzákladnější obecné schéma radioaktivní přeměny je znázorněno v levé části obr.1.2.1. Jádro A, zvané mateřské, se spontánně (tj. bez vnějšího zásahu - jen vlivem vnitřních sil a mechanismů působících v jádře*) přemění na "o něco menší" jádro B zvané dceřinné, přičemž vylétá částice C zvaná záření. Tato částice záření odnáší rozdíl energií a složení mezi jádry A a B. Musí být přitom splněn zákon zachování energie a baryonového čísla (symbolicky A = C + B pro obě tyto charakteristiky). Aby k radioaktivní přeměně mohlo dojít, musí být podle zákona zachování energie splněna hmotnostně~energetická podmínka m(B) + m(C) < m(A), kde m(A) je hmotnost mateřského jádra A (analogicky u dceřinného jádra B) a m(C) je klidová hmotnost emitované částice C. Při jaderné přeměně se uvolňuje kinetická energie DE = [m(A)-m(B)-m(C)].c², jejíž většinu odnáší emitovaná částice C, malou část též výsledné jádro B, odražené v důsledku zákona akce a reakce. Energetický rozdíl mezi základními stavy rodičovského a dceřinného systému se nazývá energie přeměny Q.
*) Příčina radioaktivity 
Mechanismy jednotlivých druhů radioaktivity budou podrobně rozebrány níže. Zde si můžeme jen předeslat stručné shrnutí příčin spontánní přeměny jader:
Radioaktivita a je způsobena vcelku pochopitelnou nestabilitou příliš těžkých jader (které silná interakce krátkého dosahu již přestává být schopna udržet), na jejichž "periferii" se zformuje velmi stabilní jádro hélia, které může být za určitých okolností emitováno přispěním kvantového tunelového jevu (obr.1.2.2). Ještě jednodušší je příčina radioaktivity g - je to pouhá "reorganizace" nukleonů při deexcitaci energeticky vzbuzeného jádra, jejíž energetický rozdíl se vyzařuje pomocí fotonu g (je to analogické deexcitaci elektronů v atomovém obalu).
Příčina radioaktivity b je složitější: leží hluboko v subnukleární oblasti - v kvarkové struktuře nukleonů, kde slabá interakce může způsobovat vzájemné přeměny kvarků "u" a "d", a tím i přeměny protonů a neutronů (viz níže "Mechanismus rozpadu b; slabé interakce", obr.1.2.5).
Z energetického hlediska si příčiny radioaktivity budeme analyzovat níže v části "Stabilita a nestabilita atomových jader". Zde si jen uvedeme, že z více než 1800 známých nuklidů (přírodních i umělých) je jen 266 stabilních, zatímco ostatní jsou radioaktivní - samovolně se méně či více rychle přeměňují na jiná jádra (podrobněji viz §1.4 "Radionuklidy").
   Než si popíšeme jednotlivé konkrétní druhy radioaktivity, zmíníme se o těch aspektech, které mají všechny druhy radioaktivity společné: jsou to především jednotky radioaktivity a exponenciální zákon radioaktivního rozpadu.

Jednotky radioaktivity
Jako u každého fyzikálního jevu, který chceme kvantifitovat, je nutno i u radioaktivity stanovit veličiny a jednotky, ve kterých budeme měřit její "sílu", "intenzitu" či velikost. Příslušná veličina se nazývá aktivita (zářiče, preparátu či obecně množiny jader) a je definována jako počet jader, který se přeměňuje za jednotku času, nebo ekvivalentně jako úbytek počtu jader (dosud nepřeměněných) za jednotku času. Aktivita radionuklidu není veličina konstantní, ale klesá s časem, jak se původní jádra postupně rozpadají. Okamžitá hodnota A(t) aktivity v čase t je tedy:
        A(t)  =  - d N(t) / d t  ,
kde N(t) je počet dosud nepřeměněných jader v daném čase t. Této aktivitě je pak úměrný i počet emitovaných částic za jednotku času, tj. intenzita radioaktivního záření.
   Jelikož radioaktivita je jev, kdy se nám v čase přeměňují atomová jádra jednoho prvku na jádra jiného prvku, přičemž čas měříme v sekundách, je přirozenou jednotkou aktivity 1 rozpad za 1 sekundu. Tato jednotka byla na počest francouzského průkopníka v oblasti radioaktivity Henri Becquerela nazvána 1 Becquerel : 1 Bq = 1rozpad/1sekundu (v průměru*). A její dekadické násobky: kilobecquerel (1kBq = 10³Bq), megabecquerel (1MBq = 10⁶Bq), gigabecquerel (1GBq = 10⁹Bq). Čím větší je radioaktivita dané látky (vzorku) v Bq, tím více jader za sekundu se nám přeměňuje a tím intenzívnější záření látka do svého okolí vysílá.
*) V definici jednotky radioaktivity je v závorce uvedeno slovo "v průměru"; radioaktivní rozpad totiž pod vlivem stochastických zákonitostí kvantové fyziky neprobíhá rovnoměrně, ale vykazuje nepravidelné statistické fluktuace. Proto bychom každou vteřinu naměřili poněkud jiný počet rozpadlých jader - výsledky je třeba zprůměrovat, nebo měřit delší dobu a výsledky normalizovat k 1sekundě.
Dřívější jednotky aktivity - Ci, mCi, mCi 
Na počátku výzkumů radioaktivity byla jedním z heroických činů separace 1 gramu čistého radia ²²⁶Ra z několika tun uranové rudy, kterou provedla Marie-Sklodowská-Curie se svým manželem Pierem Curie. Jelikož to byl první známý čistý radioisotop, byl na jejich počest vzat 1 gram radia 226 za etalon a základní jednotku radioaktivity, která byla nazvána 1 Curie (1 Ci). Příslušné dekadické zlomky pak byly milicurie (1mCi = 10^-3Ci) a mikrocurie (1mCi = 10^-6Ci). Později, když bylo objeveno či připraveno mnoho dalších radionuklidů a byla poznána vlastní podstata radioaktivity (jak je znázorněna na obr.1.2.1), vyvstaly nevýhody této náhodně vzniklé jednotky. Přepočet mezi starými a současnými jednotkami aktivity je: 1Ci @ 37GBq (tj. 1mCi @ 37MBq a 1mCi @ 37kBq).
   Vedle celkové aktivity zářiče bývá v řadě případů potřebné znát i měrnou (specifickou) aktivitu příslušného preparátu či vzorku. Měrná aktivita se většinou uvádí jako hmotnostní aktivita, což je aktivita hmotnostní jednotky zářiče - 1kg, v praxi však většinou 1gramu: A_1g = A/M [Bq/g], kde A je celková aktivita a M hmotnost preparátu. U kapalných (popř. plynných) preparátů se často používá objemová aktivita, tj. aktivita na jednotku objemu - litr, v praxi většinou mililitr: A_1ml = A/V [Bq/ml], kde A je celková aktivita a V objem preparátu.
   Čím vyšší je aktivita zářiče, tím intenzívněji září. Celkový energetický výkon P[W] zářiče o aktivitě A[Bq] je: P = A . DE, kde DE je energie uvolněná při jednom rozpadu (přepočtená na Jouly: 1eV=1,6.10^-19J), tj. rozdíl energií mateřského a dceřinného jádra, zmenšený o klidovou energii emitované částice vzniklé při rozpadu (jak bylo výše uvedeno). Např. zářič o aktivitě 1GBq tvořený radionuklidem s energií DE= 1MeV/rozpad bude mít energetický výkon cca 1,6.10^-4W=0,16mW. Část energetického výkonu zářiče se mění na teplo (kinetická energie odražených jader a absorbovaná energie záření již ve zdroji), zbytek odnáší ionizující záření - tvoří vlastní radiační výkon zářiče, při absorbci záření v látce pak dávkový příkon (viz §5.1 "Účinky záření na látku. Základní veličiny dozimetrie.").

Exponenciální zákon radioaktivního rozpadu
Radioaktivní přeměna jader je stochastický kvantově-mechanický jev, takže nelze nijak předpovědět čas, za něž se určité konkrétní jádro přemění. Lze stanovit pouze pravděpodobnost l, s jakou se jádro danéhu druhu přemění za jednotku času (1sekundu). Mějme radioaktivní látku (vzorek), v níž je v počátečním čase t=0 obsaženo celkem N_o stejných radioaktivních jader A, které se budou postupně přeměňovat na jádra B (podle schématu na obr.1.2.1). Zajímá nás, jak rychle nám bude ubývat počet mateřských jader A (a tím zároveň přibývat dceřinných jader B) - jinými slovy chceme stanovit funkční závislost N(t) okamžitého počtu N (zbylých) mateřských jader na čase t. Počet jader DN, které se nám za krátký časový okamžik Dt rozpadou, bude úměrný stávajícímu (okamžitému) počtu jader N(t) a pravděpodobnostnímu faktoru l zvanému rozpadová či přeměnová konstanta; za dostatečně krátký časový interval Dt se přemění vždy stálá část z přítomného počtu N radioaktivních jader. Původní počet jader se tedy za čas Dt změní o:
      DN(t) = - l.N(t).Dt .
Přejdeme-li od konečných diferencí k infinitezimálním difereciálům (Dčd), můžeme po vydělení dt napsat diferenciální rovnici:
      dN(t)/dt = - l . N(t) ,
jejíž integrace dává funkci N(t) = const . e^-l.t, kde e @ 2,718 je transcendentní tzv. Eulerovo číslo - základ přirozených (Napierových) logaritmů. Okrajová podmínka N(t=0)=N_o pak dává pro integrační konstantu hodnotu const=N_o, takže můžeme napsat výsledný časový zákon radioaktivního rozpadu:

Grafem je klesající křivka zvaná exponenciála (červená křivka na obr.1.2.1 vpravo). Počet jader dceřinného prvku B naopak roste podle exponenciálního zákona N_B(t) = N_o .(1 - e^-l.t ) - modrá křivka na obr.1.2.1 vpravo.
Důležitou veličinou je hodnota času, za který se přemění právě polovina původního množství jader: nazývá se poločas přeměny (rozpadu) a značí se T_1/2. Tedy N(T_1/2) = N_o/2, což po dosazení do výše odvozeného exponenciálního zákona: N_o/2 = N_o.e^-l.T1/2 a zlogaritmování, dává l = ln2/T_1/2 @ 0,693/T_1/2. Exponenciální zákon radioaktivního rozpadu můžeme tedy napsat v nejčastěji používaném tvaru :

Po uplynutí času t = T_1/2 se přemění právě polovina jader: N(T_1/2) = N_o/2. Po uplynutí dalšího poločasu zbude polovina z poloviny jader, tj. čtvrtina: N(2.T_1/2) = N_o/4. A tak dále až do nekonečna, takže teprve v limitě t®Ą bude lim N(t®Ą) = 0 a všechna jádra se opravdu přemění *).
*) Tak je tomu jen teoreticky. Ve skutečnosti je v každém radioaktivním zářiči či preparátu jen konečný počet mateřských radioaktivních jader. Po uplynutí dostatečného počtu poločasů (desítky či stovky T_1/2) se v praxi vždy nakonec rozpadne (přemění) i poslední mateřské jádro a vzorek bude neradioaktivní.
  Vedle rozpadové konstanty l a poločasu rozpadu T_1/2 se někdy zavádí střední doba života jádra t = 1/l = T_1/2/ln2, což je zároveň doba (t=t), za kterou klesne aktivita na 1/e @ 0,3679 své původní hodnoty. Všechny tyto tři veličiny (poločas přeměny T_1/2, přeměňová konstanta l a střední doba života t) udávají, jak rychle se radionuklid přeměnuje či rozpadá.
Vztah poločasu a aktivity 
Počet atomových jader rozpadající se za jednotku času (1s) je roven -dn(t)/dt = l.n(t) = n(t) . ln2/T_1/2; a to je podle definice aktivita v Bq (hodnota T_1/2 musí být udána v sekundách; pro počet jader zde používáme symbol malé n, aby se to nepletlo s nukleonovým číslem velké N). Máme-li tedy v preparátu v čase t momentálně n radioaktivních jader, bude jeho okamžitá aktivita
                         A[Bq] = n . l = n . ln2/T_1/2 ;
bude tedy přímo úměrná počtu radioaktivních jader n, nepřímo úměrná poločasu rozpadu T_1/2 a bude klesat s časem podle exponenciálního zákona n(t) = n_o.e^-l.t = n_o.e^{-(ln2/T1/2).t} .
  Máme-li radionuklid o nukleonovém čísle N, pak v hmotnostní jednotce 1gramu je obsaženo přibližně n @ 1/(N.m_n) @ 6.10²³/N atomů (m_n je hmotnost nukleonu; vazbovou energii, která je menší než 1%, zde můžeme zanedbat; konstanta 6.10²³ je známé Avogadrovo číslo vyjadřující počet atomů v jedné grammolekule isotopu). Měrná aktivita A_{1g [Bq]} (hmotnostní aktivita) 1 gramu čistého radionuklidu s nukleonovým číslem N a poločasem rozpadu T_{1/2 [sec.]} je tedy dána vztahem
                          A_1g @ (6.10²³/N).ln2/T_1/2 @ 4,16.10²³/(N.T_1/2) .
Radionuklid je tedy tím "silněji radioaktivní", čím kratší má poločas a čím menší má nukleonové číslo. Pro některé známé dlouhodobé radionuklidy vychází měrná aktivita:

Celkovou aktivitu A_[Bq] hmotnosti M_[g] čistého radionuklidu s nukleonovým číslem N a poločasem rozpadu T_1/2[sec.] pak stanovíme pomocí vztahu
                              A = M.A_1g @ 4,16.10²³.M/(N.T_1/2) .
V praxi se čisté beznosičové radionuklidy většinou nevyskytují *), naopak ve většině preparátů bývají velmi zředěné, jejich koncentrace je malá; měrná aktivita zpravidla nepřesahuje několik GBq/gram, u některých vzorků nedosahuje ani úrovně 1Bq/g.
*) Ostatně, čisté beznosičové radionuklidy o vysoké aktivitě by se uvolňovaným teplem často roztavily či vypařily - viz níže "Tepelné účinky radioaktivity". Např. 1g čistého radiojódu ¹³¹J (T1/2=8dní) by měl kolosální aktivitu 4 600 000 GBq, jeho energetický výkon by činil téměř 750W - uvolňovaným teplem by se okamžitě vypařil! Výjimkou jsou radionuklidy s dlouhým poločasem rozpadu, které mohou docela dobře existovat soustředěné ve větším množství mnoha gramů i kilogramů - např. radium nebo uran (u uranu 235 a plutonia však pozor na kritickou hmotnost a zapálení řetězové štěpné reakce! - viz pasáž "Štěpení atomových jader" v §1.3 "Jaderné reakce").

Různá rychlost rozpadu a poločasy radioaktivních rozpadů
Každý radionuklid má svůj zcela určitý, specifický a pro něj charakteristický poločas rozpadu *). Čím je poločas přeměny T1/2 kratší, tím rychleji se radionuklid přeměňuje (rozpadá). Pro různé radionuklidy jsou však hodnoty poločasu rozpadu velmi odlišné. Známe radionukidy s neobyčejně dlouhými poločasy rozpadu řádově miliardy let (patří mezi ně i některé přírodní radionuklidy jako je ⁴⁰K s T1/2=1,3.10⁹let nebo ²³⁸U s poločasem 4,5.10⁹let), statisíce let, tisíce let (např. radiouhlík ¹⁴C s T1/2=5730 let), stovky a desítky let (např. ¹³⁷Cs s poločasem 30 let), středně dlouhými poločasy roků a desítek či jednotek dní (např. ⁵⁷Co s T1/2=270 dnů, radiojód ¹³¹J s poločasem 8 dnů), několik hodin či minut (např. ^99mTc s T1/2=6 hodin, ¹⁸F s T1/2=110min., ¹⁵O s poločasem 2,2 minuty), i velmi "krátkodobé" radionuklidy s poločasy řádově sekundy či zlomky sekund (např. ^81mKr s T1/2=13sec., těžké transurany Z>111 s poločasy rozpadu někdy i řádu milisekund).
*) Ojediněle se však vyskytují radionuklidy, které mají dva rozdílné poločasy rozpadu u stejného jádra. Některá jádra se totiž mohou rozpadat dvěma různými mechanismy, každým s jinou pravděpodobností a tedy jiným poločasem. Příkladem může být jádro ⁸⁰Br₃₅, které se jednak s poločasem 17,6min. rozpadá b^- rozpadem na ⁸⁰Kr₃₆, jednak s poločasem 4,38hod. se b⁺ rozpadem a elektronovým záchytem přeměňuje na jádro ⁸⁰Se₃₄. Dalším zajímavým příkladem z oblasti transuranů je kalifornium ²⁵²Cf₉₈, které se jednak s poločasem 2,65 let rozpadá a-rozpadem na ²⁵⁰Bk (a dále pak na celou rozpadovou řadu), jednak s poločasem 85 let se rozpadá spontánním štěpením na odštěpky ze středu Mendělejevovy tabulky; jsou přitom emitovány neutrony.
   Tyto obrovské rozdíly v poločasech rozpadu jsou způsobeny rozdílnou pravděpodobností, s níž podle kvantových zákonitostí dochází k příslušným procesům v nitru jader, jež nakonec vyústí v radioaktivní přeměnu. O tom, zda je jádro stabilní nebo se bude rozpadat a jakou rychlostí (pravděpodobností), rozhoduje řada faktorů jeho stavby. Především to jsou konfigurace energetických hladin protonů a neutronů v poli jaderných sil, souvisejících s relativním počtem protonů a neutronů a celkovým počtem nukleonů. Čím vyšší energetické hladiny v poli jaderných sil protony a neutrony obsazují (důležitou okolností je zde to, že protonové a neutronové hladiny se obsazují nezávisle), tím větší je pravděpodobnost přeměny jádra na konfiguraci s nižší energií. Proto jádra s velkým přebytkem protonů či neutronů, a též jádra s enormě vysokým celkovým počtem nukleonů, se zpravidla značně rychle, tj. s krátkým poločasem, radioaktivně rozpadají mechanismy rozebíranými v dalších pasážích této kapitoly.
   Enormní rozdíly v poločasech rozpadů radioaktivních jader nastolují otázku mezních hodnot poločasů, které mají ještě fyzikální význam, tj. otázku, jaké nejkratší a nejdelší hodnoty poločasu se mohou principiálně vyskytovat:

• Jaký nejkratší může být poločas rozpadu?
  V §1.3 uvidíme, že atomová jádra (některá stabilní, většinou však radioaktivní) vznikají při jaderných reakcích. Při jaderných reakcích dochází k řadě procesů spojených s emisí různých částic. Některé emise nastávají prakticky okamžitě po interakci, jiné s menším či větším časovým zpoždění - tak je tomu zvláště v případě, kdy vzniklo radioaktivní jádro. U shora uvedených velmi krátkodobých radionuklidů může být diskutabilní, zda se vůbec ještě jedná o jádro s aspoň dočasně vázanými nukleony a má tak smysl mluvit o jeho radioaktivním rozpadu, nebo jen o okamžitě se rozpadající konfiguraci.
    Logickým kritériem pro posouzení této okolnosti je porovnání doby života "jádra" (resp. doby zpoždění emise příslušného záření) s charakteristickým časem, během něhož nukleon, letící s energií několika MeV, proletí typickým průměrem jádra, tj. vzdáleností »10^-13cm. Tento tzv. charakteristický jaderný čas činí »10^-21sec. Pouze takové jaderné konfigurace, jejichž doba života je podstatně delší než tento charakteristický jaderný čas, lze považovat za samostatná jádra a jejich následný rozpad považovat za radioaktivitu. V opačném případě se jedná jen o kinematické efekty při jaderné reakci (např. vyražení částice z jádra), které namají svůj původ ve skutečném jádře - příslušný radiační jaderný proces pak neoznačujeme jako radioaktivitu.
    Z praktického hlediska však i některé krátkodobé procesy, které při teoretickém srovnání mají dobu života poněkud delší než charakteristický jaderný čas, nelze experimentálně analyzovat a nemají v podstatě žádný reálný význam. Na tento problém se naráží při výzkumu silně nerovnovážných jader, např. při pokusech o vytváření těžkých transuranů se Z>115, které se rozpadají natolik rychle, že jejich prchavou existenci je velmi obtížné prokázat.
• Jaký nejdelší může být poločas radioaktivního rozpadu? 
  V oblasti extrémně dlouhých poločasů se nepotýkáme s problémem prokázat existenci jader - ta nepochybně existují a lze je experimentálně analyzovat. Problémem je prokázat, že nejsou zcela stabilní, ale s časem se rozpadají, byť nesmírně pomalu.
    Z teoretického hlediska by logickým kritériem pro posouzení stability či radioaktivity mohlo být porovnání střední doby života daného jádra s dobou existence vesmíru. Podle nynějších kosmologických představ zde vesmír existuje cca 13¸15 miliard let. Máme-li k dispozici celkově N jader o poločasu rozpadu T1/2, pak za dobu dosavadní existence vesmíru se z toho rozpadlo cca N.(exp)[-1n2.14.10⁹/T1/2] jader.
  ........................
    Extrémním případem enormně dlouhého poločasu rozpadu je hypotéza radioaktivity nejjednoduššího jádra vodíku, tj. nestability protonu podle některých grandunifikačních teorií (viz §3.5) - proton by se měl rozpadat s poločasem cca 10³³let. Srovnáme-li to s odhadem celkového množství cca »10²⁷ protonů ve vesmíru, pak se za dosavadní dobu existence vesmíru možná nestačil rozpadnout ani jeden proton - protony můžeme směle považovat za stabilní. Při kosmologických úvahách (či spíše spekulacích) o globální evoluci vesmíru ve vzdálené budoucnosti se však i takové extrémně dlouhé poločasy rozpadu mohou výrazně uplatnit (je na to "dost času") - viz §5.6 "Budoucnost vesmíru. Šipka času." v knize "Gravitace, černé díry a fyzika prostoročasu".
    Z praktického hlediska je třeba si uvědomit, že aktivita A preparátu obsahujícího N jader o poločasu rozpadu T1/2 je A[Bq] = N.l = N.ln2/T1/2, přičemž radioaktivitu měříme detekcí emitovaného záření (a,b,g), jehož intenzita je úměrná aktivitě A. Pro nuklidy s enormně dlouhým poločasem rozpadu (T1/2>»10¹²let) bude hustota (četnost) emitovaného záření již velmi nízká, podstatně nižší než je hladina přírodního radiačního pozadí, takže jeho experimentální prokázání je velmi obtížné. Proto u některých jader s extrémně dlouhým poločasem rozpadu (pohybujícím se většinou mezi 10¹⁴ až 10¹⁸ let) není jejich radioaktivita často ani bezpečně prokázána - např. ⁴⁸Ca, ^64,70Zn, ⁷⁶Ge, ⁸²Se, ^92,100Mo, ¹¹⁶Cd, ¹²⁴Sn, ¹²³Sb, ^136,142Ce, ^144,145,150Nd, ^147-149Sm, ¹⁵²Gd, ¹⁵⁶Dy, ¹⁶⁵Ho, ^{180,182,183,186}W, ¹⁹²Os, ^190,192,198Pt, ¹⁹⁶Hg, ²⁰⁹Bi.
    Pro stabilní jádra se klade poločas rozpadu rovný nekonečnu: T1/2® Ą (a l®0).

Radioaktivní přeměna se odehrává v atomových jádrech, které jsou skryty hluboko uvnitř atomů, jejichž elektronový obal účinně odstiňuje veškeré chemické, mechanické a teplotní vlivy, jakož i působení vnějších polí. Radioaktivní rozpad je proto nezávislý na vnějších běžných fyzikálních a chemických vlivech a podmínkách (tlak, teplota, skupenství, chemická forma, vnější pole a pod.) - nedá se ničím urychlit ani zpomalit.  Toto tvrzení však není zcela absolutní. Níže v pasáži "Nezávislost radioaktivního rozpadu na vnějších podmínkách" budou diskutovány radiační či chemické vlivy, které mohou do určité míry změnit průběh radioaktivních přeměn v jádrech.
  Dlouhodobě stabilní rychlosti či poločasy rozpadu přírodních radionuklidů se používají k určování stáří předmětů organického původu a minerálních hornin - je podrobněji popsáno v §1.3, pasáž "Radioisotopové (radiometrické) datování".

Směsi radionuklidů, rozpadové řady, radioaktivní rovnováha
Shora odvozený (mono-)exponenciální zákon rozpadu platí jen pro radioaktivní látku sestávající z radioaktivních jader stejného druhu s přesně danou hodnotou poločasu rozpadu, jejichž dceřinná jádra jsou již stabilní a dále se nerozpadají. Jsou-li však v preparátu obsaženy dva nebo více druhů radionuklidů s různými poločasy rozpadu, nebude závislost okamžité aktivity na čase již (mono)exponenciální funkce, ale bude kombinací dvou či několika exponenciálních závislostí s různými poločasy odpovídajícími zastoupeným radionuklidům - bude se jednat o biexponenciální či obecně multiexponenciální závislost - obr.2.1.B (a).
  Specifická sitace v časové zákonitosti rozpadu nastane tehdy, když se jedná o radionuklid X, jehož dceřinná jádra nejsou stabilní, ale dále se rozpadají - jedná se obecně o tzv. rozpadovou řadu "genericky" souvisejících radionuklidů - obr.2.1.B (b,c). Dynamika rozpadu zde bude záviset na poměru poločasů rozpadu primárního mateřského radionuklidu X a dceřinných, dále se rozpadajících radionuklidů Y. Pokud je poločas rozpadu primárního radionuklidu podstatně delší než poločasy dceřinných radionuklidů, ustaví se rychlost rozpadu na tomto nejdelším (řídícím) poločasu - rozpadová řada bude v radioaktivní rovnováze, při níž se bude udržovat konstantní poměr aktivity mateřského a dceřinných radionuklidů.
  Pod radioaktivní rovnováhou rozumíme obecně situaci, kdy - navzdory radioaktivnímu rozpadu - poměrné množství jader určitého radionuklidu zůstává konstantní proto, že tato radioaktivní jádra jsou neustále doplňována nějakým produkčním mechanismem, přičemž produkční rychlost dceřinného radionuklidu je rovna jeho rozpadové rychlosti. Tímto produkčním mechanismem zde mohou být:
l Jaderné reakce
Tak je tomu v přírodě u kosmogenních radionuklidů, produkovaných neustále v atmosféře účinkem kosmického záření (§1.6 "Ionizující záření", část "Kosmické záření", obr.1.6.7). Rovněž při umělé výrobě radionuklidů stálým tokem neutronů v reaktoru či protonů v cyklotronu může být dosaženo radioaktivní rovnováhy mezi produkční jadernou reakcí a rozpadem vznikajícího radionuklidu (§1.4 "Radionuklidy", pasáž "Výroba umělých radionuklidů").
l Radioaktivní rozpad mateřského radionuklidu s delším poločasem na dceřinný radionuklid s kratším poločasem.
  Z hlediska časového rozeznáváme dva druhy radioaktivní rovnováhy "generačně vázaných" radionuklidů X a Y (jakož i sitaci, kdy k rovnováze nedochází) :
¨ Dlouhodobá rovnováha,
zvaná též sekulární rovnováha - secular equilibrium (lat. saecularis = stoletý, trvalý, dlouhotrvající, světský). Tento charakter má již zmíněná rovnovážná koncentrace kosmogenních radionuklidů. U rozpadové radioaktivní řady nastává tehdy, když výchozí mateřský radionuklid X má mnohem delší poločas, než radionuklid dceřinný Y; tehdy z hlediska časového horizontu poločasu dceřinného radionuklidu můžeme jeho aktivitu považovat za konstantní - obr.2.1.B (c). Z dlouhodobého hlediska je sekulární rovnováha jen přibližná, ve skutečnosti "rovnovážné" množství dceřinného radionuklidu pomalu klesá s poločasem radionuklidu mateřského. Sekulární rovnováha se vyskytuje např. u rozpadových řad primárních dlouhodobých radionuklidů ²³²Th, ^235,238U (§1.4 "Radionuklidy").
¨ Přechodná rovnováha (dočasná, neustálená),
zvaná též transientní rovnováha - transient equilibrium (lat. transitivus = přechodný, krátce trvající) se ustaví tehdy, když poločas rozpadu mateřského radionuklidu X je jen o něco delší než dceřinného Y - obr.2.1.B (b).
¨ Žádná rovnováha
Za situace, kdy mateřský radionuklid X má kratší poločas než dceřinný Y, se nemůže neustavit žádná radioaktivní rovnováha v žádném čase. Pokud mateřský radionuklid X byl v počátečním čase t=0 připraven bez obsahu dceřinného radionuklidu, pak při jeho rozpadu se množství dceřinného radionuklidu Y nejprve zvyšuje, prochází maximem a posléze se snižuje s poločasem rozpadu dceřinného Y.
Časová dynamika radioaktivní rovnováhy 
V nejjednodušším případě následné přeměny dvou "generačně vázaných" radionuklidů X(l_X)®Y(l_Y)®Z(stabilní) bude rychlost změny počtu jader mateřského radionuklidu X a dceřinného radionuklidu Y dána soustavou dvou diferenciálních rovnic: dN_X/dt = - l_X.N_X , dN_Y/dt = l_X.N_X - l_Y.N_Y. Její integrací [za okrajové podmínky při t=0: N_X=N_X(0), N_Y=N_Y(0)] získáme biexponenciální časový zákon pro dceřinný radionuklid Y:
            N_Y(t) = N_X(0).[l_X/(l_Y-l_X)] . (e^-lX.t - e^-lY.t ) + N_Y(0).e^-lY.t  ;
pro mateřský radionuklid X samozřejmě zůstává klasický monoexponenciální zákon N_X(t) = N_X(0) . e^-lX.t .

Obr.2.1.B. Časová dynamika radioaktivity ve směsi dvou radionuklidů.
a) Ve směsi dvou nezávislých radionuklidů X,Y se každý z nich přeměňuje podle svého vlastního poločasu a celková aktivita preparátu je daná součtem obou exponenciálních funkcí.
b),c) V rozpadové řadě dvou genericky souvisejících radionuklidů X-->Y dynamika rozpadu závisí na poměru poločasů rozpadu primárního mateřského radionuklidu X a dceřinného, dále se rozpadajícího radionuklidu Y; v závislosti na této relaci l_X a l_Y se posléze může ustavit tranzientní nebo sekulární rovnováha obou radionuklidů.
d) Specifická radioaktivní dynamika u radionuklidového molybden-techneciového generátoru při opakovaných elucích dceřinného ^99mTc, vznikajícího přeměnou mateřského ⁹⁹Mo.

Pokud je l_X<l_Y, pak po dostatečně dlouhém čase je exponenciální člen e^-lY.t zanedbatelně malý ve srovnání s e^-lX.t. Časový zákon pro dceřinný radionuklid se pak zjednoduší na: N_Y(t) = N_X(0).[l_X/(l_Y-l_X)].e^-lX.t = N_X(t).l_X/(l_Y-l_X) - po dostatečně dlouhém čase se ustaví rovnovážný poměr mezi dceřinným a mateřským radionuklidem, transientní rovnováha (obr. b), při níž aktivita dceřinného radionuklidu klesá s poločasem mateřského radionuklidu. Aktivita dceřinného radionuklidu A_Y = l_Y.N_Y = N_X(t).l_Y/(l_Y-l_X) se přitom udržuje poněkud vyšší než okamžitá aktivita mateřského radionuklidu (při l_X<l_Y je poměr l_X/(l_Y-l_X) větší než 1), v poměru A_Y/A_X = l_Y/(l_Y-l_X).
  Pokud je l_X<<l_Y, pak pro časy krátké ve srovnání s poločasem radionuklidu X je l_X.t<<1 a první exponenciální člen e^-lX.t můžeme aproximovat 1; po uplynutí několika poločasů dceřinného radionuklidu Y (kdy druhý exponenciální člen je blízký 0) se pak ustaví rovnovážné množství tohoto radionuklidu N_Y = (l_Y/l_X).N_X - sekulární rovnováha (obr.c). Jeho rovnovážná aktivita A_Y = l_Y.N_Y = l_X.N_X = A_X bude rovna aktivitě mateřského radionuklidu X. Z dlouhodobého hlediska ovšem i toto "rovnovážné" množství klesá s poločasem mateřského radionuklidu X.
  Tyto zákonitosti budou níže ilustrovány na případu tzv. radionuklidového generátoru - část "Radioaktivita gama", pasáž "Čisté gama-radionuklidy; technecium ^99mTc; radionuklidové generátory". Konkrétní druhy generátorů pro získávání krátkodobých radionuklidů jsou popsány v §1.4, pasáž "Radionuklidové generátory".
Pozn.: Vztahy uvedené v tomto odstavci platí přesně jen za předpokladu, že všechny rozpady řetězce X®Y®Z probíhají ve 100% případů. Pokud tomu tak není, je třeba zavést příslušné korekční koeficienty a výsledná aktivita dceřinných isotopů bude nižší. Tak tomu bývá u rozpadových řetezců (b)-(metastabilní g), pokud určité procento rozpadů neprobíhá na vzbuzenou metastabilní hladinu, ale na základní stav dceřinného jádra (příkladem je zmíněný Mo-Tc generátor).
  Pro rozpadovou řadu většího počtu genericky spojených radionuklidů je jejich časová dynamika rozpadu dána soustavou příslušného většího počtu lineárních diferenciálních rovnic. Např. pro řadu 3 radionuklidů X(l_X)®Y(l_Y)®Z(l_Z)®W(stabilní) to bude soustava tří rovnic: dN_X/dt = - l_X.N_X, dN_Y/dt = l_X.N_X - l_Y.N_Y, dN_Z/dt = l_X.N_X - l_Y.N_Y - l_Z.N_Z. Při počátečních podmínkách N_X(0)=N_Xo, N_Y(0)=N_Z(0)=0 dostaneme pro mateřský radionuklid X obvyklý monoexponenciální rozpadový zákon, pro Y shora uvedený biexponenciální zákon, pro třetí člen řady Z to bude kombinace 3 exponenciálních členů:
            N_Z(t) = N_Xo.l_X.l_Y . {e^-lX.t/[(l_Y-l_X)(l_Z-l_X)] - e^-lY.t/[(l_Y-l_X)(l_Z-l_Y)] - e^-lZ.t/[(l_Z-l_X)(l_Y-l_Z)]} .
Pro složitější rozpadové řady jsou přítomny další exponenciální členy s příslušnými exponenty a koeficienty. Zvláště složité rozpadové řady o mnoha sekundárních radionuklidech se vyskytují u těžkých jader v oblasti uranů a transuranů; tyto rozpadové řady budou rozebírány v §1.4 "Radionuklidy", obr.1.4.1.

Některé společné jevy doprovázející radioaktivitu
Zpětný odraz jader 
Při emisi částic a kvant radioaktivního záření dochází vlivem zákona zachování hybnosti - akce a reakce - ke zpětnému odrazu dceřinného jádra, které přebírá určitou malou část kinetické energie rozpadu. Tento jev "horkých" dceřinných jader se v zásadě projevuje u každé radioaktivní přeměny, nejvýrazněji však u radioaktivity alfa, neboť a-částice mají vysokou hmotnost a jsou většinou emitovány s vysokou kinetickou energií - s vysokou hybností. U obvyklých alfa radionuklidů s nukleonovým číslem N@220-240, které emitují a-částice o energiích cca 4-7 MeV, činí kinetická energie odražených dceřinných jader kolem 100keV. Energie chemické vazby atomů ve sloučeninách je přitom jen cca 50-100 eV. Takto odražená jádra se v látce velmi rychle zabrzdí na dráze cca 500nm, podél níž způsobují ionizaci.
  Zpětný odraz jader tak může vést k uvolnění atomů z krystalové mřížky minerálů, nebo z chemické vazby v molekulách *). Kinetická energie odražených jader se též projeví ionizačními a tepelnými účinky (viz níže). V běžných jaderných aplikacích se zpětný odraz jader většinou fyzikálně neprojevuje. U některých přesných spektrometrických měření však může mít, spolu s tepelnými pohyby atomů, výrazný vliv. Příkladem je Mössbauerova spektrometrie (viz §1.6, část "Interakce záření gama a X ", pasáž "Mössbauerův jev" a §3.4, část "Mössbauerovská spektroskopie "), nebo měření přesného tvaru spektra b za účelem stanovení klidové hmotnosti neutrin (viz níže část "Neutrina", pasáž "Klidová hmotnost neutrin"). Může se ale výrazně projevovat chemicky :
*) (radio)Chemický vliv zpětného odrazu 
Když je radioaktivní atom vázán v molekule sloučeniny, může se zpětný odraz jader výrazně projevit chemicky. Kinetická energie zpětného odrazu jader, a tedy i příslušných atomů, je většinou podstatně vyšší, než jejich chemická vazbová energie v molekulách sloučenin. Proto je po radioaktivní přeměně atom dceřinného nuklidu zpravidla "vymrštěn" - disociován - z chemické vazby v původní molekule. Může se to nepříznivě projevovat ve snížené radiochemické stabilitě radioaktivních preparátů, především radiofarmak (viz §1.4, pasáž ""In vivo generátory" v nukleární medicíně" či §3.6, část "Radioisotopová terapie", pasáž "Fyzikální a biologické faktory"). Pokud k alfa-přeměně dojde v organismu, především uvnitř buňky, mohou ionizační účinky odražených jader přispívat k radiobiologickým účinkům (§3.6, pasáž "Beta a alfa radionuklidy pro terapii").
Tepelné účinky radioaktivity 
Logický, avšak v běžných aplikacích málo známý jev, doprovází všechny druhy radioaktivity: je to teplo. Při radioaktivní přeměně vyletí z jádra velkou rychlostí částice (kvantum) záření. Podle zákona akce a reakce tím bude jádro (a vlastně celý atom) "odmrštěno" opačným směrem - bude mu udělena kinetická energie pohybu. Podobně při absorbci záření je látce předávána energie na úrovni kinetické energie atomů. A kinetická energie pohybu atomů látky není nic jiného než teplo. Při každé další a další radioaktivní přeměně se takto budou rozkmitávat atomy látky na větší a větší kinetickou energii - radioaktivní látka se bude zahřívat. Při nízkých aktivitách používaných většinou v praxi je tento jev nepozorovatelně slabý, ale silné zářiče "hřejí" docela zřetelně (např. v ozařovačích pro radioterapii), nejsilnější zářiče se musejí dokonce chladit, aby nedošlo k jejich tepelnému poškození (popř. i roztavení či vypaření) - tak je tomu zvláště u vyhořelých palivových článků ze štěpných jaderných reaktorů (§.1.3, část "Jaderné reaktory ", pasáž "Problém chlazení jaderných reaktorů").
Pozn.: Na podobných tepelných účincích je ostatně založeno i energetické využívání jaderných reaktorů v elektrárnách.
  Teplo uvolňované radioaktivním rozpadem přírodních radionuklidů, uranu ^235,238U, thoria ²³²Th a draslíku ⁴⁰K, je patrně důležitým zdrojem geotermální energie, zahřívající nitro Země - viz §1.4 "Radionuklidy", část "Přírodní radionuklidy", pasáž "Geologický význam přírodní radioaktivity".
Elektrické účinky radioaktivity 
Nabité částice a nebo b (viz níže) odnášejí z radioaktivního zářiče elektrický náboj a podle zákona zachování elektrického náboje v látce zářiče pak převládají opačné náboje než je znaménko náboje emitovaných částic. Vlastní radioaktivní zářič a nebo b se tedy elektricky nabíjí. Při nízkých tocích záření, nebo pokud je zářič aspoň částečně vodivě spojen se zemí, je tento jev zanedbatelný. Avšak elektricky izolovaný zářič s intenzívním tokem záření b či a se bude postupně kladně či záporně nabíjet i na vysoký elektrický potenciál až stovek kV (podle elektrické kapacity tělesa zářiče). Tento jev se plně projeví pouze ve vakuu, neboť ve vzduchu způsobuje záření ionizaci, prostředí se stává částečně elektricky vodivým a náboj je z tělesa zářiče průběžně odváděn.
  Elektrické a tepelné účinky radioaktivity se používají v malých elektrických zdrojích - viz §1.3, pasáž "Radionuklidové voltaické články ("atomové" baterie)".

Nezávislost radioaktivního rozpadu na vnějších podmínkách
Radioaktivní rozpad je děj samovolný - je způsoben vnitřními mechanismy stavby atomového jádra. Je nezávislý na vnějších běžných fyzikálních a chemických vlivech a podmínkách (tlak, teplota, skupenství, chemická forma, vnější pole a pod.), nedá se ničím urychlit ani zpomalit. Jádro je totiž skryto hluboko v nitru atomu, jehož elektronový obal účinně odstiňuje veškeré chemické, mechanické a teplotní vlivy, jakož i působení vnějších polí. Toto zkušeností ověřené tvrzení však není zcela absolutní.
  Především nemusí platit za extrémních podmínek. Zahřejeme-li radioaktivní látku na velmi vysokou teplotu desítek či stovek miliónů stupňů, získají jádra v již zcela ionizované plasmě tak vysokou kinetickou energii, že při vzájemných srážkách překonávají Coulombickou odpudivou sílu a bude docházet k jaderným reakcím, měnícím rychlost i charakter radioaktivního rozpadu (viz následující §1.3 "Jaderné reakce"). Podobný účinek by měla extrémně silná elektromagnetická či gravitační pole (zde na Zemi zatím nedosažitelná, vyskytují se však zřejmě ve vesmíru v okolí kompaktních gravitačně zhroucených objektů, viz např. kap.4 "Černé díry" knihy "Gravitace, černé díry a fyzika prostoročasu"). Elektronový záchyt může být ovlivněn (zpomalen či zcela zastaven) zahřátím látky na cca 10⁴ stupňů, kdy dochází k úplné ionizaci atomů, včetně L a K slupky, z nichž nastává elektronový záchyt; kromě toho rychlost elektronového záchytu může být velmi mírně ovlivněna chemickými vazbami (viz níže "Specifika elektronového záchytu"). Rychlost rozpadu elektronovým záchytem může být též ovlivněna působením vnějšího tlaku na radioaktivní atomy (vyšší tlak vede ke zvýšení elektronové hustoty a tím ke zvýšení pravděpodobnosti záchytu elektronu jádrem, projevuje se však až u velmi vysokých tlaků). Úplná ionizace atomů může výrazně ovlivnit poločas beta^- rozpadu některých (ojedinělých) radionuklidů efektem tzv. b-rozpadu do vázaných elektronových stavů. Gama-radioaktivita může být vnějším prostředím ovlivňována přes efekt vnitřní konverze záření g, který závisí na elektronové konfiguraci atomového obalu. Pro plně ionizované atomy by se koeficient vnitřní konverze stal nulovým.
  Strukturu jader, a tím i radioaktivní rozpad, lze změnit ozařováním neutrony, rychlými protony či jinými částicemi *), způsobujícími jaderné reakce. Dále, chemickou vazbou radionuklidu může být do určité míry ovlivňován elektronový záchyt a proces vnitřní konverze záření gama (viz níže).
*) Dokonce i neutrina mohou v jádrech měnit průběh radioaktivity beta: záchyt (elektronového) neutrina vyvolá transmutaci neutronu na proton, což je radioaktivita beta^-, analogicky interakce antineutrina s protonem vyvolá radioaktivní přeměnu beta+. V praxi se však tento jev nepozoruje vzhledem k velmi malému účinnému průřezu interakce neutrin (mohl by se uplatnit jen v obrovském toku neutrin při výbuchu supernovy).
  Toto všechno jsou speciální či "exotické" situace. Za téměř všech situací vyskytujících se v praxi při aplikaci jaderných a radiačních metod (kapitola 3) však můžeme průběh a poločas radioaktivního rozpadu považovat za zcela nezávislý na vnějších podmínkách.

Co se stane s atomem při radioaktivní přeměně jádra? Chemické vlastnosti radioaktivních látek
Jádra jsou za většiny okolností součástí atomů, pro jejichž strukturu hrají rozhodující úlohu (jádro je "šéfem" atomu). Chemické vlastnosti radioaktivních prvků jsou, až do okamžiku radioaktivního rozpadu, zcela shodné s vlastnostmi jejich neradioativních isotopů *). Radioaktvní atomy tedy (před svou radioaktivní přeměnou) mohou vstupovat do stejných sloučenin, jako tytéž atomy neradioaktivní. Toho se využívá v řadě radiochemických technologií, včetně medicínských aplikací radionuklidů (viz §3.5 "Radioisotopové stopovací metody", §3.6 "Radioterapie", část "Radioisotopová terapie" a §4.8 "Radionuklidy a radiofarmaka pro scintigrafii").
*) Nepatrné rozdíly v kinetice (rychlosti) průběhu chemických reakcí, způsobené rozdílnou hmotností atomů isotopů (s různým počtem neutronů v jádře) jsou z chemického hlediska většinou bezvýznamné. Mohou být však využity pro isotopovou separaci.
  Při radioaktivní přeměně jádra však nutně dochází i ke změnám v atomovém obalu *). Při radioaktivitě a se náboj jádra zmenší o 2 protony, což má za následek uvolnění dvou obalových elektronů z atomu. Při b⁺ se náboj jádra zmenší o jeden proton, takže dojde k uvolnění jednoho elektronu z obalu. Při elektronovém záchytu je vnitřní elektron pohlcen jádrem a následuje série deexcitačních přeskoků elektronů v obalu, doprovázená emisí charakteristického X-záření a dalších fotonů měkkého záření. Při přeměně b^- se náboj jádra naopak zvětší o jeden proton, takže výsledný dceřinný atom si přibere jeden elektron z okolí. Při této rekonfiguraci elektronového obalu, následující okamžitě po radioaktivní přeměně jádra, dochází i k posunu energetických hladin elektronů z původních hladin mateřského atomu na nové hladiny dceřinného atomu, za příp. vyzáření měkkého elektromagnetického záření. Rekonfigurace elektronového obalu má za následek změnu v počtu valenčních elektronů a tím změnu chemických vlastností atomu (jeho oxidačního čísla). Byl-li původní mateřský atom součástí sloučeniny, po radioaktivní přeměně se zpravidla tato chemická vazba přeruší a dceřinný atom se ze sloučeniny vyloučí - dojde k disociaci, popř. naváže novou chemickou vazbu.
*) S výjimkou radioaktivity g, při níž se náboj jádra nemění, takže nedochází ani k rekonfiguraci v elektronovém obalu. Může však dojít k tzv. vnitřní konverzi záření g (viz níže část "Radioaktivita gama"), která je doprovázena emisí a přeskoky elektronů v obalu.
  Nově vznikající atomy těsně po radioaktivní přeměně původního mateřského jádra se nazývají nascentní atomy (lat. nascendi=zrod,narození). Mají zpočátku deformovaný a excitovaný elektronový obal, mají nenulový elektrický náboj - jsou ve stavu kladného či záporného iontu, vlivem výše uvedeného zpětného odrazu jader mají vysokou kinetickou energii ("horké atomy"). Vede to k vysoké chemické reaktivitě nascentních atomů po jaderné přeměně.

Druhy radioaktivity
Radioaktivita se rozděluje a klasifikuje nikoli podle toho, jaká jsou mateřská a dceřinná jádra, nýbrž podle druhu emitovaného záření (částice C na obr.1.2.1). Tyto druhy radioaktivity se označují prvními třemi písmeny řecké abecedy - a, b, g . Tato terminologie má náhodný, čistě historický původ. Radioaktivní záření bylo takto označeno podle pořadí, v němž bylo objeveno, aniž se tehdy znala jeho skutečná fyzikální podstata. Jediné co bylo tehdy známo, že záření alfa se v elektrickém poli vychyluje směrem k záporné elektrodě, záření beta ke kladné elektrodě a záření gama není ohýbáno elektrickým ani magnetickým polem. Kdyby tehdy "školometi" jen několik let počkali se závazným ustavením terminologie "alfa-beta-gama", nyní by se radioaktivita a nazývala héliová, b^- elektronová, b⁺ pozitronová a g fotonová. To by byly daleko výstižnější názvy, vyjadřující opravdovou fyzikální podstatu...

Radioaktivita alfa
Základní schéma radioaktivity a je znázorněno na obr.1.2.2. Při této jaderné přeměně se vyzařuje částice a, která je jádrem hélia ⁴He₂ - obsahuje tedy 2 protony p⁺ a 2 neutrony n^o.

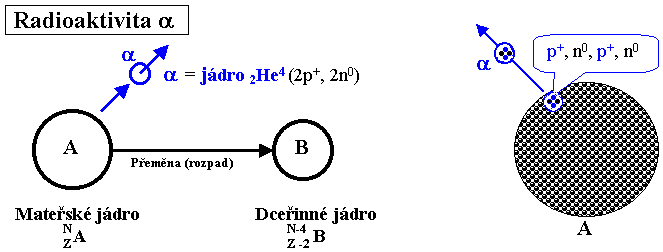
Obr.1.2.2. Základní schéma radioaktivity a.

Z mateřského jádra s N nukleony a Z protony částice a odnáší 2protony a 2neutrony, takže vzniklé dceřinné jádro bude mít N-4 nukleony a Z-2 protony - v Mendělejevově periodické tabulce prvků bude posunuto o 2 místa doleva směrem k jednodušším prvkům. Aby k radioaktivitě a mohlo dojít, musí být splněna hmotnostně~energetická podmínka m(Z-2,N-4) + m(a) < m(Z,N), kde m(Z,N) je hmotnost jádra s protonovým číslem Z a nukleonovým číslem N, m(a)şm(2,4) je klidová hmotnost částice a.
  U příliš velkých jader silná jaderná interakce, vzhledem ke svému krátkému dosahu, nestačí dostatečně silně vázat jádro proti odpudivým elektrickým silám mezi protony. Obrazně lze říci, že radioaktivitou alfa se těžká jádra "zbavují nadbytečných nukleonů", aby se staly lehčími a stabilnějšími. Tyto aspekty jsou podrobněji diskutovány níže v části "Stabilita a nestabilita atomových jader".
  Příkladem radioaktivity alfa může být a-přeměna rádia ²²⁶Ra₈₈ ® ²²²Rn₈₆ + ⁴He₂(şa) na radon 222. Dceřinná jádra po a-rozpadu bývají často rovněž radioaktivní (a či b), zpravidla tvoří celé radioaktivní řady (viz §1.4 "Radionuklidy", pasáž "Rozpadové řady"), dokud nedosáhnou stabilní konfigurace. Kromě toho jsou dceřinná jadra po a-rozpadu většinou v excitovaném stavu, takže jejich dexcitace je doprovázena zářením gama (viz níže "Radioaktivita gama").
Spektrum záření a
Částice a odnáší rozdíl energií mezi mateřským a dceřinným jádrem DE = [m(Z,N)-m(Z-2,N-4)].c², který je konstantní - všechny částice a při přeměnách daného druhu jádra mají stejné kinetické energie E_a = [m(Z,N)-m(Z-2,N-4)-m(a)].c² - spektrum záření a je čárové. Spektrometrickým měřením řady a-radionuklidů bylo zjištěno, že čím kratší poločas rozpadu má daný radionuklid, tím vyšší je energie emitovaného záření a. Tuto závislost mezi poločasem rozpadu T_1/2, resp. rozpadovou konstantou l = (ln2)/T_1/2, a energií E_a záření a udává přibližný Geiger-Nutallův vztah: ln l = A . ln E_a + B, kde A a B jsou konstanty. Tato empirická závislost dobře koresponduje s mechanismem rozpadu a tunelovým jevem vyzáření částice a, zmíněným níže. U většiny a-radionuklidů se energie emitovaných částic alfa pohybuje v rozmezí cca 4-8 MeV, dosahují rychlostí kolem 2-5% rychlosti světla. Nejnižší energie alfa 1,830MeV se pozoruje u dlouhodobého ¹⁴⁴Nd (poločas 2,3.10¹⁵let), nejvyšší energie alfa 11,650MeV byla změřena u ^212mPo (poločas 45sec.).
  Kinetická energie E_a emitovaých částic alfa je o malé procento nižší, než celková energie rozpadu Q, neboť při emisi a-částice je v důsledku zákona zachování hybnosti jádro odraženo s malou kinetickou energií do opačného směru. Pro mateřské jádro s hmotnostním číslem N bude výsledná energie alfa-částice souviset s energií rozpadu vztahem E_a @ Q.(N-4)/N.
Mechanismus rozpadu a
V pravé části obr.1.2.2 je ideově znázorněn mechanismus vyzáření částice a. Můžeme si to zjednodušeně představit tak, že těžké jádro s více než 210 nukleony je již tak velké, že celkové přitažlivé pole silných interakcí, díky svému krátkému dosahu, již nepůsobí dostatečně silně v periferních oblastech jádra. Nestačí dostatečně vyrovnat vzájemné odpuzování protonů, které má dlouhý dosah (klesá se čtvercem vzdálenosti). Toho využijí některé nukleony, které se "zkuplují" tak, že 2 protony a 2 neutrony vytvoří lokální silněji vázanou "buňku", která pak tzv. tunelovým efektem (je popsán v §1.1, pasáž "Kvantový tunelový jev") překoná potenciálovou bariéru vazbové energie jádra a vyletí ven jakožto částice a *). Překoná-li kladně nabitá částice alfa (vázaná v jádře přitažlivou silnou interakcí krátkého dosahu) potenciálovou bariéru, je odpudivou elektrostatickou silou v oblasti za dosahem jaderných sil z jádra vypuzena, či spíše vymrštěna velkou rychlostí. Analýzou průchodnosti této potenciálové bariéry tunelovým efektem lze odvodit zmíněnou Geigerovu-Nutallovu závislost mezi energií a poločasem přeměny.
*) Částice alfa je v těžkém jádře vázána silnou jadernou interakcí s výškou potenciálového valu cca 25 MeV. Energie částic při rozpadu se však pohybuje v rozmezí jen asi 4 - 9 MeV, podle konkrétního radionuklidu, takže částice sama o sobě nemá dostatečnou energii k překonání této bariéry. Podle klasické fyziky by k emisi nemohlo dojít. Podle kvantové fyziky však existuje malá, ale nenulová, pravděpodobnost, že částice může projít i vyšší potenciálovou přehradou (§1.1, pasáž "Kvantový tunelový jev").
  Dále může vzniknout otázka, proč z těžkých jader jsou emitovány právě částice aş⁴He₂ a ne třebas jednotlivé protony, neutrony, deuterony, či těžší jádra než héliová (např. uhlíku)? Příčinou je velká vazbová energie částice a (28,3MeV). K úniku z pole jádra potřebuje částice určitou kinetickou energii. Jednotlivé nukleony většinou nemají dostatečnou energii k dispozici, zatímco emise silně svázané částice a (jejíž hmotnost je menší než hmotnost nukleonů z nichž se skládá) je energeticky výhodnější. Emise jednotlivých nukleonů však nastává u silně excitovaných jader, u některých těžkých jader byla prokázána i radioaktivita vyšší než alfa - s emisí 14-C i těžších jaderných seskupení (viz níže "Exotické druhy radioaktivity").
  Pro posouzení vazbových energií nukleonů v různých jádrech doporučujeme obr.1.3.3 v §1.3., část "Jaderná energie".
  Navzdory tomu, že písmeno a je na prvním místě v řecké abecedě, je radioaktivita alfa nejméně "důležitá" ze všech druhů radioaktivity. Je to ze dvou důvodů :
1. Radioaktivita a se vyskytuje pouze u nejtěžších jader ze samého konce Mendělejevovy tabulky (N>210), převším v oblasti uranů a transuranů (lehká jádra prostě "nemají na to" aby vyzářila tak těžkou částici jakou je jádro hélia a). Typickými alfa-zářiči jsou např. radium ²²⁶Ra, plutonium ²³⁹Pu, americium ²⁴¹Am.
Jen vzácně se vyskytuje u některých středně těžkých radionuklidů (viz např. terbium ¹⁴⁹Tb). Nejlehčím prvkem, u něhož byla zaznamenaná radioaktivita alfa, je telur - tellurium ^107-109Te₅₂. V souvislosti s radioaktivitou alfa se někdy hovoří o beryliu - jeho "exotickém" isotopu ⁸Be₄ *). Ten se s extrémně krátkým poločasem 6,7.10^-17s rozpadá na dvě jádra hélia (částice a): ⁸Be₄®⁴He₂+⁴He₂. Zde se však nejedná o radioaktivitu alfa v pravém slova smyslu, ale spíše o rozštěpení vysoce nestabilního jádra na dvě stejné části.
*) Navzdory své vysoké nestabilitě je berylium ⁸Be důležité jako meziprodukt při termonukleární syntéze hélia na uhlík v nitru hvězd (viz §4.1 "Gravitace a evoluce hvězd", část "Evoluce hvězd", pasáž "Spalování hélia" knihy "Gravitace, černé díry a fyzika prostoročasu").
2. Záření a, díky svému dvojnásobnému kladnému náboji, při vniknutí do látky velmi účinně vytrhává elektrony z obalu atomů, čímž rychle ztrácí energii a zabrzdí se asi po 0,1mm v látkách hustoty vody nebo tkáně. Díky této své malé pronikavosti jej nelze využít k diagnostice ani k zevní radioterapii (vnitřně aplikované alfa-radionuklidy jsou však účinné v radioisotopové terapii - §3.6, část "Radioisotopová terapie"). Alfa-zářiče se využívají jen sporadicky v některýh detekčních přístrojích (např. detektory hustoty plynů, požární hlásiče) nebo v neutronových generátorech (smísíme-li a-zářič s vhodnou terčíkovou látkou jako je berylium, částice a vnikají do jader terčíkové látky a reakcí (a,n) odtud vyrážejí neutrony), které se laboratorně používají např. pro neutronovou aktivační analýzu.
Pozn.: Z hlediska přírodní radioaktivity je však a-radioaktivita důležitá. Většina přírodních radionuklidů zde na Zemi (s výjimkou např. draslíku ⁴⁰K) je tvořena těžkými prvy - thoriem ²³²Th a uranem ^238,235U, které jsou a-radioaktivní. Při postupném rozpadu těchto radionuklidů v rozpadových řadách (§1.4, pasáž "Rozpadové řady") se tvoří mnoho dalších jader, přičemž samotné částice a po svém zabrzdění přibírají dva elektrony, čímž vznikají neutrální atomy plynného hélia ⁴He₂. Odhaduje se, že tímto způsobem vzniká v nitru Země cca 3000 tun hélia za rok. Předpokládá se, že prakticky veškeré hélium vyskytující se na Zemi vzniklo při radioaktivním a-rozpadu přírodních radionuklidů thoria a uranu (příběh hélia je stručně zmíněn v závěru §1.1 "Atomy a atomová jádra", část "Nukleogeneze"). Většina takto vzniklého hélia zůstává nasorbována v krystalové mřížce uvnitř hornin, část se uvolňuje v plynné fázi do dutin v zemské kůře, odkud se těží se zemním plynem.

Radioaktivita beta
Naopak nejčastějším a nejdůležitějším druhem radioaktivity je radioaktivita b. Existují tři druhy radioaktivity b, které si postupně stručně probereme :

Radioaktivita b^-
Základní schéma radioaktivity b^- je na obr.1.2.3. Při této jaderné přeměně je z mateřského jádra vysokou rychlostí emitována částice b^-, což není nic jiného než obyčejný elektron e^- - stejný jako je v atomovém obalu.
Pozn.: Názvy "záření b", "částice b" pochází z doby, kdy se ještě nevědělo, že jsou to elektrony.

Obr.1.2.3. Radioaktivita beta. Vlevo: Základní schéma radioaktivity b^-. Uprostřed: Spojité energetické spektrum záření b. Vpravo: Zvětšený detail koncové části spektra pro nulovou a nenulovou klidovou hmotnost neutrin.

Vzpomeneme-li si na složení jádra (§1.1), hned vidíme zjevný paradox: jak mohou z (kladných) jader vylétat (záporné) elektrony, když tam jsou jen kladné protony a nenabité neutrony, ale žádné elektrony?
Pozn.: Nějakou dobu se fyzikové domnívali, že elektrony b^- pocházejí z obalu. Zjistilo se však, že u plně ionizovaných beta-radioaktivních atomů zbavených elektronových obalů se elektrony b^- beze změny vyzařují dál. Elektrony b^- tedy opravdu vylétají z atomového jádra.
  Když se zjistilo, že radioaktivita b^- se vyskytuje u jader s přebytkem neutronů, našlo se vysvětlení vzniku záření b^-: Některému z "nadbytečných" neutronů se "zachce" stát vzácnějším protonem *) - udělá to přeměnou: n^o ® p⁺ + e^- (+ n) (částice n si zatím nevšímejme). Proton p⁺ jakožto legitimní nukleon zůstává v jádře vázán silnou interakcí, zatímco elektron e^- vyletí velkou rychlostí ven jakožto záření b^- (odnáší rozdíl energií mezi jádry A a B).
*) Že se "neutronu zachce stát protonem" je samozřejmě jen zlehčené alegorické vyjádření; skutečný mechanismus rozpadu b bude stručně rozebrán níže v souvislosti se slabými jadernými interakcemi, obr.1.2.5. Stručné zjednodušené vysvětlení však můžeme diskutovat již zde:
Příčina radioaktivity b^-; stabilita a nestabilita neutronu v jádře 
Primární příčina radioaktivity b^- tkví v přeměně neutronu na proton, elektron a antineutrino - obecně v kvarkové struktuře nukleonů, kde slabá interakce může způsobovat vzájemné přeměny kvarků "u" a "d", a tím i přeměny protonů a neutronů (viz níže "Mechanismus rozpadu b; slabé interakce", obr.1.2.5). Ostatně, pokud je neutron volný, je nestabilní - s poločasem necelých 15 minut se vlivem slabé interakce rozpadá zmíněným b-rozpadem n^o ® p⁺ + e^- + n. Ve světle popsaného mechanismu b^- radioaktivity, spočívající v rozpadu neutronu uvnitř jádra, a faktu nestability (volného) neutronu, může vyvstat paradoxní otázka: Jak vůbec mohou existovat stabilní jádra obsahující neutrony? Proč se všechny neutrony v jejich nitru nerozpadnou na protony, elektrony a neutrina? Odpověď spočívá v tom, že na neutrony a protony v jádře nemůžeme pohlížet jako na volné - jsou součástí vyššího celku, vázaného silnou interakcí. O stabilitě tohoto celku, jádra, pak rozhoduje ani ne tak stabilita izolovaných částic, ale spolurozhoduje vazbová energie nukleonů. Pokud v dané vázané konfiguraci má jádro složené z p protonů a n neutronů menší celkovou hmotnost(~energii) než jádro složené z p+1 protonů a n-1 neutronů, nemůže k b^--rozpadu dojít, neutrony budou "donuceny" chovat se jako stabilní. V opačném případě, kdy jádro složené z p protonů a n neutronů, má vyšší celkovou energii~hmotnost než jádro z p+1 protonů a n-1 neutronů (a to nejméně o klidovou hmotnost elektronu, tj. o 511keV), nastává situace, kdy může dojít k b^--rozpadu.
Někdy se můžeme setkat i s následující argumentací : 
Pokud je neutron silnou interakcí vázán v jádře spolu s protony, dochází k tzv. paritní neutron-protonové přeměně: probíhá průběžná změna n®p®n atd., zprostředkovaná výměnou virtuálních p-mezonů (které se dříve považovaly za zprostředkovatele silné interakce mezi nukleony). Takto v jádře vázaný neutron, dřív než se "stihne" rozpadnout b-rozpadem, se (vzájemnou výměnou p-mezonu s nejbližším protonem) změní na proton, a nově zrozenému neutronu "běží rozpadový čas opět od 0", znovu se přemění na proton atd. Tím se krátký poločas rozpadu neutronu (13sec.) vzájemnou konverzí s protony neustále "obnovuje" - neutron je v jádře stabilní. Pouze tehdy, když je neutronů v jádře "přebytek", vzniká jistá pravděpodobnost, že některý z neutronů "nenajde včas" vhodného partnera pro mezonovou výměnu a rozpadne se b-rozpadem; to pak pozorujeme jako b^--radioaktivitu takového jádra.
  Při přeměně b^- se nukleonové číslo nemění, avšak jelikož se jeden neutron změnil na proton, protonové číslo se zvýší o 1 - dceřinné jádro se posune o jedno místo doprava v Mendělejevově periodické tabulce. Tato pozoruhodná skutečnost, že při b^--rozpadu vzniká "složitější" jádro než bylo původní, sehrála rozhodující úlohu při kosmické nukleosyntéze prvků těžších než železo v nitru hvězd a zvláště během výbuchů supernov (viz pasáž "Kosmická alchymie - jsme potomky hvězd!" v §1.1, §4.1 "Gravitace a evoluce hvězd" knihy "Gravitace, černé díry a fyzika prostoročasu", nebo sylabus "Kosmická alchymie"). Těžké prvky vznikly právě díky posunovacímu pravidlu "doprava" při radioaktivitě beta^-.
Typickým příkladem radioaktivity beta je b-přeměna tritia ³H₁ ® ³He₂ + e^- + n' na hélium 3, nebo uhlíku ¹⁴C₆ ® ¹⁴N₇ + e^- + n' na dusík. Často používanými beta-zářiči jsou cesium ¹³⁷Cs, kobalt ⁶⁰Co, jód ¹³¹I, iridium ¹⁹²Ir a řada dalších.
  Aby k radioaktivitě b^- mohlo dojít, musí být splněna hmotnostně~energetická podmínka m(Z+1,N) + m_e < m(Z,N), kde m(Z,N) je hmotnost jádra s protonovým číslem Z a nukleonovým číslem N, m_e je klidová hmotnost elektronu.
Energetická bilance jader se dá dobře vysvětlit slupkovým modelem struktury atomového jádra, diskutovaným v předchozím §1.1. Pokud je v jádře nadbytek neutronů nad protony, budou zaplňovat neutrony poněkud vyšší energetické hladiny než protony. Jádro pak může přejít do stavu s nižší energií tak, že neutron se přemění b^--přeměnou na proton, který přejde na volnou protovou hladinu s nižší energií.
  Z hlediska hmotnostu kvarků "u" a "d" je stabilita a nestabilita diskutována v §1.3, pasáži "Stabilita a nestabilita kvarků, hadronů, nukleonů".
Nezachování parity a asymetrie úhlového rozložení elektronů b 
Pro úplnost zmíníme jednu subtilní vlastnost radioaktivity b - porušení zákona zachování kvantového čísla parity (parita je definována v §1.5 "Elementární částice a urychlovače", část "Fyzikální parametry částic; kvantová čísla"). Tato vlastnost vede k asymetrii úhlového rozložení vylétajících elektronů b vzhledem ke směru vektoru momentu hybnosti (spinu) daného radioaktivního jádra. Tento jev byl experimentálně prokázán na jádrech ⁶⁰Co. Příslušné experimenty a teoretická analýza jsou diskutovány v §1.5, pasáž "CPT symetrie interakcí".
  Porušení zachování parity a dalších symetrií má sice značný teoretický význam ve fyzice částic a interakcí ("CPT symetrie interakcí") i v kosmologii (§5.4 "Standardní kosmologický model. Velký třesk. Formování struktury vesmíru." knihy "Gravitace, černé díry a fyzika prostoročasu"), avšak pro vlastní radioaktivitu beta je v praxi bezvýznamné. Projevuje se jen ve speciálně připravených experimentech, za velmi nízkých teplot a silných magnetických polí.. V přírodě ani ve fyzikální praxi se nikdy neuplatňuje, protože jádra radioaktivních prvků jsou chaoticky orientována a vyzařování probíhá v průměru izotropně do všech směrů.

Dvojný rozpad b
U některých jader byl zaznamenán vzácný typ radioaktivity beta - tzv. dvojný rozpad b. Ten spočívá v současné přeměně dvou neutronů v jádře na protony za vyslání dvou záporných elektronů: 2n^o ® 2p⁺ + 2e^- + 2n´ a dvou elektronových antineutrin. Tento typ rozpadu se vzácně vyskytuje u některých jader se sudým nukleonovým číslem (např. N=48 nebo N=116), u nichž se vyskytují tři isotopy ^NA_Z, ^NB_Z+1, ^NC_Z+2, jejichž hmotnosti postupně klesají specifickým způsobem (nejprve o menší, pak o větší rozdíl než 511keV). Celkově musí být splněna hmotnostně~energetická podmínka m(Z,N)>m(Z+2,N)+2m_e a zároveň situace, kdy normální rozpad beta nemůže proběhnout - buď je m(Z,N)<m(Z+1,N)+m_e, nebo se uplatňuje nějaký mechanismus jeho "znevýhodnění". V takovém případě je možná přímá přeměna jádra A na jádro C: ^NA_Z ® ^NC_Z+2 + 2e^- + 2n´ dvojným rozpadem beta. Označuje se (2n2b), nebo (nnbb) - dvouneutrinový dvojný rozpad beta. Byl pozorován např. u jader ⁴⁸Ca₂₀, ¹¹⁶Cd₄₈, ¹³⁰Xe₅₄, poločasy rozpadu jsou velmi dlouhé, cca 10²⁰let. Je možný jak dvojný b^-b^--rozpad, tak dvojný b⁺b⁺-rozpad, i dvojný elektronový záchyt.
  U některých jader (jako je ⁷⁶Ge) je uvažována možnost bezneutrinového dvojného rozpadu b, při němž by nebyla neutrina emitována - (0nbb). Vnitřní mechanismus si představujeme ve dvou fázích. V prvním kroku se v jádře b-radioaktivitou jeden neutron n₁ přemění na proton: n₁® p₁ + e₁ + n, načež v druhém kroku je vzniklé neutrino pohlceno dalším neutronem: n + n₂® p₂ + e₂. Přitom emitované a absorbované neutrino je jen virtuální, výsledkem je přeměna (Z,N) ® (Z+n,N)+e₁+e₂, při které se dva neutrony přemění na protony (protonové číslo se zvětší o 2) a emitují se jen dva elektrony. Bezneutrinový dvojný rozpad beta by porušoval zákon zachování leptonového čísla (0®1+1). Experimentální prokázání a analýza tohoto procesu by mohla pomoci upřesnit stanovení hmotnosti neutrina (snížit dosavadní horní hranici hmotnosti) a ukázala by, že neutrino je tzv. Majoranovskou částicí, tj. neutrina a antineutrina jsou shodná.

b^--rozpad do vázaných elektronových stavů
Další drobná zajímavost se ukazuje při srovnání radioaktivity beta^- u "holých" jader (u plně ionizovaných atomů) a jader obklopených elektrony v atomech. Při klasické beta-radioaktivitě je elektron emitován z jádra, opouští atom a letí do okolního prostředí. U nízkých energií však může nastat situace, kdy emitovaný beta-elektron neopustí atom, ale zůstane vázaný na některém z nižších orbitalů dceřinného atomu. K tomu nemůže dojít u neutrálních atomů, jejichž vnitřní elektronové orbity jsou již obsazeny. U plně ionizovaných b^--radioaktivních atomů však emitované b-elektrony mohou být navázány do nízkých orbitalů dceřinného atomu (které jsou všechny volné). Úplná ionizace atomu tak může vést ke vzniku dalšího "kanálu" beta-rozpadu na vázaný stav elektronu (bound-state b^- decay).
  Tento jev je pozorován u ¹⁶³Dy, který je za normálních podmínek stabilním isotopem. Pokud je však plně ionizován (¹⁶³Dy⁶⁶⁺), podléhá b-rozpadu na K a L slupku ¹⁶³Ho s poločasem 47 dní. Dalším případem je ¹⁸⁷Re, které se v neutrální atomové formě b-radioaktivitou přeměňuje s velmi dlouhým poločasem 42.10⁹ let na ¹⁶³Os. Při plné ionizaci však tento poločas činí jen 33 roků - kanál b-rozpadu na vázaný stav poločas rozpadu zkrátil miliardkrát!
  V běžných pozemských podmínkách se s ovlivňováním beta-radioaktivity úplnou ionizací látky běžně nesetkáváme, avšak předpokládá se, že se může uplatňovat v astrofyzikálních procesech kosmické nukleosyntézy - viz §1.1, část "Kosmická alchymie".

Spektrum záření b . Neutrina
Jak je to s energetickým spektrem záření beta? Elektron b by měl odnášet rozdíl energií DE = E_A - E_B mezi mateřským A a dceřinným B jádrem, který je DE = [m(Z,N)-m(Z+1,N)].c². Tento rozdíl je vždy konstantní, takže všechny elektrony b by měly vylétat se stejnou kinetickou energií E_b = [m(Z,N)-m(Z+1,N)-m_e].c² - spektrum by mělo být čárové, jak je červeně čárkovaně naznačeno na obr.1.2.3 uprostřed. Změříme-li však skutečné spektrum záření b, dostaneme jiný výsledek: spektrum bude spojité*) a u energie E_A- E_B bude končit - tlustá černá křivka na obr.1.2.3 uprostřed. Naprostá většina elektronů b tedy vylétá s energií mnohem menší než by odpovídalo zákonu zachování energie!
*) Spojité spektrum záření b poprve změřil v r.1914 J.Chadwick s použitím ohybu v magnetickém poli (první prototyp magnetického spektrometru) a detekce pomocí G.-M. trubice.
  Po některých počátečních pochybnostech o platnosti zákona zachování energie pro radioaktivitu b (tyto pochybnosti zpočátku vyslovil i N.Bohr) se přišlo na následující řešení: kromě elektronu b vylétá z jádra současně ještě další (zatím nepozorovaná) velmi lehká a elektricky neutrální částice n, která odnese patřičnou kinetickou energii, o niž se "podělí" s vylétajícím elektronem, v souladu se zákonem zachování energie. S hypotézou o této částici přišel v r.1930 švýcarský fyzik W.Pauli. Italský fyzik Enrico Fermi (průkopník ve výzkumu radioaktivity b a jaderné fyziky vůbec) připodobnil tuto podivnou částici k jakémusi malému "neutronku" (je maličká a neutrální) - italsky neutrino - a tento název i označení "n" jí již zůstal. Neutrino zůstávalo pak více než 20 let hypotetickou částicí, experimentálně bylo prokázáno až v 50.letech, viz níže. Fyzikální vlastnosti neutrin a možnosti jejich detekce jsou podrobněji rozebírány níže v části "Neutrina - duchové mezi částicemi".
  Pokud neutrino "ukradne" téměř veškerou energii rozpadu, "vyplouží" se elektron b z jádra s malou energií (případ I. vyznačený ve spektru na obr.1.2.3 uprostřed). Pokud se naopak elektronu b podaří ukořistit většinu energie, vyletí s vysokou kinetickou energií (případ II. na prostřední části obr.1.2.3). A případ III. uprostřed spektra nastává, když se elektron s neutrinem "podělí" o energii zhruba rovným dílem. Ve většině případů neutrino odnáší zhruba 2/3 celkové energie a na elektron připadne cca 1/3 maximální energie - tomu odpovídá široký vrchol spojitého spektra záření b na obr.1.2.3 uprostřed.
  Záření beta má tedy spojité energetické spektrum, obsahuje elektrony s energiemi od nuly po určitou maximální energii, která je pro daný radionuklid charakteristická. Typické hodnoty maximální energie většiny beta-zářičů činí desítky keV až jednotky MeV (nejnižší energie 2,5keV je pozorována u radionuklidu ¹⁸⁷Re, nejvyšší energie 16,6MeV byla změřena u ¹²N).
Tvar spektra záření b 
Přesný tvar křivky spektra záření b plyne z analýzy energetického rozdělení emitovaných elektronů v rámci Fermiho teorie slabé interakce. Z této teorie plyne, že intenzita N(p) záření b o hybnosti p a energii E_b je dána vztahem N(p) = (E_bmax-E_b)².p².F(Z,p), kde E_bmax je maximální energie rozpadu b a konstanta F (vyjadřující korekce na Coulombovské pole jádra) v sobě zahrnuje příslušné konstanty včetně protonového čísla Z. Z tohoto vztahu pak pro spektrum b plyne rovnice E_bmax-E_b = Ö[N(p)/p².F(Z,p)]. Vyneseme-li funkci Ö[N(p)/p².F(Z,p)] na svislé ose v závislosti na energii E_b na vodorovné ose, dostaneme lineární závislost zvanou Fermi-Kurieův graf. Je to klesající přímka, která protíná vodorovnou (energetickou) osu v bodě udávající maximální energii rozpadu b. Fermi-Kurieho grafy se někdy používají při přesné spektrometrické analýze záření b. Tvar koncového úseku tohoto spektra (viz obr.1.2.3 vpravo) - odchylka od lineární závislosti ve Fermi-Kurie grafu, může být použita i pro stanovení hmotnosti neutrin, viz níže "Klidová hmotnost neutrin".
  Pro stanovení střední energie `E<sub>b</sub> záření b z tvaru spektra záření b můžeme v prvním přiblížení vyjít z přibližné zákonitosti `E_b ~ E_bmax/3. Pro vyšší energie se tato hodnota relativně posunuje mírně doprava, takže přesnější empirický vztah je : `E_b » (E_bmax/3).(1+¹/₄ÖE_bmax); (v [MeV]). Určitý vliv na výslednou energii má i Coulombovské elektrické působení vylétajících částic b s nábojem jádra o počtu protonů Z, což vede k dalšímu korekčnímu faktoru (1 - ¹/₅₀.ÖZ).
Inverzní beta rozpad 
Shora rozebíraná standardní radioaktvita beta^-, zvaná též beta-rozpad, spočívá v přeměně neutronu n^o na proton p⁺ za emise elektronu e^- a (elektronového)neutrina n: n^o ® p⁺ + e^- + n. Existuje však i opačný proces, jaderná reakce při níž se proton může sloučit s elektronem za vzniku neutronu a emise neutrina: p⁺ + e^-® n^o + n - nazývá se inverzní beta-rozpad (pohlcení elektronu protonem je opakem emise elekronu z jádra u beta^-- rozpadu). Nastává buď spontánně v atomech při radioaktivním elektronovém záchytu (je popsáno níže v pasáži "Elektronový záchyt"), nebo je vynucen vnějšími silami - buď kinetickou energií urychlených elektronů, nebo velmi silnou gravitací. Ve vesmíru tento proces neutronizace probíhá lavinovitě při gravitačním kolapsu masívních hvězd - výbuchu supernovy a vzniku neutronové hvězdy (je podrobně diskutováno v §4.2, pasáži "Výbuch supernovy. Neutronová hvězda. Pulsary." knihy "Gravitace, černé díry a fyzika prostoročasu").
Pozn.: Jako inverzní beta rozpad se někdy též nazývají interakce neutrin s protony za vytvoření neutronu a pozitronu : n'_e + p⁺ ® n^o + e⁺ , nebo s neutrony za vzniku protonu a elektronu: n_e + n^o ® p⁺ + e^-, které se používají k detekci neutrin v neutrinových detektorech (je popsáno níže "Interakce a detekce neutrin").

N e u t r i n a - "duchové" mezi částicemi 
I když elementární částice budeme systematicky rozebírat až v §1.5 "Elementární částice", radioaktivita beta je vhodnou příležitostí zmínit se podrobněji již na tomto místě o velmi zajímavých a pozoruhodných částicích mikrosvěta - neutrinech. Učiníme tak poněkud obecněji, nejen v přímé souvislosti s radioaktivitou b *). Celkové zařazení neutrin do systematiky ostatních elementárních částic však budeme diskutovat až v §1.5.
*) Odůvodnění existence neutrin a původ jejich názvu byl diskutován výše v části "Radioaktivita b^-", pasáž "Spektrum záření b.Neutrina.". Neutrina, vzniklá kdysi jako dodatečná ne příliš přesvědčivá hypotéza snažící se vysvětlit "něco co chybělo", se staly reálnými a velmi zajímavými částicemi nejen pro jadernou fyziku, ale i astrofyziku a kosmologii.
  Neutrina jsou pranepatrné částečky (s klidovou hmotností blízkou nule - viz níže pasáž "Klidová hmotnost neutrin"), které nemají elektrický náboj a nevykazují ani silnou jadernou interakci; vykazují jen slabou jadernou interakci *). Ta je natolik slabá a krátkodosahová, že neutrina s látkou téměř neinteragují a volně jí prolétají (jako "duchové"; navíc jeví schopnost vzájemného "převtělování" - oscilace mezi třemi různými typy, viz níže).
*) A samozřejmě se předpokládá univerzální gravitační působení, které je na mikroskopické úrovni zanedbatelnou silou a zatím nás zde nezajímá. Pro astrofyziku a kosmologii však gravitační působení neutrin, kterých je ve vesmíru obrovské množství, může mít značný význam, viz níže pasáž "Klidová hmotnost neutrin".
  Každou sekundu proletí naším tělem mnoho miliard neutrin. Odhaduje se, že zde na Zemi každým cm², včetně povrchu našeho těla, prolétá každou sekundu cca 50 miliard neutrin *) (pocházejících především z termonukleárních reakcí v nitru Slunce), ale nemusíme se obávat jejich škodlivých účinků na naše zdraví, za celý život se v našem těle zachytí snad jen jedno či dvě tato neutrina. Naprostá většina neutrin je schopna volně proletět i skrz celou naši zeměkouli. Odhaduje se, že neutrina by mohla úplně zachytit až vrstva olova tloušťky 1000 světelných let!
*) Tento obrovský počet neutrin se vyskytuje zde na Zemi v blízkosti Slunce a ve vesmíru v blízkosti každé hvězdy, v níž obrovské množství neutrin vzniká při termonukleárních reakcích. A ještě daleko větší počet neutrin je v okolí vybuchující supernovy. V dalekém mezihvězdném a mezigalaktickém vesmírném prostoru se hustota neutrin odhaduje na cca 300 neutrin/m³, kde se jedná především o reliktní neutrina.
  Neutrina v obrovském množství vznikají při řadě procesů ve vesmíru - od leptonové éry při "velkém třesku", přes termonukleární reakce ve hvězdách, až po výbuchy supernov (viz níže). Vzhledem k jejich stabilitě a pronikavosti se tyto částice ve světě neustále hromadí. Lze tedy soudit, že (spolu s fotony) neutrina jsou nejhojnějšími částicemi ve vesmíru - jsme jakoby "ponořeni do neviditelného moře neutrin", která se zrodila v různých dobách a na různých místech vesmíru. Jsou to všudypřítomné, avšak téměř nepolapitelné částice..!..

Vznik a druhy neutrin
Neutrina - velmi lehké částice (o klidové hmotnosti blízké nule), bez elektrického náboje, se spinem 1/2, pohybující se rychlostí blízkou rychlosti světla - jsou nerozlučnými doprovodnými částicemi při všech procesech s elementárními částicemi s účastí slabé interakce. Jejich emise doprovází vznik elektronů při rozpadech pionů a mionů, vzájemnou přeměnu protonů a neutronů (především při radioaktivitě b), jakož i řadu procesů při srážkách elementárních částic při vysokých energiích. Neutrina patří, spolu s fotony, mezi nejhojnější částice ve vesmíru.
  Podle svého původu, konkrétního místa a mechanismu vzniku, můžeme neutrina rozdělit na pět skupin:

• Reliktní neutrina
  pocházející z nejranějších období vývoje vesmíru. V tzv. leptonové éře, necelou 1sekundu po velkém třesku, kdy teplota poklesla pod asi 10¹⁰ °K, přestala neutrina prakticky interagovat s ostatní látkou (s elektrony, neutrony, protony). Od té doby se obrovské množství "reliktních" neutrin volně pohybuje expandujícím vesmírem (nyní se jejich hustota odhaduje na asi 300neutrin/cm³ v každém kousku vesmírného prostoru, i zde na Zemi). V důsledku kosmologické expanze vesmíru poklesla energie reliktních neutrin na velmi nízké hodnoty, takže nemáme k dispozici žádnou reakci, která by umožňovala jejich detekci.
  Kosmologické aspekty těchto procesů jsou popisovány v §5.4 "Standardní kosmologický model. Velký třesk." knihy "Gravitace, černé díry a fyzika prostoročasu".
• Hvězdná neutrina 
  V nitru všech hvězd probíhá termojaderná syntéza vodíkových jader na hélium (ať již se jedná o přímý p-p řetězec nebo CNO cyklus), v pozdějších fázích evoluce hvězd i syntéza těžších prvků (viz pasáž "Kosmická alchymie - jsme potomky hvězd!" v §1.1, §4.1 "Gravitace a evoluce hvězd" knihy "Gravitace, černé díry a fyzika prostoročasu", nebo sylabus "Kosmická alchymie"). V řetězci těchto jaderných reakcí se kromě silných interakcí účastní i slabé interakce - rozpady beta, při nichž dochází ke vzniku neutrin s energiemi do cca 20MeV *). Neutrina díky své pronikavosti snadno unikají z nitra hvězd a šíří se do okolního prostoru. Z nitra Slunce je emitováno veliké množství neutrin, které "zaplavují" celou Sluneční soustavu. U naší Země činí tok těchto slunečních neutrin cca 6.10¹⁰ neutrin/sekundu/cm², z nichž většina volně prolétne zeměkoulí.
  *) Nejvíce neutrin vzniká ve "startovní" proton-protonové reakci p⁺ + p⁺® ²H + e⁺ + n_e, ale jejich energie (<0,42MeV) je pro detekční metody nízká. Pro naše detekční metody jsou vhodná neutrina vznikající v jedné z vedlejších dílčích větví reakce, v níž se jádro bóru b⁺-rozpadem mění na jádro berylia, pozitron a neutrino: ⁸B ® ⁶Be + e⁺ + n_e, kde neutrino může mít maximální energii až asi 14MeV. Tato reakce je zastoupena jen asi 0,01%, ale příslušná sluneční neutrina jsou dobře detekovatelná.
• Neutrina z výbuchu supernov 
  Výbuch supernovy je doprovázen (a vlastně způsoben) rychlým pohlcením téměř všech elektronů protony (p⁺ + e^-® n^o + n - inverzní b-rozpad), přičemž se náhle vyzáří kolosální množství neutrin (odhadované na 10⁵⁷neutrin). Dochází též k masívní neutronové fúzi jader ve vnějších vrstvách, doprovázené následným b^--rozpadem, rovněž s emisí neutrin.
  Několik neutrin tohoto původu bylo detekováno v roce 1987 po explozi supernovy SN 1978A ve Velkém Magellanově oblaku, viz níže. Procesy při výbuchu supernov jsou podrobněji popsány v §4.2 "Konečné fáze hvězdné evoluce. Gravitační kolaps" knihy "Gravitace, černé díry a fyzika prostoročasu".
  Vysokoenergetická neutrina
  Vedle neutrin nižších a středních energií (řádově MeV) mohou při výbuchu supernovy vznikat i neutrina s vysokými energiemi. Prudce expandující slupka ionizované hmoty při výbuchu supernovy může Fermiho mechanismem urychlovat protony na vysoké energie. Interakcí těchto protonů s materiálem slupky jsou produkována (přes piony a miony) mimo jiné i neutrina vysokých energií (1¸1000 TeV), která jsou pak součástí primárního kosmického záření.
• Neutrina ze sekundárního kosmického záření (atmosférická neutrina) 
  Při interakcích částic tvrdého kosmického záření (primárního) s jádry dusíku a kyslíku v horních vrstvách atmosféry (ve výškách cca 20-30km nad zemí) vznikají spršky sekundárního kosmického záření, jejichž terciální součástí jsou i neutrina. Při primárních interakcích zde dochází k produkci pionů p^± (a též K mesonů), které se rychle rozpadají na miony m^± a (mionová) neutrina : p^- ® m^- + n'_m , p⁺ ® m⁺ + n_m . Miony se dále průběžně rozpadají na elektrony, pozitrony a neutrina (mionová a elektronová): m^- ® e^- + n'_e+ n_m , m⁺ ® e⁺ + n_e+ n'_m . Neutrina tohoto původu se označují jako atmosférická neutrina. Kosmické záření je podrobněji rozebíráno v §1.6, části "Kosmické záření".
• Neutrina z přírodní radioaktivity, geoneutrina 
  V zemské kůře dochází k radioaktivním rozpadům přírodních radionuklidů, především uranu, thoria a draslíku 40 (viz §1.4 "Radionuklidy", část "Přírodní radionuklidy", pasáž "Geologický význam přírodní radioaktivity"), při nichž vznikají elektronová (anti)neutrina, které se vzhledem ke svému původu nazývají geoneutrina.
  Detekce geoneutrin, které z nám nedostupných hlubin nitra Země volně procházejí mocnými vrstvami horniny až na povrch, by mohla poskytnout cenné informace o radioaktivních prvcích v nitru Země. Analýzou směrů příchodu neutrin do detektorů, rozmístěných v různých místech, můžeme dostat informaci o prostorovém rozložení radioaktivních prvků. Spektrometrickou analýzou energie neutrin lze v principu zjistit, která radioaktivní jádra je vyzařují: neutrina z rozpadu draslíku 40 a uranu 235 mají max. energii asi 1,3MeV, z rozpadové řady ²³²Th asi 2,2MeV, z řady ²³⁸U činí maximálmí energie neutrin zhruba 3,2MeV. Po zdokonalení detekční techniky tak bude možno detekci geoneutrin použít ke geologickému hledání ložisek uranu či thoria hluboko pod zemí.
    V ovzduší, ve vodě i v tělech rostlin a živočichů dále dochází k beta- rozpadu kosmogenních radionuklidů - radiouhlíku ¹⁴C a tritia ³H, rovněž s emisí neutrin.
• Neutrina z jaderných reaktorů a z urychlovačů (neutrina umělého původu) 
  Zde na Zemi jsou v moderní době intenzívními zdroji neutrin jaderné reaktory. Při vlastním štěpení jader uranu či plutonia sice neutrina nevznikají, avšak vznikají následně při radioaktivitě produktů štěpení. Těžká jádra (jako je ²³⁵U) mají pro svou stabilitu větší poměr počtu neutronů a protonů než stabilní středně těžká jádra. Středně těžká jádra, která při rozštěpení vzniknou, tudíž mají značný přebytek neutronů, kterých se "zbavují" pomocí několika b^- radioaktivních přeměn, dokud nevzniknou jádra stabilní. Vznikají přitom elektrony "beta" a elektronová (anti)neutrina, při deexcitacích jaderných hladin pak záření gama. Po každém štěpení vzniká cca 5-6 neutrin. Při tomto následném b-radioaktivním rozpadu štěpných produktů s nadbytkem neutronů tak vzniká velké množství elektronových antineutrin (o střední energii kolem 4MeV). Nazývají se někdy "reaktorová neutrina". Výkonný reaktor produkuje zhruba 10²⁰ neutrin/sekundu.
    V menší míře vznikají neutrina jako "vedlejší produkty" při interakcích částic v urychlovačích (tam se vyskytují energie desítky MeV až stovky GeV). Urychlovače pak umožňují i cílenou produkci svazků vysokoenergetických neutrin, především mionových :
    Vysokoenergetické protony z urychlovače necháme srážet s jádry terčíku, čímž vzniká velké množství mesonů p (a řada dalších částic - kaonů, hyperonů,...). Nabité piony se nechají procházet vakuovým rozpadový tunelem, kde se během letu rozpadají (mají poločas rozpadu jen asi 2.10^-8sec.) za vzniku mionů a mionových neutrin: p^- ® m^- + n'_m , p⁺ ® m⁺ + n_m . Tato mionová neutrina, vznikající z vysokoenergetických pionů, mají rovněž vysokou energii a jsou úzce kolimována ve směru původního pionového svazku (ve směru osy rozpadového tunelu) - viz níže "Experiment CNGS+OPERA".
    Produkce vysokoenergetických svazků elektronových neutrin je obtížnější. Určitou možností by mohlo být urychlování lehčích b-radioaktivních jader s krátkým poločasem rozpadu (např. ^6,8He, ⁹Li, nebo pod.) na lineárním nebo kruhovém urychlovači, které by se pak vedly do magnetického akumulačního prstence s delšími lineárními úseky. Urychlená jádra by při své b-přeměně emitovala elektronová neutrina, která by byla (v laboratorní vztažné soustavě) též "urychlená" na vysoké energie a vylétala by ve svazcích kolimovaných podél zmíněných lineárních úseků. Zatím nebylo realizováno.

Podle své fyzikální kvantové povahy se vyskytují tři druhy neutrin n, podle druhu přidruženého nabitého leptonu :

• Elektronová neutrina
  Neutrina uplatňující se při radioaktivitě beta jsou jen jedním ze 3 druhů neutrin - jsou to neutrina elektronová n_e, doprovázející vyzáření elektronu či pozitronu při přeměně beta. Elektronová neutrina (aspoň svým primárním původem) jsou však převládajícím druhem neutrin - vznikají při termonukleárních reakcích v nitru hvězd, při výbuchu supernov, v přírodní i umělé radioaktivitě, v jaderných reaktorech.
• Mionová a tauonová neutrina 
  Při procesech s miony m a tauony t (viz §1.5 "Elementární částice") se vyzařují neutrina mionová n_m (jsou významnou součástí "atmosférických" neutrin vznikajících ve sprškách sekundárního kosmického záření) a tauonová n_t. Většinou svých vlastností se značně podobají neutrinům elektronovým, liší se způsobem svých interakcí s elementárními částicemi - místo procesů s elektrony (jako jsou b rozpady) doprovázejí slabé interakce s účastí mionů a tauonů.

Tyto jednotlivé druhy neutrin rozlišujeme podle toho, z kterého typu nabitého leptonu vznikají, nebo který lepton vzniká při jejich interakci, zda se jedná o elektron, mion či tauon. V souvislosti se zákonem zachování leptonového čísla se předpokládá, že ke každému ze tří druhů neutrin existuje i příslušné antineutrino n'.
Odlišnost neutrin a antineutrin - helicita neutrin. Goldhaberův pokus. 
Diskutuje se o tom, zda jsou neutrina Diracovské nebo Majoranovské částice - zda jsou antineutrina odlišná nebo totožná s neutriny. Jediné, čím lze dvojici neutrino/antineutrino od sebe rozlišit, je jejich helicita (točivost, spirálnost) - orientace spinu (vnitřního momentu hybnosti) částice vzhledem ke směru jejího pohybu. Přímé změření helicity neutrina by bylo velmi obtížné (mimo možnosti nynější experimentální techniky). Jedinou schůdnou možností je nepřímé stanovení helicity neutrina přes zákon zachování momentu hybnosti v radioaktivním procesu elektronového záchytu EC (viz níže "Elektronový záchyt"). Při elektronovém záchytu je z jádra emitováno pouze neutrino, které v podstatě nedokážeme detekovat. Avšak dceřinné jádro po EC bývá často v excitovaném stavu, při jehož deexcitaci je vyzářen foton záření gama, který ve své helicitě nese určité informace o bilanci momentu hybnosti. Za určitých okolností lze tyto informace dekódovat ke stanovení helicity vylétajícího neutrina.
  Toto nepřímé stanovení helicity neutrina se v r.1958 podařilo americkému týmu pod vedením M.Goldhabera (Brookhaven National Laboratory) velmi rafinovaným pokusem. Použili k tomu měření helicity deexcitačních fotonů gama o energii 963keV emitovaných z excitovaného stavu ¹⁵²Sm vznikajícího elektronovým záchytem v jaderném izomeru europia ^152mEu (§1.3, pasáž "Europium"). Tento nuklid byl zvolen proto, že počáteční i koncový stav mají stejné spinové číslo 0^-. Při elektronovém záchytu jsou pak (v důsledku zákona zachování momentu hybnosti) neutrino a deexcitační foton emitovány s opačným spinem. Pokud změříme polarizaci fotonu, zjistíme tím i helicitu neutrina. Zářič ^152mEu byl umístěn ve feritovém magnetu, který filtruje (selektuje) vylétající deexcitační kvanta podle polarizace...... Tyto fotony gama pak dopadají do prstence z neaktivního ¹⁵²Sm, v němž mohou vyvolávat rezonanční absopci s deexcitací, jejíž fotony jsou registrovány scintilačním detektorem... poměrně složitá analýza výsledků naměřených impulsů v konfrontaci s bilancí spinů (momentů hybnosti) dala pro helicitu elektronových neutrin hodnotu Hne = -1 ± 0,3 - neutrina jsou levotočivá, zatímco antineutrina pravotočivá. Je to v souladu s poznatkem o porušení parity u slabé interakce (viz §1.5, pasáž "CPT symetrie interakcí").

Oscilace neutrin
U neutrin se setkáváme s překvapivým a z klasického hlediska nepochopitelným jevem - že dochází k samovolným přeměnám mezi jednotlivými druhy neutriny - tzv. oscilaci neutrin. Neutrino při svém letu je chvíli elektronovým n_e, pak se změní na mionové či taunové neutrino a vzápětí opět na elektronové atd. (viz však poznámku "Fyzické převtělování?"na konci této pasáže). Metaforicky lze s trochou nadsázky říci, že neutrina se v jistém smyslu chovají jako bájní "duchové": mohou bez překážek čímkoli procházet a jsou schopna se "převtělovat" jedno v druhé...   Jev oscilace neutrin si představujeme jako důsledek kvantově-mechanické interference tří kvantových stavů částice neutrina, které je vnitřně superpozicí stavů "1", "2" a "3" neutrina. Tyto stavy jsou popsány kvantovými vlnami rozdílných vlnových délek *), které se při šíření prostorem střídavě dostávají do stejných fází a do různých fází, což se projevuje jako elektronové, m- nebo t-neutrino.
*) Aby tento mechanismus interference různých vlnových délek mohl fungovat, je třeba aby jednotlivé kvantové stavy měly (v duchu korpuskulárně-vlnového dualismu) různou hmotnost - aby tedy neutrina měla obecně nenulovou klidovou hmotnost (aspoň některá z nich). Ve Standardním modelu částicových interakcí se reakce neutrin s nabitými leptony (např. m^- ® e^- + n_m + n_e') označují jako reakce tzv. slabých nabitých proudů a v kvantové teorii se popisují celkovým Lagrangiánem či Hamiltoniánem, zahrnujícím jak složky nabitého leptonu, tak neutrina, s koeficienty danými tzv. Pontecorvovou- Makaiovou- Nakagawovou- Sakatovou (PMNS) směšovací maticí. Tato matice, která popisuje směšování neutrinových polí, je parametrizována třemi směšovacími úhly q a třemi komplexními fázemi d. Příslušná Schrödingerova rovnice pak poskytuje celkové vlnové řešení jako koherentní superpozice "vlnových klubek", odpovídajících jednotlivým vlastním stavům hmotností. Pravděpodobnost nalezení vlastního stavu hmotnosti je pak vyjádřena periodickou funkcí času, což se při pohybu neutrina projevuje i periodickou závislostí druhu neutrina podél dráhy - oscilace neutrin v prostoru a čase. Velikost a časový průběh oscilací závisí na míře "míchání" mezi jednotlivými čistými stavy "1","2","3", ktré jsou popisovány tzv. směšovacími úhly q₁₂, q₂₃, q₁₃, resp. druhými mocninami sinusů těchto úhlů.
  V nejjednodušším případě pohybu relativistického neutrina s kinetickou energií E_n, které je koherentní superpozicí dvou hmotnostních komponent s rozdílem kvadrátů klidových hmotností Dm_n, vychází pravděpodobnost P nalezení určitého stavu neutrina (např. n_e): P_n®ne » 1 - sin²2q.sin²[(Dm_n²/4hc.E_n).L], kde L je vzdálenost od místa vyzáření neutrina a q je směšovací úhel parametrizující PMNS matici (která je zde dvojrozměrná). Pro každou hodnotu energie E_n pak existuje určitá tzv. oscilační délka L_o, při níž se argument L.Dm_n²/4hc.E_n v sinusové funkci změní o p a pravděpodobnost P_n®ne znovu nabude hodnotu 1: L_o = 4hc.E_n/Dm_n² . Oscilační délka je přímo úměrná energii neutrina E_n a nepřímo úměrná kvadrátu rozdílu hmotností Dm_n² obou druhů (stavů) neutrin. Pro obvykle používané jednotky délky a energie lze oscilační délku vyjádřit ve zjednodušeném tvaru: L_o[m] » 2,5. E_n[MeV] / Dm_n²_[eV2_] . Hodnotu Dm_n² lze stanovit experimentálně z měření závislostí počtu pozorovaných neutrin na energii E_n pro určitou pevnou vzdálenost L a známé spektrum energií E_n neutrin. Z experimentů KamLAND vychází pro oscilace n_e«n_m hodnota Dm_n²»8.10^-5eV², v Super-Kamiokande vychází hodnota Dm_n²»2.10^-3eV², přičemž se jedná o oscilace všech tří typů neutrin. Pro běžná solární a reaktorová neutrina s energiemi jednotky MeV vychází oscilační délka poměrně krátká, řádově desítky km. Pro "atmosférická" neutrina (která vznikají při interakcích vysokoenergetického kosmického záření v zemské atmosféře) o energii desítek GeV i vyšších, pak typická oscilační délka dosahuje stovek až tisíců kilometrů (k testování oscilací je pak třeba využít neutrina detekovaná ve velkých vzdálenostech od místa vzniku; dokonce neutrina vznikající v atmosféře na opačné straně zeměkoule, jak je níže zmíněno u experimentu Super-Kamiokande).
  Oscilace neutrin je kvantově-stochastický proces, jehož pravděpodobnost po emisi neutrina je zpočátku nízká, avšak po délce jeho dráhy se zvětšuje. Ve větších vzdálenostech od zdroje, emitujícího neutrina určitého druhu (zpravidla elektronová), budeme registrovat již směs neutrin všech tří druhů, zastoupených zhruba homogenně v poměru 1:3 (závisí to na hodnotách výše zmíněných směšovacích úhlů q). O vlivu tohoto jevu na detekci jednotlivých druhů neutrin se stručně zmíníme níže.
Pozn.: Fyzické převtělování ? 
Jev oscilace neutrin je z klasického hlediska těžko pochopitelný, mohlo by se zdát že porušuje zákony zachování. Z hlediska kvantové fyziky však nedochází k tomu, že by se neutrina "fyzicky" přeměňovala jedno na druhé. Jen vlnová funkce neutrina je superpozicí 3 stavů (je to parametrizováno výše uvedenými směšovacími úhly). V závislosti na vzdálenosti od místa vzniku se pak budou projevovat různé pravděpodobnosti, že neutrino bude interagovat jako elektronové, mionové či tauonové. V jistém smyslu si můžeme představovat, že osciluje i rychlost neutrina. V kvantové fyzice se tyto jevy samotné nepovažují za porušení zachování energie či symetrií.

"Sterilní" neutrina ?
Nicotnost neutrin ("duchové mezi částicemi") vedla některé jaderné fyziky a astrofyziky k ještě bizarnější představě: že by snad mohly existovat neutrina, která nevykazují ani slabou interakci a s hmotou neintaragují jinak než prostřednictvím pouze gravitační síly. Pro tyto hypotetické neutrální částice se navrhl název sterilní neutrina. Mohly by být kandidáty na vysvětlení zatím záhadné temné hmoty ve vesmíru (§5.6 "Budoucnost vesmíru. Šipka času. Temná hmota. Temná energie." monografie "Gravitace, černé díry..."). Jsou výplodem čiré fantazie, pro jejich existenci nic nesvědčí, nemohly by být nikdy přímo detekovány..!..

Interakce neutrin s částicemi a s hmotou
Neutrina nemají elektrický náboj, nevykazují elektromagnetickou ani silnou interakci, ale jen slabou interakci (o gravitační se zmíníme níže). Z hlediska vnitřního mechanismu jsou veškeré procesy s neutriny zprostředkovány slabou interakcí s virtuální účastí těžkých intermediálních bosonů W^± a Z⁰ (v rámci koncepce tzv. elektro-slabé interakce je tato slabá interakce zprostředkována výměnami těžkých intermediálních bosonů W a Z podle Standardního modelu interakcí částic, viz §1.5 "Elementární částice"). Společným znakem je zde velmi nízký účinný průřez neutrinových interakcí. V závislosti na druhu zúčastněných částic a energiích, interakce neutrin zahrnuje širokou škálu procesů - (kvazi)elastický rozptyl, hluboce neelastický rozptyl, inverzní beta-rozpad, nukleární záchyt, produkce hadronů, vysokoenergetické interakce se vznikem mnoha dalších částic. Některé z nich stručně zmíníme :
  Neutrino-leptonové interakce. Nejjednodušší neutrinovou interakcí je (kvazi)elastický rozptyl neutrin na leptonech (v praxi téměř vždy na elektronech v atom. obalu), typicky :
n + e^- --> n´ + e^-´.
Hodnota účinného průřezu neutrino-leptonové interakce neutrina s energií E_n s elektronem hmotnosti m_e se dá vyjádřit jako s ~ 2m_e.f.(G²/p).E_n , kde G je Fermiho vazbová konstanta slabé interakce (G ~ 1,16x10^–5 GeV^–2) a f je form-faktor zahrnující doplňkové parametry. Účinný průřez zde vychází cca s ~ 2x10^-41 cm²/GeV. Tato malá hodnota účinného průřezu je způsobena malou hmotností terčíkového elektronu.
Z kinematického hlediska, rychle letící neutrino n se srazí s elektronem e^-, odrazí se od něj (většinou pod velkým úhlem nebo dokonce v opačném směru) jakožto neutrino n´ s nižší energií, přičemž předá elektronu část své energie. Odražený elektron e^-´ se pohybuje většinou ve směru původního (incidenčního) neutrina n a může být detekován.
Pro mionová neutrina dochází i k interakci n_m + e^- --> m^- + n_e (nazývané též inverzní rozpad mionu). Má prahovou hodnotu energie 10,8 GeV, danou hmotností mionu, účinný průřez je cca s ~ 15x10^-42 cm²/GeV.
  Neutrino-neutrinové interakce. Za situace velmi vysokých toků a energií neutrin by mohlo docházet ke vzájemné interakci neutrin s neutriny, např. k anihilaci neutrin s antineutriny n + n^~ -> Z⁰ -> f + f^~ obecně na dvojici fermionu f a antifermionu f^~, což může být dvojice leptonů (včetně neutrin) nebo kvarků, za účasti virtuálního bosonu Z⁰. Dvojice nabitých leptonů může vzniknout i výměnou virtuálního W^± bosonu. Účinný průřez neutrino-neutrinových interakcí je zcela nepatrný, takové procesy nemohou být pozorovány. Při vysokých koncentracích a energiích v husté neutrino-elektronové směsi (v předpokládané leptonové éře během prvmí desetiny sekundy po velkém třesku - "Etapy vývoje vesmíru") by však mohly masivně probíhat procesy anihilací a vzájemných přeměn neutrin a elektronů: n_e + n^~_e <--> e^- + e⁺.
  Neutrino-hadronové interakce (v praxi interakce přilétajících neutrin s terčíkovými protony či neutrony v atomových jádrech) :
n_(e,m,t) + nukleon (p⁺,n⁰) --> lepton^-(e,m,t) + hadron.
Neutrino-hadronové interakce mají podstatně vyšší účinný průřez než neutrino-elektronové interakce - v poměru cca 1,8x10³; je to dáno poměrem hmotnosti nukleonu a elektronu. Účinný průřez inteakce neutrina s energií E_n s nukleonem hmotnosti M_p lze vyjádřit jako s ~ f.(G²/4p).M_p.E_n /GeV, kde G je faktor slabé interakce a f je form-faktor závislý na kvarkové struktuře terčíkového nukleonu. Základní hodnota je s_o ~ (G²/4p).M_p = 1,6x10^-38 cm² /GeV.

^{Feynmanovy diagramy některých základních interakcí neutrin s leptony a nukleony.}

  Pro většinu interakcí neutrin obecně platí, že účinný průřez je lineárně úměrný energii dopadajících neutrin. Čím vyšší je energie neutrin, tím snadněji je lze detekovat pomocí interakcí ve hmotě. Až při velmi vysokých energiích (>>~10⁶ GeV) již účinný průřez přestává být úměrný energii, dosáhne nasycení; pro neutrino-hadronové interakce již má konstantní hodnotu cca s ~ 10^-38 cm² (pro elektromagnetické interakce se dosahuje nesrovnatelně vyšších hodnot až s ~ 10^-27 cm²).
  Tyto a další druhy interakcí neutrin se pravděpodobně ve velkém měřítku uplatňují v bouřlivých astrofyzikálních procesech - při výbuchu supernov, ve velmi raných stádiích vývoje vesmíru (§5.4 "Standardní kosmologický model. Velký třesk. Formování struktury vesmíru.", část "Etapy vývoje vesmíru" v knize "Gravitace, černé díry a fyzika prostoročasu"). Některé z těchto procesů mohou být použity i k detekci neutrin :
 Detekce neutrin
O detekci různých druhů záření bude podrobně pojednáváno v kapitole 2 "Detekce a spektrometrie ionizujícího záření". Detekce neutrin se však svou technikou i principy značně liší od víceméně "rutinní" detekce záření a, b, g, využívané často i v technické praxi. Neutrina, která nemají elektromagnetickou ani silnou interakci a v látce téměř na nic nepůsobí, nikdy nemůžeme "vidět" ani detekovat přímo, lze detekovat pouze sekundární produkty vznikající při jejich interakcích. Jedná se (aspoň zatím) spíše o unikátní a delikátní experimenty, snažící se prokázat samotnou existenci neutrin a odhalit některé jejich základní vlastnosti (v tomto smyslu se poněkud podobá experimentům s detekcí gravitačních vln). Proto se o metodách detekce neutrin zmíníme již na tomto místě.
  Detekovat neutrina je obecně velmi obtížné - nevykazují elektromagnetickou ani silnou interakci, jen interakci slabou. Účinný průřez této slabé interakce je velmi malý, neboť je zprostředkován výměnami těžkých intermediálních bosonů W a Z; tato velká hmotnost výměnných částic způsobuje velmi malý dosah a silně potlačuje pravděpodobnost interakcí, na rozdíl od obvyklých elektromagnetických procesů, zprostředkovaných výměnou fotonů s nulovou klidovou hmotností. Abychom vůbec byli schopni nějaká neutrina detekovat, musí být splněny 4 základní podmínky :
1. Musí být k dispozici dostatečně intenzivní tok neutrin (min cca 10¹³ neutrin/cm²/s) dopadajících do citlivého objemu detektoru.
2. Detektor musí být velký - musí obsahovat velký objem detekční látky (hmotnost - bývají to tisíce až desítky tisíc tun), se kterou mohou dopadající neutrina interagovat. Jen tak bude určitá rozumná pravděpodobnost, že některá z těch miliard prolétajících neutrin budou interagovat a vyvolají detekovatelné impulsy.
3. Musí být na co nejnižší míru sníženo rušivé radiační pozadí z přírodní radioaktivity, z materiálu detektoru, z kosmického záření. Pro odstínění především kosmického záření je nutno detektory umístit hluboko do podzemního či podmořského prostoru. Klade to též vysoké pořadavky na použité konstrukční materiály a hlavně detekční látku, její čistotu.
4. Značně dlouhá doba akvizice (desítky dnů, měsíců, i několik let), abychom zaregistrovali dostatečně velký počet neutrin, umožňující potřebně přesnou statistickou analýzu dat.
  Pro detekci neutrin to tedy bývají velké nádrže obsahující mnoho stovek až tisíců tun vysoce čistého materiálu (vody, kapalného scintilátoru), umístěné v kilometrové hloubce pod zemí, příp. pod vodou či ledem v podmořském prostoru. Jsou opatřeny velkým počtem fotonásobičů pro detekci vznikajících scintilací ve scintilační látce nebo z Čerenkovova záření. Měří se po dobu mnoha dní či měsíců.
  K detekci neutrin lze využít především tří druhů procesů :

• 1. Interakce neutrin s nukleony (proces obráceného rozpadu beta; produkce částic)
  Elektronové neutrino n_e interaguje (slabou interakcí) v atomovém jádře s neutronem n^o a způsobí tam reakci n_e + n^o ® p⁺ + e^-, nebo s protonem reakcí n'_e + p⁺ ® n^o + e⁺. Účinný průřez této interakce činí asi 10^-47 m².(E_n /1MeV)².
  Při vysokých energiích neutrin může s nukleony docházet k částicovým interakcím za vzniku elektronů, mionů či tauonů.

První úspěšná detekce neutrin
pomocí procesu n_e+p⁺ ® n^o+e⁺ se podařila v r.1956 F.Reinesovi a C.Cowanovi z laboratoří v Los Alamos, kteří jako zdroj neutrin použili výkonný jaderný reaktor v Savanah River s tokem antineutrin cca 10¹³n/cm²/s. Jako terčík a současně detektor byl použit kapalný scintilátor (triethylbenzen) s příměsí kamia ve velké nádobě objemu 1400 litrů. Při interakci neutrina s protonem obsaženým ve scintilátoru vzniká neutron n^o (s kinetickou energií několik keV) a pozitron e⁺ (s kinetickou energií 0¸8MeV). Pozitron e⁺ se v kapalině velmi rychle zbrzdí (za dobu cca 10^-10s) a pak s některým z elektronů anihiluje (e⁺+ e^-® g + g) za vzniku dvou anihilačních fotonů g, z nichž každý má energii 511keV. Ionizační energie pozitronu spolu s anihilačními fotony (celková energie 1¸8MeV) vyvolají ve scintilátoru světelný záblesk registrovaný fotonásobiči. Neutron se srážkami s jádry zpomalí (proces zpomalení a difuze trvá do 30msec) a zachytí se jádrem kamia v reakci n^o + ¹¹³Cd₄₈ ® ¹¹⁴Cd₄₈ + g; excitovaný izotop kadmia při své deexcitaci během několika mikrosekund vyzáří 2-4 kvanta gama o celkové energii 9MeV a přejde do základního stavu. Tato kvanta g rovněž vyvolají ve scintilátoru světelný záblesk zachycený fotonásobiči. Interakce neutrina s protonem (n_e+p⁺®n^o+e⁺) se tedy prozradí dvěma po sobě následujícími elektrickými signály z fotonásobičů: 1.impuls o amplitudě odpovídající 1-8MeV pocházející z registrace pozitronu; do cca 25 msec se objeví 2.impuls o amplidudě 3-10MeV pocházející ze záchytu neutronu v jádře kadmia. Během měření trvajících více než 100 hodin bylo takto detekováno v průměru 36 případů zmíněné reakce (n_e+p⁺®n^o+e⁺) neutrin za hodinu, což dávalo účinný průřez reakce cca 10^-43cm².
Radiochemická detekce neutrin 
   Pro měření interakce s neutronem (n_e+n^o ® p⁺+e^-) je potřeba zvolit takové jádro, kde přeměna neutronu na proton vede k radioaktivnímu jádru vysílajícímu záření, jež lze snadno detekovat. V praxi se pro tato měření využilo nejdříve jader chlóru ³⁷Cl - velká nádrž naplněná asi 600 tunami tetrachloretylenu C₂C_l4 (jinak běžný chemický čisticí prostředek, který ale musel být speciálně vyčištěn) byla umístěna v hloubce asi 1,5km pod zemí v opuštěném dole na zlato Homestake v Jižní Dakotě v USA - aby bylo minimalizováno radiační pozadí z kosmického záření a z pozemských zdrojů. Experimenty probíhaly pod vedením R.Davise v 60.letech. Elektronová neutrina vyvolávají v jádrech chloru reakci obráceného b-rozpadu: n + ³⁷Cl ® ³⁷Ar + e^-; prahová energie neutrin je zde 814keV. Vzniklý argon ³⁷Ar se s poločasem 35 dní rozpadá elektronovým záchytem zpět na ³⁷Cl. Přitom z atomového obalu dceřinného chlóru jsou (následkem charakteristického X-záření, které z 90% podléhá vnitřní konverzi) emitovány Augerovy elektrony o energii okolo 2,6keV, které lze detekovat plynovým proporcionálním detektorem. K tomu je ovšem nutno vyextrahovat těch několik vzniklých atomů ³⁷Ar z celého objemu cca 400000 litrů tetrachloretylenu v nádrži, což je mimořádně obtížný technický problém. V r.1968 byly výsledky experimentu vyhodnoceny, neutrina byla úspěšně detekována, avšak jejich množství představovalo jen asi 30% neutrin očekávaných podle astrofyzikálních modelů termonukleárních reakcí v nitru Slunce.
  Dalším materiálem vhodným pro radiochemickou detekci neutrin je galium ⁷¹Ga, v jehož jádrech vyvolávají elektronová neutrina reakci n + ⁷¹Ga ® ⁷¹Ge + e^- s následným rozpadem germania ⁷¹Ge elektronovým záchytem doprovázeným vyzářením Augerových detektorů podobně jako při rozpadu ³⁷Ar. Výhodou galia je podstatně nižší prahová energie 233keV detekovaných neutrin, nevýhodou vyšší cena galia ve srovnání s chlorem. Na tomto základě byly počátkem 90.let uskutečněny experimenty SAGE a GALEX, které úspěšně detekovaly nízkoenergetická neutrina, rovněž v nižším počtu vzhledem k očekávanému.
  Tímto způsobem byla úspěšně detekována neutrina jak z laboratorních zdrojů, tak z vesmíru - především ze Slunce, kde vzniká obrovské množství neutrin při termonukleárních reakcích. Jedna záhada se zde však vyskytovala permanentně: všechna měření dávala zhruba 3-krát menší hodnotu toku elektronových neutrin než se očekávalo podle rozboru termonukleárních reakcí na Slunci. Tato záhada nedostatku slunečních neutrin byla vyřešena až za mnoho let, kdy zdokonalené metody detekce neutrin prokázaly efekt oscilace neutrin - samovolnou vzájemnou přeměnu elektronových, mionových a tauonových neutrin, přičemž dřívější metody byly schopny detekovat pouze neutrina elektronová (kterých je 1/3).
CNGS (Cern Neutrinos to Gran Sasso) + OPERA (Oscillation Project with Emulsion tRacking Apparatus) 

Jedná se o nový zajímavý měřící systém typu vysílač ® přijímač(detektor) neutrin, jehož cílen je zkoumání oscilace neutrin, především na taunová neutrina a k upřesnění hmotnosti neutrin. Začal fungovat v r.2006. Vysílač neutrin je v CERN, přijímač (detektor) neutrin je instalován v podzemní laboratoři v hloubce 1400m pod horou Gran Sasso v Itálii. Vysílač neutrin je tvořem velkým urychlovačem protonů, synchrotronem SPS (Super Proton Synchrotron) v CERNu, z něhož protony, urychlené na energii 400GeV, se srážejí s jádry terčíku za vzniku velkého množství mesonů p (a řady dalších částic - kaonů, hyperonů,...). Nabité piony se pomocí magnetického pole separují a vedou do 1,2 kilometru dlouhého vakuového rozpadového tunelu, kde se během letu rozpadají (mají poločas rozpadu jen asi 2.10^-8sec.) za vzniku mionů a mionových neutrin: p^- ® m^- + n'_m , p⁺ ® m⁺ + n_m . Průměrná energie vznikajících neutrin je asi 17GeV; pro registraci tauonových neutrin pomocí tauonů potřebujeme značně vysokou energii původních mionových neutrin, vyšší než je klidová energie tauonu (m_0t »1,2GeV/c²). Neutrinový svazek je v důsledku relativistických efektů poměrně úzce kolimován přibližně ve směru původního protonového a pionového svazku.
  Celý systém [pionový svazek + rozpadová trubice] je nasměrován k 732km vzdálené podzemní laboratoři LNGS (Laboratori Nazionali del Gran Sasso) v Itálii, kam neutrina skrze zemi přilétají (ostatní částice se rychle pohltí již ve stínění na konci rozpadového tunelu, další miony pak v hornině pod zemí). Zde je instalován detekční systém OPERA složený ze 150000 střídajících se vrstev ("sendvičů", cihliček) olova *) tloušťky 1mm, proložených tenkými listy fotografické emulze. Olovo slouží jako terčík pro interakci neutrin a fotografická emulze pro registraci a zviditelnění produktů reakce.
*) Pro snížení radiačního pozadí bylo použito tzv. "římské olovo" z lodí převážejících olovo pro budování vodovodního potrubí v Římě a potopených někdy kolem 60.let před naším letopočtem. Na dně moře toto olovo leželo netknutě 2000 let, takže se v něm za tu dobu rozpadla většina přírodních radioaktivních isotopů.
  Tato "stará" technologie jaderných fotoemulzí byla použita proto, že jako jediná poskytuje velmi vysoké prostorové rozlišení »1mm registrovaných drah částic, potřebné pro zachycení kratičkých drah tauonů o velmi krátké době života (řádu pikosekund). Vyhodnocování fotoemulzí je zde ovšem plně automatizováno (pomocí technologií vyvinutých v Japonsku). Detekce drah částic pomocí jaderných fotoemulzí, včetně technologie zvané ECC (Emulsion Cloud Chamber), jakási "emulzní mlžná komora", je podrobněji rozebírána v §2.2, část "Detektory stop částic". Detekční systém OPERA je velmi mohutný, oněch 150000 sedvičů obsahuje dohromady asi 110 000 m² filmu s fotoemulzí a více než 100 000 m² olověných plátů o celkové hmotnosti více než 1200 tun. Tato mohutnost je vynucena dvěma okolnostmi: 1. Velmi nízký účinný průřez interakcí neutrin s látkou; 2. Vzdálenost 730km mezi vysílačem a detektorem (odpovídající době letu neutrin 2,43ms) je příliš krátká, takže jen velmi malá část (cca 1-2%) neutrin stihne oscilovat.
  Během letu od vysílače k detektoru dochází k oscilaci neutrin, takže kromě původních mionových sem přilétají i elektronová a taunová neutrina. Při reakcích mionových neutrin v olovu vznikají miony, při reakcích elektronových neutrin elektrony, při reakcích tauonových neutrin vznikají tauony (o které zde předvším jde). Vzniklé tauony se v 64% případů rozpadají na piony, v 18% na elektrony a v 17% na miony (za emise neutrin, které z detekčního prostoru unikají). Na základě záznamu stop částic ve fotoemulzi se mikroskopickým skenováním rekonstruuje kinematika původní interakce, což umožňuje stanovit polohu vzniku tauonu a místo jeho rozpadu. V systému jsou rozmístěny i plastové scintilátory, jejichž signál udává okamžik interakce a umožňuje stanovit, ve kterých fotoemulzích lze očekávat užitečný záznam; ty jsou vzápětí vyhodnoceny. Součástí systému jsou i elektronické "trackery" částic a magnetické spektrometry. V květnu r.2010 zde bylo poprve registrováno taunové neutrino, vzniklé oscilací z původně mionového neutrina.

• 2. Pružný rozptyl neutrina na elektronu: n + e^- ® n´ + e^-´
  (nastává pro všechny druhy neutrin). Rychle letící neutrino n se srazí s elektronem e^-, odrazí se od něj (většinou pod velkým úhlem nebo dokonce v opačném směru) jakožto neutrino n´ s nižší energií, přičemž předá elektronu část své energie. Odražený elektron e^-´ se pohybuje většinou ve směru původního (incidenčního) neutrina n a může být detekován.
  Účinný průřez této interakce činí asi 10^-48m².(E_n /1MeV).

   Pokud se tento elektron e^-´ pohybuje v nějakém prostředí (např. ve vodě) rychlostí vyšší než je rychlost světla v tomto prostředí, vysílá Čerenkovovo záření (mechanismus jeho vzniku a vlastnosti viz §1.6, pasáž "Čerenkovovo záření"), které lze detekovat fotonásobiči. Tento způsob detekce neutrin má sice vyšší prahovou energii (5MeV), jeho předností však je použitelnost i pro jiné druhy neutrin než jsou elektronová.

Detekce a spektrometrie neutrin s pomocí různých druhů jejich interakcí.
Vlevo: Některé principy detekce. Vpravo: Systém fotonásobičů SuperkamiokaNDE.

Neutrinový detektor Kamioka NDE
Detektor tohoto druhu, nazvaný Kamioka NDE (Kamioka Neutrino Detection Experiment *), byl pod vedením M.Koshiby zkonstruován v r.1982 v Japonsku - v cínovém dole Kamioka (v pohoří ... zvaném "Japonské Alpy") v hloubce 820m byla postavena nádrž obsahující asi 20000 tun vysoce čisté vody. Fotony Čerenkovova záření byly registrovány téměř 1000 velkými fotonásobiči; dalších 120 fotonásobičů, zapojených v antikoincidenci, obklopovalo tento systém v geometrii 4p. Elektronický systém zpracovávající impulsy z jednotlivých fotonásobičů umožňoval lokalizovat místo interakce neutrina, stanovit jeho energii a přibližně i směr příletu. Tento detektor tedy byl již spektrometrem, pracujícím v reálném čase (na rozdíl od dodatečné detekce Augerových elektronů v dřívějších radiochemických detektorech). Kromě zpřesnění výsledků z radiochemických detektorů a změření vysokoenergetické části spekter neutronů ze Slunce bylo na tomto detektoru dosaženo i dalšího významného úspěchu: dne 23.února 1987 byl zaregistrován záblesk 12 neutrin pocházející z výbuchu supernovy SN 1987A ve Velkém Magellanově oblaku (sousední galaxie vzdálená 170 000 světelných let).
*) Pozn. Detektor Kamioka NDE byl původně určen pro prokázání rozpadu protonu (zkratka NDE znamenala "Nucleon Decay Experiment") - podle některých verzí unitárních teorií velkého sjednocení (GUT = Grand Unifikační Teorie, sjednocují silné, slabé a elektromagnetické interakce) by proton neměl být stabilní částicí, ale rozpadal by se (např. p⁺®p^o+e⁺) s poločasem T1/2 >10^30-40let. Tento poločas je natolik dlouhý, že se ve vesmíru od jeho vzniku možná ještě nerozpadl ani jeden proton! Nepřekvapuje, že detekce rozpadu protonu nebyla úspěšná. Šťastný nápad použít toto zařízení k detekci neutrin byl však velmi úspěšný, což dalo zkratce NDE nový význam.
Super Kamioka NDE 
   Jako pokračování detektoru KamiokaNDE byl v r.1996 postaven ještě podstatně větší detektor Super KamiokaNDE, umístěný ve starém zinkovém dole 1700m pod povrchem hory Ikena Yama poblíž městečka Kamioka. Válcová nádrž o průměru 34m a výšce 36m, na jejichž vnitřních stěnách je rozmístěno 11 146 velkých fotonásobičů (průměr fotokadody téměř 50cm), je naplněna téměř 50 000 tunami superčisté vody. Fotonásobiče detekují Čerenkovovo záření elektronů nebo mionů vznikajících srážkou elektronových nebo mionových neutrin s protony a neutrony. Pomocí poměru četností produkce elektronů a mionů je systém schopen rozlišit elektronová a mionová neutrina. V r.1998 byly na této aparatuře prokázány oscilace atmosférických neutrin. Atmosférická neutrina neustále vznikají v horních vrstvách atmosféry při rozpadech pionů a posléze mionů, vytvářených interakcí tvrdého kosmického záření s atmosférou - viz §1.6, část "Kosmické záření", pasáž "Sekundární kosmické záření". Vznikají přitom mionová a elektronová neutrina (v poměru 2n_m : 1n_e). Neutrina energie E_n přicházející "zdola" procházejí skrze celou Zemi (vzdálenost L od místa jejich vzniku) a mají více času na prodělání oscilací, na rozdíl od neutrin přicházejících "zhora", které prošly jen několik kilometrů atmosféry a necelé 2km zeminy. Tato vertikální anizotropie v relativním zastoupení mionových neutrin byla detekčním systémem spolehlivě změřena. Byl pozorován znatelný úbytek detekované četnosti mionových neutrin pro L/E_n kolem 500km/GeV a navíc byl změřen opětovný nárust - "oživení" četnosti detekce mionových neutrin pro délky řádu L»10³-10⁴km/GeV, způsobený oscilačním chováním neutrin ve vzdálenosti větší než polovina oscilační délky L_o neutrin pro danou energii E_n (jak bylo diskutováno výše v pasáži "Oscilace neutrin").
Neutrinový detektor SNO 
   Další značné zdokonalení bylo realizováno v neutrinovém spektrometru SNO (Sudbury Neutrino Observatory) umístěném v hloubce 2km v dole u Sudbury v Ontariu v Kanadě. Zde je uvnitř nádoby se 7000 tun "lehké" vody (¹H₂O) umístěna další nádoba s 1000 tunami těžké vody (²H₂O, tj. D₂O). Záblesky Čerenkovova záření sleduje přes světlovodné trubice více než 9500 vnějších fotonásobičů. Neutrina způsobují v materiálu detektoru (vodě a těžké vodě) tři druhy reakcí:
a) Pohlcení elektronového neutrina neutronem v deuteriu, při němž se neutron změní na proton a energetický elektron. Deuteron, který je slabě vázaným jádrem, se pak rozpadne na dva protony a elektron: n_e + ²H ® p + p + e^-. Rychle letící elektron vyvolá Čerenkovovo záření.
b) Rychle letící neutrino se "srazí" s neutronem či protonem v deuteriu a při pružném rozptylu předá část kinetické energie, což způsobí rozpad deuteronu na proton a neutron: n + ²H ® n_rozptýlené + p + n^o. Uvolněný neutron je pak pohlcen jiným deuteronem, přičemž se emituje foton záření g. Tento foton g při fotoefektu či Comptonově rozptylu v látce vyrazí elektron, který způsobuje Čerenkovovo záření.
c) Neutrino se "srazí" s elektronem a při pružném rozptylu jej urychlí natolik, že vyvolává Čerenkovovo záření.
  Proces a) je možný pouze s elektronovým neutrinemn_e, zatímco procesy b) a c) může vyvolat libovolné neutrino. Procesy a) a b) nastávají pouze v deuteriu v těžké vodě, proces c) nastává stejně na elektronech v lehké i těžké vodě. Analýzou těchto procesů lze tak měřit nezávisle jak tok elektronových neutrin, tak i tok všech neutrin (tj. elektronových + mionových + tauonových) dohromady. Výsledky měření ukázaly, že nedostatek slunečních neutrin ve všech předchozích experimentech je způsoben neutronovými oscilacemi.
KamLAND - scintilační detektor neutrin z jaderných reaktorů 
   Japonský detektor KamLAND (Kamoioka Liquid Scintillator Neutrino Detector; původně zde byl KamiokaNDE, který byl předělán na KamLAND) je tvořen kulovou nádobou o průměru 13m, naplněnou kapalnou scintilační látkou detekující pozitrony vzniklé při záchytu antineutrina protonem. Scintilační záblesky jsou registrovány soustavou více než 18000 fotonásobičů rozmístěných na vnitřní stěně nádoby. Scintilační nádoba je obklopena vnějším Čerenkovovým detektorem s 3200 tunami vody. Energii neutrina je možno přibližně stanovit ze scintilace pozitronu. Vznikající neutrony jsou na dráze do asi 10cm zachycovány jádry vodíku, přičemž se vyzařují fotony záření g o energii asi 2MeV, způsobující rovněž scintilaci detekovanou soustavou fotonásobičů. Přístroj je určen k detekci antineutrin z okolních jaderných reaktorů, přičemž je určováno energetické spektrum a zastoupení elektronových antineutrin v závislosti na uražené vzdálenosti. Detektor umožnil detailnější studium oscilací neutrin, které potvrdilo a doplnilo výsledky z obou systémů zmíněných výše.
DUNE (Deep Underground Neutrino Experiment) 
   je budován pro studium vlastností neutrin, především v souvislosti s dosud ne dostatečně prozkoumaným a pochopeným jevem oscilací neutrin. Tento mezinárodní pokročilý projekt je založen na spolupráci především dvou nukleárních laboratoří :
-> Neutrina se budou "vyrábět" ve Fermi National Accelerator Laboratory (Fermilab) v Batavii, Illinois, v rámci projektu Long-Baseline Neutrino Facility (LBNF). Zde výkonný protonový urychlovač PIP-II (800 MeV) pomocí nárazů protonů do uhlíkového terčíku bude podukovat intenzívní svazky neutrin (mionových (anti)neutrin v rozmezí energií 1-5 MeV), kolimované severozápadně směrem na laboratoř Sanford Lab. Tyto neutrina ve Fermilabu budou nejprve procházet menším "monitorovacím" detektorem vysílaných (neoscilujících) neutrin.
-> Výsledná detekce těchto neutrin se bude provádět v Sanford Underground Research Facility (Sanford Lab) v Lead, Jižní Dakota, vzdálené 1300 km od zdroje, pomocí velkého kryogenního podzemního detektoru v hloubce 1,5 kilometru (v bývalém dole na zlato Homestake) obsahujícího 70 000 tun kapalného argonu ochlazeného na teplotu -184°C, s časově-pojekčními komorami LArTPC (tyto detektory jsou popsány v kap.2 "Detekce a spektrometrie záření", §2.3, pasáž "Driftové a časově-projekční proporcionální komory"), se simultánní detekcí scintilačních záblesků v argonu.
   Neutrina při své podzemní cestě dlouhé 1300 km budou průběžně oscilovat, takže do vzdáleného detektoru budou dopadat všechny 3 druhy neutrin. Měřením zastoupení různých druhů výsledných neutrin registrovaných ve vzdáleném detektoru, v závislosti na energii, umožní podrobnější studium dynamiky neutronových oscilací. Jedním z cílů je i zlepšit dosavadní malou úspěšnost detekce tauonových neutrin.
Velký kryogenní podzemním detektor v DUNE by též mohl detekovat neutrina z výbuchu supenovy. Rovněž se v něm plánuje hledat produkty případného rozpadu protonů ...
   Experiment DUNE lze považovat za podstatné zdokonalení dřívějšího neutrinového experimentu CNGS+OPERA (popsaného výše "CNGS+OPERA") a též proslulého neutrinového detektoru Kamioka - Super Kamioka NDE. Dokončení velkého podzemního detektoru, spuštění neutrinového svazku a zahájení měření v DUNE je plánováno na r. 2026-27.

• 3. Interakce vysokoenergetických neutrin s protony za vzniku mionů m .
  Nabité miony m pak při pohybu vysokou rychlostí v průzračném optickém prostředí vysílají Čerenkovovo záření, které lze detekovat fotonásobiči.

Detekce neutrin v ledovcích
Zajímavou a poněkud kuriózní možnost detekce rychlých neutrin představuje využití mohutných mas přírodního ledu v rozsáhlých ledovcích nacházejících se především v Antarktidě. Při nárazu vysokoenergetického neutrina na proton (v některém z jader molekuly vody - ledu) vznikne mion m o vysoké energii, který podél své dráhy pohybu ledem za sebou zanechává namodralý světelný kužel Čerenkovova záření. Jeho směr umožňuje určit směr dráhy původního neutrina. V kilometrových hloubkách v nitru ledovce za vysokých tlaků je led vysoce průhledný, kompaktní a bez bublinek, takže záblesky mionů lze detekovat do vzdáleností desítek až stovek metrů. Rozmístění fotonásobičů, spolu s koincidenční analýzou detekovaných impulsů, umožňuje prostorovou rekonstrukci kužele.
Pokud jsou optické senzory - fotonásobiče - obráceny směrem do nitra Země, detekují se neutrina přicházející z opačné strany, severní polokoule, procházející skrz zeměkouli. Z tohoto směru jsou totiž zcela odstíněny rušivé miony pocházející ze sekundárního kosmického záření. Systém je schopen detekovat nejen běžná neutrina s energiemi několik MeV, ale i vysoce energetická neutrina s energiemi řádu TeV i vyššími.
AMANDA
Prvním systémem tohoto druhu je projekt AMANDA (Antarctic Mion And Neutrino Detector Array) vybudovaný v letech 1996-2000 při Amundsen-Scotově polární stanici v Antarktidě. Sestává z více než 700 fotonásobičů, uložených v tlakuvzdorných skleněných koulích, zapuštěných pod antarktický led v 19 šachtách hloubky přes 2km*). Fotonásobiče jsou napájeny elektrickými kabely, detekované impulsy jsou světelnými kabely vedeny do vyhodnocovacího zařízení. Dosažené úhlové rozlišení pro neutrina z kosmického záření je kolem 1°.
*) Šachty do ledu jsou "vrtány" proudem horké vody 80°C, spustí se do nich fotonásobiče, načež šachta po několika hodinách opět zamrzne. V ledu zamrzlé fotonásobiče však zůstanou elektricky propojeny s vyhodnocovacím centrem.
ICECUBE
Pokračováním je ještě větší systém detekce neutrin v antarktickém ledovci, nazvaný ICECUBE (Ice Cube - krychle ledu), dokončený v prosinci 2010. Sestává z 5160 fotonásobičů, zapuštěných v 86 šachtách v různých hloubkách 1450-2450 m pod ledem. Tyto šachty jsou ve vodorovném směru rozmístěné v šestiúhelníkové mřížce s roztečí 125 metrů. Do každé této šachty byl (při rozpuštění) na laně spuštěn řetězec 60 fotonásobičů s vertikálními vzdálenostmi 17 metrů *), které pak v ledu zamrzly. Detekcí světelných záblesků je takto pokryta krychle 1x1x1 kilometr ledu. Všechny fotonásobiče jsou vybaveny digitálními mikroprocesory s rychlým přenosem dat do vzdálených vyhodnocovacích počítačů.
*) Pozn.: Ve středu pole je 8 řetězců fotonásobičů rozmístěno hustěji, s vodorovnou vzdáleností 70 metrů a svislou roztečí 7 metrů (tzv. "DeepCore"). Kromě toho je na povrchu nad každým hloubkovým řetězcem fotonásobičů umístěna fotodetekční jednotka se dvěma fotonásobiči směřujícími dolů. Toto povrchové pole "IceTop" slouží jako antikoincidenční a kalibrační detektor pro IceKube.
  Detekční systém IceCube běhen svého dosavadního provozu zaregistroval několik zajímavých případů vysokoenergetických neutrin. Poslední případ je ze září 2017, kdy bylo detekováno vysokoenergetické neutrino, pocházející pravděpodobně z velmi aktivního blazaru TXS 0506+056. Je reálná naděje na úspěšnou detekci neutrin ze supernovy ("Výbuch supernovy. Neutronová hvězda. Pulsary."), pokud by vybuchla v naší Galaxii nebo v některé sousední. Případně ze splynutí neutronových hvězd ("Srážky a splynutí neutronových hvězd").
Podmořská detekce neutrin 
Čerenkovovo záření, vznikající průletem mionů, lze detekovat i ve vodě ve velkých hloubkách v moři (kde již neproniká sluneční světlo). Prvním prototypem podmořského detektoru neutrin byl DUMAND (Deep Underwater Muon And Neutrino Detector) s 24 fotonásobiči u pobřeží Big Island of Hawaii. Prvním funkčním detektorem neutrin tohoto typu je BAJKAL se 192 fotonásobiči, který úspěšně pracuje v hloubce 1500m pod hladinou sibiřského jezera Bajkal.
  Podmořský detekční systém neutrin ANTARES (Astronomy with a Neutrino Telescope and Abyss environmental RESearch) *) byl vybudován v r.2006-2008 ve Středozemním moři asi 40km od Francouzského pobřežního města Toulon. Do hloubky 2400m pod hladinu moře (kam již neproniká denní světlo) bylo postupně spuštěno 12 vertikálních nosných lan, každé délky 450m, nesoucích celkem 900 fotonásobičů. Detekční systém pokrývá plochu asi 200´200m. Záblesky Čerenkovova záření z prolétajících mionů vyvolávají ve fotonásobičích elektrické impulsy, které jsou detekovány v koincidenci. Toto záření z mionů musí být odlišeno od pozadí způsobeného bioluminiscencí podmořských organismů a od Čerenkovova záření velkého počtu elektronů energie okolo 1MeV, vznikajících b-rozpadem radioaktivního draslíku ⁴⁰K.
*) Vedle detekce neutrin je experiment ANTARES též součástí interdisciplinárního podmořského a oceánografického výzkumu, jako je monitorování podmořského prostředí, hlavně bioluminiscence; bude obsahovat i seismografická čidla.
  Experiment ANTARES bude v dalších letech pokračovat projekty NEMO (NEutrino Mediterranean Observatory) asi 80km od pobřeží Sicilie a NESTOR (NEutrinos from Supernova and TeV Sources, Ocean Range) u pobřeží Řecka, čímž bude realizována detekce neutrin v objemu řádově 1 km³. Bude tím pokrývána geografická oblast do značné míry komplementární k výše zmíněnému antarktickému detektoru IceCube.
Rádiová detekce neutrin pomocí Askaryanova záření 
Askaryanovo záření (viz §1.6, pasáž "Askaryanovo záření") se zkouší pro deteci neutrin, především v Antarktidě, kde vzniká při průletu vysokoenergetických neutrin vrstvou ledu. Anténa ANITA (....) umístěná na balónu nad Antarktidou, detekuje tyto rádiové impulsy. Pracuje ve spolupráci s fotonásobiči detekujícími Čerenkovovo záření v antarktickém ledu v systému IceCube.
   Hlavním úkolem rozsáhlých ledovcových a podmořských detektorů je hledání vysokoenergetických neutrin, která mohla vznikat při bouřlivých kosmických událostech, především při výbuchu supernov a při samotném vzniku vesmíru, při velkém třesku. Detekce takových neutrin by mohla být cenným zdrojem informací o procesech jiným způsobem nepozorovatelných. Lokalizace zdrojů vysokoenergetických neutrin by mohla objasnit mechanismus protonové akcelerace a odpovědět tak na otázku původu vysokoenergetického kosmického záření.

Význam detekce neutrin
Vedle základního (většinou čistě teoretického) výzkumu vlastností neutrin a částicových interakcí s jejich účastí, může mít detekce neutrin význam i pro studium různých procesů zde na Zemi i ve vesmíru. Neutrina totiž, díky své extrémní pronikavosti, jsou jediné částice, které jsou schopné "vynést" informace o jaderných a částicových procesech z nitra masívních, rozsáhlých či kompaktních objektů, odkud žádné jiné záření absolutně nepronikne.
   Zde na Zemi může zvýšený počet detekovaných neutrin v určitých místech indikovat výskyt ložisek přírodních radioaktivních látek (i ve velkých hloubkách pod zemí) - uranu a thoria, při jejichž radioaktivním rozpadu, v rozpadových řadách, vznikají i neutrina (elektronová antineutrina).
   Detekce toku solárních neutrin umožňuje testovat okamžitou intenzitu termonukleárních reakcí v nitru Slunce (zvláště proto-protonového cyklu). Ani vysoká hustota a tloušťka plasmatu ve slunečním nitru nezabrání neutrinům opustit prakticky okamžitě oblast svého zrodu a "vynést" tak ven příslušnou informaci (na rozdíl od fotonů, které se po statisíce let "prodírají" plasmou, s postupnou degradací energie, z nitra k povrchu, než se vyzáří; mohou nést informaci pouze o povrchových vrstvách Slunce).
   Neutrina dále přinášejí důležité informace o bouřlivých procesech ve vzdáleném vesmíru. Jsou to především výbuchy supernov, při nichž je emitováno kolosální množství neutrin (elektronových n_e). Reliktní neutrina, pocházející z leptonové éry, mohou poskytnout důležité informace o dynamice nejranějších fází vývoje vesmíru a formování jeho struktury.
   Širší využití možností poskytovaných neutriny je však vázáno na zdokonalení detekční techniky neutrin.

Klidová hmotnost neutrin
Původní Fermiho teorie předpokládala, že klidové hmotnost neutrina je nulová. Počátkem 80.let se však rozvinuly rozsáhlé diskuse o klidové hmotnosti neutrin: zda neutrino má nulovou klidovou hmotnost (a je tedy vlnové povahy - jako kvantum záření se šíří rychlostí světla c), či nenulovou, byť velmi malou, klidovou hmotnost m_0n (a je tedy částicí pohybující se pomaleji než světlo). Tyto diskuse byly podníceny prvními úspěšnými pokusy s detekcí neutrin v 70. a 80.letech, kdy se ukázalo, že tok slunečních neutrin je asi 3-krát nižší, než se očekávalo na základě analýzy termonukleárních a následných reakcí v nitru Slunce. Tento deficit slunečních neutrin se označoval jako "záhada slunečních neutrin", nebo dokonce jako "neutrinový skandál". V r.1985 přišli Mišejev, Smirnov a Wolfstein s hypotézou, že neutrina během svého letu "oscilují" mezi stavy elektronového, mionového a tauonového neutrina, což vede k tomu, že se stávají střídavě viditelnými a neviditelnými pro tehdejší detektory schopné zaznamenat pouze elektronová neutrina. Mechanismus oscilací však může fungovat jen tehdy, když neutrina mají nenulovou klidovou hmotnost (aspoň dva druhy-stavy neutrina); bylo diskutováno výše v pasáži "Oscilace neutrin". Změřit, či alespoň odhadnout, klidovou hmotnost neutrin lze několika způsoby.
   V principu by hmotnost neutrina m_0n bylo možno stanovit na základě zákona zachování energie při b-rozpadu, pokud bychom znali rozdíl hmotností DM mateřského a dceřinného jádra. Změřením maximální energie vylétajících elektronů E_bmax lze na základě zákona zachování energie v principu stanovit klidovou hmotnost elektronového neutrina - čím těžší je neutrino, tím méně kinetické energie zbývá na elektron b; klidová hmotnost neutrina pak činí m_0n = (DM.c² - E_bmax)/c². Závislost koncové části spojitého spektra beta na klidové hmotnosti neutrina je znázorněna na obr.1.2.3 vpravo, který si zde pro názornost uvedeme znovu :

Obr.1.2.3. Radioaktivita beta. Vlevo: Základní schéma radioaktivity b^-. Uprostřed: Spojité energetické spektrum záření b. Vpravo: Zvětšený detail koncové části spektra pro nulovou a nenulovou klidovou hmotnost neutrin.

   Při přímočarém změření rozdílu hmotností DM mateřského a dceřinného járda hmotnostním spektrometrem a energie E_bmax elektronovým spektrometrem jsou však měřící chyby podstatně větší než hledaná hodnota m_0n.c² [eV]. K energetické analýze záření b se proto používá linearizace spektra pomocí shora zmíněné transformace - Fermi-Kurieův graf (pasáž "Tvar spektra záření beta"). Pokud je klidová hmotnost neutrina nulová, bude Fermi-Kurieův graf lineární až do maximální hodnoty: bude mít i koncový úsek lineární a bude protínat energetickou osu v bodě maximální energie b. V případě nenulové klidové hmotnosti neutrina bude elektron beta vždy ochuzen o energii nutnou pro produkci této nenulové hmotnosti. V počátečních úsecích spektra se to projeví jen nepatrně a linearita F-K-grafu zde zůstane zachována. V koncovém úseku F-K-grafu se však v případě nenulové hmotnosti neutrina na lineární závislosti objeví malý "ohyb", spektrum klesá rychleji a je "předčasně" ukončeno (dosáhne nulové hodnoty) u poněkud nižší energie E_bmax - m_0n.c², srovnejme s obr.1.2.3 vpravo. Vzhledem k transformaci, kterou je nutno použít pro linearizaci spektra b, při analýze tvaru Fermi-Kurieho spektra zjišťujeme druhou mocninu hmotnosti neutrina m_0n².
   Vhodným b-radionuklidem pro tato měření je tritium ³H. Měření jsou velmi obtížná, neboť hledáme efekty mnohem menší než je "rozmazání" energie způsobené zpětným rázem jader (podle zákona akce a reakce při emisi b je jádro odraženo opačným směrem) i tepelným pohybem; měření se prováděla za teplot blízkých absolutní nule a zkoumaná b-radioaktivní jádra ³H byla vázána ve vysokomolekulární látce, aby zpětný ráz převedený na celou molekulu byl malý. U některých nových plánovaných experimentů se bude používat plynný radioaktivní zdroj ³H, aby byly co nejmenší energetické ztráty elektronů ve spektru.
   Počáteční měření, vycházející z detailní analýzy tvaru koncové části spojitého spektra záření b, dávala zpočátku poměrně vysoké hodnoty m_on»40eV, později se však hodnoty snižovaly na 5eV, což při měřicích chybách větších než ⁺5eV připouštělo i nulovou hodnotu. Teprve v nedávné době se experimenty přiklonily k nenulové klidové hmotnosti neutrin - byla totiž prokázána tzv. oscilace neutrin (výše popsané experimenty Super-Kamiokande, SNO, KamLAND) - samovolná přeměna mezi neutriny elektronovými n_e, mionovými n_m a taunovými n_t , která může nastat jen při jejich nenulové klidové hmotnosti. Tato měření oscilace neutrin však neposkytují žádnou absolutní škálu neutrinových hmotností; říkají jen, že alespoň dvě ze tří neutrin mají nenulovou klidovou hmotnost a pro to nejtěžší z nich udávají odhad dolní hranice >0,05eV.
  Poslední výsledky měření tvaru spektra b tritia ³H na speciálních elektrostatických spektrometrech s magnetickou kolimací (v laboratořích v Troicku a v Mainzu) udávají horní hranici m_on<2,3eV. Nové plánované experimenty a příp. analýza bezneutrinového dvojného rozpadu beta by tuto hranici měla ještě dále snížit a upřesnit. Jedním z těchto připravovaných experimentů je KATRIN (Karlsruhe Tritium Neutrino Experiment), budovaný v mezinárodní spolupráci ve speciální Tritiové labotaroři v Karlsruhe. Bude tvořen plynným tritiovým zdrojem, jedním menším "filtračním" spektrometrem a obřím hlavním spektrometrem částic b (průměr 10m, délka 23m). Další plánovaný nezávislý experiment nese označení MARE (Microcalorimeter Arrays for a Rhenium Experiment), který bude měřit záření b radionuklidu ¹⁸⁷Re, který má ze všech nejnižší energii jen 2,5keV, avšak extrémně dlouhý poločas rozpadu T1/2=4,3.10¹⁰ let; měrná aktivita a intenzita záření je proto velmi nízká. Místo obvyklých spektrometrických metod zde bude použito velkého počtu kryogenních mikrokalorimetrů (jejich princip je stručně nastíněn v §2.5 "Polovodičové detektory"), v nichž bude elektronicky detekován nepatrný vzrůst teploty vyvolaný úplným pohlcením částice b ve vzorku Re. Od těchto budoucích experimentů se očekává citlivost na hmotnost neutrin cca 0,2eV.
  Další možnosti stanovení (či odhadu) klidové hmotnosti neutrin poskytují astronomická pozorování. Jednou z možností, bohužel velmi vzácnou, je pozorování výbuchu supernovy: v iniciální fázi při něm vzniká intenzívní světelný záblesk a mohutný výron neutrin. Pokud by se nám podařilo pozorovat světelný záblesk (či záblesk tvrdšího fotonového záření - X, g) a zároveň detekovat "záblesk" neutrin z téže supernovy, pak z časového rozdílu mezi příchodem fotonového a neutrinového záblesku můžeme stanovit, o kolik pomaleji než světlo se na cestě vesmírem pohybovaly neutrina. Z toho by pak podle zákonitostí speciální teorie relativity bylo možno stanovit klidovou hmotnost neutrin *)
*) Čistě teoreticky: nulový časový rozdíl by odpovídal nulové klidové hmotnosti; čím větší časový rozdíl, tím větší klidová hmotnost neutrin. Skutečnost je však bohužel složitější. Při iniciální fázi výbuchu supernovy - vzniku neutronové hvězdy - se rychle vyzáří obrovské množství neutrin, které téměř bez překážky a okamžitě vyletí do okolního vesmíru. Záblesk světla (a obecně elektromasgnetického záření) se však formuje delší dobu a "pracně se prodírá" hustou hmotou a plynovou obálkou. Proto neutrina ze supernovy přiletí ke vzdálenému pozorovateli zpravidla o něco dříve než světelný záblesk. Záblesk neutrin je rychlý - trvá jen několik desítek sekund, světelný záblesk je zpožděný, postupně sílí a maxima dosahuje až po několika hodinách. Měření při výbuchu supernovy ve Velkém Magellanově oblaku v r.1987 neprokázala (s ohledem na zmíněné skutečnosti) diferenci v rychlosti světla a neutrin a ukázala tím na velmi malou klidovou hmotnost neutrin.
   Nepřímé (a bohužel modelově závislé) odhady klidové hmotnosti neutrin lze v rámci kosmologie odvodit z měření anizotropie reliktního záření a z analýzy mechanismů utváření velkorozměrových struktur v raném stádiu vývoje vesmíru.

Kosmický význam neutrin
Nezaujatého člověka možná překvapí, "jaké mají ti fyzikové starosti?" - jestli takové téměř nic jako je neutrino má nicotně malou, či zcela nulovou klidovou hmotnost..?!.. Zájem o tuto problematiku však byl podnícen i z úplně opačné strany přírodovědeckého bádání než je mikrosvět - ze strany relativistické astrofyziky a kosmologie - viz kap.5 "Realativistická kosmologie" knihy "Gravitace, černé díry a fyzika prostoročasu". Standardní kosmologický model vzniku a vývoje vesmíru totiž ukazuje, že krátce po velkém třesku - v tzv. leptonové éře "..." - vzniklo ve vesmíru tak obrovské množství neutrin, že kdyby jejich klidová hmotnost byla větší než cca 5eV, byla by svým gravitačním působením schopna "uzavřít vesmír" - nynější rozpínání vesmíru by se (ve vzdálené budoucnosti) zastavilo, vesmír by se začal smršťovat a skončil by nakonec v "ohnivé peci" velkého krachu. V opačném případě by se vesmír rozpínal neustále (a konečným stavem by byla jakási "tepelná smrt" - zastavení všech procesů uvolňujících energii, pokles teploty na absolutní nulu ...); podrobnosti v §5.6 "Budoucnost vesmíru. Šipka času." zmíněné monografie "Gravitace, černé díry...". Taková gnoseologická situace je pro současnou fundamentální fyziku, astrofyziku a kosmologii příznačná - že totiž nejnepatrnější částice jakou známe (takové skoro "nic" jako je neutrino) může svou efemerní vlastností "mít či nemít klidovou hmotnost" rozhodovat o osudu toho největšího co jest - celého vesmíru. Jedním z paradoxů fyziky mikrosvěta je též to, že na ty nejmenší částice potřebujeme mít největší přístroje - viz §1.5 "Elementární částice".
  Zde jsme se letmo dotkli evoluce vesmíru v souvislosti s neutriny. Situace je však mnohem složitější - neutrina jsou jen jedním z "kandidátů" na temnou hmotu ve vesmíru, scénářů evoluce vesmíru je rovněž celá řada, podobně jako může být "více vesmírů" (viz práci "Antropický princip aneb kosmický Bůh" a "Existence více vesmírů?"). Každopádně, nyní stanovená max. klidová hmotnost neutrin ukazuje, že neutrina by na uzavření vesmíru, či metagalaxie, patrně nestačila. Vyskytly se ale spekulace, že vhodným "kandidátem" na temnou hmotu by mohli být neutralina - bosonoví superpartneři k neutrinům, jejichž existenci předpovídají tzv. supergravitační teorie (viz §1.5 "Elementární částice" a §B.6 "Sjednocování fundamentálních interakcí. Supergravitace. Superstruny." v knize "Gravitace, černé díry...."). Navíc nynější pozorování vzdáleného vesmíru naznačují, že kromě temné hmoty je vesmír zaplněn i jakousi "temnou energií" způsobující akcelerující expanzi vesmíru - viz závěr již zmíněné kapitoly 5.6 "Budoucnost vesmíru. Šipka času.", část "Akcelerovaná expanze vesmíru? Temná energie?".
  Ve stelární astrofyzice se ukazuje, že neutrina hrají důležitou úlohu v závěrečném stádiu evoluce hmotných hvězd při gravitačním kolapsu a výbuchu supernovy, kde odnášejí podstatnou část obrovské uvolněné energie z nitra kolabující hvězdy - §4.2, "Výbuch supernovy. Neutronová hvězda. Pulsary.".

Radioaktivita b⁺
Dalším druhem radioaktivity beta je radioaktivita b⁺. Její základní schéma je v levé části obr.1.2.4 :

Obr.1.2.4. Základní schéma radioaktivity b⁺ a elektronového záchytu.

Při této jaderné přeměně je jádrem emitována částice b⁺, což je antičástice k elektronu e^- - pozitron e⁺. Z hlediska elektrického náboje není sice emise b⁺ tak paradoxní jako b^-, ale ani pozitrony v jádře nejsou. Radioaktivita b⁺ se vyskytuje u radionuklidů v nichž protony převládají nad neutrony (tzv. neutron-deficitní jádra). Mechanismus vzniku b⁺ si tedy můžeme alegoricky vysvětlit takto: Některého z "nadbytečných" protonů omrzí být protonem a zachce se mu stát vzácnějším neutronem - udělá to přeměnou p⁺ ® n^o + e⁺ + n. Neutron n^o jakožto legitimní nukleon zůstává v jádře vázán silnou interakcí, zatímco pozitron e⁺ vyletí velkou rychlostí ven jako částice b⁺. Při radioaktivitě b⁺ se nukleonové číslo nemění (stejně jako u b^-), avšak protonové číslo se zmenší o 1 - dceřinnné jádro se posune o jedno místo doleva v Mendělejevově periodické tabulce.
Příkladem radioaktivity beta⁺ je pozitronová přeměna uhlíku ¹¹C₆ ® ¹¹B₅ + e⁺ + n na bór, nebo fluoru ¹⁸F₉ ® ¹⁸O₈ + e⁺ + n na kyslík.
  Aby k radioaktivitě b⁺ mohlo dojít, musí být splněna hmotnostně~energetická podmínka m(Z-1,N) + 2m_e < m(Z,N), kde m(Z,N) je hmotnost jádra s protonovým číslem Z a nukleonovým číslem N, m_e je klidová hmotnost elektronu (která je shodná s klidovou hmotností pozitronu). Tedy rozdíl hmotností mateřského a dceřinného jádra musí být větší než 1,022MeV (=2m_e).
  Energetická bilance se zde opět dá dobře vysvětlit slupkovým modelem struktury atomového jádra, diskutovaným v předchozím §1.1. Pokud je v jádře nadbytek protonů nad neutrony, budou zaplňovat protony poněkud vyšší energetické hladiny než neutrony. Jádro pak může přejít do stavu s nižší energií tak, že proton se přemění b⁺-přeměnou na neutron, který přejde na volnou neutronovou hladinu s nižší energií.
Pozn.: Na první pohled se může zdát paradoxní, že lehčí částice - proton, se může samovolně přeměnit na těžší částici - neutron, v rozporu se zákonem zachování energie! Opravdu, volný proton se nikdy nerozpadne b⁺-rozpadem na neutron (podle klasické teorie je proton stabilní, i když některé hypotézy grandunifikačních teorií předpovídají možnost nestability a rozpadu protonu, avšak jiným mechanismem a navíc s téměř nekonečně velkou dobou života větší než cca 10³³let). V jádrech však na protony a neutrony nemůžeme pohlížet jako na volné; jsou součástí vyššího celku (jádra) vázaného silnou interakcí. Právě tato vazba poskytne energii potřebnou k přeměně protonu. O stabilitě jádra pak spolurozhoduje nejen součet hmotnosti nukleonů, ale i vazbová energie nukleonů. Pokud v dané vázané konfiguraci má jádro, složené z p protonů a n neutronů, vyšší celkovou energii~hmotnost než jádro z p-1 protonů a n+1 neutronů (a to nejméně o klidovou hmotnost elektronu, tj. 511keV), nastává situace, kdy může dojít k b⁺-rozpadu. A je to zcela v souladu se zákonem zachování energie.

Pozitronové záření b⁺
Všechno o spojitém energetickém spektru a vyzáření neutrina zde platí analogicky jako u b^- (jen při přeměně b^- se vyzařuje antineutrino, zatímco při b⁺ neutrino). Co se týče dalšího osudu vyzářeného b⁺, byl by stejný jako u b^- pouze ve vakuu - pozitron e⁺ je stejně stabilní částice jako e^-, takže by ve vakuu "odletěl na druhý konec vesmíru" (o antičásticích, antiatomech, antihmotě, "antivesmírech" je pojednáno v §1.5., části "Antičástice - antiatomy - antihmota - antisvěty").
Pozn.: Opravdu až na konec vesmíru ?
Tvrzení, že emitovaná částice ve vakuu "odletí na konec vesmíru" je zde míněno spíše teoreticky a obrazně. Pohyb částic ve vesmíru je ve skutečnosti ovlivňován třemi faktory :
1. Gravitace, která svým univerzálním působením zakřivuje dráhy všech částic včetně fotonů.
2. Magnetické pole zakřivující dráhy elektricky nabitých částic.
3. Interakce nabitých částic s elektromagnetickým reliktním zářením, při němž tyto částice obráceným Comptonovým rozptylem ztrácejí energii.
   Tyto jevy způsobují, že skutečný dolet částic ani ve volném vesmíru není neomezený. Nabité částice o nižších energiích zůstávají "uvězněny" v prostoru galaxie, kde budou složitě obíhat v magnetickém a gravitačním poli. Vysokoenergetické částice sice mohou uniknout z magnetického pole galaxie, ale budou brzděny obráceným Comptonovým rozptylem na všudypřítomném reliktním elektromag. záření. A konečně, částice ani fotony elektromagnetického záření nejsou schopny překonat horizonty událostí vznikající podle obecné teorie relativity v gravitací zakřiveném prostoročase vesmíru ("Gravitace, černé díry a fyzika prostoročasu").
  V látce je však osud pozitronů b⁺ diametrálně odlišný (viz obr.1.6.1 v §1.6 , část "Interakce nabitých částic - přímo ionizující záření "). Dokud má pozitron velkou rychlost, vytrhává při průletu kolem atomů svými elektrickými silami elektrony z obalu a ionizuje tedy podobně jako elektron beta^-. Po dostatečném zabrzdění (ve vodě či tkáni po cca 1-4mm) se však pozitron e⁺ setká elektronem e^- (o krátké epizodě těsně před anihilací je níže drobná pasáž "Pozitronium"), a jelikož to jsou "antagonistické" antičástice, vzájemně se zlikvidují ("požerou se"): dojde k jejich anihilaci e⁺ + e^- ® 2g - přemění se na dvě kvanta tvrdého záření g o energiích 511keV, které vyletí z místa anihilace přesně v protilehlých směrech (pod úhlem 180^o v těžišťové soustavě). Tato skutečnost se využívá u scintigrafické metody pozitronové emisní tomografie PET, jak je popsáno v §4.3.
  Intuitivně - zjednodušeně, přibližně - si vznik záření gama při e⁺ e^- anihilaci můžeme představit z hlediska elektromagnetismu: Elektrony a pozitrony spolu svými náboji interagují elektromagnetickou silou. Když tyto dva stejné opačné náboje při anihilaci naráz vymizí, vznikne rozruch v elektromagnetickém poli, který se z místa anihilace šíří jakožto elektromagnetická vlna. Klidová hmotnost elektronu a pozitronu je rovněž elektromagnetického původu, takže při jejich náhlém vymizení vzniklá elektromagnetická vlna odnáší i jejich klidovou hmotnost 2x511 keV. Detailní mechanismus interakce (zákon zachování hybnosti - v těžišťové soustavě je po úplném zabrzdění hybnost nulová) pak vede k emisi záření gama v protilehlých směrech.
  Máme-li tedy vzorek radioaktivní látky b⁺, dochází již v nitru tohoto vzorku k anihilaci pozitronů s elektrony, takže v jeho okolí prakticky žádné pozitrony nezaregistrujeme, ale takový vzorek bude zdrojem intenzívního tvrdého záření g o energii 511keV. A stejně když radioindikátor značený b⁺ radionuklidem aplikujeme do organismu - každý pozitron ve vzdálenosti cca 1-3mm od místa svého vzniku anihiluje s elektronem v tkáni a my můžeme v koincidenci detekovat dvě kvanta záření g o energii 511keV vylétající v opačných směrech - na tom je založena scintigrafie PET (viz pasáž "Kamery PET" v kap.4 "Radioisotopová scintigrafie").
 Pozitronium
Těsně před vlastní anihilací elektron e^- a pozitron e⁺ mohou na chviličku kolem sebe obíhat (obíhají kolem společného těžiště) - utvoří zvláštní vázaný systém (podobný atomu vodíku) zvaný positronium (Ps). Rozměr "atomu" pozitronia je dvojnásobek atomu vodíku, vazbová energie pozitronia je 6,8 eV. Podle vzájemné orientace spinů elektronu a pozitronu může být pozitronium buď v singletním stavu ¹S₀ s opačně orientovanými spiny - tzv. parapozitronium p-Ps (1/4 případů), nebo v tripletním stavu ³S₁ se souhlasně orientovanými spiny - tzv. orthopozitronium o-Ps (3/4 případů).
  Tento systém pozitronia je však nestabilní, obě částice se za vyzařování elektromagnetických vln k sobě po spirále přibližují; u p-Ps za cca 120ps na sebe "dopadnou" a dojde k vlastní anihilaci na dva fotony g, každý o energii 511keV. V případě o-Ps je anihilace na dva fotony zakázána kvantovými výběrovými pravidly (souvisí se zákonem zachování spinového momentu hybnosti - každý z fotonů má spin 1), takže o-Ps by se ve vakuu rozpadalo s poměrně dlouhou dobou života cca 140ns emisí 3 fotonů se spojitým energetickým spektrem (celkovou energii 1022keV si fotony rozdělí stochastickým způsobem). V látce však pozitron vázaný v o-Ps daleko dříve stačí anihilovat s některým "cizím" elektronem z okolního prostředí, který má opačnou orientaci spinu - vznikají opět dva fotony g o energiích 511keV.
  Při anihilaci pozitronu s elektronem vznikají v naprosté většině případů 2 fotony gama, jak bylo výše uvedeno. Někdy jich však může vzniknout i více, avšak s velmi malou pravděpodobností (pravděpodobnost, že při e^-e⁺-anihilaci vznikne 2+n fotonů je úměrná a^-n, kde a=1/137 je konstanta jemné struktury). Pokud pozitron interaguje s elektronem vázaným v atomovém obalu, může být zánik takového páru doprovázen i vysláním pouze jediného fotonu, přičemž část energie a příslušná hybnost mohou být předány buď atomovému jádru nebo některému z ostatních elektronů; pravděpodobnost tohoto procesu je však velice malá a v praxi se neuplatňuje.
  Doba života pozitronů v látkách činí řádově stovky pikosekund. Přesná hodnota však záleží na lokálních elektronových hustotách a konfiguracích, čehož se využívá ve spektroskopické metodě PLS (Positron Lifetime Spectroscopy). Zkoumaný materiál se lokálně ozařuje b⁺- g zářičem (nejčastěji ²²Na), přičemž doba života pozitronů se stanovuje na základě měření zpožděných koincidencí mezi detekcí fotonu záření g z ozařujícího radionuklidu (u ²²Na je to g 1274 keV) a detekcí anihilačního fotonu g 511 keV.
  Pozitrony e⁺, emitované při radioaktivitě beta⁺, jsou vlastně jakýmisi "návštěvníky z antisvěta" - částicemi antihmoty. O vlastnostech antičástic, antihmoty, antisvětů či "antivesmírů", je diskutováno v §1.5 "Elementární částice a urychlovače", pasáži "Antičástice - antiatomy - antihmota - antisvěty" (včetně možností "výroby" a využití antihmoty, s trochu odlehčenou sci-fi story o setkání "hmoťanky" s "antihmoťanem"...).

Rozdíl energetického spektra b^- a b⁺
Spektrum záření beta nakreslené výše na obr.1.2.3 je teoretické a ideové, nebere v úvahu elektrické síly mezi elektrony či pozitrony a atomovým jádrem, které je emituje. Ve skutečnosti se spojité spektrum b^- a b⁺ svým tvarem poněkud liší v oblasti nízkých energií. U b^- je větší zastoupení elektronů nižších energií, neboť elektrony jsou při výletu z jádra zpomalovány elektrickými přitažlivými silami v poli kladně nabitého jádra. Pozitrony b⁺ jsou po opuštění jádra naopak elektrickým odpuzováním urychlovány, získávají dodatečnou kinetickou energii - je menší podíl nízkých energií v pozitronovém spektru. Elektrická Coulombovská interakce tedy způsobuje v oblasti velmi nízkých spektrálních energií obohacení emise pomalých elektronů a úbytek emise pomalých pozitronů:
        
                        Typický tvar spojitého spektra záření beta^- a beta⁺

Elektronový záchyt
Posledním, a tak trochu zvláštním, druhem radioaktivity beta je elektronový záchyt. Je alternativním procesem k rozpadu b⁺ u jader s přebytkem protonů. "Přebytečný" proton může svého cíle "stát se neutronem" dosáhnout nejen přeměnou p⁺ ® n^o + e⁺ + n vedoucí k radioaktivitě b⁺, ale i jiným způsobem. Kolem jádra obíhají v atomu elektrony. Proton, který se "chce změnit na neutron" si může "sáhnout" na oběžnou dráhu, uchvátit elektron *) a sloučit se s ním: p⁺ + e^-® n^o + n - obr.1.2.4 vpravo. Tento proces se nazývá elektronový záchyt (EC - Electron Capture); jelikož může nastat záchycení elektronu z hladiny K, nebo L či M atomového obalu, nazývá se někdy tento pochod také K-záchyt, nebo záchyt L či M. Nejčastěji nastává K-záchyt elektronu v singletním stavu s, neboť tento orbital má poměrně výrazný přesah do oblasti jádra. Elektronový záchyt se též někdy nazývá inverzní beta-rozpad (pohlcení elektronu je opakem emise elekronu z jádra u beta^-- rozpadu). Posunovací pravidla mezi nukleonovým a protonovým číslem mateřského a dceřinného jádra jsou stejné jako u b⁺, tj. (Z,N)®(Z-1,N).
*) Je to jen humorně-alegorická formulace! Podle zákonitostí kvantové mechaniky část vlnové funkce obíhajícího elektronu zasahuje až do oblasti jádra, takže popsaný proces elektronového záchytu může přímo a bezprostředně nastat.
  Při elektronovém záchytu se žádné korpuskulární záření z jádra nevysílá (pomineme-li nezachytitelná neutrina), energie se rozdělí na energii neutrina a vazbovou energii elektronu při pohlcení protonem v jádře. Jedná se tedy vůbec o radioaktivitu ve smyslu naší úvodní definice a schématu na obr.1.2.1? Odpověď zní: ano! Za prve, dochází k transmutaci jádra. Za druhé, na uprázdněné místo po elektronu na slupce K okamžitě přeskočí elektron z vyšší slupky (L) za vyzáření charakteristického X-záření; každý radionuklid rozpadající se elektronovým záchytem je zdrojem intenzívního rentgenového záření. A za třetí, jak uvidíme níže, dceřinné jádro B vzniká většinou v excitovaném stavu a při deexcitaci vyzařuje záření g. Elektronový záchyt je často doprovázen emisí tzv. Augerových elektronů (viz níže v části "Radioaktivita gama", pasáž "Vnitřní konverze záření g"), vznikajících vnitřní konverzí charakteristického X-záření.
*) Je to jen humorně-alegorická formulace! Podle zákonitostí kvantové mechaniky část vlnové funkce obíhajícího elektronu zasahuje až do oblasti jádra, takže popsaný proces elektronového záchytu může přímo a bezprostředně nastat.
  Elektronový záchyt je alternativním ("konkurenčním") způsobem rozpadu těch neutron-deficitních jader, které mají dostatek energie pro emisi pozitronu. K elektronovému záchytu dochází primárně tehdy, když hmotnost mateřského jádra m(Z,N) je sice větší než hmotnost jádra dceřinného m(Z-1,N), ale o méně než klidovou hmotnost elektronu a pozitronu 2m_e=1,022MeV. Emise pozitronu b⁺ v tomto případě nemůže nastat (není k dispozici dostatečná energie přeměny), takže elektronový záchyt je jediným možným způsobem přeměny. Pokud je rozdíl m(Z,N) - m(Z-1,N) > 2m_e, je možná přeměna mateřského jádra (Z,N) na jádro (Z-1,N) jak emisí b⁺, tak elektronovým záchytem (většinou dochází přednostně k přeměně b⁺).
  Elektronovým záchytem se přeměňuje např. 57-kobalt ⁵⁷Co₂₇ + e^- ® ⁵⁷Fe₂₆ + n na železo, nebo 125-jód ¹²⁵I₅₃ + e^- ® ¹²⁵Te₅₂ + n na telur.
Dvě zvláštnosti elektronového záchytu : 
¨ 1. Elektronový záchyt EC je jediným druhem radioaktivní přeměny jádra (vedle procesu vnitřní konverze gama při deexcitaci vzbuzených hladin - izomerním přechodu, je popsáno níže v pasáži "Vnitřní konverze záření g"), na kterém se podílí i elektronový obal atomu. Rychlost, pravděpodobnost či poločas rozpadu jádra elektronovým záchytem může být mírně ovlivněn chemickou vazbou daného atomu. Rychlost přeměny je nepatrně větší (tj. poločas je kratší) u EC-radioaktivního isotopu v elementární formě, než když by byl součástí nějaké sloučeniny. V chemické vazbě je totiž hustota orbitálních elektronů EC-radioaktivního atomu částečně posunuta k sousednímu navázanému atomu, čímž se poněkud zmenšuje pravděpodobnost záchytu elektronu daným EC-jádrem. Pozorovatelné je to u lehkých EC-radioaktivních atomů, jejichž valenční elektrony obíhají poměrně blízko jádra (podílejí se na tom zvláště s-elektrony, jejichž orbitaly mají poměrně výrazný přesah do oblasti jádra). U těžších atomů je chemický vliv na EC zanedbatelný. Dále, rychlost přeměny elektronovým záchytem lze zvýšit působením vnějšího tlaku na radioaktivní atomy či molekuly - vyšší tlak vede ke zvýšení elektronové hustoty a tím ke zvýšení pravděpodobnosti záchytu elektronu jádrem.
  Tyto vlivy byly prokázány především u berylia ⁷Be, neboť je to malý atom, jehož valenční elektrony jsou blízko jádra. Zkoumaly se různé sloučeniny nebo implantace ⁷Be v různých médiích (Au, Al₂O₃, LiO₂, grafit, fulleren C₆₀). Byl pozorován rozdíl 0,9% mezi poločasy rozpadu v kovovém a dielektrickém prostředí. Při aplikaci vysokého tlaku 270 kilobar na ⁷BeO bylo zjištěno, že rychlost rozpadu ⁷Be se zvýšila o 0,59%, u ⁷Be(OH)₂ se při tomtéž tlaku rychlost EC přeměny ⁷Be zvýšila o 0,88%. Vnější ovlivňování rychlosti rozpadu elektronovým záchytem bylo pozorováno též u isotopů ¹⁰⁹In a ¹¹⁰Sn, implantovaných do fólií Au a Al (do příslušných krystalových mřížek).
  Průběh elektronového záchytu též závisí na ionizaci příslušného atomu. Radioaktivita isotopů, které se rozpadají čistě EC, může být zpomalena (či teoreticky dokonce zastavena), jsou-li jejich atomy plně ionizované (srov. pro zajímavost s opačným efektem zrychlení nízkoenergetické b^--přeměny úplnou ionizací při raritním tzv. b-rozpadu do vázaných elektronových stavů, popsaném výše). V běžných pozemských podmínkách se s takovou situací nesetkáváme, avšak předpokládá se, že se může uplatňovat v astrofyzikálních procesech kosmické nukleosyntézy - viz §1.1, část "Kosmická alchymie".
  Při explozi supernovy jsou prvky syntetizované rychlou fúzí neutronů (tzv. r-proces), vymršťovány do vesmíru v plně ionizovaném stavu. Ty z nich, které jsou EC-radioaktivní, se proto delší dobu nemohou radioaktivně rozpadat (dokud se v chladnějších oblastech vesmíru nesetkají a nespojí s elektrony). To by mohlo způsobovat určité anomálie v distribuci prvků. Uvažuje se o holmiu ¹⁶³Ho, které se za normálních (atomárních) podmínek elektronovým záchytem přeměňuje na ¹⁶³Dy. Plně ionizované ¹⁶³Dy se výše zmíněným procesem b-rozpadu do vázaných elektronových stavů rozpadá na ¹⁶³Ho.......
¨ 2. Jelikož při EC nedochází k emisi korpuskulárního záření, rozdíl energie Q mateřského a dceřinného jádra se projeví v excitaci dceřinného jádra (s jednou či několika vzbuzenými hladinami, s následným vyzářením g) a zbytek energie je odnesen neutrinem. Kdybychom uměli změřit spektrum těchto neutrin, bylo by u EC čárové, na rozdíl od spojitého spektra neutrin z rozpadů b^-,+.
Smíšená radioaktivita beta^-, beta⁺, elektronový záchyt 
O možnostech jednotlivých typů radioaktivních přeměn rozhoduje především energetická bilance mezi příslušnými "sousedními" jádry (podrobněji je diskutováno níže v závěrečné části této kapitoly "Stabilita a nestabilita atomových jader"). Pokud je u daného výchozího jádra (Z,N) splněna hmotnostně-energetická nerovnost m(Z,N)>m(Z+1,N), bude docházet k b^- přeměnám. Za podmínky m(Z,m)>m(Z-1,N)< m(Z-1,N)+2m_e se jádro (Z,N) bude rozpadat elektronovým záchytem. Pokud je m(Z,N)> m(Z-1,N)+2m_e, je možná přeměna jádra (Z,N) na jádro (Z+1,N) jak rozpadem beta⁺, tak i elektronovým záchytem. Je-li současně splněna jak nerovnost m(Z,N)>m(Z+1,N), tak i nerovnost m(Z,m)> m(Z-1,N)+2m_e, pak mohou nastávat všechny tři druhy přeměny beta současně. Příkladem může být radioisotop ⁶⁴Cu, který se rozpadá z 39% emisí b^-, z 19% emisí b⁺ a z 42% případů elektronovým záchytem.

Mechanismus přeměny beta. Slabé interakce.
Při výkladu radioaktivity b jsme si vznik záření b^- a b⁺ objasnili vzájemnou přeměnou neutronů a protonů za situace, kdy v důsledku zvýšeného počtu neutronů či protonů jsou obsazovány vyšší energetické hladiny. Jaká je však vnitřní příčina či mechanismus těchto přeměn? První teorii rozpadu b podal E.Fermi v r.1934, který zavedl tzv. slabou interakci působící mezi elementárními částicemi.
  Podle zákonitostí kvantové fyziky Fermi popsal emitovaný elektron a neutrino vlnovými funkcemi v závislosti na jejich hybnostech, přičemž pravděpodobnost emise elektronu a neutrina v určitém intervalu hybností vyjádřil jako součin čtverců těchto vlnových funkcí a speciálního výrazu obsahujícího integrál vlnových funkcí původního neutronu a výsledného protonu, násobený konstantou g_F charakterizující sílu interakce vedoucí k emisi elektronu a neutrina - nově zavedené slabé interakce. Spektrum záření b odpovídající tomuto Fermiho výrazu má spojitý tvar podle obr.1.2.3 vpravo v souhlasu s experimentem.
  Původní Fermiho teorie byla zformulována sice v duchu kvantové fyziky, nikoli však kvantové teorie pole - slabá interakce zde byla pojímána jako "kontaktní" či "bodová" - produkty rozpadu vznikají v tomtéž bodě a okamžiku, v němž zaniká neutron (žádná zprostředkující částice se zde nepředpokládala). V duchu kvantové teorie pole by však každá interakce měla být způsobena kvantem příslušného pole - částicí zprostředkující interakci. Tuto koncepci rozpracovali v r.1967-8 S.Weinberg, A.Salam a S.Glashow, kteří pro slabou interakci zavedli tři zprostředkující částice W⁺, W^-, Z^o (s kladným a záporným nábojem a bez náboje) a přibráním fotonů vytvořili jednotnou teorii slabých a elektromagnetických interakcí - tzv. elektroslabou interakci. Tato koncepce byla r.1983 experimentálně ověřena: v interakcích vstřícných proton-antiprotonových svazků (270GeV proti 270GeV) collideru velkého protonového synchrotronu v CERN byly objeveny intermediální bosony W⁺, W^-, Z^o s hmotnostmi m_W=82GeV a m_Z=93GeV, jejichž způsoby rozpadu dobře souhlasily s předpovědí Weinberg-Salamova modelu.

Obr.1.2.5. Schématické znázornění mechanismu b^--rozpadu neutronu (nahoře) a b⁺-přeměny protonu (dole) v rámci standardního modelu elementárních částic.

Nyní se v rámci standardního modelu elementárních částic (viz §1.5) mechanismus rozpadu beta vysvětluje schématem transmutace kvarků podle obr.1.2.5. Neutron n^o (s nulovým elektrickým nábojem) se skládá z kvarků u-d-d; kvark u má náboj +2/3, kvarky d náboj -1/3. Jeden z kvarků d se působením pole (elektro)slabých interakcí přemění na kvark u za zprostředkování virtuálního intermediálního bosonu W^-, jež odnáší náboj -1. Z virtuálního bosonu W^- vzápětí vznikají elektron e^- a antineutrino n´, které se rozlétají různými směry. Výsledkem přeměny je proton p⁺ skládající se z kvarků u-u-d. Přechodné stádium mezi počátečním a koncovým stavem uprostřed obrázku trvá jen pranepatrný okamžik (cca 10^-27sec.) a není přímo pozorovatelné. Analogické schéma lze nakreslit i pro přeměnu b⁺ (dolní část obrázku), kde se proton p⁺ vlivem transmutace kvarku u na kvark d za zprostředkování intermediálního bosonu W⁺ přemění na neutron n^o, pozitron e⁺ a neutrino n. Feynmanův diagram transmutace kvarku uvnitř protonu při přeměně beta je nakreslen na obr.1.5.1.F v §1.5 "Elementární částice".
Složitost radioaktivity beta 
Když bychom porovnali jednotlivé druhy radioaktivity podle komplikovanosti jejich mechanismu, můžeme konstatovat :
  Radioaktivita alfa je v zásadě jednoduchá (obr.1.2.2). V jádře s velkým počtem nukleonů, kde jaderné síly krátkého dosahu v okrajových částech nejsou dostatečně silné, se vytvářejí silněji vázané okrky dvou protonů a dvou neutronů, které mohou (za pomoci tunelového jevu) opustit jádro a vyletět jako částice alfa - jádro hélia-4.
  Přeměna gama (obr.1.2.6) je rovněž jednoduchá. Jádro v energeticky vzbuzeném stavu deexcituje do nákladního (či nižšího) stavu, přičemž energetický rozdíl je elektromagnetickou interakcí vyzářen jako foton záření gama.
  Radioaktivita beta je však velmi složitá! Její mechanismus je skryt nejem uvnitř jádra, ale ještě hlouběji - uvnitř samotných nukleonů. Spočívá v transmutaci kvarků "u" či "d" prostřednictvím internediálního mezonu W, čím dochází k vzájemné přeměně protonů a neutronů (obr.1.2.5).

Elektromagnetické radioaktivní přeměny
Jedná se o radioaktivní procesy deexcitace jader způsobené elektromagnetickou interakcí. Známe dva typy těchto jaderných deexcitací: 1. Přímá emise fotonů gama; 2. Vnitřní konverze s emisí orbitálních elektronů z atomu. Níže si je budeme rozebírat především s souvislosti s radioaktivitou.
Pozn.: Kromě základního stavu mají atomová jádra řadu excitovaných stavů (energetických hladin), z nichž se jen část uplatňuje při radioaktivních přeměnách. Ty ostatní excitované stavy vznikají jen při ostřelování jader energetickými částicemi z urychlovačů.
Radioaktivita gama  
Dosud jsme se při výkladu radioaktivity soustředili na vlastní mechanismy radioaktivní přeměny a na vlastnosti emitovaného korpuskulárního záření (a, b^-, b⁺). Základní schémata radioaktivní přeměny na obrázcích 1.2.1 až 1.2.4 jsme proto úmyslně nakreslili poněkud zjednodušeně, abychom se mohli soustředit na podstatu radioaktivních přeměn. Nyní si všimněme chování dceřinného jádra bezprostředně po radioaktivní přeměně. Na obr.1.2.6 je nakresleno kompletní schéma radioaktivního rozpadu, včetně chování dceřinného jádra:

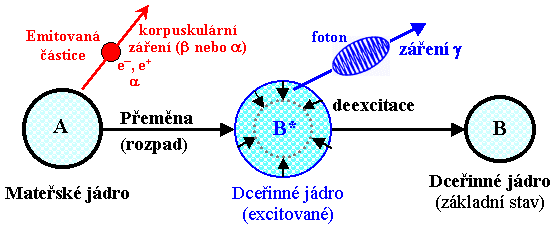
Obr.1.2.6. Typické schéma radioaktivní přeměny mateřského jádra A na excitované dceřinné jádro B* a jeho
následné deexcitace za vyzáření fotonu záření g na výsledné dceřinné jádro B.

Po tak velké "události", jakou pro atomové jádro je radioaktivní přeměna, jen málokdy zůstává vzniklé dceřinné jádro v nevybuzeném základním energetickém stavu. Po změnách v počtu nebo typu nukleonů v jádře se nukleony nemusejí ihned vyskytovat v nejnižších energetických stavech. Uvolněná energie vede k tomu, že dceřinné jádro B po radioaktivní přeměně vzniká většinou v energeticky excitovaném stavu B*; můžeme si představit, že jádro je "nafouknuté" ¹) - nukleony jsou od sebe více vzdálené, obsazují vyšší energetické hladiny - srov. obr.1.1.9. Takové "nafouknuté" jádro B* zpravidla velmi rychle "splaskne" ²), nukleony se přeskupují do nižšího energetického stavu - dochází k deexcitaci, při níž se příslušný energetický rozdíl vyzáří ve formě jednoho nebo více kvant - fotonů - tvrdého elektromagnetického záření - záření gama ³). Vyzářením kvant g se stabilizují energetické poměry v jádře. Dceřinné jádro B pak již zůstává v základním stavu.
¹) U nesférických jader, která mohou vykonávat rotační pohyb, se kromě hladinové excitace setkáváme i s excitací rotační. I zde je deexcitace doprovázena emisí fotonu g.
²) V některých případech může excitovaný jaderný stav vydržet i značně dlouhou dobu - viz níže "Metastabilita a jaderná izomerie".
³) Pokud je jádro součástí atomu (což je téměř vždy), alternativním způsobem deexcitace vzbuzených jaderných hladin může být emise obalového elektronu procesem vnitřní konverze - viz níže "Vnitřní konverze gama a X". U velmi těžkých jader v oblasti transuranů vysoce excitované stavy těchto těžkých nesymetrických jader, vedle běžné gama-deexcitace, mohou podlehnout spontánnímu štěpení (§1.3, část "Štěpení atomových jader" a "Transurany").
  Můžeme tedy vyslovit následující definici:

Spektrum záření gama
Energetické hladiny atomového jádra jsou kvantovány, takže i všechny fotony g emitované při daném druhu deexcitace budou mít stejné energie - spektrum záření g je čárové *). Pokud má jádro B* více excitovaných hladin, bude emitováno několik skupin monoenergetických fotonů g, takže spektrum bude tvořeno několika diskrétními čarami - píky v měřeném spektru (o měření spekter záření gama je pojednáno v §2.4, část "Scintilační spektrometrie záření gama").
*) Šířka linií gama
Gama-fotony při radioaktivitě pocházejí z jaderných přechodů mezi diskrétními hladinami s přesně danými energiemi, takže jsou v zásadě monoenergetické, jejich ideální fyzikální spektrum představuje ostrou linii na energii Eg. Velmi malé kolísání hodnot energie je způsobeno kvantovými relacemi neurčitosti a zpětným odrazem jader při emisi gama-fotonu. Dále, jelikož tyto fotony prakticky nikdy nepocházejí z volných jader, ale jsou emitovány z radioaktivních atomů obsažených v látce (v určitém materiálu), některé fotony interagují s látkou ještě před opuštěním vzorku. To rovněž může poněkud rozmazat jejich energii. Tepelný pohyb atomů ve vzorku způsobuje Dopplerovým jevem drobné frekvenční - energetické posuny podle různé rychlosti vyzařujících atomů (jader), které se projeví Dopplerovským rozšířením gama linie.Velikost všech těchto rozšíření je však obecně velmi malá oproti efektům při vlastní detekci záření. Skutečné, fyzikální, spektrum záření gama můžeme proto považovat za prakticky čárové - monoenergetické.
  Gama-fotony anihilačního záření, vznikající anihilací pozitronů s elektrony e⁺ e^- ® 2g, mají energii 511keV, jsou v zásadě monoenergetické. Avšak elektrony a pozitrony spolu anihilují při poněkud různých zbytkových rychlostech zabrzdění, což Dopplerovým jevem vede k frekvenčním-energetickým.posuvům. Vzniká tím Dopplerovské rozšíření anihilačního píku 511keV ze vzorků pozitronových radionuklidů. Anihilační pík 511keV je poněkud širší než ostatní "jaderné" gama píky blízkých energií ve spektru. Za běžných laboratorních podmínek toto dodatečné Dopplerovské rozšíření anihilačního píku činí cca 1,2 keV a je pozorovatelné pouze na spektrometrech s vysokým energetickým rozlišením (polovodičový Ge detektor nebo magnetický spektrometr).
  Při našich spektrometrických měřeních řady radionuklidů (např. ¹⁸F, ²²Na., ⁶⁸Ga, ¹³¹I, ¹²⁴I, ¹³⁷Cs, ¹⁵²Eu, ...) na polovodičovém HPGe detektoru jsme u "jaderných" gama-píků středních energií mezi 400-700 keV pozorovali pološřky FWHM cca 1,4-1,5 keV, u anihilačních píků 511keV pološířky FWHM činily cca 2,5-2,7 keV (projevovalo se Dopplerovské rozšíření).
  Energie g záření z radionuklidů se většinou pohybuje v rozmezí cca 5keV až 5MeV. Nejnižší energie fotonového záření z jaderných přechodů se pozoruje u ^110mAg (1,1 keV) a ^99mTc (2,17 keV; hlavní pík je zde však 140keV); tyto nízké energie však téměř úplně podléhají vnitřní konverzi (viz níže "Vnitřní konverze záření gama a X") a jejich intenzita je neměřitelně slabá. Zatím nejvyšší energie 11,26 MeV záření gama z radioaktivity byla zaznamenána u krátkodobého radionuklidu ²⁰Na. Při interakcích vysoenergetických částic však může vznikat i záření gama daleko vyšších energií řádu GeV či TeV!
  Typickým příkladem procesu podle obr.1.2.6 může být b-radioaktivita kobaltu ⁶⁰Co. Při vlastním b-rozpadu nejprve jádro kobaltu emituje elektron e^- (b-částici) a elektronové antineutrino n_e', čímž se přemění na jádro niklu ⁶⁰Ni v excitovaném stavu: ⁶⁰Co ® ⁶⁰Ni* + e^- + n_e'. Toto nově vzniklé excitované jádro se potom zbaví přebytečné energie vyzářením kvanta g: ⁶⁰Ni* ® ⁶⁰Ni + g. Dceřinný ⁶⁰Ni* má dvě excitované hladiny, takže vyzářená kvanta g zde mají energii 1173 keV a 1332 keV (viz §1.4, pasáž "Kobalt", obr ."Co-60").
  O spektrometrii záření g je pojednáno v §2.4, část "Scintilační spektra radionuklidů". Gama-spektra (scintilační a polovodičová) řady důležitých radionuklidů jsou, spolu s příslušným popisem, zobrazena v §1.4, část "Nejdůležitější radionuklidy". Z pohledu na tato spektra plyne zajímavá zákonitost: pokud radioaktivní přeměna nastává na větší počet excitovaných stavů dceřinného jádra, pak zpravidla s větší pravděpodobností na hladiny nižších energií, než na vyšší excitované stavy - v gama-spektrech jsou s vyšší intenzitou zastoupeny píky nižších energií, zatímco vysokoenergetické píky bývají daleko slabší, jsou viditelné často až při velkém zvětšení a delší akviziční době.
Ze schématu na obr.1.2.6 plynou dvě důležité skutečnosti pro záření gama emitované radionuklidy :  
1. Záření g je časově následující po emisi korpuskulárního záření při vlastní jaderné přeměně. Toto zpoždění je většinou zcela nepatrné (nanosekundy a méně), někdy však může být velmi značné (viz níže "Jaderná izomerie a metastabilita")..!..
2. Většina radionuklidů jsou zářiče smíšené - buď a+g nebo b+g. Jen některé zářiče jsou čisté a nebo čisté b - radioaktivní přeměna někdy nastává přímo na základní stav dceřinného jádra (tak je tomu např. u tritia ³H nebo uhlíku ¹⁴C). Čisté zářiče g však v přírodě neexistují! Přesto ale dokážeme vyrobit čisté gama-zářiče uměle. Umožňuje to pozoruhodná vlastnost některých jaderných excitovaných hladin: jejich metastabilita (viz níže "Jaderná izomerie a metastabilita").
Úhlové (směrové) korelace záření gama 
Kvanta ionizujícího záření, vznikající při radioaktivitě, jsou obecně emitována zcela náhodně a izotropně do všech směrů *). Pokud však při jedné a téže přeměnové události jsou z jádra emitována současně dvě či několik kvant, může mezi směry jejich výletu docházet k úhlovým korelacím. Ukážeme si to na záření gama :
  Ve většině případů, při emisi nezávislých fotonů gama z jádra, vylétají tyto fotony zcela náhodně, izotropně do všech směrů (úhlů). Pokud však dochází ke kaskádové deexcitaci za vzniku dvou fotonů gama emitovaných promptně za sebou, pak po emisi prvního fotonu je jádro polarizované - jeho vzbuzený intermediální stav je určitým způsobem orientovaný, v závislosti na momentu hybnosti odneseném emitovaným fotonem. Druhý (následný) foton gama pak bude přednostně emitován do určitého směru, korelujícího s úhlem emise prvního fotonu. Zvýšenou intenzitu druhého gama záření pak pozorujeme v určitém úhlu (např. 90°, 180°) vzhledem ke směru prvního záření. Podmínkou pro pozorování těchto g-g úhlových korelací za běžné laboratorní teploty preparátu je dostatečně krátká doba života intermediální vzbuzené hladiny ve srovnání s průměrnou četností tepelných srážek atomů zářiče (aby nedošlo k předání momentu hybnosti a porušení orientace jádra). Isotopy, u kterých se vyskytují úhlové korelace g-g, jsou např. ⁶⁰Co, ¹¹¹In, ⁷⁵Se, ¹⁶⁹Yb, ⁸¹Rb a řada dalších. Dokonalá 100% úhlová korelace je u anihilačního g-záření, vznikajícího při anihilaci elektron-pozitronových párů na dva fotony 511keV, vylétající v přesně protilehlých směrech pod úhlem 180°.
  Dále, u některých radionuklidů přeměňujících se elektronovým záchytem na excitované stavy dceřinného jádra se objevují úhlové g-X korelace mezi zářením gama a charakteristickým X-zářením doprovázejícím elektronový záchyt (např. u ¹²⁵I, ¹⁹⁸Hg). U kombinovaných beta-gama zářičů se pozoruje i úhlová korelace b-g.
*) Náhodná emise kvant záření izotropně do všech směrů souvisí se skutečností, že za běžných podmínek jsou atomová jádra (jejich spiny) orientována zcela náhodně a chaoticky se mění v důsledku tepelných pohybů. Jedině v případě, že radioaktivní vzorek je umístěn v silném magnetickém poli (několik Tesla), jsou magnetické momenty a spiny jader částečně polarizované a pak i jednofotonové záření bude vykazovat zvýšenou emisi v určitém úhlu korelujícím se směrem magnetického pole (vektoru magnetické indukce).
Koincidenční tomografická scintigrafie 
S těmito úhlovými korelacemi se svého času experimentovalo v koincidenční tomografické scintigrafii (§4.3 "Tomografická scintigrafie", pasáž "Technický vývoj tomografické scintigrafie"), avšak v praxi se to neujalo. Dokonalá úhlová korelace je u anihilačního g-záření, vznikajícího při anihilaci elektron-pozitronových párů na dva fotony 511keV, vylétající v přesně protilehlých směrech pod úhlem 180° (v těžišťové vztažné soustavě) - viz §1.5, část "Elementární částice a jejich vlastnosti", pasáž "Pozitrony"). Tato 100% úhlová korelace se široce využívá v gamagrafickém zobrazení metodou koincidenční pozitronové emisní tomografie v nukleární medicíně (§4.3, část "Pozitronová emisní tomografie PET").

Rychlost deexcitace a vyzáření g. Jaderná izomerie a metastabilita.
Většina jaderných excitovaných stavů je velmi nestabilní a prakticky okamžitě (po řádově 10^-12 s.) deexcituje vyzářením fotonového záření gama. V některých případech však jaderné excitované hladiny nedeexcitují okamžitě (příčina je diskutovaná níže), ale až po uplynutí určitého delšího průměrného času - říkáme, že jsou metastabilní. Tento jev se též nazývá jaderná izomerie - jádra mohou existovat ve dvou izomerních stavech, nazývají se izomery. Metastabilní izomery určitého isotopu se označují indexem "m" umístěným za hmotnostním (nukleonovým) číslem jádra - např. ^99mTc, či Tc-99m. Pokud má daný isotop více izomerů, označují se indexy "m1,m2,...", v pořadí podle vyšší energie příslušných excitovaných stavů - např. ^152m2Eu. Metastabilní izomery vznikají většinou po radioaktivním rozpadu v dceřinném jádře (jako je tomu u ^99mTc), avšak mohou existovat i samostatně bez předchozí radioaktivní přeměny, lze je připravit v jaderných reakcích.
Izomerie a metastabilní hladiny byly poprve pozorovány při b-rozpadu thoria ²³⁴Th na ^234mPa, u umělého radionuklidu pak u bromu ^80mBr vzniklého ozařováním ⁷⁹Br neutrony. Nyní je známo více než 300 jaderných izomerů, z nichž některé mají široké využití.
Příčina metastability a izomerie: 
Hlavním mechanismem potlačení gama-deexcitace vzbuzených jaderných hladin, kterému metastabilní izomery vděčí za svoje dlouhé poločasy, je relativní "zákaz" gama přechodu z důvodu velkého rozdílu momentů hybnosti (spinů) mezi příslušnými jadernými hladinami - "spinový nesoulad". Emise fotonu z excitovaného stavu jádra vede ke změně spinu jádra. Protože foton má spin 1, přechody s DI=1 jsou nejpravděpodobnější a nejrychlejší s dobou života excitovaných stavů cca 10^-16-10^-10s. Přechody s DI=2 jsou též velmi rychlé s dobou života excitovaného stavu v rozmezí 10^-11-10^-4s. V obou těchto případech jsou tedy fotony gama záření emitovány prakticky současně s předcházející přeměnou a nebo b (pro rychlost deexcitace a emise g tedy pozorujeme stejný poločas jako pro předcházející přeměnu korpuskulární). Přechody mezi hladinami s DI>2 jsou mnohem méně pravděpodobné, relativně "zakázané". Změny spinu větší než 2,3,4,... jsou v zásadě možné, ale každá taková jednotka změny způsobuje výraznou inhibici pravděpodobnosti přechodu (cca o 5 řádů). Pokud není jiná možnost deexcitace*), projeví se to delší dobou života excitované hladiny (10^-3s, sekundy, minuty, hodiny, roky, ojediněle i delší...). Deexcitace a emise fotonů se pak řídí vlastním poločasem, nezávislým na poločasu předcházející přeměny a nebo b. Nuklid v excitovaném jaderném stavu s delším poločasem přechodu gama se nazývá jaderný izomer a označuje se horním indexem "m" u nukleonového čísla - např. ^99mTc, ^81mKr.
*) Pokud však mezi excitovaným a základním stavem vzniklého jádra leží jedna nebo několik dalších energetických hladin, deexcitace nastává tak, že se přednostně uplatňují rychlé přechody s DI=1 nebo DI=2 a metastabilní stav nevzniká.
  Metastabilita vzbuzených hladin nastává tehdy, když v blízkosti základního stavu jádra existuje energetická hladina, která se od základního stavu značně liší svým momentem hybnosti (aspoň o 3h, tj. DI ł 3). Potom záření g, vyslané při přechodu z takové hladiny do základního stavu, musí mít vyšší multipolaritu (E3, M3 nebo vyšší) - přechody mezi takovými hladinami jsou málo pravděpodobné, takže odpovídající doby života mohou nabývat velkých hodnot. Izomerie a metastabilní stavy se nevyskytují u lehkých jader (kde neexistují vzbuzené hladiny s DI ł 3), ale až u jader s nukleonovým číslem od 24, od N>40 se pak vyskytují poměrně často. Podrobnosti vysvětluje slupkový model jádra.
Poločasy přeměny jaderných izomerů 
Poločasy deexcitace metastabilních hladin jsou u různých nuklidů velmi rozdílné, v závislosti na kvantových jaderných konfiguracích. Většinou jsou velmi krátké, řádu nanosekund či mikrosekund. Pro praktické použití přicházejí v úvahu až izomery s poločasy řádu sekund, minut, hodin a více. Nejkrátkodobějším radionuklidem, který má praktické využití, je izomer kryptonu ^81mKr s poločasem pouhých 13 sekund (viz §1.4, pasáž "Rubidium-Krypton").
  Zajímavé z fyzikálního hlediska, i pro své četné aplikace, jsou však především dlouhodobé jaderné izomery. Z nich bezesporu nejdůležitější je technecium ^99mTc s poločasem 6 hodin, popsané níže (viz též uvedené odkazy). Jádro ^99mTc má spin +1/2 a přeměňuje se na základní stav ⁹⁹Tc se spinem +9/2. Příkladem skutečně dlouhodobého izomeru je hafnium ^187m2Hf s vysokou excitační energií 2,45MeV a poločasem 31 let, nebo holmium ^166m1Ho s poločasem 1200 let.
Nejstabilnější známý jaderný izomer je tantal ^180mTa (je jako přírodní primordiální isotop obsažen v přírodním tantalu v koncentraci 0,012%) s nesmírně dlouhým poločasem rozpadu >10¹⁵ let! - je tedy téměř stabilní; přitom ¹⁸⁰Ta v základním stavu je beta^- a EC radioaktivní s poločasem pouhých 8,1 hod. Pozoruhodná stabilita ^180mTa je způsobena velkým spinovým nesouladem: excitovaná hladina ^180mTa (o energii 75keV) se spinem -9 by se měla fotonově deexcitovat na základní ¹⁸⁰Ta se spinem +1; tento velký spinový rozdíl způsobuje inhibici fotonové deexcicace faktorem 10³⁵ vzhledem k obvyklému "dovolenému" přechodu 10^-12s, což vede k poločasu 10²³s, tj. cca 10¹⁵ let. Přímý beta-rozpad na ¹⁸⁰Hf nebo ¹⁸⁰W je zde přitom rovněž zablokován z důvodu spinového nesouhlasu...
Pozn.: Poločas g-deexcitace, probíhající elektromagnetickou interakcí, je nezávislý na poločasu předchozí korpuskulární radioaktivní přeměny (alfa či beta), nýbrž záleží pouze na konkrétní.konfiguraci excitované hladiny vzhledem k hladině nižší nebo základní (viz výše uvedené mechanismy).
Jiná (nefotonová) radioaktivita izomerů 
Metastabilní vzbuzené hladiny izomerů se většinou "rozpadají" běžnou elektromagnetickou deexcitací za emise fotonu g. Podobně jako u ostatních vzbuzených stavů, alternativním způsobem deexcitace může být emise obalového elektronu procesem vnitřní konverze - viz níže "Vnitřní konverze gama a X".
  Některé jaderné izomery však mají natolik odlišné kvantové vlastnosti od základního stavu (především hodnotu spinu), že nedochází k izomernímu přechodu do základního stavu emisí fotonů g-záření, ale k radioaktivní přeměně beta^-, beta⁺ či elektronovému záchytu, na jiné sousední jádro. Příkladem je metastabilní ^152mEu, které vůbec nedexcituje na základní ¹⁵²Eu, ale ze 73% se b^--radioaktivitou přeměňuje na ¹⁵²Gd a z 27% elektronovým záchytem a b⁺ na ¹⁵²Sm (poločas je 9,3 hod.). Pozn.: Přitom jiný metastabilní izomer europia, označovaný ^152m2Eu, regulérně deexcituje s poločasem 96 min. izomerním přechodem na základní ¹⁵²Eu s emisí fotonu g-záření o energii 89,8keV...
Dalším příkladem je metastabilní lutetium ^177mLu s poločasem 160,4 dne, které sice v 22% případů přechází běžnou g-deexcitací na základní ¹⁷⁷Lu (které se pak beta-radioaktivitou s poločasem 6,68 dne přeměňuje na ¹⁷⁷Hf), avšak zároveň v 78% se přímým beta-rozpadem přeměňuje rovnou na ¹⁷⁷Hf. V tomto druhém případě je základní stav ¹⁷⁷Lu "bypassován" a kromě toho beta-přeměna z metastabilního lutetia jde na jiné (podstaně vyšší) excitované hladiny hafnia, než při obvyklé beta-radioaktivitě ¹⁷⁷Lu. Podobných případů větvené g-b přeměny metastabilních stavů je více. Ostatně, i u známého technecia ^99mTc jeho metastabilní hladina 140 keV, kromě obvyklého izomerního g-přechodu na základní stav ^99mTc, v nepatrném procentu (0,003%) beta-radioaktivitou přechází přímo na excitované stavy ruthenia ⁹⁹Ru (viz §1.4, část "Molybden-Technecium", obr. Tc99m).
  U velmi těžkých jader v oblasti transuranů vysoce excitované metastabilní stavy těchto těžkých nesymetrických jader vedle běžné gama-deexcitace mohou podlehnout spontánnímu štěpení (§1.3, část "Štěpení atomových jader" a "Transurany"), většinou s krátkým poločasem. Tyto "štěpné izomery" se označují indexem "f" (místo "m"), např. ^240fPu.
Monopólové E0 přechody 0⁺® 0⁺ 
Zvláštním případem silně zakázané deexcitace je přechod z excitovaného stavu s nulovým spinem a pozitivní paritou na základní stav, který má také nulový spin a pozitivní paritu - z elektrického hlediska se jedná o "monopólový" přechod, který v elektrodynamice nenastává. V takovém případě neprobíhá obvyklá deexcitace s emisí jednoho kvanta gama (byl by porušen zákon zachování momentu hybnosti), ale mohou přijít ke slovu tři alternativní mechanismy:
¨ Vnitřní konverze (rozebíraná níže v pasáži "Vnitřní konverze") - elektrický přenos energie přechodu na elektron v atomovém obalu, který je emitován a odnáší rozdíl energie E0 přechodu a vazbové energie elektronu. Je zde hlavním procesem v případě nízkých energií E0 excitace;
¨ Emise elektron-pozitronového páru (z Diracova vakuového pozadí) s opačně orientovanými spiny může nastávat při vysokých excitačních energiích - pokud má E0 přechod vyšší energii než dvojnásobek klidové hmotnosti elektronu, tj. >1,022MeV;
¨ Simultánní emise dvou fotonů gama s opačně orientovanými spiny. Je to proces vyššího řídu s nízkou pravděpodobností cca 10^-4-10^-3.
Praktický příklad tohoto monopólového E0 přechodu a jeho projevu ve spektru záření gama je uveden v §1.4, pasáž "Y-90". 

Čisté gama-radionuklidy; technecium ^99mTc; radionuklidové generátory
Nejdůležitějším příkladem vzniku metastabilního jaderného izomeru je radionuklid molybden ⁹⁹Mo, který se s poločasem T1/2=2,66 dne b^--radioaktivitou mění na ⁹⁹Tc - na jeho vzbuzenou hladinu ⁹⁹Tc* o energii 140keV, která je metastabilní s poločasem T1/2=6,02 hodin. Excitované jádro v metastabilním stavu se označuje indexem "m", zde tedy metastabilní technecium má označení ^99mTc. Jestliže během této doby odseparujeme dceřinné technecium od mateřského molybdenu, dostaneme čistý preparát technecia, obsahující excitovaná metastabilní jádra ^99mTc, která při postupné deexcitaci vyzařují záření g o energii 140keV - získali jsme tedy čistý zářič gama.
  Laboratorní zařízení pro získávání krátkodobějších radionuklidů z původních mateřských radionuklidů s delším poločasem se nazývají generátory. Molybden-techneciový generátor pro přípravu ^99mTc je tvořen skleněným válečkem s malou "chromatografickou" kolonkou, v níž je na vhodném sorbentu (např. Al₂O₃, SiO₃, ZrO₂) v nerozpustné chemické formě oxidu nanesen dlouhodobější mateřský izotop ⁹⁹Mo. Radioaktivní přeměnou z něj vzniká krátkodobý radionuklid ^99mTc, který se uvolní z nerozpustné vazby a propláchnutím vodou (resp. fyziologickým roztokem) - tzv. elucí - se z kolonky vymývá roztok technecistanu sodného Na^99mTcO₄ obsahující atomy čistého g-zářiče ^99mTc; b-radioaktivní ⁹⁹Mo přitom zůstává nasorbován v kolonce. Plynulá přeměna mateřského ⁹⁹Mo vede po eluci opět k nahromadění ^99mTc v generátoru, takže eluci lze po čase znovu opakovat.
Princip a technické provedení ⁹⁹Mo/^99mTc generátoru je na obr.4.8.1 v §4.8, který si zde pro názornost uvádíme :