 |
Obr.1.
Matematický postup filtrace v prostorové a
frekvenční oblasti. Horní část: Metodika filtrace v prostorové oblasti konvolucí s filtrem. Dolní část: Metodika filtrace ve frekvenční oblasti násobením filtrem. |
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | Fyzika a nukleární medicína |
FILTRY a FILTRACE v nukleární medicíně
1. Úvod - podstata a
motivace filtrace, filtrace prostorová a časová
2. Metodika filtrace - v
prostorové a frekvenční oblasti, Nyquistova frekvence
3. Filtrace u
zpětné projekce při tomografické scintigrafii SPECT
4. Druhy filtrů ve
frekvenční oblasti
4.1
Dolnofrekvenční (low-pas) filtry - vyhlazovací
4.2 Pásmové
filtry - fokusační
5. Filtrománie:
Který filtr je nejlepší ?
Co je
filtrace ?
Pod filtrací obecně rozumíme proces,
při němž se určitá část daného systému propouští a
jiná část zadržuje či zeslabuje. Nástroj pro tuto filtraci
se nazývá filtr.
Jednoduchým
příkladem může být cezení nudlí, kdy cedník-filtr
propouští vodu a zadržuje nudle. V chemii a jiných
technických aplikacích se používají různě hrubé či
jemné filtry pro různé roztoky - až po mikrofiltry či
"molekulová síta", které zadržují i nejjemnější
částečky. V politice a sdělovacích prostředcích se
běžně "filtrují" (či cenzurují) informace za
účelem manipulace veřejného mínění...
Pod filtrací dat
rozumíme nelokální matematický proces,
který transformuje data takovým způsobem, že
struktury určitého charakteru zesiluje a jiné zeslabuje či
potlačuje. Díky zmíněné nelokálnosti zde zpravidla neexistuje
inverzní (zpětná) transformace,
která by byla schopna z filtrovaných dat plně rekonstruovat
data primární - dochází ke ztrátě informace.
Proč
filtrovat ?
Scintigrafie, přes všechny své přednosti, se permanentně
potýká se dvěma základními problémy:
Scintigrafické obrazy jsou proto (ve srovnání např. s obrazy fotografickými) poměrně nekvalitní - jsou "rozmazané" a "zašuměné". Právě pro aspoň částečnou korekci těchto nepříznivých vlivů se používá filtrace.
Filtrace prostorová a
časová
Z prostoročasového hlediska můžeme provádět v zásadě dva
druhy filtrace scintigrafických dat :
Prostorová filtrace scintigrafických obrazů má dva základní cíle :
2.
Metodika filtrace
Z hlediska matematického postupu
filtrační procedury rozeznáváme dvě základní metodiky:
Filtrace v prostorové
oblasti
Každý bod obrazu se "zprůměruje" se svými
okolními body a takto vzniklá hodnota se uloží zpět do
výchozího bodu. Tím se v každém bodě obrazu sníží
statistické fluktuace (dané odmocninou z
nastřádaného počtu impulsů) - vzniká vyhlazený obraz. Po
vyhlazení se hodnota počtu impulsů daného prostředního
pixelu částečně přizpůsobí hodnotám v okolních pixelech.
Při této proceduře se obsahy jednotlivých elementů obrazu
násobí vhodnými váhovými koeficienty
(výchozí centrální bod má nejvyšší váhu, váha okolních
bodů se snižuje podle jejich vzdálenosti od centrálního
bodu), všechny hodnoty se sčítají, výsledek
se dělí součtem vah a uloží se zpět do
výchozího centrálního bodu. Filtrem pak
nazýváme zmíněnou váhovou matici zprůměrování.
Typickým příkladem je známé 9-bodové vyhlazení
s váhovou maticí:
| 1 | 2 | 1 |
| 2 | 4 | 2 |
| 1 | 2 | 1 |
Filtrace ve
frekvenční oblasti
Použití frekvenční oblasti je založeno na Fourierově
teorému, podle něhož každá funkce f(x) může být rozložena
na součet kosinusových a sinusových harmonických
funkcí A.cos(2pnx) (a podobně pro sinus), kde A je amplituda harmonické funkce
a n je
její frekvence (převrácená hodnota periody).
Příslušné grafy a vzorce jsou uvedeny na obr.1a 2.
Filtrace ve frekvenční oblasti sestává ze 3 etap:
 |
Obr.1.
Matematický postup filtrace v prostorové a
frekvenční oblasti. Horní část: Metodika filtrace v prostorové oblasti konvolucí s filtrem. Dolní část: Metodika filtrace ve frekvenční oblasti násobením filtrem. |
Matematicky lze ukázat (plyne to ze vzorců aplikovaných na obr.1), že oba způsoby filtrace - v prostorové i frekvenční oblasti - jsou ekvivalentní a dávají identický výsledek, pokud multiplikační filtr ve frekvenční oblasti je Fourierovým obrazem konvolučního filtru v prostorové oblasti. Filtrace ve frekvenční oblasti, ač je matematicky složitější (uživatel to ale nepozná - postará se o to počítač!), má některé výhody, které vyplynou z dalšího výkladu. Zde jen uvedeme, že filtry ve frekvenční oblasti se dají prostřednictvím svých form-faktorů flexibilně měnit, přičemž podle tvaru křivky filtru je názorně vidět, jaký bude mít účinek - které šumy či detaily v obraze zahladí.
 |
Frekvenční oblast se někdy též nazývá Nyquistova oblast, podle významného švédsko-amerického odborníka Harryho Nyquista (¶7.2.1889 ve Švédsku, V4.4.1976 v Texasu), který se problematikou filtrace zabýval v oblasti elektrických obvodů - LRC filtry složené z kondenzátorů, indukčností a rezistorů, filtrující elektrické signály v závislosti na frekvenci. |
Přechod z prostorové oblasti do frekvenční oblasti pomocí Fourierovy transformace je podrobněji ukázán na obr.2. Jsou zde schématicky znázorněny obrazy dvou rozdílných struktur : vlevo je velká kompaktní struktura (léze) s pozvolným oblým tvarem, vpravo malá struktura (léze) s ostrým profilem. Pod každým tímto obrazem je znázorněna jeho profilová křivka. Provedeme-li Fourierovu transformaci, budou u velké struktury vlevo dominovat nízké prostorové frekvence harmonického rozkladu, zatímco vysoké frekvence budou zastoupeny jen nepatrně (tj. s nízkou amplitudou). U malé struktury s ostrým profilem (vpravo) bude relativní zastoupení vyšších harmonických frekvencí mnohem vyšší.
 |
Obr.2. Přechod z
prostorové oblasti do frekvenční oblasti pomocí
Fourierovy transformace pro případ velké kompaktní léze (vlevo) a malé ostré léze (vpravo). |
Vyneseme-li graficky zastoupení amplitud jednotlivých harmonických funkcí v závislosti na frekvenci, vznikne spektrum, které ve frekvenční oblasti představuje Fourierovský obraz původní struktury z prostorové oblasti.
Frekvenční
K-prostor
V prostorové oblasti, obvyklém
eukleidovském prostoru - R-prostoru - je obraz
zobrazované veličiny F popsán distribuční
funkcí, neboli polem, F(x,y,z). Ve vektorovém zápisu,
zavedením prostorového vektoru r, je tato
funkce F(r). Obecnou Fourierovou
transformací vzniká nová distribuční funkce ^F(k)
= ňV F(r).exp[2pi(k.r)]
dr, kde k = (k1,k2,k3) je nový frekvenční
vektor, skalární součin k.r = x.k1+ x.k2+x.k3; integruje se přes
prostorovou oblast V. Distribuční funkce ^F(k)
je definována v novém lineárním 3-rozměrném vektorovém
prostoru. Prostorová F(k) i frekvenční ^F(k)
distribuční funkce nesou tutéž informaci a
souvisejí spolu přímou a inverzní Fourierovou transformací.
Z matematického hlediska tedy z
běžného metrického Eukleidovského R-prostoru
Fourierovskou transformací vzniká nový
"frekvenční" prostor, označovaný někdy jako K-prostor
(K-space - název vznikl podle toho, že po Fourierově
transformaci je novou nezávisle proměnnou "vlnový"
vektor který je zvykem značit k, obecně je
komplexní). Abstraktní K-prostor je v jistém smyslu
"reciproční" k obvyklému fyzikálnímu R-prostoru.
V dolní části obr.2 tedy vidíme, že velká kompaktní léze má spektrum končící u nízkých prostorových frekvencí, zatímco spektrum drobné ostré léze obsahuje i vysoké prostorové frekvence. Tato zákonitost má obecný charakter: čím více jemných detailů je v obraze, tím vyšší frekvence harmonických funkcí jsou zastoupeny ve frekvenční oblasti. Nejjemnějšími detaily ve scintigrafickém obraze jsou statistické fluktuace (šumy) měnící se chaoticky od pixlu k pixlu - těm odpovídají nejvyšší prostorové frekvence v Nyquistově oblasti. Použijeme-li tedy filtr potlačující vysoké frekvence, odstraňujeme tím z obrazu rušivé šumy - v tom spočívá vyhlazování pomocí tzv. low-pass filtrů. Základním "uměním" je zde zvolit takový filtr, který by potlačil rušivé šumy a přitom zachoval co nejvíce užitečných detailů v obraze.
Jak takové optimální filtrace dosáhnout? Určitým vodítkem nám mohou být zákonitosti znázorněné na obr.3. Odpovídá se zde na otázku: jaké nejvyšší frekvence v Nyquistově oblasti mohou ještě vyjadřovat skutečné detaily distribuce radioindikátoru zobrazené kamerou, a jaké odrážejí již jen rušivé šumy?
 |
Obr.3. K definici Nyquistovy frekvence pro scintigrafický obraz. |
Rozlišovací schopnost scintigrafického zobrazení je v principu omezena dvěma faktory.
1. Obrazová matice
Jemnost použité matrice scintigrafického
obrazu (zda použijeme matici 64x64, 128x128, 256x256 a pod.)
nám limituje, jak jemné detily budeme pomocí ní schopni
zobrazit. V levé části obr.3 je ukázáno, že jestliže
velikost pixelu použité matice činí d(cm), pak nejvyšší
frekvence harmonické funkce, která může být v takové
matrici zobrazena, je nmax Ł 1/2d .
2. Rozlišení kamery
Základním faktorem omezujícím rozlišovací schopnost ve
scintigrafii, je prostorové rozlišení kamery.
Na obr.3 vpravo nahoře jsou znázorněny profilové křivky LSF
obrazu bodového radioaktivního zdroje, zobrazeného gamakamerou
s výborným rozlišením (čárkovaně), se středním
rozlišením (plná čára) a špatným rozlišením (tečkovaná
křivka). Rozlišení kamery FWHM je definováno jako pološířka
profilové křivky PSF obrazu bodového (nebo čárového)
zdroje. Dva body, ležící od sebe v kratší vzdálenosti než
je rozlišení FWHM, již kamera nerozliší a
na scintigrafickém obraze budou zobrazeny jako jeden bod. Z
tohoto hlediska tedy nejvyšší frekvence harmonické distribuce
radioaktivity (modelové), kterou by kamera ještě zobrazila, by
byla nmax Ł~ 1/FWHM - u vyšších frekvencí by již jednotlivé
vlny (ko)sinusovky splynuly.
Fourierovou
transformací profilové křivky PSF(x) obrazu bodového zdroje
vzniká spektrální křivka zvaná modulační
přenosová funkce MTF(n), která znázorňuje s
jakou relativní amplitudou je kamera schopna zobrazit
(přenést) modelovou harmonickou distribuci radioaktivity v
závislosti na její frekvenci n. Místo, kde MTF klesá k
nule nám pak definuje maximální prostorovou frekvenci nmax, kterou je kamera ještě schopna zobrazit.
Můžeme tedy vyslovit následující tvrzení a zároveň definici :
Pro každé scintigrafické zobrazení existuje určitá maximální prostorová frekvence nmax, zvaná Nyquistova frekvence, kterou je systém schopen ještě zobrazit. |
Nyquistova frekvence je tedy zároveň maximální
frekvence ve Fourierově spektru obrazu, která ještě
odráží skutečné struktury předmětu.
Frekvence nižší než Nyquistova nám v obraze
odrážejí skutečnost, zatímco frekvence vyšší
než nmax již nemají svůj původ ve skutečnosti - jsou
důsledkem statictických fluktuací (šumů) a mohou být odstraněny
bez nebezpečí ztráty užitečných detailů v obraze.
Hodnota Nyquistovy frekvence nám
může pomoci při optimalizaci "síly" filtru: pomocí
form-faktorů (viz níže) natvarujeme graf filtru tak, aby se
blížil k nule právě pro hodnotu Nyquistovy frekvence.
Vyšší frekvence nemá smysl v obraze zachovávat, protože
nemohou odrážet žádné reálné struktury, vyjadřují pouze
rušivý šum.
Wavelet (vlnková)
transformace
Fourierova harmonická analýza je základem pro
pokročilé zpracování a konstrukční úpravy signálů,
měřených závisloszí a obrazů. Pomocí Fourierovy
transformace provádí rozklad analyzovaného signálu
či obrazu na harmonické funkce sinus a kosinus
s různými amplitudami a frekvencemi (obr.1 a 2), které pak
vhodně modifikuje a následně zpětně (inverzně)
transformuje. Fourierova transformace poskytuje informace o frekvencích
které se v signálu nacházejí (a jejich zastoupení), nikoli
však o jejich umístění - časové poloze u signálu či v
prostorovém (souřadnicovém) místě u obrazu. Je proto vhodná
především pro popis stacionárních signálů nebo poměrně
uniformních grafů a obrazů bez diskontinuit a ostrých
fluktuací. U filtrací pro eliminaci rušivých statatických
fluktuací (šumů) je hlavním problémem kompromis mezi mírou
potlačení šumu a přitom zachování užitečných detailních
informací v obrazech (jak bylo zmíněno
výše a bude diskutováno níže v části "Dolnofrekvenční
filtry vyhlazovací").
Silnější filtrace sice účinně potlačuje šum, avšak
zároveň vede k riziku zahlazení drobnějších detailů v
obraze.
Společným jmenovatelem
těchto obtíží je skutečnost, že bázové funkce Fourierovy
transformace, sinusovky a kosinusovky, mají nenulové
periodické hodnoty v celé prostorové oblasti ("od - do + nekonečna").
Proto se při Fourierovské filtraci každá změna ve
frekvenční oblasti projevií v celém obraze (v prostorové
doméně): jestliže se při filtraci pokusíme potlačit či
odřezat určité vyšší prostorové frekvence za účelem
znížení šumu v požadovaném místě obrazu, může se to
projevit zhoršením prostorového rozlišení v celém
obrazu.
Výhodným zobecněním a
zdokonalením standardní Fourierovy transformace je tzv. wavelet
(vlnková) transformace, která
místo sinusů a kosinusů pro rozklad analyzovaného signálu
používá speciální bázové funkce zvané wavelety
neboli vlnky, které jsou více lokalizovány
v prostorových souřadnicích a rychle ubývají do nekonečna.
Bázové funkce mají omezenou délku - ve srovnání s
obsáhlými sinusovkami jsou to jen krátké "vlnky" -
a s proměnnou frekvencí (škálou) se mohou přesouvat přes
celou prostorovou oblast signálu: analýza může být lokální
s různě silnou filtraci v různých místech signálu či
obrazu. Byla vytvořena řada waveletových funkcí (některé z
nich jsou na obrázku - b,c,d). Např. Morletův wavelet
je kosinusová funkce vynásobená Gaussovou funkcí s vhodnou
šířkou.

Nahoře: a)
Kosinusová bázová funkce Fourierovy transformace. Dole:
Wavelety: b) "Mexický klobouk". c)
Morletův. d) Meyerův
Při filtraci scintigrafických obrazů se vlnkové transformace zatím používají jen ojediněle a experimentálně, avšak se slibnými výsledky. V dalším textu se budeme věnovat standardním filtračním procedurám používajícím Fourierovu transformaci.
3.
Filtrace u zpětné projekce při tomografické scintigrafii
SPECT
Zhora zmíněné obecné
zákonitosti mají svá některá specifika při
aplikaci na tomografické scintigrafické obrazy
SPECT rekonstruované zpětnou projekcí (pojednání "Scintigrafie",
část "Tomografická
scintigrafie"). Na obr.4 je v levé horní části schématicky
znázorněno, jak zpětnou projekcí
nefiltrovaného profilu obrazu bodového zdroje, promítnutého
pod několika úhly (z nichž byl při SPECTu bodový zdroj
snímán), vzniká z projekčních paprsků v okolí výsledného
obrazu hvězdicový artefakt.
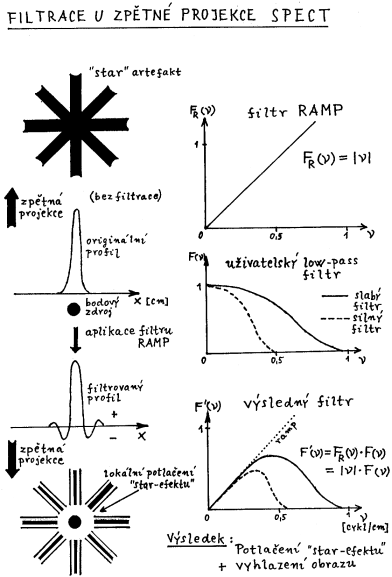 |
Obr.4 Filtrace u zpětné projekce SPECT |
Aplikujeme-li na profilovou funkci
bodového zdroje v prostorové oblasti vhodný filtr takový, že
na obou okrajích křivky je uměle zavedený "zákmit"
do záporných hodnot (velikost
těchto záporných hodnot je přímo úměrná velikosti a
rychlosti pozitivního nárustu), pak při
zpětné projekci sbíhající se paprsky se zápornými okraji
superponují tak, že v průsečíku opět vytvoří
rekonstruovaný "bodový" obraz, avšak v jeho okolí
záporné půlvlny lokálně vyruší paprsky
star-artefaktu. Ve větších vzdálenostech od obrazu bodového
zdroje sice stopy projekčních paprsků zůstávají, tam však
v zásadě nevadí - "smíchají" se s ostatními
projekčními stopami a vytvoří běžné kontinuální pozadí.
V pravé části obr.4 je tento druh
filtrace znázorněn ve frekvenční oblasti. Filtr, který lokálně
potlačuje star-efekt, zde má přímkový tvar a
nazývá se RAMP-filtr. RAMP-filtr je nezbytnou
implicitní součástí každé procedury pro rekonstrukci SPECT
metodou zpětné projekce *), avšak zároveň zesiluje vyšší
prostorové frekvence v obrazu - fluktuace, šumy. Aplikujeme-li
navíc ještě uživatelský low-pass filtr pro potlačení
statistických fluktuací, je výsledný filtr dán součinem
RAMP-filtru s uživatelským filtrem (je znázorněno v dolní
části obr.4) - takový filtr pak potlačuje star-efekt
a zároveň vyhlazuje obraz.
*) U iterativní metody rekonstrukce se
RAMP filtr nepoužívá.
Na obr.5 je schématicky znázorněn celý postup akvizice, filtrace a zpětné projekce u scintigrafie metodou SPECT.
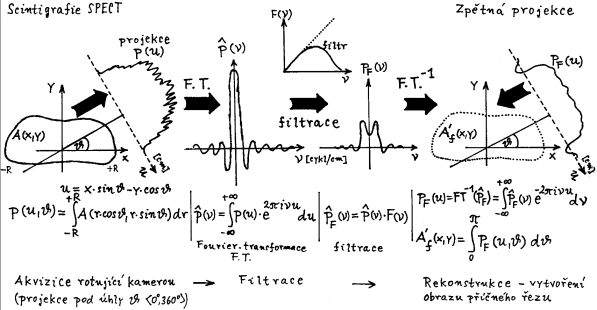
Obr.5. Postup akvizice, filtrace a zpětné
projekce u scintigrafie metodou SPECT.
Vyšetřovaný objekt (pacient), jehož příčný řez má distribuci radioindikátoru A(x,y), je kamerou snímán v řadě projekcí pod různými úhly J, čímž vznikají obrazy projekcí p(u). Tyto obrazy se pak Fourierovsky transformují do frekvenční oblasti a vzniklá spektra p(n)) se násobí filtrem složeným z RAMP-filtru a uživatelského filtru.Výsledná zfiltrovaná spektra pF(n) se pak inverzní Fourierovou transformací převádějí zpět do prostorové oblasti (vznikají filtrované obrazy projekcí pF(u)), načež se zpětnou projekcí (pod těmi samými úhly J) vytváří výsledý obraz příčného řezu A´f(x,y).
4.
Druhy filtrů ve frekvenční oblasti
Jak plyne z dosavadního výkladu,
filtrace obrazu ve frekvenční oblasti spočívá ve
vynásobení amplitudy každé harmonické funkce (na něž byl
obraz rozložen) f(n) určitým koeficentem, který v závislosti na
frekvenci n zeslabí či zesílí její amplitudu. Soubor těchto
koeficientů tvoří konkrétní filtr. Každý filtr je
realizován určitou matematickou funkcí F(n), která pro
každou hodnotu prostorové frekvence n generuje
koeficient F(n), kterým se bude násobit amplituda příslušné
harmonické ve spektru obrazu f(n). Funkční předpis filtru
F(n)
zpravidla obsahuje určité volitelné parametry - tz. form-faktory,
které spolu s matematickou funkcí určují konkrétní tvar
filtru a tím i sílu filtru. Každý
druh filtru má své specifické form-faktory, avšak jeden z
form-faktorů mají všechny filtry společný:
je to tzv. "cutoff", udávající
maximální frekvenci, od níž směrem nahoru budou již
všechny vyšší harmonické odřezané (anulované).
4.1 Dolnofrekvenční (low-pas) filtry -
vyhlazovací
Scintigrafické obrazy, zvláště
rekonstruované transverzální řezy SPECT, mají často velký
rozptyl (fluktuace) v jednotlivých voxelech - obrazový šum.
Pro lepší hodnocení těchto obrazů je žádoucí provést
snížení tohoto šumu - vyhlazení obrazu,
potlačení statistických fluktuací. Jednotlivé struktury ve
scintigrafickém obraze lze v e frekvenční oblasti rozdělit
zjednodušeně na tři skupiny :
- Nízké frekvence jsou dány rovnoměrnou aktivitou větších
struktur a pozadí.
- Střední frekvence vyjadřují změny počtu impulsů dané
různou distribucí radioindikátoru v zobrazovaných orgánech v
rozmezí jednotek až desítek pixelů - užitečnou
diagnostickou informaci.
- Nejvyšší prostorové frekvence vyjadřují statistický šum
- náhodné změny počtu impulsů v sousedních pixelech.
Ve frekvenční oblasti tedy dosáhneme vyhlazení
obrazu (snížení statistických fluktuací)
zeslabením či potlačením harmonických funkcí o vysokých
frekvencích - vynásobením spektra vhodným filtrem, který pro
nízké frekvence má hodnotu blízkou 1 (ponechává
změny počtu impulsů odpovídající strukturám zobrazovaného
orgánu) a pro vysoké frekvence dosahuje
nebo se blíží k nule (potlačuje
statistické kolísání změn v sousedních či blízkých
pixelech). Takové vyhlazující filtry se
nazývají low-pas - propouštějí především
nízké frekvence a snižují (potlačují) amplitudu vyšších
frekvencí, t.j. statistické kolísání počtu impulsů v
sousedních pixelech. V reálných obrazech se však obvykle
prostorové frekvence změn pro jednotlivé struktury
částečně překrývají, takže potlačení šumu vysoké
frekvence může vést k zahlazení reálných jemných struktur,
které mají rovněž vyšší prostorové frekvence.
Jednotlivé filtry jsou
charakterizovány frekvenční křivkou, jejíž průběh v
různých mástech určuje jejich působení. Na obr.6 jsou
uvedeny tvary a rovnice nejčastěji používaných low-pass
filtrů. U některých z nich je plnou čarou vyznačen slabší
filtr, čárkovaně pak silnější filtr.
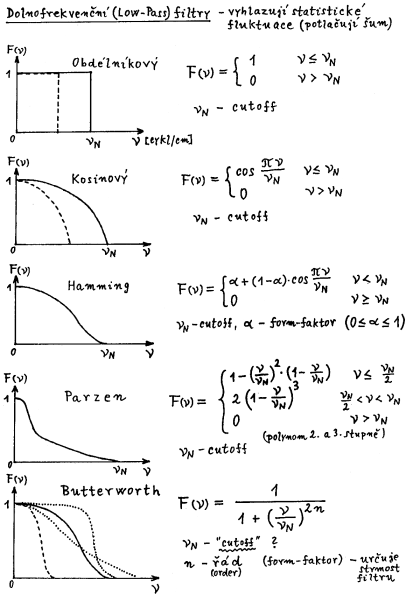 |
Obr.6. Nejčastěji používané vyhlazovací (dolnofrekvenční - low-pass) filtry. |
Nejjednodušším filtrem je prosté odřezání
(anulování) harmonických funkcí frekvencí vyšších než
určitá maximální frekvence nN zvaná "cutoff". Graf takového filtr má tvar
obdélníku - všechny frekvence až do nN = cutoff ponechává s nezměněnou amplitudou, zatímco
všechny harmonické vyšší než "cutoff" odřezává
(anuluje). Čím menší hodnotu form-faktoru "Cutoff"=nN zadáme, tím silnější bude účinek filtru.
Dále je znázorněn filtr tvaru kosinusové
funkce, který od hodnoty F=1 pro nulovou frekvenci n=0 plynule klesá až k hodnotě F=0 pro maximální
frekvenci nN (hodnota
"0" je pak přiřazena i všem frekvencím vyšším).
Síla filtru je zde opět tím vyšší, čím nižší hodnotu
form-faktoru "cutoff"=nN zadáme.
Dalšími občas používanými filtry
jsou Hamming a Parzen
(střední část obr.6). Filtr typu Hamming je modifikovaný
kosinový filtr a kromě parametru "cutoff" má ještě
jeden parametr a, který reguluje "strmost", s jakou se filtr
blíží k nule v okolí frekvencí n ~ nN. Filtr typu Parzen je kombinací dvou polynomiálních
funkcí: do poloviny rozsahu je použita rychleji klesající
funkce, na kterou pak plynule navazuje pomaleji klesající
část; form-faktorem je zde opět "cutoff".
Nejčastěji používaným low-pass
filtrem je Butterworth znázorněný v dolní
části obr.6. Má dva form-faktory - cutoff
udávající prostorovou frekvenci odřezání *) a řád
("order") regulující, jak strmě
filtr klesá od hodnot blízkých 1 k nule. Právě tato vysoká
"tvárnost" činí filtr Butterworth tak oblíbeným.
Poznámka:
Hodnota "cutoff" u filtru Butterworrth
zde není aritmeticky rovna frekvenci odřezání, jak je tomu u
ostatních filtrů. Pro n=cutoff je hodnota filtru rovná 0.5, přesně nulové
hodnoty dosahuje filtr Butterworth dokonce až v limitě pro n®Ą. Efektivně se
filtr blíží nule pro hodnoty n=2´"cutoff", a to
tím více, čím vyšší je "řád" filtru.
Síla
filtrace
Jaké jsou společné zákonitosti použití
low-pass filtrů? Co rozhoduje o jejich "síle"? Na
obr.7 je tentýž scintigrafický obraz mozku filtrován
postupně silnějším a silnějším filtrem.
| ........bez filtru ........................slabý filtr.........................střední filtr.....................silný filtr...................velmi silný filtr | ||||
 |
||||
| .........bez filtru ........................Buttw,ord=13,cutoff=0.82. .....Buttw,ord=4,cutoff=0.5........Buttw,ord=4,cutoff=0.26....Buttw,ord=4,cutoff=0.15 | ||||
| Obr.7. Výsledek filtrace obrazu mozku pomocí filtrů různé síly |
Čím dříve jde filtr k nule (při čím nižších prostorových frekvencích), tím je účinek filtrace silnější. Platí následující teorém :
Síla filtrace je nepřímo úměrná ploše pod grafem filtru ve frekvenční oblasti. |
Poznamenejme, že je to přesně
opačné než v prostorové oblasti, kde síla filtrace
je přímo úměrná ploše pod grafem
konvolučního filtru !
V pokročilých
rekonstrukčních algoritmech u SPECT a PET se používají i
sofistikovanější metody, které provádějí různě silnou
filtraci v různých místech obrazu (srov.
"Wavelet transformace").
4.2 Pásmové filtry - fokusační
Filtrace ve frekvenční oblasti
umožňuje nejen vyhlazování obrazů zredukováním vyšších
harmonických frekvencí. Pokud naopak pro určitou část
vyšších harmonických frekvencí zesílíme
jejich amplitudy, můžeme dosáhnout zvýšení
lokálního kontrastu a "zaostření"
některých detailů v obraze, které byly
"rozmazány" vlivem nedokonalého rozlišení kamery.
Takovéto pásmové filtry zesilují střední
frekvence a zeslabují vysoké i nízké frekvence, čímž zvyšují
kontrast objektů v obraze.
Lze
umělým zaostřením obrazu zcela rekonstruovat skutečnost?
Obraz vzniká konvolucí originální distribuce
(předmětu) a odezvové funkce zobrazovacího systému. Z
teoretického hlediska by použitím inverzní procedury - dekonvoluce
obrazu - mělo být možné zcela zrekonstruovat
všechny detaily původního předmětu, i ty které jsou na
obraze zahlazeny nedokonalým prostorovým rozlišením (tato
procedura se nazývá "resolution recovery"
- obnovení zhoršeného rozlišení).
Následujícím obrázek
ukazuje vyzkoušení této metody na našem pracovišti v r.1977
na scintilační kameře Pho Gamma Nuclear Chicago s
vyhodnocovacím zařízením Clincom a vlastním softwarem. Pod
scintilační kameru byly uloženy radioaktivní zdroje (jedna
miska průměru 2,5cm a 4 kuličky průměru 1cm) naplněné
roztokem 99mTc o různých měrných aktivitách -
profil jejich skutečné aktivity je na obr. vpravo nahoře
"Originální distribuce".

Dlouhotrvající akvizicí (cca 12 hodin) byl získán velmi
hladký scintigrafický obraz (profil vpravo uprostřed), bez
viditelných statistických fluktuací, na němž vlivem
špatného rozlišení (snímáno 20cm od čela kolimátoru)
nejsou viditelné detaily zdrojů. Měřením s čárovým
zdrojem byla stanovena modulační přenosová funkce
MTF(n)
kamery a Fourierovou transformací F.T. její inverzní hodnoty
1/MTF(n)
byl vypočten rekonstrukční filtr R(t) v
prostorové oblasti (obr. vlevo dole). Konvolucí
scintigrafického obrazu s tímto filtrem R(t) v prostorové
oblasti byl získám rekonstruovaný obraz (profil vpravo dole),
na němž je v detailech téměř dokonale rekonstruována
výchozí originální distribuce. Při podrobnějším pohledu
však vidíme drobné "vlnky", patrné zvláště v
plochých oblastech. Ty neodpovídají skutečnosti - jsou to artefakty,
vzniklé zesílením skrytých statistických fluktuací.
Vzhledem k velmi dobré "statistice", v praxi
nedosažitelné, jsou zde tyto artefakty drobné. Níže bude ale
ukázáno, že v praxi jsou tyto artefakty limitujícím
faktorem fokusace a "rekonstrukce" obrazů.
Filtry, které kromě vyhlazování statistických fluktuací jsou schopny zaostřovat a zvýrazňovat detaily v obraze, jsou znázorněny na obr.8. a označují se jako filtry pásmové (chovají se odlišně v různých pásmech frekvencí).
 |
Obr.8. Pásmové fokusační filtry |
Od low-pass filtrů se liší tím, že neklesají od hodnoty F(n=0) = 1 monotónně k nule, ale skládají se ze dvou částí:
Oba nejčastěji používané pásmové
filtry - typu Metz a typu Wiener
- jsou si do značné míry podobné. Vzestupná část je
odvozena od inverzní hodnoty modulační přenosové
funkce MTF a zabezpečuje podle teorie scintigrafického
zobrazení optimální rekonstrukci (dekonvoluci
- korekci obrazu na konvoluční "rozmazání"
nedokonalým rozlišením kamery) a fokusaci
obrazu - tzv. resolution recovery RR,
"obnovení rozlišení" - viz.
pojednání "Scintigrafie", pasáž "Nepříznivé
vlivy u scintigrafie".
Form-faktor "k" ("order")
umožňuje plynule nastavovat relativní zastoupení vzestupné
(fokusující) složky filtru, zatímco obvyklý parametr "cutoff"
určuje zastoupení sestupné (vyhlazující) složky filtru. Z
obr.9 vidíme, že čím větší je vzestupná část filtru,
tím výrazněji filtr fokusuje. Pokud vzestupná část chybí -
nízká hodnota parametru "k" - "order",
filtr pouze vyhlazuje podobně jako každý jiný low-pass filtr
(první část obr.9).
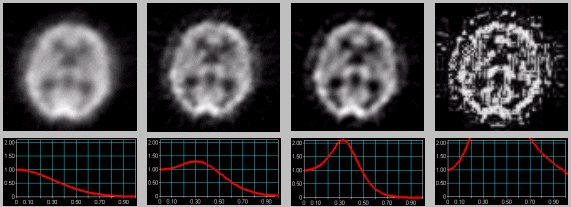 |
| .....Metz,cutoff=1,ord=3. .........Metz,cutoff=1,ord=10.......Metz,cutoff=0.74,ord=30.....Metz,cutoff=1.8,ord=90 |
| Obr.9. Filtrace pásmovým fokusačním filtrem různé síly |
Fokusaci obrazu však nelze zvyšovat
neomezeně - při vysokém podílu vzestupné fokusační části
filtru se začnou v obraze objevovat artefakty -
falešné struktury způsobené zesílením
statistických fluktuací; při pokusu o vysokou fokusaci se
obraz nakonec rozpadne na soustavu ostrůvků, z nichž mnohé
nesouvisejí se skutečnou distribucí radioindikátoru
(poslední část obr.9).
Musíme tedy upozornit, že:
Podmínkou úspěšnosti pásmových fokusačních filtrů je kvalitní scintigrafický obraz s nízkými statistickými fluktuacemi ! |
Pozn.: Filtry tohoto typu se rovněž používají v programech pro zpracování fotografických obrazů (jako je Photo Shop) ve funkci "Sharp" (dodatečné zaostření obrazu). Statistické fluktuace zde jsou většinou nízké (fotonů viditelného světla je o 3-6 řádů více než fotonů gama), avšak např. u nočních snímků mohou být podobné problémy jako u scintigrafického obrazu a dodatečná fokusace může nepřípustně zvýšit "zrnitost" obrazu.
5.
Filtrománie: Který filtr je nejlepší ?
V literatuře často různí
autoři doporučují určité filtry (filtry určitých názvů),
což u čtenářů vzbuzuje všeobecně rozšířený dojem, že
některé filtry jsou a priori lepší
než ty druhé. Pouštějí se pak do pracných experimentů s
filtry a literárních rešerší v naději, že najdou nějaký
zaručeně nejlepší "zázračný"
filtr, který jim vyrobí dokonalé obrazy. Zde si ukážeme, že
toto všechno je jen klamné zdání.
Pro objektivní rozbor
je třeba si uvědomit, že nefiltruje název filtru,
ba ani jeho matematická rovnice - ta jen generuje
koeficienty, kterými se pro jednotlivé prostorové
frekvence n bude násobit amplituda příslušné harmonické funkce
ve spektru v Nyquistově oblasti. Jestliže tedy různé filtry -
o různých názvech a různých funkčních vyjádřeních -
pomocí form-faktorů nastavíme tak, že jejich grafy
splývají, bude i výsledek filtrace identický.
Pozn.:
Příslušný obrázek zde neuvádím - byla by to nezajímavá
série identických obrazů. Každý si ale může zkusit, že
např. filtry Sheep-Logan-Hamming s parametrem cutof=1.0, Parzen
s cutof=1.2, Hamming s cutof=0.9, a=0.5 a filtr Butterwoth s
parametry cutof=0.4, order=1.5 mají téměř stejné grafy a
dávají při použití na scintigrafické obrazy stejné
výsledky.
Tato zákonitost jde ještě dál. Na obr.10 je
tentýž obraz mozku filtrován třemi různými filtry - filtry
různých názvů a různých tvarů svého grafu - volenými
však tak, aby plocha pod křivkami filtrů byla
přibližně stejná; toho lze dosáhnout
cíleným laděním form-faktorů. Vidíme, že výsledek
filtrace je téměř identický, navzdory
značné různosti funkčních předpisů i tvaru grafů
jednotlivých filtrů.
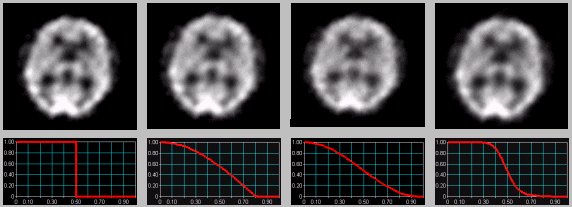 |
| ....Band-Lim,cutoff=0.51. .........Cosine,cutoff=0.80.... .......GenHann,cut=0.97,a=0.5. ...Butt,cutoff=0.49,ord=5 |
| Obr.10. Filtry různých názvů a tvarů dávají téměř stejný výsledek, pokud mají stejnou plochu |
Tyto zajímavé zákonitosti nejsou
všeobecně známy (ani v literatuře
nejsou popsány) a působí na první
pohled překvapivě; jsou však v souladu s teoretickou
analýzou. Plyne z nich poučení, že: "filtrománie"
nemá žádné opodstatnění, aspoň co se týče
low-pass filtrů.
Na otázku "Který filtr je nejlepší?", položenou v nadpisu tohoto odstavce, tedy
můžeme klidně odpovědět: Žádný ! S
každým z používaných filtrů low-pass můžeme vhodným
nastavením jejich tvarovacích parametrů dosáhnout prakticky téhož
výsledku, vyžaduje to jen zkušenost a kritické
uvažování.
A na závěr bych si dovolil ještě jednu radu*)
: Nesnažme se při praktickém vyhodnocování scintigrafických
obrazů často měnit filtry! - zhoršili bychom si tím
reprodukovatelnost obrazů, zvláště při porovnávání u
opakovaných vyšetření. Při začátku práce s novým
systémem je nejlepší vyjít z určitých doporučených či
již dříve osvědčených filtrů (např.
Butterworth, order=3, cutoff=0.4), ty si
řádně odzkoušet (a popř. modifikovat) a pak je dlouhodobě
používat. Teprve když je nějaký závažný důvod (změna metodiky, přístroje, dostatečné
nahromadění zkušeností a pod.), je
rozumné změnit používaný filtr pro dané vyšetření. A
samozřejmě můžeme cíleně zkoušet různou filtraci tehdy,
když hledáme na obraze některé atypické anomálie ...
*) Snad si mohu dovolit nějakou tu
skromnou radu vyslovit - jsem asi nejstarším
"pamětníkem" filtrace scintigrafických obrazů v
oboru nukleární medicíny u nás. Z fyzikálně-matematického
hlediska jsem se aktivně problematikou filtrace zabýval již
kolem r.1976 v souvislosti s teorií scintigrafického zobrazení a modulačními
přenosovými funkcemi.
Rizika a
úskalí filtrace obrazů
Ještě jednou varování u
filtrace obrazů:
Staré české přísloví říká: "Kde
nic není, tam ani čert nebere".
Pro náš případ toto přísloví můžeme parafrázovat takto:
"Kde nic není, tam čert může dodat - artefakt!"
- čert, v osobě přehnané filtrace,
zvýrazněním statistických fluktuací dodává artefakty
-
A kde něco je, tam to ten čert může sebrat:
Přehnanou filtrací zahladit detaily v obraze !
Tato práce byla přednášena na seminářích a symposiích České společnosti nukleární medicíny a je pravidelnou součástí postgraduálních kursů a seminářů pro obor nukleární medicíny v rámci IPVZ na KNM v Ostravě.
Poděkování:
Při vytváření této práce o filtrech a filtraci jsem úzce
spolupracoval s prim.MUDr. Jiřím Bakalou, CSc. z odd.
nukleární mediciny ve Zlíně. Dlouhé hodiny jsme spolu
proseděli u kamery Picker a počítače Odyssey, experimentovali
s různými druhy filtrů, ladili jejich parametry, diskutovali a
posuzovali jejich účinky na klinické scintigrafické studie.
Jsem Jirkovi vděčný za mnohé podněty a inspirace v mé
teoretické práci.
Vojta Ullmann