| (4.4) |
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | Gravitace, černé díry a fyzika |
Kapitola 4
ČERNÉ DÍRY
4.1. Úloha gravitace při vzniku a evoluci
hvězd
4.2. Konečné fáze hvězdné
evoluce. Gravitační kolaps
4.3.
Schwarzschildovy statické černé díry
4.4. Rotující a elektricky
nabité Kerrovy-Newmanovy černé díry
4.5. Teorém "černá díra
nemá vlasy"
4.6. Zákony dynamiky černých
děr
4.7. Kvantové vyzařování a
termodynamika černých děr
4.8. Astrofyzikální význam
černých děr
4.9. Úplný gravitační kolaps -
největší katastrofa v přírodě
4.3. Schwarzschildovy statické černé díry
To, co bylo kvalitativně řečeno v předchozím odstavci o průběhu gravitačního kolapsu, je založeno na podrobné analýze nejjednoduššího modelu gravitačního kolapsu, kolapsu sféricky symetrického. V §3.4 jsme odvodili prostoročasovou geometrii odpovídající sférické symetrii - Schwarzschildovu geometrii. Při sférické symetrii podle Schwarzschildovy-Birkhoffovy věty 3.3 bude geometrie prostoročasu Schwarzschildovská i v nestatickém případě. Pokud tedy bude gravitační kolaps probíhat tak, že sférická symetrie bude neustále přesně zachována (tj. jak distribuce hmoty, tak i její pohyb bude přesně radiální), bude geometrie okolního prostoročasu Schwarzschildova během celého průběhu gravitačního kolapsu. V počátečních fázích, kdy poloměr hvězdy je mnohem větší než gravitační poloměr, se bude realizovat jen část Schwarzschildovy geometrie vně hvězdy, zatímco uvnitř bude prostoročasová geometrie odlišná (vnitřní Schwarzschildovo řešení 4.13b, závislé na vnitřní struktuře a pohybu hmoty). V konečných fázích kolapsu, kdy se hvězda o hmotnosti M stlačí pod svůj gravitační poloměr, bude mít okolní prostoročas již všude (vnější) Schwarzschildovu geometrii (odvozenou v §3.4, vztah (3.13)) :
| (4.4) |
Schwarzschildova geometrie prostoročasu tedy popisuje statickou sféricky symetrickou černou díru. Některé rysy Schwarzschildovy geometrie, především z geometricko-topologického hlediska, byly rozebírány v §3.4 "Schwarzschildova geometrie"; zde si tento obraz rozšíříme s ohledem na fyzikální vlastnosti černé díry.
To, co dělá černou díru černou dírou, je existence horizontu událostí, v tomto případě tedy Schwarzschildovy sféry r=2M, na které je úniková ("2.kosmická") rychlost rovna právě rychlosti světla. Možnost rovnoměrného kruhového pohybu fotonu v poli Schwarzschildovy černé díry dostaneme, položíme-li ve vztahu (4.4) pro interval požadavky ds2 =0, dr=0, J =p/2 a d2j/dt2= 0 (rovnoměrnost). Vydělením dt dostaneme (dj/dt)2 = (1 - 2M/r)/r2 a po další derivaci vzhledem k požadavku d2j/dt2= 0 obrdžíme rešení r = 3M = rf . Kromě Schwarzschildovy sféry tedy kolem černé díry existuje ještě jedna význačná sféra - tzv. fotonová sféra
| r = 3 M = 3 M G / c2 , | (4.5) |
což je geometrické místo bodů, ve kterých je "1.kosmická" rychlost rovna rychlosti světla, takže v této vzdálenosti mohou fotony obíhat po kruhových orbitách kolem černé díry (obr.4.8). Toto jsou zároveň nejnižší (mezní, nejvnitřnější) kruhové orbity (viz níže); pod fotonovou sférou již žádné kruhové orbity nemohou existovat, každé těleso se zde musí pohybovat velkou rychlostí směrem ven, nechce-li být pohlceno černou dírou.
Pohyb částic
v poli Schwarzschildovy černé díry. Efektivní potenciál.
Nyní můžeme
již cíleně pokračovat v analýze geodetického pohybu
testovacích částic ve Schwarzschildově geometrii černé
díry. Použijeme k tomu rovnic (3.17)-(3.19), které si zde
vypíšeme znovu :
| (dr/dt)2 = 1/K2 - (1 - 2M/r)(1 +`L2/r2) , r2 dj/dt = const. def= `L , dt = K(1 - 2M/r) dt , |
(4.6a,b,c) |
V limitním přechodu r®Ą je (dr/dt)2 ®1/K2 -1, dt/dt®1/K. Časová složka čtyřhybnosti pi = mo.dxi/dt je E ş po = mo.dt/dt. Veličina 1/K má teď význam celkové energie v nekonečnu na jednotku vlastní hmotnosti častice: 1/K =`EĄ ;`L je moment hybnosti na jednotku hmoty. Tedy dt = EĄ-1.(1-2M/r)dt a rovnice (4.6a) zní
| (dr/dt)2 = `EĄ2 - (1 - 2M/r)(1 +`L2/r2) , | (4.7) |
což je výhodné napsat ve tvaru
| (dr/dt)2 = `EĄ2 - V2(r) , | (4.8) |
kde
| V2(r) = (1 - 2M/r)(1 +`L2/r2) . | (4.9) |
Derivování (4.8) podle t dává rovnici 2.d2r/dt2 = - ¶V2(r)/¶r . Veličina V2(r) má tedy význam efektivního potenciálu v rovnici popisující závislost mezi r a t, tedy pro radialní složku pohybu. Po dosazení dt = (r2/`L)dj z (4.6b) do (4.8) se získá rovnice mezi r a j :
| (`L2/r4) (dr/dj)2 = `EĄ2 - V2(r) . | (4.10) |
Efektivní potenciál V2(r)
se skládá ze tří částí:
a) Obvyklá přitažlivá část úměrná r-1;
b) Odpudivá část (úměrná r-2) popisující odstředivou bariéru;
c) Další, čistě relativistická
přitažlivá část úměrná r-3, vytvářející
"jámu" v efektivním potenciálu kolem r=0.
Průběh efektivního potenciálu pro různé hodnoty momentu
hybnosti testovací částice je na obr.4.6 vlevo, kde jsou též
vyznačeny oblasti v nichž dominují výše
zmíněné části a,b,c. Jestliže známe efektivní potenciál
V(r) a energii `EĄ, můžeme na základě rovnice
(4.8) stanovit radiální složku pohybu testovací částice.

Obr.4.6. Efektivní potenciál pro pohyb testovací částice v
poli Schwarzschildovy černé díry.
Vlevo:
Průběh efektivního potenciálu V(r) pro různé hodnoty
specifického momentu hybnosti `L částice.
Vpravo:
Radiální složka pohybu testovací částice mající
specifickou energii `EĄ a moment hybnosti `L je určena efektivním potenciálem VL(r).
Průsečíky přímky V=`EĄ s křivkou V=V(r) jsou body obratu, kde
radiální složka pohybu mění svůj směr. Přímka I má dva průsečíky A a B, což odpovídá eliptické orbitě s
perihéliem r=rA a "afeliem" r=rB.
Přímka II protíná křivku
V(r) jen v jednom bodě C, který je lokálním minimem - jedná se
o stabilní kruhovou orbitu o poloměru r=rC. Přímka III protíná V(r) též
v jednom bodě D, který je však maximem - příslušná
kruhová orbita o poloměru r=rD
bude nestabilní.
Některé význačné vlastnosti orbit testovacích částic lze zjistit i bez podrobného řešení příslušných pohybových rovnic (4.6). Jak je vidět z rovnice (4.8) nebo (4.10), radiální složka pohybu testovací částice mění svůj směr na opačný tehdy, když `EĄ2- V2(r) mění znaménko. Hodnota r, pro niž je efektivní potenciál roven energii testovací částice, V(r) = `EĄ, je tedy místem obratu, kde se přibližování k černé díře zastaví a nastane vzdalování, nebo naopak vzdalování od černé díry se změní v přibližování.
Různé možnosti jsou ilustrovány na obr.4.6 vpravo. Přímka I reprezentující určitou energii I`EĄ testovací částice protne funkci V(r), odpovídající danému momentu hybnosti `L testovací částice ve dvou bodech A a B. Rádiální složka pohybu bude vypadat potom asi tak, jako kdybychom na příslušnou svisle postavenou vymodelovanou křivku V(r) umístili malou kuličku ve výšce `EĄ (tj. do bodu A nebo B) a nechali ji v zemské tíži volně kutálet; kulička by se periodicky kutálela mezi body A a B a její souřadnice r by kmitala mezi hodnotami r=rA a r=rB. Testovací částice tedy obíhá po přibližně eliptické orbitě s "perihéliem" r=rA a s "aféliem" r=rB. V případě, že rovnice V(r)=`EĄ má jen jeden kořen, tj. rovnost V(r)=`EĄ nastane v bodě, kde má funkce V(r) extrém, ustaví se rovnováha mezi gravitační a odstředivou silou - bude se jednat o kruhovou orbitu. Na obr.4.6 vpravo to nastává pro přímky II a III. Přímka II protne křivku V(r) v bodě C jejího lokálního minima. Kulička položená do bodu C tam bude stále (její radiální souřadnice r=rC se nemění) - testovací částice bude kolem černé díry obíhat po stabilní kruhové dráze (neuvažujeme-li vyzařování gravitačních vln, viz níže). Přímka III protíná křivku V(r) v bodě D jejího lokálního maxima, jedná se opět o kruhovou dráhu. Tato kruhová orbita však není stabilní, kulička položená do bodu D se vlivem sebemenší výchylky skutálí dolů buďto vlevo k r=2M nebo vpravo. Kruhový pohyb testovací částice na takové labilní kruhové orbitě se i vlivem malé poruchy změní ve spirálový, buď směrem dovnitř k r=2M (částice je pohlcena), nebo směrem ven.
Z rovnice ¶V(r)/¶r = 0 plyne, že při `L> 2.Ö(3).M má funkce V(r) lokální maximum a minimum v bodech
 |
(4.11) |
V případě `L < 2.Ö(3).M neexistuje žádné minimum ani maximum a tedy neexistuje řádná stabilní kruhová orbita. Pro částici padající s `L < 2.Ö(3).M se tedy neuplatní odstředivé odpuzování, které by jí zabránilo dopadnout na poloměr r=2M, a taková částice bude pohlcena. Pro `L = 2.Ö(3).M splývají maximum a minimum v jediný inflexní bod (viz obr.4.6 vlevo) při r=6M - odpovídá to nejnižší, nejvnitřnější možné stabilní kruhové orbitě. Maximum odstředivé bariéry je v bodě r=rmax podle (4.11), takže pokud celková energie částice je `EĄ> V(rmax), je odstředivá bariéra překonána a částice je pohlcena černou dírou.
Některé typy trajektorií testovacích částic v poli Schwarzschildovy černé díry jsou znázorněny na obr.4.7. Ve velkých vzdálenostech r>>2M od černé díry se situace valně neliši od Newtonovy mechaniky: existují zde hyperbolické, eliptické nebo stabilní kruhové dráhy podobné Keplerovským (u eliptických orbit se projevuje pouze malé stáčení "perihelia", jak bylo změřeno u Merkuru, viz níže).
 |
Obr.4.7. Základní druhy orbit testovacíc částic v poli Schwarzschildovy černé díry: Trajektorie končící na horizontu (částice je pohlcena), parabolické a hyperbolické dráhy začínající a končící v nekonečnu, "eliptické" a kruhové orbity odpovídající obíhání vázané částice kolem černé díry. Není zde zachycena precese eliptických - skutečný jejich tvar viz na obr.4.12. |
V oblastech blízkých k černé díře (tj. při r v rozmezí od 2M do asi 10 M) se však trajektorie testovacích částic značně liší od Newtonovských. Jak bylo ukázáno výše, každá částice s momentem hybnosti `L < 2.Ö(3).M bude pohlcena černou dírou bez ohledu na svou energii `EĄ (zatímco v Newtonově teorii je u r=0 odstředivá bariéra nekonečně vysoká a na střed může dopadnout pouze částice s přesně nulovým momentem hybnosti). Pro částici s `L = 2.Ö(3).M existuje již jedna stabilní kruhová orbita r = rms, po níž částice (pokud má patřičnou energii `EĄ) může obíhat :
rms = 6 M = 6 M G / c2 ;
je to nejnižší - nejvnitřnější stabilní kruhová orbita - stabilní je pouze vůči poruchám směrem ven, avšak labilní vůči výchylkám dovnitř, viz obr.4.6 vlevo (ve skutečnosti je však vysoce nestabilní v důsledku vyzařování gravitačních vln - viz níže pasáž "Vyzařování gravitačních vln při pohybu v poli černé díry").
Částice s momentem hybnosti `L> 2.Ö(3).M mají již všechny možnosti pohybu, v závislosti na své energii `EĄ. Jednak se mohou pohybovat po eliptických orbitách s nejnižším a nejvyšším bodem daným vztahem (4.11). Dále pro tyto částice existují stabilní kruhové dráhy v minimech potenciálu V(r) a labilní kruhové orbity v maximech potenciálu V(r). Podle vzorce (4.11) se poloměry stabilních kruhových orbit pohybují v rozmezí od r=6M (pro `L = 2.Ö(3).M) do r=Ą (pro `L=Ą) a poloměry labilních kruhových drah v rozmezí od r=3M (pro `L=Ą) do r=6M (pro `L = 2.Ö(3).M ). Částice přicházející z r= Ą s energií `EĄ < Vmax, t.j podle vztahu ( 4.9) s energií `EĄ2 < (1 - 2M/r2max)(1 + `L2/r2max), kde rmax je dáno vztahem (4.11), se budou pohybovat po zakřivené dráze (ve větších vzdálenostech blízké hyperbolické dráze), dosáhnou "perihélia" a vzdálí se znovu k r=Ą. Částice přicházející z nekoneena s energií `EĄ > Vmax jsou však pohlceny černou dírou.
Pro výpočet periody (a úhlové rychlosti) oběhu testovací částice po kruhové dráze ve Schwarzschildově poli použijeme vztah (4.6b), kam dosadíme dt = (1/`E).(1-2M/r)dt z (4.6c). Dostaneme
w ş dj / dt = (`L/r2) (1 - 2M/r) /`EĄ .
Podmínka kruhového pohybu je `EĄ= V(r) a r=rmin (stabilní kruhová orbita) nebo r=rmax (nestabilní kruhová dráha). Ze vztahu (4.11) snadno dostaneme `L2 = M2.r2/(M.r - 3.M2) nezávisle na tom, zda se jedná o stabilní nebo labilní kruhovou orbitu. Když tyto podmínky dosadíme do vztahu pro dj/dt, dostaneme po úpravě
w = Ö(M/r3 ) , tj. T = 2pÖ(r3/M) .
Vidíme tedy, že pro kruhové orbity (stabilní i nestabilní) ve Schwarzschildově poli si zachovává přesnou platnost Keplerův zákon M =w2 r3 známý z Newtonovy nerelativistické fyziky.
Šíření
světla v poli Schwarzschildovy černé díry
Při analýze
pohybu fotonů (stejně jako i jiných částic s nulovou
klidovou hmotností) můžeme postupovat v zásadě trojím
způsobem:
a) Použít buď přímo rovnici ds2=0
s určitými zadanými podmínkami (tak jsme to udělali na
začátku tohoto odstavce při odvozování fotonové sféry);
b) Nebo použít rovnici geodetiky (3.16) v
níž je parametr ds=dt( =0) nahrazen jiným vhodným nenulovým
afinním parametrem l spojitě se měnícím podél
trajektorie fotonu (lze např. vzít l =
t);
c) Nebo konečně vyšetřovat pohyb
částice s nenulovou klidovou hmotností mo a pak přejít k limitě mo® 0.
Při tomto posledním způsobu však rovnice (4.8) a (4.10) nejsou přímo použitelné, protože veličiny `EĄ= EĄ/mo a `L = L/mo energie a momentu hybnosti na jednotku vlastní hmotnosti jsou nekonečné. Poměr těchto veličin, v němž se mo vykrátí, se však blíží konečné hodnotě, limmo® 0(`L/`EĄ) = b, rovné srážkovému parametru b definovanému jako poměr momentu hybnosti testovací částice ku její hybnosti :
| b ş L / p = L / Ö(EĄ2 - mo2) = L / Ö(`EĄ2 - 1) . | (4.12) |
Srážkový parametr b, což je vzdálenost od středu r=0 v níž by přímkový paprsek procházel nebýt ovlivňování gravitací, určuje chování fotonu v daném Schwarzschildově poli černé díry (pohyb fotonu v gravitačním poli je dán pouze jeho směrem a nezávisí na jeho energii).
Sloučením rovnic (4.6b) a (4.7) dostaneme po limitním přechodu mo® 0, `L®Ą rovnici orbity fotonu
| [(1/r2)(dr/dj)]2 = 1/b2 - (1 - 2M/r)/r2 . | (4.13) |
Místo, v němž 1/b2 = (1 - 2M/r)r2 je zde bodem obratu, kde radiální složka pohybu mění svůj směr. Aby tedy foton mohl dosáhnout místa se souřadnicí r, musí jeho srážkový parametr splňovat nerovnost
| b < r / Ö(1 - 2M/r) . | (4.14) |
Výraz na pravé straně této nerovnosti (hrající zde podobnou úlohu jako efektivní potenciál v rovnici (4.8)) má minimální hodnotu 3.Ö(3).M pro r=3M. Tedy pouze foton se srážkovým parametrem b < 3.Ö(3).M může dosáhnout libovolné (libovolně malé) hodnoty souřadnice r - je pohlcen černou dírou. Stejný výsledek dostaneme i ze vztahu (4.11), v němž limitní přechod mo® 0, tj. `L®Ą dává rmax= 3M.
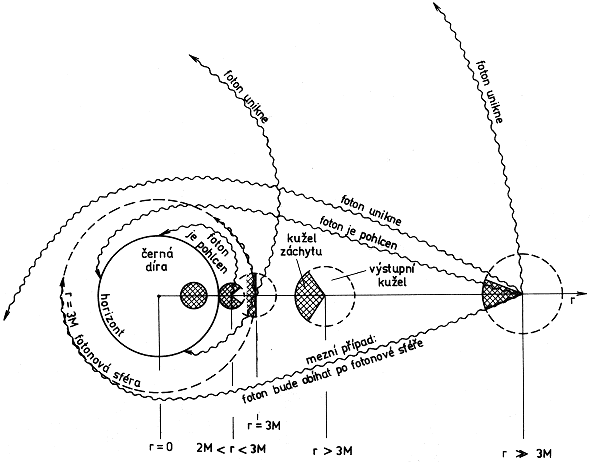
Obr.4.8. Schématické znázornění Schwarzschildovy sféry
(horizontu), fotonové sféry, výstupních světelných kuželů
a možností pohybu fotonů v poli Schwarzschildovy černé
díry.
Na obr.4.8 jsou znázorněny výstupní světelné kužely (nezaměňovat s prostoročasovými světelnými kužely!) v různých vzdálenostech od černé díry. Výstupním kuželem zde rozumíme kužel s vrcholem v daném bodě takový, že fotony vyzářené směrem ležícím uvnitř tohoto kuželu (na obr.4.8 světlá výseč) nejsou zachyceny a mohou odejít do nekonečna, zatímco světlo vyzářené směrem ležícím vně tohoto kuželu bude pohlceno černou dírou (tmavá šrafovaná výseč). Ve velkých vzdálenostech r >>3M od černé díry má výstupní kužel geometrii blízkou 4p. Do nekonečna odtud mohou odejít téměř všechny fotony s výjimkou fotonů vyzářených ve směru k černé díře v úzkém kuželu o úhlu takovém, pod jakým zorným úhlem se z dané vzdálenosti jeví koule o poloměru rz = 3.Ö(3).M ; dráhy takových fotonů se zakřiví v gravitačním poli tak, že jsou pohlceny černou dírou. Jinak řečeno, všechny fotony mající srážkový parametr menší než rz = 3.Ö(3).M jsou pohlceny (obr.4.9). Černá díra se pro fotony přicházející z nekonečna jeví jako totálně absorbující koule o poloměru 3.Ö(3).M. Učinný průřez záchytu fotonů (a každých relativistických částic) Schwarzschildovou černou dírou je tedy roven
| sr = p rz2 = 27p M2 = 27p G2 M2/ c4 . | (4.15) |

Obr.4.9. Fotony přicházející ke Schwarzschildově černé
díře se srážkovým parametrem b<3.Ö(3).M jsou pohlceny, fotony s b=3.Ö(3).M
se dostanou na fotonovou sféru,
při b>3.Ö(3).M jsou dráhy fotonů pouze zakřiveny,
avšak fotony uniknou z pole černé díry.
S přibližováním k černé díře se výstupní světelný kužel samozřejmě zužuje (obr.4.8), a to rychleji než by odpovídalo čistě geometrické představě vycházející z rozměru černé díry rg=2M v jinak rovinném prostoru. Ve vzdálenosti r=3M (na světelné sféře) má výstupní kužel úhel rovný jen 2p a s dalším přibližováním k černé díře se rychle zužuje. Ve vzdálenosti r=rg=2M (na horizontu) se výstupní kužel již zcela uzavře - jeho úhel je roven nule (nikoliv 2p jak by vyplývalo z prostého geometrického názoru bez přihlédnuti k neeukleidovským vlastnostem prostoročasu). Jen paprsek vyzářený přesně kolmo "nahoru" zde nebude pohlcen a mohl by teoreticky uniknout, avšak s nekonečným rudým posuvem; takové fotony vyzářené radiálně z horizontu směrem ven zůstávají na horizontu neomezeně dlouho, v prostoročase se stále pohybují spolu s horizontem (horizont je "generován" nulovými geodetikami - viz teorém 3.1).
Odklon částic a světla ve Schwarzschildově
poli
Řešení
rovnice (4.10), která je diferenciální rovnicí tvaru orbity,
vede na eliptické integrály a nelze jej proto obecně
analyticky vyjádřit. Pro nalezení přibližného řešení,
použitelného ve větších vzdálenostech od černé díry
(r>>M), je výhodné zavést inverzní radiální
souřadnici u = M/r, která má přímý vztah k prováděné
aproximaci. Efektivní potenciál v proměnné u je V2(r)=
(1-2u)(1 + L2u2/M2), moment hybnosti je užitečné
vyjádřit pomocí srážkového parametru a rychlosti v
nekonečnu: `L2 = vĄ2b2/(1-vĄ2). Rovnice (4.10) pak nabude tvar
| (dr / dj)2 = M2 / b2 + M2(2u - 1).(1 - vĄ2) / (vĄ2 b2) - u2 + 2 u3 . | (4.10') |
V dostatečně velké vzdálenosti od středu je člen 2u3 zanedbatelně malý a rovnice (4.10') popisuje kuželosečku s ohniskovým parametrem p ş f/2 = vĄ2b2/M2(1 - vĄ2) a výstředností e = Ö[vĄ2(2vĄ2-1).b2/M3.(1-vĄ2) + 1]. Dodatečné efekty OTR jsou způsobeny členem 2u3 v rovnici (4.10'); ve velkých vzdálenostech od středu tento člen způsobuje jen nepatrné odchylky od běžných keplerovských orbit, avšak ve vzdálenostech blízkých gravitačnímu poloměru tento člen hraje rozhodující úlohu a trajektorie testovacích částic se zde diametrálně liší od keplerovských.
Vyšetřujme nejprve hyperbolický pohyb podle horní části obr.4.10; bude nás zajímat úhel a, o který se částice odchýlí ze svého původního asymptotického směru. Tento úhel je dán úhlem mezi asymptotami orbity částice : a = j(t=+Ą) - j(t=-Ą) - p = 2 [j(r=rm) - j(r=Ą)] - p/2. Při dostatečně vysoké hodnotě srážkového parametru b bude pohyb testovací částice probíhat ve velkých vzdálenostech, tj. u<<1 bude splněno ve všech bodech trajektorie. Derivováním rovnice (4.10') se získá rovnice
d2u / dj2 + u - M2 (1 - vĄ2) / (vĄ2 b2) = 3 u2 .
Zanedbáme-li pravou stranu 3u2, bude řešení této rovnice popisovat přímočarý pohyb (nultá aproximace). Dosazením tohoto řešení nulté aproximace do členu 3u2 a opětovným řešením vzniklé diferenciální rovnice se získá trajektorie částice v prvním přiblížení, vyhovujícím již pro daný účel. Uhel a potom vychází
| a = 2M/b (1 + 1/vĄ2) . | (4.16) |
Tento vztah udává hodnotu odchylky od přímkového pohybu testovací částice pohybující se ve Schwarzschildově poli libovolnou rychlostí vĄ (<=1) s dostatečně velkým impaktním parametrem b; v tomto případě je srážkový parametr b přibližně rovný vzdálenosti rm bodu největšího přiblížení částice ke středu r=0. Vzorec (4.16) platí i pro vĄ= 1, takže úhel odklonu dráhy světla ve Schwarzschildově gravitačním poli je roven
| afot = 4 M / b = 4 G M / (b.c2) . | (4.16') |
Pro světelný paprsek
procházející těsně kolem povrchu Slunce (b » 7.105km) tento úhel odklonu vychází
afot »
8,5.10-6rad = l,75'', což bylo potvrzeno
pozorováními při úplném zatmění Slunce. V Newtonově
teorii (kde se foton považuje za částici mající v nekonečnu
rychlost c) vychází úhel odklonu dráhy fotonu
poloviční než udává vzorec (4.16'). Výsledky pozorování jednoznačně
potvrzují hodnotu úhlu odpovídajicí OTR :
Měření odklonu světelných paprsků
kolem Slunce
Pro světlo (a elekromagnetické záření obecně) Slunce
působí jako drobná achromatická gravitační čočka
nepatrné velikosti a dioptrické síly (má velkou ohniskovou
vzdálenost) - viz analýzu v následujícím odstavci.
Změření úhlu odklonu světelných paprsků při průchodu
kolem Slunce bylo velmi důležitým testem obecné teorie
relativity. U žádného jiného blízkého kosmického objektu
není zakřivení světelných papsků měřitelné. Zakřivení
světla gravitací Slunce se projevuje malým úhlovým
posunem poloh hvězd v okolí slunečného kotouče,
vzhledem k jejich polohám bez přítomnosti Slunce v těchto
místech.
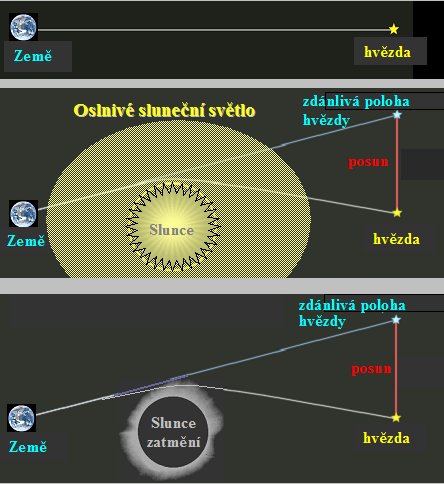 |
Nahoře: Výchozí situace - z pozorované hvězdy k Zemi dopadá paprsek světla přímočaře, bez překážky.. Uprostřed: Dole: |
Měření poloh hvězd v okolí Slunce lze
samozřejmě uskutečnit pouze během dočasného úplného
zatmění Slunce Měsícem. První vhodná
příležitost po vytvoření OTR se naskytla 29.května 1919,
kdy kotouč zatmělého Slunce se bude promítat na několik
jasných hvězd v okolí hvězdokupy Hyády. Pro pozorování
tohoto úplného zatmění se jevily výhodné dvě lokality:
Sobralu na severu Brazilie a Princ ostrov v Guinejském zálivu u
západního pobřeží Afriky. Byly tam z Británie vyslány dvě
expedice, vybavené menšími dalekohley astrografy.
Podařilo se získat cca 16 snímků na nichž bylo zaznamenáno
7 hvězd. Pečlivé zpracování výsledků, které provedl
A.S.Eddington, vedlo k úhlové odchylce pro okraj slunečního
disku 1.61" ± 0,30" pro expedici v západní
Africe a 1.98" ± 0,12" v severní Brazilii.
Pro hvězdy vzdálenější od slunečního disku je odklon
paprsků úměrně menší.
Gravitační čočky. Optika černých děr.
Zakřivování
dráhy světla v gravitačním poli vede k efektu, který je
schématicky znázorněn na obr.4.10 b). Jestliže poblíž
spojnice pozorovatele O s nějakým zdrojem světla P (třebas hvězdou
nebo quasarem) se
nachází nějaké velmi hmotné těleso M, budou světelné paprsky ze
zdroje P na své cestě k pozorovateli O gravitačním polem zakřivovány. Např. paprsek III, který by obvykle
spojoval zdroj s pozorovatelem, se v blízkosti tělesa M
odchýlí a pozorovatel O jej neuvidí. Místo toho pozorovatele O zasáhne jiný vhodně zakřivený
paprsek I, takže zdroj P se pozorovateli bude projekčně jevit v
poloze P1. Jsou-li však rozměry objektu M dostatečně malé vzhledem k jeho
hmotnosti či vzdálenosti zdroj-pozorovatel, může světlo k
pozorovateli O přicházet ještě i po druhé
cestě - paprsku II. Pozorovatel v takovém
případě místo jednoho skutečného zdroje světla P bude projekčně vidět dva zdánlivé obrazy P1 a P2. Pokud ale zdroj P, těleso M a pozorovatel O leží na jedné přímce, bude se
bodový zdroj P jevit jako prstenec kolem osy OM - tzv. Einsteinův prstenec (viz obrázek níže); při
malé odchylce od přímkové konfigurace pak bude zdroj P zobrazen jako oblouk.
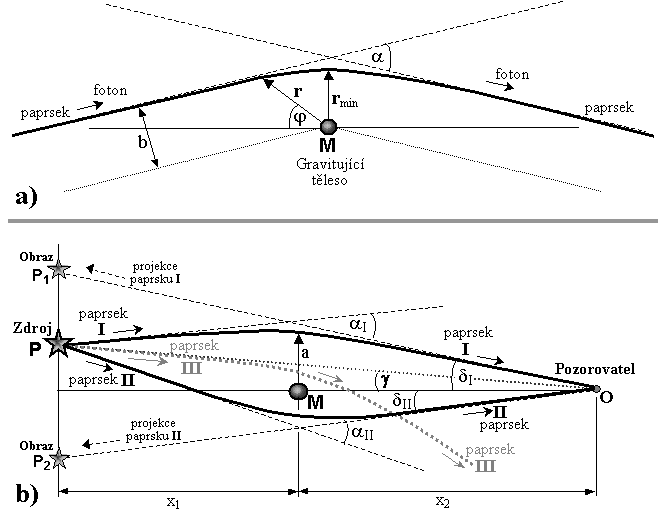
Obr.4.10. Ohyb paprsků světla v gravitačním poli.
a) Trajektorie
fotonu se při průchodu kolem hmotného objektu M odchýlí od původního směru o úhel a
(daný úhlem, který svírají asymptoty hyperbolické
trajektorie fotonu). Toto schéma je použitelné i pro
testovací částice nenulové klidové hmotnosti.
b) Efekt
gravitační čočky způsobený zakřivováním paprsků světla
vycházejícího ze zdroje P při průchodu gravitačním polem
mezilehlého tělesa M. Pozorovatele O zasahují paprsky I a II, takže skutečný zdroj P se odtud jeví jako dva zdánlivé zdroje
Pl a P2.
Označíme-li úhel mezi spojnicemi pozorovatele O se zdrojem P a s gravitujícím tělesem M jako g, bude úhel d, pod kterým se vzhledem ke spojnici OM bude jevit světelný zdroj P, dán rovnicí
d2 - g d - 4 G M / [x2(x1+x2) c2] = 0
platnou tehdy, jestliže
všechny úhly vyznačené na obr.4.10 b) jsou dostatečně
malé. Tato kvadratická rovnice má obecně dvě řešení dI
a dII odpovídající dvěma možným
světelným paprskům I a II, kterými se světlo ze zdroje P může dostat k pozorovateli O. Tento zajímavý jev se nazývá efekt gravitační
čočky, podle analogie s refrakčními
čočkami v optice.
Zde
nachází své konkrétní vyjádření poznatek odvozený v
§2.4 (část "Gravitační elektrodynamika a optika"), že gradientní gravitační pole se pro
průchod elektromagnetického vlnění chová jako opticky nehomogenní průzračné prostředí. Z
optického hlediska se gravitující sférické těleso o
hmotnosti M pro světlo jeví jako jakási spojná "čočka", jejíž optická
mohutnost je největší v oblastech kolem povrchu
tělesa (pokud se
jedná o černou díru, je to ve vzdálenosti r=3.Ö(3).M, pro niž je obrazová ohnisková
vzdálenost rovná 3M) a klesá k nule ve velkých
vzdálenostech. Z optického hlediska má tedy gravitační
čočka výraznou "kulovou
vadu"
(sférickou aberaci), avšak je dokonale achromatická - všechny vlnové délky ohýbá
naprosto stejně.
 |
Obr.4.11.
Vliv sférické gravitační čočky na rovhoběžný
svazek světelných paprsků. a) Za tělesem poloměru většího než 3M jsou tři oblasti: oblast "stínu" A; oblast B, kde každým bodem prochází pouze jeden paprsek; oblast C, kde každým bodem procházejí dva prsky. b) V případě černé díry oblasti A a B neexistují, každým bodem mohou procházet nejméně dva paprsky (celý prostor kolem ní je oblastí C ). |
Na obr.4.11 je
schématicky znázorněna situace jež nastane, je-li těleso či
černá díra ozařována širokým rovnoběžným svazkem
světla (z nekonečna). Pokud má sférické těleso hmotnosti M
poloměr větší než 3M (tj. nejedná se o černou díru),
můžeme prostor za takovým tělesem rozdělit na tři optické
oblasti (obr.4.11a). Bezprostředně za tělesem je oblast "stínu" A
způsobeného absorbcí světla v tělese. V oblasti B
každým bodem prochází pouze jeden paprsek, zatímco v oblasti
C každým bodem procházejí vždy dva
gravitací zakřivené paprsky (dvojité zobrazení) a může zde proto docházet k
interferenci. Jestliže těleso M má poloměr menší než 3M
(prakticky se tedy jedná o černou díru), oblast
"stínu" A i oblast B zde chybějí, celý prostor
kolem černé díry pro r > 3M je oblastí C
(každým bodem procházejí nejméně dva zakřivené paprsky) -
černá díra nevrhá stín !
Optika černých děr je tedy velmi pestrá a
zajímavá. Posvítíme-li např. kuželem světla z nějaké
konečné vzdálenosti na černou díru, vrátí
se nám
určitá malá část fotonů zpět: některé fotony se totiž
poblíž fotonové sféry zakřiví tak, že obkrouží černou
díru o 180° ve vzdálenosti o něco větší než 3,5.M a přijdou zpět do místa, odkud byly vyzářeny
(některé případně i po vícenásobném oběhu v blízkosti
fotonové sféry) - efekt jakési "gravitační
retročočky".
Z tohoto hlediska se tedy černá díra v "odraženém
světle" nejeví tak absolutně "černá", jak by
se dalo čekat. V každém případě (ať pozorujeme černou díru
z kterékoli strany vzhledem ke zdroji světla) kolem černé
díry osvětlované dostatečně intenzívním proudem světla
budeme vidět jakousi "svatozář" - svítící prstenec o poloměru o něco menším než 3.(Ö3).M *); ve skutečnosti to bude řada
soustředných prstenců odpovídajících jednoduchému,
dvojnásobnému a vícenásobným oběhům fotonů kolem černé
díry v blízkosti fotonové sféry, tj. fotonům odkloněným
černou dírou o úhly Dj = jo + 2kp, k=1,2,3,... (jo je úhel
mezi zdrojem a pozorovatelem). Intenzita tohoto prstence ve
srovnání s intenzitou primárního zdroje je však velmi malá.
Další zajímavostí je, že pozorovatel na fotonové sféře
(kdyby tam mohl existovat) by v dálce před sebou uviděl svá
vlastní záda.
*) Efekt se tak trochu podobá světelné
"glórii" ve vodních kapkách ozářených slunečním
světlem.
 |
Pohled na hvězdnou oblohu ve smětu k černé díře ukazuje řadu zhuštěných zobrazení celé množiny hvězd oblohy, naskládaných ve formě stále užších na sebe navazujících prstenců kolem černé díry. |
Toto silné zakřivení
světelných paprsků v blízkosti černé díry by se velmi
zvláštně projevilo na vzhledu
hvězdné oblohy pro pozorovatele nacházejícího se v
blízkosti černé díry. Černá díra, která je z optického
hlediska absorbující černé těleso, se proti hvězdné obloze
sice jeví jako tmavý kotouč, avšak sama nic
nezastiňuje
- pozorovatel vidí na obloze i nadále všechny hvězdy včetně
těch nacházejících se "za" černou dírou. Jen
jejich polohy v těchto směrech se jeví podstatně změněné -
rozptýlené a zahuštěné v okolí prstence r=3.(Ö3)M kolem černé díry.
Navíc by zde každou hvězdu bylo možno
spatřit mnohokrát v různých
směrech -
pozorovatel by viděl nejen jednu oblohu, ale (v principu)
nekonečný počet jejích smrsknutých obrazů, natlačených do soustředných
mezikruží kolem černé díry. "Nultá", základní obloha, je tvořena paprsky, které jdou od
zdroje světla přímo k pozorovateli. 1.obraz oblohy, tvořený paprsky,
které na cestě k pozorovateli udělaly jeden oběh kolem
černé díry, se zobrazuje v mezikruží o poloměru asi 5,2.M
kolem černé díry. 2.obraz oblohy je viditelný jako
další užší mezikruží uvnitř prvního a odpovídá
paprskům, které oběhly černou díru dvakrát. A tak dál,
každý další gravitační obraz oblohy je tvořen navazujícím
čím dál užším (a tmavším) mezikružím, ležícím
blíže k fotonové sféře r=3.M.
Jas těchto obrazů je celkově velmi
malý a rozměry prstenců činí řádově kilometry (pro
černé díry hvězdných hmotností), takže tento bizarní
optický efekt by byl viditelný jen pro pozorovatele v
dostatečné blízkosti černé díry; pro vzdálené
pozorovatele - tedy i pro naše astronomy - by násobné obrazy
byly naprosto nerozlišitelné.
Silné, slabé a difúzní
gravitační čočky ve vesmíru
Každá hmota gravitačně ohýbá
ve svém okolí dráhu fotonů a světelné paprsky - vytváří
efekt gravitační čočky, způsobující
posuny souřadnic a deformace tvarů objektů v pozadí,
vyvolaných gravitací objektů v popředí. Většinou se však
jedná o velmi slabé efekty, na hranici
měřitelnosti. Efekt gravitační čočky lze obecně rozdělit
na dvě kategorie :
× Silné
gravitační čočkování
vytvářející vícenásobné obrazy a rozsáhlé oblouky,
způsobené mohutnou gravitací kompaktních objektů nebo
obrovským nahromaděním hmoty v galaxiích a kupách galaxií.
× Slabé
gravitační čočkování
způsobující jen malé úhlové odklony záření. To může
být způsobeno dvěma okolnostmi:
1. Objekty relativně malých hmotností
jako jsou hvězdy a planety, způsobující efekt gravitační
"mikročočky" zmíněný níže..
2. Průchod záření kolem velmi
hmotných difúzně rozprostřených systémů ve velkých
vzdálenostech.
Slabé gravitační čočkování se může
projevovat dvěma efekty:
-- Konvergence paprsků zvětšuje úhlový
rozměr a jas objektů na pozadí ........
-- Gravitační smyk (střih - shear) paprsků se projevuje tangenciálním rozmazáváním
obrazu zdroje kolem čočkujícího objektu.
Gravitační čočky ve
vesmíru
I když efekt
gravitační čočky je již dlouho dobře známým důsledkem
obecné teorie relativity, byl poprvé pozorován teprve zcela
nedávno. Při pozorování hvězd je zakřivování dráhy
světla gravitačním polem jiných hvězd zcela nepatrné a
efekt gravitační čočky se prakticky neprojevuje, protože
gravitační pole běžných hvězd je poměrně slabé a rychle
klesá se vzdáleností. K dosažení znatelného efektu by proto
dvě hvězdy musely téměř přesně ležet na přímce
procházející pozorovatelem; pravděpodobnost tak těsného
seřazení dvou různě vzdálených hvězd na jedné přímce je
velmi malá. Učinnými gravitačními čočkami mohou být galaxie (které mají hmotnost řádově ~108-1012 -krát větší než průměrná
hvězda), přičemž ovšem světelným zdrojem, na němž se
efekt čočky pozoruje, pak musí být nějaký velmi vzdálený
objekt, aby byla určitá pravděpodobnost, že světlo při
cestě k nám bude procházet dostatečně blízko kolem nějaké
takové hmotné galaxie. Masívní galaxie nebo kupa galaxií
tedy svým gravitačním zakřivováním elektromagnetických
paprsků působí jako obrovská "čočka", přes kterou se díváme
do vzdálenějšího vesmíru (viz níže
"Gravitační čočky - mohutné astronomické
dalekohledy?"). Výsledkem je, že obraz určité velmi
vzdálené galaxie může být zesílen, znásoben či pozměněn
do podoby oblouků či prstenců, vlivem gravitace obrovsky
masívního objektu, který leží téměř přesně na spojnici mezi námi a pozorovanou vzdálenou
galaxií.
Skutečně, v r. 1979 byla na observatoři
Kitt Peak v Arizoně (D.Walsh a kol.) objevena neobvyklá dvojice
kvasarů QSO 0957+561 A,B (úhlová
vzdálenost mezi nimi činí 5,7''), které mají stejný rudý posuv z=1,41,
prakticky identická spektra a též málo rozdílný jas; navíc
poměr jasu objektu A a B je stejný ve všech
pozorovaných oblastech vlnových délek - radiových,
infračervených, optických i ultrafialových []. Přirozeným
vysvětlením těchto neobvyklých souvislostí je to, že
pozorujeme nikoli dva různé kvasary, ale kvasar
jeden,
jehož obraz je rozštěpen na dvě složky gravitační čočkou. Toto vysvětlení je dále
posíleno tím, že v úhlové vzdálenosti 0,8'' od objektu B
byla nalezena obří eliptická galaxie (jejíž hmotnost se odhaduje
na ~2.1011M¤) s rudým posuvem asi z @ 0,4. Tato mezilehlá
galaxie je
zřejmě tou gravitační čočkou způsobující zdánlivé
rozdvojení kvasaru. Při astronomických pozorováních se pak
objevily i některé další případy, kdy soustava podobných
kvasarů se dá vysvětlit jako vícenásobné zobrazení
jediného kvasaru mezilehlou galaxií jakožto gravitační
čočkou (např. trojitý kvasar QSO PG 1115 + 08).
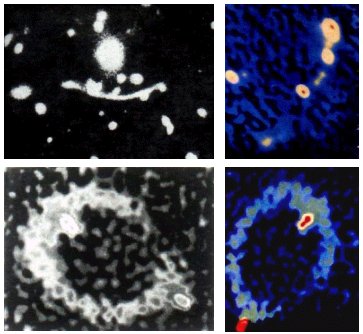 |
Vlevo: Gigantický zářivý oblouk - neúplný Einsteinův prstenec - v kupě galaxií Abell 370. Vpravo: |
| Vlevo: Téměř úplný Einsteinův prstenec MG 1131+0456. Vpravo:
|
|
| Příklady astronomicky pozorovaných Einsteinových oblouků vznikajících efektem gravitační čočky. | |
V těchto případech,
kdy gravitační čočkou je galaxie s nesférickým
gravitačním polem, je zobrazení podstatně komplikovanější
než podle obr.4.10b ve Schwarzschildově poli - dochází k
vícenásobnému rozštěpení *). Navíc se zde jedná o
rotující gravitační čočku (galaxie rotují), což může
způsobovat další efekty asymetrie a nesoučasnosti
vznikajících zobrazení, viz §4.4.
*) Radioastronomicky se
pozoruje lichý počet obrazů (často
trojitý obraz), protože
mezilehlá galaxie je pro rádiové záření průhledná. V
optickém oboru se přímý paprsek nepozoruje, skrz
neprůhlednou mezilehlou galaxii neprojde.
Charakter pozorovaného obrazu v sobě
nese některé informace o průběhu gravitačního pole
"čočky", takže podrobná analýza struktury obrazu
může zpětně poskytovat určité údaje o rozložení hmoty v mezilehlé galaxii - a to jak zářící, tak skryté
hmoty (nezářící, temné hmoty; o této
významné, ale zatím záhadné složce hmoty ve vesmíru viz
§5.6 "Budoucnost vesmíru. Šipka času. Skrytá
hmota.",
část "Temná hmota"). Z analýzy snímků vzniklých
gravitačním čočkováním tak lze potenciálně vyčíst
zajímavé informace o rozložení hmoty ve vesmíru, včetně
temné hmoty, kterou nevidíme astronomickými přístroji.
Pozorované vícenásobné zobrazení
kvasarů efektem gravitační čočky mezilehlých galaxií je,
kromě dalšího potvrzení Einsteinovy obecné teorie
relativity, též důkazem toho, že kvasary leží opravdu v kosmologických vzdálenostech (a že tedy jejich velký rudý
posuv je kosmologický Hubbleův rudý posuv).
Gravitační čočky -
mohutné astronomické dalekohledy?
Gravitační čočka je "spojná čočka", takže
vedle změny polohy obrazu vůči předmětu (a případně
rozštěpení obrazu) se projevuje i tím, že vzdálený objekt
se pozorovateli může jevit větším a jasnějším než je ve skutečnosti.
Zesílení jasu může být 10 i vícekrát. Tento efekt může
mít velký astronomicko-observační
poteciál:
obří gravitační čočka může fungovat jako opticky velmi
výkonný "objektiv" a náš běžný
astronomický dalekohled jako "okulár" tohoto hybridního teleskopického systému. Ohnisková vzdálenost
takového gravitačně-optického
dalekohledu
zde může dosahovat nepředstavitelných hodnot tisíců i
miliónů světelných let!
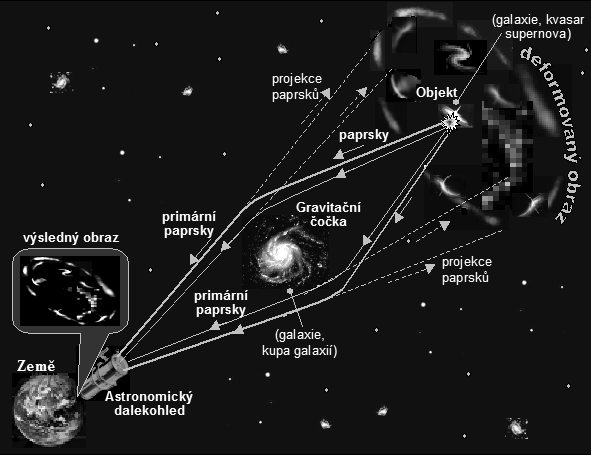 |
Schématické znázornění
hybridního gravitačně-optického astronomického
"dalekohledu". Velmi vzdálený zářící objekt (galaxie, kvasar či supernova) je nejprve zobrazen gravitační čočkou, kterou může být mezilehlá galaxie nebo kupa galaxií. Ohnuté světelné paprsky pak vstupují do klasického astronomického dalekohledu (který může být optický nebo radioastronomický - podle toho zda pozorujeme v optické nebo rádiové oblasti), kde vzniká výsledný obraz.. S trochou nadsázky lze říci, že gravitační čočka tvoří "objektiv" a velký astronomický dalekohled slouží jako "okulár" tohoto vesmírného zobrazovacího systému. |
Z hlediska potenciálního astronomického
využití ale mají gravitační čočky dvě hlavní nevýhody:
1. Jsou náhodně rozloženy v
různých konkrétních místech a směrech od pozorovatele, s
různými velikostmi a gravitačně-optickými vlastnostmi.
Nedají se nijak nastavovat, na rozdíl od klasických
astronomických dalekohledů, které můžeme snadno orientovat
do libovolných směrů. Ve obrovském vesmíru, zaplněném
miliony galaxií a kup galaxií, se však pravděpodobně
vyskytuje velké množství vhodných konfigurací, které mohou
fungovat jako gravitační čočky.
2. Gravitační čočky nejsou
schopny poskytovat ostrá zobrazení. I přesně sférické
masívní těleso se Schwarzschildovým gravitačním polem má v
optické terminologii výraznou "kulovou vadu" neboli
sférickou aberaci (jak bylo výše
ukázáno); galaxie mají navíc složité
nehomogenní rozložení hmoty. Různé části gravitační
čočky mají proto různou "optickou hohutnost", což
vede k rozmazaným a zkresleným obrazům,
složeným z různých skvrn a oblouků (jak
je výše naznačeno na obraze). Lze ale
snad doufat, že budoucí pokročilé počítačové zpracování
obrazů toto dokáže do značné míry korigovat a umožní zrekonstruovat
důležité údaje o vzdálených gravitačně zobrazených
objektech.
Zvláště mohutnými gravitačními čočkami
mohou být velké kupy galaxií. Taková kupa
galaxií může působit jako obrovská vesmírná - kosmologická
gravitační čočka, která by za vhodné konstelace
mohla pomoci nahlédnout do nejvzdálenějších hlubin vesmíru,
a tím i do nejzasší minulosti...
Vedle zesíleného a zvětšeného zobrazení
nejvzdálenějších vesmírných objektů nabízejí
gravitační čočky i další unikátní možnosti. Asi
nejpozoruhodnější z nich je možnost sledování
dynamiky rychlých explozivních procesů, jako jsou
výbuchy supernov. Gravitační čočka může vytvářet více
obrazů téhož objektu s různým časovým
zpožděním, neboť tyto obrazy jsou vytvářeny
zakřivenými paprsky s různě dlouhými drahami na cestě k
pozorovateli. V těchto rozštěpených obrazech supernovy,
které jsou vůči sobě posunuty v čase, tak můžeme prakticky
současně pozorovat různé fáze vzplanutí supernovy.
Astrometrický význam
gravitačních čoček
Gravitační čočky mohou mít i
pozoruhodný význam astrometrický. Obecně umožňují změření hmotností
astronomických objektů, aniž jsou potřeba předpoklady o
jejich složení a dynamických vlastnostech. Dráhy paprsků I a
II na obr.4.10 nejsou stejně dlouhé, takže případná změna
jasu zdroje P se na
obrazech P1 a P2 projeví s odlišným zpožděním. Změříme-li tedy časovou
diferenci změn jasnosti obrazů P1
a P2, pak trigonometrickým rozborem úhlů g, d1, d2 lze
stanovit vzdálenost zdroje P od pozorovatele. Gravitační čočky tak
umožňují poměrně přesné absolutní měření
vzdáleností kvasarů,
nezávisle na nepřímých astronomických metodách.
Značný význam by též mělo pozorování efektu gravitační
čočky vyvolaného masívní koncentrací skryté (nezářící)
hmoty (§5.6) v galaxiích a kupách galaxií.
Jak bylo výše uvedeno, gravitační čočky
mohou poskytovat více obrazů vzdálených
objektů jako jsou kvasary či vzplanutí supernovy, přičemž
tyto obrazy mohou mít různá časová zpoždění v důsledku
různě dlouhé dráhy paprsku k pozorovateli. Pokud se podaří
určit vzdálenosti zúčastněných objektů - supernovy či
kvasaru i mezilehlé gravitační čočky (změřením
příslušných rudých posuvů), pak analýzou dvou nebo více
rozštěpených obrazů téhož vzdáleného objektu (kvasaru či
supernovy) můžeme stanovit hmotnost mezilehlé galaxie -
gravitační čočky. Z těchto časových diferencí a
vzdáleností pak lze odvodit i hodnotu Hubbleovy
konstanty H rozpínání vesmíru (§5.1 část "Dynamická expanze vesmíru"); jedná se o její nezávislé
určování.
Gravitační
"mikročočky"
Takto se někdy nazývají gravitačně-ohybové jevy u těles o
mnoho řádů menších než galaxie nebo kupy galaxií - u hvězd
či dokonce planet. V úvodu této části
"Gravitační čočky ve vesmíru"
bylo zmíněno, že pravděpodobnost dostatečně těsného
"slícování" dvou různě vzdálených hvězd na
přímkové spojnici s pozorovatelem je velmi malá. Hvězdy se
však pohybují poměrně velkými rychlostmi v náhodných
směrech, takže astronomicky pozorujeme v naší Galaxii (a částečně též v sousedních Magellanových
mračnech) poměrně výrazné příčné
pohyby hvězd. Dochází tak občas k těsným optickým
zákrytům vzdálených hvězd na úhlovou rozteč
menší než miliontiny obloukové vteřiny. Při takovém
zákrytu vlivem efektu gravitační čočky bližší
hvězdy dojde k přechodnému zjasnění
vzdálenější hvězdy *). Při pozorovaných
příčných rychlostech hvězd lze dobu trvání tohoto úkazu
odhadnout na cca 20-40 dní. Kdybychon graficky vynesli křivku
závislosti jasu pozorované hvězdy na čase, viděli bychom na
jinak přímkové závislosti dočasné maximum (plochý vrchol podobný Gaussově křivce), jehož výška (resp. plocha pod
křivkou) závisí na hmotnosti
čočkující hvězdy a na úhlové vzdálenosti zákrytu.
*) Určitým problémem by mohlo být
odlišení změn jasnosti způsobených gravitační
mikročočkou od astrofyzikální proměnnosti skutečného jasu
hvězdy. Vedle analýzy dynamiky křivek by spolehlivou metodou
mohla být spektrometrická analýza. Astrofyzikální erupce
mají v různých barvách rozdílný průběh, zatímco
gravitační čočky jsou achromatické, takže průběh
světelných křivek mikročoček je stejný pro všechny barvy
(vlnové délky).
Pokud by kolem mezilehlé
(bližší) čočkující hvězdy obíhala dostatečně hmotná planeta
(exoplaneta), i ona by se mohla podílet na efektu gravitační
čočky: na vzestupné nebo sestupné části světelné křivky
základní mikročočky by se objevilo malé a krátké
sekundární zjasnění. Doba trvání (šířka) tohoto
sekundárního píku by závisela na hmotnosti planety, lze ji
odhadnout na několik hodin.
Závěrečná poznámka:
Astronomické využití gravitačních čoček je teprve v samém
začátku. Většina zde diskutovaných efektů je zatím jen
teoretická (základní efekty se daří
pozorovat jen u galaxií a kup galaxií ),
jejich astronomický potenciál bude, jak lze doufat, využíván
v příštích desítiletích - s rychlým rozvojem pozorovací
techniky a vyhodnocovací elektroniky...
Precese
eliptické dráhy ve Schwarzschildově poli
Analýzu kruhových orbit testovacích částic
(včetně fotonů) ve Schwarzschildově poli lze bez obtíží
provést přesně. Stabilní orbity odlišné od kruhových (pro
něž radiální souřadnice kmitá mezi "perihéliem"
a "aféliem", tj. mezi hodnotami r=rA
a r=rB podle obr.4.6 vpravo) jsme před
chvílí označili jako "eliptické". Není to však
tak docela pravda. Základní novou vlastnost eliptických orbit
- stáčení jejich hlavní osy - lze nejjednodušeji ukázat na
případu orbity, která se jen velmi málo liší od kruhové.
Pro kruhovou orbitu
r=R=const. o
poloměru R je (dr/dt)|r=R = 0, (d2r/dt2)|r=R = 0, `L2=
MR2/(R-3M). Slabě eliptickou dráhu
(lišící se jen nepatrně od kruhové) lze považovat za
poněkud porušenou kruhovou orbitu, takže pro ni můžeme psát
r(t)= R + e(t), kde e « R
(tj. je e/R«1) popisuje slabé radiální
kmity mezi body obratu. Toto dosadíme do rovnice vzniklé
derivací rovnice (4.6a) podle dt, rozložíme na řadu v
mocninách e/R a ponecháme pouze členy
1.řádu. Po úpravě dostaneme rovnici
d2e /dt2 = - (M/R3) (1 - 6M/R) . e ,
jejíž řešení je
e(t) = eo. sin{Ö[(M/R3)(1 - 6M/R)] . t} .
Perioda základního kruhového pohybu (oběžná doba) je podle Keplerova zákona T = 2p.Ö(R3/M). Perioda radiálních kmitů e(t) je Te = 2p.Ö[R3/M(1-6M/R)]. Pohyb se tedy neděje po stálé elipse, protože by muselo být Te = T. Za dobu jednoho radiálního kmitu Te proběhne testovací částice (obíhající úhlovou rychlostí w) úhel w.Te; rozdíl tohoto úhlu od 2p udává fázový rozdíl mezi radiálním a oběžným pohybem za jednu periodu: Dj = Te.w -2p = 2p(Te/T -1). O tento úhel Dj se za každou obrátku posunou (pootočí kolem středu r=0) body obratu, a tedy i přímka spojující perihélium přes střed s aféliem (obr.4.12) :
| Dj = 2p (Te / T - 1) = 2p [1/(1 - 6M/R) - 1] » 6p M / R . | (4.17a) |
Pokud se periody T a Te příliš neliší, můžeme orbitu částice považovat za elipsu, která však není pevná, ale jejíž hlavní osa se (kolem středu r=0 jímž prochází) neustále pozvolna otáčí úhlovou rychlostí (obr.4.12)
| w' = Dj /Te = w - we = (M/R3) [1 -Ö(1 - 6M/R)] » (3 M / R) Ö(M/R3) . | (4.17b) |
Přibližné výrazy v (4.17a,b) platí tehdy, když R>>6M, tj. dostatečně daleko od středu.
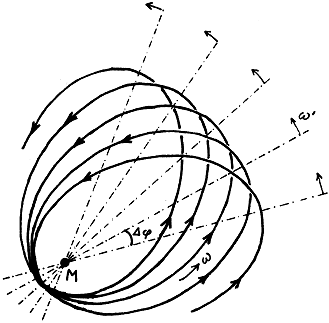 |
Obr.4.12. Znázornění skutečného pohybu testovací čás tice po "eliptické" dráze ve Schwarzschildově poli. Pohyb neprobíhá přesně po pevné elipse, ale můžeme si jej představit jako obíhání po elipse, která sama vykonává precesní pohyb - hlavní osa této elipsy pomalu rotuje v souhlasném směru kolem středu r=0. |
Precese eliptické dráhy tak vede k tomu, že "perihélium" testovací částice se za každou obrátku posune o úhel daný vztahem (4.17a). Tyto posuny se při větším počtu oběhů sčítají, takže i v případě, kdyDj pro jeden oběh činí jen nepatrný úhel, za delší dobu (po mnoha obězích) může posun perihélia nabýt měřitelnou hodnotu. Tak je tomu i při oběhu planet ve sluneční soustavě, kde tento efekt je nejvýraznější a nejsnáze měřitelný u planety Merkur (R @ 5,5.1010m). Vzorec (4.17a) pro Merkur dává Dj @ 6pGM/Rc2 @ 5.10-7rad/oběh; protože oběžná doba Merkuru je 0,241 roku, relativistický posun jeho perihélia činí asi 43'' za 100 let. Skutečně pozorovaný posun perihelia Merkura je mnohonásobně větší, avšak po odečtení všech příspěvků způsobených rušivými vlivy planet zbude právě ona část 43'' předpovězená obecnou teorii relativity.
Účinný
průřez záchytu částic černou dírou
Vztah (4.15)
udává účinný průřez záchytu černou dírou pouze pro
fotony a ultrarelativistické částice s mo« EĄ. K výpočtu účinného průřezu
záchytu nerelativistických částic černou dírou použijeme
efektivního potenciálu V(r) podle (4.9). Aby částice byla
zachycena černou dírou, musí být její energie větší než
maximum efektivního potenciálu pro daný moment hybnosti: `EĄ> Vmax. Částice s nerelativistickou
rychlostí v nekonečnu v«1 (poblíž černé díry však
rychlost může být relativistická!) má
energii EĄ=m.c2 = mo,
tj. `EĄ=1. Z podmínky `EĄ=1 > Vmax po dosazení (4.11) zjistíme,
že aby částice byla zachycena, musí její moment hybnosti
splňovat nerovnost `L<4M (viz též obr.4.6, kde
přímka `EĄ= 1 leží výše než maximum
efektivního potenciálu jen tehdy, když `L
< 4M), což vyjádřeno pomocí srážkového parametru je
b< 4M/vĄ= bk. Částice s takovým impaktním
parametrem jsou pohlceny. Účinný průřez záchytu
nerelativistických částic Schwarzschildovou černou dírou je
tedy
snr = p bk2 = 16p M2 / vĄ2 = 4p rg2 / vĄ2 = 16p G2 M2 / (c4 vĄ2) .
Vyzařování gravitačních vln při pohybu v
poli černé díry
Je třeba
zdůraznit, že pohyb těles v poli Schwarzschildovy černé
díry by vypadal tak, jak jsme si jej popsali, pouze v
idealizovaném případě nekonečně malé testovací částice
při zanedbání vyzařování gravitačních vln. Ve velkých
vzdálenostech od černé díry je toto přibližně splněno. Každé
těleso, které se však přiblíží na vzdálenost srovnatelnou
s ~2M, začne (v důsledku velkého zrychlení) při svém pohybu
vyzařovat intenzívní gravitační
vlny (§2.7, část "Zdroje gravitačních vln").
Takto vzniklé radiační brzdění výrazně ovlivní trajektorii
tělesa. Orbity (zvláště "nízké" orbity s r
<10M), které by teoreticky měly být stabilní, budou ve
skutečnosti nestabilní - těleso bude neustále
ztrácet energii vyzařováním gravitačních vln, takže bude
po spirále postupně klesat k černé díře a nakonec jí bude
pohlceno. Rychlost, s jakou částice o hmotnosti m («M) bude
při svém obíhání po kruhové dráze poloměru r
ztrácet energii gravitačním vyzařováním, je podle vzorce
(2.88) a Keplerova zákona
| dE / dt = - 32/5 . m2 M3 / r5 . | (4.19) |
Protože kinetická energie částice je E= (1/2)m.w2r2 = (1/2)m.M/r (podle Keplerova zákona je w2r3=M), dostaneme po dosazení do (4.19) rovnici pro časovou změnu poloměru orbity v důsledku gravitačního vyzařování; její řešení je
| r = ro [ 1 - 256/5 (m M2/ro4) . t ]1/4 , | (4.20) |
kde ro je stávající počáteční poloměr orbity. Je vidět, že stbilní dráha r=ro= const. může být pouze v limitě buď pro m®0 (nekonečně malá částice) nebo pro ro®Ą (dostatečně daleko od černé díry). U eliptických orbit je gravitační vyzařování nejsilnější v "periheliu", kde se proto projevuje největší radiační brzdění. V důsledku toho eliptická orbita (kromě celkového zmenšování) snižuje svou excentricitu a postupně přechází v orbitu kruhovou (pokud na to má "dost času" před svým pohlcením). Z hlediska gravitačního vyzařování je možno pohyb tělesa po oběžné dráze kolem černé díry rozdělit na dvě etapy (obr.4.13). V první etapě těleso vyzařuje energii podle vzorce (4.19) a postupně klesá po spirále až k nejnižší (nejvnitřnější a nejsilněji vázané) stabilní kruhové orbitě o poloměru r=6M. Celkové množství energie vyzářené gravitačními vlnami během této první etapy (za předpokladu, že těleso hmotnosti mo začalo svůj pohyb daleko od černé díry) je dáno vazbovou energií na orbitě o poloměru r=6M :
| E I = mo [1 - V(r=6M)L=2Ö(3)M] = mo(1 - Ö(8/9) ) @ 0,572 mo . | (4.21) |
Po dosažení nejnižší (nejvnitřnější) stabilní kruhové orbity r=6M je těleso již velmi rychle pohlceno černou dírou, přičemž vyšle intenzívní impuls ("záblesk") gravitačního záření - druhá etapa. Energie vyzářená při tomto "záblesku" gravitačních vln je přibližně rovna [289],[62]
| E II » 0,01 . m2 / M . | (4.22) |
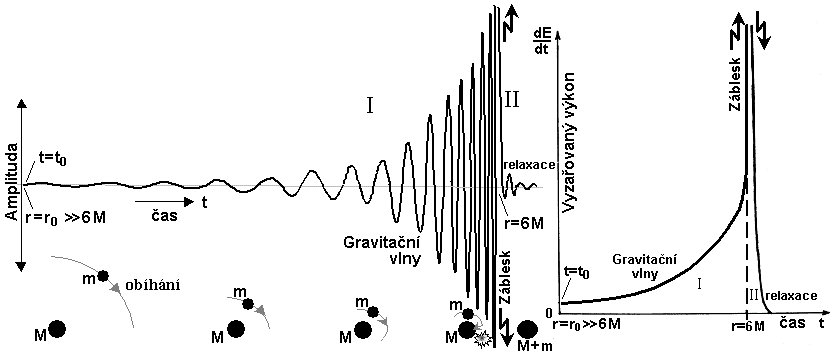 |
| Obr.4.13.
Časový průběh frekvence a intenzity gravitačního
záření tělesa m obíhajícího kolem
Schwarzschildovy černé díry M. Těleso, jež začne v čase t=0 své obíhání na nějakém velkém poloměru r0, klesá po spirále a kontinuálně vyzařuje nejprve slabé gravitační vlny, ale se stále rostoucí intenzitou a frekvencí (etapa I). Po dosažení poloměru r=6M je těleso rychle pohlceno, přičemž vyšle krátký intenzívní záblesk gravitačních vln (etapa II). Výsledná černá díra M+m je rotující a vyzařováním tlumených gravitačních vln relaxuje na stacionární konfiguraci Kerrovy černé díry. |
Celkové množství energie, které těleso o hmotnosti mo<<M může při svém pádu na Schwarzschildovu černou díru vyzářit ve formě gravitačních vln, tedy je E = EI + EII, přičemž rozhodující část se vyzáří v první etapě. Pokud ovšem těleso dopadá na černou díru přímo (radiálně - bez mnohonásobného obíhání), první etapa zde nebude a vyzářená energie bude přibližně dána vztahem (4.22). Ze vztahů (4.21) a (4.22) je vidět, že účinnost přeměny klidové hmotnosti tělesa na energii gravitačních vln je poměrně vysoká, ~5,7% - je asi pětkrát vyšší než účinnost termonukleárních reakcí (vazbová energie na nejnižší stabilní kruhové orbitě černé díry je podstatně vyšší než vazbová energie nukleonů v atomovém jádře)! Jak uvidíme v následujícím §4.4, pasáž "Pohyb částic v poli rotující černé díry", u rotujících černých děr tato účinnost může být ještě mnohonásobně větší.
Plocha
horizontu a povrchová gravitace černé díry
Plocha horizontu r = 2M Schwarzschildovy černé díry
je
| A = r=2M,ňt=const.|gJJ gjj|1/2 dJ dj = 16p M2 = 16p G2 M2 /c4 . | (4.23) |
Derivováním rovnice (4.7) podle t snadno zjistíme, že zrychlení d2r/dt2 testovací částice v radiálním směru je dáno vztahem
d2r / dt2 = - 2M/r2 + L2/r3 - 3M L2/r4 .
Pro radiálně pohybující se částici (L=0) dosahuje na horizontu její zrychlení d2r/dt2 hodnotu (d2r/dt2)|r=2M= -1/4M. "Gravitační zrychlení" na povrchu černé díry (tj. na Schwarzschildově sféře) se nazývá povrchová gravitace černé díry k; pro Schwarzschildovu černou díru je povrchová gravitace
| k = 1 / 2rg = 1 / 4M = c2/4GM . | (4.24) |
Povrchová gravitace k, která je mírou intenzity gravitačního pole na horizontu černé díry, hraje důležitou roli v termodynamice černých děr a určuje rychlost kvantové evaporace černé díry, jak uvidíme v §4.6 a 4.7.
Extenze
Schwarzschildovy geometrie a černá díra
Co se týče
geometrických konstrukcí z §3.4, vztahuje se k reálné
černé díře vzniklé sférickým gravitačním kolapsem pouze
část A a B Kruskalova diagramu
Schwarzschildovy geometrie podle obr.3.17 a 3.19. Extenzí
vzniklé části A' a B' jsou ve skutečnosti nahrazeny vnitřkem
kolabující hvězdy (kde je řešení jiné) a tedy se nerealizují. Značná část úplné extenze
Schwarzschildovy geometrie nemá žádný vztah k černé díře
vzniklé gravitačním kolapsem, protože skutečná geometrie
prostoročasu je Schwarzschildovská pouze vně kolabující
hvězdy a navíc až v asymptotické budoucnosti (viz též
obr.4.18a na konci následujícího §4.4). Úplná extenze
Schwarzschildovy geometrie by mohla popisovat jen tzv. věčnou černou díru, která nevznikla gravitačním
kolapsem, ale existovala vždy jako součást
počátečních podmínek vesmíru [].
| 4.2. Hvězdná evoluce. Gravitační kolaps |
4.4. Rotující a elektricky nabité Kerrovy-Newmanovy černé díry |
| Gravitace, černé díry a fyzika prostoročasu : | ||
| Gravitace ve fyzice | Obecná teorie relativity | Geometrie a topologie |
| Černé díry | Relativistická kosmologie | Unitární teorie pole |
| Antropický princip aneb kosmický Bůh | ||
| Jaderná fyzika a fyzika ionizujícího záření | ||
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | ||