Univerzálnost – základní vlastnost a klíč k pochopení podstaty gravitace

2.2. Univerzálnost - základní vlastnost a klíč k pochopení podstaty gravitace
Zákon volného pádu, setrvačná a gravitační hmotnost
V §1.2 "Newtonův gravitační zákon" jsme si ukázali, že ze spojení zákonů klasické mechaniky se zákonem všeobecné gravitace vyplývá pozoruhodná vlastnost univerzálního působení gravitace na pohyb těles, nezávisle na jejich hmotnosti (která z pohybové rovnice vymizí). Základní klíč k pochopení podstaty gravitace tedy měl vlastně již Galilei ve svém zákonu volného pádu, podle něhož všechna tělesa padají k zemi se stejným zrychlením nezávisle na svém složení a hmotnosti. Tato specifická vlastnost gravitace, nyní nazývaná univerzálností, zůstala dlouhou dobu fakticky nepovšimnuta. Teprve Albert Einstein pochopil, že právě univerzálnost gravitačního působení je nejdůležitější vlastností gravitace, vyvodil z toho patřičné fyzikální důsledky a vybudoval tak svoji obecnou teorii relativity jakožto fyziku gravitace a vlastností prostoročasu.
Hmotnost tělesa se ve fyzikálních jevech projevuje v podstatě trojím způsobem a podle toho můžeme rozeznávat tři druhy hmotnosti:

Podle Newtonova zákona akce a reakce je v Newtonovské teorii gravitace aktivní a pasivní tíhová hmotnost stejná. Zde si zatím všimneme jen setrvačné a pasivní gravitační hmotnosti; gravitační pole budeme považovat za dané (otázku buzení gravitačního pole budeme rozebírat v §2.5 "Einsteinovy rovnice gravitačního pole").
Hmotná testovací částice se bude v gravitačním poli pohybovat podle rovnice

Univerzálnost gravitačního působení zde pak jinými slovy říká, že pro každé těleso je setrvačná a tíhová hmotnost stejná: m_s = m_t (přesněji řečeno tyto hmotnosti jsou si úměrné a jednotkové konstanty úměrnosti, tj. rovnosti obou hmotností, se dosahuje vhodnou volbou jednotek). Hmotnosti v rovnici (2.4) se pak vykrátí a pohyb v gravitačním poli je dán rovnicí d²r/dt² = gradj, která ve shodě s kritériem univerzálnosti neobsahuje žádné individuální charakteristiky pohybujícího se tělesa.

Zkušenost i přesná měření (viz níže) ukazují, že setrvačná a tíhová hmotnost je skutečně u všech těles stejná. Z Newtonovy teorie taková rovnost nevyplývá, z jejího hlediska se jedná o pozoruhodnou náhodu, která se nedá nijak vysvětlit nebo zdůvodnit. V Newtonově teorii totiž tíhová hmotnost popisuje úplně jinou vlastnost těles než hmotnost setrvačná. Tíhová hmotnost vyjadřuje schopnost daného tělesa gravitačně se přitahovat k jiným hmotným objektům, zatímco setrvačná hmotnost charakterizuje "odpor" daného tělesa vůči mechanickému zrychlení vzhledem k inerciální soustavě. Teprve Einsteinova obecná teorie relativity na základě vlastností prostoročasu zcela přirozeným způsobem vysvětluje tuto rovnost setrvačné a tíhové hmotnosti.

Skládání setrvačných a gravitačních sil
To, že gravitační a setrvačné síly mají stejnou fyzikální povahu a mohou se spolu skládat, lze názorně ilustrovat na jednoduchém myšleném pokusu (který lze bez problému realizovat i prakticky). Připravíme si železniční vagon s dokovale rovnou podlahou i stropem, se zavřenými dveřmi a okny. Pomocí lokomotivy ho na rovných hladkých kolejích rozjedeme na konstantní rychlost (třebas 80km/h). Na pohlahu vagonu položíme těžkou kulečníkouvou kouli a vypustíme balónek naplněný vodíkem nebo héliem. Dokud se bude vagón pohybovat konstantní rychlostí, bude koule ležet v určitém místě na podlaze a balónek se nad ní bude vznášet v určitém místě na stropě. Když začne vagon brzdit, začne se vlivem setrvačnosti koule po podlaze pohybovat směrem dopředu. S překvapením ale uvidíme, že balonek se po stropě začal pohybovat opačným směrem, dozadu proti pohybu vagonu. Není to však proto, že by pro balonek neplatil zákon setrvačnosti. Důvodem je, že setrvačné síly vzniklé brzděním se složily s gravitačními silami od Země - vzniklo tak "šikmé" gravitační pole, jako kdyby byl vagon nakloněný dopředu. V tomto výsledném (změněném) gravitačním poli je balonek podle standardního Archimedova zákona nadlehčován nikoli kolmo vzhůru, ale v poněkud šikmém směru a začne se pohybovat dozadu. Kdybychom tento pokus provedli ve vakuu, pohyboval by se samozřejmě balonek ve stejném směru jako koule (a nevznášel by se u stropu, ale koulel se po podlaze...).

Gravitace a kinematika pohybu
Tedy v gravitačním poli se všechna tělesa pohybují se stejným zrychlením nezávisle na svém složení a hmotnosti. Nejrůznější tělesa vržená z téhož bodu se stejnou (vektorově) rychlostí se budou pohybovat po naprosto stejných trajektoriích. Tato univerzálnost, jak si všiml Einstein, se nápadně podobá univerzálnosti kinematiky. Osvětlíme si tento klíčový aspekt gravitace na myšleném pokusu podle obr.2.3. Představme si na chvíli, že žádná gravitace neexistuje a vesmírným prostorem se volně (s vypnutými motory) pohybuje raketa, v jejíž kabině jeden pozorovatel provádí mechanické pokusy; druhý pozorovatel to sleduje zvenku přes průhlednou stěnu kabiny.
Umístí-li vnitřní experimentátor v určité "výšce" nad podlahou kabiny nehybně vedle sebe např. olověnou kuličku a peříčko, zůstanou obě tato tělesa neustále vedle sebe "viset" v klidu vůči podlaze rakety; totéž bude pozorovat i vnější pozorovatel. Jestliže se však zapálí motory a raketa se začne pohybovat s konstantním zrychlením, situace se změní. Vnitřní pozorovatel pocítí "tíži" a bude vidět, že všechna tělesa padají k podlaze kabiny. Pokud nebude vědět o zapnutých raketových motorech, prohlásí: "V mé kabině existuje silové pole, ve kterém všechna tělesa padají se stejným zrychlením". Peříčko i olověná kulička dopadnou na podlahu kabiny přesně ve stejném okamžiku, i když jejich složení i hmotnosti jsou velmi rozdílné. Vzpomene si na Galileiho zákon volného pádu a řekne: "Toto silové pole je polem gravitačním. Asi je má raketa na povrchu (nebo opřena tyčí o povrch - situace podle obr.2.4) nějaké planety, jež je zdrojem gravitačního pole které pozoruji."

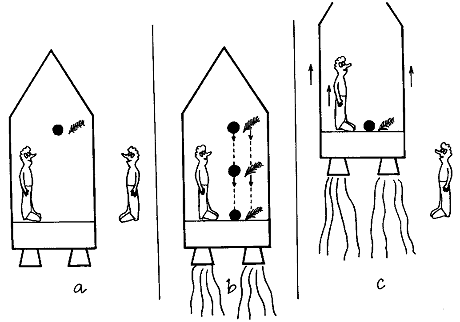
Obr.2.3. Myšlený experiment ukazující "imitaci" gravitačního pole ve zrychlené vztažné soustavě.
a) V kabině rakety volně se pohybující v prostoru bez gravitace platí Newtonův zákon setrvačnosti.
b) Po zapnutí raketových motorů bude experimentátor uvnitř kabiny pociťovat tíži a všechna tělesa (kovová kulička i peříčko) budou se stejným zrychlením padat k podlaze - z hlediska vnitřního pozorovatele panuje v kabině gravitační pole.
c) Z hlediska vnějšího pozorovatele se však o žádné "skutečné" gravitační pole v kabině nejedná, stejně zrychlené pohyby všech těles vzhledem k podlaze a stěnám kabiny jsou kinematickým efektem v neinerciální vztažné soustavě.
Pozn.: V tomto myšleném experimentu samozřejmě předpokládáme, že ve volném prostoru i uvnitř kabiny je vakuum (skafandr není zakreslen); totéž i na obr.2.4.

Vnější pozorovatel se mu však vysměje, protože on má jiné vysvětlení: "Žádné gravitační pole uvnitř kabiny neexistuje! Vnitřní pozorovatel cití tíži proto, že je spolu s kabinou urychlován silou raketových motorů. Olověná kulička i peříčko zůstávají stále na svém místě, nepadají k podlaze, ale naopak podlaha se začala se zrychlením pohybovat proti nim. Že se kulička i peříčko srazí s podlahou ve stejném okamžiku, je z kinematického hlediska samozřejmé. Tedy žádná gravitace, ale neinerciální vztažná soustava, ve které působí zdánlivé pole setrvačných sil."

Můžeme si představit i opačnou situaci (obr.2.4), kdy je kabina rakety opřena delší tyčí o povrch nějaké planety. Experimentátor uvnitř kabiny bude opět pozorovat, že všechna tělesa padají k podlaze se stejným zrychlením a může to považovat za důsledek přitomnosti gravitačního pole s univerzálními účinky. Avšak vzpomene-li si na spor s vnějším pozorovatelem v předchozím případě, může podat i jiné zdůvodnění: "Moje kabina je ve volném prostoru bez gravitace, ale jsou zapnuty raketové motory, které celou raketu rovnoměrně zrychlují. Tíže kterou cítím je setrvačným odporem hmotnosti mého těla vůči zrychlování, padání těles se stejným zrychlením je kinematický efekt v neinerciální soustavě."

Oproti předchozímu případu je zde však přece jen určitý rozdíl, který je sice zatím nepodstatný, ale v dalším bude hrát důležitou úlohu. Druhé vysvětlení bude fyzikálně ekvivalentní prvnímu vysvětlení pouze lokálně, v rámci dostatečně malé kabiny. Gravitační pole kolem planety je totiž nehomogenní - jeho intenzita slábne s výškou nad povrchem a směr je vždy do středu planety. Proto kdyby kabina byla příliš velká, zjistil by vnitřní pozorovatel, že tělesa ve větší výšce nad podlahou padají s o něco menším zrychlením než tělesa bližší podlaze a směr pádu těles v jednom koutě kabiny se poněkud liší od směru pádu v protějším koutě kabiny. Toto chování by již nebylo vysvětlitelné zrychleným pohybem kabiny bez gravitace. Pod pojmem "lokálně" budeme tedy v dalším rozumět "v dostatečně malé oblasti prostoročasu, kde je možno dané gravitační pole považovat za homogenní".

Obr.2.4. Myšlený experiment ukazující lokální nerozlišitelnost setrvačných a gravitačních sil.
a) Pozorovatel uvnitř kabiny opřené pevnou tyčí o povrch gravitující planety bude pozorovat gravitační pole s univerzálními účinky, ve kterém jak olověná kulička, tak lehké peřícko budou padat se stejným zrychlením a na podlahu dopadnou ve stejném okamžiku. Totéž by však mohl vysvětlit zapnutými raketovými motory a zrychleným pohybem kabiny; vnější pozorovatel s tím ale nebude souhlasit.
b) Po odstranění opěrné tyče bude kabina se všemi předměty uvnitř padat volným pádem, bude v ní stav beztíže. Vnější pozorovatel to samozřejmě vysvětlí volným pádem v gravitačním poli, zatímco vnitřní pozorovatel stejným právem může svou kabinu považovat za inerciální bez gravitace.

Odstraníme-li na obr.2.4 podpírající tyč, začne raketa volným pádem padat k povrchu planety. Protože všechna tělesa bez ohledu na své složení a hmotnost padají v gravitačním poli se stejným zrychlením, bude jejich vzájemné zrychlení v kabině nulové - vznikne stav beztíže. Peříčko i olověná kulička zůstávají nehybně "viset" vedle sebe ve stejné výšce nad podlahou kabiny. Vnitřní experimentátor prohlásí: "Moje kabina je inerciální soustava, která se volně pohybuje v prostoru bez gravitace." Vnější pozorovatel (spojený s planetou) však má jiné vysvětlení: "Kabina rakety a s ní všechna tělesa uvnitř padají volným pádem v gravitačním poli planety. Protože gravitační pole udílí stejné zrychlení jak peříčku, tak olověné kuličce i celé kabině, budou padat stále spolu vedle sebe a spolu s kabinou, vůči jejíž podlaze a stěnám budou tedy v klidu." Kabina volně padající v gravitačním poli je pro vnitřního pozorovatele inerciální, avšak opět jen lokálně inerciální, protože gravitační pole je nehomogenní a tedy inerciálnost je dosahována v různých místech různým zrychlením volného pádu *).
*) Všechny uvedené závěry budou platit i pro (osudu vnitřního pozorovatele daleko příznivější!) variantu, kdy místo volného pádu k povrchu zvolíme oběžný pohyb 1.kosmickou rychlostí kolem planety. Takový stav beztíže, způsobený univerzální kompenzací gravitační a odstředivé síly, si bezprostředně vyzkoušeli všichni kosmonauté.

Který z obou pozorovatelů při popsaných myšlených experimentech má pravdu? Vnitřní nebo vnější? Ať budou provádět libovolné lokální (v rámci kabiny) mechanické experimenty, bude je možno úplně stejně dobře vysvětlit jak přitomností gravitačního pole, tak působením setrvačných sil v neinerciální vztažné soustavě. V takovéto neinerciální vztažné soustavě (např. v kabině zrychlující se rakety) pozorujeme pole "setrvačných sil", které je sice pro vnějšího pozorovatele čistě kinematického původu (a tedy "zdánlivé"), avšak pro vnitřního pozorovatele je to skutečné pole mající všechny vlastnosti gravitačního pole - univerzální účinek na všechny děje. A naopak, skutečné (tj. buzené nějakou hmotou, např. v okolí planety nebo hvězdy) gravitační pole má lokálně stejné vlastnosti jako pole setrvačných sil v neinerciální soustavě.

Princip ekvivalence - univerzálnost gravitace
Setrvačnost a gravitace jsou tedy v jistém smyslu dvě stránky jedné mince: to, co se jednomu pozorovateli jeví jako setrvačnost, je pro jiného pozorovatele gravitací a naopak. Pomocí žádného lokálního experimentu od sebe nelze odlišit gravitační a setrvačné síly (neexistuje pro ně žádný "lokální indikátor"). Můžeme tak vyslovit tzv. princip ekvivalence :

Princip ekvivalence lze formulovat i jako :
Trajektorie tělesa při pohybu v gravitačním poli závisí výhradně na jeho počáteční poloze a rychlosti, nikoli na jeho struktuře, složení či jiných vlastnostech.

Důsledkem principu ekvivalence je nerozlišitelnost mezi gravitačními a setrvačnými jevy: zrychlení a gravitace se projevují stejně, takže teorie zrychleně se pohybujících soustav (což je obecná teorie relativity v užším smyslu) je zároveň i teorií gravitace. Fakt ekvivalence setrvačné a tíhové hmotnosti, který se dlouhou dobu pokládal jen za shodu okolností, povýšil Einstein na základní zákon gravitace a východisko své obecné teorie relativity.
Pozn: Někdy se rozlišijí se dvě či tři úrovně principu ekvivalence:
- Slabý princip ekvivalence - gravitační působení těles nezávisí na jejich hmotnosti a složení, gravitační a setrvačná hmotnost těles je ekvivalentní (je vzájemně úměrná, při vhodné volbě jednotek je shodná).
- Silný princip ekvivalence se vztahuje nejen na mechanické, ale i na elektromagnetické děje. Gravitační účinky by měla mít i hmotnost odpovídající energii elektromagnetického pole (jakož i dalším interakcím), viz níže.
A.Einstein na začátku budování OTR vyšel ze slabého principu ekvivalence, postupně pak přešel k jeho rozšíření i na elektromagnetické děje. Současná OTR je založena na silném principu ekvivalence.
Princip ekvivalence vyjadřuje působení "již hotového" gravitačního pole na hmotné objekty. V 2.5 "Einsteinovy rovnice gravitačního pole" si jej zobecníme na univerzálnost buzení gravitačního pole veškerou hmotou-energií, nezávisle na jejím složení a povaze. To završuje obecnou teorii relativity jakžto fyziku gravitace a (zakřiveného) prostoročasu.

Vzniká důležitá otázka, zda univerzálnost gravitačního působení se omezuje jen na jevy mechanické, nebo platí pro všechny fyzikální děje. Nepřímou indicii ve prospěch druhé možnosti nám dává již to, že tělesa velmi rozdílného složení padají v gravitačním poli se stejným zrychlením. Toto Galileiho zjištění bylo ověřeno pokusy Eötvösovými (na počátku našeho století) s přesností 10^-8, Dickeho a kol. (r.1963) s přesností 10^-11 [220] a Braginského a kol. (r.1977) s přesností 10^-12 [31]. Tělesa různého složení mají rozdílné zastoupení elektronů, protonů a neutronů, rozdílný podíl hmotnosti např. elektromagnetického původu. Naměříme-li tedy stejnou setvačnou a gravitační hmotnost pro tělesa rozdílného složení, můžeme říci, že gravitační pole má stejný účinek na protony, neutrony, elektrony i na samotné elektromagnetické pole. Působení gravitačního pole na světlo, resp. na elektromagnetické vlnění, bylo navíc přímo experimentálně ověřeno - gravitační spektrální posuv (§2.4 "Fyzikální zákony v zakřiveném prostoročase", pasáž "Gravitační frekvenční posun") a zakřivování světelných paprsků v gravitačním poli (§4.3 "Schwarzschildovy statické černé díry", pasáž "Odklon částic a světla ve Schwarzschildově poli").
Setrvačná hmotnost atomů je dána především následujícími složkami :
a) Klidová hmotnost protonů a neutronů; b) Klidová hmotnost elektronů; c) Vazbová potenciální energie protonů a neutronů v atomovém jádře způsobená silnými jadernými interakcemi; d) Potenciální elektrostatická energie elektronů a elektrostatická energie jádra; e) Kinetická energie elektronů, protonů a neutronů; f) Efekty související s polarizací vakua (tvorba virtuálních párů částic-antičástic); g) Energie slabých interakcí mezi nukleony v jádrech; h) Gravitační energie.
Příspěvky silné, elektromagnetické, slabé a gravitační interakce k hmotnosti objektu jsou v poměru :
- pro atom asi 1 : 10^-2: 10^-12 : 10^-40 ; - pro makroskopická tělesa zhruba 1 : 10^-2 : 10^-12 : 10^-29 ; - pro hvězdu hmotnosti slunce 1 : 10^-2 : 10^-12 : 10^-16 .
Měřeními Eötvösovými, Dickeho a Braginského ověřená (s přesností 10^-12) rovnost setrvačné a gravitační hmotnosti pro platinu (78 protonů a elektronů, 117 neutronů) a hliník (13 protonů a elektronů, 14 neutronů) pak při podrobnějším rozboru ukazuje, že princip ekvivalence je ověřen pro klidovou hmotnost protonů a neutronů s přesností 10^-11 a pro hmotnost elektronů asi 10^-8. Pro hmotnost související s jadernou vazbovou energií nukleonů, kinetickou energií nukleonů v jádře (související s Pauliho principem) a s elektrostatickou energií jádra pak platí ověření principu ekvivalence s přesností ~ 10^-9 až 10^-10. Pro potenciální a kinetickou energii elektronů vychází přesnost 10^-6 až 10^-7.
Antihmota: gravituje nebo antigravituje ?
Základní pilíř Einsteinovy OTR princip ekvivalence říká, že působení gravitace nezáleží na složení a struktuře hmoty. Gravitační interakce mezi hmotou a antihmotou by měla být identická. Objekt z antihmoty tak bude v gravitačným poli Země padat se stejným zrychlením jako těleso z hmoty (zde na povrchu Země bude jeho pád probíhat se známou hodnotou gravitačního zrychlení 9,81 m/s²).
Zákon volného pádu a princip ekvivalence je velmi přesně ověřen pro běžnou hmotu složenou složenou z atomů, tvořených elektrony, protony a neutrony. Logicky z toho usuzujeme, že platí i pro jednotlivé elementární částice - běžné (elektrony, protony, neutrony), a pravděpodobně i pro exotické (neutrina, mesony, hyperony, ...). Přímé experimentální ověření gravitačních vlastností u jednotlivých izolovaných částic je však velmi obtížné (ne-li nemožné), neboť tyto částice se pohybují vysokými rychlostmi a vykazují elektromagnetické a silné interakce s okolím, podstatně silnější než gravitační (je diskutováno v pasáži "Antičástice - antiatomy - antihmota - antisvěty" , odstavec "Umělá výroba antihmoty" v knize "Jaderná fyzika a fyzika ionizujícího záření").
Jak je tomu ale u antičástic (pozitrony, antiprotony, antineutrony), z nich složených "antiatomů" a obecně u antihmoty *) ? Z experimentů na urychlovačích víme, že částice a antičástice mají stejnou setrvačnou hmotnost. Bude však antihmota gravitovat nebo antigravitovat? Z rozboru pravděpodobností krátkodobé existence virtuálních elektron-pozitronových, proton-antiprotonových a jiných dvojic částic ("polarizace vakua") plyne, že výsledky Eötvösových, Dickeho a Braginského měření potvrzují platnost principu ekvivalence pro běžné antičástice (jako je pozitron a antiproton) s přesností ~ 10^-5 až 10^-6. Rozhodně tedy u antihmoty nelze očekávat "antigravitaci" - žádné "padání nahoru"! Antihmota bude normálně gravitovat - zatím jen není přesně změřeno, zda se stejnou nebo mírně odlišnou gravitační konstantou než běžná hmota..?..
*) O problematice antihmoty viz §1.5, pasáž "Antičástice - antiatomy - antihmota - antisvěty" v knize "Jaderná fyzika a fyzika ionizujícího záření".
Experimentální nejistoty o gravitačních vlastnostech antičástic a antihmoty ponechávají určitý prostor pro hypothézy o zlehka odlišné gravitační síle antihmoty od běžné hmoty. V některých alternativních či zobecněných teoriích gravitace se zavádějí další pole a interakce (např. v Kaluzově-Kleinově 5-rozměrné unitární teorii gravitace+elektromagnetismu - §B.2, část "5-rozměrná gravitace-elektromagnetismus" ), které při kvantovém přístupu mohou být dány do souvislosti s intermediálními kvanty-částicemi. Vedle standardního "tenzorového" gravitonu o spinu 2 se vyskytuje "vektorový" gravifoton spinu 1 a též "graviskalár" o spinu 0. Tyto příspěvky mohou být zdrojem narušení principu ekvivalence. Důsledkem by bylo, že gravitační potenciál mezi dvěma statickými hmotnými objekty m₁ a m₂ ve vzdálenosti r by měl anomální průběh :
V(r) = -G . ^m1^.^m2/_r . (1+ F.e^-^r/d) ,
kde kromě standardního Newtonova gravitačního potenciálu G.m₁.m₂/r vystupuje i Yukawowský potenciál e^-^r/d s dosahem d. F je škálovací konstanta této doplňkové interakce, která by se hypoteticky mohla "+/-" zlehka lišit pro hmotu a antihmotu ..?..
Lze tedy říci, že princip ekvivalence je s poměrně vysokou přesností ověřen pro silné a elektromagnetické interakce. U slabých interakcí, jejichž příspěvek k celkové hmotnosti těles je relativně velmi malý (řadově zhruba 10^-12), přesnost zmíněných experimentů nepostačuje ke zcela spolehlivému ověření principu ekvivalence, avšak jisté indicie ve prospěch jeho platnosti pro slabé interakce zde existují [105]. Co se týče principu ekvivalence pro gravitační interakci, zmíněné pokusy nedávají žádnou informaci o gravitačních vlastnostech gravitační energie (tj. o tom, zda gravitační energie přispívá stejně k setrvačné i tíhové hmotnosti), protože její podíl na celkové hmotnosti běžných makroskopických těles je zcela nepatrný (~10^-30). Avšak s rostoucí hmotností a kompaktností se relativní příspěvek gravitační energie k celkové hmotnosti tělesa zvyšuje. Pro velké planety jako je Jupiter již činí 10^-8, pro Slunce 10^-6; pro hmotné kompaktní útvary jako jsou bílí trpaslíci nebo neutronové hvězdy je ještě podstatně vyšší. Srovnání skutečných astronomicky pozorovaných trajektorií takových těles s dráhami předpovězenými nebeskou mechanikou, popř. relativistickou astrofyzikou, potvrzují platnost principu ekvivalence i pro gravitační energii, zatím sice s ne příliš vysokou přesností...

Kosmické ověření zákona volného pádu
Nynější kosmická technika umožňuje, aspoň v principu, ověřovat princip ekvivalence v přímé návaznosti na Galileiho pokusy s volným pádem. Místo kratičké dráhy z legendární nakloněné věže v Pise by se zde však použilo velmi dlouhého "volného pádu" při mnohonásobném obíhání kosmické sondy kolem Země. Ideově je princip takového uspořádání vidět z výše uvedeného obrázku 2.3a. V kabině satelitu volně obíhajícího v gravitačním poli kolem Země jsou v beztížném stavu volně umístěna dvě zkušební tělesa rozdílného složení. Pokud platí princip ekvivalence, budou obě tělesa obíhat po stejné geodetické dráze, jejich vzájemná poloha se nebude měnit ani po velkém množství oběhů. Pro přesné ověření by samozřejmě uspořádání nemohlo být tak triviální jako na obr.2.3a, kde by se projevovalo nesymetrické gravitační přitahování mezi zkušebními tělesy, předměty v kabině a s jejími stěnami. Uspořádání by muselo být přesně symetrické - koncentrické či koaxiální, poloha zkušebních těles by se hodnotila nikoli vizuálně, ale pomocí elektronického snímání.
Experiment toho druhu navrhli v r.1972 odborníci z university ve Stanfordu pod vedením P.W.Wordena pod názvem STEP (Satellite Test Equivalence Principle). S použitím precizní technologie a citlivých metod snímání polohy zkušebních těles by tímto způsobem mohl být ověřen princip ekvivalence s přesností až 10^-18. Zatím byl vytvořen pouze model zařízení, vlastní experiment na oběžné dráze bude snad realizován po r.2000.
Co nejpřesnější ověření platnosti principu ekvivalence pro všechny druhy interakcí a v co nejširším spektru fyzikálních situací je velmi důležité, protože na zcela přesné platnosti principu ekvivalence pro všechny fyzikální jevy (tj. na absolutní univerzálnosti gravitační interakce) stojí celá obecná teorie relativity jakožto fyzika prostoročasu a gravitace. Sebemenší spolehlivě zjištěná odchylka by touto teorií otřásla v samotných základech..!..

Gravitace - jediná absolutně univerzální síla
Gravitace působí na všechna tělesa, ale i na energii - na všechna pole, protože fyzikální pole má energii a tím také hmotnost, která může "gravitovat". Gravitace je tedy jediná univerzální síla, která působí absolutně na všechno na tomto světě!
Univerzálnost gravitačního působení je základní vlastností, kterou se gravitace liší od všech ostatních druhů sil v přírodě. Pole gravitačních a setrvačných sil jsou ekvivalentní pro všechny fyzikální děje, platí pro ně stejné fyzikální zákony a tedy jsou od sebe lokálně zcela nerozlišitelné. Z hlediska obecné teorie relativity lze říci, že setrvačné a gravitační síly mají stejnou (společnou) fyzikální podstatu; v dalších odstavcích uvidíme, že touto společnou podstatou jsou geometrické vlastnosti prostoročasu.
Univerzálnost gravitace nám umožnila převést si gravitaci na kinematiku. Kinematika je vyjádřením geometrických vlastností prostoru a času. Můžeme tedy již dopředu očekávat, že jestliže gravitace mění kinematiku, bude tím měnit i geometrické vlastnosti prostoru a času. Tvrzení o univerzálním působení gravitace na všechny fyzikální jevy, vyjádřené v Einsteinovu principu ekvivalence, tak má dalekosáhlé důsledky a je základem Einsteinovy obecné teorie relativity.

Obecná teorie relativity a podstata gravitace
Na otázku, zda obecná teorie relativity vysvětluje podstatu gravitace, nelze odpovědět jinak než: ano i ne! Obecná teorie relativity sice převedla gravitační působení na setrvačný pohyb - sloučila gravitaci a setrvačnost, ztotožnila je s geometrickými vlastnostmi prostoročasu. Zákony kterými se řídí gravitace převádí na zákony, kterými se řídí prostoročas. Byly tak objeveny sjednocující vztahy mezi dříve oddělenými jevy. Na otázku po příčině gravitačního působení odpovídá obecná teorie relativity zakřiveným prostoročasem, avšak nevysvětluje, proč tělesa ve svém okolí zakřivují prostoročas? Obecná teorie relativity ukazuje jak, ale ne proč. Úplnou odpověď (avšak z opačné strany) by snad mohla dát jedině důsledná unitární teorie pole - viz jednotlivé kapitoly Dodatku B "Unitární teorie pole". K nejhlubšímu prazákladu všech "proč?" a "jak dál?" se ale asi stejně nedostaneme ..?..

Gravitace, černé díry a fyzika prostoročasu :
Gravitace ve fyzice	Obecná teorie relativity	Geometrie a topologie
Černé díry	Relativistická kosmologie	Unitární teorie pole
Antropický princip aneb kosmický Bůh
Jaderná fyzika a fyzika ionizujícího záření
AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie


2.1. Zrychlení a gravitace z hlediska speciální teorie relativity		2.3. Lokální princip ekvivalence

Univerzálnost gravitace – obecná teorie relativity – podstata gravitace