Topologický tvar prostoročasu

Kapitola 3
GEOMETRIE A TOPOLOGIE PROSTOROČASU
3.1. Geometricko-topologické vlastnosti prostoročasu
3.2. Minkowského rovinný prostoročas a asymptotická struktura
3.3. Cauchyova úloha, příčinnost a horizonty
3.4. Schwarzschildova geometrie
3.5. Reissnerova-Nordströmova geometrie
3.6. Kerrova a Kerrova-Newmanova geometrie
3.7. Prostoročasové singularity
3.8. Hawkingovy a Penroseovy teorémy o singularitách
3.9. Nahé singularity a princip "kosmické cenzury"

3.1. Geometricko-topologické vlastnosti prostoročasu

Gravitační pole je projevem geometrických vlastností prostoročasu - to je stanovisko obecné teorie relativity ke kterému jsme dospěli v předchozí kapitole. Je proto užitečné studovat vlastnosti prostoročasu z hlediska geometrického a topologického. Získají se tím důležité poznatky obecné platnosti o struktuře prostoročasu a tím i o průběhu fyzikálních dějů pod univerzálním vlivem gravitace. Poznání geometrické struktury prostoročasu je nejen zajímavé samo o sobě, ale má zásadní význam ve fyzice černých děr (viz kap.4) a v kosmologii (kapitola 5).
Pozn.: Topologické přístupy a metody do studia vlastností prostoročasu v obecné teorii relativity zavedl v 60.letech Roger Penrose.

T o p o l o g i e
Než přistoupíme k vlastnímu studiu geometrických a topologických vlastností prostoročasu, zhruba si nastíníme co se rozumí topologií a jaký je její vztah ke geometrii. Podrobný výklad topologie z matematické stránky je v řadě monografií, např. [151], [155], [60], my zde nastíníme jen základní myšlenky. Geometrie (řec. geos=zemský,pozemský, metria=měření - původně tedy "zeměměřičství") vznikla jako nauka o měření (porovnávání) těles - jejich délek, tvarů, úhlů, ploch, objemů, vzdáleností a pod.*). Přitom "scénou" v níž se taková měření provádějí je prostor a některé společné geometrické vlastnosti měřených těles prohlašujeme za geometrické vlastnosti tohoto prostoru. Prostor je pojem, který vyjadřuje vzájemné poziční vztahy jednotlivých předmětů a jejich částí - vznikl abstrakcí z reálných hmotných předmětů.
*) V průběhu vývoje geometrie postupně přerostla svůj původní význam a sloučila se se všemi těmi částmi matematiky, v nichž hraje nějakou úlohu spojitost. Do těchto obecných matematických struktur vnáší geometrie svoji velikou přednost, kterou je její názornost. Na dvojrozměrných analogiích, řezech, diagramech vnoření, které obsahují téměř všechny důležité rysy vícerozměrných prostorových útvarů, lze názorně ilustrovat mnohé konstrukce, které si v jejich obecné verzi nedovedeme přímo představit - např. různé transformace a zobrazení lze interpretovat jako příslušné deformace (zprohýbání, roztažení, slepení) dvojrozměrných ploch.
  Vlastnosti prostoru můžeme rozdělit na kvantitativní - metrické (souvisejicí s měřením vzdáleností, úhlů, ploch) - a na kvalitativní - topologické (řec. topos=místo, logos= sbírat, studovat, počítat). Topologie, která se někdy též nazývá "kvalitativní geometrie", je velmi zhruba řečeno to, co zbude z geometrie, když si z ní odmyslíme všechno co má nějakou velikost (a v tomto smyslu i konkrétní tvar) *). Zabývá se kvalitativně tím, jak jsou body, množiny a objekty vnitřně a mezi sebou spojeny (propojeny), či jak spolu sousedí. Mnohé geometrické problémy totiž nezávisejí na přesném tvaru a velikosti objektů, ale jen na vnitřních či vnějších vztazích, jaké mezi sebou tyto objekty mají.
*) A opačně, geometrie je topologie opatřená pojmy vzdálenosti a úhlu - zavedením metriky.
  Topologie studuje takové vlastnosti geometrických útvarů, které se nemění při spojitých transformacích ("deformacích") - tj. různých roztaženích, stlačeních, otočeních nebo zprohýbáních *), za podmínky že nedochází k žádným roztržením nebo spojením různých částí; "blízké" body se transformují opět v "blízké" body. Není důležité, zda je předmět malý nebo velký, kulatý nebo hranatý, protože deformací se tyto vlastnosti mohou změnit. Z hlediska topologie je důležité, zda je daný objekt celistvý a spojitý, zda obsahuje otvory, "průchody, tunely", je jednorozměrný, plošný či prostorový, příp. vícerozměrný. Jinak řečeno, topologie systematizuje naše intuitivní představy a zkušenosti o "možném" a "nemožném" v prostoru, jakými cestami se dá či nedá do určitých míst "dostat".
*) Můžeme si to představit tak, že daný útvar je vyroben z plasteliny a my ho můžeme hladce a spojitě přetvarovat na jiný útvar, aniž bychom ho museli přetrhnout, proděravět či spojit nějaké části (viz níže). Při deformacích musíme zachovat "sousedství" jednotlivých bodů, jejich okolí.
  Z hlediska topologie jsou kružnice, elipsa, čtverec nebo trojúhelník "stejné" (jsou to jednorozměrné objekty, které dělí plochu na dvě části - vnitřní a vnější), jsou vzájemně homeomorfní *) - použitím topologického zobrazení lze deformovat kružnici na elipsu, čtverec nebo trojúhelník a naopak. Tím spíše jsou si topologicky ekvivalentní kružnice o různých poloměrech, elipsy s různou excentricitou, nebo čtverce s různými délkami strany. Podobně koule, elipsoid, krychle a jehlan. Takové vzájemně homeomorfní útvary jsou jen různými metrickými variantami téže topologické množiny bodů. Topologie tedy studuje nejzákladnější globální vlastnosti prostoru (a geometrických útvarů v něm) jako je souvislost, spojitost, počet rozměrů, omezenost nebo neomezenost a pod. V tomto smyslu je tedy topologie hlubší a obecnější než to, co se běžně pokládá ze geometrii. Níže uvidíme příklady prostorů, které mají stejné geometrické (metrické) vlastnosti, avšak zcela odlišné vlastnosti topologické.
*) Z řec. homeos=stejný, morphe=tvar. Homeomorfní topologické množiny a útvary jsou z pohledu topologie stejné, mají stejný "tvar" a vlastnosti. Homeomorfismus, zvaný též izomorfismus topologických prostorů, bude definován níže.
Topologické podobnosti, modelování a transformace 
Topologie se nezajímá o konkrétní "tvary", zakřivení, velikosti, ale jen o vnitřní pospojování jednotlivých částí či bodů zkoumaného útvaru. Přibližme si to na situaci z běžného života.
    Uděláme si malou podvečerní siestu s kávou či čajem a vanilkovými věnečky. Malý kávový hrníček držíme za ouško, popíjíme kávu a zakusujeme věnečky. Když se zadíváme na předměty našeho posezení, šálek na kávu má na první pohled zcela odlišný tvar, velikost, zakřivení, než věneček. Avšak kdyby byl hrníček z dokonale tvárné plasteliny, může být hladce a spojitě přetvarován na tvar věnečku, bez trhání či proděravění plasteliny (nejprve bychom stlačili stěny hrnečku dolů do dna a pak vzniklý plochý disk stlačili zboku až by splynul s ouškem; nakonec zůstane jen ouško toroidního tvaru, ekvivalentní věnečku). A naopak, z plastelinového věnečku bychom mohli opět hladce a spojitě vymodelovat hrníček s ouškem. Kdybychom měli hrníček bez ouška (jaký bývá na japonský zelený čaj), měl by jednoduchou topologii kvádru - byl by tvarově ekvivalentní třebas kostce nugátové čokolády, nebo bychom ho mohli vymodelovat do tvaru tabulky čokolády či kulatého bonbónu (postupovali bychom stejným způsobem jako v předchozím případě: stěny hrnečku bychom stlačili ke dnu a vzniklý disk pak přetvarovali do kvádru či koule). Avšak hrníček bez ouška nikdy spojitě nepřetvarujeme na hrníček s ouškem, stejně tak tabulku čokolády či nugátovou kuličku nepřemodelujeme na věneček - kvádr či kouli homeomorfně nelze přetransformovat na toroid!

Ukázka, jak spojité deformace (homeomorfické zobrazení) mohou přetvarovat předměty (bodové množiny) do různých topologicky ekvivalentních tvarů.
Nahoře: Kávový hrníček s ouškem je topologicky ekvivalentní toroidu - vanilkovému věnečku.
Dole: Hrníček bez ouška je topologicky ekvivalentní kvádru či kouli - tabulce čokolády nebo kulatému nugátovému bonbónu.

Ač se to zdá na první pohled zvláštní, právě to malé ouško je nositelem celkové toroidní topologie hrnečku! Podobně v §3.5 "Reissnerova-Nordströmova geometrie" a §3.6 "Kerrova a Kerrova-Newmanova geometrie" uvidíme, že u některých speciálně zakřivených prostoročasů jsou poměrně drobné struktury uvnitř horizontu nositeli složité globální topologie prostoročasu, dokonce i celého vesmíru či více vzájemně propojených vesmírů..!..

Množiny a zobrazení
Ústředním abstraktním pojmem, tvořícím základ matematiky, je množina - soubor objektů, které jsou přesně určené buď svým výčtem ("seznamem"), nebo charakteristickou vlastností. Pro každý objekt x lze jednoznačně stanovit, zda do dané množiny X patří - značí se xÎX, nebo do ní nepatří: xĎX. Tyto objekty patřící do množiny se nazývají prvky množiny. Prvky množin může být v běžném životě v zásadě cokoliv (jablka, hrušky, stromy, lidé,...), v matematice to bývají většinou čísla, body geometrických útvarů, funkce a transformace, řešení rovnic. Množina neobsahující žádný prvek se nazývá prázdná 0. Část množiny A se nazývá její podmnožina B - je to taková množina, jejíž všechny prvky jsou zároveň i prvky množiny A; značí se BÍA. Každá množina je zároveň svou podmnožinou. Podmnožina B, která není rovna výchozí množině A, se nazývá její vlastní podmnožina, značí se BĚA. Relace "Í,Ě" (jsou analogické "Ł,<") mezi množinou a podmnožinou se nazývá inkluze (lat. inclusio=zahrnutí - začlenění do nějakého celku).
Uvedené inkluzní symboly "Ě,Í" se v množinových aplikacích (kde se většinou používají vlastní podmnožiny), často nerozlišují. V našem textu budeme symbolem "Ě" označovat obecně jakoukoli podmnožinu.
  Množiny se obvykle nahlížejí intuitivně, avšak ve fundamentální matematice se vlastnosti množin formalizují pomocí axiomatické teorie množin.
  Mezi dvěma množinami X a Y se definují základní operace sjednocení XČY (což je množina obsahující dohromady všechny prvky z X a všechny prvky z Y) a průnik XÇY (je to množina prvků společně patřících do obou množin X i Y) (další někdy zaváděné operace, jako je rozdíl dvou množin či jejich symetrická diference a doplněk jedné množiny v druhé, zde nebudeme používat). Množiny s prázdným průnikem (XÇY=0) se označují jako vzájemně disjunktní.
  Ke vzájemnému porovnávání množin slouží operace (binární relace) zobrazování. Zobrazení j : X®Y množiny X do množiny Y znamená, že každému bodu xÎX jednoznačně přiřadíme určitý bod j(x) ş y ÎY. Prvek x se nazývá vzor a prvek y jeho obraz. Identifikátor zobrazení j se též nazývá funkce, množina vzorů X se nazývá definiční obor a množina obrazů Y obor hodnot funkce. Identifikátor zobrazení j (funkci) lze definovat či zapsat pomocí tabulky, vzorce, algoritmu výpočtu, grafu, nomogramu. "Opačné" či "zpětné" zobrazení j^-1 : Y®X se nazývá inverzní zobrazení (nelze ho však vždy vytvořit).
  Podle jednoznačnosti zobrazení se rozlišují tři druhy: Zobrazení je surjektivní (na množinu), když každý obraz má alespoň jeden vzor. Injektivní, neboli prosté zobrazení každým dvěma různým vzorům přiřazuje dva různé obrazy; k injektivnímu (prostému) zobrazení tedy lze vytvořit zobrazení inverzní. Pokud je zobrazení zároveň surjektivní i injektivní, jedná se o vzájemně jednoznačné zobrazení zvané též bijektivní - každý vzor má právě jeden obraz a každý obraz právě jeden vzor.
Čísla a číselné množiny 
Základními abstraktními objekty, sloužícími ke kvantitativnímu modelování přírodní reality v běžném životě i matematice, jsou čísla. Z matematického hlediska rozeznáváme několik druhů čísel:
l Přirozená čísla jsou kladná celá čísla 1,2,3,4,..... Jsou nejobvyklejšími čísly s nimiž se setkáváme i v běžném životě při obyčejném "číslování", určování pořadí, stanovení množství něčeho, "kupeckém počítání".
l Celá čísla -3,-2,-1,0,+1,2,3,.... jsou doplněním přirozených čísel o záporná čísla (a též o nulu, která se obvykle nezařazuje mezi přirozená čísla), kterými modelujeme snižování, chybějící množství, "dluh", hodnoty menší než nula a pod. Celá (a samozřejmě i přirozená) čísla se dělí na sudá (beze zbytku dělitelná číslem 2) a lichá (u nichž po dělení 2 zůstává zbytek 1).
l Racionální čísla jsou taková, která vznikají jako podíl dvou celých čísel (z lat. ratio=podíl) - dají se zapsat ve tvaru zlomku a/b dvou celých čísel a, bą0. Výsledkem může být buď celé číslo (např. 6/2), nebo neceločíselná hodnota vyjádřená buď jednoduše (např. 1/4 =0,25), nebo periodickým desetinným číslem (např. 5/3 = 1,666...).
l Iracionální čísla jsou obecně taková, která nelze vyjádřit jako podíl dvou celých čísel. Rozdělují se dále někdy na dvě podskupiny:
    - Algebraická iracionální čísla jsou taková, která jsou řešením (kořenem) nějakého polynomu s racionálními koeficienty. Typickým příkladem jsou odmocniny, např. Ö2 je řešením algebraické rovnice x²-2 = 0.
    - Transcendentní čísla jsou taková, která nejsou řešením žádné algebraické rovnice s racionálními koeficienty. Mohou být vyjádřena pouze nekonečným rozvojem. Typickým příkladem je Ludolfovo číslo p nebo Eulerovo číslo e (základ přirozených logaritmů). Název pochází z lat. transcendent = přesahující rozumové chápání.
l Reálná čísla jsou sjednocením všech racionálních a iracionálních čísel, jsou to všechna čísla, která mohou být zapsána konečným či nekonečným matematickým rozvojem. Reálná čísla tedy obsahují všechna výše uvedená přirozená, celá, racionální a iracionální čísla, včetně transcententních. Pomocí nich lze v zásadě kvantifikovat všechny děje "reálně" probíhající v přírodě.
l Imaginární a komplexní čísla. Komplexní čísla formálně zobecňují reálná čísla tím, že zavádějí odmocniny ze záporných čísel (které v oboru reálných čísel nelze definovat, neexistují). Základní ideou je zde zavedení imaginární jednotky i, pro jejíž druhou mocninu platí vztah i² = -1. Jinými slovy, imaginární jednotka je odmocninou z -1: i = Ö-1. Komplexní čísla jsou pak jakousi "kombinací" reálných a imaginárních čísel, zapisují se ve tvaru c = a + b.i, kde a a b jsou reálná čísla. Číslo a se nazývá reálná část komplexního čísla c, číslo b jeho imaginární část. V oboru komplexních čísel má každá algebraická rovnice příslušný počet řešení, odpovídají stupni polynomu. I když komplexní čísla nemají přímý fyzikální význam, jsou velmi užitečným nástrojem pro modelování řady procesů, kde vystupují periodické goniometrické funkce (elektrické obvody, vlnění, kvantová fyzika). Při našem výkladu teorie relativity a gravitace komplexní čísla až na výjimky používat nebudeme...
Mohutnost množin
Základní vlastností množin je jejich "velikost", počet prvků, rozsah - jak je množina "mohutná". Velikost množiny se charakterizje pojmem zvaným mohutnost. Množiny obsahující jen omezený (konečný) počet prvků se nazývají konečné množiny - lze u nich určit počet prvků a vyjádřit jej přirozeným číslem. Mohutnost konečných množin je rovna počtu prvků. Nekonečné množiny můžeme podle "velikosti" rozdělit na dvě kategorie:
¨ Spočetná množina je taková, kterou lze vzájemně jednoznačně zobrazit na některou podmnožinu přirozených čísel - prvky množiny lze "spočítat" pomocí jejich očíslování přirozenými čísly; každá konečná množina je tedy automaticky spočetná. Mohutnost nekonečných spočetných množin se označuje symbolem "alef-0" neboli c₀ (písmeno c patří zrcadlově obrácené). Základním příkladem spočetnosti jsou množiny přirozených a racionálních čísel (dá se dokázat, že mají stejnou mohutnost). Dokonce i množina algebraických iracionálních čísel je spočetná.
¨ Nespočetná množina je taková, kterou nelze vzájemně jednoznačně zobrazit na žádnou podmnožinu přirozených čísel - její prvky nelze "spočítat" očíslováním ani pomocí nekonečného počtu přirozených čísel. Základním příkladem nespočetnosti je množina reálných čísel; její mohutnost se označuje symbolem "alef-1" neboli c₁ - mohutnost kontinua. Stejnou mohutnost má i množina všech iracionálních čísel se zahrnutím transcendentních čísel - právě tato čísla jsou zodpovědná za nespočetnost. V matematice se zavádějí ještě mnohem "nekonečnější" či "nespočetnější" množiny. Podrobnější diskusí mohutnosti množin a analýzou povahy nekonečna v matematice a fyzice se zabýváme níže v části "Nekonečno v prostoročase".
  Pro naše účely modelování geometrické a topologické struktury prostoročasu v relativistické fyzice vystačíme s množinami o mohutnosti c₁, odpovídající množině reálných čísel. Některé vlastnosti složitých tzv. fraktálních množin a útvarů (označovaných někdy jako "matematická monstra") jsou stručně diskutovány v §3.3, část "Determinismus-náhoda-chaos?").
Matematické struktury na množinách
Aby množiny mohly sloužit pro modelování zákonitostí našeho světa, na obecných abstraktních množinách se zavádějí matematické struktury - dodatečné informace o vlastnostech a vztazích mezi prvky. Mohou to být algebraické operace jako je sčítání a násobení (tak vznikají především grupy - §B.6 "Sjednocování fundamentálních interakcí. Supergravitace. Superstruny.", část "Symetrie ve fyzice - Grupy transformací, kalibrační grupy", dále okruhy, tělesa, vektotové prostory, ...), relace uspořádání a logické operace (rovnosti a nerovnosti, uspořádané množiny, Booleovy algebry,...), zavedení metriky pro stanovení "vzdáleností" (metrické prostory), topologie - viz níže. Vlastní množina, na které je zavedena taková struktura, se někdy nazývá nosná množina.
  Isomorfismus (řec. isos=stejný,shodný, morfe=tvar) je zobrazení mezi dvěma množinami se stejnou strukturou, které je vzájemně jednoznačné (bijektivní) a zachovává všechny vlastnosti zavedené matematickou strukturou na množině. Tedy každému prvku první množiny odpovídá právě jeden prvek struktury druhé, přičemž toto přiřazení zachovává strukturní vztahy k ostatním prvkům. Pokud existuje takové zobrazení - množiny a struktury jsou izomorfní - mají obě množiny z hlediska struktury totožné vlastnosti. U izomorfismu se uvádí, k jaké struktuře se vztahuje, např. metrický či grupový isomorfismus. My se budeme v této kapitole zabývat topologickým isomorfismem, zvaným homeomorfismus.

Topologické prostory a jejich zobrazení
Část matematiky zvaná topologie, která vychází z upřesňování intuitivních pojmů "spojitost", "blízkost", "limita", se zabývá jakýmsi "místopisem" bodových množin. Studuje kvalitativní pojem "blízkosti" jednotlivých bodů tím, že specifikuje co se rozumí okolím každého bodu množiny. Výchozí krok množinové topologie spočívá v tom, že danou nosnou množinu pokryjeme vhodnou soustavou podmnožin.
Říkáme, že na (nosné) množině X je dána topologie, je-li určena soustava U podmnožin UĚX taková, že platí:
a) Průnik konečného počtu množin z U patří rovněž do U (U₁ÇU₂ÎU);
b) Sjednocení libovolné soustavy množin z U patří rovněž do U.
  Množina X (která je rovněž prvkem U) spolu s danou topologií se nazývá topologický prostor (X,U). Soustava U se nazývá topologie na množině (X,U). Množiny UÎU se nazývají otevřené množiny. Okolím U(x) bodu xÎX pak rozumíme otevřenou množinu UÎU, která bod x obsahuje. Pro každý bod xÎU patří do této otevřené množiny i nějaké jeho okolí. Otevřená množina tedy s každým svým bodem obsahuje i body, které jsou "dostatečně blízko" něho.
  Hranice množiny X představuje množinu všech takových prvků z X, jejichž každé okolí obsahuje alespoň jeden bod dané množiny X a alespoň jeden bod mimo množinu X. Tato hranice se značí ¶X. Uzavřená množina je taková, která obsahuje svou hranici.
  Zavedení topologie umožňuje specifikovat další důležité vlastnosti množinového zobrazení. Zobrazení j topologického prostoru (X, U) do prostoru (Y, V) se nazývá spojité zobrazení, jestliže ke každému bodu x ÎX a ke každému okolí V ÎV bodu j(x)ÎY existuje okolí U tak, že j(U)ĚV. Je to tedy zobrazení, které dostatečně blízké body zobrazuje zase blízko sebe - zachovává okolí bodů.
Jedná se o topologické zobecnění spojité funkce v matematické analýze, jejíž graf nemá ostré skoky a dá ze znázornit jako souvislá křivka. Říkáme, že funkce f(x) je spojitá v bodě x=x_o, jestliže ke každému kladnému číslu e existuje kladné číslo d tak, že pro všechny hodnoty x v intervalu x-x_o< d <x+x_o splňují funkční hodnoty nerovnost f(x)-f(x_o)< e <f(x)+f(x_o). Blízká okolí nezávisle proměnné x se zobrazují na blízká okolí funkčních hodnot f(x).
  Limita zobrazení j : X®Y mezi topologickými prostory v bodě x_oÎX je definována jako bod y_oÎY takový, že pro každé okolí U(y_o) bodu y_o existuje okolí U(x_o) bodu x_o pro které platí implikace xÎU(x_o) Ţ yÎU(y_o). Zapisuje se lim_x®xoj (x) = y_o.
Tato topologická definice je zobecněním limity funkce, sloužící v matematické analýze ke zkoumání chování funkcí v okolí určitého bodu. Limita lim_x®xof (x) = y_o vyjadřuje skutečnost, že pokud se hodnota nezávisle proměnné x blíží hodnotě x_o, hodnota funkce f(x) se blíží neomezeně blízko hodnotě y_o - limitě funkce v bodě x_o. Definuje se to pomocí chování funkce v infinitezimálním okolí vyšetřovaného bodu x_o: Funkce f(x) má v bodě x_o limitu y_o, jestliže ke každému kladnému číslu e existuje kladné číslo d tak, že pro všechny hodnoty x z okolí x-x_o< d <x+x_o splňují funkční hodnoty nerovnost f(x)-y_o)< e <f(x)+y_o. Funkce může mít dobře definovanou limitu i v bodě, kde vlastní funkční hodnota definována není (např. funkce [e^x-1]/x má v bodě x=0 limitu rovnou 1). Pro spojité funkce platí, že limita se rovná funkční hodnotě v daném bodě: lim_x®xof (x) = f(x_o ); platí i opačné tvrzení. Pro nespojité funkce se zavádějí limity zleva a zprava; v případě že tyto limity jsou shodné, označíme tuto hodnotu za limitu funkce v daném bodě. Pokud se liší, limita v tomto bodě neexistuje.
Pojem limita je výchozím základem diferenciálního a integrálního počtu, který zkoumá změny funkčních hodnot v závislosti na infinitezimálních změnách nezávisle proměnné. Pomocí limity změn funkce se zavádí derivace a k ní inverzní proces integrace.
  Vzájemně jednoznačné (bijektivní) spojité zobrazení j prostoru (X,U) na (Y,V), pro které je i inverzní zobrazení j ^-1 spojité, se nazývá homeomorfismus (je zřejmé, že j ^-1 je pak rovněž homeomorfní zobrazení prostoru Y na X). Homeomorfní zobrazení je tedy topologický izomorfismus - takové vzájemně jednoznačné zobrazení množin X a Y, při kterém se blízké body jedné množiny převádějí na blízké body druhé množiny (otevřené podmnožiny v X a Y tvořící okolí bodů x ÎX a j(x) ÎY jsou ve vzájemně jednoznačném vztahu) - zachovává se při něm okolí bodů. Množiny X a Y, mezi nimiž existuje takový homeomorfismus, se nazývají homeomorfní a považují se z topologického hlediska za ekvivalentní. Homeomorfismus je vyjádřením oněch "spojitých deformací" (stlačení nebo roztažení) zmíněných výše. Topologické pojmy a topologické vlastnosti jsou takové pojmy a vlastnosti, které zůstávají zachovány při homeomorfismu *).
* ) Například elektrický obvod je pojem topologický, protože pro jeho činnost není podstatné geometrické rozmístění jednotlivých součástek, ale jejich vzájemné elektrické propojení. Když změníme prostorové rozmístění součástek bez přerušení jejich elektrického spojení, bude obvod fungovat stejně (neplatí to tak docela pro vysokofrekvenční techniku, kde se pro různá rozmístění součástek mohou různě uplatňovat jevy kapacity, elektromagnetické indukce či vyzařování vln).

Nejnázornějším příkladem topologického prostoru je množina reálných čísel R¹ s přirozenou topologií danou soustavou podmnožin A Ě R¹, které spolu s každým svým bodem obsahují vždy i určitý interval kolem něho: pro každý bod x Î A existují čísla a,b taková, že a < x < b a interval (a, b) Î A. Zobecněním je n-rozměrný Eukleidův prostor Rⁿ všech n-tic reálných čísel (x¹,x²,...,xⁿ) při -Ą < xⁱ < +Ą s obvyklou topologií. A právě dobře známé vlastnosti eukleidovského prostoru, "odkoukané" od chování makroskopických těles, umožňují (pomocí vhodného zobrazení) na jinak amorfním topologickém prostoru zavést dodatečné struktury a učinit jej tak vhodným nástrojem k modelování fyzikálních dějů.

Regulární a singulární chování
V běžném životě mají okolní předměty obvyklé a očekávané fyzikální, geometrické a topologické vlastnosti . Jsou (relativně) hladké a spojité, mají konečné rozměry a konečné hodnoty svých fyzikálních veličin. Takové chování označujeme jako regulární. A může být matematicky modelováno pomocí regulárních zobrazení, což jsou výše zmíněná prostá vzájemně jednoznačná zobrazení, k nimž jsou k dispozici jednoznačná invezní zobrazení.
  Při matematickém modelování v teoretické fyzice se však setkáváme i se situacemi, kdy příslušné rovnice divergují a formálně dávají nekonečné či neurčité hodnoty fyzikálních veličin. Jednoduchým příkladem je idealizace bodového elektrického náboje, kdy podle Coulombova zákona je v místě o nulové vzdálenosti (r=0) nekonečně velká intenzita elektrického pole. Takovéto anomální chování fyzikální veličiny se označuje jako singulární (je to opak chování regulárního). A místo či bod anomálního chování fyzikální veličiny se nazývá singularita (lat. singularis = ojedinělý, vyjímečný, jedinečný).
  V klasické fyzice jsou singularity víceméně formální, vznikají idealizací daného modelu a v realistických případech se nevyskytují. V obecné teorie relativity se však ukazuje, že gravitační či prostoročasové singularity metriky zákonitě vznikají i za značně obecných předpokladů, které jsou v astrofyzikální praxi pravděpodobně splněny. Vedle odstranitelných souřadnicových singularit ("pseudosingularit) se vyskytují i neodstranitelné skutečné fyzikální singularity. Proto se budeme singularitami zabývat v řadě míst naší knihy - nejdříve matematickými aspekty počínaje tímto §3.1 (v jeho závěrečných pasážích), přes §3.4 "Schwarzschildova geometrie", 3.5., 3.6 "Kerrova a Kerrova-Newmanova geometrie", až po §3.7 "Prostoročasové singularity" a 3.8 "Hawkingovy a Penroseovy teorémy o singularitách". Z astrofyzikálního hlediska pak v kap.4 "Černé díry", zvláště v §4.2 "Konečné fáze hvězdné evoluce. Gravitační kolap. Vznik černé díry."a §4.4 "Rotující a elektricky nabité Kerrovy-Newmanovy černé díry".

V a r i e t y
Aby topologický prostor bylo možné numericky kvantifikovat, je užitečné zavést v něm číselné souřadnice - přiřadit bodům topologického prostoru numerické hodnoty reálných čísel. Vzniká tím tzv. varieta.
Název "varieta" zde znamená různorodost, rozličnost, různotvarost, diverzita. Je zatím zcela obecná, nejsou v ní zavedeny žádné vztahy (jako je konexe či netrika). Může modelovat objekty nejrůznějších tvarů a struktur.
  Varieta dimenze n (n- rozměrná varieta) Mⁿ je takový topologický prostor, jehož každý bod má okolí homeomorfní s Rⁿ (s určitým okolím v Rⁿ). Homeomorfní zobrazení j otevřené (pod)množiny AĚ Mⁿ do Rⁿ přiřazuje každému bodu x ÎA n-tici čísel j(x) = (x¹,x²,...,xⁿ) Î Rⁿ, které se nazývají souřadnice bodu x. Říkáme, že na množině A je zavedena souřadnicová soustava (systém souřadnic) xⁱ. Zvolením jiného homeomorfního zobrazení j' z A Ě Mⁿ do Rⁿ budou jednotlivým bodům x Î A přiřazeny jiné hodnoty souřadnic (x'¹,x'²,...,x'ⁿ) Î Rⁿ - přejdeme k jiné souřadnicové soustavě v podmnožině A. Provedli jsme transformaci souřadnic.

Dimenze topologická a Hausdorffova
Výše zmíněná dimenze - počet rozměrů - množiny či objektu, je obvyklá topologická dimenze. Je to celé číslo n udávající počet parametrů (souřadnic), kterými je jednoznačně definována poloha jednotlivých bodů tohoto útvaru. Vedle topologické dimenze se zavádí i alternativní metrická varianta dimenze, tzv. Hausdorffova-Besikovičova dimenze, která pro geometricky hladké množiny a útvary je rovna příslušné dimenzi topologické, avšak pro tzv. fraktální útvary může být vyšší a zpravidla neceločíselná. Analýzu tohoto druhu dimenze jsme (z formálně-technických důvodů výkladu fyzikálních jevů ve vztahu ke kauzální struktuře prostoročasu) odložili až na konec §3.3, pasáž "Determinismus v principu, náhoda a chaos v praxi ?", kde ji použijeme při diskusi chování chaotických systémů popisovaných tzv. podivnými atraktory ve fázovém prostoru.

Zobrazit celé Mⁿ do Rⁿ tímto způsobem však pro mnohé topologické prostory nelze (např. zobrazení S² do R² zavádějící na kulové ploše S² sférické souřadnice J,j přestává být vzájemně jednoznačné na pólech). Obecně tedy můžeme varietu Mⁿ zobrazit do Rⁿ po částech - vytvářet lokální souřadnicové "mapy" (A_a, j_a) jednotlivých "domén" (souřadnicových okolí) A_a Ě M. Soubor map jednotlivých domén A_a Ě M, pokrývajících M (t.j. _aČA_a =M), tvoří "atlas" variety M. Pouze variety topologicky ekvivalentní Rⁿ lze celé pokrýt jedinou mapou (M,j). Zavedením systému souřadnic ztrácejí body variety M svoji "anonymitu" a varieta může být zkoumána pomocí dobře známých a rozvinutých matematických operací s reálnými čísly.

Obr.3.1. V diferencovatelné varietě Mn jsou obrazy fa(p) a fb(p) bodu p z průniku dvou domém Aa a Ab svázány spojitými transformacemi včetně derivací do r-tého řádu.

Varieta Mⁿ se nazývá diferencovatelná třídy C^r, jestliže je pro ni dán atlas map (A_a, j_a) jednotlivých domén A_a Ě Mⁿ zobrazovaných vzájemně jednoznačnými zobrazeními j_a na otevřené množiny v Rⁿ splňující podmínky:
a) A_a tvoří pokrytí M, tj. _aČA_a = M;
b) Mají-li dvě domény A_a a A_b neprázdný průnik, pak bodům p Î A_a Ç A_b této překrývající se části bude zobrazením j_a přiřazena n-tice souřadnic xⁱ_a(p) Î Rⁿ a zobrazením j_b zároveň n-tice souřadnic x^k_b(p) Î Rⁿ tak, že transformace xⁱ_b(p) = xⁱ[x^k_a(p)] jsou v Rⁿ spojité funkce se spojitými derivacemi do r-tého řádu (obr.3.1).
  Aplikujeme-li vlastnost b) na dvě domény (A, j : x®xⁱ(x)) a (A', j' : x®x'ⁱ( x)) takové, že A'= A = AÇA' ale j' ą j, pak přechod od soustavy souřadnic xⁱ k jiné soustavě souřadnic x'ⁱ bude dán regulární a spojitou transformací x'ⁱ(x)= x'ⁱ[x^k(x)] r-krát derivovatelnou. V diferenciální geometrii se většinou zabýváme lokálními geometrickými vlastnostmi v rámci jedné lokální mapy, zatímco globální geometrie studuje geometricko-topologickou strukturu celé variety.

Aby varieta měla obvyklé lokální vlastnosti (a mohla být použitelná pro klasický popis fyzikálních dějů), kladou se na ni ještě dva dodatečné požadavky: Hausdorffovost a parakompaktnost. Prostor se nazývá Hausdorffův, jestliže ke každým dvěma různým bodům existují různá jejich okolí. Požadavek parakompaktnosti znamená, že ke každému pokrytí variety M soustavou otevřených podmnožin existuje takové jeho zjemnění, při němž každý bod variety má okolí protínající jen konečný počet podmnožin tohoto zjemněného pokrytí (tj. toto zjemnění je lokálně konečné) [155]. Při splnění Hausdorffovosti je parakompaktnost ekvivalentní požadavku, aby M měla spočetnou bázi, tj. aby existovala taková spočetná soustava otevřených množin, jejichž sjednocením je libovolná otevřená množina v M (prostory, jejichž topologie má spočetnou bázi, se nazývají separabilní). Parakompaktnost umožňuje zavedení konexe na M (viz níže).

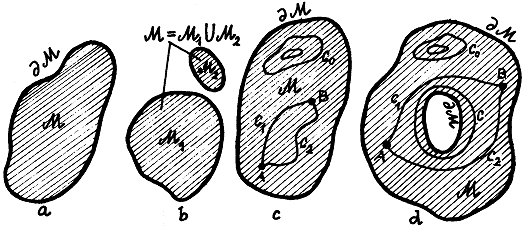
Obr.3.2. Souvislost množin (variet).
a) Souvislá množina. b) Nesouvislá množina, která je sjednocením dvou disjunktních částí.
c) Jednoduše souvislá množina - všechny spojnice mezi dvěma body jsou topologicky ekvivalentní, každá uzavřená křivka je homologická nule.
d) Dvojnásobně souvislá množina - existují dvě třídy spojnic mezi body, některé uzavřené křivky (např. C) nelze smrštit do bodu.

Stručně řečeno, n-rozměrná varieta je topologický prostor, který lokálně (v dostatečně malém okolí každého svého bodu) "vypadá" jako Eukleidovský prostor Eⁿ. Aby tato podobnost byla věrná, je třeba postavit výše zmíněné podmínky separabilnosti a parakompaktnosti.

Křivky a plochy
Pod křivkou (čarou) l(t) na varietě M se rozumí zobrazení určitého úseku R¹® M, tj. množina bodů v M, které jsou zobrazením bodů křivky xⁱ =xⁱ(t) v Rⁿ parametrizované proměnnou t Î R¹. Základní topologickou charakteristikou každé množiny (geometrického útvaru) je souvislost. Jako souvislou označujeme takovou varietu, která není tvořena sjednocením několika disjunktních neprázdných částí; potom každé její dva body lze spojit čarou, která je celá součástí této množiny (obr.3.2a). V opačném případě se jedná o nesouvislou množinu (obr.3.2b). Souvislá množina se nazývá jednoduše souvislou, jestliže pro každé dva body A a B jsou všechny spojnice mezi nimi vzájemně topogicky ekvivalentní (homologické); jinak vyjádřeno, každou uzavřenou křivku zde můžeme spojitě "stáhnout" do bodu (každá uzavřená křivka je homologická nule) - obr.3.2c. Jestliže mezi některými body existuje více druhů spojnic které nejsou vzájemně topologicky ekvivalentní, jedná se o vícenásobně souvislou množinu (obr.3.2.d), kde některé uzavřené čáry nelze "stlačit" do vymizení v bodě. Přitom "násobnost" souvislosti je definována jako s = c + 1, kde c je počet topologicky nezávislých uzavřených čar, které nelze smrštit do bodu (c je zároveň rovno počtu "rozřezání", po kterých se daná množina stává jednoduše souvislou); veličina s udává, kolika topologicky různými cestami se lze dostat z jednoho místa variety do druhého místa.
  Zobecněním jednorozměrné křivky ve varietě Mⁿ je p-rozměrná plocha C^p (p Ł n), která je zobrazením příslušného p-rozměrného podprostoru v Rⁿ. Takovou plochu C^p lze považovat za součet (sjednocení) elementárních p-rozměrných "rovnoběžníků", resp. "krychlí" K^p (které jsou ovšem obecně "křivočaré") 0 Ł x^aŁ 1 (a =1,2,...,p). Vhodným způsobem se zde zavádí orientace a sčítání, což umožňuje studovat souvislosti mezi různými plochami C a jejich hranicemi ¶C, např. při integrování [217]. Orientovaná p-rozměrná krychle K^p má (p-1)-rozměrnou hranici ¶K tvořenou jednotlivými stěnami. Tato plocha je uzavřená a proto nemá sama již žádnou hranici, takže (p-2)-rozměrná hranice (p-1)-rozměrné hranice p-rozměrné krychle je rovna nule: ¶¶K = O. Plyne to též z konstrukce hranice krychle pomocí sumy čtverců tvořících hranice jednotlivých stěn krychle, kde každá strana čtverce je započítávána dvakrát s opačnou orientací a proto se zruší.
  Obecnou plochu S můžeme rozložit na řadu krychlí (patřičné dimenze) K_i: S = _iSaⁱK_i ; potom hranici plochy S definujeme jako součet hranic "krychlí" z nichž je složena: ¶S = _iSaⁱ¶K_i (ve skutečnosti se většina těchto příspěvků z vnitřních oblastí zruší, protože jsou započítávány dvakrát s opačnou orientací podobně jako u běžného odvozování Gaussovy nebo Stokesovy věty). Jestliže hranice nějaké p-rozměrné plochy S je rovna nule (¶S = 0), jedná se o uzavřenou (kompaktní) plochu. Hranice ¶S každé plochy (nejen uzavřené) je uzavřená plocha, která již nemá svou hranici, takže vždy platí

toto se označuje jako topologický princip "hranice hranice je rovna nule", který má velký význam pro zákony zachování v obecné teorii pole [181], viz též §2.5.
  Jestliže dvě uzavřené plochy C^p₁ a C^p₂ tvoří hranici (p+1)-rozměrné oblasti v M, říkáme, že jsou vzájemně homologické (mohou být spojitou deformací převedeny jedna v druhou); pokud uzavřená plocha C^p samotná tvoří hranici (C^p = ¶A^p+1) oblasti AĚ M, nazývá se homologická nule (spojitou deformací může být stažena do jediného 0-rozměrného bodu). Homologická třída {C^pi} sestává ze všech uzavřených p-rozměrných ploch C^p které jsou vzájemně homologické.
V Eukleidově prostoru Rⁿ mohou být všechny p-rozměrné (p <= n) uzavřené plochy stlačeny do bodu, takže všechny jsou hologické nule a patří do nulové homologické třídy {C^p₀} = {0}.
Počet nezávislých homologických tříd {C^p₁}, {C^p₂}, .,., {C^p_Bp} ploch dimenze p se nazývá p-tým Bettiho číslem variety M (nezapočítává se zde třída {C^p_o} = {0} ploch homologických nule). Veličina c = _p=0Sⁿ(-1)^pBp se nazývá Eulerovou charakteristikou této variety. K popisu topologické složitosti (vícenásobné souvislosti) variet se též používá tzv. topologický genus variety, což je číslo udávající počet skupin uzavřených křivek, které nelze spojitou transformací stáhnout do bodu, neboť jsou vedeny kolem nějakého topologického tunelu či vyříznuté oblasti. Pro dvojrozměrnou varietu M² mezi genusem g a Eulerovou charakteristikou c patí vztah c = 2 - 2 g.
  Protože mezi plochami C^p je definováno sčítání, tvoří soubor těchto ploch ve varietě M grupu; množina tříd vzájemně homologických p-rozměrných uzavřených ploch pak tvoří p-rozměrnou grupu homologií daného prostoru. Vztahy mezi množinami a jejich hranicemi tak mohou být studovány algebraickými metodami v tzv. algebraické topologii [151],[106].
Pozn.: U zrodu algebraické topologie kolem r.1900 stál H.Poincaré, který křivkám na 3-varietě přiřadil prvky určité grupy (zvané fundamentální grupa variety).

Důvod vícenásobné souvislosti oblasti podle obr.3.2d je zřejmý: část z M je "vyříznuta", takže daná oblast má kromě vnější hranice též vnitřní hranici, přes kterou žádná spojnice nesmí jít. Existují však útvary i celé prostory bez hranic, které jsou vícenásobně souvislé, jak si ukážeme na následujících jednoduchých příkladech.
  Vezmeme rovný list papíru, který můžeme považovat za část Eukleidovské roviny R² (obr.3.3a). Tento list je jednoduše souvislý a platí zde axiómy Eukleidovy geometrie (proto např. součet úhlů v narýsovaném trojúhelníku bude roven 180°). Stočíme-li tento list papíru a slepíme protější strany, tj. uděláme ztotožnění (x+a,y) ş (x,y), dostaneme válcovou plochu. Eukleidovský charakter geometrie se tím lokálně nezměnil - vzdálenosti mezi jednotlivými body zůstaly stejné, nezměnily se úhly ani plochy. Avšak svými globálními topologickými vlastnostmi je tato válcová plocha zcela jiným dvojrozměrným prostorem než byla původní Eukleidova rovina. Mezi každými dvěma body existují dvě topologicky odlišné třídy spojnic, uzavřenou kružnici obepínající válec nelze nijak stáhnout do bodu, zatímco jiné uzavřené křivky ano; válcová plocha je dvojnásobně souvislá a v jednom směru (rozměru) konečná. Bettiho čísla zde jsou B₀=1, B₁= 1, B₂= 1.

Obr.3.3. Ke vztahu mezi (geo)metrickými a topologickými vlastnostmi.
a) List papíru je částí Eukleidovy roviny. Jeho stočením a slepením dostaneme válcovou plochu s lokálně zachovanou Eukleidovou geometrií, ale jinou globální topologií.
b) Jestliže se při stočení provede navíc překroucení o 180°, vznikne Möbiův list (proužek).
c) Stočením a slepením úseku válcové plochy vznikne toroid (anuloid).

Nebo podobně ohnutím, zkroucením o 180° a slepením - tj. ztotožněním (x+a,y) ş (x,-y) - papírové pásky s původně Eukleidovskou geometrií a topologií, dostaneme známý Möbiův list (proužek, obr.3.3b), jehož lokální geometrie se opět neliší od Eukleidovy, ale topologické vlastnosti má jiné. Jedná se o jednostrannou plochu (známý neúspěšný pokus s obarvením "líce" i "rubu" jedním tahem stejnou barvou), na níž nelze zavést orientaci, protože po jednom oběhu "kolem dokola" se to, co bylo vlevo objeví vpravo, směr "nahoru" se změní na "dolů" a naopak.
  Uvedené příklady ukazují, že pro úplné určení charakteru prostoru nestačí jeho (lokální) metrické vlastnosti, ale je třeba vzít v úvahu též jeho (globální) vlastnosti topologické. Kromě Eukleidova prostoru Rⁿ, na němž je pojem variety založen, tedy existují i obecnější variety s jinými topologickými vlastnostmi. Uveďme si některé další případy.

Jedním z nejdůležitějších typů variety je kulová plocha. Dvojrozměrná kulová plocha (sféra) S² jednotkového poloměru je jak známo plocha v R³, jejíž body jsou dány rovnicí (x¹)² + (x²)² + (x³)² = 1. Analogicky n-rozměrná sféra Sⁿ (jako podprostor v Rⁿ⁺¹) je geometrické místo bodů v Rⁿ⁺¹ splňujících podmínku _i=1Sⁿ⁺¹(xⁱ)² = 1. Sféra Sⁿ je konečná (kompaktní) jednoduše souvislá varieta. Pro dvojrozměrnou kulovou plochu S² jsou Bettiho čisla B₀=1, B₁=1, B₂=1 a Eulerova charakteristika c(S²) =1.
  Stočíme-li dvojrozměrnou válcovou plochu (zhotovenou z elastického materiálu) a slepíme protější základny, vznikne toroid (anuloid, obr.3.3c), který má na rozdíl od původní válcové plochy svou vnitřní geometrii zakřivenou. Tento toroid T², který vzniká ztotožněním (x+a, y+b) ş (x,y) bodů v R², je příkladem trojnásobně souvislé plochy: jsou zde dvě třídy uzavřených křivek - kružnice podél "velkého" a "malého" obvodu toroidu - které nelze smrštit do bodu. Obecně, n-rozměrný toroid Tⁿ je prostor, který vznikne ztotožněním (xⁱ+ aⁱ) ş (xⁱ), i=1,2,...,n, bodů v Rⁿ. Dvojrozměrný toroid T² má Bettiho čísla rovná B_o =1 (odpovídá třídě všech bodů - všechny body jsou vzájemně homologické), B₁=2 (jsou dvě nezávislé třídy {C¹₁} a {C¹₂} uzavřených křivek procházejících kolem menšího a většího obvodu toroidu), B₂=1 (odpovídá samotnému toroidu); Eulerova charakteristika c(T²)= 0.

Z n-rozměrné variety Mⁿ a m-rozměrné variety M^m můžeme "kartézským součinem" sestrojit (n+m)-rozměrnou varietu Mⁿ´M^m, jejíž body jsou dvojicemi (x,y), kde x je libovolný bod z Mⁿ a y libovolný bod z M^m. Např. Eukleidův prostor R³ je součinem R²´R¹, Rⁿ lze zapsat jako Rⁿ = R¹´R¹´...´R¹ (kartézský součin n-koeficientů). Válcovou plochu C² lze považovat za součin kružnice a Eukleidovy přímky, tj. C² = S¹´R¹. Co se týče toroidu, je především zřejmé, že jednorozměrný toroid T¹ a jednorozměrná sféra S¹ (kružnice) jsou vzájemně homeomorfní, tj. T¹ = S¹. Proto n-rozměrný toroid Tⁿ je z topologického hlediska kartézským součinem n kružnic: Tⁿ = S¹´S¹´...´S¹.

Topologická struktura variety Mⁿ´M^m je přirozeným způsobem dána strukturou Mⁿ a M^m: pro libovolné body xÎMⁿ a yÎM^m mající souřadnicová okolí AĚMⁿ a BĚM^m je bod (x,y)ÎMⁿ´M^m obsažen v souřadnicovém okolí A´BĚMⁿ´M^m a má tam souřadnice (xⁱ, y^j), kde xⁱ jsou souřadnice bodu x v doméně A a y^j souřadnice bodu y v doméně B.
  Funkce f (skalární pole) na varietě Mⁿ je zobrazení z Mⁿ do R¹. Říkáme, že tato funkce je diferencovatelná třídy C^r v bodě pÎM, jestliže je definována v otevřeném okolí bodu p a její vyjádření f(x) = f(x¹,x²,...,xⁿ) pomocí souřadnic xⁱÎRⁿ v nějaké lokální souřadnicové soustavě má spojité derivace do r-tého řádu podle xⁱ. Z této definice plyne, že v diferencovatelné varietě M třídy C^s je souřadnice xⁱ(x) diferencovatelnou funkcí třídy C^s.

Tenzory ve varietě
Dalšími geometrickými objekty, které přirozeným způsobem souvisejí se strukturou variety, jsou tenzory a tenzorová (speciálně též vektorová) pole. Tenzorem r-tého řádu v bodě "p" n-rozměrné variety Mⁿ se rozumí souhrn n^r čísel
            T^il_jlⁱ²_j2^._.^._.^._.^ia_jb , jl,j2,...,jb, il,i2,...,ia = l, 2, 3, ..., n
s a Ł r kontravariantními (horními ) a b = r-a kovariantními (dolními) indexy, které se při transformaci souřadnic x'ⁱ(p) = x'ⁱ(x^j(p)), tj. dx'ⁱ =(¶x'ⁱ/¶x^j) dx^j, transformují v kontravariantních indexech jako součiny a- diferenciálů souřadnic a v kovariantních indexech jako součiny b- inverzních diferenciálů v bodě p :

(3.2)

Tyto transformační vlastnosti zaručují, že tenzorové rovnice jsou invariantní (kovariantní) vzhledem k transformacím souřadnic. Pravidla pro aritmetické operace mezi tenzory jsou stejné jako v eukleidovském prostoru Rⁿ.
  Možnost zavedení libovolného tenzorového pole na varietě je obecně podmíněna topologickými vlastnostmi variety[151],[106]. Např. každá nekompaktní varieta připouští existenci konstantního vektorového pole. Pro existenci konstantního vektorového pole na kompaktní varietě je však nutnou a postačující podmínkou, aby se Eulerova charakteristika c variety rovnala nule. Například válec nebo toroid připouští konstantní vektorové pole, zatímco kulová plocha nikoli ("nelze hladce učesat vlasy na tenisovém míčku").
Konexe a metrika ve varietě. Zakřivení prostoru. 
Aby bylo možno porovnávat vektory a tenzory zadané v různých bodech variety, zavádí se konexe (z lat. connectio = spojení, styk, svázání), tj. pravidlo (předpis) pro paralelní přenos vektorů a tenzorů mezi různými body; varieta se tím stává prostorem afinní konexe (lat. affinis = sousední, spojený, příbuzný). A zde již může přijít ke slovu diferenciální geometrie - počítání kovariantních derivací tenzorových polí, kvantifikace zakřivení pomocí tenzoru křivosti, stanovení geodetických čar atd., jak to bylo nastíněno v §2.4 "Fyzikální zákony v zakřiveném prostoročase", část "Zakřivení prostoru. Tenzor křivosti".
  Pojem křivost (curvature) v diferenciální geometrii hraje důležitou úlohu. Zobecňuje, formalizuje a kvantifikuje naše intuitivní zkušenosti s tvary nerovných předmětů - čáry (křivky), plochy, tělesa. Během vývoje diferenciální geometrie bylo zavedeno několik vyjádření křivosti, především vnitřní a vnější křivost.
Vnější a vnitřní křivost 
Rozlišení těchto dvou druhů křivosti (vycházejících z různého úhlu pohledu) lze názorně ilustrovat pomocí dvojrozměrné plochy, na níž žijí dvojrozměrné bytosti, které principiálně nemohou opustit svůj 2-rozměrný svět. Vnitřní křivost plochy je taková křivost, kterou mohou naše dvojrozměrné bytosti pozorovat, aniž by opustily svůj 2-rozměrný svět: měřit např. v okolí každého bodu obvody kružnic L a jejich poloměry r. Ze zjištěných rozdílů od Eukleidovského vztahu l=2pr mohou stanovit vnitřní křivost, kvantifikovanou např. tzv. Gaussovou křivostí C_G=6.(1-L/2pr)/r². Tato vnitřní křivost může v různých bodech plochy mít různé hodnoty.
  Pro představu vnější křivosti narýsujme na list papíru, představující Eukleidovskou rovinu, několik trojúhelníků a kružnic. Ohneme-li a slepíme tento list papíru do válcové plochy, vzdálenosti ani úhly se při této operaci nezmění od původních Eukleidovských hodnot, vzniklá válcová plocha má i nadále nulovou vnitřní křivost C. Na nakreslených trojúhelnících a kružnicích však my, jako trojrozměrné bytosti, budeme pozorovat, že součet úhlů v trojúhelníku je větší než 180^o a obvod kružnice je menší než 2pr-násobek poloměru, měřeného přes trojrozměrný prostor. Budeme pozorovat vnější křivost válcové plochy. Pro naši anylýzu gravitace jakožto zakřiveného prostoročasu však je podstatná pouze vnitřní křivost.
  Konečně se do variety zavádí metrika, tj. předpis pro stanovení vzdáleností mezi jednotlivými body, čímž vzniká metrický prostor. Pomocí souřadnic vyjádřená vzdálenost mezi bodem xⁱ a sousedním nekonečně blízkým bodem xⁱ + dxⁱ je dána diferenciální formou ds² = g_ik dxⁱdx^k (i,k=1,2,...,n), kde g_ik je metrický tenzor vyjadřující vztah mezi souřadnicemi a skutečnými vzdálenostmi. Aby konexe byla slučitelná s metrikou (konexe a metrika jsou obecně nezávislé struktury zaváděné do variety), musí se při paralelním přenosu zachovávat pravidla tenzorové algebry a velikost přenášeného vektoru. Vede to na zákon paralelního přenosu (2.8) a jednoznačný vztah (2.2b) mezi koeficienty konexe a složkami metrického tenzoru [214], viz §2.1 "Zrychlení a gravitace z hlediska speciální teorie relativity" a 2.4 "Fyzikální zákony v zakřiveném prostoročase". Metrický prostor s konexí (slučitelnou s metrikou) se nazývá Riemannův prostor. Diferenciální geometrie zde podává přesné analytické nástroje pro kvantifikaci zakřivení prostoru - §2.4, část "Tenzor křivosti".

Prostoročas jako varieta
Po této letmé exkurzi do oblasti obecných geometricko-topologických struktur se již můžeme opět vrátit k vlastnímu předmětu našeho zájmu - ke gravitaci a prostoročasu. Všechny známé fyzikální jevy probíhají v prostoru a čase - v rámci čtyřrozměrného prostoročasu. Zkušenost nás přitom učí, že prostoročas má v běžných makroskopických měřítcích vlastnosti kontinua (neomezená dělitelnost prostorových měřítek a časových intervalů) a může být modelován jako čtyřrozměrná diferencovatelná varieta s Riemannovskou metrikou. Při studiu geometrických vlastností prostoročasu budeme vycházet z tohoto základního modelu :
A.  Prostoročas je souvislá čtyřrozměrná diferencovatelná varieta M⁴, která je Hausdorffovská a parakompaktní s Riemannovou metrikou g. Budeme jej značit (M,g). Souvislost variety M požadujeme proto, že nic se nemůže vyskytovat a pohybovat mimo prostor a čas, takže kdyby byla nesouvislá, byla by jakákoliv informace pro jednu část M o ostatních disjunktních částech M principiálně nedostupná, takže takové nesouvisející části by efektivně neexistovaly.
B.  V prostoročase M mohou existovat různá "fyzikální" ("látková", negravitační) pole, např. elektromagnetické pole, která se budou řídit určitými rovnicemi. Tyto rovnice budou mít charakter vztahů mezi tenzory (tenzorovými poli) *) v M (princip obecné kovariance) a jejich kovariantními derivacemi podle prostoročasových souřadnic vzhledem ke konexi G indukované metrikou g .
*) Neuvažujeme zde spinorová pole. Zavedení spinorového formalismu je v některých případech výhodné [97], avšak obecně lze spinorové vztahy nahradit ekvivalentními (i když třebas komplikovanějšími) rovnicemi tenzorovými.
  Budeme předpokládat, že reálná fyzikální pole v M budou mít tyto dvě základní vlastnosti :
1. Rovnice popisující chování polí musejí být takové, aby přenos signálu (energie) se lokálně uskutečňoval uvnitř nebo na plášti prostoročasového světelného kuželu. Tedy přenos signálu a energie mezi dvěma body (událostmi) prostoročasu je možný jen tehdy, když tyto body mohou být spojeny světočárou, která všude leží uvnitř nebo na plášti lokálního světelného kuželu (tečný vektor je v každém bodě buď časového nebo světelného typu). Tato vlastnost je vyjádřením lokální příčinnosti.
2. Pro každé fyzikální pole v M existuje symetrický tenzor T^ik - tenzor energie a hybnosti, který závisí na potenciálech (intenzitách) polí a jejich kovariantních derivacích v metrice g. Tenzor energie-hybnosti má následující vlastnosti :
a) T^ik = 0 v nějaké podmnožině M tehdy, jestliže látková pole jsou nulová.
b) Platí T^ik_;k = 0 - tedy lokální zákon zachování energie a hybnosti.
C.  Vztah mezi geometrií prostoročasu a jeho "látkovým obsahem" je realizován tím, že v prostoročase M jsou splněny Einsteinovy rovnice R_ik - ¹/₂ g_ikR = 8p T_ik .
Jak bylo ukázáno v §2.5, lze lokální zákon zachování energie a hybnosti T^ik_;k = 0 považovat za důsledek Einsteinových rovnic buzeného gravitačního pole.

Formálně lze každý prostoročas (M,g) považovat za řešení Einsteinových rovnic R_ik - ¹/₂ g_ikR = 8pT_ik v tom smyslu, že na základě komponent metrického tenzoru g_ik si vypočítáme veličinu (R_ik- ¹/₂ g_ikR)/8p a tuto si definujeme jako tenzor T_ik. V obecném případě však takto definovaný tenzor energie-hybnosti nemusí mít fyzikálně přípustné vlastnosti. Jen prostoročas zcela určitých geometrických vlastností bude popisovat skutečná gravitační pole buzená skutečným rozložením hmoty~energie.

Lokální a globální vlastnosti prostoročasu
Geometrické a topologické vlastnosti prostoročasu se obvykle rozdělují na lokální a globální *). V rámci klasické obecné teorie relativity není (s výjimkou singularit) lokální geometrie a topologie zajímavá, protože podle principu ekvivalence je prostoročas všude lokálně eukleidovský. V současné době je adekvátnost pojmu variety, tj. představa spojitého prostoru a času, experimentálně ověřena pokusy s rozptylem elementárních částic při vysokých energiích do měřítek řádu asi 10^-16cm [229]. Vezmeme-li však v úvahu kvantové zákonitosti (univerzální vliv relací neurčitosti), mohou být lokální geometrické a topologické vlastnosti prostoročasu v rámci velmi malých (subnukleárních ~10^-33cm) oblastí silně odlišné od obvyklých eukleidovských. Můžeme to ilustrovat tak, že když se díváme na dokonale vyleštěnou plochu zrcadla (jejíž lokální geometrické a topologické vlastnosti se nám normálně jeví jako dokonale eukleidovské) mikroskopem, vidíme velmi značné místní rozdíly od ideální rovinnosti a dokonce i hladkosti a spojitosti - mikrostruktura nemá eukleidovskou geometrii a dokonce ani topologii. Otázky lokální topologické struktury odsuneme do "dodatku B" (§B.4 "Kvantová geometrodynamika") a jinak budeme lokální geometrii a topologii prostoročasu považovat za eukleidovskou.
*) Toto rozlišení ale nemusí být vždy zcela jednoznačné - např. za přítomnosti lokální nahé singularity by neexistovaly globální Cauchyho hyperplochy (§3.3).
  Před vytvořením obecné teorie relativity se ani otázky globální geometrie a topologie prostoročasu nezdály být zajímavé; pod strukturou a vývojem vesmíru se většinou rozumělo rozložení a evoluce látek a polí v prostoru, přičemž struktura samotného prostoru a času se považovala za samozřejmou - eukleidovskou. I v rámci Newtonovské fyziky nebo STR lze sice formálně uvažovat i složitější topologické struktury prostoru, avšak není k tomu žádný fyzikální důvod, jednalo by se jen o samoúčelnou konstrukci (o hříčku). Obecná teorie relativity ale ukazuje, že prostoročas je zakřivený (přičemž toto zakřivení může být i silné), takže jeho globální vlastnosti se mohou značně lišit od eukleidovských. Z dvojrozměrné analogie víme, že ve srovnání s rovinnými plochami mají zakřivené plochy velkou rozmanitost tvarů s různými geometrickými a topologickými vlastnostmi - tyto plochy mohou být otevřené, uzavřené, různě "propletené" (vícenásobně souvislé) a podobně. V zakřiveném prostoročase OTR lze tedy očekávat situace, kdy nejen geometrické, ale i globální topologické vlastnosti prostoročasu mohou být úplně jiné než obvyklé eukleidovské. To se skutečně projeví v téměř všech případech, které budeme v §3.4-3.6 vyšetřovat jakožto přesná řešení Einsteinových gravitačních rovnic.
  Jak jsme si ukázali v Kapitole 2, základem OTR je lokální princip ekvivalence, který je spojovacím "můstkem" mezi negravitační a gravitační fyzikou. Einsteinovy rovnice gravitačního pole jsou (podobně jako Maxwellovy rovnice elektromagnetického pole) rovnicemi lokálními: popisují, jakým způsobem je v určitém místě prostoročasu buzeno gravitační pole (tj. metrický tenzor g_ik a jeho první a druhé derivace) rozložením hmoty a energie (tj. tenzorem energie a hybnosti T_ik) v tomtéž místě (události) prostoročasu. Einsteinovy rovnice však nedávají přímou informaci o globální geometrické a topologické struktuře prostoročasu. Globální topologická struktura prostoročasu má charakter "okrajových podmínek", které fakticky musíme zadat na základé určitých fyzikálních (či filosofických?) předpokladů. Řešení Einsteinových rovnic nám dává jen některé nepřímé informace o globální topologii, např. že v určitých případech nemůže být eukleidovská. Konkrétní globální topologie však zůstává do určité míry věcí volby.
  Nejednoznačnost globální topologie si můžeme ilustrovat na jednoduchém případě. Mějme prázdný Minkowskiho rovinný prostoročas s metrikou

ds²   =   - dt² + dx² + dy² + dz²   ,      

v němž jsou Einsteinovy rovnice identicky splněny. Prostor má Eukleidovu geometrii a může mít samozřejmě i obvyklou eukleidovskou topologii, při níž x,y,z Î (-Ą, +Ą). Avšak provedeme-li ztotožnění

(x+a, y, z)  ş  (x, y, z) ,  (x , y+b, z)  ş  (x, y, z) , (x, y, z+c)  ş  (x, y, z) ,      

zůstává lokální geometrie eukleidovská a Einsteinovy rovnice budou nadále splněny, avšak globálně se jedná o topologii trojrozměrného toroidu. Může tedy existovat rovinný a přitom uzavřený (s konečným celkovým objemem V = a.b.c) trojrozměrný prostor! Toto lze názorně ukázat na dvojrozměrné analogii: když vezmeme list papíru s Eukleidovou geometrií ds² = dx² + dy² a stočíme ho do válcové plochy (tj. provedeme ztotožnění (x+a,y) ş (x,y), kde a=2pr, r je poloměr válce), zůstane lokální geometrie eukleidovská, ale topologie bude jiná - obr.3.3a. Stočit dvojrozměrnou válcovou plochu a slepit ji do toroidu sice nelze při zachování lokální eukleidovské geometrie, avšak přidáním dalšího rozměru to již jde (trojrozměrný prostor se stane hyperplochou) a dostane se shora uvedená možnost.

Nekonečno v prostoročase
V souvislosti s tím ani pojmy "nekonečnost" a "neomezenost" prostoru a času obecně nestačí chápat v intuitivním smyslu jaký mají v klasické fyzice. Se skutečným "nekonečnem" nemá nikdo žádnou zkušenost, žádný člověk jej nikdy neviděl; pojem nekonečna vznikl jakožto idealizace velmi velkých (vzhledem k běžným), avšak konečných vzdáleností, časů nebo jiných veličin. Přitom co je "velmi velké" (resp. lépe řečeno "dostatečně velké") zcela závisí na konkrétní situaci - za prakticky nekonečně velké se považuje číslo, které je velmi velké ve srovnání se všemi ostatními hodnotami dané veličiny, vyskytujícími se při rozboru určitého problému. Například vzdálenost 10^-8cm je velmi malá z hlediska makroskopické fyziky, ale lze ji považovat za prakticky nekonečnou z hlediska struktury elementárních částic; nebo vzdálenost 100 světelných let je prakticky nekonečně velká pro astrofyziku sluneční soustavy, avšak zároveň velmi malá z hlediska struktury vesmíru jako celku.
  Podle své základní logické povahy se nekonečno rozlišuje na dvě kategorie:

• Nekonečno potenciální
  je vyjádřením trvale možného pokračování určitého procesu "až do nekonečna", např. procesu postupného přibližování k nějaké hodnotě (limitě), či principiální možnosti neustálého zvyšování určité veličiny "nade všechny meze".
• Nekonečno aktuální
  vyjadřuje nekonečnou velikost určitého skutečného (již "hotového") celku, je pojímáno jako objekt dalších matematických manipulací.

Pod nekonečností prostoru a času se skrývají vlastně dva odlišné aspekty:
a)  Globální nekonečnost "co do šíře" - tzv. extenzivní nekonečno;
b)  Lokální nekonečnost v každém místě "co do hloubky" ve smyslu neomezené dělitelnosti na stále menší a menší části - "intenzivní" nekonečno.
Intenzivní nekonečno bylo diskutováno výše v souvislosti s vlastnostmi kontinua a adekvátností modelu variety pro prostoročas. V dalším budeme pod nekonečnem rozumět extenzivní nekonečno v metrickém smyslu.

Nekonečno v matematice
Při reflexi slova "nekonečno" přemýšlivého člověka často zachvátí jakýsi podvědomý pocit tajemna, ba posvátné hrůzy z něčeho neznámého, skrytého kdesi za horizontem našeho chápání. Nekonečno jaksi nepatří do našeho racionálního světa; považuje se buď za mlhavý výplod obskurní fantazie filosofických či teologických směrů, nebo za teoretickou konstrukci podloženou nesrozumitelným matematickým aparátem.
Ano, právě matematika, která vyšla z analýzy reálných makroskopických objektů a posléze se zobecnila na abstraktní exaktní vědu, vypracovala postupy, jak s pojmem nekonečna zacházet stejně precizně, jako s počítáním s čísly v aritmetice.
Pozn.: Matematický symbol pro nekonečno "Ą" ("ležatá osmička") je starořeckého původu a symbolizuje hada, požírajícího sama sebe, jako nekonečný proces. Do matematiky jej zavedl v 17.stol. J.Wallis.
  Původní koncepce nekonečna vycházela z nekonečna potenciálního. Toto nekonečno představuje možnost pokračovat "donekonečna" v procesu postupného přibližování k určité hledané hodnotě - k limitě. Náznaky těchto úvah se objevovaly již v antické filosofii (Zenonův paradox) a matematice (počítání obsahu kruhu). Na metodách aproximací donekonečna se přibližujícími hodnotami je nyní založen diferenciální a integrální počet - nejmocnější matematický nástroj pro aplikace ve fyzice, přírodovědě i technice.
Aktuální nekonečno jakožto pojem vyjadřující velikost, početnost či "spočetnost" nekonečných souborů objektů, se začalo studovat či modelovat v polovině 19.stol. při formulaci teorie množin, založené B.Bolzanem a rozvinuté zvláště G.Cantorem. Pro dvě konečné množiny A a B platí, že jsou "stejně velké" - mají tentýž počet prvků, když ke každému prvku aÎA lze přiřadit právě jeden prvek bÎB, a naopak, ke každému prvku bÎB lze přiřadit právě jeden prvek aÎA ; jedná se o vzájemně jednoznačné (prosté) zobrazení. Toto porovnání lze zobecnit i na nekonečné množiny: pokud ke každému prvku z jedné množiny lze přiřadit právě jeden prvek z druhé množiny tak, že všechny prvky z druhé množiny jsou přiřazeny, říkáme že obě množiny mají stejnou mohutnost. Mohutnost množiny je zobecněním pojmu velikosti na nekonečné množiny. Mohutnost množiny se označuje symbolem "alef", což je první písmeno hebrejské abecedy, které v řecké transkripci můžeme zapsat podobným znakem "c" (hebrejský znak je jeho zrcadlovým obrazem; ve standardních fontech jej nemáme k dispozici).
Nejzákladnějším příkladem nekonečné množiny je množina všech přirozených čísel N (celá kladná čísla 1,2,3,4,......). Obecněji, každá množina, jejíž prvky lze seřadit do nějaké nekonečné posloupnosti a každému prvku přiřadit přirozené číslo odpovídající jeho pořadí v této posloupnosti (posloupnost lze "očíslovat"), má stejnou mohutnost jako množina všech přirozených čísel N - takové množiny se nazývají spočetné, jejich mohutnost se označuje "alef₀" neboli c₀.
Spočetná je i množina všech racionálních čísel, neboť ta lze vyjádřit jako zlomky, kde v čitateli i jmenovateli jsou celá čísla; takové zlomky pak lze seřadit do posloupnosti (např. střídavě podle rostoucího čitatele a jmenovatele), kterou lze očíslovat a tak všem racionálním číslům přiřadit čísla přirozená. I při zahrnutí čísel iracionálních algebraických (Ö2, Ö3, ...) zůstává mohutnost množiny stejná jako u čísel přirozených: odmocniny mohou být vyjádřeny jako reálná řešení polynomických rovnic a_n.xⁿ + a_n-1.x^n-1 + ... + a₂.x² +a₁.x +a₀ = 0 s celočíselnými koeficienty a_i a tyto polynomy můžeme opět seřadit do spočetných posloupností podle koeficientů a exponentů.
Množina reálných čísel R však obsahuje i tzv. transcendentní čísla (nejznámějšími z nich jsou Ludolfovo číslo p a Eulerovo číslo e - základ přirozených logaritmů), která nejsou řešením žádných polynomů s celočíselnými koeficienty, ani výsledkem žádných konečných rozvojů. Transcendentní čísla již nelze seřadit do žádné posloupnosti podle přirozených čísel. Opravdu, Cantor v r.1873 dokázal svou proslulou diagonální metodou, že množina všech reálných čísel R je nespočetná. Že reálná čísla nelze seřadit do (nekonečné) posloupnosti, jejímž členům by bylo možné přiřadit přirozená čísla - množina reálných čísel má jinou, větší mohutnost, než množina čísel přirozených. Mohutnost množiny reálných čísel R se označuje c₁, tj. alef₁, a platí c₁>c₀.
Pozn.: Některé vlastnosti složitých tzv. fraktálních množin a útvarů (označovaných někdy jako "matematická monstra") jsou stručně diskutovány v §3.3, pasáž "Determinismus-náhoda-chaos?").
  "Čísla" označující různé mohutnosti nekonečných množin (tedy c₀, c₁ a příp. další) se nazývají kardinální čísla, či zkráceně kardinály. S kardinálními čísly umí teorie množin počítat podobně jako s "obyčejnými" čísly, vyjadřujícími velikost konečných množin. Byla vytvořena svérázna "aritmetika kardinálních čísel", jejímiž základními pravidly jsou: c₀ + c₀ = c₀, c₁ = 2^c0 (to, že mohutnost množiny R je vyjádřena výrazem 2^c0 souvisí se skutečností, že 2ⁿ udává počet všech podmnožin množiny o n prvcích). Z toho pak plyne rovnost 2^c0 ´ 2^c0 = 2^c0, neboli c₁´ c₁ = c₁, což znamená, že existuje prosté zobrazení přímky na rovinu, neboli množina bodů přímky má stejnou mohutnost jako množina všech bodů roviny.
Byla vyslovena tzv. hypotéza kontinua, že neexistuje kardinální číslo k takové, že c₀< k < c₁, neboli neexistuje množina, jejíž mohutnost by byla větší než množiny přirozených čísel, ale menší než mohutnost množiny reálných čísel. Hypotézu kontinua se nepodařilo dokázat; byla posléze zahrnuta axiomaticky, podobně jako tzv. axiom výběru.........
  Moderní teorie množin je budována axiomaticky a vedla k sestrojení několika různých modelů teorie množin. Byly zavedeny i axiomy postulující existenci velkých kardinálů, popisujících mohutnosti množin, které jsou mnohem větší než mohutnost c₁ množiny reálných čísel. Zatím není známo, jaké důsledky bude mít bizarní teorie takových "šíleně velkých množin" (dokonce s nekonečnými a "nedosažitelnými" mohutnostmi) pro budoucí matematiku. A už vůbec není jasné, zda by mohla mít nějaký vztah k reálnému světu, nějaký "praktický význam". Pro studium geometrické a topologické struktury prostoročasu v relativistické fyzice ale zcela vystačíme (aspoň zatím..?..) s množinami o mohutnosti c₁, odpovídající modelování pomocí množiny reálných čísel.

Tolik tedy ve stručnosti o komplikovaných matematických strukturách nekonečna z hlediska teorie množin. V geometrickém modelování je představa nekonečna složitější z jiného hlediska. Ve dvou a vícerozměrných metrických prostorech (jako je 2-rozměrná rovina, 3-rozměrný Eukleidovský či zakřivený prostor, 4-rozměrný prostoročas) máme více různých nekonečen - míst s nekonečnou vzdáleností v různých směrech. V Eukleidovském prostoru, kde jsou všechny dimenze ekvivalentní, tato nekonečna není nutno rozlišovat; formálně doplníme k prostoru jeden "bod" který bude mít vlastnosti nekonečna. V prostoročase teorie relativity, kde se dimenze časová liší svými metrickými vlastnostmi od dimenzí prostorových, máme několik druhů nekonečna - běžné prostorové nekonečno, časové nekonečno minulosti a budoucnosti a nakonec izotropní (nulové či světelné) nekonečno budoucnosti a minulosti. Tyto druhy nekonečna budou definovány a analyzovány v následujícím §3.2. Pro názornější vhled do struktury nekonečna lze s výhodou použít takových jednoznačných zobrazení celého prostoru samého na sebe, po jejichž aplikaci odpovídají nekonečnu "obyčejné" body v konečných (třebas i jednotkových) vzdálenostech. Pro tento účel jsou nejvhodnější tzv. konformní zobrazení, kterých budeme v následujících kapitolách často používat.
  V Newtonovské fyzice (i ve STR) je prostor a prostoročas eukleidovský, takže pojmy "nekonečnost" a "neomezenost" tam není nutno rozlišovat. Podle "selského rozumu" zde z libovolného, jakkoli vzdáleného bodu prostoru můžeme "hodit kámen" ještě dále, totéž opakovat z takto dosaženého bodu atd. Není zde bod, za nímž by se nenacházela ještě vzdálenější místa, lze se neomezeně vzdálit od každého výchozího bodu. V OTR, kde se pracuje s neeukleidovskou geometrií prostoru a prostoročasu, však pojmy nekonečnost a neohraničenost mohou být podstatně odlišné. Nejjednodušším dvojrozměrným příkladem tohoto je kulová plocha, na níž dvojrozměrná bytost při lokálně přímkovém (geodetickém) pohybu podél hlavní kružnice se vrátí do výchozího bodu, přičemž urazí jen konečnou vzdálenost a nesetká se s žádnou hranicí. Celkový dvojrozměrný "objem" (plocha) je zde konečný - jedná se o neomezený, ale konečný prostor. Analogická je situace v uzavřeném trojrozměrném prostoru (jakým může být podle relativistické kosmologie náš vesmír): jedná se o neohraničený, ale co do objemu konečný prostor, do něhož se "vejde" jen konečný počet galaxií a hvězd - viz kap.5, §5.2 "Einsteinův a deSitterův vesmír. Kosmologická konstanta.".

Asymptotické vlastnosti prostoročasu
Všimněme si nyní některých obecných aspektů asymptotické struktury prostoročasu, tj. jeho vlastností v nekonečnu. Jestliže sledujeme nějaký prostorově ohraničený děj, např. vývoj hvězdy nebo i celé galaxie, budou hodnoty křivosti v dostatečně velkém okolí takového procesu o mnoho řádů větší než průměrná křivost "pozadí" (globální kosmologická křivost vesmíru). Z hlediska takového jevu lze kosmologickou křivost pozadí (vesmíru) zanedbat, považovat ji za nulovou a daný proces vyšetřovat na pozadí asymptoticky plochého prostoročasu. Fakticky téměř ve všech fyzikálních situacích, kromě sledování vesmíru jako celku (tj. v kosmologii), můžeme prostoročas považovat za asymptoticky rovinný. To má velký význam, protože pouze v asymptoticky plochém prostoročase mají některé základní fyzikální charakteristiky, jako je energie, náboj, hybnost, dobře definovaný globální smysl (viz též §2.8 "Specifické vlastnosti gravitační energie").

Obr.3.4. Prostoročasový diagram evoluce ostrovní fyzikální soustavy, během níž se část celkové hmoty~energie vyzářila ve formě elektromagnetických nebo gravitačních vln. Tato vyzářená energie je dána rozdílem celkové hmotnosti nikoliv na prostorových hyperplochách S2 a S1, ale na izotropních hyperplochách I2 a I1.

Jedna z typických situací vyskytujících se při studiu ohraničených fyzikálních dějů, je schématicky znázorněna na prostoročasovém diagramu podle obr.3.4. Nechť ostrovní fyzikální soustava, mající na hyperploše S₁ celkovou hmotnost (~energii) M₁, v průběhu své evoluce vyzáří během relativně krátkého časového intervalu část své energie ve formě gravitačních nebo elektromagnetických vln (může se jednat třebas o nesférický gravitační kolaps hvězdy), takže potom bude mít menší hmotnost M₂. Jak bylo ukázáno v §2.8, pod celkovou hmotností (energií) fyzikální soustavy se v obecné teorii relativity rozumí gravitační hmotnost měřená v asymptoticky rovinné oblasti příslušné prostorové hyperplochy. Stanovení hmotnosti M₁ na hyperploše S₁ nečiní principiální potíže (pokud soustava předtím nezářila!): časová komponenta metrického tenzoru g_oo » -1 + 2M₁/r při r®Ą. Avšak stanovíme-li podobným způsobem celkovou hmotnost na hyperploše S₂, dostaneme opět hodnotu M₁ bez ohledu na to, kolik energie bylo zářením odneseno, protože hyperplocha S₂ v příslušných vzdálenostech vždy protíná všechny odcházející vlny. K této potíži nedojde, použijeme-li místo hyperploch prostorového typu S₁ a S₂ izotropních (nulových) hyperploch I₁ a I₂, jak je znázorněno na obr.3.4. Obě hyperplochy I₁ a I₂ procházejí mimo kužel vyzařovaných vln a asymptotické chování metriky na I₁ nám definuje hmotnost M₁ a asymptotioké chování metriky na I₂ dává hmotnost M₂. A rozdíl M₁ - M₂ je celková energie vyzářených vln.
  Obecně lze říci, že při sledování fyzikálních procesů v asymptoticky rovinném prostoročase je třeba vyšetřovat asymptotické chování příslušných polí. Např. elektrický náboj fyzikální soustavy je dán asymptotických chováním elektrického potenciálu nebo vektoru elektrické intenzity ("jak rychle" jdou v nekonečnu k nule), hmotnost a moment hybnosti je určován asymptotickým tvarem metriky. Právě uvedený příklad podle obr.3.4 ukazuje, že patrně nestačí provádět asymptotickou analýzu jen v oblasti "prostorového" nekonečna r®Ą, ale je třeba zjišťovat asymptotický tvar metriky a polí i v "izotropním" nekonečnu. Konkrétně se budeme jednotlivými typy nekonečna zabývat v následujícím §3.2 "Minkowského rovinný prostoročas a asymptotická struktura".

Konformní asymptotická analýza
Při asymptotické analýze je nepříjemné to, že je třeba sledovat chování fyzikálních veličin kdesi v nekonečnu, a to nejen v obvyklém typu "prostorového" nebo "časového" nekonečna. Je nutno počítat limity pro nekonečné hodnoty souřadnic a kromě toho si lze jen obtížně představit strukturu příslušných asymptotických oblastí prostoročasu. Pro sledování globálních vlastností prostoročasu a asymptotického chování fyzikálních veličin (tj. jejich chování v nekonečně vzdálených oblastech prostoročasu) jsou velmi užitečné Penroseovy konformní metody [201],[106],[203]. Konformním zobrazením prostoročasu (M,g) na prostoročas (M^,g^) se nazývá zobrazení M®M^ takové, při němž se metrika transformuje podle vztahu g^_ik = W.g_ik a prostoročasový element intervalu ds^² = W².g_ikdxⁱdx^k = W².ds². Konformní koeficient W = W(xⁱ) může být sice v každém bodě jiný, avšak rozměry ve všech směrech (včetně časového) jsou v daném bodě násobeny vždy stejným číslem. Všechna měřítka v daném místě jsou izotropně "roztažena" nebo "smrštěna"; proto se při konformním zobrazení lokálně zachovávají okolí bodů, úhly i poměry délek: g_ikAⁱA^k/g_ikBⁱB^k = g^_ikAⁱA^k/g^_ikBⁱB^k. Konformním zobrazením se tedy nemění ani struktura světelných kuželů, tj. lokálně jejich tvary a sklony:

Penroseova metoda spočívá v použití vhodného konformního zobrazení provádějícího pro oblasti nekonečna v M nekonečně velké "stlačení" všech rozměrů (_xi_®Ąlim W(xⁱ) = 0) tak, aby tyto oblasti nekonečna mohly mít v M^ konečné souřadnice. Pomocí takového konformního zobrazení se převádí celý nekonečný prostoročas M na určitou konečnou oblast M^, jejíž hranice ¶ M^ jsou konformním obrazem oblastí nekonečna původního neomezeného prostoročasu M (obr.3.5). Asymptotické vlastnosti geometrie a fyzikálních veličin je možno potom sledovat analýzou jejich chování na hranicích konformního obrazu, kde mají souřadnice konečné hodnoty. Podmínkou je zde ovšem konformní invariantnost rovnic příslušných fyzikálních veličin.

Obr.3.5. Pomocí vhodného konformního zobrazení lze celý nekonečný prostoročas M převést na konečnou oblast M^ tak, že vlastní body M se zobrazují na vnitřek M^ a oblasti nekonečna v M na hranici ¶M^. Struktura světelných kuželů v M^ je přitom stejná jako v původním M.

Vhodnou funkcí W pro takové konformní zobrazení je např. funkce arkustangens, která převádí interval (-Ą,+Ą) na interval (-p/2,+p/2). Užitečnost Penroseovy metody se projeví na několika místech v dalším výkladu, kde konformní prostoročasové diagramy budou použity pro zobrazení globální struktury různých druhů prostoročasu a při studiu vlastností černých děr.

Analytická extenze prostoročasu
Prostoročas (M', g') se nazývá analytickým rozšířením (extenzí) prostoročasu (M,g), jestliže je (M,g) izometrický nějaké vlastní podmnožině (M',g'). Pokud existuje taková extenze, prostoročas M je rozšiřitelný, tj. může být "zvětšen" jako prostoročas; potom musíme považovat za body tohoto prostoročasu i body M'. Není totiž důvod, proč by se struktura prostoročasu měla omezit na stadiu prostoročasu M, když stejným právem by mohla pokračovat do stadia prostoročasu M'. Jedině nerozšiřitelný prostoročas lze považovat za "kompletní"; rozšiřitelný prostoročas naopak vzbuzuje podezření, že je to jen "část" skutečného prostoročasu.
  Jestliže hledáme řešení Einsteinových rovnic, pracujeme v určité soustavě souřadnic, ve které nalezneme příslušné řešení, tj. metriku prostoročasu g. Často se stává, že takto nalezená metrika není ve všech místech regulární (např. Schwarzschildovo řešení - §3.4). Vyslovit závěr, že geometrické vlastnosti prostoročasu jsou v těchto místech singulární, by však bylo předčasné (ukvapené), protože singulární chování komponent metrického tenzoru může být způsobeno jen nevhodností použité souřadnicové soustavy (viz §3.4, obr.3.15). V takových případech se pokoušíme nejprve přechodem k jiné souřadnicové soustavě singulární chování metriky odstranit; pokud se to aspoň v některých místech podaří, bude řešení v této nové souřadnicové soustavě analytickým rozšířením původního řešení, protože obsáhne větší část prostoročasu.
  Postup analytické extenze může být tedy zhruba následující: Máme nalezeno určité řešení (M,g) Einsteinových rovnic pro danou fyzikální situaci v nějaké souřadnicové soustavě xⁱ. Přejdeme k nové soustavě souřadnic x'ⁱ, např. za účelem odstranění patologického chování metrických koeficientů g_ik vlivem nevhodné původní souřadné soustavy - vznikne metrika g'_ik. Analytickou extenzi (M',g') dostaneme tak, že jako metriku použijeme g' a jako M' maximální varietu, na níž má g' požadované analytické vlastnosti (tj. má spojité derivace do druhého řádu). Může se stát, že takto získaný prostoročas M' je "větší" než M, takže původní prostoročas M nebyl "celý" a při odstraňování singulárního chování metrických komponent se nám zároveň podaří najít analytické rozšíření. Pokud je takto nalezený prostoročas M' již dále nerozšiřitelný, jedná se o úplnou (maximální) analytickou extenzi příslušného řešení (geometrie). Konkrétní ilustrace těchto postupů bude ukázána v §3.4 a 3.5 na Schwarzschildově a Reissnerově-Nordströmově řešení.

2.9. Geometrodynamická soustava jednotek		3.2. Minkowského rovinný prostoročas a asymptotická struktura

Vojtěch Ullmann