 |
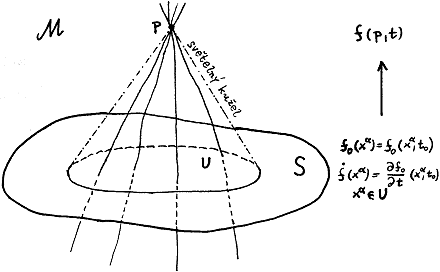
Obr.3.8. Hodnoty polí v bodě p jsou jednoznačně určeny počátečními hodnotami polí (a jejich derivací) v podmnožině U prostorové hyperplochy S. |
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | Gravitace, černé díry a fyzika |
Kapitola 3
GEOMETRIE A
TOPOLOGIE PROSTOROČASU
3.1. Geometricko-topologické vlastnosti
prostoročasu
3.2. Minkowského rovinný
prostoročas a asymptotická struktura
3.3. Cauchyova úloha, příčinnost a horizonty
3.4. Schwarzschildova geometrie
3.5. Reissnerova-Nordströmova
geometrie
3.6. Kerrova a Kerrova-Newmanova
geometrie
3.7. Prostoročasové singularity
3.8. Hawkingovy a Penroseovy
teorémy o singularitách
3.9. Nahé singularity a princip
"kosmické cenzury"
3.3. Cauchyova úloha, příčinnost a horizonty
Příčinné vztahy
mezi událostmi v prostoru a v čase jsou základem našeho
poznání objektivní reality. Ze speciální teorie relativity
víme, že pohyb hmoty a přenos energie i informace se může
dít pouze uvnitř prostoročasového světelného kuželu (viz
§1.6). Protože všechno, co platí ve speciální teorii
relativity, platí i v obecné teorii relativity, avšak
lokálně - proud hmoty, energie a informace bude probíhat vždy uvnitř
lokálního prostoročasového světelného kuželu, jak jsme si
to postulovali v §3.1. Lokální příčinnost je tedy dána
požadavkem lokální platnosti speciální teorie relativity
(STR). Otázky globální příčinnosti již nejsou tak
triviální a musí být zodpovězeny analýzou globálních
geometrických a topologických vlastností daného
prostoročasu, jež je řešením Einsteinových
rovnic.
Tvar a sklon světelných kuželů je dán
metrickým tenzorem v daném místě prostoročasu. Gravitace je tedy tou silou, která určuje
kauzální strukturu vesmíru *) - vymezuje, které události
prostoročasu mohou spolu příčinně souviset a které nikoliv.
Jak uvidíme dále, při dostatečně silném gravitačním poli
(zakřivení prostoročasu) se objevují horizonty událostí a
oblasti prostoročasu, které jsou příčinně
odděleny od ostatních částí prostoročasu.
*) Které události spolu
opravdu příčinně souvisejí, to záleží na konkrétní
situaci. Vlastnosti prostoru
a času nám dávají pouze jistá omezení - určují, které
události spolu v principu mohou nebo nemohou příčinně
souviset.
Lokální příčinnost v prostoročase M je možno vyjádřit též
následujícím způsobem podle obr.3.8. Mějme bod pÎM, takový, že každá světočára
časového nebo světelného typu procházející tímto bodem
protíná hyperplochu S (prostorového typu). UĚS označíme množinu všech bodů na S,
ve kterých ji mohou protínat světočáry časového nebo
světelného charakteru procházející bodem p. Jinými slovy, U je množina těch bodů na S, z nichž
je možno bodu p
dosáhnout pohybem po časových nebo izotropních
světočárách. Požadavek kauzality pak znamená, že hodnoty
všech polí v bodě p budou jednoznačně určeny
hodnotami polí a jejích derivací (do určitého konečného
řádu) právě v množině U. Znalost polí (a jejich
derivací) jen v části U obecně nestačí k
jednoznačnému stanovení polí v bodě p.
Taková formulace principu kauzality již úzce souvisí s tzv. Cauchyho úlohou, viz níže.
 |
Obr.3.8. Hodnoty polí v bodě p jsou jednoznačně určeny počátečními hodnotami polí (a jejich derivací) v podmnožině U prostorové hyperplochy S. |
Cauchyova úloha v matematické analýze obecně představuje postup nalezení řešení pro diferenciální rovnici při daných počátečních podmínkách (např. v daném bodě x jsou zadány hodnoty funkce f, jak je zjednodušeně naznačeno na obr.3.8 vpravo). Tyto postupy rozpracoval v r.1842 francouzský matematik A.L.Cauchy. V našem kontextu trajektorií částic a evoluce polí v prostoročase se budeme zabývat především tím, jak počáteční podmínky na určitých řezech (hyperplochách) prostoročasem mohou ovlivňovat evoluci polí a metriky v jiných oblastech časoprostoru, podle Einsteinových diferenciálních rovnic GTR.
Geometrie a kauzalita v
prostoročase
Než si ale
budeme formulovat vlastní Cauchyovu úlohu, rozebereme si
geometrické aspekty příčinných vztahů v prostoročase.
Budeme předpokládat, že prostoročas je časově orientovaný,
což znamená:
| Definice 3.1 (časově orientovaný prostoročas) |
| Prostoročas M se
nazývá časově
orientovaný, jestliže v každém
bodě prostoročasu lze všechny vektory časového nebo
izotropního typu rozdělit na dvě skupiny: vektory směřující do budoucnosti a vektory směřující do minulosti. |
V praxi toto rozlišení
může být uskutečněno za pomoci nevratných
fyzikálních dějů jako je růst entropie izolovaných
termodynamických soustav, vyzařování energie
elektromagnetickými nebo gravitačními vlnami, expanze vesmíru
(což je však značně problematický ukazatel směru toku
času) - viz §5.6, pasáž "Šipka času").
V časově orientovaném prostoročase
již můžeme zavést řadu příčinných vztahů mezi
jednotlivými událostmi i celými oblastmi prostoročasu :
| Definice 3.2 (kauzální vztahy v prostoročase) |
|
Je třeba upozornit, že výrok "událost B příčinně následuje za událostí A" neznamená, že B musí být nutně přímým důsledkem události A, ale jen to, že událost B by mohla být principiálně ovlivnitelná událostí A.
Uzavřené
světočáry a cestování časem
V §3.1 jsme viděli,
že různé druhy "ztotožnění" v prostorových
rozměrech mohou vést k různým druhům globální topologie
prostoru, aniž se to projeví na lokální geometrické
struktuře, na lokálním průběhu fyzikálních jevů.
Jestliže bychom provedli podobné "ztotožnění" v čase
(časové škále), objevily by se v prostoročasu uzavřené časové křivky - uzavřené světočáry
časového typu; ty se však zdají být z fyzikálních důvodů
nepřípustné, protože jsou ve sporu s principem kauzality. Jestliže bychom totiž na
časové ose vzali dva body (t1,x,y,z) a (t2,x,y,z) takové, že t1 < t2 a tyto
ztotožnili (t1,x,y,z)
ş (t2,x,y,z),
pak zásah do nějakého fyzikálního jevu v místě (x,y,z) v
čase t2 by v tomto místě způsobil změny v
čase t1, tedy v minulosti.
Fiktivní možnost vytvoření uzavřených časových smyček si ukážeme pomocí koncepce
tzv. červí díry (podrobněji popsané v závěru §4.4,
pasáži "Černé
díry: mosty do jiných vesmírů? Stroje času?").
Existence uzavřených světočar
časového typu tedy zřejmě vede k logickým paradoxům
toho druhu, že po uzavřené časové světočáře bychom se
mohli v čase vrátit a zabít svou babičku ještě předtím,
než stačila počít vaši maminku (a ta pak vás...); popř.
zabít vlastní rodiče před svým narozením (paradox lze formulovat pomocí různých rodinných
vztahů). Vaše
bytí, nutné k vykonání takové vraždy, by se pak stalo nekonzistentní s výsledkem tohoto zločinu. Nebo
kosmonaut v raketě by se po takové uzavřené časové
světočáře mohl vrátit v prostoru a čase zpět ke svému
startu, poškodit raketu a samému sobě v tomto původním
startu zabránit :
| Paradox kosmonauta - zmařeného startu a kosmického letu | |
 |
Kosmonaut odstartuje v raketě do vesmíru a vletí do ústí "červí díry", fungující jako "stroj času". Po uzavřené časové světočáře by se pak mohl vrátit v prostoru a čase zpět ke svému startu, poškodit raketu a samému sobě v tomto původním startu zabránit. |
Změnili jsme minulost -
nejdříve se stalo to, co jsme chtěli učinit a pak teprve se
rozhodneme, že to uděláme - nebo neuděláme. Jak by potom
bylo možné smířit dvě sporné
alternativy
v budoucnu: naši existenci, když jsme se nemohli narodit?; nebo
let kosmonauta v raketě, když si sám zabránil odstartovat?
Takový cestovatel by se tudíž ani nemohl vrátit do minulosti
a vykonat zmíněné zásahy. Cestovatel pomocí cesty časem do
minulosti by mohl zabránit tomu, aby do ní odcestoval... Jak by
bylo možné, aby se nějaká událost stala a přitom nestala?
Situace, kdy budoucí reakce
zruší předchozí akci, nemá logické řešení. Takovým
logickým paradoxům je třeba se vyhnout!
Tyto podivné, ba "patologické"
důsledky cestování časem vedou přirozeně k snaze najít
mechanismy, které by zabránily prostoročasovým událostem
"dělat takové hlouposti". S.Hawking vyslovil
hypotézu nazvanou "princip
ochrany chronologie" - ochrany
časové posloupnosti, který by kauzální smyčky zakazoval (srov. s
Penroseovým "principem kosmické cenzury"
zakazujícím nahé singularity v §3.9 "Nahé
singularity a princip "kosmické cenzury"").
Některé mechanismy tohoto druhu zde budou diskutovány níže a
též v závěru §4.4, pasáži "Černé
díry: mosty do jiných vesmírů? Stroje času?".
Zdálo by se, že takové logické
paradoxy a spory s principem kauzality při cestování časem
vznikají jen za předpokladu "svobody
vůle"
- že příslušný subjekt může podle svého rozhodnutí
udělat v principu jakýkoliv zásah do běžících dějů. V
případě, že by svoboda vůle neexistovala (a v klasické fyzice opravdu nic takového neexistuje), nemuselo by dojít ke sporu s principem
kauzality: cestovatel časem minulost nemění, protože byl
imanentně vždy její součástí (může minulost naplnit,
nikoli ji změnit). Vesmír si lze představit jako
"hotovou" a jedinečnou 4-rozměrnou varietu, do které
jsou jednotlivé světočáry již "zakomponovány". Z
tohoto pohledu všechny události na uzavřené časové
světočáře by mohly být již "synchronizovány"
tak, že by na sebe vzájemně působily bezesporně v
uzavřeném cyklu - byly by self-konzistentní. Vezmeme-li však v úvahu nevratnost evoluce vesmíru (existence
disipativních procesů, 2.zákon termodynamiky), je existence
uzavřených časových křivek fyzikálně nepravděpodobná, protože situace v pozdějším
čase t2 nemůže být totožná se situací v
dřívějším čase t1. Uzavřené křivky vedoucí ke
"stroji času" by tedy snad mohly fungovat nanejvýš v
rámci elementárních částic.
Na obrázku níže - "Paradox kulečníkové koule" je však ukázán
příklad rozporného chování, kde není
žádné subjektivní rozhodování a "svoboda vůle",
jedná se o čistě mechanický experiment ..!..
| Paradox kulečníkové koule - rozporných trajektorií těles | |
 |
Z určité
počáteční polohy je ťuknutím tága vyslána
kulečníková koule vhodnou rychlostí směrem k
pravému ústí červí díry, fungující jako
"stroj času" - po trajektorii A. Tato
koule prolétne červí dírou, vrátí se zpátky v
čase a vylétne z levého ústí ještě předtím, než
po trajektorii A vlétla do pravého ústí.
Může pak narazit "sama do sebe" (do své "mladší verze"), odklonit dráhu A do alternativní
trajektorie B, mimo červí díru. Tím však sama
sobě zabrání vletět do pravého ústí - a potažmo
narazit sama do sebe. Při pohybu, začínajícím s přesně stejnými počátečními podmínkami (ze stejné polohy a stejnou rychlostí), vznikají tak dvě rozporné trajektorie A a B, po nichž by se koule současně pohybovala. Při vhodném nasměrování může koule proletět červí dírou několikrát - existuje nekonečné množství trajektorií, lišících se počtem průletů červí dírou. |
Logický vývod z paradoxů :
Žádnému makroskopickému objektu - pozorovateli - se
nepodaří zpětně ovlivnit to, co se již jednou odehrálo.
Nemohou zřejmě existovat "poutníci časem", kteří
by mohli ohrozit chod historie. Minulost můžeme pozorovat jako
svědkové, nikoli jako aktivní účastníci. Když se díváme
do vzdáleného vesmíru, vidíme vlastně vzdálenou minulost,
kterou k nám přeneslo světlo během své cesty trvající
statisíce, miliony či dokonce miliardy let. Budoucnost za minulost však obrátit
nedokážeme!
Mnoho
vesmírů ?
Určitou sci-fi možnost, jak obejít spory a logické paradoxy
při cestování časem, by mohla představovat i Everettova a
Wheelerova kvantově-mechanická hypotéza "mnoha
světů" [79] (je diskutována i v §5.7 "Antropický
princip a existence více vesmírů"),
podle níž vesmír neobsahuje jen jedinou unikátní historii
světa, ale mnoho historií paralelních. Vždy,
když dojde k nějaké interakci (či z hlediska pozorovatele k
"rozhodnutí" či k náhodné události), dojde k
"rozvětvení historie" do různých vesmírů. Pokud
cestovatel časem odletí zpět do minulosti a změní tam svou
historii (třeba zabije svou matku před svým narozením), dojde
k "odbočení" na jinou historii v příslušném
vesmíru, který bude paralelně koexistovat s původním
vesmírem - cestovatel se vlastně přesune do jiného
vesmíru, kde bude součástí změněné historie. K
žádnému nepřípustnému ovlivnění budoucnosti
stávajícího - našeho, výchozího - vesmíru nedojde.
Fyzikální
cestování v čase ?
Myšlenka cestování časem velmi vzrušuje
lidskou fantazii a evokuje odvěké sny o věčném mládí a
překonání smrti, nápravě či odvrácení minulých chyb nebo
předpovědi budoucích důsledků našich rozhodnutí -
nahlédnutí toho, co nám osud připravuje, popř. jeho
zvrácení. V rámci Newtonovské fyziky,
vzhledem k její koncepci absolutního času,
bylo "cestování časem" zcela neuskutečnitelné
*). Objevovalo se jen v tehdy začínající
vědecko-fantastické literatuře, především v proslulém
sci-fi románu H.G.Wellse: "Stroj času" z r.1895.
*) Pozn.:
Samozřejmě s cestováním v čase nemají nic
společného časové posuny několika hodin při
cestování letadlem třebas mezi Evropou a Amerikou. Zde to
souvisí jen s rychlým prolétáním mezi dohodnutými časovými
pásmy, které jsou důsledkem našeho měření denního
času pomocí otáčení Země kolem osy. Neposunujeme se v
čase, ale jen v označení času dohodnutými čísly -
denními hodinami, které jsou posunuty podle zeměpisné délky.
Teprve v
rámci speciální teorie relativity,
umožňující ovlivňování rychlosti toku času pohybem, či obecné
teorie relativity ukazující ovlivňování běhu času
gravitací, se cestování časem začalo považovat v
určitém smyslu za fyzikálně reálnou možnost.
Pokud se nějaké těleso přiblíží rychlosti světla, nebo
pobývá v silném gravitačním poli (třebas poblíž černé
díry), čas se pro něj z hlediska ostatních zpomalí, takže
vlastně cestuje do budoucnosti. Ale žádný z těchto způsobů
neumožňuje vrátit se do výchozí doby - cesta do budoucnosti
je jednosměrná.
Relativistická
dilatace času ve STR umožňuje v principu
poměrně snadné cestování do budoucnosti.
Pozorovateli, pohybujícímu se vysokou rychlostí blízkou
rychlosti světla ubíhá čas pomaleji než
referenčnímu "klidovému" pozorovateli, takže může
i velký časový interval v klidové vztažné soustavě
překlenout za podstatně kratší interval vlastního času, tj.
"cestovat do budoucnosti" klidové
referenční soustavy; přitom by se pozorovatel stále pohyboval
uvnitř svého prostoročasového světelného kužele (viz
prostoročasový diagram na obr.1.6). K cestování do
minulosti by se však světočára pozorovatele musela
ohnout a zatočit zpět směrem dolů a vytvořit smyčku,
k čemuž by v některých bodech musela vzhledem k vertikále
být nakloněna pod úhlem větším než 45° - bylo by potřeba
dosáhnout překročení rychlosti světla, což
v rámci STR (Minkowského prostoročasu s
obvyklou Eukleidovou topologií) není
možné.
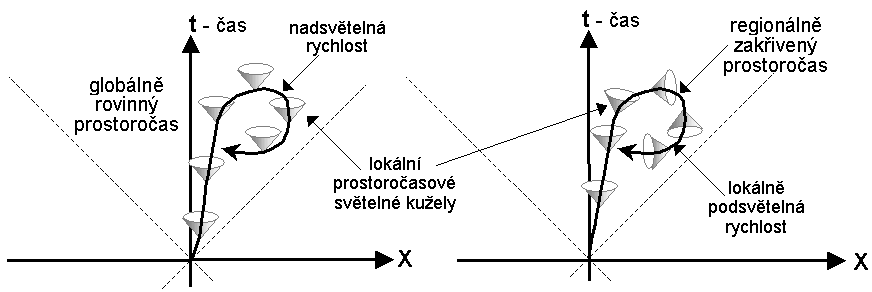 |
| Kinematické efekty
teorie relativity nabízejí - aspoň formálně - dvě
možnosti cestování v čase do minulosti: 1. V rovinném prostoročase STR pomocí pohybu nadsvětelnou rychlostí (na obrázku vlevo); 2. V zakřiveném prostoročase obecné teorie relativity pomocí pohybu lokálně podsvětelnou rychlostí uvnitř sekvence vhodně nakloněných světelných kuželů v oblasti se silně zakřivenou geometrií prostoročasu (obr. vpravo). Další hypotetickou možností je složitá topologická struktura prostoročasu - "zkratky, tunely, červí díry" (diskutováno níže). |
Obecná teorie relativity,
jakožto fyzika gravitace a zakřiveného prostoročasu, v
zásadě otvírá možnosti cestování do budoucnosti i do
minulosti. Cestování do budoucnosti je zde opět v principu
poměrně snadné: pozorovateli stačí dostatečně dlouho
pobýt v místě se silnou gravitací (vysokým gravitačním
potenciálem), kde čas podle vztahu (2.36) ubíhá pomaleji, aby
se do výchozího místa vrátil v době, kdy tam mezitím uběhl
podstatně větší interval času. V §4.3 je popsán zajímavý
jev při šíření světla v poli masívního kompaktního
objektu - efekt gravitační čočky. Takovéto
šíření světla po zakřivených drahách vede nejen k
zajímavým optickým efektům vícenásobných obrazů, ale i k různým
časovým posuvům podél různých drah paprsků.
Pozorovatel pohybující se po vhodné kratší dráze rychlostí
blízkou c by v zásadě mohl "předběhnout"
světelné fotony pohybující se po jiné (delší) dráze kolem
gravitujícího tělesa; v extrémních případech pohybů
rychlostí blízkou c kolem supermsasívního tělesa (či
dokonce kolem rotující Kerrovy černé díry) by těchto
časových rozdílů bylo možno v principu využít k
cestování v čase.
Gravitace
ovlivňuje jak běh času, tak i prostorová měřítka a
proporce. V takovém globálně zakřiveném prostoročase se
mohou vyskytovat jakési "zkratky přes prostoročas"
- hypotetické "červí díry",
které umožňují pozorovateli v jistém smyslu
"předběhnout" světelný paprsek a
"cestovat" zpět do minulosti. Přitom lokálně vše
běží podle STR, rychlost světla není nikde překročena. Je
to podobné, jako když námořník plující zde na Zemi po
oceánu stále směrem vpřed může po čase zjistit, že se
vrátil do místa, odkud vyplul. Při pohybu v zakřiveném
prostoročase může v principu pozorovatel po čase zjistit, že
se dostal nejen do výchozího místa, ale že znovu
"navštívil" událost ze své minulosti, i když
lokálně ze svého pohledu po celou dobu jeho čas tekl směrem
do budoucnosti..?..
Topologicky
složitý, vícenásobně souvislý vesmír ?
Lokální geometrie prostoročasu je určena
rozložením hmoty ve vesmíru - hmota~energie zakřivuje
prostoročas, v němž se pak tělesa a částice pohybují po
geotedikách, představujících nejrovnější možné
trajektorie. Zakřivení prostoročasu je popsáno Einsteinovými
rovnicemi, jejichž aplikace na vesmír za příslušných
zjednodušujících předpokladů vede k Fridmanovým rovnicím
(5.23) popisujícím vesmír, jehož prostor může mít kladnou,
zápornou či nulovou křivost, viz §5.3.
Tato lokální geometrie však obecně nic
neříká o globálním tvaru, tj. o celkové topologii
vesmíru. Ve standardní relativistické kosmologii se uvažuje
jednoduše souvislý vesmír (s topologií koule), na němž
pracují Einsteinovy, DeSitterovy či Fridmanovy kosmologické
modely. Teoreticky by však vesmír mohl mít složitější, vícenásobně
souvislou topologii, s různými topologickými tunely
či ztotožněními různých částí; takový vesmír by
dokonce mohl vypadat jako jakýsi "ementál".
Složitá vícenásobně souvislá
topologická struktura prostoru konečného vesmíru by měla
zajímavé důsledky pro to, co pozorovatel v takovém vesmíru
vidí: v principu by mohl uvidět mnohonásobné obrazy
galaxií, hvězd, i sama sebe, jako v zrcadlovém bludišti. A to
časově v různých fázích vývoje. Nebylo by
vyloučeno, že když pozorujeme nějakou vzdálenou galaxii,
mohlo by se jednat třebas i o naši vlastní Galaxii před
dávnou dobou miliard let! Astronomicky rozpoznat, že dvě
pozorované galaxie jsou vlastně jednou a toutéž galaxií,
zobrazenou průchodem světla přes složitou topologickou
strukturu vesmíru, by však bylo velice obtížné, ne-li
beznadějné. Viděli bychom je totiž z různého úhlu pohledu
a hlavně, vzhledem k prostorovým škálám mnoha miliard
světelných let, ve zcela různých fázích vývoje, změněné
k nepoznání.
Určitou možností, jak
získat aspoň částečné indicie pro určité topologické
struktury vesmíru, by mohlo být detailní měření vlastností
mikrovlnného reliktního záření - jeho
homogenity, fluktuací (v závislosti na úhlové vzdálenosti i
na vlnové délce), polarizace. Již v době oddělení záření
od látky byly ve vesmíru zárodky budoucích struktur, takže
tyto fotony procházely místy s různým gravitačním
potenciálem, což vedlo k malým změnám jejich energie a
vlnové délky - k nepatrnému ochlazení či ohřevu. Tyto fluktuace
by měly být patrné i nyní, jakožto nepatrně teplejší a
chladnější "skvrny" v jinak izotropním rozložení
reliktního záření - představují jakýsi
"paleontologický otisk" struktur raného vesmíru.
Rozdíl teplot je velmi malý, řádově 10-5stupně, ale podrobnou "teplotní mapu"
raného vesmíru se již podařilo pomocí citlivých
satelitních přístrojů změřit - §5.4, pasáž "Mikrovlnné reliktní záření - posel
zpráv o raném vesmíru").
Všechny tyto
teoretické spekulace nemají zatím žádné
opodstatnění v astronomických pozorováních, takže
při výkladu relativistické kosmologie v kap.5 se budeme
přidržovat nejjednoduššího a ze současného pohledu
přirozeného předpokladu jednoduše souvislé topologické
struktury vesmíru. Určitou výjimkou
budou snad jen diskuse o možnosti existence více
vesmírů; ani zde se však nebude jednat o zavádění
nějaké apriorní složité topologie, nýbrž o hypotetické
topologické vlastnosti "indukované" bouřlivými kvantově-gravitačními
procesy při počátku vesmíru.
OTR v určitých speciálních řešeních
Einsteinových gravitačních rovnic z matematického hlediska připouští
kauzální smyčky. Je to např. v Gödelově řešení
popisujícím rotující vesmír [104], nebo v prostoročase
kolem dlouhého masívního válce rotujícího vysokou
rychlostí (větší než c/2). Rotace prostoročasu v takových
řešeních s sebou unáší světlo, a tedy i příčinné
vztahy mezi objekty, takovým způsobem, že umožňuje vhodným
oběhem hmotnému objektu pohyb po uzavřené časové
světočáře, aniž by byla překročena rychlost světla v
okolí objektu. Takováto řešení jsou však jen určitými matematickými
kuriozitami, které se nikde v přírodě nerealizují.
Totéž patrně platí i o prstencových singularitách v
Kerrově geometrii (§3.6 "Kerrova
a Kerrova-Newmanova geometrie") uvnitř rotujících černých děr, či o
geometricko-topologických konstrukcích zahrnujících tzv.
"červí díry" v prostoročase - viz
§4.4.
Geometricko-topologické možnosti
"cestování" v prostoru a čase v souvislostmi s
vlastnostmi prostoročasu černých děr budou diskutovány v
§4.4., pasáž "Černé díry: mosty do jiných
vesmírů? Stroje času?", systematicky pak v práci (sylabu)
"Cesty časem: fantazie nebo fyzikální
realita?". Některé související úvahy o
směru toku času jsou dále nastíněny v §5.6, pasáž "Šipka času".
Pro topologii "cestování
časem" jsou důležité tzv. Cauchyovy
horizonty (podrobněji rozebírané níže), které m.j. vymezují a oddělují
prostoročasové oblasti, v nichž je a není možné cestování
v čase do minulosti a budoucnosti.
Cauchyho oblast a
horizont. Horizont událostí.
V dalším
budeme předpokládat, že v reálném prostoročase se
uzavřené světočáry časového ani izotropního charakteru
nevyskytují, neboli jak se někdy říká, je splněna rozumná chronologická podmínka. Potom v prostoročase pro
každou hyperplochu S prostorového typu existuje
určitá maximální oblast prostoročasu, ve které je možno
jednoznačně a úplně předpovědět fyzikální jevy na
základě znalostí počátečních podmínek na S (obr.3.9).
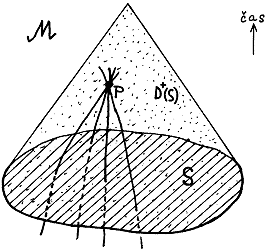 |
Obr.3.9. Na základě znalosti počátečních podmínek na prostorové hyperploše S lze v Cauchyho oblasti D+(S) jednoznačně předpovědět budoucnost, jestliže každá světočára časového nebo izotropního typu procházející libovolným bodem p Î D+(S) v minulosti protnula hyperplochu S. |
| Definice 3.3 (Cauchyho oblast *) : |
| Cauchyho oblast budoucnosti D+(S), resp. minulosti D-(S), hyperplochy S prostorového typu se nazývá množina všech takových bodů pÎM, pro které každá světočára časového nebo izotropního typu procházející bodem p protíná S v minulosti (resp. v budoucnosti). |
| Definice 3.4 (Cauchyho hyperplocha *): |
| Hyperplooha S, kterou protíná každá neprodloužitelná světočára časového nebo izotropního typu, tj. pro kterou D+(S) Č D-(S) = M, se nazývá globální Cauchyova hyperplocha. |
Jestliže tedy v
prostoročase M existuje globální Cauchyho
hyperplocha, potom na základě potřebného souboru
počátečních podmínek na této hyperploše je možno
jednoznačně určit fyzikální situaci v
celém M, tj. předpovědět
hodnoty polí a polohy a pohyby všech částic v libovolném
časovém okamžiku v budoucnosti nebo minulosti. Taková je
situace třebas v plochém Minkowskiho prostoročase STR, kde
např. každá hyperplocha t=const. je Cauchyovou hyperplochou. V
§3.5 "Reissnerova-Nordströmova geometrie" a 3.6 "Kerrova
a Kerrova-Newmanova geometrie" si však ukážeme, že tento
"deterministický ideál klasické fyziky" není v
některých složitějších případech splněn, globální
Cauchyho hyperplochy tam neexistují.
*) Úloha, která na
základě souboru počátečních podmínek na hyperploše S s pomocí rovnic pole rozšiřuje
řešení dále do budoucnosti (popř. do minulosti) se nazývá Cauchyova
úloha (podle
francouzského matematika A.L.Cauchyho, který se matematickou
stránkou těchto řešení v 19.stol. zabýval); odtud názvy
"Cauchyho oblast", "Cauchyho
hyperplocha" a "Cauchyho
horizont".

Obr.3.10. Příklady situací, kdy v prostoročase M neexistují globální Cauchyovy
hyperplochy (a jsou zde tedy přítomny Cauchyho horizonty H+C).
a) Z variety M je "vyříznut" určitý bod Q;
pak si můžeme představit světočáru C' procházející bodem
p,
která při sledování do minulosti skončí v místě, kde byl
Q, a tedy nepokračuje až k hyperploše t=const.
b) Varieta s
"lomenou" konformní hranicí ¶M (podobnou strukturu má např. Kerrova nebo
Reissnerova-Nordströmova geometrie). Do bodu p mohou kromě
světočar C protínajících S jít (nekontrolovatelně z S) i světočáry C' z hraničních
oblastí ¶M.
To, že nějaká hyperplocha S je Cauchyho hyperplochou je vlastnost nejen samotné hyperplochy S, ale i celého okolního prostoročasu M. Příklady situací, kdy v prostoročase neexistují globální Cauchyovy hyperplochy, jsou znázorněny na obr.3.10. Na obr.3.10a je obyčejný Minkowskiho prostoročas, z něhož je "vyříznutý" jen jediný bod Q. Nebýt toho, byla by každá hyperplocha S = (x,y,z,t | t=const.) globální Cauchyovou hyperplochou. Stav např. v bodě q je opravdu jednoznačně určen počátečními podmínkami na S. Vezmeme-li však libovolný bod p uvnitř kuželu s vrcholem ve vyříznutém bodě Q, bude sice většina světočar procházejících bodem p protínat hyperplochu S, avšak existují i světočáry, které při svém prodloužení z bodu p do minulosti narazí na odstraněný bod Q a nemohou být tedy prodlouženy až k S. Když si to časově obrátíme, můžeme říci, že z vyříznutého bodu Q mohou (světočárami nepokračujícími do minulosti) k bodu p nekontrolovatelně přicházet dodatečné "rušivé" vlivy (informace), které poruší předpověď učiněnou z hyperplochy S pro bod p na základě znalostí úplného souboru počátečních podmínek na S. V takovém prostoročase neexistuje žádná Cauchyho hyperplocha. Kuželová hyperplocha rozbíhající se od odstraněného bodu Q odděluje oblast prostoročasu, v níž lze předvídat evoluci na základě údajů na S od oblasti, kde toto nelze; taková plocha se nazývá Cauchyho horizont.
| Definice 3.5 ( Cauchyův horizont) |
| Cauchyho
horizontem budoucnosti H+C(S), resp. minulosti H-C(S) hyperplochy S se nazývá
hranice Cauchyovy oblasti D+(S) v budoucnosti, resp. hranice oblasti D-(S) v minulosti, tj. H+C(S) = { p | pÎD+(S), I+(P) Ç D+(S) = 0 } , H-C(S) = { p | pÎD-(S), I-(P) Ç D-(S) = 0 } · |
Je zřejmé, že hyperplocha S, která nemá Cauchyho horizont H+C(S) ani H-C(S) je globální Cauchyova hyperplocha. Každá ohraničená hyperplocha má Cauchyho horizont (viz obr.3.9), takže Cauchyovy horizonty tohoto původu lze považovat za "triviální" - neříkají nám nic o příčinné struktuře daného prostoročasu. Důležité jsou pouze netriviální Cauchyho horizonty, např. takové, které jsou jimi pro každou (i neohraničenou) hyperplochu prostorového charakteru ležící v určité části prostoročasu. Takové netriviální Cauchyovy horizonty budou ukázány v §3.5 "Reissnerova-Nordströmova geometrie" a 3.6 "Kerrova a Kerrova-Newmanova geometrie".
 |
Obr.3.11. Horizont částic pozorovatele O (pohybujícího se po světočaře C) v události p odděluje částice, které pozorovatel O může uvidět ze světobodu p od těch částic, které jsou oddtud zatím nepozorovatelné. |
Mějme pozorovatele O, který se prostoročasem M pohybuje po světočáře C (časového charakteru). Představíme si, že prostoročas M je zaplněn soustavou testovacích částic pohybujících se po časových světočárách. Pozorovatel O nacházející se ve světobodě (události) p může některé z těchto částic (ty, jež protínají světelný kužel minulosti bodu p) uvidět; v M se však mohou nacházet částice, jejichž světočáry neprotínají tento světelný kužel a proto je pozorovatel O ze světobodu p ještě nemůže vidět (některé z nich uvidí později) - obr.3.11. Říkáme, že pro pozorovatele O v události p existuje horizont částic oddělující oblast prostoročasu, v níž se nacházejí geodetiky částic pozorovatelných z p od oblasti prostoročasu, v nichž pohybující se částice nemohou být z p pozorovány. Horizont částic vzniká např. tehdy, když nekonečno minulosti J- je prostorového charakteru, jak je tomu na obr.3.11.
 |
Obr.3.12. Horizont částice P pohybující se po světočáře C odděluje oblasti prostoročasu, ze kterých se může částice P během jejího pohybu po světočáře C v principu pozorovat, od oblastí, ze kterých ji nikdy spatřit nelze. |
Částici pohybující
se po světočáře C je možno z určitých oblastí
prostoročasu pozorovat, avšak obecně v M mohou existovat oblasti, ze kterých ji
principiálně pozorovat nelze (obr.3.12). Hranice oddělující
tyto dvě oblasti prostoročasu se nazývá
horizont
částice pohybující se po světočáře C.
Jak je vidět z obr.3.13, mohou v obecném
prostoročase pro pozorovatele O pohybujícího se po
světočáře C existovat události, které nemůže
nikdy uvidět - říkáme, že tyto události
jsou pro pozorovatele O skryty za horizontem událostí. Horizontem
událostí (budoucnosti) pro pozorovatele O, pohybujícího se po
světočáře C, nazýváme plochu oddělující ty
oblasti prostoročasu, jejichž světobody (události) mohou být
pozorovatelem O při jeho pohybu po světočáře C
spatřeny, od oblastí, které pozorovatel O nemůže z C nikdy uvidět. Z obr.3.13
vidíme, že horizont událostí pro geodetického pozorovatele
vzniká např. tehdy, když J+ je prostorového charakteru. V
Minkowskiho prostoročase žádný geodeticky se pohybující
pozorovatel nemá horizont událostí, protože jeho světelný
kužel postupně probíhá celý prostoročas. Avšak pozorovatel
pohybující se např. rovnoměrně zrychleně má horizont
událostí budoucnosti (tzv. Rindlerův horizont).
 |
Obr.3.13. Horizont událostí pro pozorovatele O pohybujícího se po světočáře C odděluje ty události, které jsou pro O během jeho pohybu po C pozorovatelné, od událostí, které nemůže ze světočáry C nikdy pozorovat. |
Horizont událostí pro pozorovatele O závisí na jeho konkrétním pohybu a nedává tedy zcela jednoznačnou a objektivní informaci o kauzální struktuře daného prostoročasu. Vyslovit určitější soudy o příčinné struktuře prostoročasu můžeme tehdy, když v něm nalezneme takový horizont událostí, který jím bude pro určitou širší třídu pozorovatelů, např. pro všechny pozorovatele pohybující se v určité oblasti prostoročasu. Jak uvidíme dále (§3.5-3.6 a kapitola 4), největší význam mají takové horizonty událostí, které jsou jimi pro každého pozorovatele nacházejícího se v určité vnější asymptoticky rovinné oblasti, tj. pro všechny pozorovatele vzdálené v nekonečnu. Právě horizonty tohoto druhu budeme mít na mysli, když v dalším budeme mluvit o horizontech událostí.
| Definice 3.6 (horizont událostí) |
| Horizont
událostí (budoucnosti) je hranicí té
prostoročasové oblasti, ze které mohou být do
izotropního nekonečna budoucnosti J+ vedeny
světočáry, které v každém svém bodě leží
uvnitř nebo na plášti světelného kuželu budoucnosti
(tj. kauzální křivky):
horizont = ¶ J-(J+) - je hranicí minulosti plochy J+. Analogicky horizont událostí minulosti je ¶ J+(J-). |
Horizont událostí tedy odděluje oblasti prostoročasu, ze kterých částice mohou dosáhnout nekonečna J+ od oblastí, z nichž žádná částice do nekonečna uniknout nemůže (obr.3.14).
 |
Obr.3.14. Horizont událostí je hranicí rozdělující ty prostoročasové oblasti, v nichž události mohou být pozorovatelné z nekonečna J+, a oblasti z J+ principiálně nepozorovatelné. |
Důvody, proč vznikají
horizonty událostí, budou objasněny níže na konkrétních
řešeních Einsteinových rovnic; nejčastěji je to proto, že
v určitých oblastech je gravitace natolik silná, že odtud nepustí ven žádné
těleso, ani světlo. Zde si zatím všimneme jen některých
geometricko-topologických vlastností horizontu událostí.
Generátory
horizontu se
nazývají ty izotropní geodetiky, které leží v horizontu
(alespoň pro určitý konečný interval afinního parametru).
Lze si to představit tak, že na horizontu je úniková rychlost
rovna rychlosti světla a fotony se proto neustále
"vznášejí" na horizontu. R.Penrose [203] dokázal
důležitou větu o struktuře horizontu událostí budoucnosti :
| Teorém 3.1 (generátory horizontu) |
| Horizont
událostí je generován izotropními geodetikami,
které v budoucnosti nemají koncové body. Generující geodetika, která vstoupí do horizontu, tam již zůstává stále a nemůže se protnout s žádným jiným generátorem. Každou událostí na horizontu, která není světobodem vstupu generátoru, prochází právě jedna generující nulová geodetika. |
Vlastnosti prostoročasových horizontů hrají klíčovou úlohu ve fyzice černých děr, jak to několikrát uvidíme v kapitole 4.
Cauchyova úloha a evoluce
prostoročasu
Tolik tedy ve
stručnosti o obecných otázkách příčinnosti v prostoročase
(další podrobnosti lze nalézt především v monografii
[127]). Konkrétní realizace těchto kauzálních vtahů je
vyjádřena v tzv. Cauchyově úloze, která spočívá
zhruba v následujícím: Mějme Cauchyho hyperplochu
prostorového typu S, na níž známe (změříme)
počáteční hodnoty pole; pokud je pole popsáno
diferenciálními rovnicemi druhého řádu, musí pro ně
počáteční podmínky obsahovat distribuci potenciálů pole a
jejich prvních časových derivací. Tyto Cauchyovy
počáteční hodnoty splňují určité vazbové podmínky
vyplývající z rovnic pole (aby byly konzistentní s rovnicemi
daného pole). Potom můžeme pomocí rovnic pole toto
počáteční řešení rozšířit do bezprostřední
budoucnosti (popř. minulosti), tj. na nekonečně blízkou
hyperplochu S'. Opakovaným pokračováním tohoto postupu pak je
možno řešení prodloužit dále a dále do budoucnosti (a
minulosti) a stanovit tak hodnoty pole v celé Cauchyho
prostoročasové oblasti D+(S); pokud je S
globální Cauchyovou hyperplochou, lze stanovit pole v celém
prostoročase M.
Cauchyho úloha vyjadřuje deterministický charakter celé dosavadní fyziky: evoluce
každé fyzikální soustavy (pole) je jednoznačně určena
rovnicemi pohybu (rovnicemi pole) jen tehdy, když jsou zadány
příslušné počáteční podmínky. To je vidět již v
nejjednodušším případě Newtonových rovnic klasické mechaniky, které úplně určují trajektorii
částice jen při zadání patřičných počátečních
podmínek, např. polohy částice a její rychlosti v určitém
časovém okamžiku (třebas t=0). Podobný charakter má i elektrodynamika, kde je třeba:
a) V prostoročase zvolit
hyperplochu prostorového typu;
b) Na této počáteční
hyperploše zadat intenzity elektrického
pole E a magnetického pole B tak, aby byly
konzistentní s Maxwellovými rovnicemi div
B = 0, div E =
4pr, které hrají úlohu vazbových
podmínek pro počáteční hodnoty;
c) Potom pomocí druhé dvojice
Maxwellových rovnic rot E = - ¶B/¶t, rot B = j + ¶E/¶t
lze určit celou evoluci elektromagnetického pole v
budoucnosti (i v minulosti).
Skutečné počáteční podmínky se
přitom získávají měřením; jsou to výsledky pozorování a
nelze je nijak získat nebo odvodit z pohybových rovnic (tyto
rovnice na ně kladou jen jistá omezení). Není dosud žádná
teorie (ani nikdo neví, zda taková teorie
vůbec může existovat..?..), která by spolu s rovnicemi pohybu
určovala i počáteční hodnoty *).
*) Nový zajímavý přístup
k problému počátečních podmínek se nyní objevuje v kvantové
kosmologii v souvislosti s koncepcí inflační expanze velmi raného
vesmíru. Podle této koncepce struktura a evoluce vesmíru není
určena počátečními podmínkami při velkém třesku, nýbrž
je produktem pouze samotných fundamentálních zákonů fyziky -
viz §5.5.
Při aplikaci Cauchyovy úlohy na Einsteinovy gravitační rovnice je užitečné rozdělit tuto soustavu rovnic na dvě skupiny. První skupinou jsou čtyři rovnice
| Ri° - 1/2 di° R = 8p Ti° , | (3.8) |
které obsahují časové derivace metrického tenzoru pouze 1.řádu a neobsahují jeho druhé časové derivace. Tyto rovnice jsou vazbovými podmínkami pro počáteční hodnoty. Druhou skupinu tvoří šest rovnic
| Rab - 1/2 dab R = 8p Tab , | (3.9) |
které obsahují druhé
časové derivace metrického tenzoru a
popisují tedy evoluci pole. Cauchyho úloha zde potom spočívá v
tom, že:
a) Na
vhodné počáteční hyperploše prostorového charakteru máme
(zadáme, změříme) hodnoty metriky a jejích prvních
derivací, které musí vyhovovat vazbovým
podmínkám (3.8);
b) Integrací
rovnic (3.9) můžeme pak počáteční řešení rozšířit dále, tj. získat hodnoty metrického tenzoru na
jiných prostorových hyperplochách.
Cauchyho úloha pro
gravitační pole (tj. pro OTR) se však poněkud liší od
příslušné úlohy pro jiná fyzikální pole. Máme-li dvě
metriky g1 a g2 mezi nimiž existuje
difeomorfismus převádějící jednu na druhou, jsou tyto
metriky fyzikálně ekvivalentní. Existují tedy celé třídy
ekvivalentních metrik, takže řešení gravitačních rovnic
může být nalezeno jen s přesností do difeomorfismu. Aby
se tato nejednoznačnost odstranila, je třeba předepsat
určité podmínky, podobně jako se v elektrodynamice
zavádějí pro potenciály Lorentzovy podmínky k odstranění
libovůle v kalibračních transformacích. Rovnice většiny
fyzikálních polí jsou lineární; nelineární rovnice se objeví
až při interakci více polí mezi sebou. Gravitační pole
však díky své univerzálnosti vykazuje samogravitaci (interaguje "samo se
sebou") a Einsteinovy rovnice gravitačního pole jsou nelineární samy o sobě, i bez přítomnosti
jiných polí. Gravitační pole zároveň určuje metriku a tedy
i strukturu prostoročasu, ve kterém Cauchyho úlohu řešíme.
Proto obecně dopředu nevíme, jaká bude Cauchyho oblast
evoluce počáteční hyperplochy - neznáme prostoročasovou oblast,
v níž má být určeno řešení (evoluce nám může uchystat
"překvapení", třebas ve formě horizontu či
singularity).
Lze dokázat, že pokud počáteční
hodnoty vyhovují vazbovým rovnicím a pokud pro případné
negravitační pole je splněn postulát lokální příčinnosti
(viz §3.1), má Cauchyho úloha pro Einsteinovy rovnice (a
pohybové rovnice negravitační hmoty) jednoznačné
řešení (s přesností do difeomorfismu). Navíc toto
řešení v jistém smyslu spojitě závisí na
počátečních podmínkách, jak tvrdí věta, jejíž
zjednodušené znění je takové [127] :
| Teorém 3.2 (spojitost a stabilita řešení Cauchyovy úlohy) |
| Nechť g
představuje v oblasti U řešení Cauchyho úlohy pro
počáteční podmínky w na prostorové
hyperploše S. Potom pro změněné počáteční podmínky w + Dw takové, že jejich změna Dw bude malá v oblasti J-(U) Ç S, dostaneme v oblasti U nové řešení g', které bude blízké k původnímu řešení g. |
Tato věta
ospravedlňuje použití perturbační analýzy řešení
gravitačních rovnic zmíněné v §2.5, kdy ze známého
řešení při určitých počátečních podmínkách (např.
řešení pro případ přesné symetrie) se snažíme získat
informace o novém řešení při poněkud změněných
počátečních podmínkách (např. slabé narušeni symetrie).
Tyto metody mají značný význam hlavně při
rozboru gravitačního kolapsu, při němž ze známého
průběhu kolapsu ve sféricky symetrickém případě usuzujeme
na průběh reálného kolapsu bez přesné symetrie, viz
kapitolu 4.
Skutečně důsledné použití Cauchyho
úlohy ke stanovení evoluce fyzikálních soustav v přírodě
však není možné, Cauchyho úloha je jen teoretickým modelem
a návodem, jak takové řešení v principu nalézt. Příčina
je již v tom, že stanovit úplný soubor počátečních hodnot
fyzikálních veličin na Cauchyho hyperploše prostorového typu nelze
jednak dostatečně hustě a přesně, jednak vzhledem ke
konečné rychlosti šíření interakcí by k tomu bylo třeba
se dostat do budoucnosti ve všech (i velmi vzdálených) bodech,
což rovněž prakticky není možné. Při řešení Cauchyho
úlohy tedy počáteční podmínky na
Cauchyho hyperploše pouze zadáváme na podkladě určitého
teoretického modelu (např. všude vakuum,
nebo homogenní rozložení s určitou hustotou a pod.) a sledujeme evoluci tohoto
modelu.
Kromě toho se mohou (aspoň
teoreticky, viz §3.5-3.9) vyskytovat situace, kdy uvažovaný
prostoročas nemá globální Cauchyho hyperplochy a k určení
jeho evoluce pak nestačí ani sebelepší znalost úplného
souboru počátečních podmínek. Dále, Cauchyova úloha je
ztělesněním deterministického ducha klasické fyziky;
kvantové procesy zachovávají deterministické
vztahy jen na úrovni vlnových funkcí, zatímco globálně je
přesný determinismus klasické fyziky již narušen (viz
následující pasáž a též §4.7).
Determinismus
v principu, náhodnost a chaos v praxi ?
Cauchyova úloha ztělesňuje Laplaceovu mechanistickou
představu vesmíru jako "hodinového stroje":
"Rozum, který by v daný okamžik
znal všechny síly řídící přírodu a vzájemné polohy
objektů v ní, a který by byl dostatečně výkonný, aby tato
data mohl podrobit analýze, by mohl shrnout do jediného
systému pohyb největších vesmírných těles i nejlehčích
atomů: pro takový rozum by nebylo nic nejisté a budoucnost
stejně jako minulost by byly přítomné před jeho zrakem"
(Pierre Simon Laplace, 1812) - mechanistické pojetí
světa.
Je náš vesmír deterministický
jak tvrdil Laplace, nebo je ovládán náhodou,
jak se nám to často jeví v běžném životě? První slabina
Laplaceovy představy tkví v tom, že nikdy nemůžeme
počáteční stav systému změřit absolutně přesně,
takže ani budoucí vývody z něj nemohou být zcela přesné.
Předpokládalo se však, že když uskutečníme počáteční
měření s přesností např. na 12 desetinných míst, pak
všechny následné předpovědi budou mít též přesnost na 12
desetinných míst - počáteční chyba sice nevymizí, ale
nezvětšuje se. Bohužel se však ukázalo, že chyba či
odchylka se ve skutečnosti zvětšuje - na
každém kroku evoluce systému roste chyba předpovědi o
určitá procenta, takže po několika krocích, či desítkách
kroků, již nemůžeme předpovídat prakticky nic...
Toto
zesilování chyb je druhou slabinou, negující
dokonalý Lapaceův determinismus. Citlivost na počáteční
podmínky činí chování systému nepravidelným a
nepředvídatelným - chaotickým (řec. cháos = prázdno, zející propast,
beztvarý stav; rozumí se tím stav bez pořádku
a zákonitostí). Jednotlivé elementární
stupně chování systému se přitom řídí deterministickými
zákony, avšak vyúsťují v takové nepravidelnosti, že
vypadají jako zcela náhodné. Takovýto (zdánlivý) chaos je
tedy složité a (zdánlivě) nepravidelné chování, které má
ve skutečnosti jednoduchý deterministický podklad. Jelikož
tento chaos si generují samotné systémy řídící se
deterministickými zákony, označuje se často jako "deterministický
chaos". Tento chaos je patrně hlavní příčinou
toho, že naše příroda je tak pestrá, různorodá,
proměnná. A je možná též "hybnou silou"
duševních činností a naší lidské "svobody
vůle"..?.
Z termodynamického
hlediska jsou statistické chaotické jevy v dynamických
souborech mikročástic diskutovány v §1.1 "Jaderná
fyzika", pasáži "Termodynamika".
Všude
ve vesmíru se hmota chová podle stejných
fyzikálních a chemických zákonů. Konkrétní chování,
průběh dějů a jejich výsledek, však závisí na
aktuálních podmínkách - ty se sice vyvinuly
též podle těchto přesných zákonů, ale často složitou
kombinací okolností, které již mají charakter náhody.
Úloha náhody při vzniku a evoluci
života je diskutována v práci "Antropický
princip aneb kosmický Bůh",
pasáž "Vznik a evoluce života".
Kvantová
fyzika navíc ukazuje, že v mikroměřítcích prostoru
a času je příroda skutečně a principiálně řízena
náhodou. Např. to, zda se určitá elementární
částice či radioaktivní jádro v daném okamžiku rozpadne
či nerozpadne, je čistě náhodná záležitost; mezi jádrem
které se má vzápětí rozpadnout a tím které nikoli (nebo
až za dlouhou dobu) nelze nalézt vůbec žádný rozdíl.
Teprve v souboru velkého počtu částic či radioaktivních
jader se objevují přesné statistické pravidelnosti.
Vzniká ostatně principiální otázka, odkud tyto statistické
pravidelnosti pocházejí; jsou snad stopami nějakého skrytého
determinismu na fundamentálnější úrovni? Kvantová
fyzika to rezolutně popírá...
Ukazuje
se tedy, že deterministická představa funguje jen v
nejjednodušších idealizovaných případech -
determinismus můžeme uvažovat jen "v principu", nikoli
v praxi. Ve skutečných systémech mnoha těles,
řídících se navíc nejen zákony klasické, ale i kvantové
mechaniky, pozorujeme, že sebemenší nejistota určení stavu
systému v daném časovém okamžiku zpravidla vede k naprosté
ztrátě možnosti přesně stanovit jeho stav i po poměrně
krátkém časovém období. Malé rozdíly v počátečních
podmínkách mohou vyvolat velké změny ve výsledných jevech.
Jinak řečeno, téměř totožné stavy přítomnosti se mohou
vyvíjet k velmi odlišným budoucnostem - jakákoli předpověď
se stává nemožnou, jev se efektivně stává náhodným;
mluvíme o chaotickém chování systému *).
*) Na tuto nestabilitu a indeterminismus
chování složitých systémů často narážejí meteorologové
při snaze o dlouhodobější předpověď počasí (která se
zpravidla nedaří). Označují ji metaforicky jako "efekt
motýlího křídla" - že totiž pouhé mávnutí
motýlího křídla, způsobivšího nepatrné zvíření vzduchu
třebas v Evropě, může po čase "vyvolat" vznik
bouře či cyklonu i na druhé straně Země - v Americe či
Austrálii.
Je však třeba mít na paměti, že "efekt motýlího
křídla" je jen ad-absurdum zvětšenou mystifikací! Ve
skutečnosti jsou atmosférické děje neustále ovlivňovány lokálními
fluktuacemi okolních přírodních podmínek, které
jsou o mnoho řádů větší než onen vzdálený motýlí
efekt...
Ljapunovova nestabilita
Výpočty a počítačové simulace ukazují, že u takových
nestabilních systémů malá změna do počátečních podmínek způsobí, že původně
blízké trajektorie se s časem t od sebe exponenciálně
rozbíhají: d = do.e-l.t. Systém se po uplynutí dostatečně dlouhého času
nakonec stává chaotickým. Míru lineární
stability či nestability - "chaotičnosti" takového
systému lze charakterizovat tzv. Ljapunovovým
časem TL = 1/l, za který se systém odchýlí 2,7-krát (tímto
faktorem se zvětší každá počáteční odchylka); parametr l = 1/TL se někdy nazývá Ljapunovův
exponent.
Je
zajímavé, že i takové zdánlivě stabilní systémy jako je
Sluneční soustava, jsou patrně chaotické. Oběžné
dráhy planet se vzájemně ovlivňují gravitačními
poruchami - symetrie Keplerových orbit se zvolna
porušuje. Pro vnitřní planety Sluneční
soustavy (mimo Merkur) se Ljapunovův čas odhaduje TL » 5.106let. Vysoká hodnota tohoto času vysvětluje
neobyčejnou přesnost astronomických předpovědí pohybů
planet v časových horizontech stovky a tisíce let. V
časových intervalech stovky miliónů až miliard let by se
však chaotičnost drah planet projevila již rozhodujícím
způsobem; některá z planet by mohla dokonce vázaný systém
sluneční soustavy opustit.
V klasické fyzice se donedávna
předpokládalo, že jednoduché systémy se chovají jednoduše
a že tedy každé složité chování musí mít "složité
příčiny". Analýza chování systémů v posledních
letech však ukázala některá překvapující zjištění. Že
totiž chování i jednoduchých systémů může být velmi
složité, zdánlivě chaotické. A zase některé složité
systémy se mohou chovat překvapivě jednoduše - např. v
důsledku autoregulačních či synergických mechanismů. V
rámci této nové teorie chaosu jsou chaos a
řád jakoby spojené nádoby: za určitých okolností se řád
mění v chaos, za jiných podmínek zase chaos přechází v
uspořádané struktury. A i (zdánlivě) chaotické chování
zanechává stopy sice složité a jakoby neuspořádané, avšak
teorie chaosu v nich mnohdy nachází překvapivý řád -
jakýsi "organizovaný chaos". Tyto
stopy chaotického chování mají většinou složitou
geometrickou strukturu, pro jejíž popis již není vhodná
klasická Eukleidovská geometrie; ukazuje se však, že je lze
dobře modelovat novým typem tzv. fraktální geometrie
(viz níže).
Pro
popis chování dynamických systémů se často používá tzv. fázový
prostor (který zavedl H.Poincaré) - myšlený
matematický prostor, jehož body reprezentují všechny možné
stavy dynamického systému. Chování systému je pak
vyjádřeno určitou fázovou trajektorií -
křivkou v tomto fázovém prostoru. Dynamiku systému lze tak
znázornit pomocí geometrických útvarů ve fázovém prostoru.
Spustíme-li dynamický systém z nějakého počátečního
stavu (bodu ve fázovém prostoru) a pozorujeme jeho dlouhodobé
chování, často se stává, že jeho trajektorie ve
fázovém prostoru bude konvergovat k nějakému definovanému
geometrickému útvaru, a to někdy i při různých volbách
počátečních podmínek. Takovýto koncový útvar ve fázovém
prostoru, k němuž směřuje dynamické chování systému, se
nazývá atraktor (lat. atractio = přitahovat)
- tato struktura jakoby "přitahovala" trajektorie
systému ve fázovém prostoru, takže v ní systém buď
spočine, nebo kolem ní "obíhá".
Systém,
který se ustálí v neměnném klidovém stavu, má za atraktor
pouhý bod. U systému, který se ustálí tak, že opakuje
periodicky svůj stav, bude atraktorem uzavřená smyčka, kolem
níž systém obíhá. Systémy s kvaziperiodickým pohybem mají
složitější atraktory s násobnými a rozdělenými smyčkami.
Chaoticky se chovající systémy opisují ve fázovém prostoru
velmi složité trajektorie kolem zvláštních útvarů zvaných
podivné atraktory, které mají fraktální
strukturu.
Fraktaly -
nekonečně členité útvary
Předměty v přírodě, i když jsou většinou nepravidelné a
složitého tvaru, většinou modelujeme pomocí jednoduchých geometrických
útvarů jako je přímka, trojúhelník, čtverec a
obdélník, kružnice či elipsa, rovina, krychle, koule a
další útvary popsané Eukleidovskou geometrií. Pro tyto
základní útvary jsou též dobře známé vzorce pro výpočet
jejich délky, plochy či objemu. Podobně i u dalších
složitějších útvarů, které můžeme složit jako kombinace
z konečného či nekonečného (avšak spočetného) počtu
základních geometrických tvarů.
Všem
takovým útvarům můžeme připsat určité celé číslo - počet
rozměrů neboli (topologickou) dimenzi
daného útvaru, určenou počtem čísel, souřadnic či
parametrů, určujících polohu bodů v těchto útvarech:
přímka či křivka (byť silně zprohýbaná) má dimenzi 1,
plocha má dimenzi 2, krychle, koule a všechny prostorové
útvary mají dimenzi 3 (protože poloha každého bodu v nich je
jednoznačně určena 3 čísly - souřadnicemi).
Ukazuje
se však, že velmi členité,
"kostrbaté" a nepravidelné útvary v
přírodě (jakož i chování chaotických systémů) lépe než
klasická Eukleidovská geometrie modeluje tzv. fraktální
geometrie (lat. fractus = lomený, zlomený),
umožňující popsat i nekonečně členité tvary.
Eukleidovská geometrie je určitá abstrakce skutečných
útvarů, zatímco fraktální geometrie odráží skutečnou
složitost a členitost útvarů: fraktální útvary již nejsou
jednoduchou kombinací ideálních geometrických tvarů, ale
vyznačují se nekonečnou složitostí - čím podrobněji je
zkoumáme, tím složitější detaily se objevují. Fraktální
geometrie se snaží zachytit všechny ty jamky, hrbolky,
pokřivení, spletení, vyskytující se u přírodních
útvarů. Navzdory této bizarní složitosti fraktální
geometrie vyjevuje určité zákonitosti tzv. soběpodobnosti,
kdy každá část objektu je podobná celku (viz níže) - v
přírodě se často vyskytují větvící se fraktální
struktury. Ukazuje se, že fraktální geometrie je vhodným
matematickým prostředkem pro popis struktur a dynamiky
přírodních dějů.
Pro čtenáře, kteří
častěji nepřicházejí do styku s množinami, bude možná
užitečné, když si přečtou v §3.1 "Geometricko-topologické
vlastnosti prostoročasu",
úvodní části "Topologie", pasáž "Množiny
a zobrazení" a dále též část "Nekonečno v prostoru a čase", pasáž "Nekonečno v matematice".
Z
historie fraktalů
Kořeny těchto koncepcí sahají svým způsobem až k
zakladateli teorie množin G.Cantorovi, který m.j. v r.1883
sestrojil svéráznou čistě spekulativní množinu - tzv. Cantorovo
diskontinuum. Cantorovo diskontinuum vzniká z úsečky
jednotkové délky tak, že nejprve odstraníme prostřední
třetinu, pak ve zbylých dvou třetinových úsečkách vždy
opět prostřední třetiny atd., až do nekonečna. Zbude pak
množina izolovaných bodů, Cantorovo diskontinuum neboli Cantorův
prach. Součet délek všech vypuštěných intervalů je
přesně roven 1. Cantorův prach je na první pohled
zanedbatelnou skupinkou bodů. Cantor však dokázal, že těchto
"zrnek prachu" je přesně tolik, kolik bylo bodů na
původní úsečce (!) - je možno je vzájemně jednoznačně
přiřadit. Část je, v jistém smyslu, stejně početná jako
celek - srovnejme s diskusí o pojetí nekonečna v matematice v
§3.1 "geometrie a topologie prostoročasu", pasáž
"Nekonečno
v prostoru a čase". Poskládáme-li
všechny vynechané třetinové úseky z předchozí konstrukce
nad sebe do stupňů (o výšce stejné jako je šířka),
vznikne tzv. ďáblovo schodiště. Toto
"schodiště" má, navzdory své složité fraktální
struktuře nekonečně mnoha stupňů, konečnou délku rovnou 2.
Další
útvary neobvyklé vnitřní struktury, jako je Kochova vločka
nebo Sierpiňského koberec, budou diskutovány níže v
souvislosti s fraktální geometrií a Hausdorffovou dimenzí.
Paradoxní vlastnosti těchto uměle zkonstruovaných objektů
či struktur se tehdejším matematikům, "odchovaným"
klasickou algebrou a matematickou analýzou, zdály být natolik
bizarní a odporující intuici i zdravému rozumu, že je
označovali za jakási zvrácená "matematická
monstra".
Hlavním
zakladatelem novodobé fraktální geometrie je však Benoit
Mandelbrot, který odhalil nové a neočekávané strukturní
vlastnosti geometricky složitých útvarů a množin - anomální
dimenzi a periodicitu struktur v
různých měřítcích. Mandelbrot se v 60.letech zabýval
analýzou šumů a chyb při elektronickém přenosu signálů.
Pozoroval, že střídající se časové intervaly správného a
chybného přenosu se objevují na různých časových
škálách - jakási "sobě-podobnost"
(self-similarity). Tyto své poznatky dal šťastnou shodou
okolností do souvislosti s empirickými údaji o měření
délky mořských pobřeží (konkrétně pobřeží ostrova
Korsiky), shromážděnými L.Richardsonem. Zjistil, že
stanovení délky takového pobřeží podstatně závisí na
měřítku, tj. na "délce tyče" s níž měření
provádíme. Ve větším měřítku, na mapě, nevidíme
všechny skutečné nepravidelnosti, zákruty, výběžky a
další členitosti pobřeží, které bude větší měřítko
"překlenovat" - naměříme délku kratší. V
menších a menších měřítcích podrobnějšího pohledu
musíme při měření krátkou tyčí kopírovat čím dál
menší členitosti, takže se zjemňujícím se měřítkem bude
zjištěná délka pobřeží čím dál větší
- teoreticky až do nekonečna (tzv. Richardsonův efekt).
Pro délku pobřeží L měřenou tyčí délky e stanovil
Richardson empirickou závislost L(e) = K.e1-DR, kde konstanta K je určitá
"běžná" délka konkrétního pobřeží a konstanta
DR (zvaná
Richardsonova konstanta) charakterizuje členitost
daného pobřeží. Pro různá pobřeží se hodnota DR pohybovala v rozmezí
cca 1,05-1,3; za průměrnou hodnotu Richardsonovy konstanty se
bere 1,26. Mandelbrod analyzoval Richardsonův empirický vzorec
zavedením dalšího parametru počtu proložení měřící
tyče N(e), takže L(e) = e.N(e). Rovnici tak upravil na tvar K = L(e).eDR-1 = e.N(e).eDR-1 = N(e).eDR
, z něhož plynulo, že K lze
považovat za Hausdorffovu míru a DR za Hausdorffovu
dimenzi množiny bodů popisujících pobřeží. Dále
Mandelbrod analyzoval a doplnil tzv. Juliovy množiny.
Rozpracováním a zobecněním těchto poznatků dospěl
Mandelbrod k pojmu fraktal.
Vlastnosti fraktalů
Fraktální útvary (fraktaly) mají dvě základní pozoruhodné
vlastnosti (které zároveň mohou sloužit jako definice
fraktalů):
Z matematického hlediska sobě-podobná
množina A z n-dimenzionálního Eukleidova
prostoru En
je taková množina, pro kterou existuje konečně mnoho tzv. kontrahujících
zobrazení f1, f2, ..., fn (jsou to taková
zobrazení En do En, která zmenšují vzdálenost mezi dvěma body
ležícími v En) takových, že A vznikne jako sjednocení A = i=1Čn fi(A). Takovéto
sobě-podobné množiny vznikají opakováním "sebe
sama" při určité transformaci jako je změna měřítka,
rotace či posunutí. Soběpodobné množiny jsou invariantní
vůči změně měřítka - při libovolném zvětšení či
zmenšení vypadají podobně. Lze říci, že sobě-podobná
množina vzniká "sama ze sebe" - vzniká opakováním
téhož základního motivu. Např. Cantorovo diskontinuum se
skládá ze svých opakujících se přesných kopií,
zmenšených na 1/3.
Můžeme zjednodušeně
říci, že fraktal je geometrický útvar (či
množina), který se skládá z určitého počtu svých vhodně
zmenšených "kopií". Takovýto princip opakování
podobných tvarů ve zmenšené či zvětšené podobě
můžeme často pozorovat v přírodě, kde mnohé složité a
komplexní útvary se vytvářejí opakováním jednoduchých
struktur a pravidel. Je to např. růst větví na stromech,
korálové útesy v moři, sněhové vločky, zvětralá
skaliska, či větvení cévního systému v těle od velkých
cév aortálních až po nejjemnější kapilární. Struktury
tohoto druhu jsou velice efektivní z hlediska směstnání
plochy s velkým povrchem do malého objemu.
Topologická dimenze
Obvyklá dimenze - počet rozměrů - objektu,
zvaná též topologická dimenze (viz §3.1
"Geometrie a topologie prostoročasu") je celé číslo D udávající počet
parametrů, kterými je jednoznačně definována poloha
jednotlivých bodů tohoto útvaru. Přímka, úsečka,
kružnice, parabola, sinusovka a každá jiná křivka má
dimenzi D=1 (je jednorozměrná), neboť polohu bodu na ní lze
parametrizovat jediným číslem (souřadnicí). Každá hladká
plocha - rovina, trojúhelník, kruh, kulová či válcová
plocha, má dimenzi D=2, neboť poloha bodu zde musí být
definována pomocí dvou souřadnic. Tělesa jako je krychle,
válec, jehlan, koule, stejně jako celý obvyklý prostor kolem
nás, mají dimenzi D=3, protože poloha každého bodu v nich je
jednoznačně určena 3 souřadnicemi. Analogicky můžeme
formálně konstruovat útvary s vyššími dimenzemi, i když s
nimi nemáme přímé zkušenosti a neumíme si je představit; v
našem výkladu často používáme 4-rozměrný prostoročas.
Fraktální
dimenze
Hausdorffova dimenze
Na dimenzi se však můžeme dívat i z jiného
hlediska než topologického - z hlediska metrického,
které modeluje proces měření daného
geometrického útvaru - stanovení jeho délky, plochy, objemu,
obecně míry. Uvažujme nejprve měření
úsečky (dimenze D=1) o celkové délce L, kterou
pokryjeme N stejně dlouhými intrervaly
("měřítky") délky e. Počet intervalů N(e), které
pokrývají celou úsečku, závisí na délce intervalů podle
vztahu N(e) = L.(1/e) a délku úsečky můžeme spočítat na základě
počtu pokrytí L = N(e).e. Budeme-li obdobným způsobem měřit délku křivky,
budeme zjemňovat pokrytí, takže délka bude
vyjádřena vztahem L = lime®0N(e).e. Podobně v
případě dimenze D=2 lze pokrýt plochu čtverce o straně L
počtem N(e) čtverců o straně e, přičemž pro celkovou
plochu čtverce dostaneme S ş L(2) = N(e).e2. Pro obecný rovinný
útvar jeho plochu L(2) lze vyjádřit jako L(2) = lime®0N(e).e2. Obecně pro D-rozměrný útvar je vztah mezi jeho
velikostí (mírou) L(D) a počtem pokrytí N(e) měřítky délky e : L(D) = lime®0N(e).eD. Logaritmováním
odtud plyne možnost vyjádřit dimenzi D útvaru o
"objemu" L(D) pomocí vztahu D = lime®0[ln N(e)]/[ln L(D)+ ln(1/e)]. Normalizací k jednotkovému objemu dostáváme pro
dimenzi vztah, který můžeme považovat za alternativní nezávislou
metrickou definici dimenze - tzv. Hausdorffovy-Kolmogorovovy
dimenze DH:
DH
= lime®0[ln N(e)]/[ln(1/e)] ,
kde N(e)
je počet pokrytí měřeného útvaru měřítky (úsečkami)
délky e.
Pokud je útvar pravidelný, není nutno počítat limitu pro
nekonečné zjemnění měřítka; stačí porovnat, jakým
výsledným faktorem se změní stanovená délka
vyšetřovaného útvaru při zjemnění měřítka určitým
daným faktorem. Vztah pro stanovení Hausdorffovy dimenze se pak
zjednoduší na:
DH
= ln N / ln(1/e) ,
kde N je faktor změny stanovované délky, e je délka jednoho
nově vzniklého dílku při rozdělení původního útvaru
faktorem změny měřítka 1/e.
Spočítáme-li
Hausdorffovu-Besikovičovu dimenzi pro libovolný hladký
jednorozměrný útvar (úsečku či křivku), dostaneme DH= 1, pro hladký
plošný útvar dostaneme DH = 2, pro běžné trojrozměrné geometrické útvary DH = 3. Pro geometricky
hladké útvary obecně vždy platí DH = D - Hausdorffova dimenze je rovna dimenzi
topologické. Pro složité členité útvary - fraktaly
- je však jejich Hausdorffova dimenze vyšší
než dimenze topologická a je dána zpravidla neceločíselnou
hodnotou. Hausdorffovu dimenzi lze považovat za určité zobecnění
obvyklé (topologické) dimenze, které lépe vystihuje chování
složitých členitých útvarů, než dimenze topologická.
Fraktální dimenze kvantifikuje stupeň složitosti či
členitosti objektu tím, jak rychle roste jeho měřená délka,
obsah nebo objem v závislosti na velikosti měřítka kterým
měříme (používá se zobecněného Richardsonova
efektu).
Podobnostní dimenze
Pro soběpodobné množiny lze vyslovit další alternativní
definici dimenze - dimenzi podobnostní. Tato
dimenze kvantifikuje, kolik kopií sebe sama, zmenšených
vhodným faktorem, obsahuje daná množina. Jestliže zkoumaný
objekt obsahuje N kopií sama sebe, zmenšených faktory
1/ki (i=1,2,...,N), je podobnostní
dimenze DS
dána vztahem
i=1SN(1/ki)DS = 1 .
Pro nejobvyklejší případ, že faktory ki jsou stejné (ki=k), získáme podobnostní dimenzi řešením rovnice i=1SN(1/k)DS = 1, což dává DS = ln N / ln k = DH. Lze dokázat, že podobnostní dimenze je rovna
Hausdorffově dimenzi. Pojem podobnostní dimenze tak
umožňuje snadno stanovovat fraktální dimenzi u symetrických
fraktalů geometrického původu. Stačí zjistit, kolik
"kopií sama sebe" a v jakém měřítku daná
struktura obsahuje, a její fraktální dimenze bude dána
podílem logaritmů těchto hodnot - viz níže.
Mřížková dimenze
U složitějších fraktálních útvarů, jejichž struktury
nevykazují sobě-podobnost, lze fraktální dimenzi stanovit
empirickým způsobem "mřížkového počítání" (box-counting).
Přes daný útvar se překryje mřížka (o
dimenzi danou topologickou dimenzí studovaného útvaru) o
velikosti buněk d a spočítá se, kolik buněk obsahuje
nějaké body sledovaného útvaru. Získá se tím číslo N,
které závisí na velikosti d buněk mřížky N = N(d) -
čím hustší mřížka (menší d), tím větší je N.
Mřížku postupně zjemňujeme (zmenšujeme d) a
analyzujeme funkci N(d) tak, že ji vyneseme do log/log
grafu [lnN(d)«ln(1/d)]. Získanými body proložíme přímku, jejíž
směrnice pak udává fraktální dimenzi
vyšetřovaného útvaru.
V nejjednodušším případě, kdy se testovací mřížka
zjemňuje faktorem 2 (dvakrát hustší mřížka), se počet
započítaných buněk mezi dvěma po sobě jdoucími pokrytími
násobí číslem 2D, kde D je fraktální dimenze.
Pro
sobě-podobné objekty dává tato metoda stejné hodnoty jako
podobnostní a Hausdorffova dimenze; je však snadno
algoritmizovatelná a funguje i pro složité fraktální
útvary.
Příklady
fraktálních útvarů
Kochova vločka
Jedním z nejjednodušších a nejzajímavějších příkladů,
jak z původně Eukleidovsky tvarově jednoduché geometrické
konstrukce může vzniknout složitý fraktální útvar, je tzv.
křivka Kochové; tuto křivku v r.1904
sestrojila švédská matematička Helge van Kochová jako
geometrické modelové přiblížení obvodu sněhové vločky -
odtud též název "vločka Kochové". Vločku
Kochové můžeme sestrojit sérií postupných
trojúhelníkových iterací podle obrázku. Vyjdeme z
rovnostranného trojúhelníka s jednotkovou délkou strany
(1.iterace); obvod se tedy skládá ze tří úseků jednotkové
délky. Ve 2.iteraci připojíme k prostřední třetině každé
strany další rovnostranný trojúhelník o třetinové délce
strany - vznikne 6-cípá hvězda, jejíž obvod se skládá z 12
úseků délky 1/3. V další iteraci opět ke každé
prostřední třetině každé z 12 stran přidáme další
menší trojúhelník. Toto provádíme znova a znova - až do
nekonečna. Při každém dalším kroku bude obrys čím dál
jemněji členitý. Délka křivky se při každém kroku
prodlouží vždy o 1/3 (ze tří částí úsečky vzniknou
čtyři stejně dlouhé). V nekonečné limitě počtu kroků n®Ą dostáváme
křivku, jejíž délka 3.(4/3)n je nekonečná, avšak obsah plochy
omezené touto nekonečnou čarou zůstává konečný
(menší než plocha kruhu opsaného původnímu trojúhelníku,
neboť Kochové křivka opsanou kružnici nikde neprotíná;
sečtením konvergující nekonečné řady vychází, že je
roven 8/5 obsahu výchozího trojúhelníku). Při každé
iteraci e®e/3 vzniknou 4 (sobě-podobné) části, tj. N(e/3)®4.N(e). Podle výše
uvedeného definičního vzorce (ve zjednodušené verzi) tedy Hausdorffova
dimenze křivky Kochové vychází: DH = ln4/ln[1/(1/3)] =
ln4/ln3 @1,261, tj. vyšší
než je dimenze topologická D=1. Takováto křivka tedy
"zaplňuje" prostor (rovinu) poněkud více než pouhá
přímka či úsečka s dimenzí D = DH = 1- jedná se o množinu či útvar metricky
"hustší", než by se dalo očekávat
z jeho topologické dimenze D=1.
 |
| Konstrukce a struktura fraktální
křivky Kochové. Nahoře: 1.,2.,3. a 4. iterace křivky. Dole: Zvětšený pohled na členitou strukturu křivky. |
Takovéto "husté" fraktální
útvary s Hausdorffovou dimenzí vyšší než topologickou
vznikají tím, že v geometricky hladkých útvarech přidáváme
nekonečně mnoho zjemňujících se částí.
Cantorovo diskontinuum
Odebráním nekonečně mnoha nekonečně se
zmenšujících částí vznikají naopak "řidší"
množiny, jejichž Hausdorffova dimenze je menší
než dimenze topologická. Nejstarším příkladem je již shora
zmíněné Cantorovo diskontinuum s D=1 a DH = ln2/ln3 @ 0,63 (Cantorovo
diskontinuum je sjednocením svých dvou kopií zmenšených
koeficientem 1/3).
Sierpinského trojúhelník
vznikne tak, že z výchozího trojúhelníku vyřízneme
vnitřní menší trojúhelník tvořený středními příčkami
trojúhelníku původního. Tento postup opakujeme ve třech
zbylých trojúhelníčkách atd. - vznikne tak nekonečně mnoho
nekonečně malých trojúhelníčků. Tento útvar se skládá z
třech svých kopií zmenšených na polovinu, takže DH = ln3/ln2 @ 1,58.
Sierpiňského koberec
vzniká analogickým vyřezávacím postupem z obdélníku,
který rozdělíme vždy na 9 shodných čtverců (pomocí
kolmých příček v 1/3 a 2/3 každé strany) a ten prostřední
vyřízneme. Stejný postup opakujeme se zbývajícími 8
čtverci atd. Sierpinského čtverec s výchozí D=2 se skládá
z 8 svých kopií zmenšených na 1/3, takže DH = ln8/ln3 @ 1,89.
Mengerova houba
Zobecněním na trojrozměrné objekty vzniká Mengerova
houba: Krychli rozdělíme na 27 shodných menších
krychlí a 7 prostředních (jejichž žádná hrana není
součástí hrany původní velké krychle) vyjmeme. Tento postup
opakujeme se zbylými 20 menšími krychlemi atd. Vznikne nakonec
nekonečně členitá trojrozměrná mřížka s nekonečným
povrchem (každá stěna Mengerovy houby je zároveň
Sierpiňského kobercem), ale nulovým (nekonečně malým)
objemem. Je zajímavé, že vedle fraktálních vlastností
obsahuje i topologické ekvivalenty všech křivek existujících
v prostoru. Jelikož tento útvar (s výchozí topologickou
dimenzí D=3) je tvořen 20 kopiemi původní krychle
zmenšenými na 1/3, je fraktální dimenze Mengerovy houby DH = ln20/ln3 @ 2,73.
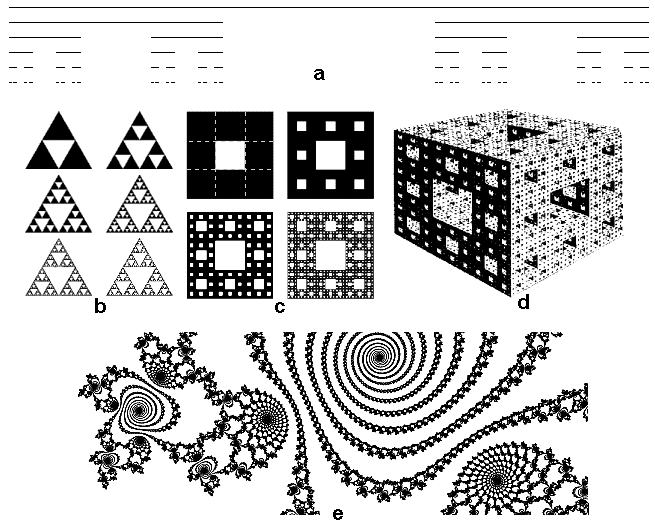 |
| Některé typické fraktální
množiny a útvary. a: Cantorovo diskontinuum (prvních 6 iterací). b: Sierpiňského trojúhelník (prvních 7 iterací). c: Sierpiňského koberec (prvních 5 iterací). d: Mengerova houba (po cca 5 iteracích). e: Příklad polynomického Juliova-Mandelbrotova fraktalu (detail - výřez z komplexní roviny). |
Polynomické fraktaly
Další
zajímavé fraktální obrazce vznikají jako geometrické místo
bodů v Gaussově rovině komplexních čísel z = x + y.i (i
je imaginární jednotka), pro něž iterativní metody řešení
některých algebraických rovnic konvergují. Nejjednodušším
příkladem je postupná iterace funkce komplexní paraboly zn+1=zn2+c, kde se do komplexní roviny zakresluje množina všech
komplexních čísel z0, pro které posloupnost zn konverguje (zn je konečné pro n®Ą). Tyto tzv. Juliovy-Mandelbrotovy
množiny tvoří velikou různorodost často nádherných
obrazců, v závislosti na hodnotě konstanty c; mohou
být spojité i diskrétní. S oblibou se nyní
vykreslují pomocí počítačové grafiky, včetně
efektních barevných modulací *). Nejvíce fraktálů
však "vymyslela" sama příroda..!..
*) Barevné zobrazení jednotlivých bodů
bit-mapy se moduluje např. počtem iterací potřebných pro
dosažení určité hodnoty |z |.
Fraktaly v přírodě
Pro složité
fraktální množiny nelze většinou výpočet Hausdorffovy
dimenze přímo provádět algebraicky podle výše uvedeného
vzorce. Je třeba postupovat "experimentálně" či
empiricky - konstruovat graf [lnN(e) « ln(1/e)] a dimenzi stanovit
extrapolací směrnice grafu pro 1/e®Ą; popř. použít mřížkové
metody stanovení fraktální dimenze. V přírodě se
setkáváme i se složitými objekty, jejichž tvar či chování
nelze popsat pomocí jediné fraktální dimenze; takovéto
"multifraktaly" jsou charakterizovány
dvěma či více dimenzemi (projevuje se rozdílnými
lineárními úseky na log/log grafu).
Z fraktálních útvarů vyskytujících se v
přírodě byly pro Hausdorffovu dimenzi empiricky stanoveny
hodnoty: mořské pobřeží DH@1,26 (Richardsonova
konstanta); povrch skály DH@2,3; povrch blan
lidského mozku DH@2,76.
Teorie
relativity, kvantová fyzika + teorie chaosu ® nové pojímání
skutečnosti?
Jak bylo výše uvedeno, v přírodě se setkáváme s řadou
jevů, vedoucích ke zformování fraktálních struktur *). V
oblasti astrofyziky a kosmologie je možné, že shluky kup
galaxií a galaxií, vznikajících ze zárodečných nehomogenit
roztažených expanzí vesmíru na různé velikosti (§5.4),
mají fraktální strukturu. V §5.5 "Mikrofyzika a
kosmologie. Inflační vesmír", pasáž "Chaotická
inflace a kvantová kosmologie" uvidíme, že
předpokládaná množina spontánně vznikajících vesmírů z
kvantových fluktuací vytváří "fraktalový strom"
nových a nových "vesmírů".
*) I fraktální geometrie je jen modelem,
do určité míry idealizovaným. Členitost přírodních
útvarů a složitost chování dynamických systémů je sice
kolosální, avšak ne nekonečná. Fraktální
model ztrácí platnost na úrovni atomárních rozměrů,
kde idea soběpodobnosti přestává platit (atomy nemají
fraktální strukturu) a stanovení metrické dimenze ztrácí
možnost realizace.
Chováním
nerovnovážných a nelineárních dynamických systémů se
zabývá synergetika, kterou můžeme s trochou
nadsázky označit za nauku o organizovaném chaosu
- na pozadí zdánlivého chaotického chování se hledají
skryté zákonitosti, které jsou často velmi netriviální a
pozoruhodné. Soběpodobnost fraktalů odpovídajících
podivným atraktorům chaotických systémů je jistým druhem
skrytého řádu, který je příznakem jakéhosi "deterministického
chaosu".
Ukazuje
se, že teorie chaosu a nekonečné členitosti
útvarů je patrně novou fundamentální představou
o okolním světě, doplňující dvě již propracované a
osvědčené fundamentální koncepce moderní fyziky: teorii
relativity a kvantovou fyziku. Všechny
tyto tři fundamentální teorie jednak vedou k obohacení a
prohloubení našeho chápání přírody a vesmíru, avšak
zároveň našemu poznání bohužel nastavují univerzální
limitní omezení, jakési "gnoseologické
bariéry", přes které se principiálně
nemůžeme dostat:
¨ Teorie
relativity
ukazuje nepřekročitelnou mez pro šíření polí a
informací danou rychlostí světla ve vakuu a odtud v kombinaci
s gravitací, jakožto teorií zakřiveného prostoročasu,
existenci horizontů událostí, které jsou v
naší knize opakovaně diskutovány.
¨ Kvantová
fyzika
svými relacemi neurčitosti a stochastickým charakterem
stanovuje meze poznatelnosti průběhu
individuálních dějů v mikrosvětě (individualitu
částic a dějů vlastně stírá).
¨ Chaos
a nelineární dynamika zásadně omezují možnosti
dlouhodobější předvídatelnosti přesného chování všech
systémů, i zdánlivě jednoduchých procesů (nepomůže nám v tom sebevýkonnější počítač ani
nejpřesnější numerické metody, jedná se o omezení
principiální!).
Těmito
posledními aspekty chování fyzikálních systémů se však
zabývat nebudeme, v naší knize nám půjde o deterministickou
analýzu gravitace a struktury prostoročasu - tedy
deterministickou aspoň v principu, v rámci
obecné teorie relativity.
| Gravitace, černé díry a fyzika prostoročasu : | ||
| Gravitace ve fyzice | Obecná teorie relativity | Geometrie a topologie |
| Černé díry | Relativistická kosmologie | Unitární teorie pole |
| Antropický princip aneb kosmický Bůh | ||
| Jaderná fyzika a fyzika ionizujícího záření | ||
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | ||