 |
(2.65) |
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | Gravitace, černé díry a fyzika |
Kapitola 2
OBECNÁ TEORIE
RELATIVTITY
- FYZIKA GRAVITACE
2.1. Zrychlení a gravitace z hlediska
speciální teorie relativity
2.2. Univerzálnost - základní
vlastnost a klíč k pochopení podstaty gravitace
2.3. Lokální princip ekvivalence
a jeho důsledky
2.4. Fyzikální zákony v
zakřiveném prostoročase
2.5. Einsteinovy rovnice
gravitačního pole
2.6. Deviace a fokusace geodetik
2.7. Gravitační vlny
2.8. Specifické vlastnosti
gravitační energie
2.9.Geometrodynamická soustava
jednotek
2.10. Experimentální
ověřování teorie relativity a gravitace
2.7. Gravitační vlny
Šíření
vln - obecný přírodní fenomén
Důležitý přírodní fenomém vlnění v látkových prostředích a
fyzikálních polích spočívá v šíření určitých změn (rozruchu, kmitů) prostorem. Šíření vln je obecně podmíněno
dvěma základními aspekty :
1. Mechanismus vzniku změn - rozruchů, kmitavého pohybu -
v daném prostředí či poli. Bez dynamického vzniku změn by
se "nemělo co šířit"...
Na vodní hladině může rozruch vzniknout třebas dopadem
kamene, načež vychýlené částečky vody periodicky kmitají
nahoru a dolů pod vlivem gravitačního pole Země. V pružných
látkových prostředích mohou silovým působením vznikat
mechanické deformace, které pak vlivem elastických sil
periodicky kmitají kolem rovnovážné polohy. V
elektromagnetickém poli vznikají změny intenzity elektrického
a magnetického pole při nerovnoměrných pohybech elektrických
nábojů a vzájemně se generují vlivem Faradayova-Ampérova
zákona elektromagnetické indukce. V gravitačním poli jsou
časové změny jeho intenzity, neboli změny zakřivení
prostoročasu, vyvolávány nerovnoměrným pohybem hmotných
těles; periodické kmitání
gravitačního pole (křivosti prostoročasu) vzniká
především při vzájemném obíhání masívních těles kolem
společného těžiště pod vlivem gravitační přitažlivosti (podle obecné teorie relativity je to opět pohyb
těles v zakřiveném prostoročase).
2. Konečná rychlost šíření změn
(rozruchu) v tomto prostředí či poli. Při nekonečné
rychlosti šíření interakce by se změna nešířila, ale
projevila by se okamžitě na všech tělesech,
jakkoliv vzdálených; vlnění by nevznikalo...
V látkových prostředích se rozruch a
kmitavý pohyb šíří do okolí v důsledku elastické
interakce se sousedními a s dalšími a dalšími
vzdálenějšími atomy a molekulami prostředí, které jsou
postupně uváděny do pohybu. Rychlost tohoto šíření
závisí na síle elastické interakce (vyjadřuje se Youngovým
modulem pružnosti) a na hustotě prostředí. Ve vzduchu, kde je
poměrně slabá elastická interakce mezi sousedeními
molekulami, činí rychlost šíření rozruchu - rychlost zvuku
- cca 330m/s., ve vodě kolem 1500m/s., v tvrdých pevných
látkách je výrazně vyšší (např. v oceli cca 5000m/s.).
Vždy je však konečná a podstaně nižší
než rychlost světla c.
V elektromagnetickém poli se rozruch šíři do prostoru
rychlostí světla c (ve vakuu) ve formě
elektromagnetických vln, kde se elektrické a magnetické pole
vzájemně budí svou proměnností (zákon
elektromagnetické indukce - Maxwellovy rovnice, §1.5 "Elektromagnetické
pole. Maxwellovy rovnice."). Jak uvidíme níže, i v gravitačním poli se rozruch
šíří rychlostí světla ve formě gravitačních vln
- kmitající křivosti prostoročasu.
Vlnová funkce,
vlnová rovnice
Šíření vlny se matematicky vyjadřuje
pomocí speciální diferenciální rovnice mezi rychlostí
časové změny (časové
derivace) výchylky f
a gradientem prostorové změny (derivace podle souřadnice) této
veličiny f - pomocí vlnové
rovnice. Ve zjednodušeném jednorozměrném
případě rovinné vlny, šířící se ve směru osy X
fázovou rychlostí c *), má vlnová rovnice tvar :
d2f/dt2 = c.d2f/dx2 .
Řešením vlnové rovnice je speciální funkce prostorových
souřadnic a času - vlnová funkce, která má
obecný tvar: f(x,t) = f(x,
t-x/c). Vyjdeme-li z nějakého výchozího bodu o součadnici xo v čae to, pak stejná hodnota
výchylky f, jako je v bodě o souřadnici xo v časovém okamžiku to, bude ve všech místech, jejichž souřadnice a čas
splňují rovnici x - xo = c.(t - to). Popisuje tedy vlnění výchylky f,
postupně se šířící prostorem ve směru osy X fázovou rychlostí
c. Nejčastěji se uvažuje harmonická
(sinusová resp. kosinusová) časová závislost: f(x,t)
= f.cos[w.(t - x/c)], kde w = 2pf je kruhová frekvence; vlnění totiž často
vzniká v důsledku periodických kmitavých pohybů
elektrických nábojů (např. v anténách
napájených vysokofrekvenčním signálem o frekvenci f), nebo kruhového obíhání
gravitujících těles. I v případech, kdy tomu tak není, lze
vznikající vlnění Fourierovsky rozložit na
harmonické složky o různých frekvencích a
amplitudách. Při použití komplexních (imaginárních
"i") čísel se harmonické vlnové funkce často
zapisují ve tvaru f(x,t) = Re (f . e-iw(t-x/c)).
*) Rychlost šíření
vlny je zde označena c, avšak nemusí
ze zde jednat o rychlost světla.
Při trojrozměrné analýze v souřadnicích x,y,z má
vlnová rovnice obecný tvar:
(1/c2) .¶2f/¶t2 = ¶2f/¶x2 + ¶2f/¶y2 + ¶2f/¶z2 ,
což se často ekvivalentně zapisuje pomocí Laplaceova
operátoru D : (1/c2) .¶2f/¶t2 = D f . Ve
4-rozměrné relativistické formulaci pak pomocí d'Alembertova
operátoru o ş -(1/c2) .¶2/¶t2 + ¶2/¶x2 + ¶2/¶y2 + ¶2/¶z2 jako of = 0.
Vlnové rovnice se odvozují z pohybových
rovnic elementů látky v mechanice kontinua a z rovnic
pole - Maxwellových rovnic elektrodynamiky
(§1.5 "Elektromagnetické
pole. Maxwellovy rovnice", část
"Elektromagnetické vlny") a Einsteinových
rovnic gravitačního pole (je
ukázáno níže v části "Vznik a vlastnosti gravitačních vln"). Plynou-li z těchto
fundamentálních rovnic látek či polí vlnové rovnice,
znamená to, že v daném látkovém prostředí nebo
fyzikálním poli se mohou šířit vlny.
Z poněkud jiného hlediska se vlnová funkce široce
používá v kvantové fyzice. V kvantové
mechanice je stav částice (resp. souboru
částic a obecně každého fyzikálního systému) popsán tzv.
vlnovou funkcí y(x,y,z). Fyzikální význam
vlnové funkce je ten, že druhá mocnina modulu vlnové funkce úyú2 určuje pravděpodobnost dW, že se
částice v daném čase t nalézá v elementu objemu dV =
dx.dy.dz kolem bodu (x,y,z): dW = úyú2.dx.dy.dz. S takto koncipovanou kvantovou vlnovou
funkcí pak operuje Schrodingerova rovnice a další
aparát kvantové mechaniky a kvantové teorie pole
za účelem stanovení kvantových stavů a pravděpodobností
přechodů mezi různými kvantovými stavy. Toto pojetí
vlnové funkce však již leží mimo rámec našeho pojednání
o fyzikálním vlnění (je diskutováno v
§1.1, část "Korpuskulárně-vlnový
dualismus" a "Kvantová povaha mikrosvěta" monografie "Jaderná
fyzika a fyzika ionizujícího záření").
Graficky se šíření vlny
znázorňuje pomocí vlnoploch. Vlnoplocha je
geometrické místo bodů v prostoru, které při vlnění
kmitají se stejnou fází. U vlnění z bodového nebo sféricky
symetrického zdroje v homogenním a izotropním prostředí se
jedná a kulovou (sférickou) vlnoplochu,
jejíž body leží na kulové ploše. Vlnoplocha, kterou vlna
dosáhne za daný čas, se nazývá čelní vlnoplocha.
Kolmice na vlnoplochu udává směr šíření vln.
Huygensův princip
Šíření vlnění se pomocí vlnoploch
názorně analyzuje pomocí tzv. Huygensova-Fresnelova
principu: V každém okamžiku lze každý bod, kam dospělo
čelo šířící se vlnoplochy, považovat za nový
zdroj sekundárního elementárního vlnění, z něhož
se sekundární vlny opět šíří na všechny strany,
přičemž superponují s původním vlněním,
jakož i se všemi dalšími elementárními vlnami. Celková
vlnoplocha v dalším časovém okamžiku pak vzniká jako
vnější obálka všech elementárních vlnoploch.
Můžeme tak zkonstruovat vlnoplochu v určitém okamžiku, je-li
známá vlnoplocha v předchozím časovém okamžiku. Z tvaru
takto vznikajících vlnoploch lze odvodit zákony odrazu,
difrakce a lomu vlnění.
Společnou obecnou
vlastností šíření vln - radiace
- je skutečnost, že příslušné vlny se odpoutávají
od zdroje a
odnášejí s sebou do prostoru část jeho
energie, hybnosti a momentu hybnosti, a to i bez přítomnosti
nějakého vzdáleného "přijímače"
těchto vln. Samotné vlny (jejich pole) totiž mají energii.
Induktivní a vlnová
zóna
Z hlediska vzájemné energetické vazby mezi
zdrojem a přijímačem si prostor kolem kmitajícího zdroje
vlnění o frekvenci f můžeme rozdělit na dvě oblasti:
¨ Induktivní zóna je blízká oblast vzdáleností r od zdroje,
menších než je vlnová délka vyzařování: r < c/f = l. Zde se v prvním přiblížení může působení
zdroje na testovací tělesa vysvětlit přímým působením
"na dálku" pod vlivem Coulombova zákona u elektřiny
nebo Newtonova zákona u gravitace. Ztráta energie zdroje zde
výrazně závisí na přítomnosti jiných těles či soustav,
které "přijímají" energii ze zdroje - v nichž
pohyby ve zdroji "indukují" svým silovým působením
určité pohyby nábojů či gravitujících těles, za
vykonávání práce. A tato indukce ze zase zpětně projevuje
ve ztrátě energie ve zdroji.
¨ Vlnová zóna je vzdáleněší oblast několika vlnových délek r >> c/f = l; často jsou to místa vzdálená stovky, tisíce,
miliony l. Pokud sem umístíme "přijímací" soustavu
(elektrické náboje v cívce či anténě
u elektromagnetických vln, nebo zkušební testovací tělesa u
gravitačních vln), žádné množství
energie přijaté touto soustavou nijak neovlivní
energetickou bilanci ve zdroji. Lze říci, že vlny již
nenávratně odnesly tuto energii ze zdroje do vzdáleného
prostoru, bez jakékoli zpětné vazby, co se tam s touto
energií stane...
Časový průběh pole
a tvar vlnoplochy
Časový průběh kmitání pole ve vlně obecně závisí na dynamice
zdroje, nemusí mít pravidelný sinusový tvar. Jak
uvidíme níže ("VesmirneZdrojeGravitVln"), vlny ze
závěrečných fází binární soustavy nejsou
přesně sinusové, skládají se z harmonických průběhů o
různých frekvencích a ampitudách. A při vzájemném
splynutí mají dokonce aperiodický charakter mocného pulsu! Na
druhé straně, pomocí Fourierovy analýzy se každý
průběh dá vyjádřit jako superpozice harmonických
funkcí (sinusových či kosinusových) s různými
amplitudami, fázemi a frekvencemi. Při obecné analýze se
proto vlny obvykle kreslí jako sinusovky.
Rovněž
tvar šíření vln může být složitější. V zásadě se
vlny šíří izotropně po kulové vlnoploše. V
blízkosti zdroje, v induktivní nebo blízké vlnové zóně,
však může mít pole ve vlně složitý nepravidelný průběh
a rovněž vlnoplocha může být deformovaná a časově
proměnná, nemusí mít pravidelný kulový tvar (projevuje se heterogenita ve struktuře a pohybech ve
zdrojové soustavě). Ve větších
vzdálenostech od zdroje se však tyto nepravidelnosti zpravidla
postupně zahladí a vlnění konverguje k
pravidelnému kulovému tvaru vlnoplochy s izotropním
šířením a harmonickým (sinusovým -
kosinusovým) časovým průběhem pole ve vlně. A ve velkých
vzdálenostech pak má kulová vlnoplocha tak velký poloměr,
že její zakřivení je téměř nulové, pozorujeme rovinnou
vlnu.
Vlny podélné a
příčné, polarizace vln
Podle směru, v němž probíhá kmitání ve
vlně vzhledem ke směru šíření vlny, rozeznáváme dva druhy
vlnění:
l Podélné
vlnění (longitudální), v němž amplituda
kmitání ve vlně probíhá ve stejném směru,
v jakém se vlna šíři. Podélné vlny vznikají nejčastěji v
pružných látkových prostředích, kde v důsledku vazebných
sil mezi částicemi (atomy, molekulami) látky se výchylka
dané částice přenáší na sousední a pak na další a
další částice. Vlna je tvořena střídajícími se oblastmi
zředění a zhuštění.
l Příčné
vlnění (transverzální), kde amplituda
kmitání ve vlně probíhá kolmo ke směru
šíření vlny. Nejjednodušším příkladem jsou vlny na
vodní hladině... Fyzikálně důležité příčné vlnění
však vzniká ve fundamentálních fyzikálních polích -
elektromagnetickém a gravitačním. Elektromagnetické
vlny jsou tvořeny kmitajícími vektory elektrické
intenzity E a magnetické indukce B,
které jsou k sobě kolmé a kmitají v rovině kolmé ke
směru šíření; vyvolávají tak kmitání
elektrických nábojů ve směrech kolmých ke směru šíření
vlny. V gravitační vlně kmitají složky
metrického tenzoru zakřiveného prostoru rovněž takovým
způsobem, že vyvolávají kmitání testovacích částic ve
směrech kolmých ke směru šíření vlny (i když složitějším způsobem - viz níže "Rovinné
gravitační vlny v linearizované gravitaci").
U příčného vlnění může být
vektor kmitání - v rámci roviny kolmé ke směru šíření -
orientován různými směry. Pokud se tento směr kmitání
náhodně a chaoticky mění, mluvíme o nepolarizovaném
vlnění. V řadě případů je však podél vlny směr
kmitání konstantní nebo se mění pravidelným způsobem -
jedná se o polarizované vlnění. Pokud
probíhá kmitání během šíření vlny pod stále
stejným úhlem v rovině kolmé na směr šíření,
označuje se jako lineární polarizace. Směr
kmitání přitom může být skloněn v libovolném konstantním
směru - úhlu polarizace. V některých případech se
směr kmitání v rovině kolmé k šíření vlny může pravidelně
a plynule měnit, kroužit po kružnici - jedná se o kruhovou
polarizaci (pravotočivou nebo
levotočivou). Obecněji pak může
docházet k eliptické polarizaci.
Vlny emitované rotujícími zdroji -
spirálovitá polarizace vln
Zcela speciální polarizace může být vlnám vtištěna
rotací. Jsou-li vlny vyzařovány rotujícím
zdrojem, zanechá tato rotace specifické stopy na
struktuře emitovaných vln. Při vzniku vlny se maximum a
minimum při rotaci zdroje vůči sobě periodicky časově
posouvají, takže fáze vlny - střídání maxima a minima
- se budou posunovat při šíření vlny rychlostí c .
Vlnoplocha nabývá šroubovnicový tvar spirály.
Vzniká jakési
"rotující, stáčející se či spirálové záření"
se specifickými vlastnostmi polarizace. Dopadá-li na
interagující částice, způsobí m.j. jejich rotaci kolem
směru šíření paprsku, což lze považovat jako projev momentu
hybnosti tohoto záření. Chová se tedy jako vlnění s orbitálním
momentem hybnosti (pro elektromagnetické vlny je
diskutováno v §1.5, pasáž "Vnitřní a orbitální moment hybnosti
vln").
Pozn.: V
laboratorních optických experimentech se toto světlo s
helikálně rotující polarizací generuje speciálními
rotujícími zdroji, válcovými čočkami, lasery, hologramy, a
měří se pomocí prostorových modulátorů světla. U radiovln
lze helikální polarizace dosáhnout speciální prostorovou
konfigurací antén napájených fázově posunovanými
střídavými signály, u zvukových vln analogicky pomocí
systémů reproduktorů. Gravitační vlny vznikající v
rotujících systémech černých děr nebo neutronových hvězd
by rovněž měly mít složku helikální rotující polarizace
(jejich měření je však komplikované, zatím se nepodařilo).
Tělesa -
částice, které se dostanou do vlnového pole, se rozkmitávají
různým způsobem, podle intenzity a polarizace
vln. Mohou se též roztáčet kolem své osy (spin) nebo do
rotace kolem osy svazku vlnění (orbitální moment hybnosti
vln).
Nyní si prozkoumáme, jak se tyto obecné fyzikálně-vlnové zákonitosti uplatňují v konkrétní oblasti gravitačního pole - u gravitačních vln :
Časově
proměnné gravitační pole
Gravitační pole je
buzeno hmotou lokalizovanou či rozloženou v prostoru, podle OTR
distribuce hmoty zakřivuje prostoročas. Pokud se rozložení
hmoty s časem mění (mění se
tvar nebo poloha hmotných objektů), reaguje na to i buzené gravitační
pole: budeme pozorovat časově
proměnné
gravitační pole, podle OTR měnící se křivost prostoročasu.
Jestliže se zdrojové těleso periodicky
pohybuje
či distribuce hmoty se periodicky mění, projeví se to v
okolním prostoru kmitavým stavem gravitačního působení - kmitavými deformacemi zakřivení prostoročasu. Jak
se bude takové časově proměnné či kmitající gravitační
působení a zakřivení prostoročasu chovat ?
Gravitační pole má mnohé společné
rysy s polem elektromagnetickým (viz §1.4), Einsteinovy rovnice
gravitačního pole jsou do určité míry zkonstruovány
"podle vzoru" Maxwellových rovnic elektrodynamiky.
Při sledování analogií mezi elektrodynamikou a gravitací se
vynoří nejdůležitější otázky :
¨ Jakou
rychlostí se šíří gravitační
interakce - gravitační odezva na změny rozložení hmoty ?
¨ Existuje
gravitační analogie elektromagnetických vln - vlny gravitační ?
¨ Jakým
způsobem gravitace zprostředkovává přenos
energie ?
Na první dvě otázky se pokusíme odpovědět v této kapitole,
problematiku gravitační energie a jejího přenosu rozebereme v
následujícím §2.8 "Specifické vlastnosti
gravitační energie".
Vznik a vlastnosti gravitačních vln
Gravitační
vlny by v zásadě měly vznikat všude tam, kde se
nerovnoměrně mění poloha nebo tvar hmotného objektu, při
zrychleném pohybu a nesférických změnách rozložení hmoty.
Podobnosti
a rozdíly elektromagnetických a gravitačních vln
Gravitační vlny se svým
charakterem do značné míry podobají vlnám elektromagnetickým:
oba typy vln mají příčný charakter a šíří se maximální
možnou rychlostí interakcí - rychlostí světla c.
Einsteinovy rovnice gravitačního pole jsou totiž svou
strukturou analogické Maxwellovým rovnicím
elektromagnetického pole. Jsou zde však určité strukturní
odlišnosti gravitačních a elektromagnetických vln :
× V univerzálnosti
působení
- elektromagnetická vlna rozkmitává jen elektricky nabité
částice (jako jsou elektrony), zatímco gravitační vlna,
představující změny geometrie prostoročasu, může rozkmitávat každou hmotu.
× V polarizačních
vlastnostech
- elektromagnetické vlny mají především dipólový charakter, zatímco gravitační vlny mají kvadrupólový charakter *), představují periodické
změny slapových účinků.
*) "Monopólový moment" představuje celkovou
hmotnost-energii systému, která se zachovává a tedy
nezpůsobuje radiaci. Určitým argumentem, proč nemohou vznikat
ani dipólové gravitační vlny, je již samotný
základní princip ekvivalence, podle něhož je
gravitace univerzální interakcí a hmotnost má vždy
stejné znaménko. Na rozdíl od elektrického dipólu tedy nelze
vytvořit skutečný gravitační dipól s rozdílnými
znaménky. Hmotnostní dipól odpovídá těžišti
hmoty systému, jehož první derivace odpovídá hybnosti,
která je také zachovávající se veličina, takže hmotnostní
dipól rovněž neemituje žádné gravitační záření. Pouze oscilace
kvadrupólových a vyšších momentů rozložení
hmotnosti mohou gravitačně vyzařovat, podobně jako vyzařují
kmitající elektrické a magnetické dipóly a vyšší
multipóly v elektrodynamice.
× V intenzitě
vyzařování
Pronikavě
se gravitační a elektromagnetické vlny liší
svou intenzitou - "sílou". Elektromagnetické
vlny poměrně vysoké intenzity vznikají elektromagnetickou
interakcí při běžných přírodních procesech a můžeme je
účinně generovat v elektronických zdrojích (vysílačích).
Můžeme je též snadno přijímat a přeměňovat jejich
energii. Intenzita vyzařování elektromagnetických vln je na
základní úrovni určena Larmorovým
vzorcem (1.61)
v §1.5 "Elektromagnetické pole. Maxwellovy rovnice.". Gravitace je však daleko
nejslabší interakcí v přírodě - vazba mezi
gravitačním polem a hmotou (látkou) je velmi malá ve
srovnání s elektromagnetickým nebo jaderným působením. Jak
bude ukázáno níže v pasáži "Zdroje
gravitačních vln", intenzita vyzařování
gravitačních vln je dána tzv. kvadrupólovou
formulí (2.77), ve které figuruje extrémě
malý koeficient G/c5; u
amplitudy vln je podle vzorce (2.77b) koeficient G/c4. Účinnost generace
gravitačních vln a jejich detekce je proto nesmírně nízká - za normálních okolností jsou gravitační vlny velice slabé, téměř neměřitelné.
Silnější gravitační vlny mohou vznikat jen za extrémního nahromadění hmoty, při působení velmi silných
gravitačních polí u některých kompaktních
objektů ve
vesmíru (bude rozebíráno níže v
části "Zdroje gravitačních vln").
Základní odlišnou strukturní vlastnost gravitačního
vlnění (podle obecné teorie relativity) můžeme vyjádřit
následujícím srovnáním: Pod
vlněním obvykle rozumíme vlnění "něčeho" v
prostoru. U gravitačních vln se vlní samotný
prostor.
Obecné vlastnosti
šíření gravitace v OTR
Mějme izolovanou hmotnou soustavu popsanou tenzorem
energie-hybnosti Tik v asymptoticky rovinném
prostoročase. Souřadnicovou soustavu zvolíme takovou, aby ve
velkých vzdálenostech od hmotného zdroje spojitě přecházela
v asymptotickou inerciální (Lorentzovu) soustavu. Složky
metrického tenzoru můžeme vyšetřovat
ve tvaru
| gik = hik + hik , | (2.63) |
| kde hik = | / | -1 | 0 | 0 | 0 | \ | je Minkowského metrika |
| | | 0 | 1 | 0 | 0 | | | ||
| | | 0 | 0 | 1 | 0 | | | ||
| \ | 0 | 0 | 0 | 1 | / |
a hik =def gik - hik jsou odchylky od této metriky; zatím nemusíme předpokládat, že hik jsou všude malé. Můžeme udělat dohodu, že indexy se budou "zvedat" a "spouštět" pomocí hik (i když to není v dané geometrii tenzor). Definujeme-li si modifikované metrické veličiny
h =def hii = hik hik , yik =def hik - 1/2 hik h
a souřadnice zvolíme tak, aby yik všude vyhovovalo čtyřem podmínkám yki,k = 0, můžeme Einsteinovy rovnice gravitačního pole vyjádřit pomocí yik :
| yik,lm hlm = -16p (T ik + t ik) , | (2.64) |
kde tik jsou veličiny druhého a vyššího řádu v yik (tik jsou složky tzv. pseudotenzoru energie-hybnosti gravitačního pole, jak bude ukázáno v příštím §2.8). Řešení těchto "násilně linearizovaných" (či "zdánlivě linearizovaných") Einsteinových rovnic může být vyjádřeno ve formě retardovaných integrálů podobně jako v elektrodynamice
 |
(2.65) |
kde R = ÖS(xa-x'a)2 je vzdálenost mezi jednotlivými místy x'a zdrojové soustavy a vztažným místem xa, v němž pole stanovujeme (obr.2.8). Pokud je tik ą0, je tento vztah vlastně integrální rovnicí, protože tik je funkcí yik. Avšak pro slabá pole v aproximaci linearizované teorie není pseudotenzor tik přítomen a vztah (2.65) přechází ve vztah (2.55) v §2.5.
Jak rychlá je gravitace ?
Podle vztahu (2.55), resp. (2.65), výsledné gravitační pole v
každém místě je dáno nikoliv okamžitým rozložením
hmoty~energie, ale rozložením zpožděným - retardovaným, posunutým do minulosti - vždy
o čas, který potřebuje pole k překonání vzdálenosti R z
jednotlivých míst x'a zdrojové soustavy do
vyšetřovaného bodu xa rychlostí c (obr.2.8). Změny v
gravitačním poli se tedy šíří konečnou
rychlostí
rovnou rychlosti světla. Jinými slovy (v terminologii gravitačních vln, viz níže), gravitační vlny se pohybují stejnou rychlostí jako vlny elektromagnetické - rychlostí
světla c.
Na první pohled se může zdát
zvláštní, že gravitační pole se šíří stejnou rychlostí
jako pole elektromagnetické, jako světlo. Není to však
zázračná náhoda, protože obecná teorie relativity, jakožto
fyzika gravitace, je stavěna na bázi speciální teorie
relativity, v níž rychlost světla hraje určující roli pro
strukturu prostoročasu *). Spíše než konkrétně o
rychlost světla se zde jedná o maximální
rychlost šíření interakcí, která má hodnotu c. Odpověď na otázku o
rychlosti šíření gravitačních vln můžeme formulovat i
obráceně: Světlo se šíří
rychlostí gravitačních vln! Gravitace totiž určuje strukturu
prostoročasu, a ta určuje, jak se mohou objekty pohybovat -
včetně světla...
*) Srov. příslušné diskuse v §1.6
"Čtyřrozměrný prostoročas a speciální teorie
relativity" a §2.2 "Univerzálnost
- základní vlastnost a klíč k pochopení podstaty gravitace".
Přímé experimentální
potvrzení rychlosti šíření gravitační interakce zatím chybí
*), nedokážeme vyrábět detekovatelné rozruchy v
gravitačním poli, nepodařilo se dosud ani zachytit
gravitační vlny od vesmírných objektů (viz
níže "Zdroje gravitačních vln"
a "Detekce gravitačních vln"). Jelikož však ve prospěch obecné teorie relativity
jako správné teorie gravitace svědčí zatím všechny
ostatní experimenty a astronomická pozorování, je světelná
rychlost šíření gravitace nanejvýš
pravděpodobná.
*) Zatím máme jen nepřímé
astronomické metody. Nejpřesvědčivější z nich je
pozorování těsných binárních pulsarů,
ukazující efekt zrychlování jejich oběhu v důsledku
vyzařování gravitačních vln, jak je popsáno níže v
pasáži "Nepřímé důkazy
gravitačních vln".
Míra tohoto efektu je velmi citlivá na hodnotu rychlosti
gravitačních vln; z měření binárního pulsaru PSR1913+16
vychází rychlost gravitace rovná rychlosti světla s
přesností asi 1%.
V principu jsou použitelné astronomické metody
srovnání rychlosti gravitace s rychlostí světla. Spočívá v
pozorování optického zákrytu vzdáleného
silného vesmírného zdroje elektromagnetického záření (jako
je kvasar) bližším masívním pohybujícím se tělesem
(třebas planetou, nebo Sluncem při úplném zatmění),
přičemž se analyzuje dynamika gravitačního ohybu
elektromagnetických papsků a vzniku gravitační
čočky (viz §4.3, část "Gravitační čočky. Optika černých děr"). Ta
závisí na shodnosti nebo rozdílnosti rychlosti pozorovaných
elektromag. vln ze vzdáleného zdroje a rychlosti gravitační
interakce od "čočkujícího" pohybujícího se
tělesa. Buď se dá pozorovat drobné posunutí pozice obrazu
vzdáleného zdroje díky pohybu zkušebního
("čočkujícího") tělesa, nebo nepatrné časové
zpoždění v příchodu elektromagnetických vln. Tyto poziční
a časové posuny závisí na rychlosti, s jakou se šíří
gravitační pole od testujícího tělesa, ve srovnání s
rychlostí měřených elektromagnetických vln
přicházejících od vzdáleného zdrojového objektu. K
pozorování těchto subtilních efektů však zatím naše
(radio)teleskopická technika nepostačuje...
Univerzálnost -
základní fyzikální vlastnost gravitačního záření
Základní fyzikální vlastností, kterou se gravitační
vlnění liší od všech ostatních druhů
záření v přírodě, je jeho naprosto univerzální
působení - interaguje úplně stejně se všemi druhy
částic a antičástic, se všemi formami hmoty.
Způsobuje totiž periodické změny v geometrických
vlastnostech (zakřivení) prostoročasu, které naprosto stejně
ovlivňují pohyby všech částic a chování
všech polí.
Rovinné gravitační vlny v
linearizované gravitaci
V dostatečně velkých vzdálenostech od zdrojových hmot bude
gravitační pole již velmi slabé, takže ve vztahu gik = hik +hik bude |hik|<<1. Budeme nejprve
předpokládat, že prostoročas je prakticky rovinný s
Minkowského metrikou, jen slabě změněnou gravitačním polem
vyjádřeným veličinami hik. V tomto případě budou
všechny nelineární efekty zpětného vlivu pole na metriku
zanedbatelně malé a takové gravitační pole potom můžeme
vyšetřovat (jakožto nezávislé pole) na pozadí
Minkowského prostoročasu podobně jako třebas pole
elektromagnetické. Linearizovanou
teorii gravitačního pole jsme si nastínili již v §2.5 jako
nejjednodušší možnost řešení Einsteinových rovnic. Při
vhodných kalibračních podminkách (2.53) platí pro slabá pole
linearizované Einsteinovy rovnice (2.54). Pro vakuum je potom oyik = 0, což je vlnová
rovnice (stejná jako v elektrodynamice - srov. rovnice
(1.46-47) v §1.5),
jejímž řešením jsou vlny
šířící se rychlostí světla, v tomto případě tedy gravitační
vlny *) .
*) Existence gravitačních
vln není specifickým důsledkem pouze obecné teorie
relativity. Gravitační vlny musejí existovat v rámci každé relativistické teorie gravitace (jako
důsledek konečné rychlosti šíření rozruchu v gravitačním
poli); pouze některé jejich vlastnosti mohou být
rozdílné.
Nejjednodušší řešení
linearizovaných gravitačních rovnic ve vakuu
| ylm = Re ( Alm . e i . kr xr ) | (2.66) |
popisuje monochromatickou rovinnou vlnu
s amplitudou Alm a vlnovým vektorem kr. Z rovnic (2.54) a 2.53) plynou vztahy krkr = 0, Almkm = 0, podle nichž k je izotropní vektor kolmý k A; gravitační vlny jsou tedy příčné vlny (rozkmitávají
tělesa pouze v rovině kolmé na směr šíření) s frekvencí w = k° = Ö(kx2+ky2+kz2) šířící se rychlostí světla ve směru k. Harmonická řešení (2.66)
tvoří úplnou soustavu (bázi) funkcí y a
libovolné řešení vlnových rovnic může být složeno jako
superpozice těchto řešení.
Lorentzovy podmínky (2.53) snižují
počet veličin yik z 10 na 6 nezávislých složek.
Lorentzovy podmínky se nezmění při transformaci yik ® yik + fi,k + fk,i, kde fi jsou čtyři libovolné funkce
splňující podmínku fi,ll = 0 (a dostatečně malé aby neporušily
podmínku |yik|<<1). Vhodnou volbou fi mohou být veličiny yik redukovány
na pouze dvě
nezávislé složky odpovídající dvěma
stavům polarizace.
Jak je ukázáno
níže, složka hxx rozkmitává testovací částice v elipsy s osami x,y,
zatímco složka hyx je rozkmitává v příčné rovině otočené o 45o
vůči x,y. Polarizace gravitační vlny se označují jako
polarizace "+" a "-".
Pro
monochromatickou rovinnou vlnu (2.66) lze vybrat kalibrační funkce fi
tak, aby yio = 0, yaa = 0. Potom hik= yik a hio = 0, haa = 0. Takováto kalibrace, která je velmi výhodná, se nazývá TT-kalibrace (Transversal
Traceless - příčná s nulovou stopou) *). V této TT-kalibraci mají
složky tenzoru křivosti velmi jednoduchou souvislost s
komponentami hik :
| Raobo = Roboa = - Raoob = - Roabo = - (1/2) hab,oo = - (1/2c2).¶2hab/¶t2 . | (2.67) |
*) Procedura kalibrační
transformace v teorii pole je obecně diskutována v
§B.6, pasáži "Kalibrační (cejchovací)
transformace; kalibrační pole".
Pokud
se rovinná vlna
šíří ve směru osy X, je popsána tenzorem
| h ik = | | | 0 | 0 | 0 | 0 | | | . |
| | | 0 | 0 | 0 | 0 | | | ||
| | | 0 | 0 | hyy | hzz | | | ||
| | | 0 | 0 | hyz | -hyy | | |
Nenulové jsou zde tedy jen dvě komponenty hik :
hyy = - hzz = Re ( A+ .e-iw(t-x)) , hyz = - hzy = Re ( A´ . e-iw(t-x)) .
Všimněme
si vlastností symetrie rovinné gravitační vlny při
pootočení kolem osy šíření. Při přechodu k nové
souřadnicové soustavě S', pootočené kolem osy šíření
gravitačních vln Z o úhel J, tj.
při transformaci t'=t, x'=x.cosJ
+y.sinJ, y'= =y.cosJ-x.sinJ, z'= z, se jednotkové vektory polarizace
gravitační vlny transformují podle vztahu e'+
= e+cos2J+e´.cos2J, e'´ = -e+sin2J+ e´cos2J . Definice klasického
spinu je
následující: Rovinná vlna
y má spin s,
jestliže se při pootočení o úhel J
kolem směru šíření transformuje podle zákona y' = eisJ.y - jinými slovy zůstává invariantní
při pootočení o úhel 2p/s kolem osy šíření. Tato
symetrie úzce souvisí se spinem
kvant, z
nichž z hlediska kvantové teorie pole příslušná vlna
sestává. Pro gravitační vlny tedy vychází tento úhel
invariance roven 180°, takže gravitační vlny mají spin s = 2 *) . Tento spin s=2 by tedy měly mít
kvanta gravitačního vlnění, zatím hypotetické gravitony (viz níže).
*) Vektory polarizace
elektromagnetické vlny se při pootočení o úhel J
kolem směru šíření transformují: ex = excosJ + eysinJ, ey = eycosJ - exsinJ - elektromagnetické vlny mají spin
s =1, jsou symetrické
vůči pootočení o 360° kolem směru šíření.
Gravitony
- kvanta gravitačního vlnění ?
Podle koncepce kvantové fyziky by se každá energie měla vyzařovat
nikoli spojitě, ale po kvantech. Všeobecně známá a experimentálně
prokázaná kvanta elektromagnetického vlnění jsou fotony (viz "Částicově-vlnový dualismus"). I když úplnou kvantovou teorii
gravitace se dosud nepodařilo vytvořit, analogické použití
kvantového modelu na gravitační vlny vedlo k představě gravitonu: hypotetického kvanta
gravitačního záření -
elementární částice zprostředkovávající gravitační
sílu v rámci kvantové teorie pole. Očekává se, že graviton
je částice s nulovou klidovou hmotností (gravitační
interakce má neomezený dosah) a bude bosonem se spinem s=2
(souvisí s výše diskutovaným kvadrupólovým charakterem
gravitační radiace); elektrický
náboj gravitonu je samozřejmě nulový (či bezpředmětný).
Jakým způsobem vzniká graviton v kvantové teorie gravitace je
diskutováno v §B.5 "Kvantování gravitačního pole".
Z hlediska fyzikální analýzy
gravitačních vln ve vesmíru (snad s
výjimkou kosmologie velmi raného vesmíru a unitárních
teorií pole) jsou gravitony
bezpředmětné.
Projevovaly by se pouze při velmi vysokých
frekvencích gravitačních
vln řádu gigahertzů a vyšších (jakési "gravitační
gama-záření").
Takové gravitační vlnění nikde v nám známém vesmíru nevzniká. Gravitony zůstanou snad trvale jen hypotetickými či modelovými
částicemi, na jejichž
přímé či nepřímé prokázání a detekci není
naděje v dohledné budoucnosti (o hypotetických a modelových
částicích ve fyzice elementárních částic viz pasáž
"Hypotetické a
modelové částice")...
V našem pojednání o gravitačních vlnách je proto nebudeme
uvažovat.
"Gravitačně
nabité" gravitační vlny
V rámci linearizované teorie gravitace jsou gravitační vlny
veskrze analogické vlnám elektromagnetickým v klasické
elektrodynamice. Ve skutečnosti se zde však musí projevovat
ten důležitý rozdíl mezi elektřinou a gravitací, který byl
zmíněn již na začátku §2.5 "Einsteinovy
rovnice gravitačního pole". Prochází-li elektromagnetická
vlna oblastí prostoru v níž působí elektrické pole, nedojde
k žádnému ovlivnění vlny tímto polem; podobně když se
dvě elektromagnetické vlny setkají, projdou "jedna přes
druhou" bez vzájemného ovlivnění a budou pokračovat ve
svém pohybu tak, jako kdyby druhé vlny nebylo. Jinými slovy,
elektromagnetické vlny jsou elektricky
neutrální
(nanabité). Gravitační vlny však nejsou gravitačně neutrální:
přenášejí energii (~hmotnost) a proto jsou
jednak ovlivňovány gravitačním polem přes které
procházejí, jednak (spolu)působí jako zdroj
gravitace.
Je to důsledkem uviverzálnosti
gravitace. Lze
říci, že gravitační vlny jsou
"gravitačně
nabité", samy vykazují
gravitaci! Níže to bude kvantifikováno tzv. Isaacsonovým
tenzorem energie-hybnosti gravitačních vln. Hypotetickým
extrémním důsledkem této skutečnosti je model gravitačního
geonu (§B.3 "Wheelerova
geometrodynamika. Gravitace a topologie."), nebo dokonce "gravitačně-vlnová"
černá díra vzniklá kolapsem mohutných gravitačních
vln (zmíněná v §4.5 "Černá díra
nemá vlasy", pasáž "Uniformita
černých děr").
Lokálně (v ne příliš velkých
oblastech) můžeme gravitační vlny považovat za rozruch vyvolaný nějakým nerovnoměrným
pohybem hmoty (např. obíháním dvojhvězd, výbuchem
supernovy, nesférickým gravitačním kolapsem a pod. - viz níže část "Zdroje
gravitačních vln"), šířící se v rovinném
prostoročase a není třeba brát zřetel na interakci s
celkovým zakřivením prostoročasu a na nelineární
interakce vln mezi sebou. Globálně však zakřivení
prostoročasu způsobené rozložením ostatní hmoty (např.
hvězd a galaxií) bude ovlivňovat šíření gravitačních vln
- bude způsobovat frekvenční posuv a měnit směr šíření.
K tomuto globálnímu zakřivení přitom bude
přispívat i energie nesená samotnými vlnami (viz níže).
Při šíření gravitačních vln budou tedy vznikat
charakteristické nelineární
efekty
[58], např. dvě gravitační vlny se budou vzájemně
rozptylovat.
Vyšetřujme tedy gravitační vlny v obecném zakřiveném prostoročase. Abychom mohli vůbec mluvit o gravitačních vlnách, musíme být schopni odlišit vlnící se část křivosti, vyvolanou gravitačními vlnami, od globální křivosti "pozadí" způsobené jinými vlivy (rozložením hmotných těles). Toto oddělení globálního zakřivení prostoročasu od lokálních fluktuací vln je možné v případech, kdy střední délka vlny l je mnohem menší než charakteristický poloměr křivosti R prostoročasu, na jehož pozadí se vlny šíří :
| l << R . | (2.69) |
Podobně můžeme
globální tvar Země odlišit od místních nerovností terénu
nebo tvar pomeranče odlišit od drobných místních nerovností
jeho povrchu. Místní křivost ve vlně může být přitom
podstatně větší než globální křivost prostoročasu
(odlišení pozadí od vln je umožněno nikoliv rozdílem hodnoty
zakřivení, ale rozdílností měřítek v nichž se zakřivení
mění) *).
*) Jak ale uvidíme níže,
samotné gravitační vlny vyvolávají podle Einsteinových
rovnic globální křivost
prostoročasu úměrnou A/l. Proto ke splnění základní podmínky
krátkovlnné aproximace (2.69) je třeba, aby amplituda A gravitačních vln byla rovněž malá.
Prostoročas vyhovující podmínce (2.69) lze potom analyzovat jednak z hlediska malých měřítek ("lokální přístup"), jednak z hlediska globálních vlastností prostoročasu. Toto přiblížení se nazývá krátkovlnná aproximace a příslušná metoda analýzy gravitačních vln Isaacsonův formalismus [140]. Metrický tenzor (potenciály pole) může být pak rozepsán ve tvaru
| g ik = gikglob + h ik , | (2.70) |
kde gikglob je globální metrika prostoročasu, na jehož pozadí se vlny hik šíří. Podobně tenzor křivosti Rik lze rozložit v řadu podle malého bezrozměrného parametru l/R<<1 :
| Rik = Rikglob + R(1)ik + R(2)ik) + F [l/R)3] , | (2.71) |
kde Rglob je globální křivost pozadí (monotónní v rozsahu většího počtu vlnových délek).
| Rik(1) = 1/2 (-h;ik - hik;ll +hlk;il+ hli;kl) | (2.72) |
je vlnící se část křivosti lineární v l/R a
| Rik(2) = (1/2) [1/2 hlm;i hlm;k + hlm(hlm;ik + hik;lm - hli;km - hlk;im) + hkl;m(hli;m - hmi;l) - (hlm;m - ......již se nevešlo na řádek- přijde doplnit | (2.73) |
je část tenzoru křivosti kvadratická v l/R. Spouštění a zvedání indexů, jakož i kovariantní derivování ";" se zde všude provádí podle metriky gikglob.
Obecné rovnice pole ve vakuu Rik = 0 mohou být potom rozděleny na části a analyzovány ze dvou hledisek:
a) Lokální
přístup
V malých měřítcích (v oblastech srovnatelných s vlnovou
délkou l), kde se globální zakřivení
prostoročasu přímo neuplatňuje, musí být lineární část
R(1)ik vyvolaná vlnami
rovna nule
| R(1)ik = 0 . | (2.74) |
S pomocí veličin yik =def hik - (1/2) h gikglob, volbou vhodné kalibrace v níž je yki;k=0 a vypuštěním členů vyšších řádů může být tato rovnice přepsána ve tvaru
| yik;ll + 2.Rgloblikm ylm = 0 . | (2.74') |
Rovnice (2.74) je tedy rovnicí šíření gravitačních vln - zobecnění vlnové rovnice (2.54) na zakřivený prostoročas.
Z rovnice (2.74) plynou základní zákony šíření gravitačních vln v zakřiveném prostoročase, analogické "geometrické optice" vln elektromagnetických [271],[181] :
Optické efekty v OTR, jako je rudý posuv nebo zakřivování paprsků v gravitačním poli, tedy platí i pro gravitační vlny.
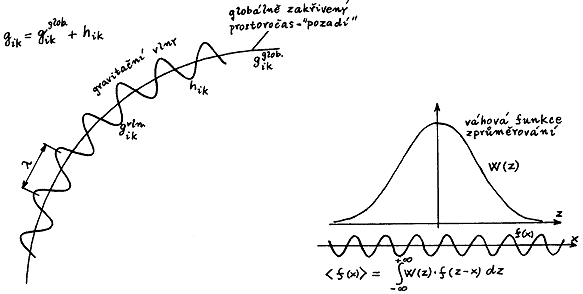
Obr.2.9. V Isaacsonově krátkovlnné aproximaci lze odlišit
globální zakřivení prostoročasu ("pozadí") od
lokálních fluktuací gravitačních vln, pokud je vlnová
délka mnohem menší než charakteristický poloměr křivosti
prostoročasu. Tato separace se provádí pomocí
zprůměrování přes oblast o několika vlnových délkách za
použití vhodné normované váhové funkce W(z) konvergující
k nule s rostoucí vzdáleností.
b) Globální
přístup
Při globálním přístupu provedeme zprůměrování "< >" všech veličin přes
oblast o rozměrech několika vlnových délek, abychom oddělili
globální křivost prostoročasu od lokálních fluktuací ve
vlnách. Veškerá struktura fluktující křivosti způsobená
gravitačními vlnami se při tomto středování zahladí -
<R(1)ik> = 0 - zatímco globální
křivost prostoročasu se prakticky nezmění:
<Rikglob> @ Rikglob. Ke středování lze použít vhodné
normované váhové funkce konvergující k nule s rostoucí
vzdáleností (s rostoucím počtem vlnových délek) a
paralelního přenosu do vyšetřovaného místa podél vhodné
geodetiky v metrice gikglob [140] - viz obr.2.9. Rovnice
pole potom budou znít Rikglob + <Rik(2))> = 0, což lze upravit na
tvar Einsteinových rovnic
| Gikglob
ş Rikglob - 1/2 Rglob
gikglob = |
(2.75) |
kde zdroj na pravé straně
| Tikvln = - (c4/8pG) [<Rik(2)> - 1/2 gikglob. <R(2)>] | (2.76) |
je tzv. Isaacsonův tenzor "efektivní
rozprostřené" energie-hybnosti gravitačních vln *).
*) To, jak se i v
"prázdném" prostoru bez hmotných zdrojů objeví na
pravé straně (2.75) zdroj globálního gravitačního pole, je
poněkud analogické tomu, jak se i ve vakuu bez proudů pro
nestacionární elektromagnetické pole objevuje Maxwellův
posuvný proud (srov. s §1.5, rovnice (1.34)) budící
magnetické pole stejně jako proud skutečných elektrických
nábojů.
Rovnice (2.75) popisují, jak gravitační vlny při svém šíření zakřivují globálně prostoročas. Tikvln můžeme tedy interpretovat jako tenzor energie-hybnosti gravitačních vln v globálním obklopujícím
prostoročase (je tenzorem pouze v
globální geometrii gikglob, nikoliv v úplné metrice gik = gikglob + hik !), pro
nějž z rovnic (2.75) plynou běžné zákony zachování Tvlnik;k = 0. Isaacsonův tenzor hraje
důležitou úlohu ve správném chápání specifické povahy gravitační energie, k čemuž se vrátíme v
následujícím §2.8 "Specifické vlastnosti
gravitační energie".
Pozn.: Zbylé
členy vyšších řádů v rovnici Rik = 0 popisují shora zmíněné nelineární
"opravy" a efekty, např. zkreslení tvaru vln a
interakce vln samých se sebou (rozptyl vlny na vlně a pod.).
Principiální otázky přenosu energie gravitačními vlnami budou podrobněji
diskutovány rovněž v §2.8, v kontextu s obecnými aspekty
gravitační energie. V tomto §2.7 se soustředíme na způsob vzniku (generování) gravitačních vln a na
možnosti jejich detekce.
Šíření gravitačních
vln
Ve vakuovém kosmickém prostoru se gravitační vlny šíří
zcela analogicky jako elektromagnetické vlny ve vakuu. V
rovinném prostoročase s Minkovského metrikou se šíří
přímočaře rychlostí světla ve vakuu, podle univerzální vlnové rovnice. Graficky se
šíření vlny znázorňuje pomocí vlnoplochy, což je
geometrické místo bodů v prostoru, které při vlnění
kmitají se stejnou fází. U vlnění z bodového nebo
sféricky symetrického zdroje se zde se jedná o kulovou
(sférickou) vlnoplochu, jejíž body leží na kulové ploše.
Kolmice na vlnoplochu udává směr šíření vln.
V zakřiveném prostoročase se
gravitační vlny šíří podél nulových (izotropních) geodetik
(2.5b) , opět analogicky elektromagnetickým vlnám: gravitace
ohýbá - zakřivuje směr šíření gravitačních
vln. Vznikají zde různé "optické" efekty, včetně
možnosti gravitační čočky (pro
světlo podsané v §4.3, pasáži "Gravitační
čočky. Optika černých děr.") a spektrálního posuvu frekvence
gravitačních vln. Vzhledem ke slabosti gravitačních vln a
obtížnosti jejich detekce se však tyto zajímavé efekty v
dohledné době asi nepodaří pozorovat.
Při šíření gravitačních vln hmotným-látkovým
prostředím dochází k mechanickému rozkmitávání
částic tohoto prostředí, což obecně může vést k absorpci
gravitačních vln. Vzhledem k velmi slabé gravitační
interakci s hmotou je však tato absorpce gravitačních vln za
normálních okolností velmi malá. Podle analogie se
světlem bychom mohli uvažovat i o zpomalení rychlosti
gravitačních vln v látkovém médiu, které by mohlo
způsobovat "lom" gravitačních vln - hypoteticky o
"gravitačním indexu lomu" v látkovém prostředí.
Ten však nijak nesouvisí s běžným optickým indexem lomu a
je prakticky přesně roven 1 pro všechna běžná prostředí (rozdíl
oproti vakuu není měřitelný). Pouze v
prostředí s obrovskou hustotou, jaké je v neutronových
hvězdách, by se projevovala výraznější interakce mezi
gravitačními vlnami a hmotou, která by mohla zpomalit rychlost
šíření gravitačních vln a generovat nezanedbatelný index
lomu..?..
Společnou obecnou
vlastností šíření vln - radiace - je skutečnost,
že příslušné vlny se odpoutávají od zdroje a odnášejí
s sebou do prostoru část jeho energie, hybnosti a momentu
hybnosti, a to i bez přítomnosti nějakého vzdáleného
"přijímače" těchto vln. Samotné vlny (jejich pole)
totiž mají energii. Zde se jedná o energii
gravitačního pole (jejíž osobité zvláštnosti jsou
diskutovány v §2.8 "Specifické vlastnosti
gravitační energie").
Vyzařování
a zdroje gravitačních vln
Za jakých okolností tedy
vznikají gravitační vlny? Podle analogie s elektrodynamikou
lze očekávat, že gravitační vlny se budou vyzařovat při zrychlených (nerovnoměrných) pohybech těles, kdy dochází k
časovým změnám buzeného gravitačního pole - když se
nerovnoměrně mění poloha nebo tvar hmotných objektů.
Nejobvyklejším druhem radiace v
elektrodynamice je záření elektrického
dipólu,
jehož intenzita je dána druhou derivací dipólového momentu d = n=1SNqn.rn
soustavy N elektrických nábojů qn,
nacházejících se v polohách rn,
podle času (§1.5, vztah (1.61)). V gravitaci úlohu
elektrického dipólového momentu hraje dipólový moment d = S mn.rn
rozložení hmoty v soustavě N částic mn. První časová derivace tohoto
dipólového momentu d. = S mn.rn.
ş p je rovna celkové hybnosti p soustavy, takže jeho druhá derivace
bude rovna nule díky zákonu zachování hybnosti. Ukazuje se
tedy, že dipólové gravitační záření nemůže existovat,
gravitační záření musí mít nejméně
kvadrupólový charakter *).
*) Souvisí to s teorémem
klasické nauky o záření [166], podle něhož nejnižší
"multipolarita" záření jež se může vyzařovat, je
větší nebo rovna klasickému spinu daného pole. Tento spin je dán mírou symetrie v rovinné vlně: spin s = 360°/(úhel
pootočení kolem osy šíření zachovávající symetrii),
takže pro elektromagnetické pole se spinem s=1 je záření
nejméně dipólové, pro gravitační pole se spinem s=2 je
nejméně kvadrupólové.
Za zdroj gravitačních vln můžeme tedy
považovat obecně každou fyzikální soustavu s časově proměnnou distribucí hmoty r(t,xa), při níž se s časem mění i kvadrupólový moment prostorového rozložení hmoty - když
se hmota-energie pohybuje zrychleně
nesférickým způsobem. Časové změny distribuce hmoty
vyvolávají příslušné časové změny geometrie okolního
prostoročasu - "rozvlňují" křivost prostoročasu.
Tyto vlny křivosti prostoročasu - tj. gravitační vlny - se odpoutávají od zdrojové soustavy
a šíří se do okolního prostoru, přičemž odnášejí
část kinetické energie pohybující se hmoty ve zdrojovém
systému.
Abychom stanovili sílu - intenzitu - amplitudu gravitačních vln vyzařovaných určitou
fyzikální soustavou, použijeme obecné řešení
linearizovaných gravitačních rovnic při Lorentzově kalibraci
ve tvaru retardovaných potenciálů
| vzorec (2.55) si zde pro názornost uvádíme znovu |
podobně jako v
elektrodynamice, kde R = Ö[a=1S3(xa - x'a)2] je vzdálenost z jednotlivých míst x'a soustavy zdroje do vyšetřovaného bodu
xa (podle
obr.2.8). Jestliže
je rozložení hmoty-energie (složek tenzoru energie-impulsu Tik) časově
proměnné,
bude budit časově proměnné potenciály yik gravitačního pole, které
mohou popisovat vyzařované gravitační vlny.
Pokud rychlost
pohybů ve vyšetřované zdrojové soustavě bude malá ve
srovnání s c a gravitační příspěvek k celkové
hmotě-energii bude malý, můžeme tenzor energie-hybnosti
vyjádřit jako pomocí hustoty hmoty r a
čtyřrychlosti ui: T ik = r . u i u k a s použitím
zákonů zachování (2.90) energie-hybnosti ve zdroji zavést tenzor kvadrupólového
rozložení hmoty ve zdroji K ab = Vň
T oo(t,x)
xa xb dV = c2 Vň r(t,x) xa xb dV.
V limitě slabého pole (a v tzv.
TT-kalibraci) pak
obecný vztah (2.55) může být vyjádřen pomocí důležité kvadrupólové formule :
| hab(t,R) = [(2G/c4)...Kab(t-R/c)] / R , | (2.77a) |
vyjadřující "amplitudu" gravitační vlny - fluktuace metriky hab(t,r) v čase t a ve vzdálenosti R od zdroje s časově proměnným tenzorem kvadrupólového momentu Kab rozložení hmoty ve zdroji:
| Kab(t) = ň r(t,x)·(3 xaxb- dab xg xg) dV . | (2.78) |
Amplituda vln tedy klesá se vzdáleností od
zdroje jako 1/r a je dána druhou časovou derivací ..Kab
kvadrupólového momentu rozložení hmotnosti-energie ve
zdrojové soustavě, s retardací R/c (podle
obr.2.8).
Kvadrupólový vzorec (2.77b) se odvodí v rámci
linearizovaných rovnic pole se zdrojem Tik, do jejichž řešení (2.55) či (2.65) ve tvaru
retardovaných potenciálů se implementuje kvadrupólový moment
(2.78) rozložení hmoty ve zdrojové soustavě ve výše
uvedené TT-kalibraci (viz pasáž "Gravitační
vyzařování ostrovní soustavy" v §2.8
"Specifické vlastnosti gravitační energie"). Kvadrupólový vzorec
poprve odvodil A.Einstein v r.1916-18.
K výpočtu energie vyzářené takovou soustavou ve
formě gravitačních vln (tj. intenzity gravitačních vln) se
používá metod nastíněných v následujícím §2.8. Pokud
pohyb hmoty ve zdroji je pomalý ve srovnání s rychlostí
světla, zdroj je malý ve srovnání s délkou vyzařovaných
vln a pole v něm je dostatečně slabé, je okamžité
množství energie gravitačně vyzařované soustavou za
jednotku času - "gravitačně
vlnový výkon" - dáno opět kvadrupólovou
formulí (odvozenou v následujícím
§2.8 "Specifické vlastnosti gravitační energie", pasáž "Gravitační vyzařování
ostrovní soustavy") :
| d E / d t = - (G/45.c5) ...Kab2 , | (2.77b) |
kde tečky znamenají derivace podle času t - jedná se zde tedy o 3.derivaci; Kab2=KabKab, sčítá se přes a,b=1,2,3. V astronomické terminologii kvadrupólový vzorec (2.77b) vyjadřuje jakousi "gravitačně-vlnovou luminozitu" zdrojové soustavy. Intenzita záření ve směru (jednotkového) vektoru n do elementu prostorového úhlu dW je dána vztahem
| (2.79) |
Vztahy (2.77) a (2.79)
ve shodě s výše uvedenou argumentací ukazují, že pro
vyzařování gravitačních vln je podstatný pouze
kvadrupólový moment zdroje, který se musí měnit s časem,
zatímco monopólový a dipólový moment k vyzařování
nepřispívají.
Koeficient G/(45.c5) ukazuje, že vyzařovávání energie
gravitačními vlnami je efektem
5.řádu vzhledem k 1/c, což spolu s malou hodnotou gravitační
konstanty G vede k velmi
malé intenzitě tohoto efektu za všech běžných
podmínek, kromě těsného oběhu a splynutí černých děr
nebo neutronových hvězd (je diskutováno
níže "Zdroje gravitačních
vln ve vesmíru").
Rozdělení zdrojů gravitačních vln
Zdroje gravitačních vln lze klasifikovat z různých hledisek.
Podle rozměrů a umístění můžeme rozlišovat zdroje laboratorní (pozemské) a astrofyzikální
(vesmírné). Z
hlediska časového průběhu pohybu hmoty ve zdroji (a tím i
frekvenčního spektra vyzařovaných vln) můžeme zdroje
gravitačního vlnění rozdělit na dva druhy :
Některé
astrofyzikální zdroje původně periodické se však v
průběhu času mohou stát aperiodickými. Např. těleso
obíhající po téměř kruhové vzdálené dráze kolem černé
díry bude po dlouhou dobu prakticky periodickým zdrojem
(slabých) gravitačních vln, dokud neklesne na mezní -
nejvnitřnější stabilní orbitu (§4.3 pasáž
"Vyzařování gravitačních vln při pohybu v
poli černé díry"). Pak je rychle pohlceno černou
dírou, přičemž vyzáří intenzívní záblesk gravitačního
záření - stane se zdrojem aperiodickým. K těmto jevům však
nejčastěji dochází u těsných dvojhvězdných systémů (viz níže "Zdroje gravitačních vln ve
vesmíru",
obr.4.13-GW).
Nejjednodušším laboratorním
zdrojem
gravitačních vln je tyč rotující kolem kolmé osy úhlovou
rychlostí w (obr.2.10a). Podle vztahu (2.77)
bude taková rotující tyč gravitačně vyzařovat energii
| d E / d t = - (32.G/ 5.c5) I2 w6 , | (2.80) |
kde I je moment setrvačnosti vzhledem k příslušné rotační ose. Jak nepatrná energie se tímto způsobem vyzařuje, lze ilustrovat na příkladu ocelové tyče průměru 1 m a délky 20 m (celková hmotnost téměř 500 tun!) rotující maximální rychlostí asi 4 otáčky za sekundu (limitovanou pevností materiálu), kdy se gravitačně vyzařuje energie dE/dt @ 2,2. 10-29W; tak nepatrná hodnota je hluboko pod současnými možnostmi ji jakkoli zaregistrovat. Z toho je vidět, že laboratorní generátory gravitačních vln (aspoň co se týče zdrojů na mechanickém základě) zatím nejsou použitelné pro experimenty s gravitačními vlnami.
Zdroje gravitačních vln ve
vesmíru
Příznivější situaci lze očekávat u některých kosmických objektů, kde vstupují do hry
nesrovnatelně větší hmotnosti než u laboratorních
generátorů. Izolovaná hvězda je schopna vyzařovat
gravitační vlny buď tehdy, když neradiálně pulzuje, nebo
když rotuje a přitom není axiálně symetrická. V případě
rotující hvězdy úhlovou rychlostí w vychází ze vzorce (2.77) pro energii gravitačního
záření vztah
| d E / d t = - (288.G/45.c5) I2 e2 w6 , | (2.81) |
kde I je moment setrvačnosti a e = (a-b)/Öab vyjadřuje odchylku od axiální
symetrie (a,b jsou hlavní osy v rovníkové rovině). Podle
příslušného modelu by gravitační záření vznikající
tímto mechanismem mohlo být příčinou zpomalování pulsaru
PSR 0532 v Krabí mlhovině (pulsar má
periodu asi 33 ms, rychlost zpomalování 1,3.10-5 s/rok, vyzařovaný
výkon gravitačních vln by měl být asi 1031W [89]).
Pozn.: Supernova je jen slabým zdrojem
gravitačních vln
V §4.2, část "Výbuch supernovy.
Neutronová hvězda. Pulsary." je ukázáno, že výbuch supernovy je
nejkatastrofálnějším jevem ve vesmíru, při němž je
vyzářena obrovská energie elektromagnetická i
korpuskulární. Avšak z hlediska emise gravitačních vln je
supernova většinou jen poměrně slabým
zdrojem pulsu gravitačních vln. Důvodem je, že kolaps jádra
a následný výbuch supernovy probíhá většinou téměř symetricky,
bez výraznějšího gravitačního vyzařování. Pokud by však
tento proces přece jen probíhal nesymetricky (třebas v důsledku předchozí srážky původních
hvězd v binárním systému..?..), příp.
detekce a analýza vzniklých gravitačních vln by mohla vynést
cenné informace (jinak nedosažitelné) o procesech v pekelné výhni "srdce"
supernovy...
 |
Obr.2.10. a) Rotující tyč jako
(laboratorní) zdroj gravitačních vln. |
Binární
hvězdné systémy
- kardinální zdroje gravitačních vln
Nejvýznamějšími zdroji gravitačních vln jsou však těsné binární systémy kompaktních astronomických
objektů - neutronových hvězd a černých děr. Značná část (více než
polovina) hvězd je součástí dvojhvězdných
nebo
vícenásobných systémů. Jednotlivé hvězdy v těchto
binárních systémech dříve či později vyčerpají zásoby
svého termonukleárního paliva a dostanou se do finálních stádií své evoluce (§4.2 "Konečné fáze
hvězdné evoluce. Gravitační kolaps. Vznik černé díry.") - a
podle jejich zbylé hmotnosti se z nich stanou bílí trpaslíci,
či zkolabují do neutronových hvězd nebo černých děr. Tyto kompaktní objekty pak budou nadále kolem sebe obíhat,
čímž budou vytvářet
gravitační vlny.
Máme-li dvě tělesa o hmotnostech m1
a m2, které se gravitačně přitahují (podle Newtonova zákona) a obíhají po kruhových orbitách
poloměru r kolem společného těžiště úhlovou
rychlostí w (obr.2.10b), bude tato soustava
podle kvadrupólového vztahu (2.77) vyzařovat energii
| d E / d t = - (32.G/5.c5)[m1.m2/(m1 + m2)]2 r-4 w6 , | (2.82a) |
ve formě téměř
monochromatických gravitačních vln o frekvenci f=2p/w (odhlédneme-li od
zrychlování rotace v důsledku přibližování obou těles,
viz níže).
Při
obíhání po eliptické dráze s hlavní poloosou a a
excentricitou e je gravitačně vyzařovaná energie dána
složitějším vztahem [285]
| d E / d t = - (32.G/5.c5)[m12.m22/(m1 + m2)] a-5 . f(e) , |
kde funkce f (e) = ( 1 + (73/24)e2
+ (37/96)e4 ) . (1 - e2)-7/2 zachycuje rostoucí vliv výstřednosti na intenzitu
záření. Při eliptickém pohybu obsahují vyzařované
gravitační vlny nejen druhou harmonickou frekvence oběžného
pohybu (jako je tomu u kruhového obíhání), ale i vyšší
harmonické. Přitom intenzita vyzařování je nejvyšší v
"perihéliu" kde jsou si obě tělesa nejblíže a
zrychlení je největší. Tento efekt vede k postupnému zmenšování
excentricity - eliptický pohyb se pomalu mění na
kruhový; celkově se perioda oběžného pohybu zkracuje.
Odnášení
energie oběžného pohybu gravitačními vlnami vede ke
vzájemnému přibližování obíhajících
těles, zkracování oběžné periody, zvyšování rychlosti
oběhu a zvyšování frekvence a intenzity
gravitačních vln. Zachycuje to obr.4.13-GW (je modifikací obr.4.13 z §4.3 pasáž "Vyzařování
gravitačních vln při pohybu v poli černé díry") :
 |
| Obr.4.13-GW.
Časový průběh amplitudy, frekvence a intenzity
gravitačního záření binárního systému dvou
kompaktních těles m1 a m2
obíhajících kolem společného těžiště. Tělesa, jež začnou v čase t=t0 své obíhání na nějakém velkém poloměru r0, velmi pomalu klesají po spirále a kontinuálně vyzařují gravitační vlny, nejprve slabé (etapa I). I u těsných binárních systémů to bývá proces trvající statisíce i miliony let. S přibližováním stále roste intenzita a frekvence vyzařování. Po dosažení vzdálenosti oběhu několika desítek gravitačních poloměrů dochází k lavinovitému růstu intenzity a frekvence gravitačních vln (etapa II). Po dosažení mezní-nejnižší stabilní orbity tělesa rychle splynou, přičemž se vyšle krátký intenzívní záblesk gravitačních vln (etapa III). V horní části obrázku jsou symbolicky nakresleny zvětšené výřezy z několika posledních oběhů, během nichž dochází k deformacím obou horizontů a nakonec k jejich spojení do deformovaného horizontu výsledné černé díry. Výsledná černá díra m1+m2 je rotující a vyzařováním tlumených gravitačních vln rychle relaxuje na stacionární axiálně symetrickou konfiguraci Kerrovy černé díry (etapa IV). |
Zmenšování poloměru oběhu r binárního systému těles m1 a m2 s časem t v důsledku vyzařování gravitačních je (v linearizované aproximaci) dáno vztahem
| d r / d t = - (64.G3/5.c5)[m1.m2.(m1 + m2)]/r3 . | (2.82b) |
Čas tr®0 do splynutí obou těles binárního systému *), obíhajících momentálně ve vzdálenosti R, pak vychází:
| tr®0 @ (5.c5/256.G3) . R4/[m1.m2.(m1 + m2)] . | (2.82c) |
Pomocí momentální oběžné periody T binárního systému to lze vyjádřit vztahem:
| tr®0 @ (5.c5/256) . (T/2p)8/3/[G5/3.(m1.m2)/(m1+m2)3] » 107[let]. T[hod.]8/3.{[(m1.m2)3/5/(m1+m2)1/5]/M¤}-5/3. | (2.82d) |
Pro běžné dvojhvězdné systémy je tento
čas splynutí - zániku - velmi dlouhý (řádu
miliard let i více), avšak pro těsné
binární systémy kompaktních objektů může být z
astronomického hlediska poměrně krátký (je
diskutováno níže).
*) Pozn.: Toto by
byla očekávaná doba splynutí idealizovaných hmotných
bodů m1 a m2 ve vzdálenosti r=0 ; pro skutečná tělesa
konečných rozměrů je tato doba splynutí poněkud kratší.
Pro
časový růst frekvence df/dt vyzařovaných
gravitačních vln při vzájemném oběhu dvou těles o hmotnostech m1
a m2 po kruhových
drahách (kolem společného těžiště) lze v post-Newtonovské aproximaci (do řádu O[(Gm/rc2)]) kvadrupólové formule [...] odvodit vztah :
| df/dt @ (m1.m2)/(m1+m2)2/5.G-3/5.c-12/5.(96/5)p8/3.f11/3 , který
se dá upravit na tvar : (m1.m2)3/5/(m1+m2)1/5 @ (c3/G). [(5/96)p-8/3. f -11/3.(df/dt)]3/5 . |
(2.82e) |
Výhodou vztahů (2.82d,e) je, že explicitně
neobsahují parametry dráhy oběhu (poloměry r), které
jsou astronomicky většinou neznámé. Analýzou vztahu mezi
frekvencí f přijímaných gravitačních vln a jejím
časovým vzrůstem df/dt je možno stanovit parametr podílu
hmotností M = (m1.m2)3/5/(m1+m2)1/5 *)
vyzařujících těles. Z něho lze v principu určit celkovou
hmotnost m1+m2 systému a další detailní
počítačovou analýzou (modelováním
podle "nelinearizované" obecné teorie
relativity a fitováním se změřeným průběhem signálu z
gravitační vlny)
lze v zásadě stanovit hmotnosti jednotlivých složek,
vyzářený výkon gravitačních vln, příp. i rotační moment
hybnosti. .....
*) Tento hmotnostní parametr M = (m1.m2)3/5/(m1+m2)1/5 se v gravitačně-vlnovém slangu někdy nazývá chirp
mass - "cvrlikající hmota",
neboť rychlý růst frekvence těsně před splynutím obou
kompaktních těles připomíná ptačí cvrliknutí. Hodnota
tohoto hmotnostního parametru M je přibližně
rovna geometrickému průměru hmotností obíhajících těles m1 a m2.
Obecně tedy nejvýznamnějšími
permanentními (periodickými či
kvaziperiodickými) zdroji gravitačních
vln ve vesmíru jsou masívní tělesa, která
kolem sebe obíhají (obíhají
kolem společného těžiště). Oběhy
planet, jako je Země kolem Slunce, vyzařují jen mizivě slabé
gravitační vlny (v řádu zlomků či jednotek Wattů). Jinak
je tomu, když blízko sebe obíhají kompaktní
gravitačně zhroucené objekty - neutronové hvězdy a
především černé díry. Každé takové těleso kolem sebe
vytváří hlubokou gravitační potenciálovou jámu - velké
zakřivení prostoročasu. Jak kolem sebe tyto objekty krouží,
periodický pohyb potenciálových jam vyvolává silné
periodické změny křivosti - jakési "brázdy" v
prostoročase, které se jakožto gravitační vlny odpoutávají
od zdrojového binárního systému a šíří se
do okolního prostoru. Gravitační vlny odnášejí
kinetickou energii rotace - jak odlétají do
vnějšího prostoru, podle zákona akce a reakce
"tlačí" zpětně (protisměrně) na obíhající
tělesa, brzdí je a nutí pohybovat se blíže k sobě, s
vyšší oběžnou rychlostí. Pomalu se po spirále blíží k
sobě (fáze I a II na
obr.4.13-GW). Polovina uvolněné gravitační energie je
odnášena vlnami, druhá polovina zvyšuje oběžnou rychlost (podle zákona o viriálu).
Mohutné zdroje a
záblesky gravitačních vln
Pokud tělesa
obíhají kolem společného těžiště ve velkých
vzdálenostech (vzhledem k jejich gravitačnímu poloměru), a
tedy s dlouhou periodou, je gravitační vyzařování podle
vztahu (2.82) velmi slabé. Např. ve Sluneční soustavě se
při obíhání Jupitera generují gravitační vlny
odnášející mizivých asi 5.10-2W, Země
při svém obíhání gravitačně vyzařuje pouhých asi 20 W. U
vzdálených (vizuálních) dvojhvězd je tok gravitačního
záření rovněž poměrně nízký (~103-107 W); u těsných (zákrytových)
dvojhvězd však gravitačně vyzařovaný výkon činí již ~1020-1025 W (i to je
na astronomické poměry málo...). Skutečně mohutnými
zdroji gravitačních vln však mohou být binární
soustavy kompaktních gravitačně zhroucených objektů jako
jsou neutronové hvězdy nebo černé díry, obíhající blízko kolem sebe, ve vzdálenosti jen několika desítek
gravitačních poloměrů *) - o
možnostech jejich vzniku viz §4.8, pasáž "Binární gravitačně vázané
systémy černých děr. Srážky a splynutí černých děr" -
fáze II na obr.4.13-GW. Hypotetická binární soustava dvou
neutronových hvězd nebo černých děr o hmotnostech Slunce
obíhajících ve vzdálenosti 104km by gravitačně vyzařovala
asi 3.1036W, při oběžném poloměru 100 km by
vyzařovaný výkon činil dokonce asi 3.1046W ! Takovéto objekty by již
byly pouze kvaziperiodické s dobou života (dobou pádu po
spirále jednoho tělesa na druhé - podle vztahu 2.82c) od
několika let do zlomků sekundy. Při
samotném zániku binárního systému (fáze III na obr.4.13-GW)
se prostřednictvím gigantického záblesku
gravitačních vln o frekvenci desítek až stovek Hz
uvolní energie dosahující výkonu až 1047W; po několik milisekund tak obě hroutící se složky
"gravitačně zazáří" tak intenzívně, jako celý
pozorovaný vesmír v elektromagnetickém oboru! Gravitační
vlny přitom odnesou cca 5% celkové hmotnosti obou
slévajících se kompaktních objektů!
*) Sblížení
oběhu kompaktních těles
Problémem ovšem je, jak se tato obíhající kompaktní tělesa
dostanou tak blízko k sobě? U běžných
dvojhvězdných systémů činí oběžná vzdálenost
minimálně 106km (těsné "spektrometrické" dvojhvězdy),
což je více než 100 000 gravitačních poloměrů. Pokud by
takovéto hvězdy zkolabovaly do neutronových hvězd nebo
černých děr, při svém oběhu by vyzařovaly jen poměrně
slabé gravitační vlny cca 1025W. Do stadia těsného oběhu by gravitačním
vyzařováním dospěly za několik milionů let (viz výše
uvedený vzorec (2.82c)). Většina dvojhvězd je však
podstatně vzdálenějších (...-...) - ty by díky
gravitačnímu vyzařování do stádia těsného oběhu a
splynutí nedospěly ani za celou dobu existence vesmíru! Jsou
dva možné mechanismy, které by kompaktní objekty mohl "sblížit"
v dohledném časovém horizontu :
¨
Tření ve velkém a dostatečně hustém
oblaku plynu, obklopujícím binární systém. V
případě, že uvniř binárního systému zůstane větší
množství plynu z obálky kolabujících hvězd, může k disipativnímu
sblížení dojít i za několik milionů let. Těsné binární
systémy vzniklé kolapsem nejstarších hvězd 1.generace se
však za těch více než 10 miliard let trvání vesmíru mohly
sblížit do fáze intenzívního gravitačního vyzařování a
vzájemného splynutí i tehdy, když tam téměř nezbylo
plynové prostředí.
¨
Gravitační interakce s okolními
hvězdami, pokud binární systém není osamocený, ale
nachází se v prostředí s hustějším soustředěním hvězd,
jako jsou kulové hvězdokupy. Okolním hvězdám, které se
přiblíží, může binární systém dynamikou svého oběhu předávat
kinetickou energii, čímž se obě složky vzájemně přibližují.
K tomu by mohlo docházet i v případě vícenásobného
systému.
V posledních
fázích těsného přibližování obou černých děr
se vlivem silné vzájemné gravitace oba horizonty
silně deformují, "vycházejí si vstříc"
*) a při rychlém obíhání divoce vibrují,
za neobyčejně silné emise gravitačních vln.
Pak dojde ke vzájemnému spojení obou
horizontů do jednoho horizontu výsledné černé díry
- etapa III, při němž dochází k mohutné "explozi
gravitačních vln". Tento výsledný horizont je rotující
a zpočátku silně deformovaný. Při své
rotaci vyzařuje tlumené rychle doznívající gravitační
vlny, čímž "relaxuje" na stacionární konfiguraci Kerrovy
axiálně symetrické rotující černé díry (fáze IV
na obr.4.13-GW) - "vypadávání
vlasů", gravitační vlny odnášejí "vlasy
nesymetrie" - §4.5 "Teorém "černá díra
nemá vlasy"".
*) Ve směru spojnice obíhajících černých děr vznikají na
jejich horizontech "hrbolky" zpočátku nevýrazné a
oblé, ale při těsnějším přiblížení jsou to již ostré
výběžky. Těmito výběžky se posléze oba horizonty spojí,
na okamžik do tvaru rotující "8 - osmičky".
Mohutnou emisí gravitačních vln se však tento tvar za
několik desetin sekundy (při hmotnostech
jednotky či desítky M¤) slije do elipsoidního horizontu
výsledné Kerrovy axiálně symetrické rotující černé
díry. Gravitační vyzařování pak navždy ustane...
Když to
shrneme, dynamiku obíhání binárního systému kompaktních
objektů a vyzařování gravitačních vln lze rozdělit do 4
etap podle obr.4.13-GW :
I. Vzdálené obíhání
po téměř Keplerovských orbitách, se slabým
gravitačním vyzařováním a velmi pomalým
spirálovým přibližováním. Doba této etapy I
závisí (podle vzorců (2.82)) na počáteční vzdálenosti obíhání, může trvat
i několik miliard let.
II. Po přiblížení
na vzdálenost několika desítek gravitačních poloměrů
intenzita gravitačního vyzařování velmi vzroste, což vede k
rychlému spirálovitému přibližování obou
těles, s emisí stále mohutnějších gravitačních vln s rychle
stoupající frekvencí, od jednotek do několika stovek
Hz. Závěrečná část této etapy II u kompaktních
objektů hvězdných hmotností trvá jen řádově sekundy.
V hantýrce lovců gravitačních vln se
tato fáze někdy nazývá "chirp" - "cvrlikání",
neboť rychlý růst frekvence těsně před splynutím obou
kompaktních těles připomíná ptačí cvrliknutí. Dynamika
růstu amplitudy a frekvence gravitačních vln je zde
charakteristická pro hmotnosti splývajících černých děr.
III. Splynutí
(fúze, srážka) obou kompaktních objektů v jednu výslednou
rotující černou díru, za vyzáření gigantického záblesku
gravitačních vln, trvajícího jen milisekundy.
IV. Relaxace
výsledné černé díry, zpočátku silně deformované, na
stacionární axiálně symetrickou konfiguraci Kerrovy černé
díry s rychlým tlumeným dozníváním
gravitačního vyzařování během zlomků sekundy. Pak se již
žádné další gravitační vlny nevyzařují. Dynamika tohoto doznívání gravitačních vln
(připomínající jakési "doznívání zvonu")
je charakteristická pro hmotnost a rychlost rotace (moment
hynosti) výsledné černé díry.
Pokud srážka a fúze černých
děr probíhá v "čistém" prostředí bez
plynů a dalších těles, jsou emitovány pouze
gravitační vlny. Při splynutí v binárním systému neutronových
hvězd lze však kromě silných gravitačních vln
očekávat i intenzívní emisi elektromagnetických vln
- gama, X-záření, viditelného světla, radiových vln (je diskutováno v §4.8, pasáž "Srážky a splynutí
neutronových hvězd").
Dalšími
kompaktními objekty, sloužícími jako potenciální zdroje
gravitačních vln, by mohly být binární
supermasívní černé díry v centru galaxií (viz §4.8, část "Kvasary"). Podle galaktické astrofyziky by mohly vznikat při srážkách
galaxií za situace, kdy galaxie se vzájemně
pronikají s malým impaktním parametrem a při nižší
vzájemné rychlosti. Černé díry v centru obou galaxií pak
při svém "míjení" mohou vytvořit vázanou
binární soustavu. Při vzájemném obíhání,
postupném přibližování po "spirále smrti" a
nakonec fúzi těchto obřích černých děr by vznikaly mohutné
gravitační vlny nízkých frekvencí, miliHertzy i
nižší... Celý tento závěrečný proces by byl daleko pomalejší,
než je tomu u binárních černých děr hvězdných hmotností.
Vzhledem k pomalosti a dlohodobosti těchto procesů lze
očekávat, že vesmírný prostor bude zaplněn záplavou nízkofrekvenčních
gravitačních vln různých intenzit a frekvenci, z mnoha
zdrojů - stochastické gravitačně-vlnové pozadí.
Očekávané frekvence
gravitačních vln z binárních astrofyzikálních zdrojů
jsou dány hmotností složek :
- Jednotky
až stovky M¤ : frekvence 10Hz - 10kHz, možnost detekce pozemskými
interferometry.
- Tisíce
až miliony M¤ : frekvence 0,0001Hz - 0,1Hz, možnost detekce
kosmickými interferometry.
- 108
až 1010 M¤ : perioda měsíce až desítky let, možnost detekce
sledováním změn frekvence pulsarů.
Středně intenzívním
zdrojem gravitačních vln může být i gravitační kolaps
hvězdy, pokud probíhá nesymetricky (při
sférickém kolapsu se gravitační vlny nevyzařují- viz §4.3
"Schwarzschildovy statické černé díry").
Extrémní příklad takového procesu je znázorněn na obr.4.14
v §4.4 "Rotující a elektricky nabité
Kerrovy-Newmanovy černé díry", kde v průběhu kolapsu rotující
hvězdy dochází k její fragmentaci a opětovnému pohlcování
jednotlivých částí, doprovázenému (a způsobovanému) velmi
intenzivním vyzařováním gravitačních vln. V každém
případě, silně nesférický kolaps hvězdy pod gravitační
poloměr je doprovázen silným zábleskem
gravitačních vln, které odnášejí nezanedbatelnou
část celkové klidové hmotnosti [289].
Již "hotová" černá díra,
pokud je osamocená, gravitační vlny nevyzařuje. Pokud však
tvoří binární či vícenásobný systém (jak bylo zmíněno
výše) nebo interaguje s okolní hmotou, může se stát
výkonným zdrojem gravitačních vln. Jestliže malé těleso
hmotnosti m padá přímo na (nerotující) černou
díru hmotnosti M, vyzáří při tom celkové
množství energie
| DE » 0,0025 m2 c2/M | (2.83) |
ve formě "záblesku" gravitačního záření se spojitým spektrem. Obíhá-li kolem černé díry těleso po oběžné dráze, vyzařuje periodické gravitační vlny s celkovou intenzitou danou vztahem (4.19). Tím neustále klesá po spirále níže, intenzita a frekvence gravitačních vln se zvyšuje, až je těleso nakonec pohlceno. V §4.3 (pasáž "Vyzařování gravitačních vln při pohybu v poli černé díry") a §4.4 bude ukázáno, že celkové množství energie, které se při takovém procesu může vyzářit gravitačními vlnami, činí pro Schwarzschildovu nerotující černou díru asi 6% klidové hmotnosti padajícího tělesa, zatímco pro rotující černou díru může představovat až 40% jeho klidové hmotnosti! Vidíme tak, že nepříznivá situace buzení gravitačních vln v laboratorních podmínkách se nám v astrofyzikálních měřítcích může zcela obrátit: nejen že mohou existovat zdroje mohutných gravitačních vln o velkých výkonech, ale i účinnost přeměny klidové hmotnosti na gravitační záření může být nesrovnatelně vyšší než účinnost, s jakou dovedeme zde na Zemi "těžit" z hmoty např. elektrickou energii (účinnost termonukleárních elektráren bude činit jen asi 0,7%).
Primordiální
gravitační vlny
Nejmohutnějším zdrojem gravitačních vln "všech
dob" byl nepochybně bouřlivý vznik
vesmíru -
"velký třesk". Kromě gravitačních vln výše
zmíněného astrofyzikálního původu může být tedy vesmír
zaplněn též "kosmologickými" či "primordiálními" gravitačními vlnami generovanými
nehomogenitami a turbulencemi superhusté látky v období kolem
velkého třesku [288]. Tyto gravitační
vlny emitované v Planckově čase, v inflační
fázi (§5.5 "Mikrofyzika a
kosmologie. Inflační vesmír.") , či při vzniku nehomogenit, turbulencí a
topologických defektů během narušení symetrií, by pravděpodobně měly stochastický charakter jakéhosi "gravitačního
šumu".
Primordiální gravitační vlny během
miliard expanze vesmíru natilik zeslábly, že
na jejich přímou detekci není asi žádná naděje v dohledné
budoucnosti; a to i tehdy, kdyby se v brzké době podařila
detekce gravitačních vln z relativně blízkých
astrofyzikálních zdrojů. Níže v části "Detekce
gravitačních vln" bude
diskutována zajímavá možnost nepřímého prokázání
primordiálních gravitačních vln změřením polarizace
reliktního mikrovlnného záření (pasáž "Měření polarizace
reliktního mikrovlnného záření").
Rovněž při všech vysokoenergetických
mikroskopických procesech (s elementárními částicemi) by se
v principu měly vyzařovat gravitační vlny, ovšem zcela
nepatrné intenzity, bez naděje na změření...
Detekce
gravitačních vln
Tolik tedy ve stručnosti o vzniku a vlastnostech gravitačních
vln. Dostáváme se tak k poslednímu bodu tohoto pojednání - k
problematice detekce gravitačních
vln.
Srovnáme-li situaci a elektrodynamikou, pak máme k dispozici
značně silné zdroje elektromagnetických vln přírodního i
umělého původu, které dokážeme citlivě detekovat a
přijímat. V oblasti radiových vln to jsou v nejjednodušším
případě obyčejné antény radiopřijímačů, v nichž
elektromagnetickou indukcí vzniká přijímaný signál.
Elektromagnetické vlny z vesmíru se velmi citlivě přijímají
radioteleskopickými anténami. Viditelné světlo účinně
emitují všechna zahřátá tělesa (třebas vlákno žárovky),
výbojky, ve vesmíru hvězdy; a citlivým detektorem jsou
naše oči. I pro krátkovlnné oblasti X a gama záření máme
k dispozici citlivé radiometry a spektrometry (Detekce a spektrometrie ionizujícího záření). Pro
gravitační vlny však máme k dispozici pouze zdroje ve velmi
vzdáleném vesmíru, jejichž vlny jsou zde na Zemi zákonitě velmi slabé. Detekce gravitačních vln - sestrojení
dostatečně citlivého "gravitačního
přijímače"
- je tedy záležitost neobyčejně delikátní!
Abychom lépe porozuměli této
problematice, všimněme si nejprve působení gravitačních vln
na pohyb testovacích částic. Podle principu ekvivalence (a v
kontextu s tím, co bylo řečeno v §2.6)
lokální působení gravitačních vln na jedinou izolovanou
částici neexistuje. Gravitační vlna nemůže být detekována
jedním daným pozorovatelem, který se "vlní s ní".
Proto musíme vzít dvě blízká či vzdálenější testovací tělesa A a B (obr.2.11a) a sledovat
periodické změny vzdálenosti mezi nimi, způsobené
kmitající křivostí metriky prostoru v gravitační vlně.
Gravitační vlna přitom způsobuje příčné
deformace
prostoru.

Obr.2.11. Působení gravitačních vln na testovací částice.
a)
Světočáry dvou volně padajících částic A a B se vlivem gravitačních vln periodicky
vzdalují a přibližují.
b) Pro
srovnání - působení (lineárně
polarizované) rovinné
elektromagnetické vlny dopadající kolmo k nákresně na
soustavu testovacích nabitých částic umístěných na
kružnici vede k periodickým posunům celého kruhu testovacích
částic ve směru závislém na polarizaci vlny.
c)
Působení rovinné gravitační vlny dopadající kolmo na
kruhově uspořádanou soustavu hmotných testovacích částic
způsobuje periodické deformace tohoto uspořádání do elipsy
střídavě ve dvou kolmých směrech daných polarizací vlny.
S částicí A, kterou vezmeme za vztažnou, spojíme referenční soustavu, která bude lokálně inerciální podél celé světočáry částice A. Vektor ei v rovnici deviace geodetik (2.57) zde pak bude roven souřadnici xiB částice B, takže
![]()
Protože pracujeme v lokálně inerciální kartézské soustavě spojené s částicí A, budou absolutní derivace přecházet v obyčejné derivace a s přesností 1.řádu souřadnicový čas t splývá s vlastním časem t. Vzhledem ke vztahu (2.67) pak rovnice deviace nabývá jednodušší tvar
![]()
Jestliže v čase t=0 bylo hab=0 a částice byly vzájemně v klidu, můžeme integrací této rovnice získat vztah
xaB(t) » xb(0) [ dab + 1/2 hab(t, xgA=0) ] ,
vyjadřující oscilace polohy částice B vzhledem k A způsobené gravitační vlnou.
Přitom oscilace vykazují jen ty komponenty xaB(t), které jsou kolmé k vektoru
šíření rovinné vlny ka (gravitační vlny jsou
příčné). Na obr.2.11c je znázorněno periodické
deformační působení rovinné gravitační vlny na soustavu
pravidelně (do kruhu) uspořádaných testovacích částic.
V případě, že sledované testovací
částice A a B nejsou volné, ale interagují
spolu negravitačními silami, je třeba rovnici deviace (2.57)
nahradit rovnicí
![]()
kde Fi je 4-síla popisující negravitační interakci částice A a B. Takový případ je znázorněn na obr.2.12a. V praxi má síla Fi vždy elektromagnetický původ (veškeré síly pevnosti a pružnosti v tělesech jsou způsobeny elektromagnetickými silami). Podobně jako v předchozím případě lze kmity částic A a B využít k detekci gravitačních vln. Pokud zahrneme ještě dissipativní procesy (viskózní tření), můžeme si reálná tělesa představovat jako složená z řady takových negravitačně interagujících hmotných částí.
Amplituda
gravitační vlny
Sílu gravitační vlny můžeme jednoduše a
výstižně vyjádřit její amplitudou h = DL/Lo, kde DL = Lmax - Lmin je maximální
změna vzdálenosti dvou testovacích částic, jejichž
původní (počáteční) vzdálenost byla Lo (obr.2.11a). Je to bezrozměrné číslo,
vyjadřující jak velkou relativní změnu vzdálenosti
dvou testovacích částic vlna svým průchodem vyvolá. Tímto
číslem se pak charakterizuje i citlivost
detektorů gravitačních vln.
Velmi přibližně můžeme očekávanou amplitudu gravitační
vlny odhadnout z výše uvedeného kvadrupólového vzorce
(2.77b)...
Síla
- slabost gravitačních vln z vesmíru
Pro posouzení šancí, možností a metodiky detekovat
gravitační vlny je užitečné odhadnout, jak silné
(či bohužel slabé...) gravitační vlny můžeme očekávat přicházet z
vesmíru? V pasáži "Vznik a vlastnosti gravitačních vln" bylo shora diskutováno, že gravitační vlny
jsou obecně velmi slabé. Podle výpočtů
uvedených výše v části "Zdroje
gravitačních vln", jakož i v §4.3, pasáž
"Vyzařování gravitačních vln
při pohybu v poli černé díry" a v §4.4, pasáž "Pohyb částic v poli rotující černé
díry", se však při relativistických pohybech hmoty ve
velmi silných gravitačních polích kompaktních objektů
může během krátkého časového intervalu ve formě
gravitačních vln vyzářit i 5% celkové hmotnosti
(u rotující černé díry to může
hypoteticky být až 40%!). V astronomické
blízkosti takových objektů bychom tedy mohli pozorovat docela
silné gravitační vlny!
Nikde v okolí však bohužel *) nemáme žádný
takový silný zdroj gravitačních vln... Základní
překážkou úspěšné detekce je proto extrémní
slabost gravitačních vln přicházejících k nám z
vesmíru. Je to způsobeno obrovskou vzdáleností
pravděpodobných silných zdrojů gravitačních vln - tisíce a
miliony světelných let.
*) Je to pro nás možná naštěstí!
Kdyby se v blízkosti několika světelných let nacházel
takový binární systém těsně obíhajících černých děr,
přicházely by k nám natolik silné gravitační vlny, že by
mohly destabilizovat sluneční soustavu!
Očekávané amplitudy gravitačních vln,
přicházejících k nám z předpokládaných zdrojů ve
vesmíru, jsou tedy velice malé. Hlavním
faktorem, ovlivňujícím konkrétní sílu vlny, je vzdálenost
zdroje r ve vztahu k jeho gravitačně-vlnovému výkonu
Pgw, tj.
množství energie, které se při daném procesu předává
gravitačním vlnám. Amplituda vlny pak přibližně vychází h
» 3.10-22..?...Pgw/r, kde vzdálenost
zdroje r je měřena ve světelných letech. Pokud by
např. poblíž středu naší Galaxie vybuchla supernova
takovým způsobem, že by gravitačním vlnám předala cca 1%
energie Slunce M¤c2,
amplituda gravitačních vln změřená zde na Zemi by se dala
odhadnout na h » 10-19. Pro gravitační vlny ze supernov v blízkých
galaxiích se jejich amplitudy odhadují na 10-19-10-21; gravitační vlny
z nesférického výbuchu supernovy by měly charakter pulsu.
Při srážce a splynutí dvou neutronových hvězd nebo
černých děr ve vzdálených galaxiích bychom mohli zachytit
záblesk gravitačních vln s rostoucí frekvencí o amplitudě
cca 10-20-10-22. Citlivost
nynějších detektorů gravitačních vln umožňuje zaznamenat
jedině tyto "katastrofické" události,
doprovázené mohutným "zábleskem" gravitačních
vln; předchozí "pokojnější" fáze s
"umírněným" gravitačním vyzařováním, jsou
zatím hluboko pod prahem detekovatelnosti.
Intenzita gravitačních vln v našem okolí se
tedy odhaduje na max. h »10-21, takže by tyč o délce jednotek metrů mohly
rozvibrovat na amplitudu asi stomiliontinu průměru atomového
jádra. Při tak malých hodnotách odezvy se může objevit
zásadní překážka detekce - kvantové relace
neurčitosti (viz např. "Kvantová fyzika") *) . Jak uvidíme níže, jedinou možností detekce
slabých vln je zvýšení vzdálenosti
testovacích těles a využití vysoce citlivých metod měření
změn polohy, především interferometrických.
*) Níže v pasáži "Interferometrické detektory
gravitačních vln", Pozn.2: "Omezení
kvantovými relacemi neurčitosti? - lze je obejít !", je diskutováno, jak při interferometrické
detekci gravitačních vln je možno obvyklé kvantové relace
neurčitosti "překonat", či přesněji řečeno obejít...
Rušivé
pozadí
Tak nepatrné pravidelné signály, jaké lze očekávat z
gravitačních vln ze vzdáleného vesmíru, se v pozemských
detektorech většinou budou ztrácet ve
všudypřítomné chaotické "kakofonii" rušivých
signálů - v pozadí šumu. Rušivé pozadí je v
našich pozemských podmínkých tvořeno především seismickými
vlnami. Dále je to hluk a vibrace z
nákladních automobilů, vlaků či průletů letadel. Při
měření signálů se dále uplatňuje elektronický
přístrojový šum a kvantový šum
způsobený statistickými fluktuacemi v důsledku kvantových
zákonitostí mikrosvěta (srov.
např. "Kvantová fyzika" a "Statistický rozptyl a
chyby měření"
v monografii "Jaderná fyzika a
fyzika ionizujícího záření").
Právě pozadí rušivých signálů, které jsou většinou
mnohem silnější než užitečný signál, je základním limitujícím
faktorem při detekci gravitačních vln.
Detektory gravitačních vln - přímá detekce
Podobně jako zdroje, tak i detektory gravitačních vln můžeme
rozdělovat na jednotlivé typy podle různých hledisek. Co se
týče základního principu jejich činnosti, rozeznáváme
detektory mechanické (měřící
pohyby těles vyvolané gravitačními vlnami) a nemechanické (analýza
vlivu gravitačních vln na elektromagnetická pole - zatím
nebylo realizováno).
Podle rozsahu a umístění se dále může jednat o detektory laboratorní (pozemské) a astronomické (kosmické). Mechanické
detektory gravitačních vln můžeme rozdělit na dvě skupiny :
Detektory gravitačních vln, zvláště pozemské, by měly pracovat nejméně ve dvojicích v dostatečně velké vzdálenosti od sebe (nejméně stovky kilimetrů) v koincidenčním režimu. Umožňuje to odlišit lokální poruchy (např. seismické či technické), projevující se jen v jednom z detektorů, od signálu vesmírného původu, který je zaznamenán současně oběma detektory.
Rezonanční
detektory gravitačních vln
Všimněme si nejprve rezonančních detektorů. Nejjednodušší
(modelový) typ takového detektoru gravitačních vln je
nakreslen na obr.2.12a, kde jsou dvě hmotná tělesa A a B spojená pružinou. V praxi však
rezonanční detektor gravitačních vln sestává ze tří
základních částí (obr.2.12b):
1. Pružného
tělesa
vhodného tvaru a vlastností, které reaguje mechanickými
pohyby - kmity, vibracemi, deformacemi - na přicházející
gravitační vlny.
2. Snímače, který tyto mechanické kmity
registruje a převádí na elektrické signály.
3. Elektronického
vyhodnocovacího zařízení, které tyto elektrické signály
zesiluje, zpracovává a zaznamenává.
Fyzika a technika těchto detektorů je
značně komplikovaná (v podrobnostech
můžeme odkázat na literaturu [270],[29],[30],[6]) a dosti se podobá teorii antén pro
příjem radiovln; z tohoto důvodu se rezonující tělesa
používaná v mechanických detektorech též nazývají "gravitační antény". Základními požadavky
na tyto gravitační antény jsou dostatečná hmotnost a co
nejvyšší parametr mechanické
jakosti (tj. co nejmenší tlumení mechanických kmitů
disipativními procesy).

Obr.2.12. Detekce gravitačních vln.
a)
Harmonický oscilátor tvořený dvěma tělesy A a B spojenými pružinou je nejjednodušším
rezonančním detektorem gravitačních vln.
b)
Rezonanční detektor gravitačních vln tvořený masívním
(pružným) válcem v němž gravitační vlny vyvolávají
kmity. Pomocí vhodných snímačů deformace jsou tyto
mechanické kmity převáděny na elektrické signály a dále
zpracovávány. Detektor tohoto typu zkonstruoval J.Weber
v r.1968.
c) Interferometrický detektor gravitačních
vln (popis viz níže "Interferometrické detektory").
Průkopníkem v oblasti
detektorů gravitačních vln byl Joseph
Weber [269],[270],
který v 60.-70.letech zkonstruoval první detektory
gravitačních vln, sestávající z hliníkových válců o
průměru 66 cm a délce 153 cm (hmotnost
asi 1,4 tun, základní rezonanční kmitočet 1660Hz), zavěšených ve vakuu a
mechanicky izolovaných od okolí. Kmity válce byly
registrovány piezoelektrickými
snímači deformace.
Pro eliminaci místních rušivých vlivů při vlastním
měření intaloval Weber dva takové detektory, z nichž jeden byl
umístěn v Marylandské universitě a druhý v Aragonské
laboratoři poblíž Chicaga (vzdálenost obou míst asi 1000
km). Za pozitivní případy detekce gravitačních vln byly
považovány impulsy které nastaly současně v obou detektorech. V r.1979
Weber skutečně zaregistroval několik takových koincidencí, které považoval za vyvolané
gravitačními vlnami. V dalším vývoji se však tento
optimismus nepotvrdil. Pozdější experimenty prováděné se
zdokonalenými detektory o vyšší citlivosti žádné vlny
nezaregistrovaly...
Dále, rozbor citlivosti Weberových válců
ukázal, že domněle přijímané gravitační záření by
muselo mít intenzitu zhruba 1 W/cm2 ; pokud by zdroj tohoto
záření byl v centru Galaxie (jak Weber odhadoval), pak za
předpokladu izotropního záření by zdroj gravitačně
vyzařoval výkon asi 1043W, což odpovídá ztrátě
hmotnosti zhruba 103M¤ za rok. Tak velký gravitační výkon by
se sotva dal vysvětlit možnými fyzikálními pochody v centru
Galaxie. Původ impulsů detekovaných
Weberem je tedy nejasný (rozechvění obou válců bylo možná
způsobeno poruchami v magnetosféře Země, vyvolanými
magnetickými erupcemi na Slunci). Podíváme-li se však shora
do pasáže "Zdroje gravitačních vln ve
vesmíru", obr.4.13,
hypoteticky mohla být zaznamenána raritní událost splynutí
dvou černých děr (jejich fúze či srážky) v
binární soustavě v naší galaxii, při níž se ve zlomku
sekundy vyzáří kolosální energie - "záblesk"
gravitačních vln..?.. Byla by to však velká náhoda...
Laboratorní mechanické detektory
gravitačních vln se dále zdokonalovaly, přičemž trend byl
spíše ve zvyšování parametrů kvality detektoru a
potlačování šumů (místo hliníkových
např. safírové rezonátory, chlazení na zlomky °K,
vylepšování snímací elektronické aparatury), než ve zvyšování hmotnosti
detektorů [29],[6]. Mechanické detektory gravitačních vln ale
mají dvě zásadní nevýhody:
¨
Principiální omezení citlivosti plynoucí ze zákonitostí
kvantové mechaniky: přesnost měření vibrací tyče je
omezena kvantovým principem
neurčitosti
*). Slabými gravitačními vlnami
způsobované vibrace válce budou velmi
malé,
subatomárních rozměrů, takže při jejich měření se budou
výrazně uplatňovat kvantové jevy.
*) Níže v pasáži "Interferometrické detektory
gravitačních vln", Pozn.2: "Omezení
kvantovými relacemi neurčitosti? - lze je obejít !", je diskutováno, jak při interferometrické
detekci gravitačních vln je možno obvyklé kvantové relace
neurčitosti "překonat", či přesněji řečeno obejít...
Podle původních odhadů jsou tyto
vibrace menší než desetina průměru atomového jádra
(pozdější odhady dávaly dokonce amplitudy vibrací jen »10-20m, tj. desetimilióntina
průměru atomového jádra! - bylo
diskutováno výše v pasáži "Amplituda
gravitačních vln"). Kvantový princip neurčitosti ukazuje,
že čím přesněji měří senzor polohu konců nebo obvodu
vibrujícího válce, tím silněji a náhodněji jeho vibrace
ovlivňuje. Žádný senzor nemůže monitorovat vibrace
přesněji, než dovolují kvantové relace neurčitosti. Pro
válce Weberových rozměrů činí nejmenší detekovatelná
amplituda vibrací cca 10-18cm (100 000-krát menší než
velikost atomového jádra). To se na první pohled zdá být
fantastické, ale na detekci gravitačních vln ze vzdálených
vesmírných objektů (předpokládané
amplitudy 10-21) asi žádné
technicky proveditelné rezonanční válce, při použití
sebelepších známých typů senzorů, stačit nebudou...
¨
Úzká šířka pásma frekvenční citlivosti - jsou naladěny na určitou
pevnou rezonanční frekvenci, danou mechanickými rozměry a
elastickými vlastnostmi použitého materiálu (většinou stovky Hz či několik kHz) a nejsou schopny účinně
registrovat signály jiných frekvencí. To výrazně snižuje
jejich celkovou efektivní citlivost a potenciální naději na
úspěšnou detekci gravitačních vln.
Abychom detekčně pokryli očekávané
proměnné spektrum frekvencí gravitačních vln, potřebovali
bychom jakýsi "gamelan" složený z mnoha válců
naladěných na různé frekvence. Nízké frekvence jednotky Hz
bychom ale ani takto nepokryli, a už vůbec ne frekvence menší
než 1Hz.
Působení gravitačních
vln na elektromagnetické vlny?
Jelikož gravitační vlny interagují nejen s látkovými
tělesy, ale i s elektromagnetickým polem, mohou být
příslušné efekty využity pro detekci gravitačních vln
nemechanickým způsobem. Jeden z návrhů takového detektoru
[30] využívá rezonanční působení gravitačních vln na
elektromagnetické vlny obíhající v kruhovém (toroidním)
vlnovodu v případě, že perioda oběhu elektromagnetických
vln vlnovodem se rovná dvojnásobku periody dopadajících
gravitačních vln. Potom jedna část elektromagnetické vlny se
bude stále nacházet v "urychlujícím" poli
gravitační vlny způsobujícím "modrý posuv",
zatímco jiná oblast bude trvale ve "zpomalujícím"
gravitačním poli vedoucím k "rudému" frekvenčnímu
posuvu. Tato rezonanční gravitačně-elektromagnetická
interakce povede ke stále rostoucímu rozdílu fází a
frekvencí elektromagnetických vln, který při dostatečně
dlouhé době působení by bylo možno v principu změřit
(vlnovod by musel být supravodivý). Všechny pobobné návrhy
jsou zatím jen ve stádiu teoretických projektů. Nevýhodou
tohoto řešení by byla úzká spektrální citlivost, podobně
jak to bylo výše diskutováno u mechanických rezonančních
detektorů. .....doplnit?.........
Země a Měsíc ?
Jako další typ mechanického detektoru by mohla sloužit samotná
Země v níž by gravitační vlny vyvolávaly
mechanické deformace a kmity. Vadí zde však značně vysoké seismické
pozadí. Souvislost mezi některými zemětřeseními a
intenzívními záblesky gravitačních vln je teoreticky možná
[74], i když neprokázaná.
Co se týče aperiodických detektorů
gravitačních vln, mohla by takovou gravitační
"anténou" sloužit soustava Země-Měsíc,
jejichž vzdálenosti by se kontinuálně proměřovaly např.
pomocí laserů. K tomu by však bylo třeba přesnost těchto
měřících metod podstatně zlepšit.....doplnit........
Interferometrické detektory
gravitačních vln
V aperiodických detektorech gravitačních vln se sledují
jemné změny vzdáleností mezi testovacími tělesy,
způsobené gravitační vlnou. Nejcitlivější metodou, kterou
máme k dispozici pro měření změn vzdáleností mezi tělesy,
je laserová interferometrie. Velkou výhodou těchto
detektorů je jejich širokospektrální
citlivost -
jsou schopné registrovat gravitační vlny o různých
frekvencích, především o nízkých
frekvencích;
právě takovéto vlny by měly nejčastěji přicházet z
reálných vesmírných zdrojů.
 Obr.2.12
Obr.2.12
Základní uspořádání
interferometrického detektoru gravitačních vln je znázorněno
na obr.2.12c (který jsme si zde pro
názornost uvedli znovu). Sestává ze dvou volně zavěšených
masívních testovacích těles M1 a M2, na
nichž jsou upevněna zrcátka odrážející světlo. Tato
testovací tělesa se jemně "zakývají" na
gravitační vlně - při průchodu gravitační vlny se
vzdálenost mezi zrcadly periodicky zvětšuje zmenšuje, jak
prostor expanduje a smršťuje se.
Geometricky kolmé
uspořádání testovacích zrcátek (měřících
ramen) je výhodné z hlediska lepší citlivosti, vzhledem ke kvadrupólovému charakteru gravitačních vln, které
rozkmitávají prostor střídavě ve dvou kolmých směrech -
přicházející gravitační vlna mírně natáhne jedno rameno
a zároveň stlačí druhé v kolmém směru. Paprsek světla
vyzařovaný laserem je polopropustnou destičkou S, sloužící
jako separátor, rozdělen na dva paprsky,
které se odrážejí od zrcátek umístěných na tělesech M1 a M2 a
vracejí se zpět k destičce S; zde dochází k jejich interferenci a výsledný světelný signál je
zaznamenáván fotoelektrickým detektorem FD. Průchod
gravitační vlny ve směru kolmém na rovinu laserových
paprsků způsobí mechanické
posuny
těles M1 a M2 takové, že v jedné
půlperiodě se vzdálenost L1 zvětší a L2 zmenší,
zatímco v druhé půlperiodě se naopak L1 zmenší a L2
zvětší. Tato změna délky drah interferujících paprsků
vede k tomu, že obě světelné vlny se setkají v různé fázi, což se projeví změnou
intenzity
výsledného interferenčního signálu měřeného fotometrem.
K měřitelnému efektu přitom postačuje
změna pouhého zlomku vlnové délky laserového světla.
Interferenční detektory se tudíž vyznačují vysokou citlivostí a jeví se jako velmi
perspektivní, zvláště po očekávaném zdokonalení
měřící techniky a dosažení velké délky L1, L2 měřících ramen. Citlivost
lze dále podstatně zlepšit optickou realizací mnohonásobného odrazu světla mezi dvojicemi
rovnoběžných zrcadel - Fabry-Perotův
interferometr.
Popsaný interferometrický detektor se dvěma
kolmými rameny je v zásadě citlivý na gravitační vlny
přicházející z různých směrů, avšak s rozdílnou směrovou
citlivostí. Nejlepší citlivost je pro vlny
přicházející kolmo zhora (nebo zdola), zatímco vlny ze
směru roviny ramen by prakticky nebyly detekovány.
Níže ve dvou poznámkách
se pokusíme zmínit některé diskutabilní aspekty při detekci
gravitačních vln :
Pozn.1: Eliminace
gravitačního frekvenčního posuvu světla v interferometru
Procházející gravitační vlna periodicky mění
nejen vzdálenost zrcadel, ale pozměňuje geometrii
prostoročasu, což přirozeně ovlivňuje i pohyb
fotonů a šíření laserového světla mezi zrcátky
interferometrického systému. Především způsobuje gravitační
frekvenční posuv světla, střídavě k nižším a
vyšším frekvencím, což by mohlo při interferometrickém
měření působit rušivě. Avšak měřící laserový paprsek
putuje mezi interferenční destičkou a zrcátky testovacích
těles ve velmi rychlém sledu tam a zpátky (v případě využití metody Fabry-Perotova
interferometru dokonce mnohokrát),
přičemž čas průchodů a odrazů paprsků v interferometru je
nesrovnatelně kratší než perioda detekované gravitační
vlny. Gravitační rudý a modrý spektrální posuv se tím
okamžitě a průběžně vzájemně vyruší.
Při interferenci se tedy nakonec projeví jen skutečná
změna vzdálenosti, způsobená rozkyvem gravitační
vlnou.
Pozn.2: Omezení
kvantovými relacemi neurčitosti? - lze je obejít !
Nutnost měřit nesmírně malé (subnukleární) posuny testovacích těles, vyvolaných slabými
gravitačními vlnami, přirozeně navozuje otázku, zda to
vůbec umožňují Heisenbergovy kvantové
relace neurčitosti..?.. Základní kvantová relace
neurčitosti mezi změnou polohy Dx částice a změnou její
hybnosti Dp je dána součinem Dx.Dpł h. Kdybychom v interferometrickém měření gravitační
vlny potřebovali současně stanovit jak změnu polohy, tak i
hybnosti testovacích zrcátek, neměli bychom šanci. My zde
však potřebujeme měřit pouze délkovou změnu polohy
zrcadel která jsou volná, nikoli jejich hybnosti (která se
při tom stává neučitou, ale my ji zde nepotřebujeme). Touto
okolností se tedy daří nikoli porušit, ale "obejít"
kvantové relace neurčitosti..!..
Přes všechna technická zdokonalení (viz níže "Nové experimenty pro detekci gravitačních vln") se gravitační vlny po mnoho let nedařilo přímo detekovat. Gravitační vlny přicházející z vesmíru byly zřejmě slabší, než byla citlivost stávajích detektorů. V gravitační fyzice jsme tedy byli v podobné situaci, jako byla elektrodynamika po Maxwellovi, ale před Hertzem. Nakonec se to však podařilo - viz níže pasáž "Radostná zvěst - přímá detekce gravitační vlny zařízením LIGO !" .
Nepřímé
důkazy gravitačních vln , nepřímá detekce
I přes obtížnost přímé detekce však máme některé nepřímé důkazy existence gravitačních vln. Jestliže
totiž nějaká soustava intenzívně gravitačně
vyzařuje,
je z ní odnášena značná energie, což vede ke změnám fyzikálních parametrů takové soustavy. Např. u
těsného binárního systému je intenzita gravitačního
vyzařování natolik veliká, že obě tělesa se budou po
spirále k sobě přibližovat a oběžná perioda se bude
znatelně zkracovat; tím se bude vyzařovaný výkon ještě
zvětšovat, takže tento efekt bude probíhat s narůstající
rychlostí. Zjištění takového zmenšování periody (tj.
zvyšování oběžné frekvence) u dvojhvězdy však ještě
samo o sobě nedokazuje, že se jedná o efekt způsobený
gravitačním vyzařováním. Změny oběžné periody mohou být
totiž způsobeny též ztrátou hmoty některé z hvězd,
viskózním brzděním v plynovém oblaku, nebo přetékáním
hmoty z jedné složky na druhou vzhledem k těsné blízkosti
obou hvězd. U těsných binárních soustav obyčejných hvězd hrají
dominantní roli zřejmě právě tato druhé možnosti.
Jestliže jsou však složky binární soustavy dostatečně kompaktní (např. neutronové hvězdy nebo černé
díry), pak vzájemné proudění hmoty i viskózní tření je
zanedbatelné - soustava je "čistá" - a zmenšování
oběžné periody bude způsobováno výhradně
vyzařováním energie gravitačními vlnami.
Binární
pulsar
A skutečně, v r.1974 J.Taylor, H.Russel, J.Weisberg s dalšími
spolupracovníky na velkém radioteleskopu observatoře Arecibo
objevili binární soustavu PSR
1913+16
obsahující pulsar (§4.2, část "Pulsary"), která se ukázala být velmi
vhodná nejen pro daný účel, ale i pro testování
relativistických efektů vůbec - je proto často označována
jako "astrofyzikální
relativistická laboratoř PSR 1913+16 ".
Pečlivá měření totiž ukázala, že druhá složka je
rovněž kompaktní objekt a na oběžné dráze pulsaru není
přítomen plyn nebo plasma, takže subtilní relativistické
efekty nejsou překryty jevy způsobenými
přenosem hmoty, viskózním brzděním, slapovými silami a pod.
[243],[]. Z hlediska OTR se tedy jedná o téměř ideální hodiny (§4.2, pasáž
"Pulsary - precizní 'hodinové
strojky' ve vesmíru") pohybující se v silném gravitačním poli značnou rychlostí po značně
výstředné dráze. Kromě řady dalších relativistických
efektů se u tohoto objektu podařilo změřit rychlost změny
periody (T =7,75 hod.) oběhu pulsaru, která činí asi DT @ -6,7.10-8s/oběh. Tato pozorovaná rychlost
změny oběžné periody pulsaru velmi dobře souhlasí s
hodnotou, kterou pro daný systém předpovídá obecná teorie
relativity v důsledku ztrát
orbitální energie gravitačním zářením. Vyzařováním gravitačních
vln se podle vztahu (2.82) z binárního systému odnáší
kinetická energie orbitálního pohybu, čímž se obě složky
k sobě spirálovitě přibližují (v daném
případě o asi 3mm při každém oběhu, což činí asi
3m/rok) a podle
Keplerova zákona perioda jejich
oběhu klesá. Jiná alternativní vysvětlení
pozorovaných změn periody oběhu pulsaru - např.
třetí těleso příslušné hmotnosti obíhající ve vhodné
vzdálenosti - se ve světle pozorovacích údajů jeví značně
nepravděpodobná.
Binární
pulsar PSR 1913+16 má tyto
základní charakteristiky [243]: hmotnosti každé ze složek
asi 1,4 M¤, eliptická dráha oběhu kolem
společného těžiště má hlavní poloosu a »1,9.106 km a výstřednost e @ 0,62, doba
oběhu činí 7,75 hod., základní pulsní perioda pulsaru je 59
milisekund. Stáčení periastra zde činí asi 4,2° za rok,
což je zhruba 107-krát rychlejší než u Merkura.
Analýzou různých proměnných složek periody příchodu
impulsů od pulsaru se rovněž podařilo změřit efekty dilatace času (příčný Dopplerův
jev), gravitačního rudého posuvu a zpožďování signálů v
silném gravitačním poli.
V posledních desetiletích byla objevena řada
binárních pulsarů, z nichž některé jsou zajímavé pro
studium dynamických gravitačních efektů OTR, včetně emise
gravitačních vln. Jmenovat můžeme např. PSR 1534+12, PSR
0337+1715, zvláště zajímavý je PSR 0737-3039 (obsahuje 2
pulsary).
Měřené údaje z pulsaru PSR 1913+16 a
dalších se staly velmi přesvědčivým (byť nepřímým) důkazem pro existenci gravitačních vln.
Časová
modulace periody signálů z pulsarů gravitačními vlnami
Vedle výše zmíněných dynamických efektů v
binárních soustavách kompaktních objektů mohou pulsary
potenciálně sloužit i ke studiu "již hotových"
gravitačních vln jiným způsobem. Pulsary - rychle rotující, silně zmagnetované
neutronové hvězdy, jsou zdroji vysoce pravidelných pulsů
elektromagnetického vlnění ve vzdáleném vesmíru (§4.2, pasáž "Pulsary
- precizní 'hodinové strojky' ve vesmíru"). Při
průchodu těchto pulsů vesmírným prostorem, obsahujícím
gravitační vlny nízkých frekvencí, dochází k určitému (i
když velmi slabému) ovlivnění jejich šíření - může
docházet k dlouho-periodické modulaci krátko-periodických
elektromagnetických signálů z pulsarů vlivem gravitačních
vln. Gravitační vlna o amplitudě h by vedla k relativní změně opakovací
frekvence pulsů no řádu Dn/no» h.
Citlivou analýzou těchto radiových signálů pomocí velkých
radioteleskopů či jejich systémů v zásadě bude možno tyto
jemné odchylky změřit. Prováděla by se korelace časů
detekce impulsů z několika pulsarů podle jejich úhlové
vzdálenosti.
K tomuto účelu jsou
vhodné především mikrosekundové pulsary, u kterých
se méně projevují efekty "hvězdotřesení" a
akrece, které mohou ovlivňit periodu pulsů. Tohoto jevu bude snad v budoucnosti možno
v principu využít k detekci dlouhoperiodických gravitačních
vln ve vesmíru - budují se soustavy většího počtu
radioteleskopů pro tuto detekci metodou Pulsar
timing array. Tato
metoda je citlivá i k velmi malým frekvencím 10-9-10-6 Hz gravitačních vln, které ve vesmíru
převažují. Vznikají při oběhu masívních objektů (např. velkých černých děr v centrech
kolidujících galaxií) s
oběžnou periodou několika měsíců až roků.
Nízkofrekvenční gravitační vlny by mohly pocházet i z
procesů při vzniku vesmíru (snížená
frekvence vlivem kosmologické expanze vesmíru). Taková měření by mohla být
doplňující k interferometrickým metodám, které nejsou
schopny detekovat nízkofrekvenční gravitační vlny.
V r.2008 byl založen
virtuální projekt NANOGrav (North
American Nanohertz Observatory for Gravitational Waves), jakožto
konsorcium asi 190 astronomů, kteří prostřednitcvím
pravidelných pozorování souboru 68 milisekundových pulsarů
se snaží detekovat nízkofrekvenční gravitační vlny pomocí
jemného sledování změn pozorovaných frekvencí pulsarů.
Sofistikovanou stochastickou analýzou velkého množství dat se
snaží odlišit signál z určitých lokalizovaných zdrojů od
stochastického pozadí náhodných gravitačních vln z mnoha
vzdálených zdrojů. Určitou možností může být analýza úhlové
korelace měřených odchylek pulsů mezi dvojicemi pulsarů
v různých částech oblohy. Jiné náhodné odchylky by
nevykazovaly stejnou korelaci.
Měření
polarizace reliktního mikrovlnného záření
Jak bylo zmíněno výše na konci části "Zdroje gravitačních
vln",
nejmohutnějším zdrojem gravitačních vln byl patrně
bouřlivý vznik vesmíru - jevy kolem "velkého
třesku". Především při gigantické a prudké inflační
expanzi velmi raného
vesmíru (§5.5 "Mikrofyzika a
kosmologie. Inflační vesmír.") by mělo dojít k intenzívnímu
rozvlnění křivosti prostoročasu - měly by vzniknout mohutné
primordiální gravitační
vlny,
které se od té doby budou šířit vesmírem. S expanzí vesmíru v nynější době
však již natolik zeslábly a enormně prodloužily své vlnové
délky, že na přímou detekci těchto primordiálních
gravitačních vln výše
popsanými metodami není žádná naděje. Rýsuje se však
zajímavá nepřímá metoda nalezení
"stop" *)
primordiálních gravitačních vln, jakou mohly zanechat ve
všudypřítomném reliktním mikrovlnném kosmickém
pozadí v době, kdy tyto vlny
byly ještě
poměrně silné, na konci éry
záření. Touto
"stopou" by mohla být částečná polarizace
reliktního mikrovlnného záření, které v té době vznikalo (oddělovalo
se od látky).
*) Můžeme to názorně přirovnat k tomu,
jak na některých kamenech pozorujeme otisky trilobitů.
Z takových otisků můžemě poměrně realisticky
zrekonstruovat velikosti a tvary těchto dávnověkých
živočichů, i když jejich organická těla se nenávratně
rozložila a již dávno zmizela. Podobně primordiální
gravitační vlny nyní již zeslábly a téměř zanikly. V
ranějších dobách vesmíru, kdy byly ještě silné, však
tyto "inflační" gravitační vlny zanechaly
charakteristické stopy - "otisky" -
na mikrovlnném reliktním záření. A ty můžeme nyní v
principu nacházet a měřit, i když je to mnohem
obtížnější a složitější než u těch otisků
trilobitů..!..
Vznik a vlastnosti reliktního mikrovlnného
kosmického pozadí jsou rozebírány §5.4, pasáž "Mikrovlnné reliktní záření -
posel zpráv o raném vesmíru" (viz též §1.1, část "Metody zkoumání přírody"). Většina reliktního
mikrovlnného záření, vznikajícího při chaotických
interakcích částic v horké plasmě, nevykazuje žádnou
pravidelnou polarizaci, jejich elektrické a magnetické vektory E
a B kmitají nahodile v různých rovinách. Na
konci éry záření při posledních rozptylech fotonů na
zbytku volných elektronů dochází k tzv. Thomsonovu
rozptylu. Pokud s elektrony kolektivně interagují fotony
různých frekvencí z různých směrů v heterogenní plasmě,
mohou vzniknout výsledné vlny s preferovanou rovinou kmitů
elektrického pole: nazývá se E-mód polarizace. Pokud
však dochází k interakci fotonů které mají změněnou
frekvenci v důsledku průchodu přes gravitační vlny
(s tenzorovým kvadrupólovým charakterem), vzniká tzv. B-mód
polarizace, který v prostoru vykazuje určitou
"obloukovost" či "zakroucenost" kolem
středu fluktuace.
Silné
gravitační vlny, putující vesmírem v době vzniku
(oddělování) reliktního záření, by měly poněkud ovlivnit
jeho vlastnosti - způsobit velmi slabou, ale charakteristickou polarizaci reliktního mikrovlnného
záření. Při dostatečné přesnosti a citlivosti měření
této polarizace (zvláště jejího vířivého módu B) by bylo možno hypotetické inflační
primordiální gravitační vlny takto nepřímo
prokázat. Bude to vyžadovat podstatné zvýšení
citlivosti a rozlišovací schopnosti přijímacích
"antén" mikrovlnného záření. Určitým problémem
by též mohlo být odlišení
gravitačně-vlnové polarizace reliktního záření od
polarizace na mezihvězdném prachu *). Všechna astronomická pozorování
mimo naši galaxii nutně probíhají prostřednictvím záření
procházejícího skrze mezihvězdný prach v naší galaxii.
*) Polarizace elektromagnetického
záření mezihvězdným prachem je způsobena převládajícím
elipsoidním tvarem zrnek prachu, které jsou mírně
orientovány v galaktickém magnetickém poli. Míra
této polarizace činí cca 3%. Dalším zdrojem polarizace
může bý synchrotronové záření elektronů
kroužících v magnetickém poli (vzhledem k velmi slabému
magnetickému poli se projevuje jen v dlouhovlnných oblastech).
Astrofyzikální význam gravitačních vln
Předpověď
Einsteinovy obecné teorie relativity, že zrychleně se
pohybující hmota musí ztrácet energii vyzařováním
gravitačních vln, tak byla potvrzena. Byl to další stimul pro
konstruktéry důmyslných detektorů gravitačních vln, kteří
si mohli být jisti konečným
úspěchem
svého snažení, protože patrně gravitační
vlny existují! Astrofyzikální význam gravitačních
vln je v zásadě dvojí :
¨
Dynamicko-evoluční
působení
Vyzařování gravitačních vln ovlivňuje nebo je zodpovědné
za důležité astrofyzikální
procesy ve
vesmíru, vedoucí k evoluci řady vesmírných systémů. Tím
se budeme stručně zabývat níže v pasáži "Gravitační vlny a dynamika vesmírných
systémů".
¨
Observačně -
gnoseologický význam
Gravitační vlny jsou "poslové" nesoucí cenné informace
o svých zdrojích. A pokud jsou tyto zdroje ve
velkých vzdálenostech (kosmologických), mohou nést též
informace, které jim "vtiskla" mezilehlá
interagující hmota *). Poznávacím významem gravitačních
vln se budeme zabývat v následující pasáži.
*) Je to podobné jako u kosmického
mikrovlnného záření, u něhož při průchodu přes
rozsáhlé kosmické struktury dochází k mírné modulaci
teplotních anizotropií (srov. §5.4,
část "Mikrovlnné reliktní záření - unikátní
posel zpráv o raném vesmíru"pasáž
"Vliv
gravitačních fluktuací metriky ve vesmíru na reliktní
záření -
Sachs-Wolfův efekt").
Z observačního hlediska je tedy
důležitá úspěšná detekce gravitačních vln a jejich
praktické využití v astronomii - k získání nového pohledu
na procesy ve vesmíru :
Gravitačně-vlnová
astronomie
Pozorování a analýza gravitačních vln má obrovský
potenciální význam pro prohloubení našeho chápání
vesmíru. Pro reflexi toho, jak nesmírně významým "oknem" do
vesmíru je
detekce a zobrazování pomocí
gravitačních vln, si nejprve stručně zrekapitulujme
důležité etapy pozorování vesmíru pomocí vln
elektromagnetických (je též diskutováno
v §1.1, část "Elektromagnetické záření - základní zdroj
informací o vesmíru").
Do poloviny 20.stol. pocházely veškeré naše
vědomosti o vesmíru z pozorování viditelného světla
- úzkého spektrálního rozmezí vlnových délek
elektromagnetického záření, na které je citlivé naše oko a
fotografické materiály. V tomto optickém oboru
se nám vesmír jeví jako poměrně klidný systém
hvězd sdružených v galaxiích a planet plynule obíhajících
po svých drahách (přímo pozorujeme
planety naší sluneční soustavy; podobný obrázek bychom
pravděpodobně dostali kdybychom uměli pozorovat planety kolem
jiných hvězd). Vlastnosti hvězd a planet
se v optickém oboru výrazněji mění v časových
měřítcích milionů nebo miliard let (až
na vzácné úkazy jako jsou novy nebo výbuchy supernov). Nejjasnějšími objekty sledovanými v optickém
oboru (očima nebo optickými teleskopy) je Slunce, planety a
blízké hvězdy, ve vzdálenějším vesmíru pak mlhoviny a
galaxie. Světlo s vlnovou délkou kolem 0,5mm je vyzařováno
převážně excitovanými atomy
nacházejícími se v horkých atmosférách hvězd a planet,
nebo v rozsáhlých plynných mlhovinách. Optická fotometrie a
spektrometrie nám proto přináší informaci o teplotách a
chemickém složení, prostřednictvím Dopplerovské
spektrometrie i o rychlostech pohybů objektů a proudění
plynů.
Od 60.let nám pozorování pomocí rádiových
vln ukázalo jinou, daleko dynamičtější
stránku vesmíru - mohutné výtrysky plynů z jader galaxií,
kvasary s nesmírně vysokou, ale kolísavou jasností, pulsary
otáčející se vysokou rychlostí a vysílající úzké
kužely záření. Nejjasnějšími objekty pozorovanými
radioteleskopy jsou gigantické mezigalaktické oblaky
("laloky") a výtrysky z galaktických jader,
poháněné pravděpodobně obřími černými dírami. Radiové
vlny (s 10-milionkrát větší vlnovou délkou než světlo)
jsou vyzařovány především rychlými elektrony
pohybujícími se téměř rychlostí světla po
spirálách v magnetických polích.
Od 70.let začala astronomická pozorování v
oboru X-záření pomocí rentgenových
teleskopů instalovaných na satelitech. Zde se nám
objevuje zase odlišný obraz vesmíru, ukazující lokální
bouřlivé procesy kolem neutronových hvězd a černých děr
hvězdných hmotností, s akrecí horkého plynu ve
dvojhvězdných soustavách. X-záření s vlnovou délkou
řádově 1000-krát kratší než světlo je vyzařováno
převážně vysokoenergetickými elektrony v extrémně
horkém plynu, jaký vzniká v akrečních
discích kolem černých děr nebo neutronových hvězd.
V důsledku turbulencí a rázových vln v akrečních
discích má toto rtg záření nepravidelnou, rychle se
měnící intenzitu. Může to být synchrotronové záření
vysílané relativistickými elektrony pohybujícími se v
silném magnetickém poli, brzdné záření, zářivá
rekombinace atomů v ionizovaném plynu. Záblesky X záření
mohou vznikat při termonukleárním zapálení vodíku
nashromážděného akrecí z červeného obra na bílý
trpaslík v těsném dvojhvězdném systému. Při
gravitačním kolapsu a zrození černé díry v
okolní rázové vlně vznikají i intenzívní záblesky
záření gama.
Astronomická pozorování v různých
spektrálních oborech vlnových délek elektromagnetického
záření tedy poskytují značně odlišné obrazy
vesmíru, které však nejsou v rozporu, ale vzájemně
se doplňují a skládají "mozaiku"
objektivního obrazu struktury a dynamiky
vesmírných soustav. V této mozaice však zatím řada
důležitých "kamenů" chybí. Z
některých míst (jako jsou vnitřky hvězd nebo oblasti
hustých plynů a prachu v centrálních částech galaxií) se
nedostane ven světlo ani žádné jiné elektromagnetické
záření. Mohou se odtud dostat neutrina, příp.
vysokoenergetické částice. Proto se určité naděje
vkládají do detekce neutrin a primárního kosmického
záření, která je však velmi obtížná a je teprve
v začátcích. Některé kompaktní objekty jako jsou černé
díry, pokud nemají akreční disky, neemitují
elektromagnetické vlnění vůbec; pokud jsou však součástí
těsného binárního objektu, budou emitovat gravitační vlny.
Důležité chybějící "kaménky do
mozaiky" poznání vesmíru by tedy mohlo přinést
nejobtížnější "okno" do vesmíru - gravitační
záření, které - jak bylo výše diskutováno v
části "Detekce gravitačních vln"
- se teprve začíná "pootevírat"! ... viz však níže "První
přímá detekce gravitační vlny zařízením LIGO"...
Analogie s hudbou
- "vidět" a slyšet hudbu?
Základní síla, která řídí stavbu a vývoj vesmíru, jakož
i dynamiku pohybu kosmických objektů, je gravitace.
Tyto gravitací řízené objekty ve vesmíru zatím pozorujeme
pouze analýzou elektromagnetického záření. Tím se
dozvídáme mnoho o pozicích a pohybech těles a chování
látky ve vesmíru, avšak o řídící síle toho všeho -
gravitaci - se dozvídáme jen nepřímo,
zprostředkovaně, neúplně. Se značnou nadsázkou (avšak s některými výstižnými rysy) to můžeme porovnat s myšleným příkladem s
orchestrální hudbou:
Představme si, že v exteriéru se koná koncert
klasické hudby pro velký orchestr, který z kopce vzdáleného
cca 4 km pozorujeme silným dalekohledem. Pozorováním pohybů
taktovky dirigenta, smyčců na houslích, paliček bubnů a
pod., by i pro dobrého znalce bylo velmi obtížné poznat,
jaká hudební skladba se hraje. Teprve zachycení zvukových vln
citlivým směrovým mikrofonem by pomohlo poznat, zda se hraje
třebas Koncert pro housle a orchestr D dur P.I.Čajkovského,
nebo 9.Symfonie L.v.Bethovena. A podobně zachycení dynamiky
gravitačních sil ve vzdálených kosmických objektech pomocí
detekce emitovaných gravitačních vln může pomoci
konkretizovat tamní dynamickou situaci...
Samotný zvuk hudby nám však nedá úplnou
informaci o jejím konkrétním vzniku v orchestru, k tomu
potřebujeme vizuální informaci. Podobně ani gravitační
vlny, v důsledku své dlouhovlnnosti, nám nemohou vytvořit
detailní ostrý obraz astronomických objektů. Teprve budoucí multimodalitní
astronomie, zkoumající astrofyzikální objekty a
události současně pomocí elektromagnetického záření,
gravitačních vln a různých emitovaných částic, nám může
poskytnout komplexní poznání.
Kromě astronomie elektromagnetického
vlnění (radio-,
optická, rentgenová a g-astronomie
- §1.1, část "Elektromagnetické záření -
základní zdroj informací o vesmíru"), detekce neutrin a částic kosmického
záření, se tak začíná rýsovat budoucí "gravitačně-vlnová astronomie", která by zřejmě
podstatně rozšířila naše znalosti o jevech probíhajících
ve vesmíru. Detekce
gravitačních vln, změření jejich frekvence
a intenzity, spolu se zobrazením směru odkud
přicházejí, umožní odhalovat důležité dynamické procesy
s kompaktními objekty, často jinými způsoby neviditelné
*), včetně nejbouřlivějších procesů gravitačního
kolapsu a srážek (splývání) neutronových hvězd a černých
děr.
*) Jsou to především binární
kompaktní objekty, které jsou většinou astromicky a opticky
"němé". Při svém dlouhodobém blízkém obíhání
pravděpodobně ztratily své akreční disky (byly
"strženy", nebo je černé díry již předtím
"spotřebovaly"), takže jejich splynutí není
doprovázeno mohutnějším elektromagnetickým zábleskem
(radiovým, optickým či gama). Jedinou možností, jak odhalit
tyto dramatické astrofyzikální události, je detekce
gravitačních vln!
Některé možnosti složitějších
scénářů splynutí binárního systému kompaktních objektů,
při nichž by mohlo být emitováno i fotonové záření, jsou
diskutovány v §4.8, pasáž "Binární gravitačně vázané
systémy černých děr. Srážky a splynutí černých děr".
Pozorování
v elektromagnetickém spektru a v gravitačních vlnách se
vzájemně doplňují: fotonové záření,
včetně X a gama-záblesků, informují o látkové
povaze objektů a okolního prostředí (jako jsou akreční disky),
gravitační vlny mohou ukazovat dynamiku,
která vede k pozorovaným bouřlivým astrofyzikálním jevům -
"zviditelnit neviditelné".
Nové informace z
gravitačních vln
Gravitační vlny k nám z vesmírných objektů přinášejí
velmi odlišné informace od těch, které nese
elektromagnetické záření. Je to dáno mechanismem jejich
vzniku a vlastnostmi jejich interakce s hmotou:
l
Mechanismus vzniku
Elektromagnetické vlny z vesmírných zdrojů jsou vysílány
(při deexcitacích atomů a interakcích elektronů) jednotlivě
a nezávisle obrovským množstvím oddělených atomů a
elektronů. Tyto jednotlivé elektromagnetické vlny, z nichž
každá kmitá poněkud odlišně, se pak skládají dohromady ve
výsledné záření které pozorujeme (tak
je tomu u radiovln a světla, u záření X a g registrujeme
jednotlivé fotony, které byly s určitou pravděpodobností
emitovány atomy a elektrony). S použitím
spektrometrické analýzy nám nesou informace o teplotě,
složení, magnetických polích a hustotě, které působí na
vyzařující atomy či elektrony (vlivem
Dopplerova jevu i o rychlostech pohybu).
Gravitační vlny jsou buzeny kolektivně, synchronními
velkorozměrovými pohyby velkého množství hmoty - kolapsem
jádra hvězdy, vzájemným obíháním masivních objektů
(hvězd, neutronových hvězd, černých děr). Proto nám
gravitační vlny přinášejí informace o pohybech velkých
hmot a dynamice velkých zakřivení prostoru.
l
Interakce s hmotou
Elektromagnetické vlny sice volně procházejí téměř
prázdným vakuem mezihvězdného prostoru, avšak při průchodu
látkou výrazně interagují s atomy a elektrony,
což způsobuje jejich absorbci. Oblasti, kde
došlo k výbuchu supernovy, gravitačnímu kolapsu, srážce
černých děr, či velkého třesku na počátku vesmíru, jsou
obklopeny silnou vrstvou látky, která pohlcuje
veškeré elektromagnetické vlny; světlo ani jiné
elektromagnetické vlny, potenciálně nesoucí informace o
bouřlivých jevech v tomto místě, se prostě "nedostanou
ven". Astronomicky můžeme pozorovat pouze
elektromagnetické vlny přicházející ze slabě
gravitujících oblastí (povrchy hvězd, zářící mlhoviny),
které navíc nejsou zastíněny oblaky mezihvězdného prachu
nebo ionizovaného plynu.
Gravitační vlny, které nejintenzivněji vznikají právě v
takových místech velkého nahromadění hmoty, silné gravitace
a bouřlivých jevů, naproti tomu snadno
procházejí oblaky plynů a prachu. Zevnitř těchto
oblastí vynášejí informace o dynamice
relativistických procesů tam probíhajících.
Ve směru, amplitudě a frekvenci
gravitačních vln (a v časových změnách amplitudy a
frekvence) jsou tedy určitým způsobem zakódovány
informace o
bouřlivých procesech probíhajících v okolí a v nitru
masívních objektů; tyto informace mohou "vynést
ven" pouze gravitační vlny, neboť se jedná o oblasti
nevysílající světlo a pro světlo a další
elektromagnetické vlny neprůhledné. Monitorování gravitačních
vln by mohlo leccos prozradit o dynamických jevech v okolí
kompaktních gravitačně zhroucených objektů. Ve zcela charaktristickém časovém průběhu amplitudy
a frekvence
mohutných gravitačních vln, vznikajících v závěrečných
stádiích těsného oběhu a
srážky
(splynutí) dvou neutronových hvězd nebo černých děr, je zakódována významná informace o průběhu tohoto dramatického
děje za účasti velkých hmotností a krajně silných
gravitačních polí - viz výše prudký růst amplitudy a
frekvence na obr.4.13-GW v části "Zdroje gravitačních vln ve
vesmíru".
Gravitační vlny mohou potenciálně
též přinášet informace o dynamice nejranějších
fází
vývoje vesmíru, kdy byl vesmír pro
všechny ostatní formy záření neprostupný *), avšak z toho
období pocházející "primordiální"
gravitační vlny mohou být v principu detekovány. Pomocí
rozsáhlých vesmírných detektorů gravitačních vln by ve
vzdálené budoucnosti bylo teoreticky možné dokonce udělat
jakýsi "snímek vesmíru" v období Planckova času a
vnést tak "světlo" i do mechanismu vzniku
vesmíru..?..
*) "Velký třesk" ve světle ani
jiném elektromagnetickém záření nikdy neuvidíme, protože
je skryt za svým vlastním mohutným zábleskem. Pomocí
gravitačních vln bychom však mohli být schopni (aspoň v principu či teoreticky)
"nahlédnout" do událostí samého začátku vesmíru.
V principu gravitační vlny vznikají při každém
zrychleném pohybu hmoty, tedy i při oběhu planet kolem
hvězd nebo oběžných pohybech vzájemně vzdálených hvězd
kolem společného těžiště v dvojhvězdných nebo
vícenásobných stelárních systémech. Takto generované
gravitační vlny jsou však nesmírně slabé a též velice
"pomalé" (nízkofrekvenční) - jejich frekvence je
dána periodou oběhu, činí jeden cykl za několik hodin, dní
nebo i roků. Na detekci, či dokonce astronomické využití
těchto gravitačních vln, není žádná naděje v dohledné
budoucnosti (a patrně nikdy!)...
Jak by vypadal gravitačně-vlnový vesmír
?
Kdybychom v hypotetické (či spíše sci-fi)
představě měli "gravitační oči"
citlivé pouze na gravitační záření, nebo byli vybaveni gravitačně-vlnovým
teleskopem, spatřili bychom při pohledu na oblohu
(lhostejno zda noční nebo denní) zcela jiný obraz
vesmíru, než jaký známe z dosavadních
astronomických pozorování. Neviděli bychom Slunce ani známé
jasné hvězdy, souhvězdí, mlhoviny. Místo toho bychom viděli
četné objekty v místech, kde v optickém oboru žádné
jasnější hvězdy nepozorujeme. Jedná se o těsné binární
systémy obíhajících kompaktních objektů -
neutronových hvězd a černých děr, vyzařující gravitační
vlny o velkém výkonu. Tyto objekty by byly četnější v těch
místech galaxie, kde se vyskytuje větší nakupení starších
hvězd (je zde větší pravděpodobnost,
že mnohé z nich již dospěly do závěrečných fází své
evoluce a zkolabovaly do kompaktních objektů). Když budeme trpěliví, čas od času spatříme
oslnivě jasné záblesky gravitačních vln. To
mohou být čtyři druhy dramatických událostí :
- Kolaps jádra hvězdy, který "odpálí" výbuch
supernovy. Pokud je tento kolaps či výbuch nesymetrický,
produkuje silný záblesk gravitačních vln. Zde se vyskytuje
korelace mezi krátkým impulsem gravitačních vln a vizuálním
astronomickým pozorováním mohutného světelného zjasnění,
doznívajícího týdny i měsíce.
- Gravitační kolaps rotující hvězdy
do černé díry s fragmentací a následnou fúzí některých
odvržených částí (viz obr.4.14 v §4.4 "Rotující
a elektricky nabité Kerrovy-Newmanovy černé díry").
- "Srážka" dvou neutronových hvězd nebo
černých děr - taková přímá srážka je však patrně velmi
vzácný úkaz.
- Časté je však těsné obíhání a splynutí
kompaktních objektů ve shora uvedeném binárním
systému, u něhož gravitační vlny již odnesly
téměř veškerou kinetickou energii obíhání. Toto by měly
být nejčastější a nejsilnější zdroje
záblesků gravitačních vln - viz výše "Zdroje gravitačních vln ve vesmíru", obr.4.13, pasáž "Mohutné
zdroje a záblesky gravitačních vln".
Kdybychom měli velmi silný "sci-fi"
gravitačně-vlnový teleskop, viděli bychom ve vzdáleném
vesmíru komíhat velké množství gravitačních záblesků z
fúzních zániků binárních systémů kompaktních objektů (tyto události zaplňují vesmír slabým
rozprostřeným gravitačně-vlnovým pozadím). Kdyby tento teleskop byl schopen zachytit i velmi
nízké frekvence řádu nanohertzů, mohli bychom vidět i
gravitační vlny z velkého počtu těsných dvojhvězdných
systémů a dokonce snad i slaboučké kontinuální pozadí reliktních
gravitačních vln z prvních okamžiků vzniku
vesmíru..!?..
Gravitační vlny a dynamika
vesmírných systémů
Vedle observačního významu (gravitačně-vlnová
astronomie) mají gravitační vlny i zásadní
astrofyzikální význam pro dynamiku a evoluci
řady systémů ve vesmíru. Především je to vývoj
masívních kompakních objektů a jejich binárních či
vícenásobných soustav. Jako příklad můžeme uvést proces
fragmentace a opětného spojování při kolapsu
rotující hvězdy na obr.4.14 v §4.4 "Rotující
a elektricky nabité Kerrovy-Newmanovy černé díry". Nebýt gravitačních vln, neproběhlo by
spojení fragmentů a "dokončení" gravitačního
kolapsu, neplatil by teorém "Černá díra nemá vlasy"
(§4.5 "Teorém "černá díra nemá vlasy""). U těsných binárních soustav
obíhajících kompaktních objektů způsobuje gravitační
vyzařování, odnášející orbitální kinetickou energii,
přibližování rotujících objektů a zkracování oběžné
periody, až nakonec dojde k jejich splynutí (jak bylo diskutováno výše v pasáži "Binární
pulsar"). U vzdálených binárních
hvězdných systémů a u planet obíhajících kolem hvězd
však gravitační radiace nemá žádný význam:
je tak slabá, že je naprosto převážena disipativními
slapovými silami v materiálech obíhajících těles a třením
při pohybu v řídkém mezihvězdném či meziplanetárním
plynu.
Vyzařování gravitačních vln má pravděpodobně význam i
pro evoluci rotujících galaxií v dlouhodobém časovém
měřítku. ....
-------- níže uvedené poznatky vznikly až po sepsání knihy "Gravitace, černé díry ...", takže v knižním vydání nebyly obsaženy -----
Nové experimenty pro detekci gravitačních vln
- LIGO, VIRGO, GEO, TAMA, LISA -
I přes zdokonalení a zvýšení
citlivosti rezonančních detektorů Weberova typu (např. detektor na Stanfordské universitě dosahuje
citlivosti 10-18) se jako nejperspektivnější
detektory gravitačních vln jeví detektory
interferometrické. Fyzikální princip a základní
uspořádání interferometrického detektoru gravitačních vln
bylo popsáno výše v základním textu, část "Detektory
gravitačních vln"a
schématicky načrtnuto na obr.2.12c. První takové detektory,
konstruované v 70.letech, svou citlivostí 10-15 nepřevyšovaly
Weberův původní detektor. Během dalších let se však
neustále zdokonalovaly, především vývojovými pracemi
fyziků a inženýrů ve skupině pod vedením R.Weisse, K.Thorna
a R.Drevera. Koncem 80.let byl v Kalifornském technologickém
institutu sestrojen laboratorní interferometr MARK2 s délkou
ramen 40 metrů, dosahují na svou dobu špičkové citlivosti 10-18.
LIGO -
velký detektor gravitačních vln
Pod vedením výše uvedené skupiny byla v r.2001 v USA
zahájena stavba největšího a nejcitlivějšího zařízení
pro detekci gravitačních vln - systému LIGO (Laser
Interferometer Gravitational
wave Observatory). Tento významný projekt,
budovaný ve spolupráci Kalifornského technologického
institutu a Technologické university Massechussets, je tvořený
dvěma vzdálenými observatořemi. Jedna z nich
je umístěna v Livingstone (stát
Louisiana), druhá stejného druhu se nachází v Hanfordu
u Washingtonu. Citlivost by měla dosahovat řádu h @ 10-21 a po rekonstrukci
dokonce 10-23! Koincidenční analýza signálů ze
vzdálených interferometrů umožňuje eliminovat falešné
signály, mající původ v lokálních poruchách.

Výrazného zvýšení citlivosti o několik
řádů oproti dřívějším detektorům se podařilo dosáhnout
kombinací řady špičkových technických inovací.
Jednak jsou to obrovské rozměry - délka ramen interferometru
je 4 kilometry (což je více než 100-krát
větší než u dřívějších interferometrů). Optická
soustava obou ramen je umístěna ve dvou trubicích délky 4km a
průměru 120cm, v nichž je udržováno vysoké vakuum.
Místo obvyklých dvou testovacích těles je v systému LIGO
použito 4 volně zavěšených těles s precizními zrcátky o
vysoké odrazivosti, dvě na každém rameni. Speciální
geometrickou konfigurací dvojice zrcátek (a vstupních a
výstupních otvorů vnitřního zrcátka) je dosaženo toho, že
laserový paprsek se mezi těmito rovnoběžnými zrcátky v
každém rameni bude mnohonásobně odrážet a
teprve potom projde otvorem ve vnitřním zrcátku k
rozdělovači paprsků, spojí se interferenčně se svým
partnerem z druhého ramena a dopadá na fotodetektor. Tento
mnohonásobný odraz na principu tzv. Fabry-Perotova
interferometru umožňuje efektivně prodloužit
optickou délku zařízení koeficientem rovným počtu
odrazů. Při 100 odrazech bude tedy optická délka ramen
100-krát větší než fyzické rozměry, tj. jako by rameno
mělo 400km!
Ve výchozím (klidovém) stavu je interferometr
nastaven tak, že oba výstupní interferující paprsky se
setkávají v protifázi a ruší se - okénko fotodetektoru je
"temné". Změna vzdáleností testovacích těles
změní tento fázový posun, okénko fotodetektoru se zjasní a
fotoelektrické čidlo vyšle elektrický signál úměrný
intenzitě interferenčního paprsku.
Systém LIGO je vybaven
řadou dalších pokročilých elektronických, optických a
mechanických vymožeností, přispívajících ke zdokonalení
citlivosti a izolaci rušivých vlivů - vibrací, slapových
sil, tepelného šumu, změn tlaku. Laserový paprsek je
"vyčistěn" do dokonale koherentního tvaru. Část
paprsku je odkloněna do modulátoru frekvence, který vytvoří
dva referenční paprsky s nepatrně vyšší a
nižší frekvencí než hlavní papsek; tyto referenční
paprsky procházejí částí optického systému, nepodléhají
však mnohonásobnému odrazu v ramenách, ale odrážejí se od
obou prvních zrcadel a dopadají do fotodetektoru, kde jsou
porovnávány s interferenčními paprsky z obou ramen.
Testovací tělesa se zrcadly jsou zavěšena jako kyvadla na
speciálních závěsech; závěsy jsou upevněny na rámy
ukotvené na sloupcích v několika mechanicky izolačních
vrstvách. Poloha zrcadel je jemně korigována magnetickými
cívkami.
Zdokonalený
detektor aLIGO
V letech 2013-2015 byla provedena generální
rekonstrukce přístrojového vybavení obou detektorů
LIGO za účelem podstatného zvýšení citlivosti.
Bylo realizováno několik podstatných technických inovací :
- Zvýšení výkonu
laseru z původních 10W na 200W. Tím se výrazně snížil
kvantový fotonový šum.
- Větší a
těžší křemenná testovací optická zrcadla, což snížilo
vliv tepelného šumu a radiačního tlaku laserového záření (a tím snížilo malé náhodné pohyby zrcadla).
- K zavěšení
zrcadel byly místo původních ocelových drátů použity
vlákna z magneticky neutrálního oxidu křemičitého.
- Použití
elektronické aktivní seismické izolace.
Takto zdokonalený detekční systém, zvaný aLIGO
(advanced LIGO), má asi 10-krát lepší
citlivost než původní LIGO (zvýšení
citlivosti faktorem 10 vede ke zvýšení
detekovatelného objemu vesmíru faktorem 1000!). Podstatně se tím zvýšil "akční
rádius" detekce i z mnoha vzdálenějších zdrojů, což
zvýšilo pravděpodobnost incidence zaznamenání gravitačních
vln; to se skutečně realizovalo první úspěšnou detekcí
gravitační vlny krátce po spuštění aLIGO (viz níže "PrvniDetekceGravitVlny") .
Vvybudováno je (nebo se staví) i několik
dalších menších pozemských interferometrických detektorů
gravitačních vln, např. :
VIRGO (Italsko-Francouzský projekt):
Délka ramene 3 km,
citlivost 10-22 při frekvenci 500Hz. Název byl zvolen podle kupy asi
1500 galaxií v souhvězdí Panny - Virgo,
vzdálené od Země asi 50 miliónů světelných let; tam se dá
očekávat zvýšená pravděpodobnost výskytu dostatečně
silných zdrojů gravitačních vln. Přístroj Virgo má velmi
dobře vyřešenou aktivní seismickou korekci. Tato
observatoř, druhá největší po LIGO, se nachází Casciny
poblíž italského města Pisa.
GEO 600 (Britsko-Německý projekt):
Délka ramene 600 m,
udávaná citlivost 10-22 při frekvenci 600Hz. Nachází se v blízkosti
Hanoveru.
TAMA 300 (Japonsko):
Délka ramene 300 m,
citlivost 5.10-21 při frekvenci 700-1000Hz. Tento přístroj souží
jako předstupeň většího systému:
KAGRA (KAmioka GRAvitational wave detector):
(Large-scale Cryogenic Gravitational wave detector)
s délkou ramen 3 km (umístěného v
těsné blízkosti proslulého podzemního detektoru
neutrin SuperKamiokaNde - viz "Detece
neutrin", pasáž "Neutrinový
detektor Kamioka NDE"). Bude součástí celosvětového systému detektorů
gravitačních vln.
Ve stadiu projektu je vybudování detektoru typu LIGO v
Indii.
Dále se počítá s postupným zdokonalováním
velkých detekčních systémů LIGO (-->aLIGO) a VIRGO, kde
zvýšením výkonu laseru, zdokonalenou aktivní seismickou
izolací+korekcí, použitím preciznějších zrcadel a
dalších špičkových technologií by mělo být dosaženo
citlivosti až h @ 10-23.
Celosvětová
síť detektorů gravitačních vln
Odborníci si hodně slibují od spolupráce a elektronického
propojení několika detektorů gravitačních vln
rozmístěných v různých částech Země. Jednak současná
detekce impulsů nezávislými vzdálenými detektory
umožňuje eliminovat náhodné falešné vibrace
lokálního původu. Dále, jak gravitační vlna postupuje po
zemském povrchu (rychlostí světla), zasáhne různé tyto
detektory v nepatrně odlišnou dobu (v
řádech několika milisekund).
Vyhodnocení zpožděných koincidencí
signálů mezi jednotlivými vzdálenými detektory tak umožní triangulačně
určit směr, z něhož gravitační vlna přichází a
provést tak astronomické přiřazení místa na obloze.
Připravuje se propojení šesti velkých detektorů
gravitačních vln: v Hanfordu (LIGO) a v Livigstonu (LIGO), v
Hannoveru (GEO), v Pise (VIRGO) a v Japonsku (TAMA-KAGRA);
všechny jsou interferometrického typu. Je plánováno
vybudování dalšího detektoru typu LIGO v Indii.
Kosmické
detektory gravitačních vln
Jedním z hlavních problémů, omezujících citlivost
sebedokonalejších pozemských detektorů gravitačních vln,
zvláště v oblasti nízkých frekvencí, je "neklidná
Země" - seismické pozadí
přírodního původu (geologického,
atmosférického,slapového), jakož i rozruchy způsobené
lidskou činností (přejezdy těžkých automobilů, zemní a
těžební práce, přelety letadel). Všudypřítomné
seismické pozadí znemožňuje pozemskými přístroji detekovat
především gravitační vlny frekvencí menších než 1Hz. Z
technických a geologických důvodů též již nelze dále
zvyšovat délku ramen pozemských interferometrů. Budoucí
velké detektory gravitačních vln proto budou muset být vybudovány
ve vesmíru - síť satelitů spojených laserovými
interferometry :
LISA - kosmická
observatoř gravitačních vln
NASA a Evropská vesmírná agentura proto připravují
projekt detekčního systému gravitačních vln umístěného ve
vesmíru, pod názvem LISA (Laser Interferometer
Space Antenna). Na oběžnou
dráhu kolem Slunce mají být vypuštěny tři kosmické sondy
vybavené lasery, které vytvoří trojúhelníkový
interferometrický systém se vzdáleností ramen 5 miliónů
kilometrů (tedy asi 10-krát větší než
je vzdálenost Země-Měsíc). Soustava
těchto tří sond má být vypuštěna kolem r.2011 a bude
obíhat kolem Slunce ve vzdálenosti 1 astronom. jednotky (jako
Země). Při svém oběhu kolem Slunce bude tato trojice sond
udržovat mezi sebou konstantní vzdálenost s přesností
jednoho mikrometru. Pro vyloučení negravitačních vlivů na
pohyb sond budou tyto sondy s použitím aktivní korekce
udržovány na ideální geodetické dráze tak, aby poloha
volně se pohybujícího testovacího tělíska, vznášejícího
se v dutině uvnitř sondy, zůstávala konstantní. Sondy budou
vysílat a speciálními zrcátky odrážet mezi sebou laserové
paprsky, jejichž interference bude zaznamenávána detektory a
vysílána na Zemi.
Systém LISA bude dosahovat daleko vyšší
citlivosti a navíc bude schopen detekovat gravitační vlny i o
mnohem nižší frekvenci (a tedy dlouhých
vlnových délek), než detektory pozemské - frekvence od 1Hz do
10-4 Hz.
Takovéto (a ještě delší) gravitační vlny by měly v
gravitačně-vlnovém spektru z vesmíru převažovat. Umožní
tak zaznamenávat m.j. pohyb neutronových hvězd či černých
děr v kompaktních binárních systémech (i
delší dobu před jejich splynutím) a masívních
černých děr (o hmotnostech milionů až miliard M¤),
které patrně kolem sebe obíhají ve středu galaxií a
generují pomalé frekvence gravitačních vln. Tímto způsobem
se možná podaří zachytit i primordiální
gravitační vlny..?..
Projekt
LISA se zatím nepodařilo zahájit, NASA od něj odstoupila. Je
plánován redukovaný projekt eLISA...
DECIGO
(Deci-hertz
Interferometer Gravitational
wave Observatory) - japonský projekt
kosmického detektoru gravitačních vln .....
Délka ramen 1000km, pásmo max.citlivosti cca 0,1 - 10 Hz.
...........................
První přímé detekce gravitačních vln
Velké a vysoce citlivé systémy pro detekci gravitačních vln
po řadu let své činnosti "mlčely", kromě šumů a
náhodných fluktuací nebyl zaznamenám žádný signál, který
by odpovídal detekci gravitační vlny.
Obrat nastal dne 14.září 2015,
kdy v 09:50:45 hod. UTC oba detektory v Laserové
Interferometrické Gravitačně-vlnové
Observatoři LIGO simultánně
zaznamenaly krátký, ale signifikantní signál z procházející gravitační vlny, jehož frekvence během 0,45 sec. stoupala od
35 do 250 Hz; pak signál rychle poklesl a prakticky
vymizel. Na vrcholu píku dosahovala amplituda h @
1.10-21, poměr signál/šum činil 24. Bylo
to krátce po zdokonalení zařízení za účelem zvýšení
citlivosti (advanced LIGO). Pracovníci zařízení aLIGO tento nově detekovaný
gravitačně-vlnový zdroj (událost, signál) nazvali GW150914
(podle data objevení).
Podrobný článek o této první úspěšné detekci, pod nímž
je podepsán kolektiv téměř 1000 výzkumných a technických
pracovníků, byl v únoru 2016 publikován v předním
fyzikálním časopise Physical Review Letters 116,
061102 (2016).
 |
Zpracování signálu GW1504914
z první úspěšné detekce gravitační vlny systémem
LIGO. Signál byl zachycen simultánně
interferometrickým detektorem v Hanfordu (vlevo) i
Livingstonu (vpravo) v koincidenci s časovou diferencí
7 milisekund, odpovídající vzdálenosti obou
detektorů 3000km. V horní části obrázku je primární zachycený signál v obou interferometrech (jen se základním pásmovým frekvenčním filtrem 35-350Hz). Uprostřed je tento signál fitovaný počítačově modelovaným průběhem pro binární systémy dvou černých děr. Úzký graf pod ním ukazuje diference mezi skutečným a nejlépe vyhovujícím modelovaným signálem. V dolní části obrázku je dvojrozměrný časově-frekvenční spektrogram (diagram) signálu, barevně a jasově modulovaný jeho amplitudou. Na vodorovné ose je čas, na svislé ose frekvence, barva a jas vyjadřuje amplitudu signálu. Názorně ukazuje zvyšování frekvence ("chirp") v průběhu času detekce. <-- Phys.Rev.Lett. 116, 061102 (2016) |
Interpretace
Detekovaný signál má podobný tvar, jako je teoretický
průběh vyzařovaných vln při vzájemném oběhu dvou
masívních kompaktních těles m1 a m2 těsně před a v průběhu jejich splynutí
na shora uvedeném obrázku 4.13-GW v základním textu, pasáž
"Zdroje gravitačních vln ve
vesmíru" (jen nárust amplitudy gravitační vlny před
splynutím není tak prudký jak se jeví na obr.4.13-GW - je to
tím, že měřený signál zachycuje jen velmi úzkou
prostorovou a časovou oblast pouhých několika (cca 8) oběhů
těsně před splynutím; na zachycení předchozích
pomalejších oběhů nestačí detekční citlivost). Tento obrázek si zde pro názornost uvedeme znovu :
 |
| Obr.4.13-GW.
Časový průběh amplitudy, frekvence a intenzity
gravitačního záření binárního systému dvou
kompaktních těles m1 a m2
obíhajících kolem společného těžiště. Tělesa, jež začnou v čase t=t0 své obíhání na nějakém velkém poloměru r0, velmi pomalu klesají po spirále a kontinuálně vyzařují gravitační vlny, nejprve slabé (etapa I). I u těsných binárních systémů to bývá proces trvající statisíce i miliony let. S přibližováním stále roste intenzita a frekvence vyzařování. Po dosažení vzdálenosti oběhu několika desítek gravitačních poloměrů dochází k lavinovitému růstu intenzity a frekvence gravitačních vln (etapa II). Po dosažení mezní stabilní orbity tělesa rychle splynou, přičemž se vyšle krátký intenzívní záblesk gravitačních vln (etapa III). V horní části obrázku jsou symbolicky nakresleny zvětšené výřezy z několika posledních oběhů, během nichž dochází k deformacím obou horizontů a nakonec k jejich spojení do deformovaného horizontu výsledné černé díry. Výsledná černá díra m1+m2 je rotující a vyzařováním tlumených gravitačních vln rychle relaxuje na stacionární axiálně symetrickou konfiguraci Kerrovy černé díry (etapa IV). |
Charakter zachyceného signálu tedy odpovídá
gravitačním vlnám vyzařovaným v binárním
systému při těsném přiblížení a spojení
("srážce", fúzi) dvou obíhajících masívních
kompaktních objektů. Lze říci, že tento detekovaný signál
s sebou nesl věrný "podpis" či "otisk"
tohoto svého původu, patrný již při pouhém vizuálním
pohledu: je jím rychlý růst frekvence a amplitudy (po převedení do akustického signálu
připomínající "pípnutí" - chirp) a po dosažení maxima pak náhlý pokles a rychlé
doznívání amplitudy.
Detekované signály byly podrobeny velmi pečlivé
vysoce sofistikované počítačové analýze. S
pomocí výše uvedeného vzorce (2.82e) (v
pasáži "Zdroje gravitačních vln ve
vesmíru") byl na základě frekvence a dynamiky nárustu
frekvence proveden základní odhad celkové hmotnosti zdroje M=m1+m2 >@ 70M¤. Binární systém samozřejmě nemůže být menší,
než odpovídá součtu Schwarzschildových poloměrů obou
binárních složek, což zde dává 2GM/c2
>@ 210 km.
Aby bylo dosaženo orbitální frekvence 75
Hz (polovina změřené frekvence
gravitační vlny max. 150Hz), musely obíhat objekty m1 a m2 velmi blízko sebe (což je
možné jen když jsou velmi kompaktní),
ve vzdálenosti cca 350km od sebe. V závěrečním stádiu
přitom dosahovaly oběžné rychlosti až 2/3 rychlosti světla!
Tyto parametry, odvozené z analýzy signálu,
kladou významná omezení na charakter binárního zdroje.
Dvojice neutronových hvězd, které jsou sice kompaktní, by
neměly potřebnou hmotnost. U dvojice černé díry a
neutronové hvězdy s požadovanou celkovou hmotností by se
neutronová hvězda (@2M¤) s velkou černou dírou (@60M¤)
spojila při podstatně nižší frekvenci. Černé díry jsou
tedy jedinými známými kompaktními objekty,
které při vzájemném oběhu mohou dosáhnout orbitální
frekvenci 75 Hz,
aniž jsou v kontaktu před svým spojením. Po náhlém poklesu
signálu za vrcholem, odpovídajícím spojení obou černých
děr, se objevují menší vlny s rychle klesající amplitudou,
odpovídající tlumeným oscilacím výsledné deformované
černé díry při jejím přechodu do stacionární axiálně
symetrické Kerrovy konfigurace (gravitační vlny odnášejí "vlasy
nesymetrie" - §4.5 "Teorém "černá díra
nemá vlasy"").
Dále následovalo složité počítačové vyhledávání
parametrů zdroje, z něhož detekované gravitační
vlny pocházely. V rozmezí hmotností jednotlivých složek
1-99M¤ a celkové hmotnosti do 99M¤ byly
modelovány binární systémy o různých parametrech oběhu s
použitím post-Newtonovských aproximací, poruchové analýzy
černých děr a dalších metod numerické teorie
relativity. Byl vytvořen celý "atlas" mnoha
tisíc teoretických binárních zdrojů s nejrůznějšími
parametry. Výsledky tohoto modelování byly fitovány
s naměřenými křivkami signálu a odchylky posuzovány
statistickými metodami chí-kvadrátů a Bayesovskou
analýzou koherence. Tato podrobná analýza detekovaných
signálů vedla k následujícím závěrům:
Detekovaný signál GW1504914
pocházel z gravitačních vln vyzařovaných binárním
objektem dvou černých děr v poslední fázi jejich
blízkého vzájemného oběhu a splynutí - fúzi (srážce).
Stanovené parametry zdrojové soustavy:
| Hmotnost černé díry m1 | -436+5 M¤ |
| Hmotnost černé díry m2 | -429+4 M¤ |
| Hmotnost výsledné černé díry M | -462+4 M¤ |
| Rotační moment hybnosti (spin) J/M výsledné černé díry | -0,070,67+0,05 |
| Celková energie vyzářená gravitačními vlnami | -0,53,0+0,5 M¤c2 |
| Špičkový výkon vyzářený gravitačními vlnami při splynutí | -20200+30 M¤c2/s |
| Luminozitní vzdálenost binárního zdroje | -180410+160 Mpc |
Pozoruhodná je celková hodnota energie
odnesená gravitačními vlnami - vyzářily se tři
hmotnosti našeho Slunce! A naprosto kolosální je
okamžitý gravitačně-vlnový výkon -
gravitační "luminozita" zdroje v
závěrečné fázi při splynutí - 200 M¤c2
za sekundu, což je 10-krát více, než je zářivý výkon
všech hvězd ve všech galaxiích celého vesmíru!
Z koincidenční analýzy časové
diference 6,9ms signálu mezi detektory v Hanfordu a
Livingstonu bylo možno triangulačně stanovit jen velmi hrubě přibližnou
polohu (směr, úhel) zdroje na obloze, které
neumožňuje přesné astronomické přiřazení; je to oblast
(pás) o ploše asi 600 čtverečních úhlových stupnů na
jižní obloze, přibližně ve směru k Magellanovým oblakům (zdroj však byl mnohem dále než tyto menší
sousední galaxie). K přesnější
lokalizaci místa na obloze by bylo potřeba více detektorů (zprovoznění detektoru Virgo v Itálii - již se
stalo, viz níže, připravovaná KAGRA v Japonsku a LIGO Indie). Ale ani pak bychom na tomto místě asi nic
neviděli *), neboť černé díry při svém
dlouhodobém blízkém obíhání pravděpodobně ztratily své
akreční disky (byly odvrženy, nebo je
černé díry již předtím "spotřebovaly"), takže jejich splynutí není doprovázeno
mohutnějším elektromagnetickým zábleskem. U splynutí
bílých trpaslíků a neutronových hvězd však lze očekávat
výrazný optický efekt.
*) Objevila se sice zpráva, že ve stejné
době byl zaregistrován slabý záblesk gama paprsků
ze zhruba stejného místa oblohy; vzhledem k neurčitosti polohy
se však asi jednalo o náhodu.
Pokud by se ale při dalších
pozorováních tento doprovodný efekt fotonové emise potvrdil,
bude zajímavé spekulovat, co by mohlo ten X či gama záblesk
vyvolat, když původní akreční disky byly pravděpodobně
při dlouhodobém blízkém obíhání velkými úhlovými
rychlostmi odvrženy (a možná byly již dlouho předtím
"spotřebovány" černými dírami). Mohl tam
snad vzniknout nějaký "společný akreční disk"
kolem těsného binárního systému..?.. Nebo se jedná o
vícenásobný systém dvou černých děr a navíc bílého
trpaslíka či neutronové hvězdy,
které mohly při své destrukci dodávat binárnímu
černoděrovému systému látku (plyn), která při srážce
interagovala za emise tvrdého fotonového záření..?..
Některé možnosti scénářů splynutí binárního systému
kompaktních objektů jsou diskutovány v §4.8, pasáž "Binární gravitačně vázané
systémy černých děr. Srážky a splynutí černých děr".
Úchvatný
příběh ze vzdáleného vesmíru
Můžeme si tedy vyprávět fascinující příběh, který se
odehrál v dávné době ve velmi vzdáleném místě ve
Vesmíru; avšak gnoseologické vyústění měl "tady a
teď" na naší Zemi..!.. Kdesi v nezměrných hlubinách
vesmíru, v obrovské vzdálenosti (cca 1
miliarda světelných let) se ve vesmíru
nachází bezejmenná galaxie, která by se i v největších
astronomických dalekohledech jevila jen jako maličká skvrnka (třebaže obsahuje řádově stovky miliard hvězd). Před asi 10 miliardami let (kdy
ještě neexistovalo Slunce ani naše sluneční soustava) se tam z hustého plyno-prachového oblaku zformovaly
blízko sebe dvě hvězdy 1.generace o hmotnostech cca 30-50
hmotností Slunce, které kolem sebe obíhaly v
těsném dvojhvězdném systému. Tyto hvězdy v
intenzívních termonukleárních reakcích velice rychle
spotřebovaly vodík, hélium, uhlík i těžší prvky (srov. §4.1, část "Termonukleární reakce v nitru hvězd") a za cca 1 milion let
vybuchly jako supernovy a následně zkolabovaly do
černých děr. Vzniklé černé díry kolem sebe (kolem společného těžiště) i
nadále obíhaly ve vzdálenostech několika miliónů kilometrů
- jakožto binární systém kompaktních objektů.
Nejprve měly kolem sebe akreční disky ze zbylých plynů z
oblaku (o nich je v §4.8 část "Akreční
disky kolem černých děr"), avšak postupně je "spotřebovaly" (či příp. v závěrečných fázích odvrhly). Tyto černé díry kolem sebe obíhaly miliardy let,
přičemž vyzařovaly zpočátku poměrně slabé gravitační
vlny. To způsobovalo postupné zmenšování poloměru
oběhu, zpočátku velmi pomalé (jen cca
milimetry za rok). V průběhu času -
miliard let, s postupným přibližováním, však gravitační
vyzařování sílilo a přibližování se tím
zrychlovalo. Když se obě černé díry ve svém obíhání
přiblížily na několik set tisíc kilometrů, intenzita
gravitačních vln začala lavinovitě narůstat,
spolu s růstem frekvence oběhu, což vedlo k
čím dál rychlejšímu spirálovitému poklesu
oběžné dráhy. Tato "spirála smrti"
pak velmi rychle vyústila ve "srážku"
- sloučení, spojení, fúzi - obou černých
děr. V této závěrečné fázi několika posledních oběhů a
sloučení se vyzářilo kolosální množství energie
gravitačních vln. Šťastná náhoda
tomu chtěla, že tyto gravitační vlny dorazily k naší Zemi právě
teď, kdy se nezměrným úsilím mnoha stovek fyziků,
techniků a dělníků podařilo zkonstruovat natolik citlivý
detektor gravitačních vln (LIGO), že byl schopen i na
obrovskou vzdálenost tyto gravitační vlny zaregistrovat..!..
To tedy byl signál GW1504914.
Význam přímé detekce
gravitačních vln
Gnoseologický význam první přímé detekce
gravitačních vln GW1504914 můžeme shrnout do 5 bodů:
¨ 1. Přímý
důkaz "fyzické" existence gravitačních vln
a vlastností jejich interakce s tělesy.
¨ 2. Měření
ukazuje existenci binárních systémů černých děr
o hvězdné hmotnosti, potvrzující správnost představ stelární
relativistické astrofyziky o evoluci masívních hvězd
a jejich binárních systémů (častější
výskyt tak masívních dvojných systémů černých děr se
však neočekával..!..).
¨ 3. Je to
první pozorování "katastrofického procesu"
těsného oběhu a splynutí dvou černých děr
za vyzáření kolosálního záblesku gravitační energie.
¨ 4. Další potvrzení
správnosti obecné teorie relativity, a to za velmi
"exotických" podmínek velmi silné časově
dynamické gravitace a vysoce relativistických
rychlostí (všechny dosavadní testy bylz
založeny na citlivé anylýze subtilních relativistických
efektů ve slabých gravitačních polích).
¨ 5. Tento
úspěch bude pravděpodobně stimulovat zdokonalování
stávajících detektorů a výstavbu nových - vybudování
hustší celosvětové sítě detektorů gravitačních
vln, umožňující přesné
koincidenčně-triangulační stanovení polohy detekovaných
zdrojů na obloze a tím jejich astronomické přiřazení. A
snad i vybudování velkých kosmických detektorů
gravitačních vln s mnohonásobně vyšší citlivostí
a spektrálním rozsahem. Otevře se tím nové "okno do
vesmíru" - gravitačně-vlnová astronomie
(nastíněná výše v pasáži "Astrofyzikální
význam gravitačních vln").
Úskalí a pochybnosti při detekci
gravitačních vln
Při měření tak subtilních efektů (na
hranici detekovatelnosti), jaké poskytují gravitační vlny,
vznikají zákonitě mnohá úskalí a technické obtíže. A i
po jejich překonání zůstávají některé problémy s
interpretací a pochybnosti o validitě získaných výsledků...
Určitou "nevýhodou" první přímé
detekce gravitačních vln GW1504914 byly osamocenost
- skutečnost, že nemohla být ověřena jiným nezávislým
měřením, ani zkorelována s nějakým konkrétním
astronomicky pozorovaným objektem. Staré binární kompaktní
objekty jsou astromicky a opticky "němé".
Při svém dlouhodobém blízkém obíhání již ztratily své
akreční disky (odvrhly je, nebo je již předtím
"spotřebovaly"), takže jejich splynutí není
doprovázeno mohutnějším elektromagnetickým zábleskem
(radiovým, optickým či gama). Jedinou možností, jak odhalit
tyto dramatické astrofyzikální události, je tedy detekce
gravitačních vln. Jejich přímé astronomické přiřazení
zpravidla není možné...
Jedná se o raritní astrofyzikální
událost *), která se skrytě "připravovala"
miliony či miliardy let (podle výše
uvedeného vzorce (2.82c) v části "Vesmírné
zdroje gravitačních vln") při vzájemném obíhání kompaktních hvězd v
binárním systému za slabého gravitačního vyzařování,
které bylo hluboko pod citlivostí našich detektorů. Zachytit
je možné až úplně poslední fázi tohoto
procesu - těsné přiblížení, několik desítek posledních
oběhů a vzájemné spojení obou černých děr, za vyzáření
obrovského "záblesku" gravitačních vln.
*) Raritní událost ?
Ta "raritnost" je z globálního pohledu jen relativní.
Při obrovském množství hvězd v astromicky pozorovaném
vesmíru, odhadovaném na @1022 (naše
galaxie má cca 2.1011hvězd, v zorném poli velkých
astronomických dalekohledů je asi 1011galaxií),
dochází velmi často ke gravitačnímu kolapsu hmotnějších
hvězd, které jsou většinou součástí dvojhvězdného či
vícenásobného systému, za vzniku černých děr (hmotnosti
větších než @5M¤). Dá se očekávat, že již po miliardy let dochází
pravděpodobně několikrát denně k fúzi v binárních
systémech vzájemně obíhajících kompaktních objektů, za
vyzáření mohutných gravitačních vln (vesmírný prostor je
jakoby "zaplaven" slabým pozadím
gravitačně-vlnového "šumu" z těchto zdrojů) - viz
"Gravitačně-vlnový vesmír". Většinou je to ale v příliš velkých
vzdálenostech na to, abychom je dnešními detektory mohli
zachytit. V okruhu 1Megaparseku se odhaduje četnost fúze
binárních kompaktních objektů na cca 2-400/rok. Jen ty
nejsilnější máme šanci detekovat; kdyby se to v brzké době
znova a vícekrát podařilo, umožnilo by to upřesnit toto
zatím velmi neurčité rozmezí incidence fúzí kompaktních
objektů... Již se to podařilo, níže je
uvedeno několik dalších detekcí gravitačních vln.
To, že
systém aLIGO detekoval signifikatní gravitačně-vlnový
signál GW1504914 tak záhy po svém zdokonalení, je jistě na
jedné straně velká náhoda... Původní detektor LIGO
by jej nezachytil buď vůbec, nebo s tak velkým rušivým
pozadím, že detailnější analýza by nebyla možná.
Původní LIGO by snad za několik desítek let signifikantně
zachytil jiný, podstatně silnější, signál z fúze v mnohem
bližším binárním systému kompaktních objektů..?..
Rekonstrukce a zdokonalení systému LIGO podstatně zvýšila
"akční rádius" - pravděpodobnost detekce
gravitačních vln i z mnohem vzdálenějších binárních
zdrojů, příp. z bližších slabších zdrojů. Incidence
záchytu gravitačních vln na aLIGO by se tak mohla značně
zvýšit.
I když je tedy GW1504914 velmi dobře
fyzikálně a technicky podloženo, možnost nějakého neznámého
rušivého vlivu *) zatím nelze s naprostou
jistotou vyloučit..!.. Např. slabé, ale rozsáhlé proměnné
magnetické pole z poruch v magnetosféře Země, vyvolaných
erupcemi na Slunci, by možná též bylo schopné drobně
rozkmitat kovové součásti v ramenech interferometrického
detektoru..?.. Taková pole jsou však v okolí LIGO
monitorována.
*) Jak tomu pravděpodobně bylo v r.1979 u
Weberových válců..?.., viz "Detektory
gravitačních vln".
Astronomové však doufali, že v blízké
budoucnosti v naší nebo v některé blízké galaxii dojde k
podobné bouřlivé astrofyzikální události, jejíž
gravitační vlny budou detekovány nezávisle více
systémy - a snad se ji podaří i astronomicky
přiřadit..?.. To se skutečně podařilo - viz
níže "Další přímé detekce gravitačních vln".
Další přímé detekce gravitačních vln
Následně po signálu GW1504914 byl na
aLIGO dne 12.10.2015 detekován další slabší signál, který
by mohl rovněž snad pocházet z gravitačních vln emitovaných
při těsném oběhu a splynutí dvou kompaktních objektů, byl
nazván LVT151012 (výraznější
signál byl zaznamenán v Livigstonu).
Amplituda však byla více než 10-krát slabší než u
GW1504914 a nepodařilo se jej spolehlivě vyhodnotit na pozadí
šumového signálu.
 |
Počítačové vyhodnocení gravitačně-vlnového signálu LVT151012 |
 |
Počítačové
vyhodnocení gravitačně-vlnového signálu GW151226 PhysRevLett.116.241103 |
Dne 26.12.2015 byl detekován další
gravitačně-vlnový signál GW151226. Tento signál byl
sice výraznější než LVT151012, ale ve srovníní s prvním
signálem GW1504914 rovněž nebyl příliš kvalitní - prostým
okem bychom na grafu změřeného signálu gravitační vlnu
nenašli, "vydolovat" z něj užitečná data se
podařilo až velmi pečlivou počítačovou analýzou.
Třetí přímá detekce gravitačních vln nastala
4.ledna 2017, signál byl nazván GW170104.
Jednalo se opět o typický signál ze splynutí binárního
systému černých děr:
 |
Zdroj: LIGO |
|||||||||||||||||||||
Čtvrtá přímá detekce gravitačních vln ze splynutí černých děr se podařila 14.srpna 2017, signál byl nazván GW170814. Je pozoruhodná tím, že poprve byl detekován signál gravitační vlny současně třemi přístroji: napřed LIGO Livingstone, s odstupem 8 milisekund LIGO Hanford a nakonec Virgo v Itálii po 14 ms. (od Livingstone). Umožňuje to přesněji lokalizovat místo na obloze, odkud gravitační vlny přicházejí. U GW170814 tato stereotaktická analýza ukázala oblast oblohy o velikosti pouhých 60 stupňů2 v oblasti souhvězdí Eridanus na jižní obloze. Lokalizace je zde asi 10-krát lepší než jen ze dvou detektorů LIGO; ani zde však žádný astronomický (optický, rádiový) doprovodný efekt nebyl pozorován, což se u fúze černých děr ani nedá čekat. Různé orientace ramen těchto tří detektorů dále umožňují analyzovat polarizaci gravitační vlny (měřená data odpovídala shora uvedené polarizaci střídající se ve dvou kolmých směrech podle obr.2.11).
| LIGO Hanford | LIGO Livingstone | Virgo (Itálie) | ||||||||||||||||||||||
 |
Zdroj: LIGO |
|||||||||||||||||||||||
GW170817
- Sloučení neutronových hvězd
O tři dny později, 17.srpna 2017, byl detektory LIGO a Virgo
zachycen další gravitačně-vlnový signál GW170817,
který byl interpretován jako poslední fáze oběhu a sloučení
dvou neutronových hvězd. K tomuto pozoruhodnému
vývodu vedly dvě pozorované skutečnosti :
1. Analýza průběhu
gravitačně-vlnového signálu.
Signál gravitační vlny byl pozorovatelný asi 100 sekund, s
nízkou amplitudou začínal frekvencí 24Hz a během asi 3000
cyklů se amplituda a frekvence zvyšovala na cca 400Hz; pak
signál ustal. Tento průběh odpovídal kolizi a sloučení obou
kompaktních objektů o hmotnosti menší a
průměru větším než černé díry. Podrobnou analýzou
průběhu tohoto gravitačně-vlnového signálu byly stanoveny
hmotnosti obíhajících a splývajících kompaktních těles v
rozmezí cca 1,2-1,6M¤ a celková hmotnost binárního systému 2,75M¤. To
odpovídá hmotnostem astronomicky pozorovaných neutronových
hvězd.
Signál přišel nejprve do detektoru Virgo v Itálii, pak o
22ms. později do detektoru LIGO-Livingstone a za další 3ms. do
detektoru LIGO-Hanford. Tyto tři detekce umožnily
triangulačně lokalizovat zdroj na plochu 30 stupňů2 na jižní obloze v
oblasti souhvězdí Hydra.
2. Emise elektromagnetického záření.
Poprve při zachycení gravitačních vln zde byl astronomicky
registrován i optický-elektromagnetický
protějšek ve formě záblesku gama-záření GRB170817A
(1,7s. po sloučení) a po
asi 10 hodinách i v optickém a infračerveném oboru - objekt SSS17a
v galaxii NGC4993, v oblasti lokalizované pomocí detekce
gravitačnívh vln. Po několika dnech se objekt podařilo
pozorovat rentgenovými kamerami Chandra, pak i v oblasti
rádiových vln na VLA. Spektrální maximum elektromagnetického
záření se z gama, rentgenové a UV oblasti rychle přesouvalo
do optické a infračervené oblasti. Tato pozorování v
elektromagnetické oblasti odpovídají situaci při splynutí
dvou neutronových hvězd, kdy vyvržený
materiál, bohatý na neutrony, explozivně "nukleonizuje"
a přeměňuje se radioaktivně na jádra těžkých prvků a
intenzívně září (§4.8, pasáž "Srážky a splynutí
neutronových hvězd"), což se observačně projevuje podobně jako výbuch
novy *).
*) Taková astronomicky
pozorovaná událost se někdy nazývá "kilonova"
- může být až 1000-krát silnější než běžná nova,
zvláště pokud se pozoruje ze směru rotační osy binárního
systému. Toto však nebyl tento případ, optický záblesk byl
poměrně slabý ve vztahu k relativní blízkosti zdroje. Lze to
vysvětlit tím, že rotační osa byla od pozorovacího směru
nakloněna nejméně o 30°.
 |
Zdroj: LIGO PhysRevLett.119.161101 (2017) |
Vlevo: Časově-frekvenční
diagram detekovaných signálů GW170817 z jednotlivých
detektorů. Bohužel nebyl zatím publikován graf primárních detekovaných gravitačně-vlnových signálů (snad z důvodu rušivé krátkodobé elektronické fluktuace, ke které došlo na LIGO-Livingstone asi 1sekundu před maximem...). |
||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Dole: Fúze
neutronových hvězd. a) Dvě neutronové hvězdy obíhající v binárním systému ve velké vzdálenosti velmi pomalu klesají po spirále a kontinuálně vyzařují gravitační vlny, nejprve slabé. b) S přibližováním stále roste intenzita a frekvence gravitačního vyzařování. c) Při těsném přiblížení dochází k deformaci a nakonec ke srážce a splynutí obou neutronových hvězd. d) Při prudké rotaci během fúze může být vyvrženo velké množství neutronové látky, které okamžitě nukleonizuje za vzniku převážně težkých jader, s následným radioaktivním rozpadem. e) Výsleným objektem po odeznění nestabilit je buď neutronová hvězda nebo černá díra (podle zbylé hmotnosti). Tento výsledný objekt bude mít kolem sebe jen málo mohutný akreční disk (neboť většina látky byla odmrštěna pryč obrovskou energií uvolněnou při explozivní nukleonizaci). (zdroj: AstroNuklFyzika, §4.8, pasáž "Srážky a splynutí neutronových hvězd") |
||||||||||||||||||||||||||
Neutronové hvězdy při svém oběhu a
sloučení vyzařují slabší gravitační vlny
než černé díry. Ve srovnání s dřívějšími detekcemi
gravitačních vln byla však událost GW170817 mnohem blíž
- ve vzdálenosti 130 milionů místo několika miliard
světelných let, takže ji bylo možno detekovat. Výsledným
produktem pozorované fúze neutronových hvězd je
pravděpodobně černá díra, ale mohla by to být i větší
neutronová hvězda..?..
Tento případ detekce sloučení neutronových
hvězd je předzvěstí multimodalitní astronomie
- zde dvoumodalitní [gravitačně-vlnové +
elektromagnetické]. Bude to též nový způsob, jak
zkoumat vztahy mezi hmotou, gravitací a elektromagnetismem.
Perspektivou je i třetí modalita - detekce neutrin,
pokud by ke sloučení neutronových hvězd došlo v bližší
vzdálenosti (srov. §1.2, část "Detece neutrin";
perspektivní je zde hlavně antarktický ledovcový detekční
systém IceCube, viz pasáž "Detekce neutrin v ledovcích").
GW170817 má důležitý astrofyzikální
význam. Je to první přímé pozorování
fúze neutronových hvězd, při níž je vyvrženo
velké množství neutronového materiálu s následnou
explolzivní nukleonizací za vzniku velkého množství těžkých
prvků - viz výše uvedený obrázek z §4.8, pasáže
"Srážky a splynutí
neutronových hvězd".
Tyto těžké prvky (včetně zlata,
platiny, uranu, ...) obohatily vesmírný
prostor. Další taková pozorování pomohou upřesnit odhady, jak
časté jsou tyto události ve vesmíru a v jaké míře
se fúze neutronových hvězd podílejí na kosmické nukleogenezi
těžších prvků; spolu se stelární syntézou
a výbuchy supernov (srov. §4.1,
4ást "Evoluce hvězd" a §4.2, část "Astrofyzikální význam supernov").
Pozn.: Nadhodnocený
podíl nukleogeneze z fúze neutronových hvězd
Když se podařila první multimodalitní detekce gravitačních
vln ze sloučení neutronových hvězd, v prvním entuziasmu se
začaly vyskytovat názory, že většina (nebo
dokonce všechny) těžkých prvků ve
vesmíru pochází z fúzí neutronových hvězd.
Střízlivější analýzy však ukázaly že tyto odhady jsou
silně nadhodnocené. Fúze neutronových hvězd neprobíhá
tak často, aby stačila vysvětlit pozorované množství
těžkých prvků ve vesmíru. Je sice důležitou součástí,
avšak hlavním zdrojem těžkých prvků je pravděpodobně
přece jen hvězdná nukleosyntéza a výbuchy supernov...
Gravitační
"standardní siréna"
Detekce gravitačních vln z fúze neutronových hvězd, spolu se
současnou detekcí elektromagnetického záření z jejich
optickývh protějšků, má i astrofyzikálně-kosmologický
význam pro nezávislé stanovení vzdálenosti příslušných
objektů. Toto meření totiž umožňuje kombinovat stanovení
vzdálenosti ke zdroji odvozené z analýzy signálu gravitační
vlny, s rychlostí vzdalování odvozenou z měření rudého
posuvu pomocí spektrometrie elektromagnetického signálu. Tento
přístup nevyžaduje použití "žebříku"
kosmických vzdáleností (diskutovaného v §4.1, pasáži
"Stanovení
vzdáleností vesmírných objektů - základní podmínka
astrofyziky"). Analýza
gravitačních + elektromagnetických vln tak může být
použita k přímému stanovení vztahu vzdálenosti <-->
svítivosti v kosmologických měřítcích, bez použití
mezilehlých měření vzdáleností, s někdy problematickou
návazností. Takto nezávisle stanovená hodnota Hubbleovy
konstanty je zde 70.0+12.-8 km/s/Mpc, v dobrém souladu se stávajícími
měřeními jinými metodami. Neurčitost cca 10% je zde
způsobena především nejistotou orientace osy rotace
binárního systému vzhledem k Zemi. Detekce gravitačních vln
se proto někdy metaforicky označuje jako "standardní
siréna" - gravitačně-vlnový analog
elektromagnetické "standardní svíčky"
(cefeidy, supernovy Ia) používané pro stanovení velkých
kosmologických vzdáleností...
GW190425
- další sloučení neutronových hvězd ?
Další detekce gravitačních vln ze
sloučení neutronových hvězd nastala 25.dubna 2019. Bohužel
byly plnohodnotně snímány jen detektorem LIGO Livingstone (druhý detektor v Handfordu byl momentálně odstaven,
v detektoru Virgo byl nízký poměr signílu k šumu). Nemohla být proto provedena lokalizace zdroje na
obloze. Analýza signálu ukázala, že se patrně jednalo o
srážku dvou atypicky hmotných neutronových hvězd 1,6-2 M¤ a
1,4-1,7 M¤, celková hmotnost 3,4 M¤ (uvažuje se též, že by to mohly být i malé černé
díry..?..), luminositní vzdálenost 160
Mpc. Nebyla nalezena žádná emise elektromagnetického
záření, která by korelovala s detekcí gravitačních vln.
Mohlo by se tedy jednat o situaci zmíněnou v §4.8 (pasíž "Srážky a splynutí neutronových hvězd"), kdy při
srážřce hmotnějších neutronových hvězd se výsledný
objekt může téměř okamžitě zhroutit do černé díry,
která rychle pozře téměř všechnu hmotu obou neutronových
hvězd. Z místa srážky pak již neunikne žádné záření - kilonova
není pozorována...
GW190521
Další zajímavá událost detekce gravitačních vln byla
zaznamenána 21.května 2019 ze směru na Vlasy Bereniky.
Podrobná analýza výsleků ukázala, že se jednalo o
sloučení dvou zatím největších černých děr o hmotnostech
85 a 66 M¤, které se odehrálo ve vzdálenosti 17 miliard
světelných let :
 |
Zdroj: LIGO |
|||||||||||||||||||||||
Z astrofyzikálního hlediska je tato událost
zajímavá poměrně velkými hmotnostmi zúčastněných
černých děr a výsledné černé díry. Černé díry
hmotností větších než cca 60-70 M¤ by podle
současných astronomických poznatků měly být vzácné, je
pozována jakási "mezera" v hmotnostech mezi 60 a 100
000 M¤. Jaderně-astrofyzikální analýzy
ukazují, že masivní hvězdy se zbylou hmotností větší než
cca 65 M¤ ve finálním stádiu evoluce při kontrakci
pravděpodobně nezkolabují do černé díry, ale ještě před
dosažením horizontu podlehnou tzv. elektron-pozitronové
párové nestabilitě (viz §4.1, pasáž "Elektron-pozitronová párová nestabilita"). Při tomto procesu je hvězda rozmetána při
výbuchu supernovy a nezanechá po sobě černou díru. Pokud k
tomu skutečně dochází, černé díry středních hmotností
by se měly vyskytovat jen zřídka. Měření GW190521 ukazuje,
že závěrečná stádia masivních hvězd snad mohou produkovat
černé díry i vyšších hmotností a ještě hmotnější
černé díry vznikají při sloučení mezi dvojicemi
menších černých děr. Tento proces vícenásobného
sloučení pak může hierarchicky pokračovat...
Další zajímavostí zde je
zachycení záblesku světla (na Palomarské
observatoři), který by mohl souviset s touto událostí.
Jelikož se při vlastním sloučení černých děr žádné
světlo nevyzařuje (bylo dskutováno výše), byla vyslovena
hypotéza, že výsledná černá díra se mohla dostat na dráhu
vedoucí přes akreční disk blízké supermasivní černé
díry, v jehož materiálu by tím mohl vzniknout světelný
efekt..?..
Gravitačně-vlnová
astronomie
Stále rostoucí počet dalších zachycených signálů -
navzdory jejich poněkud slabímu odstupu signál/šum -
ukazují, že první úspěšná detekce gravitační vlny
GW151226 nebyla náhoda, nýbrž že se slibně začíná
rozvíjet možnost "gravitačně-vlnové astronomie"..!..
A též multimodalitní - "více-poslové"
- astronomie.
Zatím sice stávající pozemní detektory
gravitačních vln jsou schopny detekovat pouze mohutné jednorázové
gravitační vlny z katastrofických událostí jako jsou
srážky - splynutí - černých děr nebo neutronových hvězd.
A to až z posledních fází těchto splynutí,
trvajících kolem jedné minuty, s relativně vysokými
frekvencemi. Budoucí detekční systémy (jako je
plánovaná LISA), kromě vyšší citlivosti, budou schopny
detekovat i nízkofrekvenční gravitační vlny - z
mnoha stovek i tisíců těsných binárních hvězdných
systémů.
| Gravitace, černé díry a fyzika prostoročasu : | ||
| Gravitace ve fyzice | Obecná teorie relativity | Geometrie a topologie |
| Černé díry | Relativistická kosmologie | Unitární teorie pole |
| Antropický princip aneb kosmický Bůh | ||
| Jaderná fyzika a fyzika ionizujícího záření | ||
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | ||