| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | Gravitace, černé díry a fyzika |
Kapitola 4
ČERNÉ DÍRY
4.1. Úloha gravitace při vzniku a evoluci
hvězd
4.2. Konečné fáze hvězdné
evoluce. Gravitační kolaps
4.3. Schwarzschildovy statické
černé díry
4.4. Rotující a elektricky
nabité Kerrovy-Newmanovy černé díry
4.5. Teorém "černá díra nemá vlasy"
4.6. Zákony dynamiky černých
děr
4.7. Kvantové vyzařování a
termodynamika černých děr
4.8. Astrofyzikální význam
černých děr
4.9. Úplný gravitační kolaps -
největší katastrofa v přírodě
4.5. Teorém "černá díra nemá vlasy"
V předchozích
kapitolách jsme si ukázali, jak gravitačním kolapsem
dostatečně hmotných hvězd vznikají černé
díry.
Avšak jaký konkrétní "tvar" mají černé díry?
Kolapsem kulové nerotující hvězdy vznikne kulová (sféricky
symetrická) Schwarzschildova černá díra, kolapsem rotující
hvězdy vzniká axiálně symetrická Kerrova či
Kerrova-Newmanova černá díra. Toto všechno jsou však idealizované případy. Vzniká otázka, jaká černá
díra vznikne kolapsem reálné
hvězdy? Na
první pohled by se mohlo zdát, že kolapsem "deformované" hvězdy, mající třebas
"hrbol" na povrchu (protuberanci,
stopu po dopadu planety či akreci plynů), by mohla vzniknout "deformovaná" černá
díra s
"hrbolem" na svém horizontu. Jak uvidíme níže,
podle zákonitostí obecné teorie relativity se toto stát nemůže: buď nevznikne žádná černá díra,
nebo vznikne přesně symetrická
černá díra.
Zjednodušeně řečeno, černá díra
nevykazuje žádné stopy toho, zda vznikla z hvězdy kulatého
nebo deformovaného nepravidelného tvaru.
Jediné, čím se černá díra navenek projevuje - jediné, co pro vnější svět ze zkolabovaného objektu zbylo - je vnější pole. Ukazuje se, že ve srovnání s objektem před kolapsem má černá díra velmi jednoduchou strukturu :
| Teorém 4.1 ("černá díra nemá vlasy") |
| Po "dokončení" gravitačního kolapsu (tj. po utvoření horizontu a po vymizení všech gravitačních a elektromagnetických vln) je vnější elektromagnetické a gravitační pole stacionární černé díry ve vakuu zcela určeno jen třemi nezávislými parametry : celkovou hmotností M, elektrickým nábojem Q a vlastním rotačním momentem hybnosti J, bez ohledu na to, z čeho a jakým způsobem černá díra vznikla. |
Metaforicky se to
vyjadřuje větou "černá
díra nemá vlasy", tj. nemá žádné další
nezávislé charakteristiky kromě hmotnosti, náboje a
rotačního momentu hybnosti *). Tvrzení "černá díra
nemá vlasy" odůvodníme nejprve fyzikálními argumenty,
potom zmíníme některé geometricko-topologické teorémy o
jednoznačnosti, na nichž je založen obecný
matematický důkaz, a nakonec si ukážeme dalekosáhlé
fyzikální důsledky tohoto teorému.
*) Metaforické znění
"černá díra nemá vlasy" pochází od J.A.Wheelera.
"Vlasy" jsou zde míněny nějaké příznaky, které
vystupují z horizontu a ukazují individuální charakteristiky
hmoty, ze které černá díra vznikla. Přesněji bychom měli
říkat "černá díra nemá téměř žádné vlasy", pouze hmotnost,
moment hybnosti a elektrický náboj.
Teorém
o "bezvlasovosti" byl po několik let vlastně
hypothézou, pro kterou sice svědčila řada fyzikálních
argumentů a poznatky Zeldoviče, Novikova, Ginzburga, Price,
Israela a Cartera, avšak obecný důkaz chyběl. Definitivní
dokončení důkazu teorému 4.1 bylo provedeno v pracech
B.Cartera [44], W.Israela [142], S.Hawkinga [121] a D.Robinsona
[219].
Zachování
interakce s hmotou pohlcenou černou dírou
Hmotnost, náboj a moment
hybnosti
jsou jediné zachovávající se veličiny (neměnící se s
časem v průběhu kolapsu), které jsou jakožto zdroje spojeny s poli sil dlouhého dosahu (hmotnost a
moment hybnosti s gravitačním polem, elektrický náboj s
elektromagnetickým polem), na nichž zanechávají jednoznačný
"odraz" či "stopu". Pomocí těchto
jednoznačných odrazů (zachovávajících se integrálních toků
přes uzavřené plochy) tato pole potom nadále udržují po utvoření horizontu hodnoty těchto
tří veličin, i když jejich vlastní zdroje zmizely pod
horizontem nebo byly dokonce již možná zničeny v singularitě
(z hlediska jejich vlastního času). Utvoření horizontu je zde tedy rozhodujícím
momentem: ať se pak pod horizontem již cokoliv stane se zdroji,
nijak se to nemůže projevit na vnějším poli, které proto
zachovává svoji hodnotu odpovídající zdrojům těsně před překročením horizontu. Je tím rovněž ospravedlněno
použití Gaussovy věty pro integrální toky vnějších
polí uzavřenými plochami, protože se nemusíme starat o
možné nepřípustné topologické chování (např.
vícenásobná souvislost nebo singularita) prostoročasu uvnitř
horizontu. Proto můžeme např. integrál
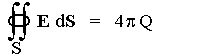
intenzity elektrického pole E přes uzavřenou plochu S,
obklopující v dostatečné vzdálenosti černou díru,
považovat za její elektrický náboj Q, i když tento
skutečný náboj (jeho nositelé) nenávratně zmizel pod
horizontem, byl pohlcen singularitou, popř. se vynořil v jiném
vesmíru nebo jiném místě téhož vesmíru (to všechno pro vnějšího pozorovatele ovšem nemá
smysl, protože by se to odehrávalo v absolutní budoucnosti). Podobné je to s gravitačním
polem a s jejím zdrojem, hmotností M.
Máme-li
tedy dvě vzdálená tělesa nebo částice A a B,
které jsou ve vzájemné gravitační nebo elektromagnetické
interakci, po pohlcení jednoho z nich (třebas A) černou
dírou tato interakce nezaniká. Po vyzáření
dynamických složek vznikajících při kolapsu či akreci i
nadále zůstává interakce dalekého dosahu s
partnerem B. Nebude to však již interakce s původním
individuálním tělesem nebo částicí A, ale částice B
bude interagovat s celkovým polem černé díry,
jejíž součástí se pohlcený objekt A stal. A toto
pole je určeno celkovou hmotností M, rotačním momentem
hybnosti J a elektrickým nábojem Q. Lze říci, že částice A,
i se svým polem, se jakoby "rozpustí" v celkovém
poli černé díry.
Tento mechanismus též poskytuje odpověď na
často kladenou paradoxní otázku: "Jak se
může gravitační síla dostat ven z pod horizontu černé
díry a působit na vnější tělesa?- když horizont přece ven
nic nepustí!". Gravitační pole se však
nemusí "prodírat" zevnitř přes horizont. Ono v tom
daném vnějším místě již je a bylo tam
před kolapsem hvězdy nebo pádem tělesa do černé díry. A
při kolapsu nebo pohlcení tělesa toto pole nezaniká, ale udržuje
si tu hodnotu, kterou mělo těsně před aktem kolapsu
či pohlcení.
Pozn.: Výše
uvedená odpověď je z hlediska klasické teorie pole.
V kvantové teorii pole (§1.1 "Atomy a
atomová jádra", pasáž "Kvantová teorie pole" v monografii "Jaderná
fyzika a fyzika ionizujícího záření")
se interakce modelově vysvětluje pomocí intermediálních
částic, které si interagující tělesa (částice)
neustále vyměňují. Ty by horizont černé díry neměl
"pustit". Odpověď můžeme nahlížet ze
dvou aspektů:
1. Je to jen model, který je
užitečný pro dynamické děje mezi mikročásticemi (je
diskutováno v pasáži "Virtuální či skutečné částice?" zmíněného odkazu); u statického
silového-polního působení mezi makroskopickými tělesy je
patrně irelevantní.
2. Intermediální částice jsou virtuální,
takže pro ně "zákaz" průchodu horizontem v principu
neplatí. Jak bude ukázáno v §4.7 "Kvantové
vyzařování a termodynamika černých děr", zákonitosti kvantové fyziky umožňují
poblíž horizontu generování (Hawkingova) záření efekty
kvantového tunelového jevu virtuálních
párů částic.
Multipólové
vyzařování
Způsob, jakým černé díře v průběhu kolapsu
"vypadávají vlasy", se dá nejlépe pochopit rozborem
gravitačního kolapsu, který se od symetrického případu
liší jen malou odchylkou (perturbací). Vnější pole lze pak
rozložit na složky související s multipólovými
momenty. V
průběhu kolapsu se budou jednotlivé multipólové momenty s
časem měnit, což bude doprovázeno
vyzařováním vln. Právě vyzařování
vln je tím
mechanismem, který mění hodnoty některých fyzikálních veličin v
průběhu kolapsu. Příp. nesymetrie elektrického náboje
způsobují při kolapsu vyzařování elektromagnetických
vln.
Důležitější je však vyzařování gravitačních
vln (§2.7 "Gravitační vlny", část "Zdroje gravitačních vln ve
vesmíru"), které odnášejí veškeré
počáteční nesymetrie v
rozložení hmotnosti ve zkolabovaném objektu.
Podle teorie záření [166] mohou
vyzařovat jen ty multipólové momenty, jejichž
"multipolarita" je větší nebo rovna spinu příslušného pole **), zatímco
složky s multipolaritou menší se zachovávají a k
vyzařování nepřispívají.
**) Spin pole zde stačí
uvažovat klasicky jako míru symetrie v rovinné vlně
příslušného pole: dané pole má spin s, jestliže jeho rovinná vlna je
invariantní vůči pootočení o úhel 2p/s kolem
směru šíření.
Pokud se multipólové momenty, kterým je
to "dovoleno" úplně vyzáří, bude výsledné
limitní pole zcela charakterizováno jen zbylými
zachovávajícími se multipólovými momenty, jejichž
multipolarita je menší než spin pole (a které se tedy nemohou
vyzářit). Pro elektromagnetické pole se
spinem s=1 se vyzáří ve formě elektromagnetických vln
všechny multipóly rozložení náboje, počínaje dipólovým
momentem a zachovává se pouze monopólová část - celkový elektrický náboj. Pro gravitační pole se spinem s=2 se
vyzáří ve formě gravitačních vln všechny multipóly
rozložení hmotnosti, počínaje kvadrupólovým momentem;
zachovává se jen monopólová část - celková hmotnost, a dipólová část související s
vlastním rotačním momentem
hybnosti v
těžišťové soustavě. Pro (modelové) skalární pole se
spinem s=0 by se nezachovávala žádná část,
vše se vyzáří.
Podrobný rozbor slabě perturbovaného
gravitačního kolapsu ukazuje, že před utvořením horizontu
se všechny vyšší multipólové momenty, kterým je to
dovoleno, skutečně vyzáří. Price [212], ukázal, že pro
příspěvky takových polí neexistují řešení s fyzikálně
přípustnými asymptotickými vlastnostmi (buď
jsou nekonečná na horizontu nebo divergují pro nekonečné
vzdálenosti).
"Kvantové
vlasy" ?
Z kvantové fyziky vyplývají další zachovávající se
veličiny, spojené s kvantovými poli. Mohly by po zformování
černé díry přetrvávat v podobě jakýchsi "kvantových
vlasů". Jedná se však o kvantová pole krátkého
dosahu; "kvantové vlasy" by mohly ovlivnit
vlastnosti vypařující se kvantové černé mikrodíry
(takové mikrodíry jsou diskutovány v
§4.7 "Kvantové vyzařování a termodynamika
černých děr"). Pro makroskopické černé díry však případné
kvantové mikrovlasy nemají žádné důsledky, neboť kvantová
fyzika se neuplatňuje v makroskopických měřítcích.
Rozšíření analýzy na případ silných interakcí [245] a
slabých interakcí [116] ukazuje, že makroskopická černá
díra nemůže vykazovat síly slabých ani
silných interakcí od leptonů a baryonů pohlcených v díře
[10],[244].
Teorémy o jednoznačnosti
Existují tedy
pádné fyzikální argumenty ve prospěch teorému "černá
díra nemá vlasy". Protože však detailní rozbor
průběhu gravitačního kolapsu je možný jen ve značně
zjednodušených případech, nedokazuje se tím platnost
teorému 4.1 pro obecnou černou díru. Obecný matematický
důkaz teorému "černá díra nemá vlasy" je založen
na globálních geometricko-topologických metodách studia
struktury prostoročasu, pomocí nichž lze získat některé
informace o globální struktuře prostoročasu na základě
určitých obecných předpokladů bez nutnosti detailního
řešení gravitačních rovnic. Pomocí těchto metod byly
odvozeny některé důležité věty
o jednoznačnosti řešení v prázdném stacionárním
asymptoticky prognostickém prostoročase.
Za
nejjednodušší "prototyp" takových teorémů o
unitaritě lze považovat již Schwarzschildovu-Birkhoffovu
větu 3.3 (odvozenou v §3.4
"Schwarzschildova geometrie"), podle níž vakuový
asymptoticky rovinný prostoročas se sférickou symetrií má
Schwarzschildovu geometrii a je tedy popsán jen jediným
parametrem - celkovou hmotností M bez ohledu na to, jak
je např. hmota radiálně rozložena (pokud je zachována
sférická symetrie). Příslušné obecnější věty o
jednoznačnosti jsou tyto :
| Teorém 4.2 (Israel [141]) : |
| Každý prázdný (Tik=0) statický prostoročas, ve kterém je regulární horizont událostí s topologií koule, má Schwarzschildovu geometrii (a je tedy centrálně symetrický a charakterizovaný jen parametrem celkové hmotnosti M). |
| Teorém 4.3 (Israel [142]) : |
| Každý statický prostoročas, který obsahuje pouze statické elektromagnetické pole a který má regulární horizont událostí s topologií koule, má Reissnerovu-Nordströmovu geometrii (je tedy centrálně symetrický a charakterizovaný celkovou hmotností M a elektrickým nábojem Q). |
| Teorém 4.4 (Hawking [120],[121]) : |
| Stacionární černá díra musí být buďto axiálně symetrická nebo statická (přičemž horizont událostí má topologii koule). |
Kdyby totiž černá díra nebyla axiálně symetrická, bude při rotaci vyzařovat gravitační vlny (časově proměnný kvadrupólový moment) a nebude tedy stacionární; jen axiálně symetrická černá díra může rotovat a být přitom stacionární.
Pro ilustraci teorému 4.4 si představme myšlený pokus podle obr.4.20. Rotující axiálně symetrickou černou díru obklopíme v dostatečné velké vzdálenosti od horizontu hmotou s pevným axiálně nesymetrickýrn rozložením - např. kolem ní uděláme tuhý hmotný rám (třeba z železných tyčí), obr.4.20a. Gravitační působení rámu způsobí, že metrika již není axiálně symetrická. Není to však narušení věty 4.4, protože pokud černá díra rotuje, nebude již situace podle obr.4.20a stacionární. Vlivem strhávání momentem hybnosti totiž rám začne rotovat ve stejném směru jako černá díra. Jelikož je rám axiálně nesymetrický, bude při této rotaci vyzařovat gravitační vlny a ztrácet tak kinetickou energii rotace. Nakonec se rotace jak černé díry, tak rámu radiačně zabrzdí; černá díra se stane nerotující (statickou) v souhlase s Hawkingovou větou 4.4. Poněkud složitější situace by byla v případě, že hmotný rám by nebyl volný, ale upevněný (nějakými negravitačními silami) tak, že nemůže začít rotovat a vyzařovat gravitační vlny - obr.4.20b. I v tomto případě se dá věta 4.4 obhájit. Gravitační působenení rámu deformuje horizont. Horizont však rotuje a deformace horizontu při svém pohybu bude vyzařovat gravitační vlny (dovnitř díry), čímž se bude zpomalovat jeho rotace. Nakonec se opět rotace černé díry zabrzdí.

Obr.4.20. Myšlený pokus k fyzikální ilustraci teorému 4.4.
a) Kolem rotující
černé díry je volně umístěn tuhý hmotný rám. Vlivem
strhávání rotací černé díry se rám roztočí, bude
vyzařovat gravitační vlny a celá soustava se bude radiačně
brzdit. Toto uspořádání je zároveň jednou z možností, jak
z rotující černé díry získávat energii (viz §4.4).
b) Pevný hmotný rám fixovaný kolem černé
díry vnějšími silami.
| Teorém 4.5 (Carter [44]) : |
| Pro prázdný (Tik=0) stacionární axiálně symetrický prostoročas, ve kterém je regulární horizont událostí s topologií koule, existují dvě různé skupiny řešení, z nichž každé závisí jen na dvou parametrech; za tyto parametry lze vzít celkovou hmotnost M a rotační moment hybnosti J. |
Jednou takovou skupinou řešení je Kerrova geometrie při a2 Ł M2 ; jak ukázal Robinson, žádná jiná odlišná skupina řešení již neexistuje. Carterova věta 4.5 byla dále v pracech Robinsona [219], Boseho a Wanga [24] zobecněna na případ přítomnosti elektromagnetického pole (tj. pro elektricky nabitou černou díru), přičemž jako obecné řešení se získá Kerrova-Newmanova geometrie prostoročasu (analyzovaná v §3.6 "Kerrova a Kerrova-Newmanova geometrie").
Spojením těchto
(částečně se prolínajících) teorémů 4.2 až 4.5
přicházíme k závěru, že (pokud lze zanedbat gravitační
pole hmoty nacházející se vně horizontu) všechny
stacionární černé díry musejí být axiálně symetrické a
geometrie prostoročasu je obecně vyjádřena Kerrovým-Newmanovým řešením, které je popsáno jen třemi volnými parametry: hmotností
M,
rotačním momentem hybnosti J a elektrickým nábojem Q. A to je teorém 4.1 "černá díra nemá vlasy".
Ukazuje se tedy, že kromě hmotnosti,
náboje a momentu hybnosti se všechny ostatní charakteristiky
(které by nebyly z těchto tří parametrů odvoditelné) - jako
jsou nehomogenity a nesymetrie rozložení hmoty a náboje
tělesa před kolapsem, magnetická pole, proudy, tlaky,
turbulence a pod. - zcela "vyzáří" ve formě gravitačních a
elektromagnetických vln z nichž část se rozšíří do
prostoru, část je pohlcena černou dírou. Toto záření
odnese "vlasy" černé díry. Nehomogenity, stejně
jako žádné další jevy vznikající již pod horizontem,
nemají na vnější pole vliv, protože informace o nich (ve
formě příslušných rozruchů a vln) geometrie prostoročasu
nepustí k vnějšímu pozorovateli.
Uniformita černých děr
Černé díry různého původu jsou od sebe nerozlišitelné, mají-li stejnou hmotnost, náboj a
rotační moment hybnosti. Není poznat, zda černá díra
vznikla z vodíku nebo z železa, z obyčejné hmoty nebo z
antihmoty, z protonů, elektronů, neutronů a v jakém
zastoupení *). Černé díry jsou tedy, ve srovnání s velkou
rozmanitostí různých druhů a typů hvězd, velmi uniformní. Všechny černé díry jsou si podobné
jako vejce vejci: skoro všechny jsou Kerrovské různě
rychle rotující (eliptické), občas se mezi nimi může
objevit díra Schwarzschildovská (kulová), popř. elektricky
nabitá. Jiné kvalitativní rozdíly mezi černými děrami nejsou, jsou jen rozdíly v jejich
"velikosti". Vznikem černé díry se ztrácejí téměř všechny informace o tom, z čeho
tato černá díra vznikla; zjistitelná je pouze celková
hmotnost, moment hybnosti a elektrický náboj.
*) V principu je možno
např. dosáhnout takového zkoncentrování světla, že část
jeho elektromagnetické energie podlehne gravitačnímu kolapsu a
vytvoří černou díru. Nebo podobně může gravitačnímu
kolapsu podlehnout i část (nelokální) gravitační energie
při dostatečném zkoncentrování gravitačních vln (viz §2.7 "Gravitační vlny" a B.3 "Wheelerova geometrodynamika.
Gravitace a topologie."). Taková "čistě
elektromagnetická" (popř. "čistě
gravitační") černá díra bude potom nerozlišitelná od
černé díry vzniklé kolapsem (elektricky neutrální) hvězdy
s příslušnou hmotností a momentem hybnosti. Podmínky pro tak
mohutné zkoncentrování gravitačních
nebo elektromagnetických vln by však asi mohly vzniknout jen v
počátečních fázích vývoje vesmíru po hypotetickém
"velkém třesku", nebo snad při gravitačním kolapsu
celých galaxií...
Černé
díry jsou jedinými makroskopickými objekty, které jsou velmi
jednoduché. Po dokončení gravitačního kolapsu a
odlétnutí záření, které odnáší pryč jejich
"vlasy", vznikne v konečném stavu velmi jednoduchý
objekt, který lze zcela přesně a úplně
popsat jen třemi parametry a několika málo matematickými
vzorci - bez jakékoli idealizace či omezení
zjednodušujících modelů! S tím se nikde jinde v makrosvětě
nesetkáváme *). Analogii to má jedině v mikrosvětě
"elementárních" částic, které mohou být též
úplně popsány několika málo svými kvantovými čísly
(§1.5 "Elementární částice a urychlovače" v knize "Jaderná fyzika a fyzika
ionizujícího záření").
*) Je podivuhodné a paradoxní,
že tak tajemný a exotický objekt jakou je černá díra, je z
fyzikálně-teoretického hlediska nejlépe popsaným a
prozkoumaným "tělesem" v přírodě..!..
Ztráta determinismu ? -
Informační paradox ?
Deterministické zákony klasické fyziky umožňují na
základě znalosti úplného souboru stavových podmínek daného
systému v určitém okamžiku (na Cauchyho
hyperploše prostorového typu) předpovědět
stav
systému v libovolném okamžiku v budoucnosti i minulosti.
Jsou-li však ve vesmíru přítomny černé díry, nelze ani na
základě dokonalé znalosti jeho stavu v určitém časovém
okamžiku zjistit stav, který byl v minulosti, protože
o vlastnostech hmoty, ze které vznikla černá díra (a též o hmotě, která byla kdykoliv v minulosti
černou dírou pohlcena), nelze téměř nic zjistit; černá
díra pohltila nejen tuto hmotu, ale pohltila
i všechny informace o ní s výjimkou pouze sumární
hmotnosti, náboje a momentu hybnosti. Přítomnost černé díry
- její vlastnost "nemít vlasy" - tedy i v rámci
klasické fyziky principiálně omezuje možnost rekonstruovat minulost
na základě sebelepší znalosti současného stavu; lze pouze
předpovídat budoucnost (a to ještě jen
ve vnější asymptoticky rovinné oblasti prostoročasu - viz
§3.5). Tento "informační paradox" tak vede k částečné ztrátě determinismu. Jak ale uvidíme v §4.7 "Kvantové
vyzařování a termodynamika černých děr", efekt kvantového
vyzařování černých děr nám dokonce (aspoň
v principu) bere i
tuto poslední deterministickou schopnost..!.. Z hlediska kvantové fyziky je "paradox ztráty
informace" diskutován v §4.7, pasážích
"Kvantové
vypařování: návrat hmoty a informace z černé díry ?" a "Paradox ztráty informace ?".
| Gravitace, černé díry a fyzika prostoročasu : | ||
| Gravitace ve fyzice | Obecná teorie relativity | Geometrie a topologie |
| Černé díry | Relativistická kosmologie | Unitární teorie pole |
| Antropický princip aneb kosmický Bůh | ||
| Jaderná fyzika a fyzika ionizujícího záření | ||
| AstroNuklFyzika ® Jaderná fyzika - Astrofyzika - Kosmologie - Filosofie | ||